Performance Comparison Between a Nonlinear Energy Sink and a Linear Tuned Vibration Absorber for Broadband Control

Abstract

The performance of a linear tuned vibration absorber (LTVA) and a nonlinear energy sink (NES) for the vibrationcert mitigation of an unain linear primary system is investigated. An analytic tuning rule for the LTVA when the primary system contains uncertainty is derived. The behavior of the linear system coupled to the NES is analyzed theoretically. A tuning methodology for the NES in the deterministic as well as for the uncertain case is presented.

9.1 Introduction

Mitigation of resonant vibrations of a linear system is a widely encountered problem in engineering [8]. In the early 1900, Frahm proposed the use of linear resonator to reduce the amplitude of the oscillations around the resonance of a primary system [3]. This problem was later formalized by Den Hartog [2] who developed a tuning procedure based on invariant points to find appropriate stiffness and damping of the absorber.

A recent trend in the literature is to exploit and take advantage of nonlinear phenomena for vibration mitigation and energy harvesting [7, 11, 12, 19]. Among them, the nonlinear energy sink (NES), which consists of an absorber with essential nonlinearity, received particular attention. It was shown that a NES can lead to targeted energy transfer, which is an irreversible channelling of vibrational energy from the host structure to the absorber [5, 17]. Such an appealing feature makes the NES a suitable candidate for vibration isolation. However, due to the nonlinearity, it can also exhibit classic nonlinear behavior such as jumps or sensitivity to motion amplitude and therefore, it must be carefully designed.

Passive control of resonance using a NES was analyzed both theoretically [15, 16] and experimentally [6]. In addition to periodic response, systems with NES were shown to exhibit relaxation oscillations. The performance comparison between a linear absorber and a NES for the vibration mitigation of a linear system was addressed in [14]. However, in this study, both absorbers are constrained to have the same damping and the presence of detached resonance curve was not taken into account. In [13], a linear flexible beam with an embedded NES/linear absorber was investigated, but no proper design procedure was proposed, which makes difficult the comparison of both solutions.

The present work aims at giving an objective comparison between a NES and a linear absorber for passively controlling the resonance of a linear primary system. Two case studies are considered: first, the primary system is assumed to be deterministic; second, the stiffness of the primary system is assumed to be a random variable. In other words, the first case corresponds to the nominal case whereas in the second case, the stiffness of the primary system can vary to take into account model uncertainties or ageing effects.

The paper is organized as follows. In Sect. 9.2, a general model encompassing both linear and nonlinear absorber is presented. In Sect. 9.3, a tuning procedure for the linear absorber in the case of an uncertain primary system is presented. In Sect. 9.4, the theoretical treatment of the system coupled with the NES is presented. In Sect. 9.5, a tuning procedure for the NES in both the deterministic and uncertain case is discussed. In Sect. 9.6, the performance of the linear absorber and the NES for vibration mitigation are compared. Finally, conclusions are drawn.

9.2 Description of the Model

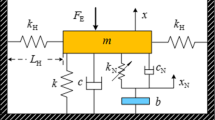
A schematic of the studied system is depicted in Fig. 9.1. m _j , k _j , c _j and x _j (j = 1, 2) are the mass, stiffness, damping and absolute displacement of the primary system and the absorber, respectively. F denotes the forcing amplitude and k _nl2 the nonlinear stiffness of the absorber. The equations of motion of the corresponding system are

$$\displaystyle\begin{array}{rcl} & & m_{1}\ddot{x}_{1} + c_{1}\dot{x}_{1} + k_{1}x_{1} + c_{2}(\dot{x}_{1} -\dot{ x}_{2}) + k_{2}(x_{1} - x_{2}) + k_{nl2}(x_{1} - x_{2})^{3} = F\cos \Omega t \\ & & m_{2}\ddot{x}_{2} + c_{2}(\dot{x}_{2} -\dot{ x}_{1}) + k_{2}(x_{2} - x_{1}) + k_{nl2}(x_{2} - x_{1})^{3} = 0 {}\end{array}$$

(9.1)

where the dots represent the differentiation with respect to the time t and $\Omega$ is the pulsation of harmonic excitation. In order to take into account an uncertainty of the primary system, the linear stiffness is expressed as $k_{1} = k_{10} + k_{11}$, where k ₁₀ is the nominal stiffness and k ₁₁ ( | k ₁₁ |  < k ₁₀) a random variable.

Fig. 9.1

Linear oscillator coupled to a nonlinear vibration absorber

The configuration of the primary system coupled either to the LTVA or the NES is obtained by setting k _nl2 or k ₂ to zero in Eq. (9.1), respectively. Introducing non-dimensional time $\tilde{t} =\omega _{1}t$, the equations of motion are recast into

$$\displaystyle\begin{array}{rcl} & & x_{1}'' + 2\xi _{1}x_{1}' + (1+\delta )x_{1} +\epsilon \lambda (x_{1}' - x_{2}') +\epsilon \rho ^{2}(x_{ 1} - x_{2}) +\epsilon K(x_{1} - x_{2})^{3} = G\cos \tilde{\Omega }\tilde{t} \\ & & x_{2}'' +\lambda (x_{1}' - x_{2}') +\rho ^{2}(x_{ 1} - x_{2}) + K(x_{1} - x_{2})^{3} = 0 {}\end{array}$$

(9.2)

here, primes denote differentiation with respect to the non-dimensional time $\tilde{t}$ and

$$\displaystyle{ \begin{array}{c} \epsilon = \dfrac{m_{2}} {m_{1}},\quad \omega _{1i} = \sqrt{\dfrac{k_{1i } } {m_{1}}},\quad \xi _{1} = \dfrac{c_{1}} {2m_{1}\omega _{10}},\quad \tilde{\Omega } = \dfrac{\Omega } {\omega _{10}},\quad \lambda = \dfrac{c_{2}} {m_{2}\omega _{10}}, \\ \rho = \sqrt{ \dfrac{k_{2 } } {m_{2}\omega _{10}^{2}}},\quad K = \dfrac{k_{nl2}} {m_{2}\omega _{10}^{2}},\quad G = \dfrac{F} {m_{1}\omega _{10}^{2}},\quad \delta = \dfrac{k_{11}} {k_{10}}\end{array} }$$

9.3 Linear Tuned Vibration Absorber

In this section the linear primary system coupled to a linear tuned vibration absorber (LTVA) is analyzed. The equation of motion of the primary system coupled to a LTVA is simply obtained by letting K = 0 in Eq. (9.2).

9.3.1 Deterministic Primary System

First, we deal with the case of deterministic primary system, thus imposing δ = 0 in Eq. (9.2). Den Hartog showed that the FRF of the primary mass has two invariant fixed points which are independent of the absorber damping $\lambda$ [2]. He proposed to adjust the stiffness of the absorber so that these two invariant points have equal heights in the FRF. The damping of the absorber is then determined so that the FRF presents an horizontal tangent through one of the fixed points. An approximate value of the optimal damping is obtained by taking an average value that leads to the horizontal tangent to both fixed points. This method is the so-called equal-peak method. Quite surprisingly, it is only recently that an exact closed-form formula for this classical problem has been found by Asami and Nishihara [1]

$$\displaystyle{ \begin{array}{lll} \rho _{opt}& =& \dfrac{2} {1+\epsilon }\sqrt{ \dfrac{2\left [16 + 23\epsilon + 9\epsilon ^{2} + 2\left (2+\epsilon \right )\sqrt{4 + 3\epsilon }\right ]} {3\left (64 + 80\epsilon + 27\epsilon ^{2}\right )}} \\ \lambda _{opt}& =&\dfrac{\rho _{opt}} {2} \sqrt{\dfrac{8 + 9\epsilon - 4\sqrt{4 + 3\epsilon } } {1+\epsilon }}\end{array} }$$

(9.3)

9.3.2 Uncertain Primary System

In this section, the tuning of the LTVA for the case of an uncertain primary system is addressed. The problem is formulated as follows

$$\displaystyle{ [\rho _{opt},\lambda _{opt}] =\mathrm{ arg}\left [\min _{\rho,\lambda }\left (\max _{\delta \in I_{\delta }}\vert H\vert _{\infty }(\rho,\lambda,\delta,\epsilon,\xi _{1})\right )\right ] }$$

(9.4)

By solving numerically problem (9.4), we observed that the solution is such that

$$\displaystyle{ \vert H\vert _{\infty }(\rho _{opt},\lambda _{opt},\delta _{min}) = \vert H\vert _{\infty }(\rho _{opt},\lambda _{opt},\delta _{max}) }$$

(9.5)

Therefore, in the uncertain case, the optimal tuning of the absorber is obtained when the FRF of the system at the uncertainty bounds has equal peaks. Based on this observation, we express an analytic tuning rule for the LTVA in the uncertain case. Neglecting the damping of the primary system to simplify the calculation (i.e. $\xi _{1} = 0$), the normalized steady state amplitude of the primary mass is given by

$$\displaystyle{ H^{2} = \left \vert \frac{X1} {G} \right \vert ^{2} = \frac{\Omega ^{2}\lambda ^{2} + \left (\Omega ^{2} -\rho ^{2}\right )^{2}} {\Omega ^{2}\lambda ^{2}\left (\Omega ^{2}\left (1+\epsilon \right ) -\delta -1\right )^{2} + \left (\Omega ^{4} - \Omega ^{2}\left (\rho ^{2}\left (1+\epsilon \right ) +\delta +1\right ) +\rho ^{2}\left (\delta +1\right )\right )^{2}} }$$

(9.6)

Using the optimal values for the tuning of the LTVA in the nominal case given in Eq. (9.3), Fig. 9.2 shows the FRF of the primary system for different values of $\lambda$. Black and gray lines correspond to δ = ∓0. 15, respectively. Solid lines correspond to $\lambda =\lambda _{opt}$ from Eq. (9.3) and dash-dotted and dashed lines correspond to $\lambda =\lambda _{opt} \pm 50\%$. P _j , Q _j (j = 1, 2) indicates the invariant fixed points. Using the classical equal-peaks methodology, the FRF of the primary system (9.6) is rewritten as follows

Fig. 9.2

FRF of the primary system coupled to the LTVA for different value of $\lambda$

$$\displaystyle{ H^{2} = \frac{A\lambda ^{2} + B} {C\lambda ^{2} + D} }$$

(9.7)

where A, B, C, D are simply identified from Eq. (9.6). The above expression is independent of damping if $A/C = B/D$. Substituting the expressions of A, B, C, D into this relation and solving for $\Omega$ gives

$$\displaystyle{ \Omega _{Pj,Qj} = \sqrt{\frac{\rho ^{2 } \left (1+\epsilon \right ) +\delta _{j } + 1 \mp \sqrt{\rho ^{4 } \left (1+\epsilon \right ) ^{2 } - 2\rho ^{2 } \left (1 +\delta _{j } \right ) + \left (1 +\delta _{j } \right ) ^{2 }} } {\epsilon +2}},\quad j = 1,2 }$$

(9.8)

where the subscript j = 1, 2 refer to the lower and upper bound of δ, respectively. Equation (9.8) defines the abscissa of the invariant fixed points.

The ordinates of points P _j and Q _j can be found by letting $\lambda \rightarrow \infty$ in Eq. (9.7)

$$\displaystyle{ H(\Omega _{Pj,Qj}) = \frac{1} {\Omega _{Pj,Qj}^{2}\left (1+\epsilon \right ) - 1 -\delta _{j}} }$$

(9.9)

The optimum value of ρ is obtained by requiring $H(\Omega _{P1}) = H(\Omega _{Q2})$. Substituting Eq. (9.8) into Eq. (9.9) and solving for ρ yields a complicated expression. This expression can be greatly simplified when considering symmetric bound, i.e. | δ ₁ |  =  | δ ₂ | . In this case, the optimal value of ρ is expressed by

$$\displaystyle{ \rho _{opt} = \frac{\sqrt{1 - \vert \delta _{1 } \vert \sqrt{\vert \delta _{1 } \vert ^{2 } \left (1+\epsilon \right ) ^{2 } +\epsilon \left (\epsilon +2 \right )}}} {\left (1+\epsilon \right )\sqrt{1 + \vert \delta _{1 } \vert ^{2}}} }$$

(9.10)

Following Den Hartog approach, we impose an horizontal tangent successively at points P1 and Q2. Differentiating Eq. (9.7) with respect to $\Omega$ gives

$$\displaystyle{ \frac{dH^{2}} {d\Omega } =\alpha _{1}\lambda ^{4} +\alpha _{ 2}\lambda ^{2} +\alpha _{ 3} = 0 }$$

(9.11)

where

$$\displaystyle\begin{array}{rcl} \alpha _{1}& =& -2\Omega ^{4}\left (\epsilon +1\right )\left (\Omega ^{2}\left (\epsilon +1\right ) -\delta -1\right ) {}\\ \alpha _{2}& =& -4\Omega ^{2}\rho ^{4}\left (\epsilon +1\right )\left (\Omega ^{2}\left (\epsilon +1\right ) -\delta -1\right ) {}\\ & & \quad + 2\Omega ^{4}\rho ^{2}\left (2\Omega ^{2}\left (\epsilon ^{2} + 3\epsilon + 2\right ) -\left (3\epsilon + 4\right )\left (1+\delta \right )\right ) {}\\ & & -\Omega ^{6}\left (\Omega ^{2}\left (\epsilon ^{2} + 2\epsilon + 4\right ) - 4\left (1+\delta \right )\right ) {}\\ \alpha _{3}& =& -2\left (\Omega ^{2} -\rho ^{2}\right )\left (\Omega ^{4} +\rho ^{4}\left (\epsilon +1\right ) - 2\Omega ^{2}\rho ^{2}\right )\left (\Omega ^{4} - \Omega ^{2}\left (\rho ^{2}\left (\epsilon +1\right ) +\delta +1\right )\right. {}\\ & & \quad \left.+\rho ^{2}\left (1+\delta \right )\right ) {}\\ \end{array}$$

Substituting $\Omega = \Omega _{P1}$ from Eqs. (9.8) and (9.10) into (9.11) and solving for $\lambda ^{2}$ a first value $\lambda _{1}$ is obtained. Repeating the same operation for $\Omega = \Omega _{Q2}$, the value $\lambda _{2}$ is obtained. The optimum value of damping parameter is taken as the average value $(\lambda _{1} +\lambda _{2})/2$. The comparison between the FRF of the uncertain primary system in the case of deterministic tuning and uncertain tuning is depicted in Fig. 9.3. Black and gray lines are referred to robust and nominal tuning, respectively. Continuous lines correspond to δ = 0 whereas dash-dotted and dashed lines correspond to δ = ∓0. 15. The parameters of the linear absorber are $\lambda = 0.25$, ρ = 0. 95 in the case of nominal tuning and $\lambda = 0.31$, ρ = 0. 92 in the case of robust tuning. Therefore, to increase the bandwidth of the LTVA, the stiffness of the absorber is reduced and the damping is increased compared to the nominal case.

Fig. 9.3

Comparison of the FRF of the LTVA for the nominal tuning and robust tuning for ε = 0. 05, δ = ±0. 15

9.4 Theoretical Analysis of the Nonlinear Energy Sink

In this section, the behavior of the primary system coupled to the NES (i.e. ρ = 0 in Eq. (9.2)) is analyzed using the mixed multiple scale/harmonic balance method [10]. First a new coordinate $r = x_{1} - x_{2}$ representing the relative displacement of the NES is introduced in Eq. (9.2).

$$\displaystyle{ \begin{array}{l} x_{1}'' + 2\xi _{1}x_{1}' + (1+\delta )x_{1} +\epsilon \lambda r' +\epsilon Kr^{3} = G\cos \tilde{\Omega }\tilde{t} \\ r'' - x_{1}'' +\lambda r' + Kr^{3} = 0\end{array} }$$

(9.12)

Considering small mass ratio ε ≪ 1, according to the multiple scale method, independent time scales $t_{0} =\tilde{ t}$, $t_{1} =\epsilon \tilde{ t}$ are introduced and the variables are expanded in series

$$\displaystyle{ \begin{array}{l} x_{1}(\tilde{t};\epsilon ) = x_{10}(t_{0},t_{1}) +\epsilon x_{11}(t_{0},t_{1})+\ldots \\ r(\tilde{t};\epsilon ) = r_{0}(t_{0},t_{1}) +\epsilon r_{1}(t_{0},t_{1})+\ldots \end{array} }$$

(9.13)

The variable are rescaled so that $\xi _{1} =\epsilon \xi _{1}$, G = ε G. Substituting the previous scaling, Eq. (9.13) into Eq. (9.12) and equating coefficients of like power of ε to zero yields to the following set of equations

$$\displaystyle{ \begin{array}{ll} O(\epsilon ^{0}):&d_{0}^{2}x_{10} + x_{10}(1+\delta ) = 0 \\ &d_{0}^{2}r - d_{0}^{2}x_{10} +\lambda d_{0}r_{0} + Kr_{0}^{3} \end{array} }$$

(9.14)

$$\displaystyle{ \begin{array}{ll} O(\epsilon ^{1}):&d_{0}^{2}x_{11} + x_{11}(1+\delta ) = -2d_{0}d_{1}x_{10} - 2\xi _{1}d_{0}x_{10} -\lambda d_{0}r_{0} - Kr_{0}^{3} + G\cos \tilde{\Omega }t_{0}\end{array} }$$

(9.15)

where $d_{j}^{i} = \partial ^{i}/\partial t_{j}^{i}$. Note that only the first equation at O(ε ¹) is given since it is the only one to be used.

9.4.1 Order ε ⁰

The solution of the first equation of (9.14) is given by

$$\displaystyle{ x_{10} = A(t_{1})\mathrm{e}^{i\omega t_{0} } + [c.c],\quad \omega = \sqrt{1+\delta } }$$

(9.16)

where [c. c] denotes the complex conjugate of the preceding terms. The second equation of (9.14) is now investigated. As mentioned in [10], this equation does admit solution neither in terms of standard trigonometric function nor in term of Jacobi function. Therefore, we seek a solution using the method of harmonic balance. Since 1:1 resonance between the primary system and the NES is expected, it reads

$$\displaystyle{ r_{0} = B(t_{1})\mathrm{e}^{i\omega t_{0} } + [c.c] }$$

(9.17)

here, only a single harmonic expansion is used. The effect of higher harmonics has been discussed in [9]. Substituting Eqs. (9.16) and (9.17) into the second equation of (9.14) and balancing terms of the fundamental harmonic gives

$$\displaystyle{ A = B\left (1 -\frac{i\lambda } {\omega } -\frac{3K\vert B\vert ^{2}} {\omega ^{2}} \right ) }$$

(9.18)

Equation (9.18) defines the slow invariant manifold (SIM) of the problem [4]. Substituting polar form A = ae^{i α}, B = be^{i β}, a real valued expression is obtained as

$$\displaystyle{ a^{2} = \frac{b^{2}} {\omega ^{2}} \left [\lambda ^{2} + \frac{\left (3Kb^{2} -\omega ^{2}\right )^{2}} {\omega ^{2}} \right ] }$$

(9.19)

It can be shown that the slow invariant manifold can admit extrema. Vanishing the derivative of the right hand side of Eq. (9.19) with respect to b and solving for b gives

$$\displaystyle{ Z_{j} = \frac{\omega } {9K}\left (2\omega \mp \sqrt{\omega ^{2 } - 3\lambda ^{2}}\right ),\quad j = 1,2,\quad Z_{j} = b_{j}^{2} }$$

(9.20)

The corresponding amplitude of the primary system is obtained when substituting Eq. (9.20) into Eq. (9.19) and is given by

$$\displaystyle{ a_{i}^{2} = \frac{2} {81K\omega }\left [\omega \left (9\lambda ^{2} +\omega ^{2}\right ) \pm \left (\omega ^{2} - 3\lambda ^{2}\right )^{\frac{3} {2} }\right ] }$$

(9.21)

Therefore, if $\lambda <\lambda _{c} =\omega /\sqrt{3}$, the SIM admit extrema and is composed of two stable and one unstable branches. It is well known that systems with NES can perform relaxation cycles. In the framework of NES, such a response is often denoted strongly modulated response (SMR). When the system exhibits SMR, the maximum amplitude of the relaxation cycle, when $\epsilon \rightarrow 0$ is given by Eq. (9.21).

9.4.2 Order ε ¹

In order to analyze SMR regimes, Eq. (9.15) is considered. The proximity of the forcing frequency and the natural frequency of the primary system is emphasized by defining $\tilde{\Omega } =\omega +\epsilon \sigma$. Substituting Eqs. (9.16) and (9.17) into Eq. (9.15) and eliminating secular terms yields

$$\displaystyle{ 2id_{1}A\omega + 2i\xi _{1}A\omega + i\lambda B\omega - 3KB\vert B\vert ^{2} + \frac{G} {2} \mathrm{e}^{i\sigma t_{1} } = 0 }$$

(9.22)

We are interested in the behavior of the system on the stable branches of the SIM. Substituting Eq. (9.18) into (9.22) gives

$$\displaystyle{ -2id_{1}\left (\omega B - i\lambda B -\dfrac{3K} {\omega } B\vert B\vert ^{2}\right ) -\left (2i\xi _{ 1}\omega - i\lambda \left (1-\omega \right )\right )B + \left (1 -\dfrac{2i\xi _{1}} {\omega } \right )3KB\vert B\vert ^{2} = 0 }$$

(9.23)

Expressing B in polar form and splitting into real and imaginary parts yields

$$\displaystyle{ d_{1}b = \frac{f_{1}(b,\psi )} {g(b)},\quad d_{1}\psi = \frac{f_{2}(b,\psi )} {g(b)} }$$

(9.24)

where $\psi = t_{1}\sigma -\beta$ and

$$\displaystyle\begin{array}{rcl} & & f_{1}(b,\psi ) = 36K^{2}\xi _{ 1}b^{5} - 24K\omega ^{2}\xi _{ 1}b^{3} + 3GK\omega b\sin \psi + 2\omega ^{2}\left (2\lambda ^{2}\xi _{ 1} +\lambda \omega ^{2} + 2\omega ^{2}\xi _{ 1}\right )b \\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad - G\omega ^{2}\left (\omega \sin \psi +\lambda \cos \psi \right ) \\ & & f_{2}(b,\psi ) = \dfrac{1} {b}\left [-54K^{2}\left (\omega +2\sigma \right )b^{5} + 6K\omega \left (4\lambda \xi _{ 1} +\omega +8\sigma \right )b^{3} + 9GK\omega b^{2}\cos \psi \right. \\ & & \qquad \qquad \qquad \qquad \qquad \left.-2\omega ^{2}\left (\lambda ^{2}\omega + 2\lambda ^{2}\sigma + 2\omega ^{2}\sigma \right )b + G\omega ^{2}\left (\lambda \sin \psi -\omega \cos \psi \right )\right ] \\ & & g(b) = -4\left (27K^{2}b^{4} - 12Kb^{2}\omega ^{2} +\lambda ^{2}\omega ^{2} +\omega ^{4}\right ) {}\end{array}$$

(9.25)

According to [16], Eq. (9.24) admits two types of fixed points. The first type is referred as ordinary fixed points and is computed by solving for $f_{1} = f_{2} = 0$ and g ≠ 0. The types of fixed points are referred as folded singularities and are found for $f_{1} = f_{2} = g = 0$.

The ordinary fixed points are obtained by solving $f_{1} = f_{2} = 0$ for $\cos \psi$, $\sin \psi$ and using trigonometric identity. A third order polynomial in Z = b ² is then obtained. The folded singularities are generated by setting $f_{1} = g = 0$ or equivalently $f_{2} = g = 0$, giving

$$\displaystyle\begin{array}{rcl} \psi _{ij}& =& -\arctan \left (\dfrac{3Kb_{i}^{2} -\omega ^{2}} {\lambda \omega } \right ) \\ & & \pm \arccos \left [\dfrac{2b_{i}\left (2K\xi _{1}b_{i}^{2}\left (9Kb_{i}^{2} - 6\omega ^{2}\right ) + 2\lambda ^{2}\omega ^{2}\xi _{1} +\lambda \omega ^{4} + 2\omega ^{4}\xi _{1}\right )} {G\omega \sqrt{3Kb_{i }^{2 }(3Kb_{i }^{2 } - 2\omega ^{2 } ) +\lambda ^{2 } \omega ^{2 } +\omega ^{4}}} \right ]{}\end{array}$$

(9.26)

From Eq. (9.26), a condition on the forcing amplitude is obtained as follows

$$\displaystyle{ G_{ifs} \geq \dfrac{2b_{i}\left (2K\xi _{1}b_{i}^{2}\left (9Kb_{i}^{2} - 6\omega ^{2}\right ) + 2\lambda ^{2}\omega ^{2}\xi _{1} +\lambda \omega ^{4} + 2\omega ^{4}\xi _{1}\right )} {\omega \sqrt{3Kb_{i }^{2 }(3Kb_{i }^{2 } - 2\omega ^{2 } ) +\lambda ^{2 } \omega ^{2 } +\omega ^{4}}} }$$

(9.27)

here, the subscript fs stands for folded singularities.

9.4.3 Detached Resonance Curve

An important feature that can affect the performance of the NES is the possible presence of detached resonance curves (DRC). This can be analyzed by locating the boundary of the saddle-node bifurcation in Eq. (9.24). Introducing perturbations around the fixed points and linearizing with respect to the perturbation, the so-called variational equation is obtained. By imposing the roots of the characteristic polynomial to be zero, an equation for Z is obtained as

$$\displaystyle\begin{array}{rcl} & & \qquad \qquad 27K^{2}\left (\omega ^{2} + 4\omega \sigma + 4\sigma ^{2} + 4\xi _{ 1}^{2}\right )Z^{2} - 24K\omega ^{2}\left (\omega \sigma +2\sigma ^{2} + 2\xi _{ 1}^{2}\right )Z \\ & & +\omega ^{2}\left (\lambda ^{2}\omega ^{2} + 4\lambda ^{2}\omega \sigma + 4\lambda ^{2}\sigma ^{2} + 4\lambda ^{2}\xi _{ 1}^{2} + 4\lambda \omega ^{2}\xi _{ 1} + 4\omega ^{2}\sigma ^{2} + 4\omega ^{2}\xi _{ 1}^{2}\right ) = 0{}\end{array}$$

(9.28)

Solving for Z and substituting into the fixed points equation, an expression for G _sn is obtained. An example of boundary of saddle node bifurcation in the space of parameters $(\sigma,G)$ is displayed in Fig. 9.4. Continuous lines correspond to the boundary of the saddle-node bifurcations. The creation or merging of detached resonance curves is computed for $\partial G_{sn}/\partial \sigma = 0$ and it is represented by the dotted lines. The lower one corresponds to the appearance of a DRC, while the upper one corresponds to the merging of the DRC with the principal resonance curve.

Fig. 9.4

Boundary of saddle-node bifurcation

9.5 Tuning of the NES

In this section, the theoretical developments are used to define a tuning rule for the NES. Both the deterministic and the uncertain case are addressed.

9.5.1 Deterministic Primary System

First, the case δ = 0 is analyzed. The theoretical analysis allows us to determine critical forcing amplitudes G that will determine different response characteristics. Since in our case, the forcing amplitude is considered fixed, the tuning procedure consists in finding appropriate value of ($\lambda,K$) for the NES. Critical forcing amplitude can be converted into critical nonlinear stiffness by using the forcing-nonlinearity equivalence principle [18] which states that if the ratio $G^{2}/K =\mathrm{ cst}$, the behavior of the system, compared to the supplied energy, remains unchanged. By doing so, the sizing chart depicted in Fig. 9.5 is obtained.

Fig. 9.5

Sizing zones for the primary system coupled to the NES

Continuous and dash-dotted lines represent the boundary of folded-singularities and DRC, respectively. Vertical dashed line represents the maximum value of damping for which the SIM admits extrema (i.e. the maximum value of the damping for which the system may perform relaxation cycles). In order to highlight the influence of the different boundaries on the response of the primary system, the frequency response curve corresponding to each zones is presented in Fig. 9.6.

Fig. 9.6

FRF of the primary system coupled to the NES for the different sizing zones

In zone I, the couple $(\lambda,K)$ is below the boundary of folded singularities and DRC. In this case, the system behaves quasi-linearly, so that this zone is not interesting from a vibration mitigation point of view. In zone II, the system can exhibit SMR without detached resonance curve. The amplitude of the oscillations is halved compared to the case in zone I and SMR takes place on the unstable part of the frequency response curve denoted by dotted lines. In zone III, high amplitude DRC is present, so that this zone must be avoided. In zone IV, the parameters of the NES are above the boundary of folded singularities but under the boundary of DRC so that fixed points on the right stable branch of the SIM exist. This can be seen on Fig. 9.6 where stable fixed points exist on the upper part of the frequency response curve. The zone V is located inside the boundary of DRC and above the boundary of folded singularities. Therefore the frequency response curve presents both a DRC and fixed points on the right stable branch of the SIM. Finally, in zone VI, the parameters of the NES are higher than the second boundary of DRC, yielding to the merging of the DRC with the main branch of the frequency response curve.

From the above observation, the parameters of the NES have to be chosen in zone II or IV. This choice can be further restricted to zone II by making the following observations. In zone IV, we do not have any a priori information about the amplitude of the fixed points lying on the right stable branch of the SIM. In addition, in zone II, in the absence DRC and fixed points on the right stable branch of the SIM, the maximum amplitude of the oscillation (when $\epsilon \rightarrow 0$) is determined by the maximum of the SIM in Eq. (9.21). As a conclusion, although potentially conservative, zone II is regarded as the optimal tuning region.

Optimal values of the parameters of the NES have now to be chosen inside zone II. As mentioned in the previous paragraph, the maximum amplitude of the primary system is determined by looking at the maximum of the SIM. The superposition of the amplitude of the extremums on zone II is depicted in Fig. 9.7. It is observed that the optimal value of the parameters of the NES is located at the intersection of the upper boundary of folded singularities and the boundary of creation of DRC.

Fig. 9.7

Maximum amplitude of the linear oscillator inside zone II

9.5.2 Uncertain Primary System

The case where the stiffness of the primary system is uncertain is now analyzed. This uncertainty is represented by parameter δ in Eq. (9.2). The sizing curves in the space of parameters $(\lambda,K)$ for $\delta \in [-0.15,+0.15]$ are depicted in Fig. 9.8. Continuous lines correspond to the nominal case (δ = 0), dash-dotted and dashed lines correspond to $\delta = -0.15$ and $\delta = +0.15$, respectively.

Fig. 9.8

Sizing zones of the NES for different uncertainties

We note that the upper part of zone II for $\delta = -0.15$ is included in the zone II for δ = 0. 15. Therefore, passive control through SMR exists for the whole range of detuning. So that the system can perform SMR as long as the zone II for δ = δ _min is contained in the zone II corresponding to δ = δ m a x, which occurs for | δ | ≈ 0. 3. The tuning rule may be summarized as follows. The optimum parameters of the NES ($\lambda _{opt},K_{opt}$) are found at the intersection of the folded singularities and DRC. If the natural frequency of the primary system is uncertain, the tuning of the NES is determined by the lower bound of the uncertainty, i.e. δ = δ _min .

9.6 Performance Comparison of the NES and LTVA

In this section, the performance of the NES and LTVA from a vibration mitigation point of view are compared. The deterministic case is first addressed, then the case of uncertain primary system is considered. For both cases, a damping factor $\xi _{1} = 0.5\,\%$ is considered. Also, a single forcing amplitude $G = 10^{-4}$ is considered whereas the frequency detuning parameter is assumed to vary in the range δ = ∓0. 15.

9.6.1 Deterministic Primary System

As shown in Fig. 9.5, given a forcing amplitude, the optimum stiffness and damping of the NES are found at the intersection between the boundary of creation of DRC and the folded singularities. For ε = 5 %, this gives $\lambda \approx 0.51$, K ≈ 3. 03 × 10⁵. For the LTVA, the optimum parameters are given in Eq. (9.3). Note that these equations are valid in the case of an undamped primary system. However, for lightly damped primary system, the performance of the LTVA is not really affected since almost equal peaks is observed, as depicted in Fig. 9.9. Both the displacements of the primary system and the absorber are illustrated. Gray correspond to the system coupled to the LTVA. Black solid and dotted lines correspond to stable and unstable periodic solution of the system coupled to the NES. Black dots correspond to the results of time step integration of the equation of motion (9.2).

Fig. 9.9

Comparison of the frequency response curve of the LTVA and the NES for a deterministic primary system with ε = 0. 05. Left: amplitude of the linear oscillator and right: amplitude of the absorber

It is clear from Fig. 9.9 that in the case of deterministic, linear primary system, the LTVA is far more efficient than the NES for vibration mitigation.

9.6.2 Uncertain Primary System

The frequency response curves of the uncertain primary system coupled to the optimal NES or LTVA are depicted in Fig. 9.10. Black and gray lines refer to the primary system coupled to the NES and LTVA, respectively. Even if SMR is expected over the range of detuning δ = ∓15 %, the LTVA performs better than the NES since the maximum is reduced of about 20 % compared to the NES.

Fig. 9.10

Comparison of the frequency response curve of the robust NES vs robust LTVA

The results for ε = 5 % and ε = 1 % are summarized in Table 9.1. It is observed that for a smaller mass ratio (i.e. ε = 1 %) the difference between the LTVA and the NES is even larger.

Table 9.1 $\vert H\vert _{\infty }$ of the primary system coupled to the LTVA/NES for ε = 5 % and ε = 1 % in the deterministic and uncertain case

9.7 Conclusion

The paper proposed an objective comparison between a NES with cubic stiffness nonlinearity and a linear absorber for vibration mitigation of a linear host system. A design procedure for the NES, which minimizes the maximum amplitude of the linear oscillator while preventing the presence of detached resonance curves has been presented. Surprisingly, the proposed design procedure yields highly damped NES which is contrary to conventional wisdom. A novel tuning procedure for the LTVA, when the natural frequency of the primary system contains uncertainty has also been presented.

For both deterministic and uncertain primary system, the LTVA outperforms the NES. The only way to achieve a better performance of the NES is to allow the presence of DRC, however, this is a risky solution since the system may be attracted to high amplitude solution under some perturbations.