Keywords

6.1 Introduction

In all around the world, approximately 40 % of the total world population uses internet [1], and cell phones are used by around 97 people out of every 100 people [2], which can provide a valid evidence for the idea that wireless communication is used worldwide. These infrastructures communicate with each other via antennas. In other words, the Internet and cell phones services are not functional without antennas. Thus, it can be said that the antenna structure is an irreplaceable and vital component of such electronic systems. IEEE defines what antenna does as “transmitting or receiving electromagnetic waves”. In other words, the antenna structure converts electrical signal into electromagnetic or electrical signal. For military applications, antenna structures are used in electronic warfare (EW), radar, naval, satellite and spacecraft systems so that devices and vehicles associated with these systems can communicate with each other. Common antenna types used in civil and military systems are dipole antennas, monopoles antennas (see Fig. 6.1), loops antennas, helix antennas, etc. As can be seen from Fig. 6.1, most of these antenna structures have inherently cantilever beam type configuration since one end is connected to the antenna hub, while the other end is free to receive or transmit electromagnetic wave, known as radio frequency (RF). Moreover, these antenna structures are generally made up of high conductive materials since the performance of an antenna structure is proportional to conductivity of the material [4]. Table 6.1 summarizes the most widely used materials in antenna structures. Copper and aluminum are the most widely used materials because of cost and weight concerns.

Fig. 6.1
figure 1

Monopole antenna structure [3]

Full size image
Table 6.1 Conductivity of the some common materials [4]
Full size table

However, antenna structures used in military and civil systems can encounter many mechanical shocks from various sources such as near miss underwater explosion, ballistic shock due explosion of mine, pyrotechnic shock, dropping of an antenna structure and so forth. Mechanical shock can be described as “a sudden and violent change in the state of motion of the component parts or particles of a body or medium resulting from sudden application of a relatively large external force, such as a blow or impact” according to first Shock and Vibration Symposium in 1947 [5]. Generally mechanical shocks contain high amplitude and rich spectral energy since the duration of mechanical shock is measured in milliseconds and the amplitude may be as high as 1000 G (see Fig. 6.2). Therefore, even if only one of the antennas in the electronic warfare and communication systems is broken down due to a mechanical shock, the whole system will be unable to function properly. For example, a printed circuit board (PCB), printed on the antenna structure, may be damaged due to exposure of a high level of mechanical shock, and as a result of this, the system becomes dysfunctional. Therefore, antenna structures must be designed to withstand mechanical shock types, which are explained briefly below, to ensure their reliability.

Fig. 6.2
figure 2

Time history of mechanical shock [6]

Full size image

Transportation and handling shock is received by electronic and mechanical systems used in military and civil applications as a result of transportation and human errors in handling of materials. For instance, while a military armored vehicle is running over a bump at unwary speed, all systems including antennas are exposed to mechanical shocks. Furthermore, ballistic shock is another type of mechanical shock containing high amplitude and high frequency content which is mainly caused by the impact of non-perforating mine blast, projectiles or ordnances on armored vehicle [7]. In addition to that pyroshock which is the response of a system to high-frequency stress waves one example of mechanical shock. Generally, pyroshock is generated as a result of explosive charges in order to separate two stages of a rocket [8]. Moreover, gunfire shock is a repetitive wave originated from artillery shooting of military vehicle. Consequently, the antenna structure should withstand these mechanical shocks originating from various environmental effects.

In literature, studies on the nonlinear dynamic characteristics of antenna structures exposed to mechanical shocks are limited since most researchers have investigated modal and random vibrations analyses of the antenna structure. Concerning the linear dynamic analyses of antenna structure, the simulations were performed by commercial finite element programs such as ABAQUS® and NASTRAN®. Static and dynamic analyses of dipoloop antenna radome were simulated by a linear finite element analysis by Reddy and Hussain [9]. Mechanical shock analysis was conducted on ABAQUS®. In this study, only stresses were evaluated on the dipoloop antenna radome. Lopatin and Morozov [10] studied the free vibration of thin-walled composite spoke of an umbrella-type deployable space antenna. The composite spoke of the deployable space antenna was modeled as a cantilever beam via including effects of transverse shear. On the other hand, the nonlinear dynamic response of the antenna structure under dynamic loads is characterized by limited number of researchers. Random and modal analyses of a gimbaled antenna including gap nonlinearity resulting from small clearances in the joints are studied by Su [11] where the nonlinearity is linearized and then the resulting linear systems is solved commercial finite element software. Moreover, Sreekantamurthy et al. [12] investigated static and dynamic loads such as inflation pressure, gravity and pretension loads on a parabolic reflector antenna by using commercial finite element software. In their work, geometric nonlinearity was included into the model, since the deformation of parabolic reflector antenna was large.

Inherently, antenna structures have a larger dimension in longitudinal direction. When they receive high mechanical shock such as ballistic and pyrotechnical shocks, nonlinear effects play an important role on shock response of antenna structures.

Although the nonlinear dynamic characteristics, under mechanical shock are different from the linear ones, there appears almost no study on this specific topic. However, especially in micro and nanoscale areas, many researchers investigated the dynamics response of micro electro mechanical systems, micro beams, micro switches and so forth which are under mechanical shock even by considering the nonlinear effects. As an initial attempt, some authors used single degree of freedom assumption to get a rough estimation of the dynamic response of micro systems. For example, Younis et al. [13] studied the performance of capacitive switches modeled as a single degree of freedom (SDOF) system under mechanical shock through including the effects of squeeze-film damping and electrostatic forces. Moreover, Li and Shemansky [14] treated the micro-machined structure as a single degree of freedom system as well as a distributed parameter model. For more accurate analysis, many authors used continuous beam models to simulate the response of micro systems to a mechanical shock. As an example, Younis et al. [15] investigated the simultaneous effects of mechanical shock and electrostatic forces on microstructures simulated as cantilever and clamped-clamped beams. In this particular study, reduced order model results based on Galerkin’s Method were compared with the ones obtained from commercial finite element software. Due to the large deformation of micro systems resulting from the applied mechanical shock, some researchers included nonlinearity to the models to predict the dynamic behavior in real life. For instance, Younis and Arafat included both geometric and inertia nonlinearities into their studies while analyzing the response of the cantilever microbeam activated by mechanical shock and electrostatic forces [16]. In their work, they analyzed the effects of cubic geometric and inertia nonlinearities on the cantilever microbeam by using reduced order model which is based upon Galerkin’s Method. In another study of Younis et al. [17], the response of the clamped-clamped microbeam was investigated through using four modes in the Galerkin based reduced order model including geometric nonlinearity. Moreover, Younis et al. [17] studied the effects of shape of shock pulse and package on the response of microbeam and validated the results via commercial finite element software. Furthermore, some researchers employed approximate solutions to the response of systems under mechanical shock through frequency domain approaches rather than time domain approach which is computationally expensive. As an example, Liang et al. [18] estimated shock response of the mast in ships using frequency domain method such as square root of the sum of squares (SRSS), complete quadratic combination method (CQC), naval research laboratory method (NRL) and absolute summation method (ABS). Alexander [19] mentioned the frequency domain methods which are applied to the nonlinear systems as well. Younis and Pitarresi [20] emphasized synthetic methods utilizing the static response and shock spectrum based on maximum responses of many single degree of freedom systems. In this study [20], linear and nonlinear response of microbeam found in synthetic method and Galerkin-based reduced order method employing six modes were compared in terms of different values of shock amplitude.

Mechanical shock excitation is inherently applied to the base of structures. In literature, mechanical shock was simulated for continuous systems by base excitation which is either applied to the fixed boundary condition [21, 22] or distributed force applied through the structure [15–17, 20].

Antenna structures, which are used for military and civil applications, are vital component of the many the electronic systems. These antenna structures are subjected to mechanical shock from various environments such as transportation, ballistic, pyrotechnic shocks. Therefore, correct modeling of dynamic characteristic of the antenna structure under mechanical shock is needed because of the need to accurately predict the performance of the antenna structure. Inherently, most of the antenna structures have slender shape and larger dimension in longitudinal direction. Moreover, they are subjected to high frequency, high amplitude mechanical shocks. Thus, mathematical modeling of the antenna structure through linear theory can yield incorrect results, since antenna structures experience large deformation, where nonlinear effects become dominant. In other words, nonlinearities due to large deformation must be included in order to predict dynamic behavior accurately.

6.2 Mathematical Modeling

In this section, antenna structure is modeled by equivalent lumped mass model, Euler-Bernoulli Beam Theory, finite element method and approximate methods.

6.2.1 Equivalent Lumped Mass Model

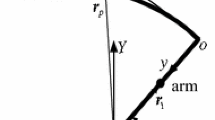
In this section, the antenna structure is treated as a single degree of freedom system utilizing an equivalent lumped mass model. Basically, most of the antenna structures such as monopole antennas (see Fig. 6.3) have a cantilever beam structure since one end is fixed to the antenna hub while the other end is free to transmit or receive electromagnetic waves.

Fig. 6.3
figure 3

Cantilever beam type the antenna structure

Full size image

Equivalent mass and stiffness of the antenna structure described in Fig. 6.3 is given as [23].

$$ {m}_{eq}=0.2427 mL, $$
(6.1)
$$ {k}_{eq}=\frac{3EI}{L^3}, $$
(6.2)

where m is the mass per unit length of the antenna structure, l is the length of the antenna structure and E is Young’s modulus of the antenna’s material. Therefore, the antenna structure shown in Fig. 6.3 is reduced to a single degree of freedom system as shown in Fig. 6.4.

Fig. 6.4
figure 4

Equivalent lumped mass model of the antenna structure

Full size image

6.2.2 Linear Continuous Model

In this part, the antenna structure is modeled by Euler-Bernoulli beam theory, which is widely used in literature, in order to predict dynamic characteristic of slender beam like structure [13, 15–17, 20, 21]. However, due to inherent assumptions of the theory, accuracy of the results is poor when the thickness to length ratio is larger than 10 %. In such cases Timoshenko beam model is applied to get accurate results [24]. In this paper, Euler-Bernoulli beam theory is used to model the antenna structure, since most of the antenna structures naturally have thickness to length ratio much less than 10 %.

Consider the antenna structure, whose length, density, cross sectional area and flexural rigidity are represented as l, ρ, A and EI, respectively. As can be seen in Fig. 6.5, the transverse deflection of the antenna structure is defined as w(x, t), where x is the axial position, t represents time and F(x, t) is the distributed force that is applied through the length of the antenna structure. Equation of motion of the antenna structure is given as [25]

Fig. 6.5
figure 5

Nomenclatures of the antenna structure in bending direction [25]

Full size image
$$ \frac{\partial^2}{\partial {x}^2}\left(EI\frac{\partial^2w\left(x,t\right)}{\partial {x}^2}\right)+c\frac{\partial w\left(x,t\right)}{\partial t}+\rho A\frac{\partial^2w\left(x,t\right)}{\partial {t}^2}=F\left(x,t\right). $$
(6.3)

In this paper, mechanical shock is applied as distributed force through the length of the antenna structure (see Fig. 6.5). Hence, equation of motion of the antenna structure subjected to mechanical shock can be given as

$$ \frac{\partial^2}{\partial {x}^2}\left(EI\frac{\partial^2w\left(x,t\right)}{\partial {x}^2}\right)+c\frac{\partial w\left(x,t\right)}{\partial t}+\rho A\frac{\partial^2w\left(x,t\right)}{\partial {t}^2}=-\left(\rho A{a}_{\max}\right){a}_{pulse}(t), $$
(6.4)

where, a max is the maximum value of mechanical shock and a pulse is a unit mechanical shock profile such as half sine, terminal peak sawtooth and so forth. The equation of motion given by Eq. (6.4) can be nondimensionalized by using following non dimensional parameters

$$ \widehat{x}=\frac{x}{l},\ \widehat{\mathrm{w}}=\frac{w}{l},\ \widehat{\mathrm{t}}=\frac{t}{T}, $$
(6.5)

where T is the time scale parameter. Substituting Eq. (6.5) into Eq. (6.4), the outcome is

$$ \frac{\partial^4w\left(x,t\right)}{\partial {t}^4}+{c}_{non}\frac{\partial w\left(x,t\right)}{\partial t}+\frac{\partial^2w\left(x,t\right)}{\partial {t}^2}={F}_{non}{a}_{pulse}(t), $$
(6.6)

where, nondimensional damping and forcing terms are as follows

$$ {c}_{non}=\frac{c{l}^4}{EIT},\ {\mathrm{F}}_{non}=\frac{-\rho A{a}_{\max }{l}^3}{EI}. $$
(6.7)

The nondimensional force given in Eq. (6.7) implies that effects of the mechanical shock increases sharply with increasing length and decreasing thickness of the antenna structure. This is in agreement with the experimental findings available in the literature [26].

The resulting partial differential equation of motion can be converted into a set of ordinary differential equations by using Galerkin’s method. In this method, the following form of solution is assumed

$$ w\left(x,t\right)={\displaystyle \sum_{i=1}^n{a}_i(t){\phi}_i(x)}, $$
(6.8)

where, ϕ i (x) is a comparison function which satisfies both geometric and natural boundary conditions as well as differentiable at least to the order of the partial differential equation. a i (t) is generalized coordinate to be determined, and n is the number of modes used in the analysis [27]. After substituting Eq. (6.8) into Eq. (6.6), multiplying the resulting equation with ϕ j and integrating from 0 to 1, the following result is obtained

$$ {\displaystyle \sum_{i=1}^n{u}_i(t)\left({\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x){\phi_i}^{\prime \prime \prime \prime }(x)dx}\right)+{c}_{non}{\displaystyle \sum_{i=1}^n{\overset{.}{u}}_i(t)\left({\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x){\phi}_i(x)dx}\right)}}+{\displaystyle \sum_{i=1}^n{\ddot{u}}_i(t)\left({\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x){\phi}_i(x)dx}\right)={\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x){F}_{non}{a}_{pulse}(t)dx}}. $$
(6.9)

If orthogonal comparison functions are used, Eq. (6.9) is reduced to an uncoupled form as follows

$$ {\ddot{u}}_j(t)+2{\zeta}_j{\omega}_{non,j}{\overset{.}{u}}_j(t)+{\omega_{non,j}}^2u(t)={\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x){F}_{non}{a}_{pulse}(t)dx}, $$
(6.10)

where, ζ j is the modal damping ratio of the j th mode and it is given by

$$ {\zeta}_j=\frac{c_{non}}{2{\omega}_{non,j}}. $$
(6.11)

6.2.3 Nonlinear Continuous Model

In this section, shock response of an antenna structure considering geometric and inertia nonlinearities is analyzed. In real life, response of almost all systems to any forcing is nonlinear, where superposition property of linear systems does not hold. For simplicity, many engineering systems are treated as linear which is a valid assumption in most cases. For instance, in order to obtain linear equation of motion of an antenna structure under mechanical shock, small deformation is assumed. This assumption gives accurate results if the deformation in the real case is small with respect to the thickness of the antenna structure. However, if the deformation is large, small deformation assumption results in highly inaccurate results. Therefore, linear modeling may result in a design which is not optimum and hence, increases weight and cost. In addition to this, estimated acceleration of a PCB on the antenna structure is not accurate. Since mechanical shocks result in large deformations, antenna structure needs to be modeled by including nonlinearities.

Nonlinearities common in structures are geometric nonlinearity, damping nonlinearity, inertia nonlinearity, curvature nonlinearity, material nonlinearity and boundary condition nonlinearity. Since, the antenna structure experiences large deformation due to its long and slender structure, curvature and inertia nonlinearities are included into the model.

In the light of above mentioned information, equation of motion of the antenna structure, which has uniform density and constant cross section, under mechanical shock including geometric curvature and inertia nonlinearities is given as [25]

$$ EI\frac{\partial^4w}{\partial {x}^4}+c\frac{\partial w}{\partial t}+\rho A\frac{\partial^2w}{\partial {t}^2}=-EI\frac{\partial }{\partial x}\left(\frac{\partial w}{\partial x}\frac{\partial }{\partial x}\left(\frac{\partial w}{\partial x}\frac{\partial^2w}{\partial {x}^2}\right)\right)-\frac{1}{2}\rho A\frac{\partial }{\partial x}\left(\frac{\partial w}{\partial x}{\displaystyle \underset{L}{\overset{x}{\int }}\left(\frac{\partial^2}{\partial {t}^2}{\displaystyle \underset{0}{\overset{x}{\int }}{\left(\frac{\partial w}{\partial x}\right)}^2dx}\right)dx}\right)-\left(\rho A{a}_{\max}\right){a}_{pulse}(t). $$
(6.12)

Equation (6.12) is converted into a set of nonlinear ordinary differential equations by using Galerkin’s method. Similar to the previous case, substituting Eq. (6.8) into Eq. (6.12) multiplying the result by ϕ j and integrating from 0 to 1 the following result is obtained

$$ \begin{array}{l}{\displaystyle \sum_{i=1}^n{u}_i(t){\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x)}{\phi_i}^{\prime \prime \prime \prime }(x)dx+{c}_{non}{\displaystyle \sum_{i=1}^n{\overset{.}{u}}_i(t){\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x)}{\phi}_i(x)dx+{\displaystyle \sum_{i=1}^n{\ddot{u}}_i(t){\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x)}{\phi}_i(x)dx=}}}\\ {}-{\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j}\left({\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{{\prime\prime} }}\right)}^2+4\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{\prime }}\right)\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{{\prime\prime} }}\right)\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{{\prime\prime\prime} }}\right)+{\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{\prime }}\right)}^2\left({\displaystyle \sum_{i=1}^n{u}_i{\phi_i}^{\prime \prime \prime \prime }}\right)\right)dx\\ {}-{\alpha}_{in}{\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j}\left(\frac{\partial }{\partial {x}^2}\left(\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{\prime }}\right){\displaystyle \underset{1}{\overset{x}{\int }}\left(\frac{\partial^2}{\partial {t}^2}{\displaystyle \underset{0}{\overset{x}{\int }}{\left({\displaystyle \sum_{i=1}^n{u}_i{\phi}_i^{\prime }}\right)}^2dx}\right)dx}\right)\right)dx+{\displaystyle \underset{0}{\overset{1}{\int }}{\phi}_j(x)}{F}_{non}{a}_{pulse},\end{array} $$
(6.13)

where nondimensional damping, inertia and forcing parameters are given as

$$ {c}_{non}=\frac{c{l}^4}{EIT},\ {\alpha}_{in}=\frac{l^4\rho A}{2{T}^2EI},\ {\mathrm{F}}_{non}=\frac{-\rho A{a}_{\max }{l}^3}{EI}. $$
(6.14)

Equation (6.13) can be represented in matrix form, where in this study MUPAD® available in MATLAB® is used for the symbolic calculations.

6.2.4 Finite Element Simulation by ANSYS

In this section, shock response of an antenna structure is obtained by using ANSYS, which is commonly used commercial finite element software. In this paper, the antenna structure is modeled by 3-D 2 Node beam elements known as BEAM188 (see Fig. 6.6). This element type is used to analyze slender beam like structures. Moreover, this element has six degrees of freedom which are three translational degrees of freedom in X, Y and Z directions and three rotational degrees of freedom about X, Y and Z axes. In addition to that, the element is suitable for the consideration of stress stiffening and large deformation effects. The theory behind this element is Timoshenko beam theory, which includes shear deformation[28].

Fig. 6.6
figure 6

Geometry of BEAM188 [28]

Full size image

ANSYS Workbench does not have a tool for mechanical shock simulation, since mechanical shocks are applied to a structure from its base. In literature, Application Customization Toolkit exists for transient base excitation analysis. However, this toolkit is applicable for only linear transient analysis. As a result of that, ANSYS Parametric Design Language (APDL) is used to simulate mechanical shock. The APDL code which is embedded into “Transient Structural” module is written by “ACCEL” command. This command gives acceleration to the selected nodes. Furthermore, Rayleigh damping is used to model damping which is defined as

$$ \left[C\right]={\alpha}_m\left[M\right]+{\beta}_m\left[K\right], $$
(6.15)

where, α and β are mass and stiffness constants, respectively. In this example, the first two modes are used in order to find these damping coefficient, which is implemented into ANSYS Transient Structural.

6.2.5 Approximate Methods

In this part, approximate methods based on modal combination are introduced. In these methods, the maximum response of the antenna structure is estimated by combination of mass normalized eigenfunction coefficient, modal participation factor and dynamic constant obtained from shock response spectrum. Moreover, mass normalized eigenfunction coefficient is obtained by using a mode shape function of the antenna structure at a desired location. Furthermore, the modal participation factor shows effectiveness of a particular mode on the response [29]. Thus, the modal participation factor, Γ n , of the antenna structure is given as [30]

$$ {\varGamma}_n=\rho A{\displaystyle \underset{0}{\overset{L}{\int }}{\phi}_n(x)dx}, $$
(6.16)

where, ρ and A are uniform density and cross sectional area of an antenna structure, respectively and ϕ n (x) is the mode shape of the n th mode.

Absolute sum (ABS), square root of sum of squares (SRSS), naval research (NRL) and complete quadratic combination methods are examples of approximate methods. These methods are used to get maximum shock response of an antenna structure. The main advantage of these methods is their computational efficiency compared to transient analysis. Moreover, these methods are conservative compared to transient analysis, since modal maximum responses are assumed to act simultaneously and have the same sign.

6.3 Case Studies

In this section, several case studies are conducted in order to analyze shock response of the antenna structure in detail. Moreover, linear and nonlinear ordinary differential equations are solved by Newmark method, which is also used in finite element software ANSYS.

Firstly, finite element method is compared with the linear continuous model. Consider the antenna structure given in Fig. 6.3 with constant cross section and uniform density. The antenna structure has 350 mm length, 40 mm width and 2 mm thickness. Moreover, the antenna structure is made up of aluminum, the density and Young’s modulus of which are 2700 kg/m3 and 70 GPa, respectively. In addition to that, the antenna structure is subjected to 50 G 11 ms half sine mechanical shock which is the transportation shock for wheeled vehicle and aircraft according to International Standard IEC-60068-2-27 [31]. Acceleration responses of the antenna structure to the given input mechanical shock using reduced order model and finite element simulation are given in Fig. 6.7. It is observed that the result of ROM is in agreement with the result of the finite element method.

Fig. 6.7
figure 7

Shock response of the antenna structure

Full size image

In nonlinear finite element analysis, there are some drawbacks which affect shock response of an antenna structure. One of them is Rayleigh damping, which depends on mass and stiffness matrices as seen from Eq. (6.15). Using constant β m leads to undesirable results in the nonlinear analysis, since ANSYS updates stiffness matrix for each iteration. Therefore, β m constant cannot be used in nonlinear analysis. In this case study, damping is assumed to be zero and artificial damping is introduced as 0.5.In Newmark method, the amount of numerical dissipation is controlled by artificial damping. Furthermore, this damping leads to reduction of numerical errors. Linear and nonlinear shock responses of the antenna structure are compared in Fig. 6.8. According to the results obtained, nonlinearity reduces the shock response of the antenna structure significantly.

Fig. 6.8
figure 8

Linear and nonlinear shock response of the antenna structure

Full size image

Nonlinear mathematical model used in this study is validated by Ref. [16]. Younis et al. [16] studied nonlinear analysis of the cantilever MEMS under mechanical shock. The maximum nondimensional deflection versus shock amplitude graph given in [16] is used to validate the nonlinear mathematical model used in this study. Consider the cantilever MEMS, whoselength, thickness and width are \( L=100\;\upmu \mathrm{m} \), \( h=0.1\;\upmu \mathrm{m} \) and \( b=10\;\upmu \mathrm{m} \), respectively. The cantilever MEMS is made up of silicon, whose density and Young’s modulus are 2332 kg/m3 and 169 GPa, respectively. The results obtained are compared with the ones given in [16] in Figs. 6.9 and 6.10b. The results obtained are in well agreement with the ones given in [16]; hence, the nonlinear model and the solution method used are validated.

Fig. 6.9
figure 9

Calculated shock response of the cantilever MEMS

Full size image
Fig. 6.10
figure 10

The paper shock response of the cantilever [16]

Full size image

The maximum relative displacement and acceleration tip response of an antenna structure is critical for design, since PCB, which is placed on the tip of an antenna structure, is sensitivity to the amplitude of the mechanical shock. Therefore, plot of the maximum response of the antenna structure vs. shock amplitude gives a better idea in terms of durability of the antenna structure. It can be observed from Figs. 6.11 and 6.12, both acceleration and relative displacement responses of the antenna structure is reduced when geometric nonlinearity is considered. Moreover, approximate methods can be used as a starting point of shock analysis of an antenna structure. Although approximate methods give conservative results compared to linear transient counterparts, computation time is significantly reduced. Furthermore, equivalent lumped mass model leads to enormous error in this case study, since the second, the third and the fourth modes also contribute to the shock response of the antenna structure in addition to the first mode. In other words, acceleration response of the antenna structure is composed of the first, the second, the third and the fourth modes of the structure which can be deduced from Fig. 6.13.

Fig. 6.11
figure 11

Maximum acceleration response of the antenna structure

Full size image
Fig. 6.12
figure 12

Maximum relative displacement of the antenna structure

Full size image
Fig. 6.13
figure 13

Frequency content of acceleration response of the antenna structure

Full size image

6.4 Conclusion

In this study, shock response of an antenna structure including geometric nonlinearity is investigated. Firstly, lumped mass model of an antenna structure is studied. Although lumped mass model is a fundamental and computationally efficient model, this is not applicable for case studies where contribution of the modes higher than the first mode cannot be neglected. Therefore, modeled continuous beam model by using Euler-Bernoulli beam theory results in highly accurate results due to the fact that the effects of higher modes can as well be retained in the solution. Although both linear reduced order model (ROM) and finite element model are in agreement with each other, ROM is computationally very efficient, since a fine mesh is required in order to capture the propagation of shock wave properly. However, this leads to increased solution times. Furthermore, geometric nonlinearity plays an important role on shock response of an antenna structure, since many antenna structures have larger dimension in longitudinal direction. It is interesting to note that geometric nonlinearity reduces both relative displacement and acceleration response, especially in the case of high shock acceleration. It is similar to the case where as if shock isolator is used. In other words, when the antenna structure is modeled properly including geometric nonlinearity, response is similar to the case where an antenna structure is modeled by linear theory including shock isolator. Therefore, nonlinear modeling can eliminate the usage of shock isolator. It can be concluded that approximate methods are inherently conservative methods and may be used as a starting point of shock analysis due to their little computation time.