Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The available codes and guidelines on design of structures for fire are based on performance evaluation at the component level and using deterministic approaches, while fire events and performance of structures at elevated temperatures involve considerable uncertainties. Measured data specifically indicates large uncertainties in the intensity and characteristics of fire load and of material properties at elevated temperatures. A risk-informed performance-based design that models the uncertainties can optimize safety, efficiency, and the overall cost of the design. Researchers have recently been focusing on applying risk-based decision-making optimization techniques (De Sanctis et al. 2011), using reliability analysis (Gue et al. 2013), and developing probabilistic frameworks (He 2013) to design structures for fire.

Aside from fire itself, fire following earthquake (FFE) is also an extreme hazard, which is a low probability, high consequence event. In a recent study on historical FFE events, 20 cases from seven different countries were collected, 15 of which occurred between 1971 and 2014 (Elhami Khorasani and Garlock 2015). Fire that followed the earthquake in a majority of these cases caused considerable damage. Based on our current design guidelines, buildings are generally designed for individual extreme events (i.e., earthquakes or fires only), but the structural response of buildings under cascading multi-hazard fire and earthquake events is not evaluated during the design process, and this is something to consider for resiliency planning in densely populated regions (Elhami Khorasani 2015; Elhami Khorasani et al. 2015c). Previous studies on the response of structures in FFE scenarios analyze the problem using deterministic approaches and model thermal and seismic analyses in different programming environments (Della Corte et al. 2003, 2005; Yassin et al. 2008) due to the limited available tools which can analyze both loading events. Most commercially available finite element programs require extensive computational resources to model and run seismic and thermal analysis sequentially.

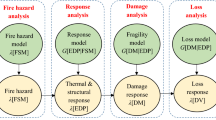
This work is a step toward developing guidelines to include uncertainties in the new generation of performance-based design, for fire and cascading multi-hazard events such as post-earthquake fires. Any guideline for fire design includes three steps: (1) determining the design fire (demand model, design fire), (2) performing thermal analysis (demand model, thermal analysis), and (3) performing a structural analysis that considers the thermal load (capacity model, structural analysis). Given the three steps, this work (1) provides probabilistic models for fire load and mechanical properties of steel at elevated temperatures using literature data, (2) develops a framework to evaluate performance of structures under fire and FFE incorporating the developed probabilistic models, and (3) applies the framework to a 9-story moment resisting frame (MRF) and studies response of the MRF under FFE by modeling the seismic and thermal analyses in one programming environment.

2 Probabilistic Models

This section provides the developed probabilistic models for fire load density (demand), yield strength and modulus of elasticity of steel (capacity), and a quick overview of the mathematical procedure needed to develop the models.

2.1 Background

A brief overview of the mathematical procedure used to develop probabilistic models in this work is discussed in this section. Gardoni et al. (2002) proposed a formulation that developed probabilistic models by correcting deterministic models with correction terms calibrated using observed experimental data. The deterministic formulations may come from codes or standards, and correction terms are added to remove the inherent bias in the deterministic model. A model error is included and calculated to account for the remaining inaccuracy of the model. The general form of the model is shown in Eq. (10.1):

$$ C\left(\mathbf{x},\boldsymbol{\Theta} \right)= \stackrel{\frown }{c}\left(\mathbf{x}\right)+\gamma \left(\mathbf{x},\boldsymbol{\uptheta} \right)+\sigma \varepsilon $$
(10.1)

where C(x, Θ) is the quantity of interest (or a transformation into a new space using transformations like the natural logarithm, square root function, or the logistic function); Θ = (θ,σ), in which θ = (θ1,θ2,…), denote the set of unknown model parameters; ĉ(x) is a selected deterministic model that is expressed as a function of the variables x (ĉ(x) is transformed accordingly if C(x, Θ) is transformed); γ(x,θ) is a correction term for the bias inherent in the deterministic model; and σε is the model error that captures the remaining scatter in the residuals, where ε is a random variable with zero mean and unit variance and σ represents the standard deviation of the model error. The formulation in Eq. (10.1) is general and can also be used when there are no deterministic models available; in such case, ĉ(x) = 0.

Equation (10.1) is based on three assumptions: (1) ε follows a standard normal distribution (normality assumption), (2) σ does not depend on x (homoskedasticity assumption), and (3) γ(x,θ) can be added to ĉ(x) instead of being, for example, a multiplicative term (additivity assumption). These assumptions can typically be satisfied by considering an appropriate variance-stabilizing transformation of the original quantity of interest (Box and Cox 1964) and verified by using diagnostic plots (Rao and Toutenburg 1997). The selection of the variance-stabilizing transformation is often guided by the physical range of the quantity of interest, and the transformation is selected so that the transformed quantity ranges from −∞ to +∞. For example, if the physical quantity is nonnegative, then the natural logarithm or the square root function can be used as a transformation. If the quantity of interest is between 0 and 1, then the logistic function can be used (Stone 1996).

Different procedures, such as linear regression, nonlinear regression, or the maximum likelihood method, can be used to calculate the unknown model parameters Θ. However, a Bayesian approach may also be used when prior information is present (Box and Tiao 1992). In this work, a Bayesian updating framework is used to estimate the unknown parameters Θ = (θ,σ). The details of the mathematical formulation are provided in Gardoni et al. (2002). When using that approach, as opposed to a purely empirical model, the probabilistic model includes the physical understanding that is often behind the deterministic models. Also, the newly developed probabilistic model is based on an already existing model; therefore, it is easier for the engineering practice to accept and apply the new model.

2.2 Fire Load

The temperature-time evolution of fire in this work is calculated using the Eurocode1 (EC1) formulation (CEN 2002), which depends on geometric characteristics of the compartment, thermal properties of the boundary of enclosure, and fire load density. Among the three factors, determination of fire load density most strongly influences the fire temperature. A sensitivity study by Guo et al. (2013) confirms that the value of fire load density has a significant influence on the structural response to fire.

The authors collected and studied available surveys in the literature on fire load density in office buildings (Elhami Khorasani et al. 2014). The results of four surveys on office buildings from different countries, and using different surveying methods, were compared to older data from eight other surveys, as well as the design values suggested by codes. The available surveys showed a wide range in the recorded mean fire load density values (348–852 MJ/m2), which implies that a considerable amount of uncertainty exists in predicting fire load density. Another important observation was that survey results showed a correlation between fire load density and the room size and use. The majority of data showed that meeting rooms or relatively large offices have a smaller fire load density than storage rooms, file areas, or smaller offices in an office building.

Data from a US survey with the most comprehensive collection for fire load density in office buildings (Culver 1976) were used to generate a new probabilistic model for fire load density q in office buildings. The model for q includes the effect of room size A f on the fire load density and consists of two equations: Eq. (10.2a) for lightweight categories (general offices, clerical, etc.) and Eq. (10.2b) for heavy weight categories (library, storage, and file rooms):

$$ q= \exp \left[6.951-0.0047\left({A}_f\times 10.76\right)+0.5712\varepsilon \right] $$
(10.2a)
$$ q= \exp \left[8.252-0.0081\left({A}_f\times 10.76\right)+0.5508\varepsilon \right] $$
(10.2b)

where q is in units of MJ/m2, A f is the room size in m2, and ε is a random variable that follows the standard normal distribution. Eqs. (10.2a) and (10.2b) represent the characteristic fire load density value (q f,k ) in the EC1 formulation, which is discussed in Annex E of EC1 (CEN 2002). The equations can therefore be used with EC1 to develop fire characteristic time-temperature curves.

2.3 Mechanical Properties at Elevated Temperatures

This section provides probabilistic models for mechanical properties of steel at elevated temperatures based on available data in the literature. The two major mechanical properties of steel when performing structural analysis at elevated temperatures are yield strength at a strain equal to 2 % and modulus of elasticity. The two properties are part of the Eurocode3 (EC3) formulation (CEN 2005), which will be used in this work to evaluate performance of a structure at elevated temperatures. It should be noted that EC3 uses yield strength at a strain equal to 2 %, as opposed to yield strength at 0.2 % offset, to define the constitutive material model of steel at elevated temperatures.

The reported analytical equations for the parameters at elevated temperatures are in terms of normalized values, meaning that the parameter at every temperature is a factor of the parameter at the ambient temperature. The normalized parameters for yield strength and modulus of elasticity are assumed to vary between one and zero (one at ambient and zero at temperatures above 1000 °C). The reported measured data are also normalized values between zero and one, with occasional values larger than one at lower temperatures. Values larger than one imply that the strength of the specimen is larger than the assumed strength at the room temperature.

A study by the National Institute of Standards and Technology (NIST) (Luecke et al. 2011) provides measurements of yield strength at a strain equal to 2 % at elevated temperatures. Those data and the EC3 model (Eq. 10.3) are used to develop a probabilistic model for the normalized 2 % yield strength (k y,2%,T ). The data in Fig. 10.1 is normalized based on the 0.2 % offset yield strength of steel at the ambient temperature, and the EC3 model consists of eight linear functions for different temperature ranges. The developed probabilistic model is provided in Eq. (10.4) and shown in Fig. 10.1. In Eq. (10.4), \( {\overset{\frown }{k}}_{y,2\%,T}^{*}=\left({\overset{\frown }{k}}_{y,2\%,T}+{10}^{-6}\right)/1.7 \) where \( {\overset{\frown }{k}}_{y,2\%,T} \) is the normalized 2 % yield strength based on EC3 (Eq. 10.3), \( \mathrm{logit}\left({\overset{\frown }{k}}_{y,2\%,T}^{*}\right)= \ln \left[\frac{{\overset{\frown }{k}}_{y,2\%,T}^{*}}{1-{\overset{\frown }{k}}_{y,2\%,T}^{*}}\right] \), T is temperature in Celsius, and ε is the standard normal distribution. In this model, γ(x,θ) (in Eq. 10.1) consists of three terms, and σ = 0.43:

Fig. 10.1
figure 1

Proposed probabilistic model for yield strength at a strain of 2 % using EC3 (Eq. 10.3)

Full size image
$$ {\widehat{k}}_{y,2\%,T}=\frac{F_{y,2\%,T}}{F_y}=\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{ll}1.0\hfill & T<400\ {}^{\circ}\mathrm{C}\hfill \\ {}-2.2\times {10}^{-3}T+1.88\hfill & 400{}^{\circ}\mathrm{C}\le T<500{}^{\circ}\mathrm{C}\hfill \\ {}-3.1\times {10}^{-3}T+2.33\hfill & 500{}^{\circ}\mathrm{C}\le T<600{}^{\circ}\mathrm{C}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{ll}-2.4\times {10}^{-3}T+1.91\hfill & 600{}^{\circ}\mathrm{C}\le T<700{}^{\circ}\mathrm{C}\hfill \\ {}-1.2\times {10}^{-3}T+1.07\hfill & 700{}^{\circ}\mathrm{C}\le T<800{}^{\circ}\mathrm{C}\hfill \\ {}-5\times {10}^{-4}T+0.51\hfill & 800{}^{\circ}\mathrm{C}\le T<900{}^{\circ}\mathrm{C}\hfill \end{array}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{ll}-2\times {10}^{-4}T+0.24\hfill &\ 900{}^{\circ}\mathrm{C}\le T<1200{}^{\circ}\mathrm{C}\hfill \\ {}0.0\hfill & 1200{}^{\circ}\mathrm{C}\le T\hfill \end{array}\hfill \end{array}\right\} $$
(10.3)
$$ {k}_{y,2\%,T}=1.7\times \frac{e^{\left[ logit\left({\hat{k}}_{y,2\%,T}^{*}\right)+0.412-0.81\times {10}^{-3}T+0.58\times {10}^{-6}{T}^{1.9}+0.43\times \varepsilon \right]}}{e^{\left[ logit\left({\hat{k}}_{y,2\%,T}^{*}\right)+0.412-0.81\times {10}^{-3}T+0.58\times {10}^{-6}{T}^{1.9}+0.43\times \varepsilon \right]}+1} $$
(10.4)

Figure 10.1 shows the measured data and median of the proposed probabilistic model (ε = 0 in Eq. 10.4) based on the logistic transformation, along with the one standard deviation confidence interval of the models in the transformed space (ε = \( \pm 1 \) in Eq. 10.4). The model asymptotically approaches zero at higher temperatures, while the confidence interval is also closing faster at higher temperatures, reflecting smaller dispersion of data.

Similar to yield strength, data from the study by NIST (Luecke et al. 2011) are used to develop the probabilistic model for normalized modulus of elasticity at elevated temperatures (k E,T ). In developing the probabilistic model, the deterministic base, ĉ(x), in Eq. (10.1) is set to zero, and using the logistic function, one arrives at Eq. (10.5) with three terms for γ(x,θ) and σ of 0.36. Figure 10.2 shows the proposed models and one standard deviation confidence interval (in the transformed space) in relation to the measured data. The figure shows that the standard deviation envelope for the proposed model follows the scatter of data and is the smallest at low and high temperatures:

Fig. 10.2
figure 2

Proposed probabilistic models for modulus of elasticity with no deterministic base

Full size image
$$ {k}_{E,T}=1.1\times \frac{e^{\left(2.54-2.69\times {10}^{-3}\times T-2.83\times {10}^{-6}{T}^2+0.36\times \varepsilon \right)}}{e^{\left(2.54-2.69\times {10}^{-3}\times T-2.83\times {10}^{-6}{T}^2+0.36\times \varepsilon \right)}+1} $$
(10.5)

Both of the proposed models have important advantages over the existing models: they are single continuous curves, as opposed to the available deterministic models such as EC3, and they are unbiased and account for uncertainty. More detail about derivation and application of the models using the EC3 formulation can be found in Elhami Khorasani et al. (2015a).

3 Methodology

One of the objectives of this work is to develop a framework to evaluate the performance of a MRF under both fire-only and FFE scenarios. In the fire-only scenario, the MRF is intact with no prior damage, while the MRF has gone through nonlinear seismic analysis in an FFE scenario and may have permanent residual deformations before the fire starts. The comparison between the two events shows the influence of the earthquake on performance of the frame during fire.

The steps to perform post-earthquake fire analysis of the MRF are as follows: (1) select an earthquake scenario, (2) select a fire scenario, (3) perform seismic structural analysis, (4) change certain model constraints to allow for thermal expansion, and (5) perform structural-fire analysis. Uncertainties in the above process are grouped in steps 1 and 2 as part of demand and step 5 as part of capacity. A routine Monte Carlo simulation can be used for reliability analysis where the process is repeated multiple times to incorporate the uncertainties. The frame structure in this work is analyzed for one ground motion in step 1 (i.e., deterministic assumption), while multiple fire scenarios considering uncertainties in fire load and fire location (step 2) are modeled, and variability in material properties at elevated temperatures (step 5) are included. Fire load and material properties are randomly generated using the developed probabilistic models provided in Eqs. (10.2a, 10.2b), (10.4), and (10.5).

Four different engineering design parameters (EDP) related to the beam are defined to evaluate performance of the MRF. The performance of the columns was also considered, and no limit state was detected in any of the cases; this is due to large and heavy column sections of the MRF. Therefore, the results do not include column performance. Similar results were observed in a study by Keller and Pessiki (2015). A corresponding limit state is defined for each considered EDP as shown in Table 10.1 and discussed as follows:

Table 10.1 Defined EDPs and the corresponding limit states
Full size table
  1. 1.

    Plastic hinges: In a MRF with moment connections, three plastic hinges in a beam form a mechanism, in which case the beam eventually becomes unstable and loses its capacity to provide lateral restraint to the column.

  2. 2.

    Pseudo-velocity: The pseudo-velocity is calculated as the rate of displacement of the beam and is used as a measure of instability at elevated temperatures. The EDP is defined as the pseudo-velocity of the beam at the beam mid-span. Based on previous studies, and values provided in the study by Usmani et al. (2003), a limiting value of 0.254 mm/s (0.01 in/s) is defined for pseudo-velocity of the beam.

  3. 3.

    Tension force: Large tension forces can develop in the beam during the cooling phase of the fire and consequently cause connection failure. The finite element model does not capture connection failure. Therefore, based on a sample calculation of connection capacity, a limit state of 20 %P u of the column is defined for the maximum tension force in the beam before a connection fails (connections should generally be able to carry at least 2 %P u to allow for tensile forces due to column out of plumbness). The limiting value of 20 %P u is based on conservative calculations for a prototype 9-story building that will be discussed in Sect. 10.4 and can be refined based on particular designs under study.

  4. 4.

    Deflections: Excessive deflections can cause instability, and the limit state is defined as L/20 (L is the span length) (BRE 2005).

During the structural analysis of the frame at elevated temperatures, the concrete slab is not modeled, and non-composite behavior is assumed since the concrete slab goes into tension and cracks (Quiel and Garlock 2010a). However, it is assumed that there remains sufficient mechanical locking between the cracked concrete and shear studs to prevent lateral torsional buckling of the beams.

The MRF is modeled in the programming environment OpenSees, which is a finite element program and object-oriented software for nonlinear analysis of structures under seismic loadings, primarily developed at the University of California, Berkeley (McKenna and Fenves 2006). The seismic and thermal analyses of the MRF are both performed in OpenSees, using the recently added thermal module (Jiang et al. 2015). The new thermal module was modified by Elhami Khorasani et al. (2015b) to enhance the thermal analysis by allowing strain reversals, a seamless transition from seismic to thermal analysis, and including reliability analysis. The current constitutive material model for steel at elevated temperature was modified to incorporate the effect of plastic strain during both heating and cooling phases of fire. This modification facilitates sequential seismic and thermal analyses. Also, the current reliability module was adjusted to incorporate uncertainties in the thermal analysis.

4 Case Study: 9-Story MRF

This work applies the framework discussed above to study the performance of an example MRF under fire and FFE. The geometry and building description of the prototype MRF is based on the SAC steel project (SAC 2000). The SAC project considered different building heights, location, and both stiff and soft soil. The MRF in the present study is a 9-story frame that is assumed to be located on stiff soil in downtown Los Angeles and has plan and elevations that are based on SAC buildings. As the seismic design provisions have been updated in the code since the SAC steel project, the MRF is redesigned based on ASCE7-10 specifications (ASCE 2010).

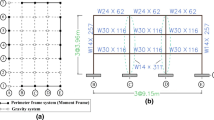
The building geometry consists of a square plan with 5 bays, each at 9.14 m (30 ft), in either direction. Columns and girders are spaced at 9.14 m (30 ft) and beams are spaced at 3.05 m (10 ft) intervals. The floor beams provide lateral support for the MRF girders. The 9-story building has a typical floor height of 3.96 m (13 ft) with a basement height of 3.66 m (12 ft) and ground floor height of 5.50 m (18 ft). The building consists of 4 MRFs, one on each side, and placed such that biaxial bending is avoided at corners. The MRFs in the two orthogonal directions are identical. The columns are pinned at the foundation and laterally braced at the ground level. The frame has a first mode period of 1.75 s. Figure 10.3 shows plan and elevation of the 9-story structure.

Fig. 10.3
figure 3

Plan and elevation of the 9-story MRF

Full size image

Given the MRF example, the following provides details of each step, discussed in Sect. 10.3, to perform post-earthquake fire analysis applied to the case study:

Step 1: Select an Earthquake Scenario

In this study, the earthquake scenario is kept as deterministic and the case study is completed for one ground motion. In general, the variability in ground motions should be considered, and the analysis should be repeated for various earthquakes in order to capture uncertainty in the earthquake scenario. The ground motion selected for this study is the 1989 Loma Prieta, CA earthquake ground motion that was recorded at station 47381 Gilroy (Array #3), and will be referred to as Gilroy earthquake. Only one component of the ground motion (the G03090 component) is applied since two-dimensional models are being used. The location was on stiff soil, and the earthquake had a magnitude of 6.9 with the closest distance from a fault rupture zone of 14.4 km. The hazard level chosen for this study is the maximum considered earthquake (MCE) (the 2 % in 50-year earthquake). The scale factor for the Gilroy ground motion is calculated to be 2.78 for the MCE level. The scaling procedure is based on the work of Somerville et al. (1997).

Step 2: Select a Fire Scenario

As discussed in Sect. 10.3, the frame structure is analyzed for multiple fire scenarios considering uncertainties in fire load and fire location. The probabilistic fire load density developed in Sect. 10.2.1 is used to generate random fire load density q. This study assumes a single compartment 6.1 m deep by 9.1 m wide (20 ft deep by 30 ft wide) in every floor that is subject to fire. Given the floor area of the compartment, Eq. (10.2a), developed for lightweight compartments (general office space), is a better choice. Therefore, the full fire temperature-time history is constructed using q values from Eq. (10.2a), the EC1 formulation (CEN 2002), and based on the work of Quiel and Garlock (2010a) to resemble an actual fire event. Given that the fire occurs after an earthquake, it is assumed that the compartment has no functional active firefighting measures and that the passive fire protection has been damaged enough to render it ineffective. Previous research by Braxtan and Pessiki (2011a, b) showed that spray fire resistive material, as passive fire protection, can delaminate or dislodge during inelastic seismic response and extensive damage can be expected especially in the beam plastic hinge regions. In addition, steel has a high thermal conductivity, and a local damage to passive fire protection can cause the structural element to heat up during fire.

Figure 10.4a shows the probability density function (PDF) for the maximum fire temperature reached in the compartment based on 50,000 random realizations of q generated using Eq. (10.2a) based on random generations of ε. The generated fire scenarios show that the 90 percentile maximum fire temperature value (T max) is approximately 1000 °C. Figure 10.4b shows the cumulative distribution function (CDF) for T max larger than 1000 °C. The MRF in this study is analyzed for 50 randomly generated fire temperature-time curves with T max larger than 1000 °C.

Fig. 10.4
figure 4

(a) PDF for T max, (b) CDF for T max above 1000 °C

Full size image

Four different fire locations are assumed in the frame by varying floors and bays of the fire compartment, shown in Fig. 10.5 where “B” stands for bay and “F” stands for floor. The locations of compartment allow evaluating the effect of story level (floor 4 vs. floor 6) and the effect of bay location (interior bay 2 vs. exterior bay 4). In a complete probabilistic analysis, uncertainty in the location of fire in the building should be considered. The aim of this research is to demonstrate the methodology while investigating post-earthquake fire performance of a tall building. Therefore, four compartments that are representative of interior/exterior bays and lower/higher stories for the 9-story building are selected as example studies.

Fig. 10.5
figure 5

Analytical model of the MRF frame in OpenSees

Full size image

The heat transfer analysis is performed for all the considered cases to obtain steel temperatures for the beams, perimeter columns, and interior columns of the compartment under study. Heat transfer for the two columns and a beam in the fire compartment is mainly per the closed-form solution developed by Quiel and Garlock (2010b) based on a lumped-mass method. The procedure is slightly modified for the beam to include the effect of the concrete slab (which acts as a heat sink) on the top flange temperature. An empirical equation developed by Ghojel and Wong (2005) is used to calculate the heat flux between the top flange and the slab.

Step 3: Perform Seismic Structural Analysis

Figure 10.5 shows the analytical model for the 9-story frame in OpenSees and the design sections of the MRF. The concentrated plasticity concept with rotational springs is used to model the nonlinear behavior of the 9-story MRF under dynamic loading. The frame is modeled with elastic beam-column elements that are connected with zero-length elements. The zero-length elements serve as the rotational springs that follow a bilinear hysteretic response. Panel zones are also modeled to capture the shear distortion in beam-column joints (Gupta and Krawinkler 1999). A leaning-column that carries gravity load is linked to the frame to simulate P-Delta effects.

Step 4: Change Model Constraints to Allow for Thermal Expansion

The model constraints need to be adjusted when transferring from seismic to thermal analysis. During the seismic analysis, a constraint is placed on the nodes of every floor to ensure that they move together horizontally, representing the effect of concrete slab diaphragm in the composite structure. However, after the seismic analysis is completed, the constraint on the nodes of the compartment that would experience fire is removed. This is explained in the previous research by Quiel and Garlock (2010a), which showed the steel in the composite girder during the thermal analysis experiences a faster increase in temperature than the slab. The steel expands at a faster rate than concrete, which eventually results in cracking of concrete, thus rendering the slab negligible for structural response.

Step 5: Perform the Structural-Fire Analysis

In performing an efficient and proper FFE analysis, the procedure must seamlessly transition from seismic to thermal in the OpenSees environment, and the modeling technique should be applicable to both dynamic and thermal analysis. Thermal modeling in OpenSees is only possible with the dispBeamColumnThermal-type element (Jiang and Usmani 2013), which is defined using fibers and considers plasticity along its length. Meanwhile, an efficient seismic model discussed above uses various other element types, including zero-length deterioration spring elements to capture nonlinear behavior. The 9-story frame in this work is modeled with springs and elements applicable for seismic analysis, except for the beams and columns of the fire compartment that are assumed to be heated (which will be modeled with dispBeamColumnThermal elements), as shown in Fig. 10.5. The authors tested the thermal elements for dynamic loading, and the results showed that the elements could reasonably capture the nonlinear dynamic behavior during an earthquake.

The two major parameters with uncertainties in the structural-fire analysis of the frame are yield strength and modulus of elasticity of steel at elevated temperatures. Equations (10.4) and (10.5) are used to randomly generate k y,2%,T and k E,T , for the beam and each column in the fire compartment. The material properties are randomly generated for every considered fire scenario.

5 Results

This section provides results of the probabilistic study for the 9-story frame under fire-only and FFE scenarios. As explained in Table 10.1 (Sect. 10.3), four limit states are considered for performance evaluation of the structure: (1) formation of three plastic hinges (PH), (2) pseudo-velocity (PSV), (3) tension force, and (4) deflection. The selected earthquake is the Gilroy ground motion scaled to the maximum considered earthquake (Gilroy-MCE). The thermal loading scenarios are obtained based on 50 randomly generated fire curves, applied to four fire compartments. The randomly generated material properties for the beam and columns, k y,2%,T and k E,T , are kept the same in the four compartments for comparison purposes (e.g., so that the effects of location can clearly be observed).

Figure 10.6 identifies the limit states reached under 50 fire scenarios for fire-only and FFE-Gilroy, respectively. The plots show results based on the bay under study (bay 2 and bay 4) and the two considered floors (floor 4 and floor 6). Also, the plots differentiate between the cases that the program stops converging during the heating phase of fire (circle markers) versus cases that continue through the cooling phase of the temperature-time curve of fire (plus-sign markers). Non-convergence does not imply collapse of the structure, but means that the beam element is not locally stable any longer. On the right margin of each plot, the total number of cases reaching the limit state is indicated.

Fig. 10.6
figure 6

Plots of limit states reached for fire-only and FFE-Gilroy scenarios

Full size image

The results show that, considering all the scenarios, at least 50 % of the cases reach the three plastic hinge limit state during the heating phase (25 out of 50 cases in B4-F4), while the number could reach up to 88 % (44 out of 50 cases in B2-F6). All cases that reach the PSV limit state form three plastic hinges, whereas formation of three plastic hinges does not guarantee reaching the PSV limit state. In addition, the program stops converging in all cases that reach the PSV limit state (implying that the beam is locally unstable and OpenSees can no longer advance the analysis). The results show that large tension forces can develop during the cooling phase, which may lead to potential connection failures. Overall, the upper floors reach limit states for plastic hinges and PSV more frequently than the lower floors due to the smaller beam sizes. The interior bays reach limit states more frequently than the exterior bays due to adjacent restraints. Finally, response of the MRF under fire in a seismically induced damaged state is similar to having a fire within an undamaged MRF.

Another parameter that is studied, and is affected by the earthquake, is the inter-story drift of compartments during fire. The analyses showed that the exterior bays experience drifts that are larger than the interior bays and fire causes more drift on floor 6 than floor 4. The maximum recorded drift reached after the earthquake and during the fire was approximately 3.5 % in the B4-F6 compartment. Overall, the earthquake does not increase the probability of reaching a limit state, but affects the drift demands during the fire event.

6 Summary and Conclusions

This work has provided a procedure to evaluate performance of a 9-story steel moment resisting frame (MRF) subject to fire and fire following earthquake (FFE) within a probabilistic framework. As part of the framework, parameters with uncertainties were identified, and probabilistic models were developed for fire load density, as well as for yield strength and modulus of elasticity of steel at elevated temperatures. The developed models were based on literature data, in conjunction with available deterministic equations in codes and standards. The proposed models are unbiased and account for uncertainties. The procedure used to develop the models can be applied to derive probabilistic models for other material properties and parameters with uncertainty.

The framework, together with the developed models, was applied to evaluate performance of a 9-story MRF under fire and FFE. The frame was modeled in OpenSees, and both seismic and thermal analyses were performed in one seamless programming environment. Four fire locations and 50 fire scenarios were considered to investigate the effects of fire intensity and location on the performance of the MRF. The results were compiled based on four engineering design parameters related to the beam, including formation of three plastic hinges, pseudo-velocity, tension force, and deflection. Performance of the columns was not included in the results, as analysis showed that the columns did not reach any limit state.

Results show that interior bays reached limit states more often than exterior bays due to the added restraint of the adjacent structure and upper floors were more vulnerable than lower floors due to the smaller section sizes. Overall, post-earthquake damage does not affect the fire performance of the MRF for the considered design parameters. During fire, the only parameter affected by the post-earthquake initial condition was the inter-story drift. The residual drift after the earthquake increased the total drift during fire, but the total drift did not exceed 4 %. This work focused on the performance of the MRF under FFE, assuming that fire occurs on the building perimeter where the MRF is located. However, it is equally likely to have a fire ignition inside the building where gravity frames are located. Gravity frames have considerably smaller sections compared to the MRF, and it is the subject of future work of this research. Finally, the proposed framework can be extended to evaluate structures under other multi-hazard scenarios. The case study in this work was performed for one earthquake scenario; however, the procedure can be expanded to include uncertainty in ground motion. Also, the framework can be adopted for fire following blast scenarios, a similar cascading multi-hazard loading event.