Reactive Transport

Abstract

This benchmark problem is based on the reactive transport example presented in Sect. 15.6 of benchmark book volume I (Kolditz et al. 2012c), which was originally described in van Breukelen et al. (2005).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Sequential Chlorinated Hydrocarbons Degradation

Wenkui He and Thomas Kalbacher

This benchmark problem is based on the reactive transport example presented in Sect. 15.6 of benchmark book volume I (Kolditz et al. 2012c), which was originally described in van Breukelen et al. (2005). It simulates the sequential dechlorination of chlorinated hydrocarbons (CHCs) from tetrachloroethene (PCE) to ethane (ETH) along an around 800 m long aquifer with a period of 20 years. Here, we use the benchmark to validate the coupling interface OGS#IPhreeqc described in He et al. (2015a).

1.1 Definition

The hydraulic conductivity and porosity of the aquifer are 10 m d$^{-1}$ and 0.25, respectively. The groundwater flow velocity is 0.1 m d$^{-1}$. Initially there is no CHC in the aquifer. The concentrations of PCE and its heavy isotope in the infiltration water are 0.9892 mol m$^{-3}$ and 0.0108 mol m$^{-3}$, respectively. The whole dechlorination chain is as follows:

PCE $\Rightarrow$ TCE (trichloroethylene) $\Rightarrow$ DCE (dichloroethylene) $\Rightarrow$ VC (vinyl chloride) $\Rightarrow$ ETH (ethylene)

The $^{12}C$ and $^{13}C$ isotopes of each CHC are modeled as separate species. Totally there are 11 chemical species including one tracer chloride, which is produced in each dechlorination reaction. All degradation reactions are simulated as first-order kinetics . For each CHC the kinetic isotope fractionation factor $\alpha _k$ is assumed to be constant during the whole degradation process, which can be calculated by Eq. (10.1.1):

$$\begin{aligned} \alpha _k = 1 + \frac{\epsilon }{1000} \end{aligned}$$

(10.1.1)

where $\epsilon$ is the isotope enrichment factor. The kinetic of each $^{12}C$ as well as $^{13}C$ CHC can be calculated by Eqs. (10.1.2) and (10.1.3), respectively.

$$\begin{aligned} \frac{d\text{ CHC }_l}{dt} = -{\upgamma }_l\ \text{ CHC }_l \end{aligned}$$

(10.1.2)

$$\begin{aligned} \frac{d\text{ CHC }_h}{dt} = -{\upgamma }_l\ \text{ CHC }_h (1+\frac{\epsilon }{1000}) \end{aligned}$$

(10.1.3)

The first-order degradation rate and enrichment factor for each CHC are listed in Table 10.1.

Table 10.1 The first-order degradation rate and enrichment factor for CHCs

Fig. 10.1

Concentration profiles of the light CHCs and $\delta ^{13}C$ isotope signatures along the model domain simulated by PHREEQC (symbols) and OGS#IPhreeqc (lines) after 20 a (from He et al. 2015a)

1.2 Results

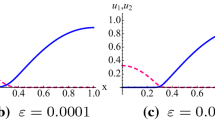
The concentration profiles of the light CHC as well as the $\delta ^{13}C$ isotope signatures along the model domain simulated by PHREEQC (from van Breukelen et al. 2005) and OGS#IPhreeqc are illustrated in Fig. 10.1. As we can see, there is a very good agreement between the results simulated by both codes. More details of the coupling interface OGS#IPhreeqc and its applications can be found in He et al. (2015a).

2 PSI—Reactive Transport Benchmark

Jenna Poonoosamy, Georg Kosakowski, Luc R. Van Loon, Urs Mäder

In this chapter we briefly summarize the reactive transport experiments we conducted in a flow cell and which are described in Poonoosamy et al. (2015).Then we present our numerical simulations whose results were benchmarked against our experimental work. We considered three case studies with increasing complexity: case 1 considers a 2D system with density driven flow and conservative mass transport, case 2 in addition includes the dissolution and precipitation of mineral phases leading to porosity changes and case 3 extends the case 2 by considering the formation of solid solutions. We used the OpenGeoSys-GEM simulator, which uses finite element solvers for fluid flow and mass transport implemented in OpenGeoSys, coupled with GEMS for chemical equilibrium calculations (Kosakowski and Watanabe 2014). The numerical calculation with OpenGeosys-GEM will be compared with other reactive transport codes within the framework of SeS benchmark projects (see Sect. 1.2).

2.1 Definition of the Problem Set-Up

We designed a 2D reactive transport experimental benchmark which aims to be reproducible, fast to conduct and with a simple chemical set up. In what follows, we briefly summarize the experiment formulated to benchmark numerical simulations of flow of a fluid with variable density coupled with reactive transport (Poonoosamy et al. 2015). The experiment was conducted using the flow cell depicted in Fig. 10.2, which allowed us to visualize dye tracer tests. It consists of a reactive porous layer of strontium sulphate (SrSO$_{4}$) between two inert porous layers composed of silicon dioxide (SiO$_{2}$). The flow cell has dimensions of $0.1\,\times {}\,0.1\,\times {}\,0.01$ m, and it contains several ports for fluid injection and sampling. The inlet and outlet positions were chosen to create an asymmetric flow field. The chemical transformations in the flow cell were monitored by taking samples of the pore solution at ports ‘c’ and ‘d’, as well as by collecting the effluent at the outlet. The pressure difference between ports ‘a’ and ‘b’ was also measured. We performed post mortem analysis to determine the nature and location of the mineralogical transformations of the reactive media. Our numerical simulations will follow up this setup, and we will use our experimental measurements to quantitatively benchmark them. A qualitative benchmark will also be shown using images of the dye tracer distribution throughout the flow cell.

Fig. 10.2

Geometry of the numerical benchmark

In Table 10.2, we list the properties of the different regions Q1, Q2, and Q3 shown in Fig. 10.2, as well as properties of the fluid and initial conditions used for the numerical calculations. The coordinates (x, z) of the ports ‘a’ and ‘b’, where pressure sensors were installed, are (0.02, 0.02 m) and (0.08, 0.08 m) respectively. The ports ‘c’ and ‘d’, where sampling was performed, are located at (0.08, 0.02 m) and (0.02, 0.08 m) respectively. These are the coordinates one should use to compare numerical results with the experimental measurements presented in Poonoosamy et al. (2015).

Table 10.2 Properties of the different regions of porous media

We define three different benchmark cases with increasing complexity. In Case 1, we study density driven flow with conservative mass transport. In Case 2, we in addition consider dissolution and precipitation of mineral phases leading to porosity changes. Finally, Case 3 extends the Case 2 by inclusion of the possible formation of solid solutions. Table 10.3 provides additional information on the inlet and outlet conditions for the three case studies. For all simulations, we considered a discretization of the squared geometry in Fig. 10.2 by triangular elements. For Cases 1 and 3, a node distance of 1 mm was chosen, while for Case 2 a more refined mesh was adopted, with a node distance of 0.5 mm.

Table 10.3 Characteristics of the inlet and outlet

Table 10.4 Thermodynamic database of aqueous, gaseous and solid species present under standards conditions

Case 1: Conservative mass transport coupled with a density driven flow.

Here we consider the injection of a highly concentrated solution of sodium chloride (NaCl of density 1.056 kg dm$^{-3}$) in a flow cell, initially saturated with water (density 1 kg dm$^{-3}$). An injection of 0.5 mL of a conservative tracer at the inlet is carried out at a rate of 20 ${\upmu }$L min$^{-1}$, followed by the inflow of a NaCl solution for 24 h. This NaCl solution was saturated with strontium sulphate (SrSO$_{4}$). The Q2 region, composed of SrSO$_{4}$, was assumed to be unreactive in this case study. The system was simulated for 24 h.

Case 2: Reactive transport with porosity changes.

A highly concentrated solution of barium chloride (BaCl$_{2}$) is injected in a flow cell. The injection of BaCl$_{2}$ enhances the dissolution of SrSO$_{4}$ and causes barium sulphate (BaSO$_{4}$) to precipitate according to the reaction:

$$\begin{aligned} Ba{Cl}_{2(aq)}+SrSO_{4(s)}\rightarrow {}BaSO_{4(s)}+SrCl_{2(aq)} \end{aligned}$$

(10.2.1)

Porosity changes are likely to occur given that BaSO$_{4 }$ has a larger molar volume than SrSO$_{4}$. As a result, material medium properties such as permeability and diffusivity will equally change. The reactive layer Q2 has an initial porosity of 33 % and is composed of two grain size populations of SrSO$_{4}$ (i.e., celestite 1 and celestite 2). Celestite 1 corresponds to SrSO$_{4}$ with a grain size of 10–63 ${\upmu }$m, while celestite 2 has a much higher grain size in the range 250–400 ${\upmu }$m. Different kinetic rates of dissolution are used for these two grain populations (see Sect. 10.2.2). The following reactive surface areas (per volume unit) were attributed to the small and large crystals respectively: 20,000 m$^{2}$ m$^{-3}$ and 100 m$^{2}$ m$^{-3}$. We assumed no kinetic constraints on the precipitated barite (BaSO$_{4}$(s)) phase. The simulation time is set to 200 h.

Case 3: Reactive transport involving the formation of a solid solution.

Here the reactive media is composed of celestite with a single grain size population of 63–125 ${\upmu }$m. The reactive surface area (per volume unit), a$_{(SrSO4)}$, is 10,000 m$^{2}$ m$^{-3}$. A solution composed of 0.099 mol L$^{-1}$ SrCl$_{2}$ and 0.001 mol L$^{-1}$ BaCl$_{2}$ is injected at the inlet at a flow rate of 10 ${\upmu }$L min$^{-1}$. The simulation time is set to 600 h (Table 10.4).

The chemical configurations for Case 1, Case 2 and Case 3 are summarized in Tables 10.5, 10.6 and 10.7 in the annex.

2.2 Description of the Coupled Code

The fluid flow and mass transport equations are solved by OpenGeoSys, and the chemical processes by the GEMS3K kernel code of GEM-Selektor V3 (Kulik et al. 2013).The coupling of these two codes is referred as OpenGeoSys-GEM, and its capabilities are described in Shao et al. (2009) and Kosakowski and Watanabe (2014). Mass transport and chemical reactions are solved in a sequential non-iterative approach (SNIA), i.e. the transport and reaction equations are solved separately in a sequential manner without iteration between them.

The GEM approach consists of calculating the equilibrium state of a chemical system via minimization of its Gibbs free energy. The minimization is constrained by mass balance equations where the given total amounts of chemical elements are conserved. An additional charge balance equation is also imposed to enforce the electrically neutral condition of the system. The calculated equilibrium state by GEMS3K not only provides the molar amounts of every species in the system, which indicates which phases are stable or unstable, but also important chemical quantities such as species activities that are needed for calculation of kinetic rates of mineral dissolution. The thermodynamic data (standard Gibbs energy of formation [kJ mol$^{-1}$]) of aqueous, gaseous and solid species considered in our chemical system and the molar volumes [m$^{3}$ mol$^{-1}$] based on the PSI/NAGRA thermodynamic database (Hummel et al. 2002), are given in Table 10.4.

In OpenGeosys-GEM the density of the aqueous phase is calculated by GEM3K. This is done by calculating the partial molar volumes of each aqueous species at the temperature and pressure of interest, and summing the product of these partial molar volumes by the corresponding molar amounts of the aqueous species to obtain the volume of the aqueous phase. The total mass of the phase divided by this volume gives the density of the aqueous phase, which is dependent on its molar composition. This density is updated after each chemical equilibrium calculation and passed along to the fluid flow solver.

Density flow

During the numerical simulations, the velocity field is calculated by solving the flow equation (Eq. 14.16 in Kolditz 2002). The concentrations of all chemical species are determined by solving the mass transport equation (Eq. 3.46 in Kolditz 2002) for the components (i.e. chemical elements) followed by equilibrium calculations by the chemical solver at every node of the mesh using the result of the transported components. The equilibrated concentrations are retrieved for the next time step of mass transport calculation. In OpenGeoSys, the Boussinesq approximation is considered, i.e. the density variation is neglected in the mass conservation equation of the fluid phase. Density variations are included by the buoyancy term of the Darcy equation only. For variable-density flow in porous medium the Darcy velocity $\mathbf q$(m s$^{-1}$) is given as:

$$\begin{aligned} \mathbf q = -\frac{\mathbf k}{\mu {}}\left( \nabla {}p-\rho {} \mathbf g \right) , \end{aligned}$$

(10.2.2)

where $\mathbf k$ is the permeability tensor (m$^{2}$), $\mu$ is the dynamic viscosity (Pa s) of fluid, $\nabla p$ (Pa) is the pressure gradient, $\rho$ is density of fluid (kg m$^{-3}$) and $\mathbf g$ is the gravity vector (m s$^{-2}$).

Porosity, diffusivity and permeability

As a result of dissolution/precipitation reactions, porosity changes occur. Transport properties such as effective diffusion coefficients, $D_e,$ and the permeability, k $_{s}$, of the medium are parameterized as a function of porosity.

For the dependence of the effective diffusion coefficient, $D_e,$ on porosity we used a simplified Archie’s law (Archie 1942):

$$\begin{aligned} D_e = D_w n^m \end{aligned}$$

(10.2.3)

where D $_{w}$ [m$^{2 }$ s$^{-1}$] is the diffusion coefficient in water, n [-] is the porosity and m [-] is an empirical coefficient. In our case m was set to 1.

Changes of permeability k $_{s}$ [m$^{2}$] with porosity are given by a modified Kozeny – Carman equation:

$$\begin{aligned} k_s=k_0{\left( \frac{n}{n_0}\right) }^3 \end{aligned}$$

(10.2.4)

where k $_{0}$ [m$^{2}$] is the initial permeability, and w and $w_0$ are the current and initial porosities, respectively.

Activity corrections

Activity coefficients for all dissolved species ${\upgamma _i}$ are calculated by the extended Debye- Hückel equation (Helgeson et al. 1981). A detailed description is reported in Wagner et al. (2012). Equation ( 10.2.5) relates the activity coefficients of an aqueous ion to its charge (Z$_{i}$) and ionic strength (I):

$$\begin{aligned} {log}_{10}{\upgamma }_i=\frac{-A_{\upgamma }Z_i^2\sqrt{I}}{1+\dot{a}_iB_{\upgamma }\sqrt{I}}+b_{\upgamma _{i}}{I} \end{aligned}$$

(10.2.5)

where $\dot{a}_i$ (in 10$^{-8}$ cm) is an average distance of approach of two ions of opposite charges, $b_\upgamma$ is a semi-empirical coefficient, either individual for a given electrolyte or common for all charged species. $\dot{a}_i$ and $b_{\upgamma {i}}$ were set to 3.72 and 0.064 respectively for all the ionic species (Helgeson et al. 1981).These are values for the well calibrated sodium chloride electrolyte. $A_\upgamma$ and $B_\upgamma$ are temperature dependent coefficients obtained internally from SUPCRT92 subroutines (Johnson et al. 1992) incorporated into the GEMS code. At a temperature of 25 $^{\circ }$C and pressure of 1 bar, $A_\upgamma \ \approx {}\ 0.5114$ and $B_\upgamma \ \approx \ 0.3288$. Activity coefficients, $\upgamma _{(i)}$for neutral species (dissolved gasses) and water were set to unity.

Kinetics of precipitation and dissolution reactions of minerals

The temporal quantities of strontium and barium sulphate, and consequently also the porosity evolution, depend on the reaction kinetics. The kinetic rates dm/dt [mol s$^{-1}$] are calculated following Palandri and Kharaka (2004a). In our simulations, the simplest reactive surface area SA [m$^{2}$] model of those implemented in OGS-GEM was chosen:

$$\begin{aligned} SA=V_ia_i \end{aligned}$$

(10.2.6)

where V $_{i}$ [m$^{3}$] is the volume of the mineral and a $_{i}$ [m$^{2}$ m$^{-3}$] is the relative surface area per volume unit.

In our simulations, barium sulphate was assumed to precipitate instantaneously (very fast kinetics) and only the kinetic dissolution of strontium sulphate was taken into account. The dissolution rate of strontium sulphate at pH = 5.6 (pH of the experiment) is calculated based on the equation given in Palandri and Kharaka (2004a) with parameters from Dove and Czank (1995).

$$\begin{aligned} \frac{dm}{dt}=-SA\ k^{^\circ {}}(1-\varOmega {}) \end{aligned}$$

(10.2.7)

where SA[m$^{2}$] is the reactive surface area of the strontium sulphate mineral phase, $k^{^\circ {}}={10}^{-5.66}$ mol m$^{-2}$ s$^{-1}$ is the dissolution rate constant at 298.15 K and $\varOmega {}$ is the mineral saturation index.

Solid solution

A solid solution phase is defined as a mixture of solids forming a homogeneous crystalline structure. The thermodynamics of a solid solution has been described in details by Bruno et al. (2007). Briefly, the Gibbs energy of a solid solution (composed of n-components) that deviates from ideality ($\varDelta {}$G$_{total}$ $^{real}$), can be split into the Gibbs energy of pure end-members (G $_{i}$ $^{0}$X$_{i}$), the ideal Gibbs energy of mixing ($\varDelta {}$G$_{mix}$ $^{id}$), and the excess Gibbs energy of mixing (G $^{ex}$):

$$\begin{aligned} \varDelta {}G_{total}^{real}=\sum _{i=1}^nG_i^0X_i+\varDelta {}G_{mix}^{id}+G^{ex} \end{aligned}$$

(10.2.8)

The $\varDelta {}$G$_{mix}$ $^{id}$ is given by the following formula:

$$\begin{aligned} \varDelta {}G_{mix}^{id}=RT\sum _{i=1}^nX_ilnX_i \end{aligned}$$

(10.2.9)

where X $_{i}$ $_{ }$the mole fraction of component i, R and T are the gas constant and temperature respectively.

The G $^{ex }$term depends on the mixing model of choice. In our approach, the subregular mixing model is considered (Bruno et al. 2007). The excess Gibbs energy of a binary subregular solution with component A and B mixing randomly is given by the Margules formula:

$$\begin{aligned} \varDelta {}G^{ex}=X_AX_B(X_Aw_{BA}+X_Bw_{AB}) \end{aligned}$$

(10.2.10)

where X $_{A}$ andX $_{B}$ are the molar fractions of the end-members and $w_{AB}$ and $w_{BA}$ are the Margules interaction parameters, $w_{AB}\not =w_{BA}$. Note that this model reduces to the regular model when $w_{AB} = w_{BA}$. The Margules parameters (in J mol$^{-1}$) are usually defined as linear functions of temperature, T, and pressure, P,

$$\begin{aligned} w_{AB}=w_{u,AB}-Tw_{s,AB}+Pw_{v,AB} \end{aligned}$$

(10.2.11)

where $w_{u}$, $w_{s}$ and $w_{v}$ are empirical coefficients related to excess internal energy, entropy and volume of mixing, respectively. The Margules parameters $w_{AB}, w_{BA}$ for barium and strontium sulphate solid solution at 298.15 K were set to 3787 J mol$^{-1}$ and 3665 J mol$^{-1}$ according to Zhu (2004). Corrections to pressure and temperature were neglected in our model.

2.3 Results

In this part we present the reference solution for the different case studies.

Case 1

Case 1 considers the injection of a concentrated non-reacting sodium chloride solution into a porous medium initially saturated with a liquid of lower density (water). Figure 10.3 compares, at different times, the experimentally observed dye tracer distribution in a highly concentrated NaCl solution (bottom figures) with results from our numerical simulations (top figures). The simulated tracer profile is in good qualitative agreement with the experimental observation. A quantitative tracer concentration comparison could not be performed because of large uncertainties on the experimental tracer concentration calibration. Figure 10.4 gives the simulated breakthrough curve of the tracer at ports ‘c’ and ‘d’, and at the outlet for comparison with other transport codes.

Fig. 10.3

The temporal evolution of the tracer profiles of the model (top) and the experiment (bottom)

Fig. 10.4

The simulated tracer concentration at port ‘d’, ‘c’ and the outlet as a function of time

Case 2

Case 2 extends Case 1 by considering dissolution and precipitation of minerals that change porosity and permeability in the flow cell. When a concentrated BaCl$_{2}$ solution reaches the reactive SrSO$_{4}$ layer Q2, the dissolution of SrSO$_{4}$ is triggered and barium sulphate (BaSO$_{4}$) precipitates. Figure 10.5 shows the total amount of BaSO$_{4}$ and SrSO$_{4}$ in the flow cell with time, which changes due to either mineral dissolution or precipitation. During the first 150 h, dissolution of SrSO$_{4}$ at a constant rate of 0.2 mmol per hour is observed. After 150 h, this dissolution rate slows down. Similarly the total amount of precipitated barium sulphate increases for the first 150 h and slowly builds up to 0.036 mol at 200 h. The initial fast precipitation of barium sulphate for the first 150 h results from the dissolution of the smaller strontium sulphate particles (celestite 1). As the smaller strontium sulphate grains are consumed, aqueous SO$_{4}$ $^{2-}$ is supplied by the dissolution of larger dissolution strontium sulphate (celestite 2) which is much slower due to its lower reactive surface area. The simulated results reproduced well the experimental data. In the experiments, small strontium sulphate crystals dissolved completely, while larger strontium sulphate grains were coated by a layer of barium sulphate, which prevented further dissolution. These observations were approximated in our model by applying a different reactive surface area for small and big strontium sulphate grains. The reactive surface areas attributed to celestite 1 and celestite 2 are fitted values, because the measured BET surface area overestimated strontium sulphate dissolution. The experimental observation also showed the absence of a precipitation front of barium sulphate at 200 h. This was reproduced in our simulation as shown in Fig. 10.6.

Fig. 10.5

Time evolution of the total bulk amount [mol] of barium sulphate and strontium sulphate in the flow cell

Fig. 10.6

Time evolution of barium sulphate profiles [mol m$^{-3}$] in the flow cell

The transformation of strontium sulphate to barium sulphate involves a volume increase of about 12 %. The resulting porosity decrease and associated permeability changes are shown in Fig. 10.7. This model does not reproduce the experimentally observed 100 % net pressure increase (between port ‘a’ and port ‘b’) measured during the experiment (Poonoosamy et al. 2015), because the calculated porosity change is too small to significantly change the permeability as calculated by the Kozeny-Carman porosity – permeability relation (Eq. 10.2.4). In (Poonoosamy et al. 2015), a second scenario that involved the insertion of a 1 mm thick zone at the quartz/ strontium sulphate interface (between the Q1 and Q2 region) with an initial lower porosity of 0.1 reproduced the experimental pressure changes. This scenario is not included here.

Fig. 10.7

Porosity left and associated permeability changes right across z = 0.01 m at 0, 100 and 200 h

Figure 10.8 shows the calculated and simulated ion concentrations at port ‘c’ and at the outlet as a function of time. Note that the uncertainties on the measured concentration at port ‘c’ are relatively high because it involved the sampling of small volumes of liquid (100 ${\upmu }$L) that were afterwards diluted for measurement by ion chromatography. The simulated breakthrough curves of Cl$^{-}$, Sr$^{2+}$ and Ba$^{2+}$ differ significantly from the experimental data. The chloride concentration of the liquid samples collected at port ‘c’ exceeds its injecting concentration (0.6 mol L$^{-1}$). This can be due to sampling artefacts at the ports. As such, the experimental ion concentrations at the port cannot be used for comparison. On the other hand, the calculated ion concentrations at the outlet are in good agreement qualitatively and quantitatively with experimental data.

Fig. 10.8

Measured and calculated ion concentrations at port ‘c’ and at the outlet as a function of time

Case 3

Case 3 is a hypothetical case study that considers the formation of a solid solution between barium sulphate and strontium sulphate. It still needs to be tested experimentally. In this case, the pure mineral phase strontium sulphate is replaced by a solid solution. No pure barium sulphate phase is likely to precipitate. The injection of a solution composed of 1 mmol/L barium chloride and 99 mmol/L of strontium chloride, likely triggers a barium rich solid solution. Figure 10.9 shows the total amount of mineral phases present in the flow cell with time. After 600 h, 0.0043 mol of pure strontium sulphate phase has reacted to form 0.0043 mol of a (Sr$_{1-x}$Ba$_{x}$)SO$_{4}$ solid solution. The composition of the formed solid solution changes with time.

Fig. 10.9

Evolution of the bulk mineral composition in the flow cell with time. The left axis refers to the dissolving pure celestite while the right axis refers to the precipitating phases (end members of solid solution)

Figure 10.10 shows the porosity change between 0 and 600 h and the associated permeability decrease across line $z=0.01$m. The porosity decrease and the corresponding permeability change are negligible.

Fig. 10.10

Porosity (left) and associated permeability changes (right) across z = 0.01 m at 0 and 600 h

2.4 Summary

We conducted 2D experiments to benchmark fluid flow and reactive transport calculations. Barium chloride was injected in a flow cell filled with a porous reactive layer of strontium sulphate sandwiched between two layers of inert porous material, silicon dioxide. Our experiments are flexible enough to investigate several process couplings such as the effect of the liquid phase density on advective-diffusive transport of solutes, kinetically controlled dissolution/precipitation reactions causing porosity changes, and mineral changes involving formation of solid solution. We thus present 3 case studies with increasing level of complexity as a benchmark for reactive transport codes. In Case 1 tests with a non-reactive tracer and density-driven flow (due to the high concentration of a sodium chloride solution), were well reproduced by the numerical model. Case 2 involved the dissolution and precipitation of mineral phases that caused changes in porosity and permeability of the porous media. The presented model could reproduce well the temporal mineral bulk composition in the flow cell, but failed to reproduce the measured net pressure increase with the implemented Kozeny-Carman equation. However, by modifying the initial medium properties of the interface in the simulation, the experimental results could be fitted. This scenario described in Poonoosamy et al. (2015) is not presented here. Case 3 extends the problem of case 2 by considering the formation of a non-ideal solid solution and still needs to be verified experimentally. The presented cases are based on the benchmark study in the framework of the SeS benchmark initiative (Xie et al. 2014).

Annex

Table 10.5 Equilibrium amount of solutes and phases (mol) for boundary (BC) and initial conditions (IC) for case 1

Table 10.6 Equilibrium amount of solutes and phases (mol) for boundary (BC) and initial conditions (IC) for case 2

Table 10.7 Equilibrium amount of solutes and phases (mol) for boundary and initial conditions for case 3