On Welschinger Invariants of Descendant Type

Abstract

We introduce enumerative invariants of real del Pezzo surfaces that count real rational curves belonging to a given divisor class, passing through a generic conjugation-invariant configuration of points and satisfying preassigned tangency conditions to given smooth arcs centered at the fixed points. The counted curves are equipped with Welschinger-type signs. We prove that such a count does not depend neither on the choice of the point-arc configuration nor on the variation of the ambient real surface. These invariants can be regarded as a real counterpart of (complex) descendant invariants.

Dedicated to Gert-Martin Greuel in occasion of his 70th birthday

1 Introduction

Welschinger invariants of real rational symplectic manifolds [17–19, 21] serve as genus zero open Gromov–Witten invariants. In dimension four and in the algebraic-geometric setting, they are well defined for real del Pezzo surfaces (cf. [12]), and they count real rational curves in a given divisor class passing through a generic conjugation-invariant configuration of points and are equipped with weights ± 1. An important outcome of Welschinger’s theory is that, whenever Welschinger invariant does not vanish, there exists a real rational curve of a given divisor class matching an appropriate number of arbitrary generic conjugation-invariant constraints.

There are several extensions of the original Welschinger invariants: modifications for multicomponent real del Pezzo surfaces [9, 12], mixed and relative invariants [10, 20] (R. Rasdeaconu and J Solomon, Relative open Gromov–Witten invariants, unpublished), invariants of positive genus for multicomponent real del Pezzo surfaces [15], and for $\mathbb{P}^{2k+1}$, k ≥ 1 [4, 5]. The goal of this paper is to introduce Welschinger-type invariants for real del Pezzo surfaces, which count real rational curves passing through some fixed points and tangent to fixed smooth arcs centered at the fixed points. They can be viewed as a real counterpart of certain descendant invariants (cf. [6]).

The main result of this note is Theorem 1 in Sect. 2, which states the existence of invariants independent of the choice of constraints and of the variation of the surface. Our approach in general is similar to that in [12], and it consists in the study of codimension one bifurcations of the set of curves subject to imposed constraints when one varies either the constraints or the real and complex structure of the surface. In Sect. 5, we show a few simple examples. The computational aspect and quantitative properties of the invariants will be treated in a forthcoming paper.

2 Invariants

Let X be a real del Pezzo surface with a nonempty real point set $\mathbb{R}X$ and $F \subset \mathbb{R}X$ a connected component. Pick a conjugation-invariant class $\varphi \in H_{2}(X\setminus F; \mathbb{Z}/2)$. Denote by $\mathop{\mathrm{Pic}}\nolimits _{+}^{\mathbb{R}}(X) \subset \mathop{\mathrm{Pic}}\nolimits (X)$ the subgroup of real effective divisor classes. Pick a nonzero class $D \in \mathop{\mathrm{Pic}}\nolimits ^{\mathbb{R}}(X)$, which is F-compatible in the sense of [11, Sect. 5.2]. Observe that any real rational (irreducible) curve C ∈ | D | has a one-dimensional real branch (see, e.g., [12, Sect. 1.2]), and hence we can define C ₊, C ₋, the images of the components of $\mathbb{P}^{1}\setminus \mathbb{R}\mathbb{P}^{1}$ by the normalization map.

Given a smooth (complex) algebraic variety $\Sigma$, a point $z \in \Sigma$, and a positive integer s, the space of s-arcs in $\Sigma$ at z is

$$\displaystyle{\mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma,z) = \mathop{\mathrm{Hom}}\nolimits (\mathop{\mathrm{Spec}}\nolimits \mathbb{C}[t]/(t^{s+1}),(\Sigma,z))/\mathop{\mathrm{Aut}}\nolimits (\mathbb{C}[t]/(t^{s+1}))\ .}$$

Denote by $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\Sigma,z) \subset \mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma,z)$ the (open) subset consisting of smooth s-arcs, i.e., of those which are represented by an embedding $(\mathbb{C},0) \rightarrow (\Sigma,z)$.

Choose two collections of positive integers $\boldsymbol{k} =\{ k_{i},\ 1 \leq i \leq r\}$ and $\boldsymbol{l} =\{ l_{j},\ 1 \leq j \leq m\}$, where r, m ≥ 0 and

$$\displaystyle{ \sum _{i=1}^{r}k_{ i} + 2\sum _{j=1}^{m}l_{ j} = -DK_{X} - 1\, }$$

(1)

and all k ₁, …, k _r are odd. Pick distinct points z ₁, …, z _r  ∈ F and real arcs $\alpha _{i} \in \mathop{\mathrm{Arc}}\nolimits _{k_{i}}^{\mathrm{sm}}(X,z_{ i})$, 1 ≤ i ≤ r, and also distinct points $w_{1},\ldots,w_{m} \in X\setminus \mathbb{R}X$ and arcs $\beta _{j} \in \mathop{\mathrm{Arc}}\nolimits _{l_{j}}^{\mathrm{sm}}(X,w_{ j})$. Denote $\boldsymbol{z} = (z_{1},\ldots,z_{r})$, $\boldsymbol{w} = (w_{1},\overline{w}_{1},\ldots,w_{m},\overline{w}_{m})$ and

$$\displaystyle{ \mathcal{A} = (\alpha _{1},\ldots,\alpha _{r}) \in \prod _{i=1}^{r}\mathop{\mathrm{Arc}}\nolimits _{ k_{i}}^{\mathrm{sm}}(X,z_{ i})\, }$$

(2)

$$\displaystyle{ \mathcal{B} = (\beta _{1},\overline{\beta }_{1},\ldots,\beta _{m},\overline{\beta }_{m}) \in \prod _{j=1}^{m}\left (\mathop{\mathrm{Arc}}\nolimits _{ l_{j}}^{\mathrm{sm}}(X,w_{ j}) \times \mathop{\mathrm{Arc}}\nolimits _{l_{j}}^{\mathrm{sm}}(X,\overline{w}_{ j})\right )\ . }$$

(3)

In the moduli space $\mathcal{M}_{0,r+2m}(X,D)$ of stable maps of rational curves with r + 2m marked points, we consider the subset $\mathcal{M}_{0,r+2m}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))$ consisting of the elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow X,\boldsymbol{p}]$, $\boldsymbol{p} = (\,p_{1},\ldots,p_{r},q_{1},\ldots,q_{m},q_{1}^{{\prime}},\ldots,q_{m}^{{\prime}}) \subset \mathbb{P}^{1}$, such that

$$\displaystyle{\boldsymbol{n}^{{\ast}}\left (\bigcup \mathcal{A}\cup \bigcup \mathcal{B}\right ) \geq \sum _{ i=1}^{r}k_{ i}p_{i} +\sum _{ j=1}^{m}l_{ j}(q_{j} + q_{j}^{{\prime}})\ .}$$

Let $\mathcal{M}_{0,r+2m}^{\;im,\mathbb{R}}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B})) \subset \mathcal{M}_{0,r+2m}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))$ be the set of elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow X,\boldsymbol{p}]$ such that $\boldsymbol{n}$ is a conjugation-invariant immersion, the points $p_{1},\ldots,p_{r} \in \mathbb{P}^{1}$ are real, and $q_{j},q_{j}^{{\prime}}\in \mathbb{P}^{1}$ are complex conjugate, j = 1, …, m. For a generic choice of point sequences $\boldsymbol{z}$ and $\boldsymbol{w}$, and arc sequences $\mathcal{A}$ and $\mathcal{B}$ in the arc spaces indicated in (2) and (3), the set $\mathcal{M}_{0,r+2m}^{\;im,\mathbb{R}}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))$ is finite (cf. Proposition 1(1) below).

Given an element $\xi = [\boldsymbol{n}: \mathbb{P}^{1} \rightarrow X,\boldsymbol{p}] \in \mathcal{M}_{0,r+2m}^{\;im,\mathbb{R}}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))$, denote $C = \boldsymbol{n}(\mathbb{P}^{1})$ and define the Welschinger sign of ξ by (cf. [12, Formula (1)])

$$\displaystyle{W_{\varphi }(\xi ) = (-1)^{C_{+}\circ \;C_{-}+C_{+}\circ \;\varphi }\ .}$$

Notice that, if C is nodal, then C ₊ ∘ C ₋ has the same parity as the number of real solitary nodes of C (i.e., nodes locally equivalent to x ² + y ² = 0).

Finally, put

$$\displaystyle{ W(X,D,F,\varphi,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B})) =\sum _{\xi \in \mathcal{M}_{0,r+2m}^{\;im,\mathbb{R}}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))}W_{\varphi }(\xi )\ . }$$

(4)

Theorem 1

• (1) Let X be a real del Pezzo surface with $\mathbb{R}X\neq \emptyset$, $F \subset \mathbb{R}X$ a connected component, $\varphi \in H_{2}(X\setminus F, \mathbb{Z}/2)$ a conjugation-invariant class, $D \in \mathop{\mathrm{Pic}}\nolimits _{+}^{\mathbb{R}}(X)$ a nef and big, F-compatible divisor class, $\boldsymbol{k} = (k_{1},\ldots,k_{r})$ a (possibly empty) sequence of positive odd integers such that

  $$\displaystyle{ \max \{k_{1},\ldots,k_{r}\} \leq 3\, }$$

  (5)

  and $\boldsymbol{l} = (l_{1},\ldots,l_{m})$ a (possibly empty) sequence of positive integers satisfying (1), $\boldsymbol{z} = (z_{1},\ldots,z_{r})$ a sequence of distinct points of F, $\boldsymbol{w} = (w_{1},\ldots,w_{m},\overline{w}_{1},\ldots,\overline{w}_{m})$ a sequence of distinct points of $X\setminus \mathbb{R}X$ , and, at last, $\mathcal{A}$, $\mathcal{B}$ are arc sequences as in (2), (3). Then the number $W(X,D,F,\varphi,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z},\boldsymbol{w}),(\mathcal{A},\mathcal{B}))$ does not depend neither on the choice of generic point configuration $\boldsymbol{z}$, $\boldsymbol{w}$ nor on the choice of arc sequences $\mathcal{A}$, $\mathcal{B}$ subject to conditions indicated above.

• (2) If tuples (X,D,F,φ) and (X ^′ ,D ^′ ,F ^′ ,φ ^′ ) are deformation equivalent so that X and X ^′ are joined by a flat family of real smooth rational surfaces, then we have (omitting $(\boldsymbol{z},\boldsymbol{w})$ and $(\mathcal{A},\mathcal{B})$ in the notation)

  $$\displaystyle{W(X,D,F,\varphi,(\boldsymbol{k},\boldsymbol{l})) = W(X^{{\prime}},D^{{\prime}},F^{{\prime}},\varphi ^{{\prime}},(\boldsymbol{k},\boldsymbol{l}))\ .}$$

Remark 1

 

• (1) If k _i  = l _j  = 1 for all 1 ≤ i ≤ r, 1 ≤ j ≤ m, then we obtain original Welschinger invariants in their modified form [9], and hence the required statement follows from [12, Proposition 4 and Theorem 6]. This, in particular, yields that we have to consider the only case − DK _X − 1 ≥ 3.

• (2) In general, one cannot impose even tangency conditions at real points z ₁, …, z _r . Indeed, suppose that r ≥ 1 and k ₁ = 2s is even. Suppose that − DK _X − 1 ≥ 2s and p _a (D) = (D ² + DK _X )∕2 + 1 ≥ s. In the linear system | D | , the curves, which intersect the arc A ₁ at z ₁ with multiplicity ≥ s and have at least s nodes, form a subfamily of codimension 3s. On the other hand, the family of curves, having singularity A _2s at z ₁ and (s − 1) additional infinitely near to z ₁ points lying on the arc α ₁, has codimension 3s + 1, and it lies in the boundary of the former family. Over the reals, this wall-crossing results in the change of the Welschinger sign of the curve that undergoes the corresponding bifurcation. Indeed, take local coordinates x, y such that z ₁ = (0, 0) and α ₁ = { y = 0}, and consider the family of curves

  $$\displaystyle{y = t^{2s},\quad x = \varepsilon t + t^{2} + t^{3},\quad \varepsilon \in (\mathbb{R},0)\ .}$$

  For ɛ = 0, the curve has singularity A _2s at z ₁ and its next (s − 1) infinitely near to z ₁ points belong to α ₁. In turn, for ɛ ≠ 0, the node, corresponding to the values $t = \pm \sqrt{-\varepsilon }$, is solitary as ɛ > 0 and non-solitary as ɛ < 0, whereas the remaining (s − 1) nodes stay imaginary or solitary.

Conjecture 1

Theorem 1 is valid without restriction (5).

The proof of Theorem 1 in general follows the lines of [12], where we verify the constancy of the introduced enumerative numbers in one-dimensional families of constraints and families of surfaces. The former verification requires a classification of codimension one degenerations of the curves in count, while the latter verification is based on a suitable analogue of the Abramovich–Bertram–Vakil formula [1, 16]. Restriction (5) results from the lack of our understanding of nonreduced degenerations of the counted curves.

3 Degeneration and Deformation of Curves on Complex Rational Surfaces

3.1 Auxiliary Miscellanies

• (1) Tropical limit. For the reader’s convenience, we shortly remind what is the tropical limit in the sense of [14, Sect. 2.3], which will be used below. In the field of complex Puiseux series $\mathbb{C}\{\{t\}\}$, we consider the non-Archimedean valuation $\mathop{\mathrm{val}}\nolimits (\sum _{a}c_{a}t^{a}) = -\min \{a\:\ c_{a}\neq 0\}$. Given a polynomial (or a power series) $F(x,y) =\sum _{(i,j)\in \Delta }c_{ij}x^{i}y^{j}$ over $\mathbb{C}\{\{t\}\}$ with Newton polygon $\Delta$, its tropical limit consists of the following data:

  • A convex piecewise linear function $N_{F}: \Delta \rightarrow \mathbb{R}$, whose graph is the lower part of the polytope $\mathop{\mathrm{Conv}}\nolimits \{(i,j,-\mathop{\mathrm{val}}\nolimits (c_{ij}))\:\ (i,j) \in \Delta \}$, the subdivision S _F of $\Delta$ into linearity domains of N _F , and the tropical curve T _F , the closure of $\mathop{\mathrm{val}}\nolimits (F = 0)$;

  • Limit polynomials (power series) $F_{\mathop{\mathrm{ini}}\nolimits }^{\delta }(x,y) =\sum _{(i,j)\in \delta }c_{ij}^{0}x^{i}y^{\,j}$, defined for any face δ of the subdivision S _F , where $c_{ij} = t^{N_{F}(i,j)}(c_{ij}^{0} + O(t^{>0}))$ for all $(i,j) \in \Delta$.

• (2) Rational curves with Newton triangles.

Lemma 1

• (1) For any integer k ≥ 1, there are exactly k polynomials F(x,y) = ∑ _i,j c _ij x ⁱ y ^j with Newton triangle $T = \mathop{\mathrm{Conv}}\nolimits \{(0,0),(0,2),(k,1)\}$ , whose coefficients c ₀₀ ,c ₀₁ ,c ₀₂ ,c ₁₁ are given generic nonzero constants and which define plane rational curves. Furthermore, in the space of polynomials with Newton triangle T, the family of polynomials defining rational curves intersects transversally with the linear subspace given by assigning generic nonzero constant values to the coefficients c ₀₀ ,c ₀₁ ,c ₀₂ ,c ₁₁ . If the coefficients c ₀₀ ,c ₀₁ ,c ₀₂ ,c ₁₁ are real, then,

  • For an odd k, there is an odd number of real polynomials F defining rational curves, and each of these curves has an even number of real solitary nodes,

  • For an even k, there exists an even number (possibly zero) of polynomials F defining rational curves, and half of these curves have an odd number of real solitary nodes while the other half an even number of real solitary nodes.

• (2) For any integer k ≥ 1, there are exactly k polynomials F(x,y) = ∑ _i,j c _ij x ⁱ y ^j with Newton triangle $T = \mathop{\mathrm{Conv}}\nolimits \{(0,0),(0,2),(k,1)\}$ , whose coefficients c ₀₀ ,c ₀₂ ,c ₁₁ are given generic nonzero constants and the coefficient c _k−1,1 vanishes and which define plane rational curves. Furthermore, in the space of polynomials with Newton triangle T and vanishing coefficient c _k−1,1 , the family of polynomials defining rational curves intersects transversally with the linear subspace given by assigning generic nonzero constant values to the coefficients c ₀₀ ,c ₀₂ ,c ₁₁ . If the coefficients c ₀₀ ,c ₀₂ ,c ₁₁ are real, then,

  • For an odd k, there is a unique real polynomial F defining a rational curve, and this curve either has k − 1 real solitary nodes or has no real nodes at all,

  • For an even k, either there are no real polynomials defining rational curves or there are two real polynomials, one defining a rational curve with k − 1 real solitary nodes and the other defining a rational curve without real solitary nodes.

Proof

Both statements can easily be derived from [14, Lemma 3.9]. ■

• (3) Deformations of singular curve germs. Our key tool in the estimation of dimension of families of curves will be [8, Theorem 2] (see also [7, Lemma II.2.18]). For the reader’s convenience, we remind it here. Let C be a reduced curve on a smooth surface $\Sigma$, and z ∈ C. By $\mathop{\mathrm{mt}}\nolimits (C,z)$, we denote the intersection multiplicity at z of C with a generic smooth curve on $\Sigma$ passing through z, by δ(C, z) the δ-invariant, and by $\mathop{\mathrm{br}}\nolimits (C,z)$ the number of irreducible components of (C, z).

Lemma 2

Let C _t, $t \in (\mathbb{C},0)$ be a flat family of reduced curves on a smooth surface $\Sigma$ , and z _t ∈ C _t, $t \in (\mathbb{C},0)$ a section such that the family of germs (C _t ,z _t ), $t \in (\mathbb{C},0)$ , is equisingular. Denote by U a neighborhood of z ₀ in $\Sigma$ and by (C ⋅ C ^′ ) _U the total intersection number of curves C,C ^′ in U. The following lower bounds hold:

• (i) $(C_{0} \cdot C_{t})_{U} \geq \mathop{\mathrm{mt}}\nolimits (C_{0},z_{0}) -\mathop{\mathrm{br}}\nolimits (C_{0},z_{0}) + 2\delta (C_{0},z_{0})$ for $t \in (\mathbb{C},0)$ ;

• (ii) If L is a smooth curve passing through z ₀ = z _t, $t \in (\mathbb{C},0)$ , and $(C_{t} \cdot L)_{z_{0}} = \mathop{\mathrm{const}}\nolimits$ , then

  $$\displaystyle{(C_{0} \cdot C_{t})_{U} \geq (C_{0} \cdot L)_{z_{0}} + \mathop{\mathrm{mt}}\nolimits (C_{0},z_{0}) -\mathop{\mathrm{br}}\nolimits (C_{0},z_{0}) + 2\delta (C_{0},z_{0})}$$

  for t ∈ (C,0).

• (iii) If L is a smooth curve containing the family z _t, $t \in (\mathbb{C},0)$ , and $(C_{t} \cdot L)_{z_{t}} = \mathop{\mathrm{const}}\nolimits$ , then

  $$\displaystyle{(C_{0} \cdot C_{t})_{U} \geq (C_{0} \cdot L)_{z_{0}} -\mathop{\mathrm{br}}\nolimits (C_{0},z_{0}) + 2\delta (C_{0},z_{0})}$$

  for t ∈ (C,0).

Let $x,y \in (\mathbb{C},0)$ be local coordinates in a neighborhood of a point z in a smooth projective surface $\Sigma$. Let L = { y = 0}, and $(C,z) \subset (\Sigma,z)$ a reduced, irreducible curve germ such that (C ⋅ L) _z  = s ≥ 1. Denote by $\mathfrak{m}_{z} \subset \mathcal{O}_{\Sigma,z}$ the maximal ideal and introduce the ideal $I_{\Sigma,z}^{L,s} =\{ g \in \mathfrak{m}_{z}\:\ \mathop{\mathrm{ord}}\nolimits g\big\vert _{L,z} \geq s\}$. The semiuniversal deformation base of the germ (C, z) in the space of germs (C ^′, z) subject to condition (C ^′⋅ L) _z  ≥ s can be identified with the germ at zero of the space

$$\displaystyle{B_{C,z}(L,s):= I_{\Sigma,z}^{L,s}\big/\big\langle \,f, \frac{\partial f} {\partial x} \cdot \mathfrak{m}_{z}, \frac{\partial f} {\partial y} \cdot I_{\Sigma,z}^{L,s}\big\rangle \,}$$

where $f \in \mathcal{O}_{\Sigma,z}$ locally defined the germ (C, z) (cf. [7, Corollary II.1.17]).

Lemma 3

• (1) The stratum B _C,z ^eg (L,s) ⊂ B _C,z (L,s) parameterizing equigeneric deformations of (C,z) is smooth of codimension δ(C,z), and its tangent space is

  $$\displaystyle{ T_{0}B_{C,z}^{eg}(L,s) = I_{ C,z}^{L,s}\big/\big\langle \,f, \frac{\partial f} {\partial x} \cdot \mathfrak{m}_{z}, \frac{\partial f} {\partial y} \cdot I_{\Sigma,z}^{L,s}\big\rangle \, }$$

  (6)

  where

  $$\displaystyle{I_{C,z}^{L,s} =\{ g \in \mathcal{O}_{ \Sigma,z}\:\ \mathop{\mathrm{ord}}\nolimits g\big\vert _{C,z} \geq s + 2\delta (C,z)\}\ .}$$

• (2) If $\Sigma$ , (C,z), and L are real, and s is odd, then a generic member of B _C,z ^eg (L,s) is smooth at z and has only imaginary and real solitary nodes; the number of solitary nodes is $\delta (C,z)\mod 2$.

Proof

 

• (1) In [10, Lemma 2.4], we proved a similar statement for the case s = 2 and (C, z) of type A _2k , k ≥ 1, and we worked with equations. Here, we settle the general case, and we work with parameterizations. First, observe that a general member of B _C, z ^eg(L, s) has δ(C, z) nodes as its singularities and is smooth at z. Thus, $\mathop{\mathrm{codim}}\nolimits _{I_{\Sigma,z}^{L,s}}B_{C,z}^{eg}(L,s) =\delta (C,z)$, the tangent space to B _C, z ^eg(L, s) at its generic point C ^′, is formed by the elements $g \in \mathcal{O}_{\Sigma,z}$, which vanish at the nodes of C ^′ and whose restriction to (L, z) has order s. Clearly, the limits of these tangent spaces as C ^′ → (C, z) contain the space $I_{C,z}^{L,s}\big/\langle \,f, \frac{\partial f} {\partial x}\mathfrak{m}_{z}, \frac{\partial f} {\partial y}I_{\Sigma,z}^{L,s}\rangle$. On the other hand, $\dim I_{\Sigma,z}^{L,s}/I_{C,z}^{L,s} =\delta (C,z)$ (see, e.g., [13, Lemma 6]). Let us show the smoothness of B _C, z ^eg(L, s). Notice that the germ (C, z) admits a uniquely defined parameterization x = t ^s, y = φ(t), $t \in (\mathbb{C},0)$, where φ(0) = 0, and each element C ^′ ∈ B _C, z ^eg(L, s) admits a unique parameterization x = t ^s, y = φ(t) + ∑ _i = 1 ^m a _i t ⁱ, where m = dimB _C, z ^eg(L, s), $a_{1},\ldots,a_{m} \in (\mathbb{C},0)$. Choose m distinct generic values $t_{1},\ldots,t_{m} \in (\mathbb{C},0)\setminus \{0\}$ and take the germs of the lines $L_{i} =\{ (t_{i}^{s},y)\:\ y \in (\mathbb{C},\varphi (t_{i})\}$, i = 1, …, m. It follows that the stratum B _C, z ^eg(L, s) is diffeomorphic to ∏ _i = 1 ^m L _i , hence the smoothness and (6).

• (2) The second statement follows from the observation that the equation t ₁ ^s = t ₂ ^s has no real solutions t ₁ ≠ t ₂. ■

Let $C^{(1)},C^{(2)} \subset \Sigma$ be two distinct immersed rational curves, z ∈ C ⁽¹⁾ ∩ C ⁽²⁾ a smooth point of both C ⁽¹⁾ and C ⁽²⁾, and $W_{z} \subset \Sigma$ a sufficiently small neighborhood of z. Denote by V ⊂ | C ⁽¹⁾ + C ⁽²⁾ | the germ at C ⁽¹⁾ ∪ C ⁽²⁾ of the family of curves, whose total δ-invariant in $\Sigma \setminus U$ coincides with that of C ⁽¹⁾ ∪ C ⁽²⁾.

Lemma 4

• (1) The germ V is smooth of dimension

  $$\displaystyle{c = (C^{(1)} \cdot C^{(2)})_{ z} - C^{(1)}K_{ \Sigma } - C^{(2)}K_{ \Sigma } - 2\,}$$

  and its tangent space isomorphically projects onto the space $\mathcal{O}_{\Sigma,z}/I_{z}$ , where

  $$\displaystyle{I_{z} =\{ f \in \mathcal{O}_{\Sigma,z}\:\ \mathop{\mathrm{ord}}\nolimits f\big\vert _{(C^{(i)},z)} \geq (C^{(1)} \cdot C^{(2)})_{ z} - C^{(i)}K_{ \Sigma } - 1,\ i = 1,2\}\ .}$$

• (2) Let f ₁ ,…,f _c ,f _c+1 ,… be a basis of the tangent space to |C ⁽¹⁾ + C ⁽²⁾ | at C ⁽¹⁾ ∪ C ⁽²⁾ such that f ₁ ,…,f _c project to a basis of $\mathcal{O}_{\Sigma,z}/I_{z}$ , and f _j ∈ I _z , j > c, satisfy

  $$\displaystyle\begin{array}{rcl} & \mathop{\mathrm{ord}}\nolimits f_{c+1}\big\vert _{(C^{(1)},z)} = (C^{(1)} \cdot C^{(2)})_{z} - C^{(1)}K_{\Sigma } - 1\, & {}\\ & \mathop{\mathrm{ord}}\nolimits f_{j}\big\vert _{(C^{(1)},z)} \geq (C^{(1)} \cdot C^{(2)})_{z} - C^{(1)}K_{\Sigma },\quad j > c + 1\,& {}\\ \end{array}$$

  and let

  $$\displaystyle{\sum _{i=1}^{c}t_{ i}f_{i} +\sum _{j>c}a_{j}(\overline{t})f_{j},\quad \overline{t} = (t_{1},\ldots,t_{c}) \in (\mathbb{C}^{\;c},0)\,}$$

  be a parameterization of V, where C ⁽¹⁾ ∪ C ⁽²⁾ corresponds to the origin, and a _j , j > c are analytic functions vanishing at zero. Then

  $$\displaystyle{ \frac{\partial a_{c+1}} {\partial t_{i}} (0)\neq 0\quad \mbox{ for all}\ 1 \leq i \leq c\ \mbox{ with}\ \mathop{\mathrm{ord}}\nolimits f_{i}\big\vert _{(C^{(1)},z)} \leq (C^{(1)} \cdot C^{(2)})_{ z}-C^{(1)}K_{ \Sigma }-2\ . }$$

  (7)

Proof

Let $\nu ^{(i)}: \mathbb{P}^{1} \rightarrow C^{(i)}\hookrightarrow \Sigma$ be the normalization, p _i  = (ν ⁽ⁱ⁾)^∗(z), i = 1, 2. Note that by Riemann–Roch

$$\displaystyle{h^{k}(\mathbb{P}^{1},\mathcal{N}_{ \mathbb{P}^{1}}^{\nu ^{(i)} }(-(-C^{(i)}K_{ \Sigma } - 1)p_{i})) = 0,\quad k = 0,1,\ i = 1,2\,}$$

where $\mathcal{N}$ denotes the normal bundle of the corresponding map, and observe that the codimension of I _z in $\mathcal{O}_{\Sigma,z}$ equals c. The first statement of lemma follows.

For the second statement, we note that a generic irreducible element C ∈ V satisfies

$$\displaystyle\begin{array}{rcl} (C \cdot C^{(1)})_{ W_{z}}& \leq & C^{(1)}C^{(2)} + (C^{(1)})^{2} - (C^{(1)}C^{(2)} - (C^{(1)} \cdot C^{(2)})_{ z}) \\ & & -((C^{(1)})^{2} + C^{(1)}K_{ \Sigma } + 2) = (C^{(1)} \cdot C^{(2)})_{ z} - C^{(1)}K_{ \Sigma } - 2\ .{}\end{array}$$

(8)

Next, we choose i ∈ { 1, …, c} as in (7) and take C ∈ V given by the parameter values t _i  = t, t _j  = t ^s with some s > 1 for all j ∈ { 1, …, c}∖{i}. Then, if a _c+1 = O(t ^m) with m > 1, one encounters at least $(C^{(1)} \cdot C^{(2)})_{z} - C^{(1)}K_{\Sigma } - 1$ intersection points of C and C ⁽¹⁾ in W _z . Thus, (7) follows. ■

• (4) Geometry of arc spaces. Let $\Sigma$ be a smooth projective surface. Given an integer s ≥ 0, denote by $\mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma )$ the vector bundle of s-arcs over $\Sigma$ and by $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\Sigma )$ the bundle of smooth s-arcs over $\Sigma$ (particularly, $\mathop{\mathrm{Arc}}\nolimits _{0}(\Sigma ) = \mathop{\mathrm{Arc}}\nolimits _{0}^{\mathrm{sm}}(\Sigma ) = \Sigma$). For any smooth curve $C \subset \Sigma$, we have a natural map $\mathop{\mathrm{arc}}\nolimits _{s}: C \rightarrow \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\Sigma )$, sending a point z ∈ C to the s-arc at z defined by the germ (C, z). The following statement immediately follows from basic properties of ordinary analytic differential equations:

Lemma 5

Let s ≥ 1, U a neighborhood of a point $z \in \Sigma$ , and σ a smooth section of the natural projection $\mathop{\mathrm{pr}}\nolimits _{s}: \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(U) \rightarrow \mathop{\mathrm{Arc}}\nolimits _{s-1}^{\mathrm{sm}}(U)$ . Then there exists a smooth analytic curve $\Lambda$ passing through z, defined in a neighborhood V ⊂ U of z, and such that $\mathop{\mathrm{arc}}\nolimits _{s}(\Lambda ) \subset \sigma (\mathop{\mathrm{Arc}}\nolimits _{s-1}^{\mathrm{sm}}(V ))$.

Now, let $\Sigma$ be a smooth rational surface, $\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma$ an immersion, $C = \boldsymbol{n}(\mathbb{P}^{1}) \in \vert D\vert$, where $-DK_{\Sigma } = k > 0$. Pick a point $p \in \mathbb{P}^{1}$ such that $z = \boldsymbol{n}(\,p)$ is a smooth point of C. Denote by $U \subset \mathop{\mathrm{Arc}}\nolimits _{k-1}(\Sigma )$ the natural image of the germ of $\mathcal{M}_{0,1}(\Sigma,D)$ at $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,p]$. Choose coordinates x, y in a neighborhood of z so that z = (0, 0), C = { y + x ^k = 0}, and introduce two one-parameter subfamilies $\Lambda ^{{\prime}} = (z_{t}^{{\prime}},\alpha _{t}^{{\prime}})_{t\in (\mathbb{C},0)}$ and $\Lambda ^{{\prime\prime}} = (z_{t}^{{\prime\prime}},\alpha _{t}^{{\prime\prime}})_{t\in (\mathbb{C},0)}$ of $\mathop{\mathrm{Arc}}\nolimits _{k-1}(\Sigma )$:

$$\displaystyle{z_{t}^{{\prime}} = (t,0),\ \alpha _{ t}^{{\prime}} =\{ y = (x - t)^{l}\},\quad z_{ t}^{{\prime\prime}} = (0,0),\ \alpha _{ t}^{{\prime\prime}} =\{ y = tx^{k-1}\},\quad t \in (\mathbb{C},0)\,}$$

where l > k.

Lemma 6

The germ U is smooth of codimension one in $\mathop{\mathrm{Arc}}\nolimits _{k-1}(\Sigma )$ , and it transversally intersects both $\Lambda ^{{\prime}}$ and $\Lambda ^{{\prime\prime}}$.

Proof

It follows from Riemann–Roch and from Lemma 2(iii) that V admits the following parameterization:

$$\displaystyle\begin{array}{rcl} & ((x_{0},y_{0}),\{y=y_{0} + a_{1}(x - x_{0}) +\ldots +a_{k-2}(x - x_{0})^{k-2}+\varphi (x_{0},y_{0},\overline{a})(x - x_{0})^{k-1}\})\,& {}\\ & x_{0},y_{0},a_{1},\ldots,a_{k-2} \in (\mathbb{C},0),\quad \overline{a} = (a_{1},\ldots,a_{k-2}),\quad \varphi (0) = 0,\quad \frac{\partial \varphi } {\partial x_{0}} (0)\neq 0\ . & {}\\ \end{array}$$

Thus, V is a smooth hypersurface. The required intersection transversality results from a routine computation. ■

3.2 Families of Curves and Arcs on Arbitrary del Pezzo Surfaces

Let $\Sigma$ be a smooth del Pezzo surface of degree 1, and $D \in \mathop{\mathrm{Pic}}\nolimits (\Sigma )$ be an effective divisor such that $-DK_{\Sigma } - 1 > 0$. Fix positive integers $n \leq -DK_{\Sigma } - 1$ and $s \gg -DK_{\Sigma } - 1$. Denote by $\mathring\Sigma ^{n} \subset \Sigma ^{n}$ the complement of the diagonals and by $\mathop{\mathrm{Arc}}\nolimits _{s}(\mathring\Sigma ^{n})$ the total space of the restriction to $\mathring\Sigma ^{n}$ of the bundle $(\mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma ))^{n} \rightarrow \Sigma ^{n}$. In this section, we stratify the space $\mathop{\mathrm{Arc}}\nolimits _{s}(\mathring\Sigma ^{n})$ with respect to the intersection of arcs with rational curves in | D | , and we describe all strata of codimension zero and one.

Introduce the following spaces of curves: given $(\boldsymbol{z},\mathcal{A}) \in \mathop{\mathrm{Arc}}\nolimits _{s}(\mathring\Sigma ^{n})$, $\boldsymbol{z} = (z_{1},\ldots,z_{n})$, $\mathcal{A} = (\alpha _{1},\ldots,\alpha _{n})$, and a sequence $\boldsymbol{s} = (s_{1},\ldots,s_{n}) \in \mathbb{Z}_{>0}^{n}$ summing up to $\vert \boldsymbol{s}\vert \leq s$, put

$$\displaystyle\begin{array}{rcl} \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})& =& \{[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}(\Sigma,D)\:\ {}\\ & & \quad \boldsymbol{n}(\,p_{i}) = z_{i},\quad \boldsymbol{n}^{{\ast}}(\alpha _{ i}) \geq s_{i}p_{i},\quad i = 1,\ldots,n\}\, {}\\ \mathcal{M}_{0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})& =& \{[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\:\ {}\\ & & \quad \boldsymbol{n}\ \mbox{ is birational onto its image}\}\, {}\\ \mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})& =& \{[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\:\ {}\\ & & \quad \boldsymbol{n}\ \mbox{ is an immersion}\}\, {}\\ \mathcal{M}_{0,n}^{sing,1}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})& =& \{[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\:\ {}\\ & & \quad \boldsymbol{n}\ \mbox{ is singular in}\ \mathbb{P}^{1}\setminus \boldsymbol{p}\ \mbox{ and smooth at}\ \boldsymbol{p}\}\, {}\\ \mathcal{M}_{0,n}^{sing,2}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})& =& \{[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\:\ {}\\ & & \quad \boldsymbol{n}\ \mbox{ is singular at some point}\ p_{i} \in \boldsymbol{p}\}\ . {}\\ \end{array}$$

We shall consider the following strata in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$:

• (i) The subset $U^{im}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following conditions:

  For any sequence $\boldsymbol{s} = (s_{1},\ldots,s_{n}) \in \mathbb{Z}_{>0}^{n}$ summing up to $\vert \boldsymbol{s}\vert \leq s$ and for any element $(\boldsymbol{z},\mathcal{A}) \in U^{im}(D)$, where $\boldsymbol{z} = (z_{1},\ldots,z_{n}) \in\mathring\Sigma ^{n}$, $\mathcal{A} = (\alpha _{1},\ldots,\alpha _{n})$, $\alpha _{i} \in \mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma,z_{i})$, the family $\mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is empty if $\vert \boldsymbol{s}\vert \geq -DK_{\Sigma }$ and is finite if $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$. Furthermore, in the latter case, all elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ are represented by immersions $\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma$ such that $\boldsymbol{n}^{{\ast}}(\alpha _{i}) = s_{i}p_{i}$, 1 ≤ i ≤ n.

• (ii) The subset $U_{+}^{im}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following condition:

  For any element $(\boldsymbol{z},\mathcal{A}) \in U_{+}^{im}(D)$, there exists $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert \geq -DK_{\Sigma }$ such that $\mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\neq \emptyset$.

• (iii) The subset $U_{1}^{sing}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following condition:

  For any element $(\boldsymbol{z},\mathcal{A}) \in U_{+}^{im}(D)$, there exists $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ such that $\mathcal{M}_{0,n}^{sing,1}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\neq \emptyset$.

• (iv) The subset $U_{2}^{sing}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following condition:

  For any element $(\boldsymbol{z},\mathcal{A}) \in U_{2}^{sing}(D)$, there exists $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ such that $\mathcal{M}_{0,n}^{sing,2}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\neq \emptyset$.

• (v) The subset $U^{mt}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following condition:

  For any element $(\boldsymbol{z},\mathcal{A}) \in U^{mt}(D)$, there exists $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ and $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ such that $\boldsymbol{n}$ is a multiple cover of its image.

Proposition 1

• (1) The set U ^im (D) is Zariski open and dense in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$.

• (2) If U ⊂ U ₊ ^im (D) is a component of codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , then, for a generic element $(\boldsymbol{z},\mathcal{A}) \in U$ and any sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma }$ , the set $\mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is either empty or finite, and all of its elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ are presented by immersions and satisfy $\boldsymbol{n}^{{\ast}}(z_{i}) = s_{i}p_{i}$ , i = 1,…,n.

• (3) If U ⊂ U ₁ ^sing (D) is a component of codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , then, for a generic element $(\boldsymbol{z},\mathcal{A}) \in U$ and any sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ , the set $\mathcal{M}_{0,n}^{sing,1}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is either empty or finite, whose all elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ satisfy $\boldsymbol{n}^{{\ast}}(z_{i}) = s_{i}p_{i}$ , i = 1,…,n.

• (4) If U ⊂ U ₂ ^sing (D) is a component of codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , then, for a generic element $(\boldsymbol{z},\mathcal{A}) \in U$ and any sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ , the set $\mathcal{M}_{0,n}^{sing,2}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is either empty or finite, whose all elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ satisfy $\boldsymbol{n}^{{\ast}}(z_{i}) = s_{i}p_{i}$ , i = 1,…,n.

• (5) If U ⊂ U ^mt (D) is a component of codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , then, for a generic element $(\boldsymbol{z},\mathcal{A}) \in U$ and any sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ , the following holds: Each element $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ satisfying $C^{{\prime}} = \boldsymbol{n}(\mathbb{P}^{1}) \in \vert D^{{\prime}}\vert$ , where D = kD ^′ , k ≥ 2, admits a factorization

  $$\displaystyle{\boldsymbol{n}: \mathbb{P}^{1}\mathop{\longrightarrow }\limits^{\rho }\mathbb{P}^{1}\mathop{\longrightarrow }\limits^{\nu }C^{{\prime}}\hookrightarrow \Sigma }$$

  with ρ a k-multiple ramified covering, ν the normalization, $\boldsymbol{p}^{{\prime}} =\rho (\,\boldsymbol{p})$ , for which one has

  $$\displaystyle{[\nu: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}^{{\prime}}] \in \mathcal{M}_{ 0,n}(\Sigma,D^{{\prime}},\boldsymbol{s}^{{\prime}},\boldsymbol{z},\mathcal{A})\,}$$

  where $\vert \boldsymbol{s}^{{\prime}}\vert = -D^{{\prime}}K_{\Sigma }$ , and all branches $\nu \big\vert _{\mathbb{P}^{1},p_{i}^{{\prime}}}$ are smooth.

Proof

 

• (1) A general element of $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D)$ is represented by an immersion sending $\boldsymbol{p}$ to n distinct points of $\Sigma$ (cf. [12, Lemma 9(1ii)]). Let $(\boldsymbol{z},\mathcal{A}) \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$, and a sequence $\boldsymbol{s} = (s_{1},\ldots,s_{n}) \in \mathbb{Z}_{>0}^{n}$ satisfy $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$. The fiber of the map $\mathop{\mathrm{arc}}\nolimits _{\boldsymbol{s}}: \mathcal{M}_{0,n}(\Sigma,D) \rightarrow \prod _{i=1}^{n}\mathop{\mathrm{Arc}}\nolimits _{s_{i}-1}^{\mathrm{sm}}(\Sigma )$, sending an element $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ to the collection of arcs defined by the branches $\boldsymbol{n}\vert _{\mathbb{P}^{1},p_{i}}$, is either empty or finite. Indeed, otherwise, by Lemma 2(ii), we would get a contradiction:

  $$\displaystyle{D^{2} \geq (D^{2} + DK_{ \Sigma } + 2) + \vert \boldsymbol{s}\vert = D^{2} + 1 > D^{2}\ .}$$

  On the other hand,

  $$\displaystyle{\dim \mathcal{M}_{0,n}(\Sigma,D) =\dim \prod _{ i=1}^{n}\mathop{\mathrm{Arc}}\nolimits _{ s_{i}-1}^{\mathrm{sm}}(\Sigma ) = -DK_{ \Sigma } - 1 + n\,}$$

  and hence the map $\mathop{\mathrm{arc}}\nolimits _{\boldsymbol{s}}$ is dominant. It follows, that, for a generic element $(\boldsymbol{z},\mathcal{A}) \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ and any sequence $\boldsymbol{s} \in \mathbb{Z}_{\geq 0}^{n}$ such that $\vert \boldsymbol{s}\vert \leq s$, one has: $\mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is empty if $\vert \boldsymbol{s} \geq -DK_{\Sigma }$ and $\mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is finite nonempty if $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$. The same argument proves Claims (2) and (3) together with the fact that U ₊ ^im(D) and U ₁ ^sing(D) have positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$.

  Next, we will show that the sets U ₂ ^sing(D) and U ^mt(D) have positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$, thereby completing the proof of Claim (1), and will prove Claims (4) and (5).

• (2) To proceed further, we introduce additional notations. Let $f: (\mathbb{C},0) \rightarrow (C,z)\hookrightarrow (\Sigma,z)$ be the normalization of a reduced, irreducible curve germ (C, z), and let m ₀, m ₁, … be the multiplicities of (C, z) and of its subsequent strict transforms under blowups. We call this (infinite) sequence the multiplicity sequence of $f: (\mathbb{C},0) \rightarrow \Sigma$ and denote it $\overline{m}(\,f)$. Note that, if z ₀ = z and the infinitely near points z ₁, …, z _j , 0 ≤ j ≤ s, of (C, z) belong to an arc from $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\Sigma,z)$, then m ₀ = … = m _j−1 (see, for instance, [2, Chap. III]). Such sequences m ₀, …, m _j will be called smooth sequences. Given smooth sequences $\overline{m}_{i} = (m_{0i},\ldots,m_{j(i),i})$ such that $\vert \overline{m}_{i}\vert:=\sum _{l}m_{li} \leq s$, i = 1, …, n, denote by $\mathcal{M}_{0,n}(\Sigma,D,\{\overline{m}_{i}\}_{i=1}^{n})$ the family of elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D)$ such that $\boldsymbol{n}$ is birational onto its image and $\overline{m}(\boldsymbol{n}\vert _{\mathbb{P}^{1},p_{i}})$ contains $\overline{m}_{i}$ for every i = 1, …, n. Put

  $$\displaystyle\begin{array}{rcl} \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n},D,\{\overline{m}_{ i}\}_{i=1}^{n})& =& \{(\boldsymbol{z},\mathcal{A}) \in \mathop{\mathrm{Arc}}\nolimits _{ s}^{\mathrm{sm}}(\mathring\Sigma ^{n})\:\ \mbox{ there exists} {}\\ & & [\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{ 0,n}(\Sigma,D,\{\overline{m}_{i}\}_{i=1}^{n}) {}\\ & & \mbox{ such that}\ \boldsymbol{n}(\,\boldsymbol{p}) = \boldsymbol{z}\ \mbox{ and}\ \boldsymbol{n}^{{\ast}}(\alpha _{ i}) \geq \vert \overline{m}_{i}\vert p_{i},\ i=1,\ldots,n\} {}\\ \end{array}$$

• (3) We now prove Claim (4) together with the fact that U ₂ ^sing(D) has positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$.

  Let $(\boldsymbol{z},\mathcal{A})$ be a generic element of a top-dimensional component U ⊂ U ₂ ^sing(D), a sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ satisfy $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$, and $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ have singular branches among $\boldsymbol{n}\vert _{\mathbb{P}^{1},p_{i}}$, i = 1, …, n. Let $\overline{m}_{i} = (m_{0i},\ldots,m_{j(i),0})$ be a smooth multiplicity sequence of the branch $\boldsymbol{n}\vert _{\mathbb{P}^{1},p_{i}}$ such that $\vert \overline{m}_{i}\vert \geq s_{i}$. Denote by $\mathcal{V}$ the germ at $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ of a top-dimensional component of $\mathcal{M}_{0,n}(\Sigma,D,\{\overline{m}_{i}\}_{i=1}^{n})$. Without loss of generality, we can suppose that $\mathcal{M}_{0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A}) \subset \mathcal{M}_{0,n}(\Sigma,D,\{\overline{m}_{i}\}_{i=1}^{n})$ and $U \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n},D,\{\overline{m}_{i}\}_{i=1}^{n})$.

  Note that $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$ is isolated in $\mathcal{M}_{0,n}^{br}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$. Indeed, otherwise Lemma 2(ii) would yield a contradiction:

  $$\displaystyle{D^{2}\,\geq \,(D^{2}+DK_{ \Sigma }+2)+\sum _{i=1}^{n}(m_{ 0i}-1+\vert \overline{m}_{i}\vert )\,\geq \,(D^{2}+DK_{ \Sigma }+2)+\vert \boldsymbol{s}\vert \,=\,D^{2}+1 > D^{2}\ .}$$

  Next, we can suppose that m _0i  ≥ 2 as 1 ≤ i ≤ r for some 1 ≤ r ≤ n and that m _0i  = 1 for r < i ≤ n.

  Consider the case when $\vert \overline{m}_{i}\vert = s_{i}$ for all i = 1, …, n. We claim that then

  $$\displaystyle{ \dim \mathcal{V}\leq \sum _{i=1}^{n}j(i) + n + r - 1\ . }$$

  (9)

  If so, we would get

  $$\displaystyle{\dim U \leq \sum _{i=1}^{n}(s-j(i)) + n-r +\dim \mathcal{V}\leq n(s + 2) - 1 =\dim \mathop{\mathrm{Arc}}\nolimits _{ s}^{\mathrm{sm}}(\mathring\Sigma ^{n}) - 1\,}$$

  and the equality would yield $(\boldsymbol{n}^{{\prime}})^{{\ast}}(\boldsymbol{z},\mathcal{A}) =\sum _{ i=1}^{n}s_{i} = -DK_{\Sigma } - 1$ for each element $[\boldsymbol{n}^{{\prime}}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}^{{\prime}}] \in \mathcal{M}_{0,n}^{sing,2}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ with generic $(\boldsymbol{z},\mathcal{A}) \in U$, as required in Claim (3). To prove (9), we show that the assumption

  $$\displaystyle{ \dim \mathcal{V}\geq \sum _{i=1}^{n}j(i) + n + r }$$

  (10)

  leads to contradiction. Namely, we impose ∑ _i = 1 ⁿ j(i) + n + r − 1 conditions, defining a positive-dimensional subfamily of $\mathcal{V}$ containing $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}]$, and apply Lemma 2. It is enough to consider the following situations:

  • (a) 1 ≤ r < n;

  • (b) 1 < r = n, j(1) > 0;

  • (c) 1 = r = n, j(1) > 0, m ₀₁ > m _j(1), 1;

  • (d) r = n, j(1) = … = j(n) = 0;

  • (e) 1 = r = n, j(1) > 0, m ₀₁ = … = m _j(1), 1.

  In case (a), we fix the position of z _i and of the next j(i) infinitely near points for i = 1, …, r, and the position of additional ∑ _i = r+1 ⁿ j(i) + n − r − 1 smooth points on $C = \boldsymbol{n}(\mathbb{P}^{1})$, obtaining a positive-dimensional subfamily of U and a contradiction by Lemma 2:

  $$\displaystyle\begin{array}{rcl} D^{2}& \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{r}(m_{ 0i} - 1 + \vert \overline{m}_{i}\vert ) +\sum _{ i=r+1}^{n}j(i) + n - r - 1 {}\\ & =& D^{2} +\sum _{ i=1}^{r}(m_{ 0i} - 1) > D^{2}\ . {}\\ \end{array}$$

  In case (b), we fix the position of $\boldsymbol{z}$ and of additional infinitely near points: j(1) − 1 points for z ₁, and j(i) points for all 2 ≤ i ≤ n. These conditions define a positive-dimensional subfamily of U, which implies a contradiction by Lemma 2:

  $$\displaystyle\begin{array}{rcl} D^{2}& \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=2}^{r}(m_{ 0i} - 1 + \vert \overline{m}_{i}\vert ) + (m_{01} - 1) + \vert \overline{m}_{1}\vert - m_{j(1),1} {}\\ & \geq & D^{2} +\sum _{ i=2}^{n}(m_{ 0i} - 1) > D^{2}\ . {}\\ \end{array}$$

  In case (c), the same construction similarly leads to a contradiction:

  $$\displaystyle{D^{2} \geq (D^{2}+DK_{ \Sigma }+2)+(m_{01}-1)+\sum _{0\leq k<j(1)}m_{k1} \geq (D^{2}+DK_{ \Sigma }+2)+\vert \overline{m}_{1}\vert = D^{2}+1 > D^{2}\ .}$$

  In case (d), we fix the position of z _i , 1 < i ≤ n and of one more smooth point of $C = \boldsymbol{n}(\mathbb{P}^{1})$. Thus, Lemma 2, applied to the obtained positive-dimensional family, yields a contradiction:

  $$\displaystyle{D^{2} \geq (D^{2}+DK_{ \Sigma }+2)+\sum _{i=1}^{n}(m_{ 0i}-1)+\sum _{1<i\leq n}m_{0i}+1 = D^{2}+\sum _{ 1<i\leq n}(m_{0i}-1)+1 > D^{2}\ .}$$

  In case (e), relation (10) reads $\dim \mathcal{V}\geq j(1) + 2 =\dim \mathop{\mathrm{Arc}}\nolimits _{j(1)}(\Sigma )$. As noticed above, the map $\mathop{\mathrm{arc}}\nolimits _{j(1)}: \mathcal{V}\rightarrow \mathop{\mathrm{Arc}}\nolimits _{j(1)}(\Sigma )$ is finite. Hence, $\dim \mathcal{V} = j(1) + 2$, and (due to the general choice of $\xi = [\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,p] \in \mathcal{V}$) the germ $(\mathcal{V},\xi )$ diffeomorphically maps onto the germ of $\mathop{\mathrm{Arc}}\nolimits _{j(1)}(\Sigma )$ at π(ξ). Observe that the fragment (m ₀₁, …, m _j(1), 1, m _j(1)+1, 1) of the multiplicity sequence of $\boldsymbol{n}\vert _{\mathbb{P}^{1},p}$ is a smooth sequence. That means, the map of $(\mathcal{V},\xi )$ to $\mathop{\mathrm{Arc}}\nolimits _{j(1)+1}(\Sigma )$ defines a section $\sigma: (\mathop{\mathrm{Arc}}\nolimits _{j(1)}(\Sigma ),\pi (\xi )) \rightarrow \mathop{\mathrm{Arc}}\nolimits _{j(1)+1}(\Sigma )$, satisfying the hypotheses of Lemma 5. So, we take the curve $\Lambda$, defined in Lemma 5, and apply Lemma 2(iii):

  $$\displaystyle\begin{array}{rcl} D^{2}& \geq & (D^{2} + DK_{ \Sigma } + 2) + (m_{01} +\ldots +m_{j(1),1} + m_{j(1)+1,1}) - 1 {}\\ & \geq & (D^{2} + DK_{ \Sigma } + 2) + \vert \overline{m}_{1}\vert = D^{2} + 1 > D^{2}\, {}\\ \end{array}$$

  which completes the proof of (9).

  Consider the case when $\sum _{i=1}^{n}\vert \overline{m}_{i}\vert > -DK_{\Sigma } - 1$ and show that then $\dim U \leq \dim \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n}) - 2$. The preceding consideration reduces the problem to the case

  $$\displaystyle{r = n\quad \mbox{ and}\quad \sum _{i=1}^{n}\vert \overline{m}_{ i}\vert - m_{j(n),n} < -DK_{\Sigma } - 1 <\sum _{ i=1}^{n}\vert \overline{m}_{ i}\vert \,}$$

  in which we need to prove that

  $$\displaystyle{ \dim \mathcal{V}\leq \sum _{i=1}^{n}j(i) + 2n - 2\ . }$$

  (11)

  We assume that

  $$\displaystyle{ \dim \mathcal{V}\geq \sum _{i=1}^{n}j(i) + 2n - 1 }$$

  (12)

  and derive a contradiction in the same manner as for (10). We shall separately treat several possibilities:

  • (a) j(n) = 0;

  • (b) j(n) > 0.

  In case (a), we fix the position of z _i and of the additional j(i) infinitely near points for all i = 1, …, n − 1, thereby cutting off $\mathcal{V}$ a positive-dimensional subfamily, and hence by Lemma 2 we get a contradiction:

  $$\displaystyle\begin{array}{rcl} D^{2}& \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{n-1}(m_{ 0i} - 1 + \vert \overline{m}_{i}\vert ) + m_{0n} - 1 {}\\ & \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{n}\vert \overline{m}_{ i}\vert - 1 \geq D^{2} + 1 > D^{2}\ . {}\\ \end{array}$$

  In case (b), we again fix the position of z _i and of the additional j(i) infinitely near points for all i = 1, …, n − 1, thereby cutting off $\mathcal{V}$ a subfamily $\mathcal{V}^{{\prime}}$ of dimension ≥ j(n) + 1. Consider the map $\mathop{\mathrm{arc}}\nolimits _{j(n)-1}: \mathcal{V}^{{\prime}}\rightarrow \mathop{\mathrm{Arc}}\nolimits _{j(n)-1}(\Sigma )$ and note that $\dim \mathop{\mathrm{Arc}}\nolimits _{j(n)-1}(\Sigma ) = j(n) + 1 \leq \dim \mathcal{V}^{{\prime}}$. If $\dim \pi (\mathcal{V}^{{\prime}}) \leq j(n)$, fixing the position of z _n and of j(n) − 1 additional infinitely near points, we obtain a positive-dimensional subfamily of $\mathcal{V}^{{\prime}}$ and hence a contradiction by Lemma 2:

  $$\displaystyle\begin{array}{rcl} D^{2}& \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{n-1}(m_{ 0i} - 1 + \vert \overline{m}_{i}\vert ) + (m_{0n} - 1) + \vert \overline{m}_{n}\vert - m_{j(n),n} {}\\ & \geq & (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{n}\vert \overline{m}_{ i}\vert - 1 \geq D^{2} + 1 > D^{2}\ . {}\\ \end{array}$$

  If $\dim \pi (\mathcal{V}^{{\prime}}) = j(n) + 1$, the preceding argument yields that $\dim \mathcal{V}^{{\prime}} = j(n) + 1$, and we can suppose that the germ of $\mathcal{V}^{{\prime}}$ at the initially chosen element $\xi = [\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{V}$ is diffeomorphically mapped onto the germ of $\mathop{\mathrm{Arc}}\nolimits _{j(n)-1}(\Sigma )$ at $\mathop{\mathrm{arc}}\nolimits _{j(n)-1}(\xi )$. Thus, we obtain a section $\sigma: (\mathop{\mathrm{Arc}}\nolimits _{j(n)-1}(\Sigma ),\pi (\xi )) \rightarrow \mathop{\mathrm{Arc}}\nolimits _{j(n)}(\Sigma )$ defined by the map $(\mathcal{V}^{{\prime}},\xi ) \rightarrow \mathop{\mathrm{Arc}}\nolimits _{j(n)}(\Sigma )$. It satisfies the hypotheses of Lemma 5, which allows one to construct a smooth curve $\Lambda$ as in Lemma 5 and apply Lemma 2(iii):

  $$\displaystyle{D^{2} \geq (D^{2} + DK_{ \Sigma } + 2) +\sum _{ i=1}^{n-1}(m_{ 0i} - 1 + \vert \overline{m}_{i}\vert ) + \vert \overline{m}_{n}\vert - 1 \geq D^{2} + 1 > D^{2}\,}$$

  a contradiction.

  The proof of Claim (4) is completed.

• (4) It remains to consider the set U ^mt(D). Let $(\boldsymbol{z},\mathcal{A}) \in U^{mt}(D)$, $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ satisfy $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$, and $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ be such that $\boldsymbol{n}$ is a k-multiple (ramified) covering of its image $C = \boldsymbol{n}(\mathbb{P}^{1})$, k ≥ 2. We have C ∈ | D ^′ | , where kD ^′ = D, and ν ^∗(α _i ) ≥ s _i ^′ p _i ^′, ρ ^∗( p _i ^′) ≥ l _i p _i , where l _i s _i ^′ ≥ s _i for all i = 1, …, n. Since l _i  ≤ k for all i = 1, …, n, it follows that

  $$\displaystyle{\sum _{i=1}^{n}s_{ i}^{{\prime}}\geq \frac{\vert \boldsymbol{s}\vert } {k} = \frac{-DK_{\Sigma } - 1} {k} = -D^{{\prime}}K_{ \Sigma } -\frac{1} {k} > -D^{{\prime}}K_{ \Sigma } - 1\ .}$$

  This yields that U ^mt(D) has positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$, and, furthermore, if not all branches $\nu \big\vert _{\mathbb{P}^{1},p_{i}^{{\prime}}}$, i = 1, …, n, are smooth, the codimension of U ^mt(D) in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is at least 2. The proof of Claim (4) and thereby of Claim (1) is completed. ■

3.3 Families of Curves and Arcs on Generic del Pezzo Surfaces

Let $\Sigma$ be a smooth del Pezzo surface of degree 1 satisfying the following condition:

(GDP) There are only finitely many effective divisor classes $D \in \mathop{\mathrm{Pic}}\nolimits (\Sigma )$ satisfying $-DK_{\Sigma } = 1$, and for any such divisor D, the linear system | D | contains only finitely many rational curves, all these rational curves are immersed, and any two curves C ₁ ≠ C ₂ among them intersect in C ₁ C ₂ distinct points.

By Itenberg et al. [12, Lemmas 9 and 10], these del Pezzo surfaces form an open dense subset in the space of del Pezzo surfaces of degree 1.

Let us fix an effective divisor $D \in \mathop{\mathrm{Pic}}\nolimits (\Sigma )$ such that $-DK_{\Sigma } - 1 \geq 3$.

Proposition 2

In the notation of Sect.  3.2, let $(\boldsymbol{z}_{0},\mathcal{A}_{0})$ be a generic element of a component U of U ^mt (D) having codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , a sequence $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ satisfy $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ , and $[\boldsymbol{n}_{0}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}_{0}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z}_{0},\mathcal{A}_{0})$ be such that $\boldsymbol{n}_{0}$ covers its image with multiplicity k ≥ 2 so that $\boldsymbol{n}_{0}(\mathbb{P}^{1}) \in \vert D^{{\prime}}\vert$ , where D = kD ^′ , and $\boldsymbol{n}_{0} =\nu \circ \rho$ with $\nu: \mathbb{P}^{1} \rightarrow C^{{\prime}}$ the normalization, $\rho: \mathbb{P}^{1} \rightarrow \mathbb{P}^{1}$ ak-fold ramified covering. Assume that $(\boldsymbol{z}_{t},\mathcal{A}_{t}) \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$, $t \in (\mathbb{C},0)$ , is the germ at $(\boldsymbol{z}_{0},\mathcal{A}_{0})$ of a generic one-dimensional family such that $(\boldsymbol{z}_{t},\mathcal{A}_{t})\not\in U^{mt}(D)$ as t ≠ 0, and assume that there exists a family $[\boldsymbol{n}_{t}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}_{t}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z}_{t},\mathcal{A}_{t})$ extending the element $[\boldsymbol{n}_{0}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}_{0}]$ . Then n = 3, k = 2, $-D^{{\prime}}K_{\Sigma } = 3$, $\boldsymbol{s} = (2,2,1)$ , and $[\nu: \mathbb{P}^{1} \rightarrow C^{{\prime}}\hookrightarrow \Sigma,\boldsymbol{p}_{0}^{{\prime}}] \in \mathcal{M}_{0,3}(\Sigma,D^{{\prime}},\boldsymbol{s}^{{\prime}},\boldsymbol{z}_{0},\mathcal{A}_{0})$ , where $\boldsymbol{p}^{{\prime}} =\rho (\,\boldsymbol{p}_{0})$ and $\boldsymbol{s}^{{\prime}} = (1,1,1)$ . Furthermore, the family $[\boldsymbol{n}_{t}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}_{t}]$, $t \in (\mathbb{C},0)$ , is smooth and isomorphically projects onto the family $(\boldsymbol{z}_{t},\mathcal{A}_{t})$, $t \in (\mathbb{C},0)$.

Proof

Note, first, that by the assumption (GDP) and Proposition 1(2, 5), the map $\boldsymbol{n}_{0}: \mathbb{P}^{1} \rightarrow \Sigma$ is an immersion, and (in the notation of Proposition 1(5))

$$\displaystyle{ \nu ^{{\ast}}(\alpha _{ i}) = s_{i}^{{\prime}}p_{ i}^{{\prime}},\ i = 1,\ldots,n,\quad \sum _{ i=1}^{n}s_{ i}^{{\prime}} = -D^{{\prime}}K_{ \Sigma }\ . }$$

(13)

Furthermore, if $C^{{\prime}} = \boldsymbol{n}_{0}(\mathbb{P}^{1}) \in \vert D^{{\prime}}\vert$, where D = kD ^′, then (D ^′)² > 0, since the assumption $-DK_{\Sigma } \geq 4$ yields D ² ≥ 2 by the adjunction formula. Hence, in the deformation $\boldsymbol{n}_{t}: \mathbb{P}^{1} \rightarrow \Sigma$, $t \in (\mathbb{C}.0)$, in a neighborhood of each singular point z of C ^′, there appear singular points of $C_{t} = \boldsymbol{n}_{t}(\mathbb{P}^{1})$, t ≠ 0, with total δ-invariant at least k ² δ(C ^′, z), which implies

$$\displaystyle{ k^{2}\left (\frac{(D^{{\prime}})^{2} + D^{{\prime}}K_{ \Sigma }} {2} + 1\right ) \leq \frac{k^{2}(D^{{\prime}})^{2} + kD^{{\prime}}K_{\Sigma }} {2} + 1\, }$$

(14)

and hence

$$\displaystyle{ -D^{{\prime}}K_{ \Sigma } \geq \frac{2k + 2} {k} \quad \mbox{ or, equivalently,}\quad - D^{{\prime}}K_{ \Sigma } \geq 3\ . }$$

(15)

Let ρ ^∗( p _i ^′) ≥ l _i p _i , i = 1, …, n. We can suppose that k ≥ l ₁ ≥ … ≥ l _n . Then

$$\displaystyle{ \sum _{i=1}l_{i}s_{i}^{{\prime}}\geq -kD^{{\prime}}K_{ \Sigma } - 1\quad \Longrightarrow\quad \sum _{i=1}^{n}(l_{ i} - 1)s_{i}^{{\prime}}\geq -(k - 1)D^{{\prime}}K_{ \Sigma } - 1\ . }$$

(16)

If l ₁ ≤ k − 1, then (13) and (16) yield

$$\displaystyle{-(k - 2)D^{{\prime}}\geq -(k - 1)D^{{\prime}}K_{ \Sigma } - 1\quad \Longrightarrow\quad - D^{{\prime}}K_{ \Sigma } \leq 1\,}$$

forbidden by (15), and hence

$$\displaystyle{ l_{1} = k\ . }$$

(17)

By Riemann–Hurwitz, ∑ _i > 1(l _i − 1) ≤ k − 1, and then it follows from (16) that

$$\displaystyle{ (k - 1)(-D^{{\prime}}K_{ \Sigma } - (n - 1)) + (k - 1) \geq -(k - 1)D^{{\prime}}K_{ \Sigma } - 1\, }$$

(18)

or, equivalently

$$\displaystyle{ (n - 2)(k - 1) \leq 1\, }$$

(19)

which in view of Riemann–Hurwitz and (17)–(19) leaves the following options:

• either n = 1,

• or n = 2, $\boldsymbol{s} = (k(-D^{{\prime}}K_{\Sigma } - 1),(k - 1))$,

• or n = 2, $\boldsymbol{s} = (ks_{1}^{{\prime}},ks_{2}^{{\prime}})$, $s_{1}^{{\prime}} + s_{2}^{{\prime}} = -D^{{\prime}}K_{\Sigma }$,

• or n = 3, $\boldsymbol{s} = (2(-D^{{\prime}}K_{\Sigma } - 2),2,1)$.

Let us show that s ₁ ^′ > 1 is not possible. Indeed, otherwise, in suitable local coordinates x, y in a neighborhood of z ₁ in $\Sigma$, we would have z ₁ = (0, 0), C ^′ = { y = 0}, $\boldsymbol{n}_{0}: (\mathbb{P}^{1},p_{1}) \rightarrow (\Sigma,z_{1})$ acts by $\tau \in (\mathbb{C},0) \simeq (\mathbb{P}^{1},p_{1})\mapsto (\tau ^{k},\tau )$, and we also may assume that the family of arcs α _1, t is centered at z ₁ and given by $y =\sum _{i\geq s_{1}^{{\prime}}}a_{i}(t)x^{i}$ with a _i (0) ≠ 0, i ≥ s ₁ ^′. Then $\boldsymbol{n}_{t}: (\mathbb{P}^{1},p_{1,t}) \rightarrow (\Sigma,z_{1})$ can be expressed via $\tau \in (\mathbb{C},0) \simeq (\mathbb{P}^{1},p_{1,t})\mapsto (\tau ^{k} + tf(t,\tau ),tg(t,\tau ))$, which contradicts the requirement $\boldsymbol{n}_{t}^{{\ast}}(\alpha _{1,t}) \geq (ks_{1}^{{\prime}}- 1)p_{1,t}$ equivalently written as

$$\displaystyle{t \cdot g(t,\tau ) \equiv \sum _{i\geq s_{1}^{{\prime}}}a_{i}(t)(\tau ^{k} + tf(t,\tau ))^{i}\mod (\tau ^{k} + tf(t,\tau ))^{ks_{1}^{{\prime}}-1 }\,}$$

since the term $a_{s_{1}^{{\prime}}}(0)\tau ^{ks_{1}^{{\prime}} }$ does not cancel out here in view of k ≥ 2.

Thus, in view of (15), we are left with n = 3, k = 2, $\boldsymbol{s}^{{\prime}} = (1,1,1)$, and $\boldsymbol{s} = (2,2,1)$. Without loss of generality, for $(z_{t},\mathcal{A}_{t})$, $t \in (\mathbb{C},0)$, we can choose the family consisting of two fixed points z _1, 0, z _2, 0 and fixed arcs α _1, 0, α _2, 0 (transversal to C ^′) and of a point z _3, τ moving along the germ $\Lambda$ of a smooth curve transversally intersecting C ^′ at z _3, 0 (τ being a regular parameter on $\Lambda$). We then claim that the evaluation

$$\displaystyle{[\boldsymbol{n}_{t}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}_{ t}]\mapsto \boldsymbol{n}_{t}(\,p_{3.t}) = z_{3,\tau (t)}}$$

is one-to-one, completing the proof of Proposition 2. So, we establish the formulated claim arguing on the contrary: If some point z _3, τ , τ ≠ 0, has two preimages, then the curves $C_{1} = \boldsymbol{n}_{t_{1}}(\mathbb{P}^{1})$, $C_{2} = \boldsymbol{n}_{t_{2}}(\mathbb{P}^{1})$ intersect with total multiplicity ≥ 5 at z _1, 0, z _2. 0, z _3, τ and intersect with multiplicity ≥ δ(C ^′, z) in a neighborhood of each point $z \in \mathop{\mathrm{Sing}}\nolimits (C^{{\prime}})$, which altogether leads to a contradiction:

$$\displaystyle{\hspace{38.0pt} C_{1}C_{2} \geq 5 + 4((D^{{\prime}})^{2} + D^{{\prime}}K_{ \Sigma } + 2) = 5 + D^{2} - 4 = D^{2} + 1\ .\hspace{45.0pt} \blacksquare }$$

The compactification $\overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ of the space $\mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is obtained by adding the elements $[\boldsymbol{n}:\widehat{ C} \rightarrow \Sigma,\boldsymbol{p}]$, where

• $\widehat{C}$ is a tree formed by k ≥ 2 components $\widehat{C}^{(1)},\ldots,\widehat{C}^{(k)}$ isomorphic to $\mathbb{P}^{1}$;

• the points of $\boldsymbol{p}$ are distinct but allowed to be at the nodes of $\widetilde{C}$;

• $[\boldsymbol{n}:\widehat{ C}^{(\,j)} \rightarrow \Sigma,\widehat{C}^{(\,j)} \cap \boldsymbol{p}] \in \mathcal{M}_{0,\vert C^{(\,j)}\cap \boldsymbol{p}\vert }(\Sigma,D^{(\,j)},\boldsymbol{s}^{(\,j)},\boldsymbol{z},\mathcal{A})$, where we suppose that the integer vector $\boldsymbol{s}^{(\,j)} \in \mathbb{Z}_{\geq 0}^{n}$ has coordinates s _i ^( j) > 0 or s _i ^( j) = 0 according as p _i belongs to $\widehat{C}^{(\,j)}$ or not, j = 1, …, k;

• ∑ _j = 1 ^k D ^( j) = D, where D ^( j) ≠ 0, j = 1, …, k, and $\sum _{j=1}^{k}\boldsymbol{s}^{(\,j)} = \boldsymbol{s}$.

One can view this compactification as the image of the closure of $\mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ in the moduli space of stable maps $\overline{\mathcal{M}}_{0,n}(\Sigma,D)$ under the morphism, which contracts the components of the source curve that are mapped to points. Notice that in our compactification, the source curves $\widehat{C}$ may be not nodal, and the marked points may appear at intersection points of components of a (reducible) source curve.

Introduce the set $U^{red}(D) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ defined by the following condition: For any element $(\boldsymbol{z},\mathcal{A}) \in U^{red}(D)$, there exists $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ with $\vert \boldsymbol{s}\vert \geq -DK_{\Sigma } - 1$ such that $\overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\setminus \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\neq \emptyset$.

Proposition 3

The set U ^red (D) has positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ . Let $(\boldsymbol{z},\mathcal{A})$ be a generic element of a component of U ^red (D) having codimension one in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ , and let $(\boldsymbol{z}_{t},\mathcal{A}_{t}) \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$, $t \in (\mathbb{C},0)$ , be a generic family which transversally intersects U ^red (D) at $(\boldsymbol{z}_{0},\mathcal{A}_{0}) = (\boldsymbol{z},\mathcal{A})$.

• (1) Given any vector $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ such that $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$ , the set $\overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\setminus \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is either empty or finite. Moreover, let

  $$\displaystyle{[\boldsymbol{n}:\widehat{ C} \rightarrow \Sigma,\boldsymbol{p}] \in \overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\setminus \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})}$$

  extend to a family

  $$\displaystyle{ [\boldsymbol{n}_{\tau }:\widehat{ C}_{\tau } \rightarrow \Sigma,\boldsymbol{p}_{\tau }] \in \overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z}_{\varphi (\tau )},\mathcal{A}_{\varphi (\tau )}),\quad \tau \in (\mathbb{C},0)\, }$$

  (20)

  for some morphism $\varphi: (\mathbb{C},0) \rightarrow (\mathbb{C},0)$ . Then $[\boldsymbol{n}:\widehat{ C} \rightarrow \Sigma,\boldsymbol{p}]$ is as follows:

  • (1i) either $\widehat{C} = C^{(1)} \cup C^{(2)}$ , where $C^{(1)} \simeq C^{(2)} \simeq \mathbb{P}^{1}$, $\boldsymbol{n}(C^{(1)})\neq \boldsymbol{n}(C^{(2)})$ , and

    • the map $\boldsymbol{n}:\widehat{ C}^{(\,j)} \rightarrow \Sigma$ is an immersion and $\boldsymbol{z} \cap \mathop{\mathrm{Sing}}\nolimits (C^{(\,j)}) =\emptyset$ for j = 1,2,

    • $\vert \boldsymbol{p} \cap \widehat{ C}^{(1)} \cap \widehat{ C}^{(2)}\vert \leq 1$,

    • $[\boldsymbol{n}:\widehat{ C}^{(\,j)} \rightarrow \Sigma,\boldsymbol{p} \cap \widehat{ C}^{(\,j)}] \in \mathcal{M}_{0,\vert \boldsymbol{p}\cap \widehat{C}^{(\,j)}\vert }(\Sigma,D^{(1)},\boldsymbol{s}^{(\,j)},\boldsymbol{z},\mathcal{A})$ , j = 1,2, where D ⁽¹⁾ + D ⁽²⁾ = D, $\boldsymbol{s}^{(1)} + \boldsymbol{s}^{(2)} = \boldsymbol{s}$, $\vert \boldsymbol{s}^{(1)}\vert = -D^{(1)}K_{\Sigma }$, $\vert \boldsymbol{s}^{(2)}\vert = -D^{(2)}K_{\Sigma } - 1$ , and, moreover, $(\boldsymbol{n}\vert _{C^{(\,j)}})^{{\ast}}(\mathcal{A}) =\sum _{ i=1}^{n}s_{i}^{(\,j)}p_{i}$ for j = 1,2;

  • (1ii) or n = 1, $\boldsymbol{z} = z_{1} \in \Sigma$, $\mathcal{A} =\alpha _{1} \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\Sigma,z)$, $\boldsymbol{p} = p_{1} \in \widehat{ C}$ , D = kD ^′ , where k ≥ 2 and $-D^{{\prime}}K_{\Sigma } \geq 3$ , and the following holds

    • $\widehat{C}$ consists of few components having p ₁ as a common point, and each of them is mapped onto the same immersed rational curve C ∈|D ^′ |;

    • z ₁ is a smooth point of C, and $(C \cdot \alpha _{1}) = -D^{{\prime}}K_{\Sigma }$.

  • (1iii) or D = kD ^′ + D ^″ , where k ≥ 2, $-D^{{\prime}}K_{\Sigma } \geq 2$ , D ^″ ≠ 0, $\widetilde{C} =\widetilde{ C}^{{\prime}}\cup \ldots \cup \widetilde{C}^{{\prime\prime}}$ , where

    • $\widehat{C}^{{\prime}}\simeq \mathbb{P}^{1}$, $\boldsymbol{n}:\widehat{ C}^{{\prime\prime}}\rightarrow CX^{{\prime\prime}}\hookrightarrow \Sigma$ is an immersion, where C ^″ ∈|D ^″ |,

    • the components of $\widehat{C}^{{\prime}}$ have a common point p ₁ and are disjoint from p ₂ ,…,p _n , and each of them is mapped onto the same immersed rational curve C ^′ ∈|D ^′ |,

    • z ₁ is a smooth point of C ^′ , and $(C^{{\prime}}\cdot \alpha _{1}) = -D^{{\prime}}K_{\Sigma }$.

• (2) In case (1i),

  • if $\boldsymbol{p} \cap \widehat{ C}^{(1)} \cap \widehat{ C}^{(2)} =\emptyset$ , there is a unique family of type (20), and it is smooth, parameterized by τ = t;

  • if $\widehat{C}^{(1)} \cap \widehat{ C}^{(2)} =\{ p_{1}\}$ , then there are precisely κ = min {s ₁ ⁽¹⁾ ,s ₁ ⁽²⁾ } families of type (20), and for each of them t = τ ^κ∕d , where d = gcd(s ₁ ⁽¹⁾ ,s ₁ ⁽²⁾ ).

Proof

If $[\boldsymbol{n}:\widehat{ C} \rightarrow \Sigma,\boldsymbol{p}] \in \overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ with a generic $(\boldsymbol{z},\mathcal{A}) \in \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ and $\widehat{C}$ consisting of m ≥ 1 components, then by Propositions 1 and 2 one obtains m = 1 and $\boldsymbol{n}$ immersion. Hence, U ^red(D) has positive codimension in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$. Suppose that $(\boldsymbol{z},\mathcal{A})$ satisfies the hypotheses of proposition. Then the finiteness of $\overline{\mathcal{M}}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})\setminus \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ and the asserted structure of its elements follows from Propositions 1 and 2, provided we show that

• (a) There are no two components $\widehat{C}^{{\prime}},\widehat{C}^{{\prime\prime}}$ of $\widehat{C}$ such that $\boldsymbol{n}(\widehat{C}^{{\prime}})\neq \boldsymbol{n}(\widehat{C}^{{\prime\prime}})$, $\boldsymbol{n}_{{\ast}}(\widehat{C}^{{\prime}}) \in \vert D^{{\prime}}\vert$, $\boldsymbol{n}_{{\ast}}(\widehat{C}^{{\prime\prime}}) \in \vert D^{{\prime\prime}}\vert$, and $\deg (\boldsymbol{n}\vert _{\widehat{C}^{{\prime}}})^{{\ast}}\mathcal{A}\geq -D^{{\prime}}K_{\Sigma }$, $\deg (\boldsymbol{n}\vert _{\widehat{C}^{{\prime\prime}}})^{{\ast}}\mathcal{A}\geq -D^{{\prime\prime}}K_{\Sigma }$,

• (b) In cases (1ii) and (1iii), we have inequalities $-D^{{\prime}}K_{\Sigma } \geq 3$ and $-D^{{\prime}}K_{\Sigma } \geq 2$, respectively.

The proof of Claim (a) can easily be reduced to the case when $\boldsymbol{n}\vert _{\widehat{C}^{{\prime}}}$ and $\boldsymbol{n}\vert _{\widehat{C}^{{\prime\prime}}}$ are immersions, and $\deg (\boldsymbol{n}\vert _{\widehat{C}^{{\prime}}})^{{\ast}}\alpha _{1} = -D^{{\prime}}K_{\Sigma } =\deg (\boldsymbol{n}\vert _{\widehat{C}^{{\prime\prime}}})^{{\ast}}\alpha _{1} = -D^{{\prime\prime}}K_{\Sigma }$. However, in such a case, the dimension and generality assumptions yield that there exists the germ at C ^{′ ′} of the family of rational curves C _t ^{′ ′} ∈ | D ^{′ ′} | , $t \in (\mathbb{C},0)$, such that $(C_{t}^{{\prime\prime}}\cdot C^{{\prime}})_{y_{t}} \geq -D^{{\prime\prime}}K_{\Sigma }$ for some family of points y _t  ∈ (C ^′, z ₁), $t \in (\mathbb{C},0)$, which together with Lemma 2(iii) implies a contradiction:

$$\displaystyle{(D^{{\prime\prime}})^{2} \geq ((D^{{\prime\prime}})^{2} + D^{{\prime\prime}}K_{ \Sigma } + 2) + (-D^{{\prime\prime}}K_{ \Sigma } - 1) = (D^{{\prime\prime}})^{2} + 1\ .}$$

Claim (b) in the case (1ii) follows from inequalities (14) and (15). In case (1iii), we perform similar estimations. If the curves C ^′ and C ^{′ ′} intersect at z ₁, then $(C^{{\prime}}\cdot C^{{\prime\prime}})_{z_{1}} =\min \{ -D^{{\prime}}K_{\Sigma },-D^{{\prime\prime}}K_{\Sigma } - 1\}$, and we obtain

$$\displaystyle\begin{array}{rcl} & \frac{(kD^{{\prime}}+D^{{\prime\prime}})^{2}+(kD^{{\prime}}+D^{{\prime\prime}})K_{ \Sigma }} {2} + 1 \geq k^{2}\left (\frac{(D^{{\prime}})^{2}+D^{{\prime}}K_{ \Sigma }} {2} + 1\right ) & {}\\ & +k(D^{{\prime}}D^{{\prime\prime}}- (C^{{\prime}}\cdot C^{{\prime\prime}})_{z_{1}}) + \frac{(D^{{\prime\prime}})^{2}+D^{{\prime\prime}}K_{ \Sigma }} {2} + 1 & {}\\ & \Longleftrightarrow\quad \left \{\begin{array}{@{}l@{\quad }l@{}} (k - 1)(-D^{{\prime}}K_{ \Sigma }) + 2(-D^{{\prime\prime}}K_{ \Sigma } - 1) \geq 2k,\quad \quad &\mbox{ if}\ - D^{{\prime}}K_{ \Sigma } \geq -D^{{\prime\prime}}K_{ \Sigma } - 1, \\ (k + 1)(-D^{{\prime}}K_{\Sigma }) \geq 2k,\quad \quad &\mbox{ if}\ - D^{{\prime}}K_{\Sigma } \leq -D^{{\prime\prime}}K_{\Sigma } - 1\end{array} \right.& {}\\ & \Longrightarrow\quad - D^{{\prime}}K_{\Sigma } \geq 2\ . & {}\\ \end{array}$$

If the curves C ^′ and C ^{′ ′} do not meet at z ₁, then we obtain

$$\displaystyle\begin{array}{rcl} & \frac{(kD^{{\prime}}+D^{{\prime\prime}})^{2}+(kD^{{\prime}}+D^{{\prime\prime}})K_{ \Sigma }} {2} + 1 \geq k^{2}\left (\frac{(D^{{\prime}})^{2}+D^{{\prime}}K_{ \Sigma }} {2} + 1\right )& {}\\ & +k(D^{{\prime}}D^{{\prime\prime}}- 1) + \frac{(D^{{\prime\prime}})^{2}+D^{{\prime\prime}}K_{ \Sigma }} {2} + 1\quad \Longleftrightarrow\quad - D^{{\prime}}K_{ \Sigma } \geq 2\ . & {}\\ \end{array}$$

Let us prove statement (2) of Proposition 3. If $\boldsymbol{p} \cap \widehat{ C}^{(1)} \cap \widehat{ C}^{(2)} =\emptyset$, then the (immersed) curves $C^{(1)} = \boldsymbol{n}(\widehat{C}^{(1)})$ and $C^{(2)} = \boldsymbol{n}(\widehat{C}^{(2)})$ intersect transversally and outside $\boldsymbol{z}$, and the point $\widehat{z} =\widehat{ C}^{(1)} \cap \widehat{ C}^{(2)}$ is mapped to a node of $C^{(1)} \cup C^{(2)}\setminus \boldsymbol{z}$. Then the uniqueness of the family $[\boldsymbol{n}_{t}:\widehat{ C}_{t} \rightarrow \Sigma,\boldsymbol{p}_{t}]$, $t \in (\mathbb{C},0)$, and its smoothness follows from the standard properties of the deformation smoothing out a node (see, e.g., [12, Lemma 11(ii)]). Suppose now that the point $\widehat{C}^{(1)} \cap \widehat{ C}^{(2)}$ belongs to $\boldsymbol{p}$. We prove statement (2) under condition n = 1, leaving the case n > 1 to the reader as a routine generalization with a bit more complicated notations. Denote $\xi:= s_{1}^{(1)} = -D^{(1)}K_{\Sigma }$, $\eta:= s_{1}^{(2)} = -D^{(2)}K_{\Sigma } - 1$. We have three possibilities:

• Suppose that ξ < η. In suitable coordinates x, y in a neighborhood of z ₁ = (0, 0), we have

  $$\displaystyle{\alpha _{1} \equiv y -\lambda x^{\eta }\mod \mathfrak{m}_{z_{1}}^{s},\quad C^{(1)} =\{ y + x^{\xi } + \mbox{ h.o.t.} = 0\},\quad C^{(2)} =\{ y = 0\}\,}$$

  where λ ≠ 0 is generic. Without loss of generality, we can define the family of arcs $(\boldsymbol{z}_{t},\mathcal{A}_{t})_{t\in (\mathbb{C},0)}$ by $\boldsymbol{z}_{t} = (t,0)$, $\mathcal{A}_{t} =\{ y \equiv \lambda (x - t)^{\eta }\mod \mathfrak{m}_{\boldsymbol{z}_{t}}^{s}\}$ (cf. Lemma 6). The ideal $I_{z_{1}}$ from Lemma 6 can be expressed as 〈y ², yx ^ξ−1, x ^ξ+η〉. Furthermore, by Lemma 6, for any family (20), the curves $C_{\tau } = \boldsymbol{n}(\widehat{C}_{\tau }) \in \vert D\vert$ are given, in a neighborhood of z ₁, by

  $$\displaystyle\begin{array}{rcl} & & y^{2}(1 + O(x,y,\overline{c})) + yx^{\xi }(1 + O(x,\overline{c})) +\sigma (\overline{c})yx^{\xi -1} \\ & & \qquad +\sum _{ i=0}^{\xi -2}c_{ i1}(\tau )yx^{i} +\sum _{ i=0}^{\xi +\eta -1}c_{ 0i}(\tau )x^{i} + O(x^{\xi +\eta },\overline{c}) = 0\, {}\end{array}$$

  (21)

  where $\overline{c}$ denotes the collection of variables {c _i1,  0 ≤ i ≤ ξ − 2,  c _i0,  0 ≤ i ≤ ξ +η − 1}, the functions c _ij (τ) vanish at zero for all i, j in the summation range, and σ(0) = 0. Changing coordinates x = x ^′ + t, where t = φ(τ), we obtain the family of curves

  $$\displaystyle\begin{array}{rcl} & & y^{2}(1 + O(x^{{\prime}},y,t,\overline{c})) + y(x^{{\prime}})^{\xi }(1 + O(x^{{\prime}},t,\overline{c})) +\sigma ^{{\prime}}y(x^{{\prime}})^{\xi -1} \\ & & \qquad +\sum _{ i=0}^{\xi -2}c_{ i1}^{{\prime}}y(x^{{\prime}})^{i} +\sum _{ i=0}^{\xi +\eta -1}c_{ 0i}^{{\prime}}(x^{{\prime}})^{i} + t \cdot O((x^{{\prime}})^{\xi +\eta },t,\overline{c}) = 0\, {}\end{array}$$

  (22)

  where

  $$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} c_{i1}^{{\prime}}\quad &=\sum _{0\leq u\leq \xi -2-i}\binom{i + u}{i}t^{u}c_{i+u,1} + \binom{\xi -1}{i}t^{\xi -1-i}\sigma \\ \quad &\quad + t^{\xi -i}\left (\binom{\xi }{i} + O(t)\right ) + O(t^{\xi -i},\overline{c}),\quad i = 0,\ldots,\xi -2, \\ c_{i1}^{{\prime}}\quad &=\sum _{u\geq 0}\binom{i + u}{i}t^{u}c_{i+u,0},\quad i = 0,\ldots,\xi +\eta - 1, \\ \sigma ^{{\prime}} \quad &=\sigma +t(\xi +O(t,\overline{c})).\end{array} \right. }$$

  (23)

  Next, we change coordinates y = y ^′ +λ(x ^′)^η and impose the condition $(C_{\tau } \cdot (\boldsymbol{z}_{\varphi (\tau )},\mathcal{A}_{\varphi (\tau )})) \geq \xi +\eta$, which amounts in the following relations on the variables $\overline{c}^{{\prime}} =\{ c_{i1}^{{\prime}},\ 0 \leq i \leq \xi -2,\ c_{i0}^{{\prime}},\ 0 \leq i \leq \xi +\eta - 1\}$:

  $$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \quad &c_{i0}^{{\prime}} = 0,\ i = 0,\ldots,\eta -1,\quad c_{i0}^{{\prime}} +\lambda c_{i-\eta,1}^{{\prime}} = 0,\ i = l,\ldots,\eta +\xi - 2, \\ \quad &c_{\xi +\eta -1}^{{\prime}} +\lambda \sigma ^{{\prime}} = 0.\ \end{array} \right. }$$

  (24)

  The new equation for the considered family of curves is then

  $$\displaystyle\begin{array}{rcl} & F(x,y) = (y^{{\prime}})^{2}(1 + O(x^{{\prime}},y^{{\prime}},t,\overline{c})) + y^{{\prime}}(x^{{\prime}})^{\xi }(1 + O(x^{{\prime}},t,\overline{c})) & \\ & \qquad \qquad + (x^{{\prime}})^{\xi +\eta }(a + O(x^{{\prime}},t,\overline{c})) + y^{{\prime}}\left (\sum _{i=0}^{\xi -2}c_{i1}^{{\prime}}(x^{{\prime}})^{i} +\sigma ^{{\prime}}(x^{{\prime}})^{\xi -1}\right ) = 0.& {}\end{array}$$

  (25)

  with some constant a ≠ 0. Consider the tropical limit of the family (25) (see [14, Sect. 2.3] or Sect. 3.1). The corresponding subdivision of $\Delta$ must be as shown in Fig. 1a. Indeed, first, c ₀₁ ^′ ≠ 0, since otherwise the curves C _τ would be singular at $\boldsymbol{z}_{t}$ contrary to the general choice of $(\boldsymbol{z}_{t},\mathcal{A}_{t})$. Second, no interior point of the segment [(0, 1), (ξ, 1)] is a vertex of the subdivision, since otherwise the curves C _τ would have a positive genus: The tropicalization of C _τ would then be a tropical curve with a cycle which lifts to a handle of C _τ (cf. [14, Sects. 2.2 and 2.3, Lemma 2.1]). By a similar reason, the limit polynomial $F_{\mathop{\mathrm{ini}}\nolimits }^{\delta }/y^{{\prime}} =\sum _{ i=0}^{\xi }c_{i1}^{0}(x^{{\prime}})^{i}$, where δ is the segment [(0, 1), (ξ, 1)], must be the ξ-th power of a binomial. The latter conclusion and relations (22) and (23) yield that N _F (i, 1) = ξ − i for i = 0, …, ξ and

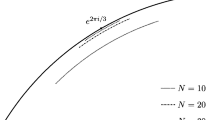
  $$\displaystyle{c_{i1}^{{\prime}} = t^{\xi -i}(c_{ i1}^{0} + c_{ i1}^{{\prime\prime}}(t)),\ i = 0,\ldots,\xi -2,\quad c_{\xi +\eta -1,0}^{{\prime}} = t(c_{\xi +\eta -1,0}^{0} + c_{\xi +\eta -1,0}^{{\prime\prime}})\,}$$

  where c _i1 ⁰, i = 0, …, ξ − 2, and c _{ξ+η−1, 0} ⁰ are uniquely determined by the given data, the functions c _i1 ^{′ ′}, 0 ≤ i ≤ ξ − 2, vanish at zero, and c _{ξ+η−1, 0} ^{′ ′} is a function of t and c _i1 ^{′ ′}, 0 ≤ i ≤ ξ − 2, that is determined by the given data and vanishes at zero too. To meet the condition of rationality of C _τ and to find the functions c _i1 ^{′ ′}(t), 0 ≤ i ≤ ξ − 2, we perform the refinement procedure as described in [14, Sect. 3.5]. It consists in further coordinate change and tropicalization, in which one encounters a subdivision containing the triangle $\mathop{\mathrm{Conv}}\nolimits \{(0,0),(0,2),(\xi,1)\}$ (see Fig. 1b). The corresponding convex piecewise linear function N ^′ is linear along that triangle and takes values N ^′(0, 2) = N ^′(ξ, 1) = 0, N ^′(0, 0) = η −ξ. By Shustin [14, Lemma 3.9 and Theorem 5], there are ξ distinct solutions {c _i1 ^{′ ′}(t),  0 ≤ i ≤ ξ − 2} of the rationality relation. More precisely, the initial coefficient (c _i1 ^{′ ′})⁰ is nonzero only for 0 ≤ i ≤ ξ − 2, $i \equiv \xi \mod 2$. The common denominator of the values of N ^′ at these point is ξ∕d, where d = gcd(ξ, η), and hence c _i1 ^{′ ′} are analytic functions of t ^d∕ξ. It follows thereby that t = τ ^ξ∕d.

  Fig. 1

  

  Tropical limits: (a) the case ξ < η, (b) refinement, (c) the case ξ = η, (d) the case ξ > η

• Suppose that ξ = η (see Fig. 1c). In this situation, the argument of the preceding case ξ < η applies in a similar way and, after the coordinate change x = x ^′ + t, y = y ^′ +λ(x ^′)^ξ, leads to Eq. (25), whose Newton polygon is subdivided with a fragment $\mathop{\mathrm{Conv}}\nolimits \{(0,1),(0,2),(2\xi,0)\}$ on which the function N _F is linear with values N _F (0, 2) = N _F (2ξ, 0) = 0, N _F (0, 1) = ξ. By Lemma 1, we get ξ solutions {c _i1 ^′(t),  i = 0, …, ξ − 2}, which are analytic functions of t. Then, in particular, t = τ.

• Suppose that ξ > η. In suitable coordinates x, y in a neighborhood of z ₁ = (0, 0), we have

  $$\displaystyle{\alpha _{1} \equiv y\mod \mathfrak{m}_{z_{1}}^{s},\quad C^{(1)} =\{ y +\lambda x^{\xi } + O(x^{\xi +1}) = 0\},\quad C^{(2)} =\{ y + x^{\eta } = 0\}\,}$$

  where λ ≠ 0. Without loss of generality, we can define the family of arcs $(\boldsymbol{z}_{t},\mathcal{A}_{t})_{t\in (\mathbb{C},0)}$ by $\boldsymbol{z}_{t} = (0,0)$, $\mathcal{A}_{t} =\{ y \equiv tx^{\xi -1}\mod \mathfrak{m}_{z_{1}}^{s}\}$ (cf. Lemma 6). The ideal $I_{z_{1}}$ from Lemma 6 can be expressed as 〈y ², yx ^ξ, x ^ξ+η−1〉. Thus, by Lemma 6, for any family (20), the curves $C_{\tau } = \boldsymbol{n}(\widehat{C}_{\tau }) \in \vert D\vert$ are given in a neighborhood of z ₁ by

  $$\displaystyle\begin{array}{rcl} & & y^{2}(1 + O(x,y,\overline{c})) + yx^{\eta }(1 + O(x,\overline{c})) +\lambda x^{\xi +\eta }(1 + O(x,\overline{c})) \\ & & \quad +\sigma (\overline{c})x^{\xi +\eta -1} +\sum _{ i=0}^{\eta -1}c_{ i1}(\tau )yx^{i} +\sum _{ i=0}^{\xi +\eta -2}c_{ 0i}(\tau )x^{i} = 0\, {}\end{array}$$

  (26)

  where $\overline{c}$ now denotes the collection of variables {c _i1,  0 ≤ i ≤ η − 1,  c _i0,  0 ≤ i ≤ ξ +η − 2}, the functions c _ij (τ) vanish at zero for all i, j in the summation range, and σ(0) = 0. Inverting t = φ(τ), changing coordinates y = y ^′ + tx ^ξ−1, and applying the condition $(C_{\tau } \cdot \mathcal{A}_{\varphi (\tau )}) \geq k + l$, we obtain an equation of the curves C _τ in the form

  $$\displaystyle\begin{array}{rcl} & & F(x,y^{{\prime}}) = (y^{{\prime}})^{2}(1 + O(t,x,y^{{\prime}},\overline{c}^{{\prime}})) + y^{{\prime}}x^{\eta }(1 + O(t,x,\overline{c}^{{\prime}})) \\ & & \qquad \qquad +\lambda x^{\xi +\eta }(1 + O(t,x,\overline{c}^{{\prime}})) +\sum _{ i=0}^{\eta -1}c_{ i1}(t)y^{{\prime}}x^{i} = 0\, {}\end{array}$$

  (27)

  where $\overline{c}^{{\prime}} =\{ c_{i1},\ 0 \leq i \leq \eta -1\}$, and the following relations must hold:

  $$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \quad &c_{i0} = 0,\ i = 0,\ldots,\eta -2, \\ \quad &c_{i0} + tc_{i-\xi +1,1} = 0,\ i =\xi -1,\ldots,\eta +\xi - 2, \\ \quad &\sigma +t(1 + O(t,\overline{c}^{{\prime}})) = 0\ .\end{array} \right. }$$

  (28)

  By Lemma 4(2), $\frac{\partial \sigma } {\partial c_{\eta -1,1}} (0)\neq 0$. The rationality of the curves C _τ yields that the subdivision S _F of the Newton polygon of F(x, y ^′) given by (27) must contain two triangles $\mathop{\mathrm{Conv}}\nolimits \{(0,1),(\eta,1),(0,2)\}$ and $\mathop{\mathrm{Conv}}\nolimits \{(0,1),(\eta,1),(\xi +\eta,0)\}$ (see Fig. 1d), and, furthermore, $F_{\mathop{\mathrm{ini}}\nolimits }^{\delta }/y^{{\prime}}$ must be the η-th power of a binomial, where δ = [(0, 1), (η, 1)] (cf. the argument in the treatment of the case ξ < η above). These two conclusions and Eq. (28) uniquely determine the initial coefficients c _i1 ⁰ as well as the values N _F (i, 1) = η − i for all i = 0, …, η − 1, and leave the final task to find the functions c _i1 ^{′ ′}(t), i = 0, …, η − 2, which appear in the expansion c _i1(t) = t ^η−i(c _i1 ⁰ + c _i1 ^{′ ′}(t)), i = 0, …, η − 2 (notice here that the last equation in (28) allows one to express c _η−1, 1 ^{′ ′} via c _i1 ^{′ ′}, i = 0, …, η − 2). To this extent, we again use the argument of the case ξ < η, performing the refinement procedure along the edge δ = [(0, 1), (η, 1)] (see [14, Sect. 3.5]) and apply the rationality requirement to draw the conclusion: There are exactly η families (20), and, for each of them, t = τ ^η∕d, where d = gcd{ξ, η}.

Statement (2) of proposition is proven. ■

3.4 Families of Curves and Arcs on Uninodal del Pezzo Surfaces

A smooth rational surface $\Sigma$ is called a uninodal del Pezzo surface if there exists a smooth rational curve $E \subset \Sigma$ such that E ² = −2 and $-CK_{\Sigma } > 0$ for each irreducible curve $C \subset \Sigma$ different from E. Observe that $EK_{\Sigma } = 0$. Denote by $\mathop{\mathrm{Pic}}\nolimits _{+}(\Sigma,E) \subset \mathop{\mathrm{Pic}}\nolimits (\Sigma )$ the semigroup generated by irreducible curves different from E. Assume that $\Sigma$ is of degree 1 and fix $D \in \mathop{\mathrm{Pic}}\nolimits _{+}(\Sigma,E)$ such that $-DK_{\Sigma } - 1 \geq 3$. Fix positive integers $n \leq -DK_{\Sigma } - 1$ and $s \gg -DK_{\Sigma } - 1$.

Accepting notations of Sect. 3.2, we introduce the set $U^{im}(D,E) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ is defined by the following conditions. For any sequence $\boldsymbol{s} = (s_{1},\ldots,s_{n}) \in \mathbb{Z}_{>0}^{n}$ summing up to $\vert \boldsymbol{s}\vert \leq s$ and for any element $(\boldsymbol{z},\mathcal{A}) \in U^{im}(D,E)$, where $\boldsymbol{z} = (z_{1},\ldots,z_{n}) \in\mathring\Sigma ^{n}$, $\boldsymbol{z} \cap E =\emptyset$, $\mathcal{A} = (\alpha _{1},\ldots,\alpha _{n})$, $\alpha _{i} \in \mathop{\mathrm{Arc}}\nolimits _{s}(\Sigma,z_{i})$, the family $\mathcal{M}_{0,n}^{im}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ is empty if $\vert \boldsymbol{s}\vert \geq -DK_{\Sigma }$ and is finite if $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$. Furthermore, in the latter case, all elements $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z},\mathcal{A})$ are represented by immersions $\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma$ such that $\boldsymbol{n}^{{\ast}}(\alpha _{i}) = s_{i}p_{i}$, 1 ≤ i ≤ n, and $\boldsymbol{n}^{{\ast}}(E)$ consists of DE distinct points.

Proposition 4

The set U ^im (D,E) is Zariski open and dense in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$.

Proof

The statement that U ^im(D) is Zariski open and dense in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring\Sigma ^{n})$ can be proved in the same way as Proposition 1(1). We will show that U ^im(D, E) is dense in U ^im(D), since the openness of U ^im(D, E) is evident. For, it is enough to show that any immersion $\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma$ such that $\boldsymbol{n}_{{\ast}}(\mathbb{P}^{1}) = D$ can be deformed into an immersion with an image transversally crossing E at DE distinct points.

Suppose, first, that a generic element $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma ] \in \mathcal{M}_{0,0}(\Sigma,D)$ is such that the divisor $\boldsymbol{n}^{{\ast}}(E) \subset \mathbb{P}^{1}$ contains an m-multiple point, m ≥ 2. Since $\dim \mathcal{M}_{0,0}(\Sigma,D) = -DK_{\Sigma } - 1 \geq 3$, we fix the images of $-DK_{\Sigma } - 2$ points p _i , $i = 1,\ldots,-DK_{\Sigma } - 2$, obtaining a one-dimensional subfamily of $\mathcal{M}_{0,0}(\Sigma,D)$, for which one derives a contradiction by Lemma 2(iii):

$$\displaystyle{D^{2} \geq (D^{2} + DK_{ \Sigma } + 2) + (-DK_{\Sigma } - 2) + (m - 1) = D^{2} + m - 1 > D^{2}\ .}$$

Hence, for a generic $[\boldsymbol{n}: \mathbb{P}^{1} \rightarrow \Sigma ] \in \mathcal{M}_{0,0}(\Sigma,D)$, the divisor $\boldsymbol{n}^{{\ast}}(E)$ consists of DE distinct points. Suppose that m ≥ 2 of them are mapped to the same point in E. Fixing the position of that point on E, we define a subfamily $V \subset \mathcal{M}_{0,0}(\Sigma,D)$ of dimension

$$\displaystyle{\dim V \geq \dim \mathcal{M}_{0,0}(\Sigma,D) - 1 = -DK_{\Sigma } - 2 \geq 2\ .}$$

As above, we fix the images of $-DK_{\Sigma } - 3$ additional point of $\mathbb{P}^{1}$ and end up with a contradiction due to Lemma 2(ii):

$$\displaystyle{D^{2} \geq (D^{2} + DK_{ \Sigma } + 2) + (-DK_{\Sigma } - 3) + m = D^{2} + m - 1 > D^{2}}$$

■

Let $\mathfrak{X} \rightarrow (\mathbb{C},0)$ be a smooth flat family of smooth rational surfaces such that $\mathfrak{X}_{0} = \Sigma$ is a nodal del Pezzo surface with the (−2)-curve E and $\mathfrak{X}_{t}$, t ≠ 0, are del Pezzo surfaces. We can naturally identify $\mathop{\mathrm{Pic}}\nolimits (\mathfrak{X}_{t}) \simeq \mathop{\mathrm{Pic}}\nolimits (\Sigma )$, $t \in (\mathbb{C},0)$. Fix a divisor $D \in \mathop{\mathrm{Pic}}\nolimits _{+}(\Sigma,E)$ such that $-DK_{\Sigma } - 1 \geq 3$. Given n ≥ 1 and $s \gg -DK_{\Sigma } - 1$, fix a vector $\boldsymbol{s} \in \mathbb{Z}_{>0}^{n}$ such that $\vert \boldsymbol{s}\vert = -DK_{\Sigma } - 1$. Denote by $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathfrak{X}) \rightarrow \mathfrak{X} \rightarrow (\mathbb{C},0)$ the bundle with fibres $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathfrak{X}_{t})$, $t \in (\mathbb{C},0)$. Pick n disjoint smooth sections $z_{1},\ldots,z_{n}: (\mathbb{C},0) \rightarrow \mathfrak{X}$ covered by n sections $\alpha _{1},\ldots,\alpha _{n}: (\mathbb{C},0) \rightarrow \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathfrak{X})$ such that $(\boldsymbol{z}(0),\mathcal{A}(0)) \in U^{im}(\Sigma,E)$, and $(\boldsymbol{z}(t),\mathcal{A}(t)) \in U^{im}(\mathfrak{X}_{t})$, t ≠ 0.

Proposition 5

Each element $[\nu:\widehat{ C} \rightarrow \Sigma,\boldsymbol{p}] \in \overline{\mathcal{M}_{0,n}(\Sigma,D,\boldsymbol{s},\boldsymbol{z}(0),\mathcal{A}(0))}$ such that

• either $\widehat{C} \simeq \mathbb{P}^{1}$ , or $\widehat{C} =\widehat{ C}^{{\prime}}\cup \widehat{ E}_{1} \cup \ldots \cup \widehat{E}_{k}$ for some k ≥ 1, where $\widehat{C}^{{\prime}}\simeq \widehat{ E}_{1} \simeq \ldots \simeq \widehat{ E}_{k} \simeq \mathbb{P}^{1}$, $\widehat{E}_{i} \cap \widehat{ E}_{j} =\emptyset$ for all i ≠ j, and $\#(\widehat{C}^{{\prime}}\cap \widehat{ E}_{i}) = 1$ for all i = 1,…,k;

• $\boldsymbol{p} \subset \widehat{ C}^{{\prime}}$ and $[\nu:\widehat{ C}^{{\prime}}\rightarrow \Sigma,\boldsymbol{p}] \in \mathcal{M}_{0,n}^{im}(\Sigma,D - kE,\boldsymbol{s},\boldsymbol{z}(0),\mathcal{A}(0))$ , and each of the $\widehat{E}_{i}$ is isomorphically taken onto E;

extends to a smooth family $[\nu _{t}:\widehat{ C}_{t} \rightarrow \mathfrak{X}_{t},\boldsymbol{z}(t)] \in \overline{\mathcal{M}_{0,n}}(\mathfrak{X}_{t},D,\boldsymbol{s},\boldsymbol{z}(t),\mathcal{A}(t))$, $t \in (\mathbb{C},0)$ , where $\widehat{C}_{t} \simeq \mathbb{P}^{1}$ and ν _t is an immersion for all t ≠ 0, and, furthermore, each element of $\mathcal{M}_{0,n}(\mathfrak{X}_{t},D,\boldsymbol{s},\boldsymbol{z}(t),\mathcal{A}(t))$, $t \in (\mathbb{C},0)\setminus \{0\}$ is included into some of the above families.

Proof

The statement follows from [16, Theorem 4.2] and from Proposition 4, which applies to all divisors D − kE, since $-(D - kE)K_{\Sigma } = -DK_{\Sigma }$ for any k. ■

4 Proof of Theorem 1

By blowing up additional real points if necessary, we reduce the problem to consideration of del Pezzo surfaces X of degree 1.

• (1) To prove the first statement of Theorem 1, it is enough to consider only del Pezzo surfaces satisfying property (GDP) introduced in Sect. 3.3 (cf. [12, Lemma 17]) and real divisors satisfying − DK _X − 1 ≥ 3 (cf. Remark 1(1)). So, let a real del Pezzo surface X satisfy property (GDP) and have a nonempty real part. Let $F \subset \mathbb{R}X$ be a connected component. Denote by $\mathcal{P}_{r,m}(X,F)$ the set of sequences $(\boldsymbol{z},\boldsymbol{w})$ of n = r + 2m distinct points in $\Sigma$ such that $\boldsymbol{z}$ is a sequence of r points belonging to the component $F \subset \mathbb{R}X$, and $\boldsymbol{w}$ is a sequence of m pairs of complex conjugate points. Fix an integer s ≫ −DK _X and denote by $\mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(X,F,r,m) \subset \mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring{X^{n}})$ the space of sequences of arcs $(\mathcal{A},\mathcal{B})$ centered at $(\boldsymbol{z},\boldsymbol{w}) \in \mathcal{P}_{t,m}(X,F)$ such that $\mathcal{A} = (\alpha _{1},\ldots,\alpha _{r})$ is a sequence of real arcs $\alpha _{i} \in \mathop{\mathrm{Arc}}\nolimits _{s}(X,z_{i})$, $z_{i} \in \boldsymbol{z}$, i = 1, …, r, and $\mathcal{B} = (\beta _{1},\overline{\beta }_{1},\ldots,\beta _{m},\overline{\beta }_{m})$ is a sequence of m pairs of complex conjugate arcs, where $\beta _{i} \in \mathop{\mathrm{Arc}}\nolimits _{s}(X,w_{i})$, $\overline{\beta }_{i} \in \mathop{\mathrm{Arc}}\nolimits _{s}(X,\overline{w}_{i})$, i = 1, …, m, and $\boldsymbol{w} = (w_{1},\overline{w}_{1},\ldots,w_{m},\overline{w}_{m})$.

  We join two elements of $\mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m) \cap U^{im}(D)$ by a smooth real analytic path $\Pi =\{ (\boldsymbol{z}_{t},\boldsymbol{w}_{t}),(\mathcal{A}_{t},\mathcal{B}_{t})\}_{t\in [0,1]}$ in $\mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ and show that along this path, the function $W(t):= W(X,D,F,\varphi,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z}_{t},\boldsymbol{w}_{t}),(\mathcal{A}_{t},\mathcal{B}_{t}))$, t ∈ [0, 1], remains constant. By Propositions 1 and 3, we need only to verify the required constancy when the path $\Pi$ crosses sets U ₊ ^im(D), U ₁ ^sing(D), U ₂ ^sing(D), U ^mt(D), and U ^red(D) at generic elements of their components of codimension 1 in $\mathop{\mathrm{Arc}}\nolimits _{s}^{\mathrm{sm}}(\mathring{X^{n}})$. Let t ^∗ ∈ (0, 1) correspond to the intersection of $\Pi$ with some of these walls.

  If is clear that crossing of the wall $U_{+}^{sm}(D) \cap \mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ does not affect $W(X,D,F,\varphi,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z}_{t},\boldsymbol{w}_{t}),(\mathcal{A}_{t},\mathcal{B})_{t})$.

  The constancy of W(t) in a crossing of the wall $U_{1}^{sing}(D) \cap \mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ follows from Proposition 1(3) and [12, Lemmas 13(2), 14 and 15]. The transversality hypothesis in [12, Lemma 15] can be proved precisely as [12, Lemma 13(1)].

  The constancy of W(t) in a crossing of the wall $U_{2}^{sing}(D) \cap \mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ follows from Proposition 1(4) and Lemma 3.

  The constancy of W(t) in a crossing of the wall $U^{mt}(D) \cap \mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ follows from Propositions 1(5) and 2. Indeed, by Proposition 2 exactly one real element of the set $\mathcal{M}_{0,n}(X,D,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z}_{t},\boldsymbol{w}_{t}),(\mathcal{A}_{t},\mathcal{B}_{t}))$ undergoes a bifurcation. Furthermore, the ramification points of the degenerate map $\boldsymbol{n}: \mathbb{P}^{1} \rightarrow X$ are complex conjugate. Hence, the real part of a close curve doubly covers the real part of $C = \boldsymbol{n}(\mathbb{P}^{1})$, which means that the number of solitary nodes is always even.

  At last, the constancy of W(t) in a crossing of the wall $U^{red}(D) \cap \mathbb{R}\mathop{\mathrm{Arc}}\nolimits _{s}(X,F,r,m)$ we derive from Proposition 3. Notice that the points $p_{1} \in \widehat{ C}$ and z ₁ ∈ X must be real, and hence the cases (1ii) and (1iii) are not relevant, since we have the lower bound − kD ^′ K _X  ≥ 2k ≥ 4 contrary to (5). In the case (1i), we use Proposition 3(2):

  • if $\boldsymbol{p} \cap \widehat{ C}^{(1)} \cap \widehat{ C}^{(2)} =\emptyset$, then the germ of the real part of the family (20) is isomorphically mapped onto the germ $(\mathbb{R},t^{{\ast}})$ so that the central curve deforms by smoothing out a node both for t > t ^∗ and t < t ^∗, and hence W(t) remains unchanged;

  • if $\boldsymbol{p} \cap \widehat{ C}^{(1)} \cap C^{(2)} =\{ p_{1}\}$, then $p_{1} \in \mathbb{P}^{1}$ and z ₁ ∈ X must be real, and hence ξ +η must be odd, in particular, d = gcd{ξ, η} is odd too, where ξ = s ₁ ⁽¹⁾, η = s ₁ ⁽²⁾; if κ = min{ξ, η} is odd, then the real part of each real family (20) is homeomorphically mapped onto the germ $(\mathbb{R},t^{{\ast}})$, and, in the deformation of the central curve both for t > t ^∗ and t < t ^∗, one obtains in a neighborhood of z ₁ an even number of real solitary nodes, which follows from Lemma 1(2); if κ is even, then either the real part of a real family (20) is empty or the real part of a real family (20) doubly covers one of the halves of the germ $(\mathbb{R},t^{{\ast}})$, so that in one component of $(\mathbb{R},t^{{\ast}})\setminus \{t^{{\ast}}\}$, one has no real curves in the family (20), and in the other component of $(\mathbb{R},t^{{\ast}})\setminus \{t^{{\ast}}\}$, one has a couple or real curves, one having an odd number κ − 1 real solitary nodes, and the other having no real solitary nodes [see Lemma 1(2)], and hence W(t) remains constant in such a bifurcation.

• (2) By Itenberg et al. [12, Proposition 1], in a generic one-dimensional family of smooth rational surfaces of degree 1 all but finitely many of them are del Pezzo and the exceptional one are uninodal. Hence, to prove the second statement of Theorem 1 it is enough to establish the constancy of

  $$\displaystyle{W(t) = W(\mathfrak{X}_{t},D,F_{t},\varphi,(\boldsymbol{k},\boldsymbol{l}),(\boldsymbol{z}(t),\boldsymbol{w}(t)),(\mathcal{A}(t),\mathcal{B}(t)))}$$

  in germs of real families $\mathfrak{X} \rightarrow (\mathbb{C},0)$ as in Proposition 5, where the parameter is restricted to $(\mathbb{R},0) \subset (\mathbb{C},0)$. It follows from Proposition 5 that the number of the real curves in count does not change, and real solitary nodes are not involved in the bifurcation. Hence, W(t) remains constant.

5 Examples

We illustrate Theorem 1 by a few elementary examples. Consider the case of plane cubics, for which new invariants can easily be computed via integration with respect to the Euler characteristic in the style of [3, Proposition 4.7.3].

Let r ₁ + 3r ₃ + 2(m ₁ + 2m ₂ + 3m ₃ + 4m ₄) = 8, where r ₁, r ₃, m ₁, m ₂, m ₃, m ₄ ≥ 0. Define integer vectors $\boldsymbol{k} = (r_{1} \times 1,r_{3} \times 3)$, $\boldsymbol{l} = (m_{1} \times 1,m_{2} \times 2,m_{3} \times 3,m_{4} \times 4)$. Denote by L the class of line in $\mathop{\mathrm{Pic}}\nolimits (\mathbb{P}^{2})$. Then

$$\displaystyle{W(\mathbb{P}^{2},3L,(\boldsymbol{k},\boldsymbol{l})) = r_{ 1} - r_{3}\ .}$$

As compared with the case of usual Welschinger invariants, in the real pencil of plane cubics meeting the intersection conditions with a given collection of arcs, in addition to real rational cubics with a node outside the arc centers, one encounters rational cubics with a node at the center of an arc of order 3. Notice that this real node is not solitary since one of its local branches must be quadratically tangent to the given arc. We also remark that, in a similar computation for a collection of arcs containing a real arc of order 2, one also encounters rational cubics with a node at the center of such an arc, but this node can be solitary or non-solitary depending on the given collection of arcs, and hence the count or real rational cubics will also depend on the choice of a collection of arcs.

Of course, the same argument provides formulas for invariants of any real del Pezzo surface and D = −K, or, more generally, for each effective divisor with p _a (D) = 1.

We plan to address the computational aspects in detail in a forthcoming paper.