Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Problem Description

Especially in the grocery retail trade , repetitive weekly delivery patterns are used to increase planning stability for the stores and to balance picking workload at the distribution center (DC). A delivery pattern is defined as a store-specific combination of weekdays on which a delivery takes place. Assuming that there must be at least one delivery every week, and six weekdays, there is a total of 63 potential delivery patterns for each store.

As several processes in the logistics subsystems DC, transportation and instore logistics of the retail supply chain are influenced by the delivery pattern decision, an integrated approach is necessary to solve the problem. Existing approaches in literature, however, neglect important areas influenced by the delivery patterns and often focus on short-term vehicle routing. E.g., Ronen and Goodhart [4] propose a hierarchical approach in a cluster-first, route-second manner. They first cluster stores with similar characteristics and preselect patterns. Then they assign patterns to stores using a MIP, and afterwards build transportation routes applying a periodic vehicle routing problem (PVRP). Cardos and Garcia Sabater [1] design a decision support system to determine delivery schemes for stores focusing on inventory and transportation costs. They preselect feasible solutions in the first step. Then they evaluate minimal cost paths for each delivery frequency for each store and afterwards solve a PVRP for each delivery frequency combination. A major disadvantage of both approaches is that they do not consider instore handling costs, despite the fact that these determine the main cost block of operational logistics costs according to several empirical studies (see [3]). Finally Sternbeck and Kuhn [5] try to act on some of the limitations of the papers previously named. They present an integrative approach taking into account relevant cost components and capacity restrictions in three subsystems of the retail supply chain (DC, transportation and the stores). A limitation is that they do not model bundling effects across stores.

The model we propose in the following section is based on the approach of Sternbeck and Kuhn [5], but avoids preselection of patterns and incorporates bundling issues, thus creating a more exact decision tool for retailers trying to resolve the problem of selecting optimal delivery patterns for their stores.

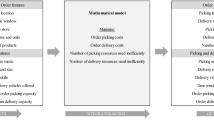
Our focus within this paper is on the three major subsystems of the retail supply chain that are affected by the selection of delivery patterns, namely the DC, transportation and the stores (see [5]). We concentrate on one DC supplying its affiliated stores with a dry goods assortment. We focus on operational costs that are directly dependent on the selection of delivery patterns. Basing our model on the findings of Sternbeck and Kuhn [5], we include the following cost terms: picking costs at the DC, transportation costs, instore inventory holding costs and instore handling costs that can be separated into ordering and receiving costs, initial shelf restocking costs and costs of restocking shelves from the backroom.

There is a trade-off between different cost components that are aligned to the delivery pattern decision. While most cost components increase with higher delivery frequency, instore inventory holding costs and shelf restocking costs have an inverse relationship. Picking costs, transportation costs, ordering and receiving costs as well as initial shelf restocking costs increase with higher delivery frequency as they consist of a fixed portion for each delivery and a variable component depending on the quantities delivered. As a consequence, less frequent deliveries lead to a reduction in fixed costs and therefore decreasing total costs per week. As delivery frequency goes down, however, the quantities delivered exceed daily demand and shelf space capacity to a greater degree, leading to higher inventory holding costs and more shelf restocking activities instore as well as higher costs.

Without considering capacity limits at the DC and in transportation, each store could realize its own optimal delivery pattern. Retailers, however, try to balance the workload at the DC to be able to use existing capacity efficiently. We therefore assume minimum and maximum picking capacity as well as limited transportation capacity on each day. Limited space in a store’s backroom can limit the potential delivery frequencies for the store. We therefore include store-specific receiving capacity in our decision model. The mathematical model reflects the relevant cost components as well as the restricting capacities, and models a twofold decision:

  • Selection of delivery patterns: Which stores are supplied on which days?

  • Construction of base tours: Which stores build a delivery cluster?

As our decision is a tactical one, we assume deterministic but dynamic store- and article-specific demand. Furthermore, each store has its specific shelf layout with specific shelf space capacity as well as different backroom capacities. We assume a homogeneous transportation fleet, but this assumption can easily be avoided by slightly adapting the model proposed in the following section. Each delivery includes the demand of all articles until the next delivery day. In contrast to the model proposed by Sternbeck and Kuhn [5], we explicitly model bundling effects in transportation across stores and determine the base tours that build the basis for short-term vehicle routing.

2 Model Formulation

Considering the setting and assumptions above, we propose the following binary program to model the joint delivery pattern and base tour decision:

$$\begin{aligned} Minimize \sum _{f \in F} \sum _{r \in R} x_{f, r} \cdot \hat{c}_{f, r} + \sum _{k \in K} \sum _{t \in T} y_{k, t} \cdot c_{k}^{transtour} + \sum _{f \in F} \sum _{k \in K} \sum _{r \in R} x_{f, k, r} \cdot c_{f, k, r}^{transstop} \end{aligned}$$
(1)

s.t.

$$\begin{aligned} \sum _{r \in R} x_{f, r} = 1&&\forall f \in F\end{aligned}$$
(2)
$$\begin{aligned} \sum _{k \in K} x_{f, k, r} = x_{f, r}&&\forall f \in F, r \in R\end{aligned}$$
(3)
$$\begin{aligned} \sum _{f \in F} \sum _{r \in R} x_{f, k, r} \cdot pall_{f, r, t} \le y_{k, t} \cdot cap^{trans}&&\forall k \in K, t \in T\end{aligned}$$
(4)
$$\begin{aligned} \sum _{f \in F} \sum _{r \in R} x_{f, r} \cdot pick_{f, r, t} \le maxcap_{t}^{pick}&&\forall t \in T\end{aligned}$$
(5)
$$\begin{aligned} \sum _{f \in F} \sum _{r \in R} x_{f, r} \cdot pick_{f, r, t} \ge mincap_{t}^{pick}&&\forall t \in T\end{aligned}$$
(6)
$$\begin{aligned} \sum _{r \in R} x_{f, r} \cdot pall_{f, r, t} \le cap_{f}^{rec}&&\forall f \in F, t \in T\end{aligned}$$
(7)
$$\begin{aligned} x_{f, r} \in \{0; 1\}&&\forall f \in F, r \in R\end{aligned}$$
(8)
$$\begin{aligned} x_{f, k, r} \in \{0; 1\}&&\forall f \in F, k \in K, r \in R\end{aligned}$$
(9)
$$\begin{aligned} y_{k, t} \in \{0; 1\}&&\forall k \in K, t \in T \end{aligned}$$
(10)

The objective function (1) minimizes the sum of total operational costs. These consist of the costs independent of the delivery tour settings \(\hat{c}_{f, r}\) and tour-specific costs. While costs independent of the tour settings solely depend on which pattern r is assigned to store f, reflected in the binary decision variable \(x_{f, r}\), tour-specific costs also depend on the assignment of a store f to a delivery cluster k, reflected in the two other types of decision variables \(x_{f, k, r}\) and \(y_{k, t}\), which decides if a cluster k is supplied on day t. The associated tour-specific costs are costs reflecting tour length and stops, \(c_{k}^{transtour}\) and \(c_{f, k, r}^{transstop}\). The underlying idea of the determination of tour-specific transportation costs is the logic developed by Fisher and Jaikumar [2]. They approximate tour costs on a tactical level by assigning stores to seed points. They thereby construct clusters that build so-called base tours for which the exact sequence is not known, but transportation costs can be approximated quite accurately. Figure 1 illustrates the determination of transportation costs.

Fig. 1
figure 1

Determination of transportation costs: schematic illustration and calculation example

Full size image

Besides the objective function, the model consists of several constraints (2)–(10). The first two conditions (2) and (3) ensure that each store f gets exactly one delivery pattern r, and is assigned to exactly one cluster k. Constraint (4) ensures that transportation capacity is met and a delivery to cluster k on day t only takes place if at least one of the stores assigned to cluster k is served on this day. Conditions (5) and (6) ensure that the picking effort at the DC is within the range \([mincap_{t}^{pick}; maxcap_{t}^{pick}]\) on each day. Constraint (7) ensures that the receiving capacity restriction holds. The decision variables are defined in conditions (8)–(10).

3 Solution Approach

As computational efforts can be extensive when applying the MIP proposed with its simultaneous clustering decision and pattern selection, we propose a sequential approach. The methodology is a cluster-first, assign-second procedure. In a first step, stores are assigned to clusters. This assignment can be done on the basis of predefined delivery areas of service providers or via a two-step algorithm. First, seed points are set (e.g., by applying a clustering algorithm), and then an adapted algorithm on the basis of Fisher and Jaikumar [2] can be used to assign stores to clusters. The clustering step results in an assignment parameter \(z_{f, k}\) that assigns store f to cluster k. After determining the clusters a model for assigning delivery patterns to stores can be applied that is analogous to the model presented in Sect. 2, with the main difference being that no store-cluster assignment decision is incorporated. The decision variable \(x_{f, k, r}\) is replaced by the combination of decision variable \(x_{f, r}\) and parameter \(z_{f, k}\).

Fig. 2
figure 2

Numerical results: delivery patterns of stores of two clusters

Full size image

4 Numerical Example

To illustrate the results of the model and approach proposed, we use real-life data from a major European grocery chain. The sample taken for this example consists of 35 small- and medium-sized stores attached to one central DC. The product ranges are store-specific and amount to a maximum of 618 different articles. Shelf space capacities and demand are also store-specific. For supplying the 35 stores, five trucks are available with capacity constraints according to the share of the products focused on the total assortment. To limit the analysis, a sequential approach is used, clustering the stores into 10 clusters according to geographical and sales issues in a first step. Applying the data obtained, CPLEX solves the model within a few seconds.

The results show a distribution of operational costs to the subsystems of the retail supply chain that is analogous to findings presented in literature: DC 27 %, transportation 30 %, and instore 43 %. The stores are served 1.86 times per week on average, with a maximum of three and a minimum of one delivery per week. As the sample consists of merely small- and medium-sized stores, this result is reasonable. The capacity utilization of the trucks is 87 % on average. There are 2.24 stops per tour on average. This means that the logic of Fisher and Jaikumar can serve as a good approximation of transportation costs because of a manageable amount of stops per tour on average. Post-calculations show that the transportation cost approximation only differs by less than 1 % from the real transportation costs that apply to the resulting tours.

A main criticism of the existing approach of Sternbeck and Kuhn [5] was the missing incorporation of bundling effects in transportation across stores. Figure 2 illustrates the delivery patterns of the stores of two clusters and shows the synchronization that is obtained with our new model and solution approach. The stores of cluster 1 are served by specific tours on Monday, Wednesday and Thursday. The stores of cluster 2 are mainly served on Tuesday, Wednesday and Saturday. An extra delivery for store 5 is needed on Friday due to transportation capacity limits.

5 Summary

We proposed a binary programming model that considers the decision-relevant costs and capacities at the DC, in transportation and instore to solve the problem of determining optimal store delivery patterns for grocery chains. To resolve the trade-off between the different cost components aligned to the delivery pattern decision, we proposed a sequential solution approach. We revealed significant bundling potential by applying the model and approach proposed using a case from a major European grocery retailer. The logistics levers identified can be applied to further optimize delivery patterns in retail distribution.