Adaptively Controlled Synchronization of Delay-Coupled Networks

Abstract

We discuss an adaptive control delay-coupled networks of Stuart-Landau oscillators, an expansion of systems close to a Hopf bifurcation. Based on the considered, automated control scheme, the speed-gradient method, the topology of a network adjusts itself by changing the link weights in a self-organized manner such that the target state is realized. We find that the emerging topology of the network is modulated by the coupling delay. If the delay time is a multiple of the system’s eigenperiod, the coupling within a cluster and to neighboring clusters is on average positive (excitatory), while the coupling to clusters with a phase lag close to $\pi$ is negative (inhibitory). For delay times equal to odd multiples of half of the eigenperiod, we find the opposite: Nodes within one cluster and of neighboring clusters are coupled by inhibitory links, while the coupling to clusters distant in phase state is excitatory. In addition, the control scheme is able to construct networks such that they exhibit not only a given cluster state, but also oscillate with a prescribed frequency. Finally, we demonstrate the efficiency of the speed-gradient method in cases where only part of the network is accessible.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Networks are ubiquitous. They can be found in a large variety of different research areas such as social science, economics, psychology, biology, physics, and mathematics [1–3], where networks are used to model the interactions of coupled systems or large number of agents. Two important lines of research have formed: (i) investigations of network topologies including data-mining and constructive models of their generation [1–6] and (ii) studies of dynamics on networks with fixed topology [7–16]. The concept of adaptive networks aims to bring these two directions together by considering topologies that evolve according to the states of the network nodes, which are in turn influenced by the topology [17].

In the wide spectrum of dynamical scenarios of coupled systems, zero-lag synchronization, which is also known as in-phase or complete synchronization, has been at the center of attention for a long time. Within the last decade, other, more complex synchronization patterns have moved into the focus of increasing research activities. These include cluster and group synchronization, which was studied in theory [11, 18–21] and realized in experiments [22, 23]. Prominent examples of these types of synchrony have been reported in many biological systems including dynamics of neurons [24], central pattern generation in animal locomotion [25], or population dynamics [26]. The difference between cluster and group synchronization can be described as follows: Group synchronization corresponds to the case where each cluster potentially exhibits different local dynamics. This dynamical state is more general than an M-cluster state, for which the compound system exhibits M clusters with zero-lag synchronization between the nodes within one cluster, but—in the case of oscillating dynamics—with a constant phase lag of $2\pi /M$ between the clusters.

If the network dynamics does not settle in the desired cluster state in a self-organized way, control methods can help to adaptively change the topology of the network in order to realize the target state. This has previously been investigated, to our knowledge, only by a few researchers: Lu et al., for instance, considered the control of cluster synchronization by means of changing topology. As a limiting restriction for the applicability, their method requires a-priori knowledge to which cluster each node should belong in the final state [27]. Furthermore, the majority of algorithms, which have been developed to control synchrony by adaptation of the network topology, take advantage of local mechanisms. A large number of these control schemes can be related to Hebb’s rule: Cells that fire together, wire together [28]. The method that we propose below, however, uses a global goal function to realize self-organized control. It is hence a powerful alternative and complements existing control schemes.

In short, we will present an algorithm that adapts the weights of the links in the network such that a desired cluster state is reached. We will show that our method is robust towards different initial conditions and also works for a large parameter range. This includes the potential adding of new links, if the initial weight had been zero, or the removal of links, if the respective weight is set to zero. The adaptation algorithm for the network structure is based on the speed-gradient method [29, 30]. The goal function, which we employ, has a strong advantage compared to other methods: it does not rely on a-priori ordering of nodes, i.e., it is not necessary to assign each node to a specific cluster in advance.

As a proof of concept, we will consider the normal form of a Hopf bifurcation, which is also known as Stuart-Landau oscillator. This model is generic for many oscillating systems present in nature and technological applications. In addition, we take into account time delays in the coupling between the nodes because delays naturally arise in many applications. Note that our scheme also works for instantaneous coupling. Furthermore, we will demonstrate that our method does not require to control all links of a network. The control scheme is still successful if only a subset of links is accessible, which we will explicitly illustrate for random networks [31]. We will also show how networks can be constructed in which cluster states oscillate with a prescribed frequency. This includes zero frequency and gives rise to a freezing of the dynamical motion. The final topology, i.e., distribution of link weights, of these controlled networks will contain some randomness because we start with random initial conditions for the state of the nodes. Despite this randomness, we will show that on average the topology is characterized by common features. As a crucial parameter shaping a topology, which enables synchronization, we identify the delay time.

Delay is an ubiquitous phenomenon in nature and technology and arises whenever time in the propagation or the processing of a signal is needed [32, 33]. For example, in laser networks the finite speed of light gives rise to a propagation delay [34–36]. Time delay in neural networks emanates from the finite speed of the transmission of an action potential between two neurons where the propagation velocity of an action potential varies between 1 and 100 m/s depending on the diameter of the axon and whether the fibers are myelinated or not [37]. The influence of delay on the dynamics on networks has been investigated by several authors [13, 16, 19, 38–57]. Depending on the context, delay can play a constructive or a destructive role [58–69].

The rest of this chapter is organized as follows: In Sect. 3.2 we introduce the model of Stuart-Landau oscillator and discuss the application of the speed-gradient method on the coupling matrix. In Sect. 3.3, we present the main results including applications of the control scheme to select a frequency of the ensemble of oscillators and restricted accessibility of the controller. We wrap up in Sect. 3.4 and finish with an outlook for future research directions and additional questions.

2 Model Equation and Control Scheme

In this chapter, we will first introduce the model equations of the Hopf normal form. Then, we will show the application of the speed-gradient method for an automated adjustment of the network topology by changing the weights of the links. The control scheme is based on a goal function that will be designed such that it becomes minimal for the desired M-cluster state.

2.1 Stuart-Landau Oscillator

We consider the Stuart-Landau oscillator given by the following equations

$$\begin{aligned} \dot{z}= \left[ \lambda + i\omega - |z|^2\right] z \end{aligned}$$

(3.1)

with the complex variable $z \in \mathbb {C}$ and parameters $\lambda ,\omega \in \mathbb {R}$ [70]. This system arises generically in a center manifold expansion close to a supercritical Hopf bifurcation with $\lambda$ as the bifurcation parameter. Below the bifurcation, i.e., for negative $\lambda$, the system exhibits a stable focus at the origin, which becomes unstable at the bifurcation point $\lambda =0$. Above the bifurcation, a stable limit cycle with radius $r=\sqrt{\lambda }$ coexists with the unstable focus. The parameter $\omega$ is the frequency of the limit cycle and determines the intrinsic timescale.

Throughout this chapter, we discuss networks of N delay-coupled Stuart-Landau oscillators $z_j$, $j=1,\dots ,N$, described by

$$\begin{aligned} \dot{z}_j(t)= & {} [\lambda + i\omega - |z_j|^2]z_j +K\sum _{n=1}^N G_{jn}(t)[z_n(t-\tau )-z_j(t)] \end{aligned}$$

(3.2)

with a real coupling strength K and coupling delay $\tau$. For notational convenience, we use in the following the abbreviation $z_{n,\tau } \equiv z_n(t-\tau )$. The matrix $\{G_{jn}(t)\}_{j,n=1,\ldots ,N}$ describes the topology of the network. Its elements might change over time, because it is subject to the adaptive control as discussed in Sect. 3.2.2 below.

In order to investigate the amplitude and phase dynamics of the complex variable z, it is convenient to rewrite Eq. (3.1) using $r_j=|z_j|$ and $\varphi _j=\arg (z_j)$:

$$\begin{aligned} \dot{{r_j}}(t)= & {} \left[ \lambda - r_j^2\right] r_j+K\sum _{n=1}^N{G_{jn}\left\{ r_{n,\tau }\cos \left[ \varphi _{n,\tau }-\varphi _j\right] -r_{j}\right\} },\end{aligned}$$

(3.3a)

$$\begin{aligned} \dot{{\varphi _j}}(t)= & {} \omega +K\sum _{n=1}^NG_{jn}\left\{ \frac{r_{n,\tau }}{r_j}\sin \left[ \varphi _{n,\tau }-\varphi _j\right] \right\} . \end{aligned}$$

(3.3b)

One class of solutions of Eqs. (3.3) are M-cluster states that exhibit a common amplitude $r_j\equiv r_{0}$. The phases of the oscillators in an M-cluster state are given by $\varphi _j=\varOmega _M t+j 2\pi /M$, where $\varOmega _M$ is the collective frequency. A special cluster state is complete, in-phase, or zero-lag synchronization, i.e., $M=1$, where all nodes are in one cluster. The other extreme case are splay states with $M=N$, where each cluster consists of a single node only. In the continuum limit, the splay state on a unidirectionally coupled ring corresponds to a rotating wave. For a schematic diagram of (a) in-phase synchronization, (b) a 3-cluster state, and (c) a splay state, see Fig. 3.1.

Fig. 3.1

Schematic examples of a in-phase synchronization ($M=1$), b a 3-cluster ($M=3$), and c a splay state ($M=N$). Each cluster consists of the same number of nodes

2.2 Speed-Gradient Method

For a dynamical system in general notation

$$\begin{aligned} \dot{ {\varvec{x}}}(t)={\varvec{F}}\left( {\varvec{x}},{\varvec{u}},t\right) , \end{aligned}$$

(3.4)

an additional set of equations for the control vector ${\varvec{u}}$ can be derived using the gradient (with respect to the accessible parameters) of the speed (temporal change) of an appropriately chosen goal function Q [29]:

$$\begin{aligned} \frac{d{\varvec{u}}}{dt}=-\varGamma \nabla _u \dot{Q}\left( {\varvec{x}},{\varvec{u}},t\right) \end{aligned}$$

(3.5)

with a positive definite gain matrix $\varGamma$. Intuitively, the control scheme works as follows: The speed $\dot{Q}$ may decrease along the direction of its negative gradient. As $\dot{Q}$ becomes negative, the control function Q will decrease as well and will finally reach its minimum indicating that the control goal is realized. For details and conditions, see Refs. [71, 72].

In the following, we will apply this speed-gradient control to the elements of the coupling matrix $\{G_{jn}(t)\}_{j,n=1,\ldots ,N}$ of Eq. (3.2), i.e.,

$$\begin{aligned} \dot{G}_{jn}=-\gamma \frac{\partial }{\partial G_{jn} } \dot{Q}_M \nonumber \end{aligned}$$

with $\gamma >0$ and choose the goal function $Q_M$ to realize the M-cluster state as [73]:

$$\begin{aligned} Q_M= & {} 1-\underbrace{\frac{1}{N^2} \sum _{j=1}^N e^{M i\varphi _j}\sum _{k=1}^N e^{-Mi\varphi _k}}_{I} +\underbrace{ \frac{1}{2} \sum _{p=1}^{M-1} \sum _{j=1}^N e^{pi\varphi _j}\sum _{k=1}^N e^{-pi\varphi _k}}_{II} \nonumber \\&+\underbrace{\frac{1}{2}\sum _{i,k=1}^N(r_i-r_k)^2}_{III} + \underbrace{\frac{c}{2}\int \limits _0^t \sum _{k=1}^N \left( \sum _{i=1}^N G_{ki}-1\right) ^2dt}_{IV} \end{aligned}$$

(3.6)

Fig. 3.2

Effects of the penalty term (II) in Eq. (3.6). Both $Q_1$ and $Q_2$ without penalty terms have a minimum for $\varphi _1=\varphi _2$. Taking the penalty terms for $p<M=2$ into account, this minimum vanishes and $Q_2$ becomes zero only for anti-phase synchronization

with $c>0$. The goal function becomes minimized, once an M-cluster state is reached, and consists of the following terms: (I) a Kuramoto-type order parameter generalized for an M-cluster state, (II) a penalty term for all p-cluster states with $p<M$, (III) a penalty term to realize identical amplitudes of all oscillators, and (IV) a term added to guarantee a constant row-sum of $\{G_{jn}(t)\}_{j,n=1,\ldots ,N}$ designed such that $\sum _{n=1}^{N}G_{jn}=1$. Figure 3.2 illustrates the effects of the penalty term (II) for in-phase and anti-phase synchronization of a network motif of two coupled nodes. The penalty term (IV) takes into account all deviations from the unity row-sum during the growth of the network, such that $Q_M$ will not vanish completely in the goal state. Thus, we define $q_M\equiv Q_M-\frac{c}{2}\int _0^t \sum _k \left( \sum _i G_{ki}-1\right) ^2dt$, i.e., the sum over the terms (I)–(III), as better measure for the quality of synchronization.

Calculating the derivation of $Q_M$ and the gradient with respect to the matrix elements $G_{jn}$, we obtain the following $N^2$ equations after some algebraic manipulation [73]

$$\begin{aligned} \dot{G}_{jn}=&-\gamma K \left[ \frac{r_{n,\tau }}{r_j}\sin (\varphi _{n,\tau } -\varphi _j)\right] \nonumber \\&\times \sum _{k=1}^N\left\{ \sum _{1\le p<M}p\sin [p(\varphi _k-\varphi _j)]-\frac{2M}{N^2} \sin [M(\varphi _k-\varphi _j)]\right\} \nonumber \\&-2\gamma K\sum _{k=1}^N(r_j-r_k)\left[ r_{n,\tau }\cos (\varphi _{n,\tau } -\varphi _j)-r_j\right] -\gamma c\left( \sum _{i=1}^N G_{ji} -1\right) . \end{aligned}$$

(3.7)

The case, when not all $N^2$ elements of the coupling matrix are accessible, will be discussed in Sect. 3.3.3.

Next, we will present some results on the generation of various cluster states, that is, different combinations of number of elements N and number of clusters M.

3 Results

In this chapter, we will present the main findings of our study. At first, we will demonstrate the success of the proposed control method along the lines of an exemplary 8-cluster state. Then, we will address the impact of the time delay on the distribution of the coupling weights. Finally, we will discuss two applications of the controller: (i) a frequency selection of the cluster state and (ii) targeted control, when only a fraction of the network is accessible.

Fig. 3.3

Control of an 8-cluster state for $N=40$. Parameters: $\lambda =0.1$, $\omega =1$, $c=0.01$, $K=0.1$, $\tau =\pi$, $\gamma =10$

3.1 Automated Adjustment of Network Topology

Figure 3.3 presents a successful realization of an 8-cluster state and depicts the time series of the radii, the phase differences with respect to the reference node 0, the weights of the coupling matrix, and the goal function with ($Q_8$) and without ($q_8$) the unity row-sum term IV of Eq. (3.6) during the growth of the network. The simulations starts from a unidirectional ring as initial topology and random initial conditions $z_j(-50)=r_j(-50)e^{i\varphi _j(-50)}, j=1,\dots ,N$. The control is switched on at time $t=0$. One can see that after a short transient, the radii and phases rapidly converge to the desired 8-cluster state, and $Q_8$ and $q_8$ approach their minimum. Once the target state is reached, the coupling weights do not change anymore. The specific choice of the parameter $\gamma$ influences the transient times to reach the final network that supports the desired cluster state. Note that the generated network contains excitatory links, i.e., $G_{jn}>0$, and inhibitory ones with $G_{jn}<0$. The distribution of the weights in the final topology and the perturbation of the network (marked by the dotted line at $t=80$) will be discussed in detail in Sect. 3.3.2.

We also study the fraction of successful realizations $f_c$ and the time to reach the target state $t_c$ in dependence on the coupling strength K and the delay time $\tau$. We find that the fraction of successfully controlled networks $f_c$ is close to 1 and $t_c$ is roughly 10 units in the considered range $0.1 <K\le 5$, $0\le \tau \le 3\pi$ (cf. Fig. 10.4 in Ref. [74]), demonstrating that our method works very reliably independently of the coupling parameters. The quantities $f_c$ and $t_c$ will be helpful in Sect. 3.3.3, where we will apply the control only to a fraction of the links in the network.

3.2 Dependence on Time Delay

In the following, we discuss the structural properties of the networks after successful control for different coupling delays. For this purpose, we consider the coupling weights of the final topology as a function of the final phase difference between all pairs of oscillators. This will allow us to investigate the influence of delay on networks that enable synchronization in the prescribed cluster state.

Fig. 3.4

Dependence of the elements of coupling matrix averaged over 100 realizations on the phase difference $\varDelta _{jn}=\lim _{t \rightarrow \infty }{[\varphi _j(t)-\varphi _n(t)]}$ for $N=30$, $M=10$, and different time delays $\tau$. Other parameters as in Fig. 3.3

Figure 3.4 shows the weights $G_{jn}$ of an 8-cluster state as an average over 100 realizations. This ensemble average $\langle G_{jn} \rangle$ is presented in dependence on the final phase difference $\varDelta _{jn}\equiv \lim _{t \rightarrow \infty }[{\varphi _j(t)-\varphi _n(t)}]$, where the different colors correspond to different coupling delays. The network of the exemplary case shown in Fig. 3.3 is included in the dark-blue curve for $\tau =\pi$.

It can be seen that the curves have the form of a shifted cosine, i.e., $\langle G_{jn} \rangle \propto \cos \left( \frac{2\pi (j\,-\, n)}{M}-\tau \right)$. Focusing on the 8-cluster states of Fig. 3.3, we find a negative coupling between nodes with a small phase difference and a positive coupling between nodes with a phase equal or close to $\pi$.

For further insight into the network structure, we consider a row-wise discrete Fourier transform of the coupling matrix $\left\{ G_{jn}\right\}$ after successful control. For this purpose, we introduce an auxiliary $N \times M$ matrix $\varGamma _{jk}=\sum _{l=0}^{m-1} \tilde{G}_{j,k+lM}$, where m is the number of nodes in one cluster, i.e., $m=N/M$, and the final topology of the network is given by $\tilde{G}=G(t_{\infty })$. For notational convenience, we label the nodes such that the synchronized state can be described by $r_j\equiv r_{0,M}$ and $\varphi _j\equiv \varOmega _M t+j\frac{2\pi }{M}$, $j=1,\dots ,N$, where $r_{0,M}$ and $\varOmega _M$ denote the common radius and the common frequency, respectively. In other words, $\varGamma _{jn}$ represents the total input which node j receives from all nodes in cluster n. Representing each row of $\varGamma$ as a discrete Fourier series, the corresponding Fourier coefficients are given by

$$\begin{aligned} a_l^j&=\frac{2}{M}\sum _{k=1}^{M}\varGamma _{jk}\sin \left( \frac{l(k-j)2\pi }{M}-\varOmega _M \tau \right) \nonumber \\&=\frac{2}{N}\sum _{k=1}^{N}\tilde{G}_{jk}\sin \left( \frac{l(k-j)2\pi }{M}-\varOmega _M \tau \right) , \\ \nonumber \end{aligned}$$

(3.8a)

$$\begin{aligned} b_l^j&=\frac{2}{M}\sum _{k=1}^{M}\varGamma _{jk}\cos \left( \frac{l(k-j)2\pi }{M}-\varOmega _M \tau \right) \nonumber \\&=\frac{2}{N}\sum _{k=1}^{N}\tilde{G}_{jk}\cos \left( \frac{l(k-j)2\pi }{M}-\varOmega _M \tau \right) , \end{aligned}$$

(3.8b)

where l labels the lth coefficient in the Fourier series of the jth row. Note that the coefficients $a_0^j$ are equal to zero and due to the constant row-sum condition of $G_{jn}$, we have $b_0^j=\frac{1}{2M\cos (\varOmega _M \tau )}$.

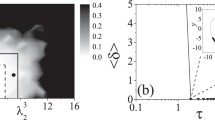
It is straight-forward, but lengthy to perform a linear stability analysis to compute the impact of perturbation on the radii, phases, and Fourier coefficients on the desired cluster state. One will finally derive a characteristic equation, whose infinite number of roots are the Floquet exponents. We are only interested in the one with the largest real part, which we denote by $\text {Re}\varLambda$. If this quantity is negative, the cluster solution will be stable, otherwise the solution is unstable. For details, on the derivation see Sect. 10.6.2 of Ref. [74].

Figure 3.5 shows the result of this stability analysis for (a) all higher Fourier coefficients being zero, i.e., $a_l^j = b_l^j = 0$ for $l > 1$ and $j = 1,\dots , N$, (b) random higher Fourier coefficients, and (c) constant higher Fourier coefficients, i.e., $a_l^j = b_l^j = 10$ for $a_l^j = b_l^j = 10$ and $j = 1,\dots , N$, in dependence on the common radius $r_{0,M}$ and the common frequency $\varOmega _M$. Random means that for each value of $r_{0,M}$ and $\varOmega _M$ the coefficients are drawn from a uniform distribution on the interval $[-10, 10]$. We find that the stability is only affected by the higher Fourier coefficients if $r_{0,M}$ is small: For small $r_{0,M}$ the unstable regions (yellow to orange color code) have a qualitatively different form in panels (a), (b), and (c), while for large $r_{0,M}$ stability is found in all three cases.

Fig. 3.5

Stability as a function of common frequency $\varOmega _M$ and radius $r_{0,M}^2$ for a vanishing higher Fourier coefficients, i.e., $a_l^j= b_l^j=0$ for $l>1$, b random higher Fourier coefficients, c constant higher Fourier coefficients, i.e., $a_l^j= b_l^j=10$ for $l>1$. $N=8$, $M=4$. Other parameters as in Fig. 3.3

Another possibility to test the influence of the higher coefficients is to disturb them during or after the course of the adaptation process. This is shown for the 8-cluster state in Fig. 3.3, where at $t=80$, we set each of the higher Fourier coefficients to a random value in the interval $[-3,3]$. One can see that the common frequency and radius do not change as a result of this perturbation.

In summary, these results can be seen as evidence that the higher Fourier coefficients do not affect the stability of the desired cluster state. Analyzing the first Fourier coefficients, one can derive the following equations for the common radius $r_{0,M}$ and frequency $\varOmega _M$ [73, 74]:

$$\begin{aligned} r_{0,M}^2= & {} \lambda +K\left[ \frac{b_1^jN}{2}-1\right] , \end{aligned}$$

(3.9a)

$$\begin{aligned} \varOmega _M= & {} \omega +K\left[ \frac{a_1^jN}{2}\right] . \end{aligned}$$

(3.9b)

Considering that these equations have to be satisfied for all $j=1,\ldots ,N$, we conclude that a solution with a common radius and a common frequency exists, only if $a_1^1=a_1^2=\ldots =a_1^N \equiv a$ and $b_1^1=b_1^2=\ldots =b_1^N \equiv b$. In fact, the average topology is mainly given by b, because a and $b_0$ are typically small and the higher coefficients average out as discussed above. Therefore, we obtain $G_{jn} \approx b \cos \left( \frac{2\pi (j\,-\,n)}{M}-\varOmega _M \tau \right)$, which explains the cosine form of the curves shown in Fig. 3.4.

3.3 Applications of Controller

3.3.1 Frequency Selection

In the following, we will exploit Eq. (3.9b) to select a common frequency via constructing an appropriate matrix. For this purpose, we set $a=\frac{2}{N}\left( \frac{\varOmega _M-\omega }{K}\right)$. To demonstrate the effect of this choice, we consider the case of a stationary cluster with a common frequency $\varOmega _M$. Figure 3.6 depicts the corresponding time series of the radii, phases, coupling weights, goal function, and $\varOmega _M$. At $t=0$ (first dotted line), we start the adaptive control with $M=N$, that is, with the goal function leading to a splay state. Then, at $t=40$ (second dotted line), the adaptive control is switched off and a is set to $a=\frac{2 \omega }{\textit{NK}}$ forcing $\varOmega _M$ to approach zero.

Fig. 3.6

Freezing of the motion of a splay state with $N=12=M$. Parameters: $\lambda =0.1$, $\omega =1$, $c=0.01$, $K=0.1$, $\tau =\pi$, $\gamma =10$

3.3.2 Targeted Control

In the previous sections, we have assumed that every link of the network is subject to the control scheme, that is, all elements of the coupling matrix $\{G_{jn}(t)\}_{j,n=1,\ldots ,N}$ are accessible. This might be not realistic for applications. We will show in the following that it suffices to control a subset of links, while the other links are left unchanged. This will be demonstrated for the example of a directed random network that consists of P links chosen from the $L=N(N-1)$ possible links excluding self-coupling. From this set of P links, we select, again randomly, A links which are subject to adaptation as given by Eq. (3.7).

Fig. 3.7

Control of $A/L=30\,\%$ of the links for $N=15$, $M=3$, and $P/L=0.4$. Parameters: $\lambda =0.1$, $\omega =1$, $c=0.01$, $K=0.1$, $\tau =\pi$, $\gamma =10$

Figure 3.7 depicts the realization of 3-cluster state in a network of 15 nodes with the time series of the radii, the phase differences, the elements of the coupling matrix, and the goal function shown in the different panels, respectively. The nodes are coupled on a random network with density 0.4 and with $30\,\%$ of the links accessible, i.e., $A/L=0.3$. It can be seen that using the goal function $Q_3$ the network consists of 3 equally sized clusters after successful control.

Fig. 3.8

a Fraction $f_c$ of successfully controlled networks and b times $t_c$ needed to reach the control goal as a function of number of random links P and number of controlled links A, normalized by $L=N(N-1)$. We simulated 10 realizations for each parameter combination. $K=0.2$. Other parameters as in Fig. 3.7

Next, we explore the performance of our method with respect to the links present in the networks and the fraction of these links subject to adaptation. Figure 3.8a depicts the fraction $f_c$ of successfully controlled networks as a function of P / L and A / L. We define a network as successfully controlled in an M-cluster state at time $t_c$ if it was in this state for $t \in [t_c-1,t_c]$. Figure 3.8b shows the corresponding control time $t_c$.

One can see that the success rate $f_c$ does not depend strongly on the total number of links P in the network and is rather constant for fixed A. The rate, however, depends on the ratio of adapted links A / L. We conclude that the links additionally present in the network, but not subject to control, have very little effect on the synchronizability of the network. For example, consider a horizontal cut at $A/L=0.4$. Then, the control still works in more than $90\,\%$ of the cases.

Fig. 3.9

Control of a subset of links for fixed ratio of a $P/L=0.4$, b $P/L=0.6$, and c $P/L=1$. Red circles Success rate $f_c$. Blue circles Probability $p_{>1}$ that no node in the network has less than 2 incoming links which are adapted. Blue line Analytic calculation of $p_{>1}$ (cf. [74]). $K=0.2$. 80 realizations for each value of A / L. Other parameters as in Fig. 3.7

Figure 3.9 further corroborates these results. A good approximation of the success rate $f_c$ can be obtained if we assume that for successful control each node in the networks needs at least two incoming links which are subject to adaptation. One adapted link is not sufficient because it is not able to change due to the unity row-sum condition. Only if a second incoming link is present, the links can change in order to control the dynamics of the node because the effect of the adaptation of the first link on the row-sum can be counterbalanced by the second link. Figure 3.9 depicts $f_c$ versus A / L as red circles for a fixed ratio of $P/L = 0.4, 0.6, 1$ in panels (a)–(c), respectively. The blue circles depict the fraction $p_{>1}$ of networks where all nodes have at least two incoming links. Obviously, $p_{>1}$ well approximates $f_c$ although they are not identical indicating that cases exist where the network can be controlled though one node has less than two adapted incoming links, or where the control fails although each node has two incoming links. Note that an analytic expression for $p_{>1}$ can be derived, which yields the blue curves in Fig. 3.9. For details, see Sect. 10.8 in Ref. [74].

4 Summary and Conclusions

We have applied a speed-gradient algorithm to adapt the topology of time-delay coupled oscillators to control cluster synchronization. The controller minimizes a goal function that is based on a generalized Kuramoto order parameter. The goal function is chosen according to the target cluster state, but independent of the ordering of the nodes. An additional term ensures amplitude synchronization. We find that this speed-gradient control scheme is very robust with respect to perturbations, different initial conditions, and coupling parameters. We have focused on the dependence on the coupling strength and delay time.

We have found that the distribution of link weights of the successfully controlled network is modulated by the coupling delay. A row-wise discrete Fourier transform of the coupling matrix gives insight into these delay modulations. Necessary conditions for the existence of a common radius and a common frequency give rise to restrictions affecting the first Fourier coefficients, while there is no restriction for the higher Fourier coefficients. We also found that the stability of the cluster states is only weakly affected by the higher Fourier coefficients. Thus, we conclude that the higher Fourier coefficients are mainly dependent on the random initial conditions and are therefore randomly distributed. On average, the network topology is therefore dominated by the first Fourier coefficients leading to the observed delay modulation.

Appropriate selection of the first Fourier coefficients leads to cluster states with a given common frequency. As an example, we have quenched the oscillations in a Stuart-Landau oscillator. This allows for construction of networks that exhibit a desired dynamical behavior.

In many real-world networks not all links are accessible to control. Therefore, we have considered random networks, where we have chosen a random subset of links to which we applied the adaptation algorithm. The other links remained fixed. We have found that the control is successful if the number of adapted links is equal or higher than approximately 30 % of all possible links, independently of the number of actual fixed links. For practical applications this opens up the possibility to apply the method more easily.

Since we have considered the paradigmatic Stuart-Landau oscillator as a generic model of the Hopf bifurcation, we expect broad applicability to control, for instance, synchronization of networks in medicine, chemistry or mechanical engineering or as self-organizing mechanisms in biological networks.