Analytical, Optimal, and Sparse Optimal Control of Traveling Wave Solutions to Reaction-Diffusion Systems

Abstract

This work deals with the position control of selected patterns in reaction-diffusion systems. Exemplarily, the Schlögl and FitzHugh-Nagumo model are discussed using three different approaches. First, an analytical solution is proposed. Second, the standard optimal control procedure is applied. The third approach extends standard optimal control to so-called sparse optimal control that results in very localized control signals and allows the analysis of second order optimality conditions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Beside the well-known Turing patterns, reaction-diffusion (RD) systems possess a rich variety of self-organized spatio-temporal wave patterns including propagating fronts, solitary excitation pulses, and periodic pulse trains in one-dimensional media. These patterns are “building blocks” of wave patterns like target patterns, wave segments, and spiral waves in two as well as scroll waves in three spatial dimensions, respectively. Another important class of RD patterns are stationary, breathing, and moving localized spots [1–7].

Several control strategies have been developed for purposeful manipulation of wave dynamics as the application of closed-loop or feedback-mediated control loops with and without delays [8–11] and open-loop control that includes external spatio-temporal forcing [10, 12–14], optimal control [15–17], and control by imposed geometric constraints and heterogeneities on the medium [18, 19]. While feedback-mediated control relies on a continuous monitoring of the system’s state, open-loop control is based on a detailed knowledge of the system’s dynamics and its parameters.

Experimentally, feedback control loops have been developed for the photosensitive Belousov-Zhabotinsky (BZ) reaction. The feedback signals are obtained from wave activity measured at one or several detector points, along detector lines, or in a spatially extended control domain including global feedback control [8, 9, 20]. Varying the excitability of the light-sensitive BZ medium by changing the globally applied light intensity forces a spiral wave tip to describe a wide range of hypocycloidal and epicycloidal trajectories [21, 22]. Moreover, feedback-mediated control loops have been applied successfully in order to stabilize unstable patterns in experiments such as unstable traveling wave segments and spots [11]. Two feedback loops were used to guide unstable wave segments in the BZ reaction along pre-given trajectories [23]. An open loop control was successfully deployed in dragging traveling chemical pulses of adsorbed CO during heterogeneous catalysis on platinum single crystal surfaces [24]. In these experiments, the pulse velocity was controlled by a laser beam creating a movable localized temperature heterogeneity on an addressable catalyst surface, resulting in a V-shaped pattern [25]. Dragging a one-dimensional chemical front or phase interface to a new position by anchoring it to a movable parameter heterogeneity was studied theoretically in [26, 27].

Recently, an open-loop control for controlling the position of traveling waves over time according to a prescribed protocol of motion $\vec {\phi }(t)$ was proposed that preserves simultaneously the wave profile [28]. Although position control is realized by external spatio-temporal forcing, i.e., it is an open-loop control, no detailed knowledge about the reaction dynamics as well as the system parameters is needed. We have already demonstrated the ability of position control to accelerate or decelerate traveling fronts and pulses in one spatial dimension for a variety of RD models [29, 30]. In particular, we found that the analytically derived control function is close to a numerically obtained optimal control solution. A similar approach allows to control the two-dimensional shape of traveling wave solutions. Control signals that realize a desired wave shape are determined analytically from nonlinear evolution equations for isoconcentration lines as the perturbed nonlinear phase diffusion equation or the perturbed linear eikonal equation [31]. In the work at hand, we compare our analytic approach for position control with optimal trajectory tracking of RD patterns in more detail. In particular, we quantify the difference between an analytical solution and a numerically obtained result to optimal control. Thereby, we determine the conditions under which the numerical result approaches the analytical result. This establishes a basis for using analytical solutions to speed up numerical computations of optimal control and serves as a consistency check for numerical algorithms.

We consider the following controlled RD system

$$\begin{aligned} \partial _t \vec {u}(\vec {x},t) - {\mathcal {D}} \varDelta \vec {u}(\vec {x},t) + \vec {R}(\vec {u}(\vec {x},t)) = {\mathcal {B}}\vec {f}(\vec {x},t). \end{aligned}$$

(10.1)

Here, $\vec {u}(\vec {x},t)=(u_1(\vec {x},t),\dots ,u_n(\vec {x},t))^T$ is a vector of n state components in a bounded or unbounded spatial domain $\varOmega \subset \mathbb {R}^N$ of dimension $N \in \{1,2,3\}$. ${\mathcal {D}}$ is an $n\times n$ matrix of diffusion coefficients which is assumed to be diagonal, ${\mathcal {D}}=\mathrm {diag}(D_1,\ldots ,D_n)$, because the medium is presumed to be isotropic. $\varDelta$ represents the N-dimensional Laplace operator and $\vec {R}$ denotes the vector of n reaction kinetics which, in general, are nonlinear functions of the state. The vector of control signals $\vec {f}(\vec {x},t)=(f_1(\vec {x},t),\dots ,f_m(\vec {x},t))^T$ acts at all times and everywhere within the spatial domain $\varOmega$. The latter assumption is rarely justified in experiments, where the application of control signals is often restricted to subsets of $\varOmega$. However, notable exceptions as, e.g., the already mentioned photosensitive BZ reaction, exist. Here, the light intensity is deployed as the control signal such that the control acts everywhere within a two-dimensional domain.

Equation (10.1) must be supplemented with an initial condition $\vec {u}(\vec {x},t_0)=\vec {u}_0(\vec {x})$ and appropriate boundary conditions. A common choice are no-flux boundary conditions at the boundary $\varSigma = \partial \varOmega \times (0,T)$, $\partial _n \vec {u}(\vec {x},t) = \vec {0}$, where $\partial _n \vec {u}$ denotes the component-wise spatial derivative in the direction normal to the boundary $\varGamma = \partial \varOmega$ of the spatial domain.

Typically, the number m of independent control signals in Eq. (10.1) is smaller than the number n of state components. We call such a system an underactuated system. The $n\times m$ matrix ${\mathcal {B}}$ determines which state components are directly affected by the control signals. If $m=n$ and the matrix ${\mathcal {B}}$ is regular, it is called a fully actuated system.

Our main goal is to identify a control $\vec {f}$ such that the state $\vec {u}$ follows a desired spatio-temporal trajectory $\vec {u}_d$, also called a desired distribution, as closely as possible everywhere in space $\varOmega$ and for all times $0 \le t\le T$. We can measure the distance between the actual solution $\vec {u}$ of the controlled RD system Eq. (10.1) and the desired trajectory $\vec {u}_d$ up to the terminal time T with the non-negative functional

$$\begin{aligned} J(\vec {u}) =&\Vert \vec {u} - \vec {u}_d\Vert _{L^2(Q)}^2, \end{aligned}$$

(10.2)

where $\Vert \cdot \Vert _{L^2(Q)}^2$ is the $L^2$-norm defined by

$$\begin{aligned} \Vert \vec {h} \Vert _{L^2(Q)}^2 =&\int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ \vec {h}(\vec {x},t)^2 \right\} , \end{aligned}$$

(10.3)

in the space-time-cylinder $Q{:}= \varOmega \times (0,T)$. The functional Eq. (10.2) reaches its smallest possible value, $J=0$ if and only if the controlled state $\vec {u}$ equals the desired trajectory almost everywhere in time and space.

In many cases, the desired trajectory $\vec {u}_d$ cannot be realized exactly by the control, cf. Ref. [32], for examples. However, one might be able to find a control which enforces the state $\vec {u}$ to follow $\vec {u}_d$ as closely as possible as measured by J. A control $\vec {f} = \vec {\bar{f}}$ is optimal if it realizes a state $\vec {u}$ which minimizes J. The method of optimal control views J as a constrained functional subject to $\vec {u}$ satisfying the controlled RD system Eq. (10.1).

Often, the minimum of the objective functional J, Eq. (10.2), does not exist within appropriate function spaces. Consider, for example, the assumption that the controlled state, obtained as a solution to the optimization problem, is continuous in time and space. Despite that a discontinuous state $\vec {u}$, leading to a smaller value for $J(\vec {u})$ than any continuous function, might exist, this state is not regarded as a solution to the optimization problem. Furthermore, a control enforcing a discontinuous state may diverge at exactly the points of discontinuity; examples in the context of dynamical systems are discussed in Ref. [32]. For that reason, the unregularized optimization problem, Eq. (10.2), is also called a singular optimal control problem. To ensure the existence of a minimum of J within appropriate function spaces and bounded control signals, additional (inequality) constraints such as bounds for the control signal can be introduced, cf. Ref. [33]. Alternatively, it is possible to add a so-called Tikhonov-regularization term to the functional Eq. (10.2) which is quadratic in the control,

$$\begin{aligned} J(\vec {u},\vec {f}) = \Vert \vec {u} - \vec {u}_d\Vert _{L^2(Q)}^2 + \nu \Vert \vec {f}\Vert _{L^2(Q)}^2. \end{aligned}$$

(10.4)

The $L^2$-norm of the control $\vec {f}$ is weighted by a small coefficient $\nu >0$. This term might be interpreted as a control cost to achieve a certain state $\vec {u}$. Since the control $\vec {f}$ does not come for free, there is a “price” to pay. In numerical computations, $\nu >0$ serves as a regularization parameter that stabilizes the algorithm. For the numerical results shown in later sections, we typically choose $\nu$ in the range $10^{-8} \le \nu \le 10^{-3}$. While $\nu >0$ guarantees the existence of an optimal control $\vec {f}$ in one and two spatial dimensions even in the absence of bounds on the control signal [33], it is not known whether Tikhonov-regularization alone also works in spatial dimensions N larger than two. Here, we restrict our investigations to one and two spatial dimensions. The presence of the regularization term causes the states to be further away from the desired trajectories than in the case of $\nu = 0$. Thus, the case $\nu =0$ is of special interest. Naturally, the solution $\vec {u}$ for $\nu = 0$ is the closest (in the $L^2(Q)$-sense) to the desired trajectory $\vec {u}_d$ among all optimal solutions associated with any $\nu \ge 0$. Therefore, it can be seen as the limit of realizability of a certain desired trajectory $\vec {u}_d$.

In addition to the weighted $L^2$-norm of the control, other terms can be added to the functional Eq. (10.4). An interesting choice is the weighted $L^1$-norm such that the functional reads

$$\begin{aligned} J(\vec {u},\vec {f}) = \Vert \vec {u} - \vec {u}_d\Vert _{L^2(Q)}^2 + \nu \Vert \vec {f}\Vert _{L^2(Q)}^2 + \kappa \Vert \vec {f}\Vert _{L^1(Q)}. \end{aligned}$$

(10.5)

For appropriate values of $\kappa >0$, the corresponding optimal control becomes sparse, i.e., it only acts in some localized regions of the space-time-cylinder, while it vanishes identically everywhere else. Therefore, it is also called sparse control or sparse optimal control in the literature, see Refs. [34–37]. In some sense, we can interpret the areas with non-vanishing sparse optimal control signals as the most sensitive areas of the RD patterns with respect to the desired control goal. A manipulation of the RD pattern in these areas is most efficient, while control signals applied in other regions have only weak impact. Furthermore, the weighted $L^1$-norm enables the analysis of solutions with a Tikhonov-regularization parameter $\nu$ tending to zero. This allows to draw conclusions about the approximation of solutions to unregularized problems by regularized ones.

In Sect. 10.2, we present an analytical approach for the control of the position of RD patterns in fully actuated systems. These analytical expressions are solutions to the unregularized ($\nu =0$) optimization problem, Eq. (10.2), and might provide an appropriate initial guess for numerical optimal control algorithms. Notably, neither the controlled state nor the control signal suffering from the problems are usually associated with unregularized optimal control; both expressions yield continuous and bounded solutions under certain assumptions postulated in Sect. 10.2. In Sect. 10.3, we explicitly state the optimal control problem for traveling wave solutions to the Schlögl [1, 38] and the FitzHugh-Nagumo model [39, 40]. Both are well-known models to describe traveling fronts and pulses in one spatial dimension, solitary spots and spiral waves in two spatial dimensions, and scroll waves in three spatial dimensions [4, 10, 41, 42]. We compare the analytical solutions from Sect. 10.2 with a numerically obtained regularized optimal control solution for the position control of a traveling front solution in the one-dimensional Schlögl model in Sect. 10.3.3. In particular, we demonstrate the convergence of the numerical result to the analytical solution for decreasing values $\nu$. The agreement becomes perfect within numerical accuracy if $\nu$ is chosen sufficiently small. Section 10.4 discusses sparse optimal control in detail and presents numerical examples obtained for the FitzHugh-Nagumo system. Finally, we conclude our findings in Sect. 10.5.

2 Analytical Approach

Below, we sketch the idea of analytical position control of RD patterns proposed previously in Refs. [28, 29]. For simplicity, we consider a single-component RD system of the form

$$\begin{aligned} \displaystyle \ \partial _t u(x,t) - D \partial _x^2 u(x,t) + R(u(x,t)) = f(x,t), \end{aligned}$$

(10.6)

in a one-dimensional infinitely extended spatial domain $\varOmega = \mathbb {R}$. The state u as well as the control signal f are scalar functions and the system Eq. (10.6) is fully actuated. Usually, Eq. (10.6) is viewed as a differential equation for the state u with the control signal f acting as an inhomogeneity. Alternatively, Eq. (10.6) can also be seen as an expression for the control signal. Exploiting this relation, one simply inserts the desired trajectory $u_d$ for u in Eq. (10.6) and obtains for the control

$$\begin{aligned} f(x,t)=\displaystyle \partial _t u_d(x,t) - D \partial _x^2 u_d(x,t) + R(u_d(x,t)). \end{aligned}$$

(10.7)

In the following, we assume that the desired trajectory $u_d$ is sufficiently smooth everywhere in the space-time-cylinder Q such that the evaluation of the derivatives $\partial _t u_d$ and $\partial _x^2 u_d$ yields continuous expressions. We call a desired trajectory $u_d$ exactly realizable if the controlled state u equals $u_d$ everywhere in Q, i.e., $u(x,t) = u_d(x,t)$. For the control signal given by Eq. (10.7), this can only be true if two more conditions are satisfied. First, the initial condition for the controlled state must coincide with the initial state of the desired trajectory, i.e., $u(x,t_0) = u_d(x,t_0)$. Second, all boundary conditions obeyed by u have to be obeyed by the desired trajectory $u_d$ as well. Because of $u(x,t) = u_d(x,t)$, the corresponding unregularized functional J, Eq. (10.2), vanishes identically. Thus, the control f is certainly a control which minimizes the unregularized functional J and, in particular, it is optimal.

In conclusion, we found a solution to the unregularized optimization problem Eq. (10.2). The solution for the controlled state is simply $u(x,t) = u_d(x,t)$, while the solution for the control signal is given by Eq. (10.7). Even though we are dealing with an unregularized optimization problem, the control signal as well as the controlled state are continuous and bounded functions, provided that the desired trajectory $u_d$ is sufficiently smooth in space and time.

Generalizing the procedure to multi-component RD systems in multiple spatial dimensions, the expression for the control reads

$$\begin{aligned} \vec {f}(x,t) = {\mathcal {B}}^{-1}(\displaystyle \partial _t \vec {u}_d(x,t) - \vec {\mathcal {D}} \varDelta \vec {u}_d(x,t) + \vec {R}(\vec {u}_d(x,t))). \end{aligned}$$

(10.8)

Once more, the initial and boundary conditions for the desired trajectory $\vec {u}_d$ have to comply with the initial and boundary conditions of the state $\vec {u}$. Clearly, the inverse of $\vec {\mathcal {B}}$ exists if and only if $\vec {\mathcal {B}}$ is a regular square matrix, i.e., the system must be fully actuated. We emphasize the generality of the result. Apart from mild conditions on the smoothness of the desired distributions $\vec {u}_d$, Eq. (10.8) yields a simple expression for the control signal for arbitrary $\vec {u}_d$.

Next, we exemplarily consider the position control of traveling waves (TW) in one spatial dimension. Traveling waves are solutions to the uncontrolled RD system, i.e., Eq. (10.1) with $\vec {f}= \vec {0}$. They are characterized by a wave profile $\vec {u}(x,t)=\vec {U}_c(x-c\,t)$ which is stationary in a frame of reference $\xi =x-ct$ co-moving with velocity c. The wave profile $\vec {U}_c$ satisfies the following ordinary differential equation (ODE),

$$\begin{aligned} \displaystyle \vec {\mathcal {D}} \vec {U}_c''(\xi )+c\vec {U}_c'(\xi ) - \vec {R}(\vec {U}_c(\xi )) = \vec {0},\quad \xi \in \varOmega \subset \mathbb {R}. \end{aligned}$$

(10.9)

The prime denotes differentiation with respect to $\xi$. Note that stationary solutions with a vanishing propagation velocity $c = 0$ are also considered as traveling waves. The ODE for the wave profile, Eq. (10.9), can exhibit one or more homogeneous steady states. Typically, the wave profile $\vec {U}_c$ approaches either two different steady states or the same steady state for $\xi \rightarrow \pm \infty$. This fact can be used to classify traveling wave profiles. Front profiles connect different steady states for $\xi \rightarrow \pm \infty$ and are found to be heteroclinic orbits of Eq. (10.9). Pulse profiles join the same steady state and are found to be homoclinic orbits [43]. Furthermore, all TW solutions are localized in the sense that their spatial derivatives of any order $m\ge 1$ decay to zero, $\lim _{\xi \rightarrow \pm \infty } \partial _\xi ^m \vec {U}_c(\xi )=0$.

We propose a spatio-temporal control signal $\vec f(x,t)$ which shifts the traveling wave according to a prescribed protocol of motion $\phi (t)$ while simultaneously preserving the uncontrolled wave profile $\vec {U}_c$. Correspondingly, the desired trajectory reads

$$\begin{aligned} \vec {u}_d(x,t)=\vec {U}_c(x-\phi (t)). \end{aligned}$$

(10.10)

Note that the desired trajectory is localized for all values of $\phi (t)$ because the TW profile $\vec {U}_c$ is localized. The initial condition for the state is $\vec {u}(x,t_0)=\vec {U}_c(x-x_0)$ which fixes the initial value of the protocol of motion as $\phi (t_0)=x_0$. Then, the solution Eq. (10.8) for the control signal becomes

$$\begin{aligned} \vec {f}(x,t) = {\mathcal {B}}^{-1}(\displaystyle -\dot{\phi }(t)\vec {U}_c'(x-\phi (t)) - {\mathcal {D}}\vec {U}_c''(x-\phi (t)) + \vec {R}(\vec {U}_c(x-\phi (t))) \end{aligned}$$

(10.11)

with $\dot{\phi }(t)$ denoting the derivative of $\phi (t)$ with respect to time t. Using Eq. (10.9) to eliminate the non-linear reaction kinetics $\vec {R}$, we finally obtain the following analytical expression for the control signal

$$\begin{aligned} \vec {f}(x,t) = (\displaystyle c-\dot{\phi }(t)){\mathcal {B}}^{-1}\vec {U}_c'(x-\phi (t)) =: \vec {f}_\mathrm {an}. \end{aligned}$$

(10.12)

Remarkably, any reference to the reaction function $\vec {R}$ drops out from the expression for the control. This is of great advantage for applications without or with only incomplete knowledge of the underlying reaction kinetics $\vec {R}$. The method is applicable as long as the propagation velocity c is known and the uncontrolled wave profile $\vec {U}_c$ can be measured with sufficient accuracy to calculate the derivative $\vec {U}_c'$.

Being an open loop control, a general problem of the proposed position control is its possible inherent instability against perturbations of the initial conditions as well as other data uncertainty. However, assuming protocol velocities $\dot{\phi }(t)$ close to the uncontrolled velocity c, $\dot{\phi }\sim c$, the control signal Eq. (10.12) is small in amplitude and enforces a wave which is relatively close to the uncontrolled TW. Since the uncontrolled TW is presumed to be stable, the controlled TW might benefit from that and a stable open loop control is expected. This expectation is confirmed numerically for a variety of controlled RD systems [28] and also analytically in Ref. [29].

Despite the advantages of our analytical solution stated above, there are limits for it as well. The restriction to fully actuated systems, i.e., systems for which ${\mathcal {B}}^{-1}$ exists, is not always practical. In experiments with RD systems, the number of state components is usually much larger than one, while the number of control signals is often restricted to one or two. Thus, the question arises if the approach can be extended to underactuated systems with a number of independent control signals smaller than the number of state components. This is indeed the case but entails additional assumptions about the desired trajectory. In the context of position control of TWs, it leads to a control which is not able to preserve the TW profile for all state components, see Ref. [28]. The general case is discussed in the thesis [32] and is not part of this paper.

Moreover, in applications, it is often necessary to impose inequality constraints in form of upper and lower bounds on the control. For example, the intensity of a heat source deployed as control is bounded by technical reasons. Even worse, if the control is the temperature itself, it is impossible to attain negative values. Since the control signal $\vec {f}_\mathrm {an}$ for position control is proportional to the slope of the controlled wave profile $\vec {U}_c'$, the magnitude of the applied control may locally attain non-realizable values. In our analytic approach no bounds for the control signal are imposed. The control signal $\vec {f}$ as given by Eq. (10.8) is optimal only in case of a vanishing Tikhonov-regularization parameter $\nu =0$, cf. Eq. (10.4). Moreover, desired trajectories $\vec {u}_d$ which do not comply with initial as well as boundary conditions or are non-smooth might be requested. Lastly, the control signal $\vec {f}$ cannot be used in systems where only a restricted region of the spatial domain $\varOmega$ is accessible by control. While all these cases cannot be treated within the analytical approach proposed here, optimal control can deal with many of these complications.

3 Optimal Control

In the following, we recall the optimal control problem and sketch the most important analytical results to provide the optimality system.

3.1 The Control Problem

For simplicity, we explicitly state the optimal control problem for the FitzHugh-Nagumo system [39, 40]. The FitzHugh-Nagumo system is a two-component model $\vec {u} = (u,v)^T$ for an activator u and an inhibitor v,

$$\begin{aligned} \begin{array}{rcl} \displaystyle \partial _t u(\vec {x},t) - \varDelta u(\vec {x},t) + R(u(\vec {x},t)) + \alpha \, v(\vec {x},t) &{} = &{}f(\vec {x},t), \\ \displaystyle \partial _t v(\vec {x},t) + \beta \, v(\vec {x},t) - \gamma \,u(\vec {x},t) + \delta &{} = &{} 0, \end{array} \end{aligned}$$

(10.13)

in a bounded Lipschitz-domain $\varOmega \subset \mathbb {R}^N$ of dimension $1 \le N \le 3$. Since the single-component control f appears solely on the right-hand side of the first equation, this system is underactuated. Allowing a control in the second equation is fairly analogous. The kinetic parameters $\alpha$, $\beta$, $\gamma$, and $\delta$ are real numbers with $\beta \ge 0$. Moreover, the reaction kinetics are given by the nonlinear function $R(u)=u(u-a)(u-1)$ for $0 \le a \le 1$. Note that the equation for the activator u decouples from the equation for the inhibitor v for $\alpha = 0$, cf. Eq. (10.13), resulting in the Schlögl model [1, 38], sometimes also called the Nagumo model. We assume homogeneous Neumann-boundary conditions for the activator u and $u(\vec {x},0) = u_0(\vec {x})$, $v(\vec {x},0) = v_0(\vec {x})$ are given initial states belonging to $L^\infty (\varOmega )$, i.e., they are bounded.

The aim of our control problem is the tracking of desired trajectories $\vec {u}_d = (u_d,v_d)^T$ in the space-time cylinder Q and to reach desired terminal states $\vec {u}_T= (u_T,v_T)^T$ at the final time T. In contrast to the analytic approach from Sect. 10.2, these desired trajectories are neither assumed to be smooth nor compatible with the given initial data or boundary conditions. For simplicity, we assume their boundedness, i.e., $(u_d,v_d)^T \in \left( L^\infty (Q)\right) ^2$ and $(u_T, v_T)^T \in \left( L^\infty (\varOmega )\right) ^2$. The goal of reaching the desired states is expressed as the minimization of the objective functional

$$\begin{aligned} \begin{aligned} J(u,v,f) =&\, \frac{1}{2}\left( c_T^U\Vert u(\,\cdot ,T)-u_T\Vert _{L^2(\varOmega )}^2 + c_T^V\Vert v(\,\cdot ,T)-v_T\Vert _{L^2(\varOmega )}^2\right) \\&+ \frac{1}{2}\left( c_d^U\Vert u-u_d\Vert _{L^2(Q)}^2 + c_d^V\Vert v-v_d\Vert _{L^2(Q)}^2\right) + \frac{\nu }{2}\Vert f\Vert _{L^2(Q)}^2. \end{aligned}\end{aligned}$$

(10.14)

This functional is slightly more general than the one given by Eq. (10.2) because it also takes into account the terminal states. We emphasize that the given non-negative coefficients $c_d^U,\, c_d^V, \, c_T^U$, and $c_T^V$ can also be chosen as functions depending on space and time. In some applications, this turns out to be very useful [44]. The control signals can be taken out of the set of admissible controls

$$\begin{aligned} \mathcal {F}_{\mathrm{ad}}= \{f \in L^\infty (Q) : f_a \le f(\vec {x},t) \le f_b,\ \text { for } (\vec {x},t) \in Q\}. \end{aligned}$$

(10.15)

The bounds $-\infty< f_a< f_b < \infty$ model the technical capacities for generating controls.

Under the previous assumptions, the controlled RD equations (10.13) have a unique weak solution denoted by $(u_f,v_f)^T$ for a given control $f \in \mathcal {F}_{\mathrm{ad}}$. This solution is bounded, i.e., $u_f,\, v_f \in L^\infty (Q)$, cf. [44]. If the initial data $(u_0, v_0)^T$ are continuous, then $u_f$ and $v_f$ are continuous on ${\bar{\varOmega }} \times [0,T]$ with ${\bar{\varOmega }}=\varOmega \cup \partial \varOmega$ as well. Moreover, the control-to-state mapping $G:=f \mapsto (u_f,v_f)^T$ is twice continuously (Frèchet-) differentiable. A proof can be found in Ref. [44, Theorem 2.1, Corollary 2.1, and Theorem 2.2]. Expressed in terms of the solution $(u_f,v_f)^T$, the value of the objective functional depends only on f, $J(u,v,f) =J(u_f,v_f,f) =: F(f)$, and the optimal control problem can be formulated in a condensed form as

$$\begin{aligned} \mathrm{(P)} \qquad \mathrm{Min} \ F(f), \quad f \in \mathcal {F}_{\mathrm{ad}}. \end{aligned}$$

(10.16)

Referring to [44, Theorem 3.1], we know that the control problem (P) has at least one (optimal) solution $\bar{f}$ for all $\nu \ge 0$. To determine this solution numerically, we need the first and second-order derivatives of the objective functional F. Since the mapping $f \mapsto (u,v)^T$ is twice continuously differentiable, so is $F:L^p(Q) \longrightarrow \mathbb {R}$. Its first derivative $F'(f)$ in the direction $h\in L^p(Q)$ can be computed as follows:

$$\begin{aligned} F'(f)h = \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ (\varphi _f + \nu f)h \right\} , \end{aligned}$$

(10.17)

where $\varphi _f$ denotes the first component of the so-called adjoint state $(\varphi _f,\psi _f)$. It solves a linearized FitzHugh-Nagumo system, backwards in time,

$$\begin{aligned} \begin{array}{rcl} \displaystyle -\partial _t \varphi _f - \varDelta \varphi _f + R^\prime (u_f)\varphi _f - \gamma \, \psi _f &{} = &{}c_d^U(u_f-u_d), \\ \displaystyle -\partial _t \psi _f + \beta \, \psi _f + \alpha \,\varphi _f &{} = &{} c_d^V(v_f-v_d) \end{array} \end{aligned}$$

(10.18)

with homogeneous Neumann-boundary and terminal conditions $\varphi _f(\vec {x},T) = c_T^U(u_f(\vec {x},T)-u_T(\vec {x}))$ and $\psi _f(\vec {x},T) = c_T^V(v_f(\vec {x},T)-v_T(\vec {x}))$ in $\varOmega$.

This first derivative is used in numerical methods of gradient type. Higher order methods of Newton type need also the second derivative $F^{\prime \prime }(f)$. It reads

$$\begin{aligned} \begin{aligned} F''(f)h^2 =&\int \limits _\varOmega d\vec {x}\,\left\{ c_T^U\eta _{h}(\vec {x},T)^2 + c_T^V\zeta _{h}(\vec {x},T)^2 \right\} \\&+ \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ [c_d^U - R''(u_f)\varphi _f]\eta _{h}^2+ c_d^V\zeta _{h}^2 \right\} + \nu \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ h^2 \right\} \end{aligned}\end{aligned}$$

(10.19)

in a single direction $h \in L^p(Q)$. In this expression, the state $(\eta _{h},\zeta _{h}) := G^\prime (f)h$ denotes the solution of a linearized FitzHugh-Nagumo system similar to Eq. (10.18), see Ref. [44, Theorem 2.2] for more information.

3.2 First-Order Optimality Conditions

We emphasize that the control problem (P) is not necessarily convex. Although the objective functional J(u, v, f) is convex, in general, the nonlinearity of the mapping $f \mapsto (u_f,v_f)^T$ will lead to a non-convex functional, F. Therefore, (P) is a problem of non-convex optimization, possibly leading to several local minima instead of a single global minimum.

As in standard calculus, we invoke first-order necessary optimality conditions to find a (locally) optimal control f, denoted by $\bar{f}$. In the case of unconstrained control, i.e., $\mathcal {F}_{\mathrm{ad}}:= L^p(Q)$, the first derivative of F must be zero, $F^\prime (\bar{f}) = 0$. Computationally, this condition is better expressed in the weak formulation

$$\begin{aligned} F^\prime (\bar{f})f = \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ (\bar{\varphi }+ \nu \bar{f})f \right\} = 0\quad \forall f \in L^p(Q) \end{aligned}$$

(10.20)

where $\bar{\varphi }$ denotes the first component of the adjoint state associated with $\bar{f}$. If $\bar{f}$ is not locally optimal, one finds a descent direction d such that $F^\prime (\bar{f})d < 0$. This is used for methods of gradient type.

If the restrictions $\mathcal {F}_{\mathrm{ad}}$ are given by Eq. (10.15), then Eq. (10.20) does not hold true in general. Instead, the variational inequality

$$\begin{aligned} F^\prime (\bar{f})(f - \bar{f}) = \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ (\bar{\varphi }+ \nu \bar{f})(f - \bar{f}) \right\} \ge 0\quad \forall f \in \mathcal {F}_{\mathrm{ad}}\cap U(\bar{f}) \end{aligned}$$

(10.21)

must be fulfilled, cf. [45]. Here, $U(\bar{f}) \subset L^p(Q)$ denotes a neighborhood of $\bar{f}$. Roughly speaking, it says that in a local minimum we cannot find an admissible direction of descent. A gradient method would stop in such a point. A pointwise discussion of Eq. (10.21) leads to the following identity:

$$\begin{aligned} \displaystyle \bar{f}(\vec {x},t) = \mathrm{Proj}_{[f_a,f_b]}\left( -\frac{1}{\nu }[\bar{\varphi }(\vec {x},t)]\right) \quad \text { for } \nu > 0. \end{aligned}$$

(10.22)

Here, $\mathrm{Proj}_{[f_a,f_b]}(x) = \min \{\max \{f_a , x\}, f_b\}$ denotes the projection to the interval $[f_a,f_b]$ such that $\bar{f}(\vec {x},t)$ belongs to the set of admissible controls $\mathcal {F}_{\mathrm{ad}}$ defined in Eq. (10.15). According to Eq. (10.22), as long as $\bar{\varphi }$ does not vanish, a decreasing value $\nu \ge 0$ yields an optimal control growing in amplitude until it attains its bounds $f_a$ or $f_b$, respectively. Thus, the variational inequality Eq. (10.21) leads to so-called bang-bang-controls [45] for $\nu =0$ and $\bar{\varphi }\ne 0$. These are control signals which attain its maximal or minimal possible values for all times and everywhere in the spatial domain $\varOmega$. A notable exception is the case of exactly realizable desired trajectories and $\nu =0$, already discussed in Sect. 10.2. In this case, it can be shown that $\bar{\varphi }$ vanishes [32] and Eq. (10.22) cannot be used to determine the control signal $\bar{f}$.

Numerically, solutions to optimal control are obtained by solving the controlled RD system Eq. (10.13) and the adjoint system, Eq. (10.18), such that the last identity, Eq. (10.22), is fulfilled. In numerical computations with very large or even missing bounds $f_a,\,f_b$, Eq. (10.22) becomes ill-conditioned if $\nu$ is close to zero. This might lead to large roundoff errors in the computation of the control signal and can affect the stability of numerical optimal control algorithms.

3.3 Example 1: Analytical and Optimal Position Control

In 1972, Schlögl discussed the auto-catalytic trimolecular RD scheme [1, 38] as a prototype of a non-equilibrium first order phase transition. The reaction kinetics R for the chemical with concentration u(x, t) is cubic and can be casted into the dimensional form $R(u) = u(u-a)(u-1)$. The associated controlled RD equation reads

$$\begin{aligned} \partial _t u- \partial _x^2 u + u\left( u-a\right) \left( u-1\right) =\,f(x,t),\quad 0<a<1, \end{aligned}$$

in one spatial dimension, $\varOmega = \mathbb {R}$. A linear stability analysis of the uncontrolled system reveals that $u=0$ and $u=1$ are spatially homogeneous stable steady states (HSS), while $u=a$ is an unstable homogeneous steady state. In an infinite one-dimensional domain, the Schlögl model possesses a stable traveling front solution whose profile is given by

$$\begin{aligned} U_c(\xi ) = 1/\left( 1+\exp \left( \xi /\sqrt{2}\right) \right) \end{aligned}$$

(10.23)

in the frame of reference $\xi =x-c\,t$ co-moving with front velocity c. This front solution establishes a heteroclinic connection between the two stable HSS for $\xi \rightarrow \pm \infty$ and travels with a velocity $c = \left( 1-2\,a\right) /\sqrt{2}$ from the left to the right.

As an example, we aim to accelerate a traveling front according to the following protocol of motion

$$\begin{aligned} \phi (t) = -10 + c \,t + \displaystyle \frac{10-1/\sqrt{2}}{200} \, t^2, \end{aligned}$$

(10.24)

while keeping the front profile as close as possible to the uncontrolled one. In other words, our desired trajectory reads $u_d(x,t) = U_c(x-\phi (t))$ and, consequently, the initial conditions of both the controlled and the desired trajectory are $u_0(x)=u_d(x,0)=U_c(x+10)$. In our numerical simulations, we set $T=20$ for the terminal time T, $\varOmega = (-25,25)$ for the spatial domain, and the threshold parameter is kept fixed at $a=9/20$. Additionally, we choose the terminal state to be equal to the desired trajectory, $u_T(x) = u_d(x,T)$, and set the remaining weighting coefficients to unity, $c_d^U = c_T^U = 1$, in the optimal control problem. The space-time plot of the desired trajectory $u_d$ is presented in Fig. 10.1a for the protocol of motion $\phi (t)$ given by Eq. (10.24).

Fig. 10.1

a Space-time plot of the desired trajectory $u_d(x,t) = U_c(x-\phi (t))$ with the protocol of motion $\phi (t)$ as given in Eq. (10.24), b analytic position control signal $f_\text {an}(x,t)$, Eq. (10.12), and c numerically obtained optimal control $\bar{f}$ for Tikhonov regularization parameter $\nu = 10^{-5}$ are presented. The magnitude of the control signal is color-coded. In the center panel (b), the dashed line represents $\phi (t)$. The remaining parameter values are $a=9/20$, $T=20$, and $c_d^U = c_T^U = 1$

Below, we compare the numerically obtained solution to the optimal control problem (P) with the analytical solution from Sect. 10.2 for the Schlögl model. The Schlögl model arises from Eq. (10.12) by setting $\alpha =0$ and ignoring the inhibitor variable v. Consequently, all weighting coefficients associated with the inhibitor trajectory are set to zero, $c_d^V = c_T^V = 0$, in the functional J, Eq. (10.14).

Figure 10.1b depicts the solution for the analytical position control $f_\text {an}$ which is valid for a vanishing Tikhonov regularization parameter $\nu = 0$. The numerically obtained optimal control $\bar{f}$ for $\nu = 10^{-5}$, shown in Fig. 10.1c, does not differ visually from the analytic one. Both are located at the front position where the slope is maximal, $\vec {u}_d=0.5$ (dashed line in Fig. 10.1b), and their magnitudes grow proportional to $\dot{\phi }(t)$. For a quantitative comparison, we compute the distance between analytical and optimal control signal $\Vert \bar{f} - f_\text {an}\Vert _2$ in the sense of $L^2(Q)$, Eq. (10.3), and normalize it by the size of the space-time-cylinder $|Q| = T\,|\varOmega |$,

$$\begin{aligned} \Vert h\Vert _2 := \frac{1}{|Q|}\Vert h\Vert _{L^2(Q)}. \end{aligned}$$

(10.25)

The top row of Table 10.1 displays the distance $\Vert \bar{f} - f_\text {an}\Vert _2$ as a function of the regularization parameter $\nu$. Even for a large value $\nu =1$, the distance is less than $5\times 10^{-4}$. Decreasing the value of $\nu$ results in a shrinking distance $\Vert \bar{f} - f_\text {an}\Vert _2$ until it saturates at $\simeq$ $8\times 10^{-6}$. The saturation is due to numerical and systematic errors. Numerical computations are affected by errors arising in the discretization of the spatio-temporal domain and the amplification of roundoff errors by the ill-conditioned expression for the control, Eq. (10.22). A systematic error arises because the optimal control is computed for a bounded interval $\varOmega =(-25,25)$ with homogeneous Neumann-boundary conditions while the analytical result is valid only for an infinite domain.

Table 10.1 The distance $\Vert \bar{f} - f_\text {an}\Vert _2$ between the analytical control signal $f_\text {an}$, valid for $\nu =0$, and the optimal control $\bar{f}$ obtained numerically for finite $\nu >0$ decreases with decreasing values of $\nu$ (top row). Similarly, the optimally controlled state trajectory $u_f$ approaches the desired trajectory $u_d$, measured by $\Vert u_f - u_d\Vert _2$, for smaller values of $\nu$ (bottom row)

Another interesting question is how close the controlled state $u_f$ approaches the desired trajectory $u_d$. The bottom row of Table 10.1 shows the distance between the optimally controlled state trajectory $u_f$ and the desired trajectory for different values $\nu$. Similarly as for the control signal, the difference lessens with decreasing values $\nu$. Note that the value does not saturate and becomes much smaller than the corresponding value for the difference between control signals. Here, no discretization errors arise because a discretized version of the desired trajectory is used as the target distribution. Nevertheless, systematic errors arise because neither the initial and final desired state nor the desired trajectory obey Neumann-boundary conditions. This results in an optimal control signal exhibiting bumps close to the domain boundaries. However, the violation of boundary conditions can be reduced by specifically designed protocols of motion. The further the protocol of motion keeps the controlled front away from any domain boundary the smaller is the violation of homogeneous Neumann-boundary conditions since the derivatives of traveling front solution Eq. (10.23) decay exponentially for large |x|. An alternative way of rigorously avoiding artifacts due to the violation of boundary conditions is the introduction of additional control terms acting on the domain boundaries, see Ref. [31].

For the example discussed above, the numerically obtained optimal control $\bar{f}$ for $\nu >0$ is computed with a Newton-Raphson-type root finding algorithm. This iterative algorithm relies on an initial guess for the control signal which is often chosen to be random or uniform in space. The closer the initial guess is to the final solution, the fewer steps are necessary for the Newton-Raphson method to converge to the final solution. The similarity of the numerically obtained and analytical control solution, see Fig. 10.1 and Table 10.1, motivates the utilization of the analytical result $f_\text {an}$ as an initial guess in numerical algorithms. Even for a simple single component RD system defined on a relatively small spatio-temporal domain Q as discussed in this section, the computational speedup is substantial. The algorithm requires only 2/3 of the computation time compared to random or uniform starting values for the control. In particular, we expect even larger speedups for simulations with larger domain sizes.

4 Sparse Optimal Control

In applications, it might be desirable to have localized controls acting only in some sub-areas of the domain. So-called sparse optimal controls provide such solutions without any a priori knowledge of these sub-areas. They result in a natural way because the control has the most efficient impact in these regions to minimize the objective functional.

For inverse problems, it has been observed that the use of an $L^1$-term in addition to the $L^2$-regularization leads to sparsity [46–48]. The idea to use the $L^1$-term goes back to Ref. [49].

To our knowledge, sparse optimal controls were first discussed in the context of optimal control in Ref. [34]. In that paper, an elliptic linear model was discussed. Several publications followed, investigating semi-linear elliptic equations, parabolic linear, and parabolic semi-linear equations; we refer, for instance, to Refs. [35–37] among others.

In this section, we follow the lines of Refs. [44, 50] and recall the most important results for the sparse optimal control of the Schlögl-model and the FitzHugh-Nagumo equation.

4.1 The Control Problem

In optimal control, sparsity is obtained by extending the objective functional J by a multiple of $j(f):= \Vert f\Vert _{L^1(Q)}$, the $L^1$-norm of the control f. Therefore, recalling that $J(u_f,v_f,f) =: \mathcal {F}(f)$, we consider the problem

$$ \mathrm {(P_{sp})} \qquad \mathrm{Min} \ \mathcal {F}(f) + \kappa \, j(f), \quad f \in \mathcal {F}_{\mathrm{ad}}$$

for $\kappa > 0$. The first part F of the objective functional is differentiable, while the $L^1$-part is not.

Our goal is not only to derive first-order optimality conditions as in the previous section but also to observe the behavior of the optimal solutions for increasing $\kappa$ and $\nu$ is tending to zero. For that task, we also need to introduce second-order optimality conditions.

As before, there exists at least one locally optimal solution f to the problem $\mathrm {(P_{sp})}$, denoted by $\bar{f}$. We refer to Ref. [44, Theorem 3.1] for more details. While $\mathcal {F}$ is twice continuously differentiable, the second part j(f) is only Lipschitz convex but not differentiable. For that reason, we need the so-called subdifferential of j(f). By subdifferential calculus and using directional derivatives of j(f), we are able to derive necessary optimality conditions.

4.2 First-Order Optimality Conditions

We recall some results from Refs. [44, 50]. Due to the presence of j(f) in the objective functional, there exists a $\bar{\lambda }\in \partial j(\bar{f})$ such that the variational inequality Eq. (10.21) changes to

$$\begin{aligned} \int \limits _0^T \int \limits _\varOmega d\vec {x}\,dt\,\left\{ (\bar{\varphi }+ \nu \bar{f} + \kappa \bar{\lambda })(f - \bar{f}) \right\} \ge 0\quad \forall f \in \mathcal {F}_{\mathrm{ad}}\cap U(\bar{f}). \end{aligned}$$

(10.26)

For the problem $\mathrm {(P_{sp})}$, a detailed and extensive discussion of the first-order necessary optimality condition leads to very interesting conclusions, namely

$$\begin{aligned} \displaystyle \bar{f}(\vec {x},t)&= 0, \text { if and only if } |\bar{\varphi }(\vec {x},t)| \le \kappa ,\end{aligned}$$

(10.27)

$$\begin{aligned} \displaystyle \bar{f}(\vec {x},t)&= \mathrm{Proj}_{[f_a,f_b]}\left( -\frac{1}{\nu }[\bar{\varphi }(\vec {x},t)+\kappa \bar{\lambda }(\vec {x},t)]\right) ,\end{aligned}$$

(10.28)

$$\begin{aligned} \displaystyle \bar{\lambda }(\vec {x},t)&= \mathrm{Proj}_{[-1,+1]}\left( -\frac{1}{\kappa }\bar{\varphi }(\vec {x},t)\right) \end{aligned}$$

(10.29)

if $\nu > 0$. We refer to Refs. [36, Corollary 3.2] and [51, Theorem 3.1] in which the case $\nu = 0$ is discussed as well.

The relation in Eq. (10.27) leads to the sparsity of the (locally) optimal solution $\bar{f}$, depending on the sparsity parameter $\kappa$. In particular, the larger the choice of $\kappa$ is, the smaller does the support of $\bar{f}$ become. To be more precise, there exists a value $\kappa _0 > \infty$ such that for every $\kappa \ge \kappa _0$ the only local minimum $\bar{f}$ is equal to zero. Obviously, this case is ridiculous and thus, one needs some intuition to find a suitable value $\kappa$. We emphasize that $\bar{\lambda }$ is unique, see Eq. (10.29), which is important for numerical calculations.

4.3 Example 2: Optimal and Sparse Optimal Position Control

For the numerical computations, we follow the lines of Ref. [44] and use a non-linear conjugate gradient method. The advantage of using a (conjugate) gradient method lies in the simplicity in its implementation and in the robustness of the method to errors in the solution process. Moreover, it allows to solve the systems Eq. (10.13) and the adjoint system separately. The disadvantage is clearly the fact that it might cause a huge amount of iterations to converge, cf. Ref. [44, Sect. 4].

Hence, we modify our approach by the use of Model Predictive Control [52, 53]. The idea is quite simple: Instead of optimizing the whole time-horizon, we only take a very small number of time steps, formulate a sub-problem, and solve it. Then, the first computed time-step of the solution $\bar{f}$ of this smaller problem is accepted on $[0,t_1]$ and is fixed. A new sub-problem is defined by going one time-step further and so on. Although the control gained in this way is only sub-optimal, it leads to a much better convergence-behavior in many computations.

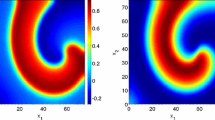
Next, we revisit the task to extinguish a spiral wave by controlling its tip dynamics such that the whole pattern moves out of the spatial domain towards the Neumann boundaries [9, 21, 54]. To this goal, following Ex. 6 from Ref. [44, Sect. 4], we set the protocol of motion to $\vec {\phi }(t) = \left( 0,\min \{120, 1/16\,t\}\right) ^T$ and $u_d(\vec {x},t) := u_\text {nat}(\vec {x}-\vec {\phi }(t),t),$ where $u_\text {nat}$ denotes the naturally developed spiral wave solution of the activator u to Eq. (10.13) for $f = 0$. In our numerical simulation, we take only 4 time-steps in each sub-problem of the receding horizon. Moreover, we set the kinetic parameters in the FHN model, Eq. (10.13), to $a = 0.005$, $\alpha = 1$, $\beta = 0.01$, $\gamma = 0.0075$, and $\delta = 0$. Further, we fix the simulation domain $\varOmega = (-120,120)\times (-120,120)$, the terminal time $T = 2000$, $\nu = 10^{-6}$ as Tikhonov parameter, and $f_a = -5$ and $f_b = 5$ as bounds for the control, respectively. As initial states $(u_0,v_0)^T$ a naturally developed spiral wave whose core is located at (0, 0) is used; $u_0$ is presented in Fig. 10.2a.

In addition, an observation-function $c_d^U \in L^\infty (Q)$ instead of the constant factor $c_d^U \in \mathbb {R}$ is used with a support restricted to the area close to the desired spiral-tip. To be more precise, $c_d^U(\vec {x},t) = 1$ holds only in the area defined by all $(\vec {x},t) \in Q$ such that $|\vec {x}-\bar{\vec {x}}(t)| \le 20$ and vanishes identically otherwise. The other coefficients $c_d^V$, $c_T^U$, and $c_T^V$ are set equal to zero.

The reason for the choice of such an observation-function is clear: a most intriguing property of spiral waves is that, despite being propagating waves affecting all accessible space, they behave as effectively localized particles-like objects [55]. The particle-like behavior of spirals corresponds to an effective localization of so called response functions [56, 57]. The asymptotic theory of the spiral wave drift [58] is based on the idea of summation of elementary responses of the spiral wave core position and rotation phase to elementary perturbations of different modalities and at different times and places. This is mathematically expressed in terms of the response functions. They decay quickly with distance from the spiral wave core and are almost equal to zero in the region where the spiral wave is insensitive to small perturbations.

Fig. 10.2

a Spiral wave solution of the activator u to Eq. (10.13) with $\vec {f}=0$. The latter is used as initial state $u_0(\vec {x})=u_\text {nat}(\vec {x}-\vec {\phi }(0),0)$ in the problem $\mathrm {(P_{sp})}$. b Numerically obtained sub-optimal control ($\kappa = 0$) and c sparse sub-optimal control solution ($\kappa = 1$), both shown in the $x_2$–t–plane for $x_1 = 0$ with associated spiral-tip trajectory (black line). The magnitude of the control signal is color-coded. The remaining system parameters are $a = 0.005$, $\alpha = 1$, $\beta = 0.01$, $\gamma = 0.0075$, and $\delta = 0$. In the optimal control algorithms, we set $\nu = 10^{-6}$, $f_a = -5$, and $f_b = 5$

The numerical results for the sup-optimal control ($\kappa = 0$) and for the sparse sub-optimal control ($\kappa = 1$) are depicted in Fig. 10.2b, c, respectively. One notices that the prescribed spiral tip trajectory is realized for both choices for the sparsity parameter $\kappa$, viz., $\kappa = 0$ and $\kappa = 1$. The traces of the spiral tip is indicated by the solid lines in both panels. Since the spiral tip rotates rigidly around the spiral core which moves itself on a straight line according to $\vec {\phi }(t)$, one observes a periodic motion of the tip in the $x_2$–t–plane. In addition, the area of non-zero control (colored areas) is obviously much smaller for non-zero sparsity parameter $\kappa$ compared to the case $\kappa = 0$ , cf. Fig. 10.2b, c. However, in this example we observed that the amplitude of the sparse control is twice as large compared to optimal control ($\kappa =0$).

4.4 Second-Order Optimality Conditions and Numerical Stability

To avoid this subsection to become too technical, we only state the main results from Ref. [50]. We know for an unconstrained problem with differentiable objective-functional that it is sufficient to show $F^\prime (\bar{f}) = 0$ and $F^{\prime \prime }(\bar{f}) > 0$ to derive that $\bar{f}$ is a local minimizer of F if F is a real-valued function of one real variable. More details about the importance of second order optimality conditions in the context of PDE control can be found in Ref. [59].

In our setting, considering all directions $h \ne 0$ out of a certain so-called critical cone $C_f$, the condition for $\nu > 0$ reads

$$ F^{\prime \prime }(\bar{f})h^2 > 0. $$

Then, $\bar{f}$ is a locally optimal solution of $\mathrm {(P_{sp})}$. The detailed structure of $C_f$ is described in Ref. [50]; also the much more complicated case $\nu = 0$ is discussed there.

The second-order sufficient optimality conditions are the basis for interesting questions, e.g., the stability of solutions for perturbed desired trajectories and desired states [50]. Moreover, we study the limiting case of Tikhonov parameter $\nu$ tending to zero.

4.5 Tikhonov Parameter Tending to Zero

In this section, we investigate the behavior of a sequence of optimal controls and the corresponding states as solutions of the problem $\mathrm {(P_{sp})}$ as $\nu \rightarrow 0$. For this reason, we denote our control problem $\mathrm{(P}_\nu \mathrm{)}$, the associated optimal control with $\bar{f}_\nu$, and its associated states with $(\bar{u}_\nu ,\bar{v}_\nu )$ for a fixed $\nu \ge 0$. Since $\mathcal {F}_{\mathrm{ad}}$ is bounded in $L^\infty (Q)$, any sequence of solutions $\{\bar{f}_\nu \}_{\nu > 0}$ of $\mathrm{(P}_\nu \mathrm{)}$ has subsequences converging weakly$^*$ in $L^\infty (Q)$. For a direct numerical approach, this is useless, but we can deduce interesting consequences of this convergence using second order sufficient optimality conditions.

Assume that the second order sufficient optimality conditions of Ref. [50, Theorem 4.7] are satisfied. Then, we derive a Hölder rate of convergence for the states

$$\begin{aligned} \displaystyle \lim _{\nu \rightarrow 0}\frac{1}{\sqrt{\nu }}\left\{ \Vert \bar{u}_\nu - \bar{u}_0\Vert _{L^2(Q)} + \Vert \bar{v}_\nu - \bar{v}_0\Vert _{L^2(Q)}\right\} = 0 \end{aligned}$$

(10.30)

with $(\bar{u}_\nu ,\bar{v}_\nu ) = G(\bar{f}_\nu )$ and $(\bar{u}_0,\bar{v}_0) = G(\bar{f}_0)$. We should mention that this estimate is fairly pessimistic. All of our numerical tests show that the convergence rate is of order $\nu$, i.e., we observe a Lipschitz rather than a Hölder estimate [50]. As mentioned in Ref. [50], it should also be possible to prove Lipschitz stability and hence, to confirm the linear rate of convergence for $\nu \rightarrow 0$ with a remarkable amount of effort.

4.6 Example 3: Sparse Optimal Control with Tikhonov Parameter Tending to Zero

Finally, we consider a traveling pulse solution in the FitzHugh-Nagumo system in one spatial dimension $N=1$. Here, the limiting case of vanishing Tikhonov parameter, $\nu = 0$, is of our special interest. We observe that Newton-type methods yield very high accuracy even for very small values of $\nu > 0$. This allows us to study the convergence behavior of solutions for $\nu$ tending to zero as well.

Following Ref. [50] and in contrast to the last example in Sect. 10.4.3, we solve the full forward-backward-system of optimality. We stress that this is numerically possible solely for non-vanishing value of $\nu$. However, we constructed examples where an exact solution of the optimality system for $\nu = 0$ is accessible as shown in Ref. [50, Sect. 5.3]. In this sequel, our reference-solution, denoted by $\bar{u}_\text {ref}$, will be the solution of $\mathrm{(P}_\nu \mathrm{)}$ for $\nu := \nu _\text {ref} = 10^{-10}$. For smaller values, the numerical errors do not allow to observe a further convergence. The distance $\Vert \bar{u}_\nu - \bar{u}_\text {ref}\Vert _{L^2(Q)}$ stagnates between $\nu = 10^{-10}$ and $\nu _\text {ref} < 10^{-10}$.

Next, we treat the well-studied problem of pulse nucleation [60, 61] by sparse optimal control. We aim to start and to stay in the lower HSS for the first two time-units, i.e., $u_d(\vec {x},t) = -1.3$ for $t \in (0,2)$. Then, the activator state shall coincide instantaneously with the traveling pulse solution $u_\text {nat}$, i.e., $u_d(\vec {x},t) = u_\text {nat}(\vec {x},t-2)$. To get the activator profile $u_\text {nat}$, we solve Eq. (10.13) for $f = 0$ and its profile is shown in Fig. 10.3a.

In our optimal control algorithms, we set the parameters to $\varOmega = (0,75)$, $T = 10$, $\alpha = 1$, $\beta = 0$, $\gamma = 0.33$, and $\delta = -0.429$. Moreover, here we use a slightly different nonlinear reaction kinetics $R(u) = u(u-\sqrt{3})(u+\sqrt{3})$ in Eq. (10.13) but this does not change the analytical results. The upper and lower bounds for the control f are set to very large values, viz., $f_a = -100$ and $f_b = 100$. In addition, the coefficients in Eq. (10.14) are kept fixed, viz., $c_d^U = 1$ and $c_T^U = c_d^V = c_T^V = 0$.

Fig. 10.3

a Segment of a traveling pulse solution $(u_0, v_0)^T$ in the uncontrolled FitzHugh-Nagumo system, Eq. (10.13) with $f = 0$. b Numerically obtained sparse optimal control solution $\bar{f}_\nu$ for almost vanishing Tikhonov parameter, $\nu = 10^{-10}$, and c the associated optimal state $\bar{u}_\nu$. The amplitude of the control signal is color-coded. The kinetic parameter values are set to $\alpha = 1$, $\beta = 0$, $\gamma = 0.33$, $\delta = -0.429$, and $R(u) = u(u-\sqrt{3})(u+\sqrt{3})$

Our numerical results obtained for a sparse optimal control $\bar{f}_\nu$ acting solely on the activator u, cf. Eq. (10.13), are presented in Fig. 10.3b, c. In order to create a traveling pulse solution from the HSS $u_d = -1.3$, the optimal control resembles a step-like excitation with high amplitude at $x \simeq 40$. Since the Tikhonov parameter is set to $\nu = 10^{-10}$, large control amplitudes are to be expected and indicate that in the unregularized case, even a delta distribution might appear. Because this excitation is supercritical, a new pulse will nucleate. In order to inhibit the propagation of this nucleated pulse to the left, the control must act at the back of the pulse as well. Thus, we observes a negative control amplitude acting in the back of the traveling pulse. We emphasize that the desired shape of the pulse is achieved qualitatively. The realization of the exact desired profile can not be expected due to a non-vanishing sparse parameter $\kappa = 0.01$. Even for this respectively small value, the sparsity of the optimal control shows.

Since the displayed control and state are computed for an almost vanishing value $\nu = 10^{-10}$, we take the associated state as reference-state $\bar{u}_\text {ref}$ in order to study the dependence of the distance $\Vert \bar{u}_\nu - \bar{u}_\text {ref}\Vert _{L^2(Q)}$ on $\nu > 0$. From Table 10.2, one notices the already mentioned Lipschitz-rate of convergence for decreasing values $\nu > 0$, $\Vert \bar{u}_\nu - \bar{u}_\text {ref}\Vert _{L^2(Q)} \propto \nu$. This observation is consistent with results from [50] for various other examples.

Table 10.2 The comparison of the distance $\Vert \bar{u}_\nu - \bar{u}_\text {ref}\Vert _{L^2(Q)}$ between the numerically obtained states $\bar{u}_\nu$ and the numerically obtained reference-solution $\bar{u}_{\text {ref}}$, computed for $\nu = 10^{-10}$, for decreasing values of $\nu > 0$

5 Conclusion

Optimal control of traveling wave patterns in RD systems according to a prescribed desired distribution is important for many applications.

Analytical solutions to an unregularized optimal control problem can be obtained with ease from the approach presented in Sect. 10.2. In particular, the control signal can be obtained without full knowledge about the underlying nonlinear reaction kinetics in case of position control. Moreover, they are a good initial guess for the numerical solution of regularized optimal control problems with small regularization parameter $\nu > 0$, thereby achieving a substantial computational speedup as discussed in Sect. 10.3.3. Generally, the analytical expressions may serve as consistency checks for numerical optimal control algorithms.

For the position control of fronts, pulses, and spiral waves, the control signal is spatially localized. By applying sparse optimal position control to reaction-diffusion systems, as discussed in Sect. 10.4, the size of the domains with non-vanishing control signals can be further decreased. Importantly, the method determines sparse controls without any a priori knowledge about restrictions to certain subdomains. Additionally, sparse control allows to study second order optimality conditions that are not only interesting from the theoretical perspective but also for numerical Newton-type algorithms.