Keywords

1 Introduction

This paper is part of an ongoing research [6, 12, 13] aiming at the development of a methodology for creating semantic measures taking as source any given semantic graph. This methodology, called SemArachne, does not require any particular knowledge of the semantic graph and is based on the notion of proximity rather than distance. It considers virtually all paths connecting two terms with weights depending on edge types. SemArachne automatically tunes these weights for a given semantic graph. The validation of this process was performed using WordNet 2.1 [8] with WordSimilarity 353 [9] data set with results better than those in the literature [13].

WordNet 2.1 has a smaller graph when compared with the recent versions of it or even other semantic sources, such as DBpedia or Freebase. Not only the number of nodes and edge types increases as the number of graph arcs expands enabling them to relate semantically a large number of terms, making graphs not only larger but also denser. Compute proximity in these conditions comes with a price. Since SemArachne considers all the paths, the number of paths to process tends to increase.

A rough measure of graph density is the maximum degree of all its nodes. However, consider it can be misleading since there may be a special node where all the edge types are applied. The real challenge is then the graph average node degree. SemArachne computes all paths connecting a pair of terms up tp a given length. The node degree is the branching factor for the paths crossing that node. Hence, a high average node degree reduces the efficiency of the SemArachne measure.

The alternative explored in this paper to reduce graph density is to reduce the number of edge types while keeping all nodes, thus preserving the potential to relate a larger set of terms. The approach is to incrementally build a subgraph of the original semantic graph. This process starts with a full disconnected graph containing all the nodes. At each iteration, a new edge type is added until the semantic measure quality stops to improve. The result of this process is a subgraph where the semantic quality is maximized. The semantic measure used by SemArachne [12] had also some minor adjustments.

The rest of the paper is organized as follows. The next section surveys the state of the art on semantic relatedness. Section 3 summarizes previously published work and Sect. 4 details the approach followed to measure semantic relatedness is larger graphs. The experimental results and their analysis can be found in Sect. 5. Finally, Sect. 6 summarizes what was accomplished so far and identifies opportunities for further research.

2 Related Work

Semantic measures are widely used today to measure the strength of the semantic relationship between terms. This evaluation is based on the analysis of information describing the elements extracted from semantic sources.

There are two different types of semantic sources. The first one are unstructured and semi-structured texts, such as plain text or dictionaries. Texts have evidences of semantic relationships and it is possible to measure those relationships using simple assumptions regarding the distribution of words. This source type is mainly used by distributional approaches.

The second type of semantic sources is more general and includes a large range of computer understandable resources where the knowledge about elements is explicitly structured and modeled. Semantic measures based on this type of source rely on techniques to take advantage of semantic graphs or higher formal knowledge representations. This source type is mainly used by knowledge-based approaches.

Distributional approaches rely on the distributional hypothesis [11] that states that words in a similar context are surrounded by the same words and are likely to be semantically similar. There are several methods following this approach, such as the Spatial/Geometric methods [10], the Set-based methods [5], and the Probabilistic methods [7].

The knowledge-base approaches rely on any form of knowledge representation, namely semantic graphs, since they are structured data from which semantic relationships can be extracted. They consider the properties of the graph and elements are compared by analysing their interconnections and the semantics of those relationships. Several methods have been defined to compare elements in single and multiple knowledge bases, such as Structural methods  [14, 15, 22, 24], Feature-based methods  [4, 23, 27] and Shannon’s Information Theory methods [16, 19–21].

Knowledge-based approaches have the advantage of controlling which edge types should be considered when comparing pairs of elements in the graph. They are also easier to implement than distributional methods and have a lower complexity. However they require a knowledge representation containing all the elements to compare. On the other hand, using large knowledge sources to compare elements is also an issue due of high computational complexity.

There are also hybrid approaches [2, 3, 18, 24] that mix the knowledge-based and the distributional approaches. They take advantage of both texts and knowledge representations to estimate the semantic measure.

3 Previous Work

This section summarizes previously published work [12, 13] that is the core of SemArachne and relevant for the graph reduction process described in the next section. The first subsection details on the semantic measure and the following subsection on the quality measure. The last subsection details on the fine tune process.

3.1 Semantic Measure

A semantic graph can be defined as \(G=(V,E,T,W)\) where V is the set of nodes, E is the set of edges connecting the graph nodes, T is the set of edge types and W is a mapping of edge types to weight values. Each edge in E is a triplet (u, v, t) where \(u,v \in V\) and \(t \in T\).

The set W defines a mapping \(w:T\mapsto \mathbb {Z}\). The bound of the absolute weight valuesFootnote 1 for all edge types is defined by

$$\begin{aligned} \varOmega (G) \equiv max_{t_i \in T} \;\; |\;w(t_i)\;| \end{aligned}$$

To measure the proximity between a pair of terms it is necessary to build a set of distinct paths that connects them by walking through the graph. A path p of size \(n \in \mathbb {N}^+\) is a sequence of unrepeated nodes \(u_0 \ldots u_n \forall _{0 \le i,j \le n} u_i \not = u_j\), linked by typed edges. It must have at least one edge and cannot have loops. A path p is denoted as follows:

$$\begin{aligned} p = u_0 \xrightarrow {t_1} u_1 \xrightarrow {t_2} u_2 \ldots u_{n-1} \xrightarrow {t_n} u_n \end{aligned}$$

The weight of an edge depends on its type. The weight of a path p is the sum of weights of each edge, \(\omega (p) = w(t_1)+w(t_2)+\ldots +w(t_n)\). The set of all paths of size n connecting the pair of concepts is defined as follows and its weight is the sum of all its sub paths.

$$\begin{aligned} P_{u,v}^n = \{ u_0 \xrightarrow {t_1} u_1 \ldots u_{n-1} \xrightarrow {t_n} u_n : u = u_o \wedge v = u_n \wedge \forall _{0 \le i,j \le n} \; u_i \ne u_j \} \end{aligned}$$

The semantic measure is based on the previous definition and also considers the path length. \(\varDelta \) is the degree of each node in each path. The proximity function r is defined by the following formula.

$$\begin{aligned} r(u,v) = {\left\{ \begin{array}{ll} 1 &{} \leftarrow u = v \\ \frac{1}{\varOmega (G)}\sum \limits _{n=1}^\infty \frac{1}{2^n.n.\varDelta (G)^n} \sum \limits _{p \in P_{u,v}^n} \omega (p) &{} \leftarrow u \ne v \end{array}\right. } \end{aligned}$$
(1)

Given a graph with a set of nodes V, where \(r: V \times V \mapsto [-1,1]\), the proximity function r takes a pair of terms and returns a “percentage” of proximity between them. The proximity of related terms must be close to 1 and the proximity of unrelated terms must be close to –1.

This definition of proximity depends on weights of transitions. The use of domain knowledge to define them has been proved a naïve approach since an “informed opinion” frequently has no evidence to support it and sometimes is plainly wrong. Also, applying this methodology to a large ontology with several domains can be hard. To be of practical use, the weights of a proximity based semantic relatedness measure must be automatically tuned. To achieve it, it is necessary to estimate the quality of a semantic measure for a given set of parameters.

3.2 Quality Measure

The purpose of the quality measure is to compute the quality of a semantic measure defined by (1) for a particular set of parameters. In order to simplify and optimize the quality measure, it is necessary to factor out weights from the semantic measure definition. Thus its quality may be defined as function of a set of weight assignment.

The first step is to express the semantic measure in terms of weights of edge types. Consider the set of all edge types T with \(\sharp T = m\) and the weight of its elements \(w(t), \forall _t \in T\). The second branch of (1) can be rewritten as follows, where \(c_i(a,b),i \in \{1..m\}\) are the coefficients of each edge type.

$$\begin{aligned} r(a,b) = \alpha \sum \limits _{n_1}^\infty \beta \sum \limits _{P_j\in \mathbb {P}} \sum \limits _{t \in P_j} w(t) = \sum \limits _{i=1}^m c_i(a,b) \cdot w(t_i) \end{aligned}$$

Edge type weights are independent of the arguments of r but the coefficients that are factored out depend of these arguments. It is possible to represent both the weights of edges and their coefficients, \((w(t_1), w(t_2),\ldots ,w(t_k)) = {\varvec{w}}\) and \((c_1(a,b),c_2(a,b),\ldots ,c_m(a,b) = {\varvec{c}}(a,b))\) respectively, by defining a standard order on the elements of T. This way the previous definition of r may take as parameter the weight vector, as follows

$$\begin{aligned} {{\varvec{w}}}(a,b) = {\varvec{c}}(a,b) \cdot {\varvec{w}} \end{aligned}$$

The method commonly used to estimate the quality of a semantic relatedness algorithm is to compare it with a benchmark data set containing pairs of words and their relatedness. The Spearman’s rank order correlation is widely used to make this comparison.

Consider a benchmark data set with the pairs of words \((a_i,b_i)\) for \(1 \le i \le k\), with a proximity \(x_i\). Given the relatedness function \(r_{{\varvec{w}}}: S \times S \mapsto \mathfrak {R}\) let us define \(y_i = r_{{\varvec{w}}}(a_i,b_i)\). In order to use the Spearman’s rank order coefficient both \(x_i\) and \(y_i\) must be converted to the ranks \(x_i^\prime \) and \(y_i^\prime \).

The Spearman’s rank order coefficient is defined in terms of \(x_i\) and \(y_i\), where \(x_i\) are constants from the benchmark data set. To use this coefficient as a quality measure it must be expressed as a function of \({\varvec{w}}\). Considering that \({\varvec{y}} = (r_{{\varvec{w}}}(a_i,b_i), \ldots , r_{{\varvec{w}}}(a_n,b_n))\) then \({\varvec{y}} = C {\varvec{w}}\), where matrix C is a \(n\times m\) matrix and where each line contains the coefficients for a pair of concepts and each column contains coefficients of a single edge type. Vector \({\varvec{w}}\) is a \(m\times 1\) matrix with the weights assigned to each edge type. The product of these matrices is the relatedness measure of a set of concept pairs.

Considering \(\rho ({\varvec{x}},{\varvec{y}})\) as the Spearman’s rank order of \({\varvec{x}}\) and \({\varvec{y}}\), the quality function \(q : \mathfrak {R}^n \mapsto \mathfrak {R}\) using the benchmark data set \({\varvec{x}}\) can be defined as

$$\begin{aligned} q_{{\varvec{x}}}({\varvec{w}}) = \rho ({\varvec{x}}, C {\varvec{w}}) \end{aligned}$$
(2)

The next step in the SemArachne methodology is to determine a \({\varvec{w}}\) that maximizes this quality function.

3.3 Fine Tuning Process

Genetic algorithms are a family of computational models that mimic the process of natural selection in the evolution of species. This type of algorithms uses concepts of variation, differential reproduction and heredity to guide the co-evolution of a set of problem solutions. This algorithm family is frequently used to improve solutions of optimization problems [29].

In the SemArachne the candidate solution – individual – is a weight values vector. Consider a sequence of weights (the genes), \(w(t_1), w(t_2), \ldots , w(t_k)\), taking integer values in a certain range, in a standard order of edge types. Two possible solutions are the vectors \({\varvec{v}} = (v_1, v_2, \ldots , v_k)\) and \({\varvec{t}} = (t_1, t_2, \ldots , tn)\). Using crossover, it is easy to recombine the “genes” of both “parents” resulting in \({\varvec{u}} = (v_1, t_2, \ldots , t_{n-1}, v_k)\).

This is a closer representation of the domain than the typical binary one. It can also be processed more efficiently with large number of weights. In this tuning process the genetic algorithm only have a single kind of mutation: randomly selecting a new value for a given “gene”.

The fitness function plays a decisive role in the selection of the new generation of individuals. In this case, individuals are the vector of weight values \({\varvec{w}}\), hence the fitness function is in fact the quality function previously defined in (2).

4 Graph Reduction Procedure

The previous section explained how to tune the weights of a semantic measure by using a genetic algorithm with an appropriate quality function. This section introduces a procedure for selecting a subgraph of the original semantic source with a reduced density by repeatedly applying that procedure.

Fig. 1.
figure 1

Semantic graph reduction procedure

Full size image

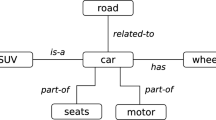
Figure 1 depicts the overall strategy. It starts with a fully disconnected graph by omitting all the edges. The small graph on the left in Fig. 1 shows the arcs as dotted lines to denote the original connections. When a single property (edge type) is added to this graph a number of paths is created. If the original graph has n property types then one can create n different subgraphs. The quality of these graphs can be measured using the approach described in the last section. The best of these candidates is the selected graph for the first iteration. This process continues until the quality of the candidate graphs cannot be further improved.

More formally, consider a semantic graph \(G=(V,E,T,W)\) where V is the set of nodes, E is the set of edges connecting the graph nodes, T is the set of edge types and W is a mapping of edge types to weight values. The initial graph of this incremental algorithm is \(G_0=(V,\emptyset ,\emptyset ,\emptyset )\). This is a totally disconnected graph just containing the nodes from the original graph, i.e., edges, types and weights are all the empty set.

Each iteration builds a new graph \(G_{k+1}=(V,E_{k+1},T_{k+1},W_{k+1})\) based on \(G_k=(V,E_k,T_k,W_K)\). The new set of types \(T_{k+1}\) has all the types in \(T_{k}\). In fact, several candidate \(G^i_k\) can be considered, depending on the types in \(T - T_k\) that are added to \(T_{k+1}\). The arcs of \(E^i_{k+1}\) are those in E whose type is in \(T^i_{k+1}\). The general idea is to select the \(G^i_{k+1}\) that produces an higher increment on semantic measure quality. This algorithm stops when no candidate is able to improve it.

In general, computing the semantic measure quality of \(G^i_{k+1}\) is a time consuming task. However, there are some ways to make it more efficient. As shown in Fig. 1, if \(G^i_{k+1}\) is not a connected graph then the quality measure cannot be computed. This means that for the first iteration many \(G^1_{k+1}\) can be trivially discarded. Moreover, if \(E^i_{k+1}\) = \(E^i_k\) then the semantic quality measure is the same. This insight can be used to speedup the iterative process. The paths connecting pairs of concepts using arcs in \(E_{k+1}\) are basically the same that used \(E_k\). The new paths must appear on the nodes of previous paths and can only have arcs of types in \(T_{k+1}\). This insight can be used to compute the quality of \(G^i_{k+1}\) incrementally based on the computation of \(G^i_{k}\).

The generation of the sets \(T^i_{k+1}\) is a potential issue. Ideally \(T^i_{k+1}\) would have just one element more than \(T^i_{k}\). However this may not always be possibleFootnote 2. Consider \(T^i_1\), the candidate sets of types for the first iteration. In most cases they will produce a disconnected graph, hence with a null semantic measure quality. They will only produce a connected graph if the selected type creates a taxonomy. In many cases this involves 2 types of arcs: one linking an instance to a class, another linking a class to its super-class. To deal with this issue the incremental algorithm attempts first to generate \(T^i_{k+1}\) such that \(\sharp T^i_{k+1} = \sharp T^i_{k}+1\), where \(\sharp \) stands for set cardinality. In none of these improve the semantic measure quality then it attempts to generate \(T^i_{k+1}\) such that \(\sharp T^i_{k+1} = \sharp T^i_{k}+2\), and so forth.

5 Validation

The validation of SemArachne was performed using the semantic graphs of different versions of WordNet along with three different data sets.

WordNetFootnote 3 [8] is a widely used lexical knowledge base of English words. It groups nouns, verbs, adjectives and adverbs into synsets – a set of cognitive synonyms – that expresses distinct concepts. These synsets are linked by conceptual and lexical relationships. The validation process used three different data sets: WordSimilarity-353Footnote 4 [9] Rubenstein & Goodenough [25] (RG65) and Miller & Charles [17] (MC30).

Table 1. Spearman correlation of SemArachne compared with literature
Full size table

Table 1 compares the performance of SemArachne against the state of the art for methods using the same knowledge-based approach. For WordNet 2.1, SemArachne achieves a better result than those in the literature when using WordSim-353 data set. Using WordNet 3.1 as semantic graph, SemArachne produces also a better semantic quality than those in the literature. Although results are not the best in the WordNet 3.0, despite the data set used, they have the same order of magnitude.

The quality of the semantic measure produced with graph reduction was validated against several approaches in the literature. An advantage of this methodology is the ability of measure the semantic relatedness regardless the semantic graph used and produce comparable results for each semantic graph and data set. It is also scalable, since it handles gradually larger graphs.

6 Conclusion

As semantic graphs evolve they become larger. Since larger graphs relate more terms this improves their potential as semantic sources for relatedness measures. However, these larger graphs are also a challenge, in particular to semantic measures that consider virtually all paths connecting two nodes, as is the case of SemArachne.

The major contribution of this paper is an incremental approach to select a subgraph with a reduced number of edge types (arcs) but with the same number of entities (nodes). This approach starts with a totally disconnected graph, at each iteration adds an arc type that increases the quality of the semantic measure, and stops when no improvement is possible.

These contributions were validated with different versions of WordNet, a medium size graph typically used as semantic source for relatedness measures. Although this is not the kind of large semantic graphs to which this approach is targeted, it is convenient for initial tests due to its relatively small size.

In the WordNet graph the reduction of properties is not so expressive, since the total number of properties is comparatively small. The obtained subgraphs do not always improve the quality of the SemArachne measure, but produce a result that is similar, and in most cases better, than best method described in the literature for that particular graph.

The immediate objective of the SemArachne project is to extend the validation presented in this paper to other data sets and, most of all, to other graphs. Massive graphs with very high density, such as Freebase, are bound to create new and interesting challenges. Another important consequence of this graph reduction procedure is that it decouples the original graph from the actual semantic source. Thus SemArachne can be extended to process multiple semantic graphs (with shared labels) and create an unified semantic measure combining their semantic power.