Keywords

1 Introduction

Forces and moments of force acting on vehicle wheels have critical impact on its motion and durability of its structure. For this reason, knowledge of these forces and moments of force is important in the process of designing and optimization of mechanical structures of the wheeled mobile robots. Optimization of the design can be aimed at guaranteeing, for example, the required strength of the chassis while keeping the minimum mass or the adequate damping of structural vibrations.

Knowledge of the phenomena associated with robot motion, in particular, the occurring forces and moments of force, is also the foundation for the development of dynamic models of this kind of system. Models like that can be useful both in the process of robot design and in the synthesis of algorithms for control of its motion, especially when the designed controller relies on robot dynamics model (e.g., adaptive control or robust control). The developed models of dynamics of the mobile robots enable simulation of their motion.

In the case of robots moving in conditions of wheel slip, it is necessary to consider the so-called tire model in the model of robot dynamics. Models like that have been developed for automobiles for many years, which is reflected, for instance, in the works [1, 2], whereas they are rarely used in the case of mobile robots. As pointed out in the work [3], tire models should be taken into account especially in the case of robots with nonsteered wheels, called skid-steered robots.

Tire models take into account the phenomena in the tire-ground interface, including forces and moments of force, and in the case of more advanced models also the tire structure is included. In order to develop or validate a tire model, the knowledge of robot motion parameters as well as the forces and moments of force acting on wheels is necessary.

Particularly difficult is the measurement of forces and moments of force acting on wheels during robot motion. Commercial solutions to this problem are not available at the moment. In the case of automobiles, solutions using the so-called multiaxis wheel force transducers [4, 5] are available. In the case of small-wheeled robots, because of their size and lack of standards concerning the wheel geometry, it would be difficult to use them with existing robot designs.

After taking into account the above considerations, in this work a concept of measurement system and method enabling determination of forces and moments of force acting on the wheel of a small mobile robot during motion will be presented.

2 Wheeled Mobile Robot

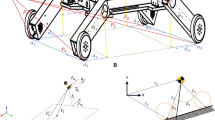
The object of the research is a small four-wheeled mobile robot called PIAP GRANITE. The robot has all wheels driven independently by DC servomotors with gear units and encoders. A visualization of the robot is shown in Fig. 1a, and its kinematic structure as well as illustration of reaction forces acting in the wheel–ground plane of contact is presented in Fig. 1b.

Fig. 1
figure 1

Four-wheeled mobile robot: a visualization of the robot, b kinematic structure of the robot and illustration of reaction forces acting in the wheel-ground plane of contact

Full size image

It is possible to distinguish the following main components of the robot: 0—body with frame for installation of the research equipment, 1–4—wheels with toothed belt pulleys, and 5–6—toothed belts.

The drive transmission in each drive unit can be decoupled, which permits obtaining the following configurations of the robot chassis:

  • driving of front or rear wheels only,

  • driving of front or rear wheels and transmission of the drive to the remaining wheels using the toothed belts,

  • independent driving of all wheels.

The following designations for the ith wheel have been introduced in the robot model: A i is the geometrical center, r i is the radius, θ i is the rotation angle (i = {1, …, 4}).

The most important robot parameters are:

  • dimensions: L = 0.425 m, W = 0.553 m (where L = A 1 A 3 = A 2 A 4, W = A 1 A 2 = A 3 A 4, see Fig. 1b), r i  = r = 0.0965 m,

  • masses of the components: m 0 = 40 kg, m i  = 1 kg, m 5 = m 6 = 0.18 kg.

The robot is equipped with:

  • a laptop computer for control and data acquisition purposes,

  • iNEMO sensors module with 3-axis MEMS accelerometer, gyro, and magnetometer for determination of motion parameters of the robot [6],

  • a GNSS receiver and antenna for robot navigation [7],

  • a 2D laser scanner for localization in known environment [8],

  • bumpers for obstacles detection,

  • router and USB modem for Internet connection,

  • video cameras and lights for robot teleoperation.

The robot drives are DC servomechanisms. The mechanical power from the motor is transmitted by means of the gear unit to the axle of the wheel, which is illustrated in Fig. 2. It is assumed that version of the robot with independent driving of all 4 wheels is analyzed in this paper.

Fig. 2
figure 2

Schematic diagram of the robot drive unit and wheel

Full size image

3 Method of Determination of Forces and Moments of Force Transmitted by the Wheel of a Mobile Robot During Motion

To the described robot will be applied the method allowing determination of forces and moments of force transmitted by its wheels. The method of determination of those forces and moments of force takes into account the vehicle motion and properties of a drive units.

The idea of the solution relies on measurement of forces carried by flexible pressure sensors, which are placed between axle bearings and the supporting frame inside the measuring head. Forces and moments of force are then transmitted from the wheel via bearings to particular force sensors placed between bearings and the supporting frame which, based on the force measurements on those sensors, enables determination of forces and moments of force carried by the wheel, which in the end allows determination of forces and moments of force resulting from interaction of the wheel with the ground. The schematic diagram of the system for the left front wheel is shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of the system for measurement of forces and moments of force carried by the axle of robot wheel

Full size image

Forces and moments of force acting on a wheel are transmitted to the axle and then to the two bearings denoted B and C in Fig. 3, and finally via force sensors to the robot body. In the analyzed system occurs also the interaction at the point D, that is, in the gears contact area.

In general case, on the wheel act forces and moments of force resulting from the gravity force of this wheel, inertia forces, driving torque, and contact of the wheel with the ground. As a result, from the axle to which the wheel is mounted, reaction forces and reaction moments of force acting on the wheel appear as well. All forces and moments of force acting on the wheel excluding gravity force are shown in Fig. 4.

Fig. 4
figure 4

Illustration of forces and moments of force acting on robot wheel

Full size image

External reaction forces and moments of force acting at the point of contact of the wheel with the ground T, that is, F T  = [F Tx , F Ty , F Tz ]T and T T  = [T Tx , T Ty , T Tz ]T can be reduced to the agreed-on point of mounting of this wheel, i.e., to the point A, according to the following relationships:

$${\mathbf{F}}_{A} = {\mathbf{F}}_{T} ,\quad {\mathbf{T}}_{A} = {\mathbf{r}}_{T} \times {\mathbf{F}}_{T} + {\mathbf{T}}_{T} ,\quad {\mathbf{r}}_{T} \times {\mathbf{F}}_{T} = \left| {\begin{array}{*{20}c} {{\mathbf{e}}_{x} } & {{\mathbf{e}}_{y} } & {{\mathbf{e}}_{z} } \\ 0 & 0 & { - r} \\ {F_{Tx} } & {F_{Ty} } & {F_{Tz} } \\ \end{array} } \right| = [F_{Ty} r, - F_{Tx} r,0]^{T} ,$$
(1)

where F A  = [F Ax , F Ay , F Az ]T, T A  = [T Ax , T Ay , T Az ]T, r T  = [x T , y T , z T ]T are the vectors that determine the position of the point of contact T with respect to the point A of the wheel which is also the origin of the coordinate system of this wheel, e x , e y , e z are unit vectors of the axes.

For the wheel, the following dynamic equations of motion can be written in the matrix-vector form:

$$m_{W} {\mathbf{a}}_{A} = {\mathbf{F}}_{A} + {\mathbf{R}}_{A}^{(W)} + m_{W} \,{\mathbf{g}},$$
(2)
$${\mathbf{I}}_{W} \left( {{{\ddot{\boldsymbol{\uptheta} }}}_{A}^{{}} + {\ddot{\boldsymbol{\upvarphi }}}} \right) + \left( {\dot{{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}} \right) \times {\mathbf{I}}_{W} \left( {{\dot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}} \right)\, = {\mathbf{T}}_{A} + {\mathbf{M}}_{A}^{(W)} + {\boldsymbol{\uptau }}_{{}}^{(W)} ,$$
(3)

where m W is the mass of the wheel, I W is the inertia tensor of the wheel (3 × 3 matrix), and a A is the vector of acceleration of the wheel geometric center, \({\dot{\boldsymbol{\uptheta }}}_{A}^{{}} = [0,\;{\dot{\uptheta }},\,0]^{T} ,\;{\ddot{\boldsymbol{\uptheta }}}_{A}^{{}} = [0,\;{\ddot{\uptheta }},\,0]^{T}\) are the vectors of angular velocity and angular acceleration of wheel spin, \({\dot{\boldsymbol{\upvarphi }}} = [{\dot{\upvarphi }}_{x} ,\;{\dot{\upvarphi }}_{y} ,\;{\dot{\upvarphi }}_{z} ]^{T} ,\;{\ddot{\boldsymbol{\upvarphi }}} = [{\ddot{\upvarphi }}_{x} ,\;{\ddot{\upvarphi }}_{y} ,\;{\ddot{\upvarphi }}_{z} ]^{T}\)—vectors of angular velocity and angular acceleration of the spin of the mobile platform, g = [g x , g y , g z ]T—gravitational acceleration vector, F A  = [F Ax , F Ay , F Az ]T, T A  = [T Ax , T Ay , T Az ]T—vectors of force and moment of force resulting from the contact of the wheel with the ground reduced to the point A, τ (W) = [0, τ, 0]T—driving torque vector, \({\mathbf{R}}_{A}^{(W)} = [R_{Ax}^{(W)} ,\;R_{Ay}^{(W)} ,\;R_{Az}^{(W)} ]^{T} ,\;{\mathbf{M}}_{A}^{(W)} = [M_{Ax}^{(W)} ,\;M_{Ay}^{(W)} ,\;M_{Az}^{(W)} ]^{T}\)—vectors of reaction force and moment of force acting on the wheel.

Those equations enable determination of internal reaction forces and moments of force acting on the wheel in the agreed-on point of its mounting to the axle.

It is assumed that all parameters of motion of the system are known, that is, they are measured and/or determined during robot motion.

Forces and moments of force acting on the axle of the wheel (after reduction of the forces acting on the wheel to the point A), the gear, and the bearings are shown in Fig. 3. Based on this figure, it is possible to write the following dynamic equations of motion for the wheel axle:

$$m_{S} \,{\mathbf{a}}_{S} = {\mathbf{F}}_{A}^{{}} + {\mathbf{R}}_{B}^{(S)} + {\mathbf{R}}_{C}^{(S)} + {\mathbf{R}}_{D}^{(S)} + m_{S} \,{\mathbf{g}},$$
(4)
$${\mathbf{I}}_{S}^{*} ({\ddot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\ddot{\boldsymbol{\upvarphi }}}) + ({\dot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}) \times {\mathbf{I}}_{S}^{*} ({\dot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}) = {\mathbf{T}}_{A}^{{}} + {\mathbf{M}}_{B}^{(S)} + {\mathbf{M}}_{C}^{(S)} + {\mathbf{M}}_{D}^{(S)} + {\mathbf{r}}_{CM} \times m_{S} \,{\mathbf{g}},$$
(5)

where m S is the mass of the system: axle, wheel, toothed belt pulley, gear and bearings, \({\mathbf{I}}_{S}^{*}\) is the inertia tensor for the system calculated with respect to the reference system of origin at the point A, based on the known inertia tensor I S with respect to the mass center of this system using the parallel-axis theorem (Steiner’s theorem) [9], r CM is the vector describing position of the mass center of the system with respect to the point A, a S is the vector of acceleration of the mass center of the system, \({\mathbf{R}}_{B}^{(S)} = [R_{Bx}^{(S)} ,R_{By}^{(S)} ,R_{Bz}^{(S)} ]^{T}\), \({\mathbf{R}}_{C}^{(S)} = [R_{Cx}^{(S)} ,R_{Cy}^{(S)} ,R_{Cz}^{(S)} ]^{T}\), \({\mathbf{M}}_{B}^{(S)} = [M_{Bx}^{(S)} ,M_{By}^{(S)} ,M_{Bz}^{(S)} ]^{T}\), \({\mathbf{M}}_{C}^{(S)} = [M_{Cx}^{(S)} ,M_{Cy}^{(S)} ,M_{Cz}^{(S)} ]^{T}\) are the vectors of reaction forces and moments of force of the bearings, \({\mathbf{R}}_{D}^{(S)} = [R_{Dx}^{(S)} ,R_{Dy}^{(S)} ,R_{Dz}^{(S)} ]^{T}\), \({\mathbf{M}}_{D}^{(S)} = [M_{Dx}^{(S)} ,M_{Dy}^{(S)} ,M_{Dz}^{(S)} ]^{T}\) are the vectors of reaction force and moment of force acting on the spur gear.

It is assumed that the current i consumed by the motor driving the wheel is known. On this basis, knowing the torque constant and transmission gear ratio and after assuming certain efficiency, it is possible to determine the torque acting on the axle of the wheel from the following relationship:

$${\tau } = {\eta }_{D} \,n_{D} \,k_{M} \,i,\quad{\varvec{\uptau}} = [0,{\tau },0]^{T} ,$$
(6)

where η D is the efficiency of the gear transmission, n D is the gear ratio of the transmission from the motor to the wheel axle, and k M is the torque constant of the motor.

The force \({\mathbf{R}}_{D}^{(S)}\) can be projected both on the directions of axes of the adopted coordinate system, and on the directions: tangent, normal, and binormal of the natural coordinate system associated with the driven gear and of origin at the point D; that is, in the point of contact of the gears. Between those projections, the following relationships hold true:

$${\mathbf{R}}_{D}^{(S)} = [R_{D\tau }^{(S)} \sin \delta - R_{Dn}^{(S)} \cos \delta ,R_{Db}^{(S)} ,{- R_{D\tau }^{(S)}} \cos \delta - R_{Dn}^{(S)} \sin \delta ]^{T} ,$$
(7)

where the angle δ describes the position of the point D (Fig. 3), δ = 45° for the right wheel and δ = 135° for the left one.

Between the tangent and normal components of the force, \({\mathbf{R}}_{D}^{(S)}\) is the valid relationship resulting from the pressure angle ζ, which enables determination of the normal component of the force:

$$R_{D\tau }^{(S)} /R_{Dn}^{(S)} = \text{tg}\zeta \Rightarrow R_{Dn}^{(S)} = R_{D\tau }^{(S)} /\text{tg}\zeta .$$
(8)

In turn, the binormal component of the force depends on the coefficient of friction between the gears μ D , that is:

$$|R_{Dy}^{(S)} | \le\mu_{D} \sqrt {(R_{Dx}^{(S)} )^{2} + (R_{Dz}^{(S)} )^{2} } .$$
(9)

The friction coefficient for the interacting gears is in the interval μ Ds  ≥ μ D  ≥ μ Dk . In the case of the spur gears, the value of this coefficient is small enough for the longitudinal component of the force to be small compared to the remaining components. For this reason, in the following considerations, it is assumed that this component is approximately equal to zero.

It should be noted that the driving torque τ acting on the wheel is equivalent to the moment carried by the driven gear, that is:

$$\tau = M_{Dy}^{(S)} = R_{D\tau }^{(S)} r_{D} \Rightarrow R_{D\tau }^{(S)} = \tau /r_{D} ,$$
(10)

where r D is the radius of the driven gear (equal to half of its pitch diameter).

So, eventually the vector of force carried by the driven gear located on the axle of the wheel reads:

$${\mathbf{R}}_{D}^{(S)} = [\tau /r_{D} (\sin \delta - \cos \delta /\text{tg}\zeta ),0, - \tau /r_{D} (\cos \delta - \sin \delta /\text{tg}\zeta )]^{T} ,$$
(11)

whereas the vector of the moment of force is equal to:

$${\mathbf{M}}_{D}^{(S)} = {\mathbf{r}}_{D} \times {\mathbf{R}}_{D}^{(S)} = [R_{Dz}^{(S)} y_{D} ,\;R_{Dx}^{(S)} z_{D} - R_{Dz}^{(S)} x_{D} ,\; - R_{Dx}^{(S)} y_{D} ]^{T} ,$$
(12)

where \({\mathbf{r}}_{D} = \left[ {x_{D} ,y_{D} ,z_{D} } \right]^{T} = \left[ {r_{D} \cos \delta , \pm d,r_{D} \sin \delta } \right]^{T}\), d is the distance of the gear plane from the wheel plane, sign “+” is for the right wheel, and “−” is for the left one.

Around each bearing, six pressure sensors are mounted. Their arrangement is presented in Fig. 5. Sensors measuring the axial component of the reaction force are situated at the opposite sides of the bearings.

Fig. 5
figure 5

Arrangement of force sensors and related notation

Full size image

It is assumed that the nominal operating point of all sensors is in the middle of their range; i.e., all sensors are pre-stressed. It prevents the situation when, due to existence of clearances, effects of impact on the surfaces of sensors occur during robot motion.

On the basis of known forces acting on the sensors, it is possible to determine the forces carried by the bearings B and C using the following relationships:

$${\mathbf{R}}_{B}^{(S)} = \sum\limits_{j = 1}^{6} {{\mathbf{R}}_{Bj}^{{}} } ,\quad{\mathbf{R}}_{C}^{(S)} = \sum\limits_{j = 1}^{6} {{\mathbf{R}}_{Cj}^{{}} }$$
(13)
$${\mathbf{R}}_{B}^{(S)} = [ - R_{B2} + R_{B4} , \pm \,(R_{B5} + R_{B6} ), - R_{B1} + R_{B3} ]^{T} ,$$
(14)
$${\mathbf{R}}_{C}^{(S)} = [ - R_{C2} + R_{C4} , \pm \,( - R_{C5} - R_{C6} ), - R_{C1} + R_{C3} ]^{T} ,$$
(15)

where sign “+” is for the right wheel whilst “−” is for the left one.

In turn, the reaction moments of force of the bearings B and C are, respectively, equal to:

$${\mathbf{M}}_{B}^{(S)} = {\mathbf{r}}_{B} \times {\mathbf{R}}_{B}^{(S)} = [R_{Bz}^{(S)} y_{B} ,0, - R_{Bx}^{(S)} y_{B} ]^{T} ,$$
(16)
$${\mathbf{M}}_{C}^{(S)} = {\mathbf{r}}_{C} \times {\mathbf{R}}_{C}^{(S)} = [R_{Cz}^{(S)} y_{C} ,0, - R_{Cx}^{(S)} y_{C} ]^{T} ,$$
(17)

where r B  = [x B , y B , z B ]T = [0, ± b, 0]T, r C  = [x C , y C , z C ]T = [0, ±c, 0]T, b and c are distances of the geometric centers of the bearings B and C from the point A of the wheel, sign “+” is for the right wheel while “−” is for the left one.

Knowing the geometric and inertial parameters, parameters of motion of the system and estimated values of the driving torques, it is finally possible to determine forces and moments of force carried by the robot wheels. To this end, one should determine the unknown quantities for each robot drive unit in the following sequence:

  1. 1.

    value of the driving torque on the basis of the measured current consumption for the robot drive and knowing the parameters of the motor and transmission—Eq. (6):

$$\tau = \eta_{D} \,n_{D} \,k_{M} \,i,\quad{\boldsymbol{\tau }} = [0,\tau ,0]^{T} ,$$
  1. 2.

    vectors of reaction force and moment of force carried by the driven gear mounted on the wheel axle—relationships (11)–(12), on the assumption that δ ≈ const

$${\mathbf{R}}_{D}^{(S)} = [\tau /r_{D} (\sin \delta - \cos \delta /\text{tg}\zeta ),0, - \tau /r_{D} (\cos \delta - \sin \delta /\text{tg}\zeta )]^{T} ,$$
$${\mathbf{M}}_{D}^{(S)} = [R_{Dz}^{(S)} y_{D} ,R_{Dx}^{(S)} z_{D} - R_{Dz}^{(S)} x_{D} , {- R_{Dx}^{(S)} y_{D} ]^{T}} ,$$
  1. 3.

    vectors of reaction forces and moments of force of the bearings B and C (Fig. 3) on the basis of measurements from the pressure sensors—relationships (14)–(17)

$${\mathbf{R}}_{B}^{(S)} = [ - R_{B2} + R_{B4} , \pm \,(R_{B5} + R_{B6} ), - R_{B1} + R_{B3} ]^{T} ,$$
$${\mathbf{M}}_{B}^{(S)} = {\mathbf{r}}_{B} \times {\mathbf{R}}_{B}^{(S)} = [R_{Bz}^{(S)} y_{B} ,0, - R_{Bx}^{(S)} y_{B} ]^{T} ,$$
$${\mathbf{R}}_{C}^{(S)} = [ - R_{C2} + R_{C4} ,\; \pm ( - R_{C5} - R_{C6} ), - R_{C1} + R_{C3} ]^{T} ,$$
$${\mathbf{M}}_{C}^{(S)} = {\mathbf{r}}_{C} \times {\mathbf{R}}_{C}^{(S)} = [R_{Cz}^{(S)} y_{C} ,0, - R_{Cx}^{(S)} y_{C} ]^{T} ,$$
  1. 4.

    vectors of forces and moments of force acting on the wheel, reduced to the point A (Fig. 3) on the basis of dynamic equation of motion for the wheel axle—resulting from Eqs. (4) to (5):

$${\mathbf{F}}_{A}^{{}} = m_{S} \,{\mathbf{a}}_{S} - ({\mathbf{R}}_{B}^{(S)} + {\mathbf{R}}_{C}^{(S)} + {\mathbf{R}}_{D}^{(S)} + m_{S} \,{\mathbf{g}}),$$
$${\mathbf{T}}_{A}^{{}} = {\mathbf{I}}_{S}^{*} \,({\ddot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\ddot{\boldsymbol{\upvarphi }}}) + ({\dot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}) \times {\mathbf{I}}_{S}^{*} ({\dot{\boldsymbol{\uptheta }}}_{A}^{{}} + {\dot{\boldsymbol{\upvarphi }}}) - ({\mathbf{M}}_{B}^{(S)} + {\mathbf{M}}_{C}^{(S)} + {\mathbf{M}}_{D}^{(S)} + {\mathbf{r}}_{CM} \times m_{S} \,{\mathbf{g}}),$$

where

$${\mathbf{r}}_{CM} \times m_{S} \,{\mathbf{g}} = m_{S} \left| {\begin{array}{*{20}c} {{\mathbf{e}}_{x} } & {{\mathbf{e}}_{y} } & {{\mathbf{e}}_{z} } \\ 0 & {y_{CM} } & 0 \\ {g_{x} } & {g_{y} } & {g_{z} } \\ \end{array} } \right| = [g_{z} y_{CM} ,0, - g_{x} y_{CM} ]^{T}$$
  1. 5.

    vectors of external reaction forces and moments of force acting on the point of contact of the wheel with the ground, resulting from relationship (1)

$${\mathbf{F}}_{T} = {\mathbf{F}}_{A} ,\quad{\mathbf{T}}_{T} = {\mathbf{T}}_{A} - {\mathbf{r}}_{T} \times {\mathbf{F}}_{T} .$$

In the initial approximation, for simplicity, it is possible to neglect the parameters of system motion occurring in Eqs. (4)–(5) and consequently the resulting inertia forces. This assumption is particularly justified during steady-state motion of the robot.

4 Practical Realization of Measuring System

Within the present work, a practical realization of the measuring system allowing determination of forces and moments of force acting on the robot wheel will be presented. It is the patent pending solution [10].

In Fig. 6 mechanical design of the robot drive unit is shown, and in Fig. 7, the realized structure. The drive unit contains 2 measuring heads shown in Fig. 8. Both heads enable measurement of forces carried by the bearings, which are marked B and C in Fig. 3.

Fig. 6
figure 6

Mechanical design of the robot drive unit

Full size image
Fig. 7
figure 7

Realization of the robot drive unit

Full size image
Fig. 8
figure 8

Mechanical design of the measuring head

Full size image

Through both measuring heads passes the axle driven by the motor on which the wheel is mounted. According to Fig. 8, the measuring head consists of bearing 1 which transmits the forces and moments of force acting on the axle, bearing housings 2 and 3, the supporting frame 4, six flexible pressure sensors 7 and fine-pitch screws 5 which allow calibration of the head measuring system.

5 Conclusions

Within the work, the method of determination of forces and moments of force transmitted by the wheel of a mobile robot during its motion is presented. The proposed method of calculations will enable determination of those quantities in the experimental investigations of motion of the robot. Also the practical implementation of the proposed system developed for the four-wheeled robot with independently driven nonsteered wheels is presented. The proposed solution will enable verification of the tire models used in the simulation investigations of the lightweight wheeled mobile robots.