Fully Inverse Parametric Linear/Quadratic Programming Problems via Convex Liftings

Abstract

In this chapter, we present in an unified manner the latest developments on inverse optimality problem for continuous piecewise affine (PWA) functions. A particular attention is given to convex liftings as a cornerstone for the constructive solution we advocate in this framework. Subsequently, an algorithm based on convex lifting is presented for recovering a continuous PWA function defined over a polyhedral partition of a polyhedron. We also prove that any continuous PWA function can be equivalently obtained by a parametric linear programming problem with at most one auxiliary one-dimensional variable.

1 Introduction

Piecewise affine (PWA) functions have been studied in Mathematics since many years. They are useful to fit nonlinear functions which are difficultly obtained via an analytic expression. In control theory, PWA functions appeared early in [40] as a new approach for nonlinear control design. Subsequently, this class of functions has been particularly of use to approximate nonlinear systems [1]. This approximation is of help to simplify control design and stability analysis for nonlinear systems. Afterward, many studies exploit PWA functions as a good candidate to approximate optimal solution of constrained optimization-based control, e.g., [7, 13, 19, 20, 35]. Subsequently, this class of functions is proved to represent an optimal solution to a minimization problem subject to linear constraints and a linear/quadratic cost function, leading to a class of hybrid systems called piecewise affine systems. This class of control laws has received significant attention in control community [8, 33, 39, 43].

However, PWA control law is shown to have two major limitations in terms of implementation, once the state-space partition includes many regions:

• the memory requirement for storing the regions and the associated control law gains, is demanding,

• the point-location problem, determining which region the current state belongs to, becomes more expensive.

Therefore, it is necessary to find other methods of implementing these control laws to overcome the above limitations. Some studies on the complexity reduction of PWA control laws are found in [21, 22, 25, 26]. In general, these studies search for complexity reduction via the simplification of state-space partition by preserving the stability property but by trading for performance degradation. An alternative direction for complexity reduction is generated by inverse optimality problem. This idea is fundamentally different by the fact that the given PWA function will be embedded into the frame of an optimization problem.

Inverse optimality problems aim at finding suitable optimization problems such that their optimal solutions are equivalent to those to the associated given functions. In particular, inverse parametric linear/quadratic programming problem focuses on recovering a continuous PWA function defined over a polyhedral partition. Some recent results are found in [6, 17, 27–29, 32]. Two different approaches are distinguished therein. The first one [17] relies on the decomposition of each component of the given continuous PWA function into the difference of two convex functions. This approach requires $2n_u$ auxiliary variables where $n_u$ represents the dimension of the co-domain space of the given PWA function. The latter one relies on convex liftings which needs only one auxiliary variable. However, this method is restricted to continuous PWA functions defined over polytopic partitions (bounded polyhedral partition). In the same line of the works in [27, 28, 32], the result in this manuscript is also based on convex liftings. However, this chapter extends to continuous PWA functions defined over a polyhedral partition of a polyhedron (possibly unbounded).

2 Notation and Definitions

Apart from the common notation of the book, in this chapter we use $\mathbb {N}_{>0}$ to denote the set of positive integers. Also, for ease of presentation, we use $\mathcal {I}_N$ to denote the following index set with respect to a given $N \in \mathbb {N}_{>0}$: $\mathcal {I}_N=\left\{ i \in \mathbb {N}_{>0} \mid i \le N\right\} .$

For a given $d\in \mathbb {N}_{>0},$ we use $1_d$ to denote a vector in $\mathbb {R}^d$ whose elements are equal to 1.

Given two sets $P_1, P_2 \subset \mathbb {R}^{d},$ their Minkowski sum, denoted as $P_1 \oplus P_2,$ is defined as follows:

$$\begin{aligned} P_1 \oplus P_2 :=\left\{ y \in \mathbb {R}^d \mid \exists x_1 \in P_1, x_2 \in P_2, \quad \text { s.t. } y=x_1+x_2 \right\} . \end{aligned}$$

Given a set $\mathcal {S},$ we write by $\mathrm {int}(\mathcal {S}), \mathrm {conv}(\mathcal {S})$ to denote the interior, the convex hull of the set $\mathcal {S},$ respectively. Also, by $\mathrm {dim}(\mathcal {S}),$ we denote the dimension of the affine hull of $\mathcal {S}.$ With a space $\mathbb {S}$, being a subspace of $\mathbb {R}^d$, we use $\mathrm {Proj}_{\mathbb {S}}\,\mathcal {S}$ to denote the orthogonal projection of $\mathcal {S} \subseteq \mathbb {R}^d$ onto the space $\mathbb {S}.$

A polyhedron is the intersection of finitely many halfspaces. A polytope is a bounded polyhedron. An unbounded polyhedron is known to obtain rays. An extreme ray is a ray which cannot be written by a convex combination of any two other rays. Given a full-dimensional polyhedron $\mathcal {S} \subset \mathbb {R}^d,$ we write $\mathcal {V}(\mathcal {S}), \mathcal {R}(\mathcal {S})$ to denote the sets of vertices and extreme rays, of polyhedron $\mathcal {S},$ respectively. If $\mathcal {S}$ is a full-dimensional polyhedron, then its number of vertices and extreme rays are known to be finite. If $\mathcal {S}$ is a finite set of rays, i.e., $S = \left\{ y_1,\ldots ,y_n\right\}$ then $\mathrm {cone}(\mathcal {S})$ represents the cone defined as follows:

$$\begin{aligned} \mathrm {cone}(S) = \left\{ t_1y_1 + \cdots + t_ny_n: \,\, t_i \ge 0,\quad \forall \, 1 \le i \le n\right\} \end{aligned}$$

(2.1)

Given two sets $\mathcal {S}_1, \mathcal {S}_2,$ we write $\mathcal {S}_1 \backslash \mathcal {S}_2$ to denote the points which belong to $\mathcal {S}_1$ but do not belong to $\mathcal {S}_2.$ More precisely, its mathematical description is presented as follows:

$$\mathcal {S}_1 \backslash \mathcal {S}_2:=\left\{ x \mid x \in \mathcal {S}_1, \quad x \notin \mathcal {S}_2\right\} .$$

For two vectors $x,u \in \mathbb {R}^d,$ $\left\langle x,u \right\rangle = x^Tu.$ Given a vector $u \in \mathbb {R}^d$ and a scalar $\alpha \in \mathbb {R},$ a hyperplane, denoted by $\mathcal {H}$, is defined as follows:

$$\mathcal {H}=\left\{ x \in \mathbb {R}^d \mid \left\langle x,u \right\rangle = \alpha \right\} .$$

Such a hyperplane $\mathcal {H}$ is called a supporting hyperplane of a polyhedron/polytope $\mathcal {S}$ if either $\mathrm {inf}\left\{ \left\langle x,u \right\rangle \mid x \in \mathcal {S}\right\} = \alpha$ or $\mathrm {sup}\left\{ \left\langle x,u \right\rangle \mid x \in \mathcal {S}\right\} = \alpha .$ A face of polyhedron/polytope $\mathcal {S}$ is the intersection of this set and one of its supporting hyperplanes. If $\mathcal {S}\subset \mathbb {R}^d$ denotes a full-dimensional polyhedron/polytope, then a face of dimension $k, 0 \le k \le d,$ is briefly denoted by $k-$face. A $(d-1)-$face is called a facet, an 1-face is called an edge, a $0-$face is called a vertex. If $\mathcal {S}$ denotes a polyhedron/polytope, then by $\mathcal {F}(\mathcal {S}),$ we denote the set of its facets.

For ease of presentation, given an $\epsilon \in \mathbb {R}_+,$ we use $B_d(\epsilon )$ to denote a full-dimensional box in $\mathbb {R}^{d},$ i.e., $B_d(\epsilon )=\left\{ x \in \mathbb {R}^{d} \mid \Vert x \Vert _{\infty } \le \epsilon \right\} .$

Some necessary definitions of help for our development are presented below.

Definition 2.1

A collection of $N\in \mathbb {N}_{>0}$ full-dimensional polyhedra $\mathcal {X}_i \subset \mathbb {R}^d,$ denoted by $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$, is called a polyhedral partition of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^d$ if

• 1. $\bigcup _{i \in \mathcal {I}_N} \mathcal {X}_i=\mathcal {X}$.

• 2. $\text {int}(\mathcal {X}_i) \bigcap \text {int}(\mathcal {X}_j)= \emptyset \text {with} i \ne j, (i,j) \in \mathcal {I}^2_N$,

Also, $(\mathcal {X}_i, \mathcal {X}_j)$ are called neighbors if $(i,j)\in \mathcal {I}^2_N$, $i\ne j$ and $\text {dim}(\mathcal {X}_i \cap \mathcal {X}_j)=d-1$.

If $\mathcal {X}_i$ for every $i \in \mathcal {I}_N$ are polytopes, then the partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ is alternatively called polytopic partition. A polyhedral partition is called cell complex, if its facet-to-facet property [41] is fulfilled,¹ namely, any two neighboring regions share a common facet.

Definition 2.2

For a given polyhedral partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^d,$ a piecewise affine lifting is described by function $z: \mathcal {X} \rightarrow \mathbb {R}$ with

$$\begin{aligned} z(x)= a^T_i x+b_i \quad \text { for any } x \in \mathcal {X}_i, \end{aligned}$$

(2.2)

and $a_i \in \mathbb {R}^{d}, \, b_i \in \mathbb {R}, \quad \forall i \in \mathcal {I}_N$.

Definition 2.3

Given a polyhedral partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X},$ a piecewise affine lifting $z(x)= a^T_i x+b_i \forall x \in \mathcal {X}_i,$ is called convex lifting if the following conditions hold true:

• z(x) is continuous over $\mathcal {X}$,

• for each $i \in \mathcal {I}_N$, $z(x) > a_j^Tx +b_j$ for all $x \in \mathcal {X}_i \backslash \mathcal {X}_j$ and all $j \ne i,\, j \in \mathcal {I}_N$.

The strict inequality in Definition 2.3 implies the convexity of z(x) and the fact that for any two neighboring regions $(\mathcal {X}_i, \mathcal {X}_j),$ $(a_i,b_i) \ne (a_j,b_j).$ Namely, any two neighboring regions should be lifted onto two distinct hyperplanes. The strict inequality is of help to guarantee the partition between different regions. Note that there always exits a piecewise affine lifting for any polyhedral partition. A trivial example is the one defined as in Definition 2.2 with $a_i = 0, b_i = 0.$ However, it is not the case that any polyhedral partition admits a convex lifting. It is observed that a polyhedral partition with respect to the existence of a convex lifting should be a cell complex. This observation is proved via the following lemma.

Lemma 2.1

If a given polyhedral partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^d$ admits a convex lifting, then it is a cell complex.

Proof

By $z(x)=a^T_ix+b_i,$ for $x \in \mathcal {X}_i,$ we denote a convex lifting of the given partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$. Consider a pair of neighboring regions $(\mathcal {X}_i, \mathcal {X}_j), (i,j) \in \mathcal {I}^2_N.$ As defined, due to the continuity of z(x) at any point $x \in \mathcal {X}_i \cap \mathcal {X}_j,$ the hyperplane,

$$\mathcal {H}:= \left\{ x \in \mathbb {R}^d \mid a^T_ix+b_i = a^T_jx+b_j \right\} ,$$

separates $\mathcal {X}_i, \mathcal {X}_j$ and contains $\mathcal {X}_i \cap \mathcal {X}_j.$ Also, by the second property of a convex lifting, the halfspace,

$$C_i:=\left\{ x \in \mathbb {R}^d \mid a^T_ix+b_i > a^T_jx+b_j \right\} ,$$

contains $\mathcal {X}_i \backslash (\mathcal {X}_i \cap \mathcal {X}_j).$

Suppose the facet-to-facet property of $\mathcal {X}_i, \mathcal {X}_j$ is not fulfilled. Then, there exists a point $x \in \mathcal {H},$ s.t. either $x \in \mathcal {X}_i, x \notin \mathcal {X}_j,$ or $x \in \mathcal {X}_j, x \notin \mathcal {X}_i.$ Without loss of generality, the former one happens. $x \in \mathcal {H}$ leads to $a^T_ix+b_i = a^T_jx+b_j.$ Also, $x \in \mathcal {X}_i, x \notin \mathcal {X}_j$ leads to $a^T_ix+b_i > a^T_jx+b_j.$ These last two inclusions are clearly contradictory. The proof is complete.    $\square$

Definition 2.4

A cell complex $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^d$ admits an affinely equivalent polyhedron if there exists a polyhedron $\widetilde{\mathcal {X}} \subset \mathbb {R}^{d+1},$ such that for each $i \in \mathcal {I}_N$:

• 1. $\exists F_i \in \mathcal {F}(\widetilde{\mathcal {X}})$ satisfying: $\mathrm {Proj}_{\mathbb {R}^{d}} F_i = \mathcal {X}_i,$

• 2. if $\underline{z}(x)=\underset{z}{\min }\,z \,\,$ s.t. $\left[ x^T \,z \right] ^T \in \widetilde{\mathcal {X}},$ then $\left[ x^T \,\, \underline{z}(x)\right] ^T \in F_i$ for $x \in \mathcal {X}_i$.

An illustration can be found in Fig. 2.1 thereby the multicolored segments along the horizontal axis represent the given polytopic partition including six regions. The pink polytope above is one of its affinely equivalent polyhedra.

Fig. 2.1

An illustration for affinely equivalent polyhedron

Remark 2.1

Note that the lower boundary of an affinely equivalent polyhedron represents a convex lifting for a given cell complex as shown in Fig. 2.1. Therefore, starting from an affinely equivalent polyhedron $\widetilde{\mathcal {X}}$ of the given cell complex $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$, one of its convex liftings is the optimal cost function of the following parametric linear programming problem:

$$\begin{aligned} \underset{z}{\min }\,z \quad \text { subject to } \quad \left[ x^T \,\, z\right] ^T \in \widetilde{\mathcal {X}}, \end{aligned}$$

where z denotes the last coordinate of $\widetilde{\mathcal {X}}$ and $x \in \mathcal {X}.$ Note also that if a given cell complex is convexly liftable, the existence of convex lifting is not unique, meaning that different convex liftings can be defined over a given cell complex. However, for the practical interest in control theory, the existence is the most important property.

An algorithm for construction of convex liftings will be presented in Sect. 2.4.

3 Problem Statement

This section formally presents the definition of inverse optimality problem. As earlier mentioned, the main goal is to recover a continuous PWA function through an optimization problem (see also [6]). The solution relies on convex liftings.

Given a polyhedral partition $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^{n_x}$ and a continuous PWA function $f_{pwa}(\cdot ): \mathcal {X}\rightarrow \mathbb {R}^{n_u}$, the objective is to find a set of four matrices $H_x, H_u, H_z, K,$ defining linear constraints and a linear/quadratic cost function J(x, z, u) such that $f_{pwa}(x)$ can be equivalently obtained via the optimal solution to the following convex optimization problem:

$$\begin{aligned} f_{pwa}(x)= \mathrm {Proj}_{\mathbb {R}^{n_u}}\mathrm {arg}\underset{\left[ z^T \,\,u^T\right] ^T}{\,\min } \, J(x,z,u) \,\, \text { s.t. } \,\, H_xx+H_zz+H_uu \le K. \end{aligned}$$

(2.3)

It is well known that optimal solution to a parametric linear/quadratic programming problem is a PWA function defined over a polyhedral partition (see [8]). Therefore, we restrict our interest, in this manuscript, to linear constraints. Note also that a given PWA function is usually not convex/concave, the presence of an auxiliary variable z is thus of help to reinforce the convexity of the recovered optimization problem. It will be proved that scalar $z \in \mathbb {R}$ is sufficient for the recovery.

4 Algorithm for the Construction of a Convex Lifting

4.1 Existing Results on Convex Liftings

As shown in Lemma 2.1, a polyhedral partition, admitting a convex lifting, should be a cell complex. However, not every cell complex is convexly liftable. An illustration can be found in Fig. 2.2. This partition is a cell complex but not convexly liftable. Thus, being a cell complex is a necessary condition for the existence of convex liftings, but not a sufficient condition. Back to the history, we can find the trace of a large number of studies on this topic. Some prominent results for convex liftability of polyhedral partitions in $\mathbb {R}^2$ are found in [9, 10, 24, 38]. Also, some particular diagrams, e.g., Voronoi diagrams, Delaunay diagrams, and Power diagrams in the general dimensional space, are studied in [3, 5, 11, 12, 16]. Necessary and sufficient conditions for a cell complex to be convexly liftable are referred to [2, 4, 23, 28, 30, 36].

Note that these results are equivalent as proved in [36]; therefore, if a cell complex is convexly liftable, then it satisfies all these conditions. Also, due to Lemma 2.1, a polyhedral partition, whose facet-to-facet property does not hold, will not fulfill these conditions.

From the practical interest, these above conditions are only of help for recognizing a convexly liftable cell complex. They do not provide any hint for the construction of such convex liftings. As convex liftings are a tool in our constructive solution of inverse optimality, an algorithm dedicated to convex liftings will be presented in the next subsection.

Fig. 2.2

A nonconvexly liftable cell complex

4.2 An Algorithm for Construction of Convex Liftings

This subsection concentrates on a construction of convex liftings for a given cell complex. The following algorithm is based on the reinforcement of continuity and convexity constraints at the vertices of the given cell complex. Clearly, the vertex representation of this cell complex is of use. Therefore, this algorithm (Algorithm 2.1) restricts the construction to a bounded cell complex $\left\{ \mathcal {X}_i \right\} _{i\in \mathcal {I}_N}$, e.g., a cell complex of a polytope $\mathcal {X}$. A simple convexly liftable cell complex is presented in Fig. 2.3. One of its convex liftings is shown in Fig. 2.4.

Fig. 2.3

A convexly liftable cell complex

Fig. 2.4

A convex lifting of the cell complex in Fig. 2.3

Note that the insertion of $c > 0$ in (2.5) ensures the strict inequalities called convexity conditions, as defined in Definition 2.3. As for the complexity of Algorithm 2.1, if N denotes the number of regions in $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_N}$, then step 1 considers at most $\frac{1}{2} N(N-1)$ cases. For each pair of neighboring regions, the number of imposed constraints (including equality and inequality constraints) is equal to the number of vertices of $\mathcal {X}_i.$ If $v_\mathrm{max}$ denotes the maximal number of vertices among the regions in $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_N}$, then an upper bound for the number of constraints for (2.6) is $\frac{1}{2} N(N-1)v_\mathrm{max},$ thus scales quadratically with the number of regions. Recall that (2.6) is a quadratic programming problem and is considered to be computationally tractable with respect to the working-memory capacity of calculator.

Note also that the requirement that $\mathcal {X}$ is a polytope can be relaxed to compact, (not necessarily convex) polyhedral sets. As defined, a polyhedral partition is a collection of several polyhedra/polytopes. If we restrict our attention to a collection of polytopes, then their union represents a bounded set. This compact set has the boundary described by linear constraints, but it is not necessarily a polytope. Algorithm 2.1 can also construct convex liftings for such convexly liftable cell complexes if feasible. For illustration, a cell complex of a nonconvex polyhedral set is shown in Fig. 2.5. This cell complex is clearly convexly liftable.

Fig. 2.5

A convexly liftable cell complex of a nonconvex polyhedral set

Notice also that the feasibility of the optimization problem (2.6) is instrumental to determine whether the given partition is convexly liftable. More clearly, the given cell complex is convexly liftable if and only if problem (2.6) is feasible. Due to Lemma 2.1, for any polyhedral partition, whose facet-to-facet property does not hold, the associated optimization problem (2.6) is infeasible.

For a convexly liftable cell complex of a polyhedron, it can be observed that Algorithm 2.1 cannot be directly applicable. Let us take a simple example to illustrate this limitation of Algorithm 2.1. Consider a partition of four quadrants, which covers the whole $\mathbb {R}^2.$ It is observed that each quadrant has only one vertex, known to be the origin 0. Therefore, if $(Q_1, Q_2)$ are two neighboring quadrants, only one continuity constraint at the origin will be imposed along Algorithm 2.1. It follows that $z(x)=0$ may be resulted from the optimization problem (2.6). However, this real-valued function is not a convex lifting.

We will present an intermediate result related to the construction of convex liftings for cell complexes of polyhedra.

The following assumption is of help for our development.

Assumption 2.1

For all $x \in \bigcup _{i \in \mathcal {I}_N} \mathcal {V}(\mathcal {X}_i),$ $x \in \mathrm {int}(B_{n_x}(\epsilon )) \subset \mathbb {R}^{n_x},$ with some suitable $\epsilon >0.$

In view of Assumption 2.1, the following theorem is of help to construct convex liftings for cell complexes of a polyhedron.

Theorem 2.1

Given a convexly liftable cell complex $\left\{ \mathcal {X}_i\right\} _{i\in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}\subseteq \mathbb {R}^{n_x}$ and a box $B_{n_x}(\epsilon )$ satisfying Assumption 2.1, $f: \mathcal {X}\cap B_{n_x}(\epsilon ) \rightarrow \mathbb {R}$

$$\begin{aligned} f(x)=a^T_i x +b_i \quad \text { for } \quad x \in \mathcal {X}_i \cap B_{n_x}(\epsilon ), \nonumber \end{aligned}$$

is a convex lifting of the cell complex $\left\{ \mathcal {X}_i \cap B_{n_x}(\epsilon )\right\} _{i\in \mathcal {I}_N}$, if and only if the function $g:\mathcal {X}\rightarrow \mathbb {R}$ defined as follows:

$$\begin{aligned} g(x)= a^T_ix+b_i \quad \text { for } \quad x \in \mathcal {X}_i, \nonumber \end{aligned}$$

is also a convex lifting of $\left\{ \mathcal {X}_i \right\} _{i\in \mathcal {I}_N}$.

Proof

$\longrightarrow$ First, due to Assumption 2.1, the intersection $\mathcal {X}\cap B_{n_x}(\epsilon )$ does not have any effect on the internal subdivision of $\mathcal {X}$, since any vertex of the partition $\left\{ \mathcal {X}_i \right\} _{i\in \mathcal {I}_N}$ lies in the interior of $B_{n_x}(\epsilon )$.

Consider now two neighboring regions in the partition $\left\{ \mathcal {X}_i \cap B_{n_x}(\epsilon ) \right\} _{i \in \mathcal {I}_N}$, denoted as $\mathcal {X}_i \cap B_{n_x}(\epsilon ), \mathcal {X}_j \cap B_{n_x}(\epsilon )$. As assumed, f(x) is a convex lifting of $\left\{ \mathcal {X}_i \cap B_{n_x}\right. \left. (\epsilon )\right\} _{i \in \mathcal {I}_N}$, then it can be deduced from its definition that:

$$\begin{aligned} \begin{aligned}&a^T_ix + b_i = a^T_jx+b_j \quad \forall x \in (\mathcal {X}_i \cap B_{n_x}(\epsilon )) \cap (\mathcal {X}_j \cap B_{n_x}(\epsilon )) \\&a^T_ix + b_i > a^T_jx+b_j \quad \forall x \in (\mathcal {X}_i \cap B_{n_x}(\epsilon )) \backslash (\mathcal {X}_j \cap B_{n_x}(\epsilon )). \end{aligned} \end{aligned}$$

Note also that constraint $a^T_ix + b_i = a^T_jx+b_j$ describes the hyperplane, separating $\mathcal {X}_i \cap B_{n_x}(\epsilon )$ and $\mathcal {X}_j \cap B_{n_x}(\epsilon )$, then it separates also $\mathcal {X}_i$ and $\mathcal {X}_j$. This end leads to

$$\begin{aligned} \begin{aligned} a^T_ix + b_i&= a^T_jx+b_j \quad \forall x \in \mathcal {X}_i \cap \mathcal {X}_j, \\ a^T_ix + b_i&> a^T_jx+b_j\quad \forall x \in \mathcal {X}_i \backslash \mathcal {X}_j. \end{aligned} \end{aligned}$$

Applying this inclusion to every pair of neighboring regions, the following inclusion can be obtained:

$$\begin{aligned} a^T_ix+b_i > a^T_jx +b_j,\quad \forall x \in \mathcal {X}_i \backslash \mathcal {X}_j, \forall j \ne i, j\in \mathcal {I}_N, \nonumber \end{aligned}$$

meaning g(x) is a convex lifting of $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N}.$

$\longleftarrow$ The sufficient condition can be similarly proved.    $\square$

This theorem shows that we can construct a convex lifting for a cell complex of a polyhedron from a convex lifting of an appropriate partition of a bounded set. This partition is resulted from the intersection of the given cell complex and some suitable boxes. The remaining problem is to find out one among these boxes. This task can be easily carried out from Assumption 2.1. A simple algorithm is put forward below.

Note that a strictly positive scalar c needs to be inserted in Algorithm 2.2 to ensure that all $x \in \bigcup _{i \in \mathcal {I}_N} \mathcal {V}(\mathcal {X}_i)$ lie in the interior of $B_{n_x}(\epsilon )$ via constraint reinforcements. More precisely, constraints $-(\epsilon - c)1_{n_x} \le x \le (\epsilon - c)1_{n_x}$ imply that $\epsilon - c > 0,$ leading to $\Vert x \Vert _{\infty } \le \epsilon - c < \epsilon ,$ thus $x \in \mathrm {int}(B_{n_x}(\epsilon ))$ for all $x \in \bigcup _{i \in \mathcal {I}_N} \mathcal {V}(\mathcal {X}_i).$

4.3 Nonconvexly Liftable Partitions

Taking into account the dichotomy between convexly liftable and nonconvexly liftable partitions, a natural question is how to deal with PWA functions defined over nonconvexly liftable partitions. As mentioned before, not every cell complex is convexly liftable, therefore, solving inverse parametric linear/quadratic programming problems via convex liftings needs an adaptation to deal with such particular partitions. Note that this issue has already been investigated in [28, 32]. We recall the main result here for completeness.

Theorem 2.2

Given a nonconvexly liftable polytopic partition $\left\{ \mathcal {X}_i\right\} _{i\in \mathcal {I}_N}$, there exists at least one subdivision, preserving the internal boundaries of this partition, such that the new cell complex is convexly liftable.

We refer to [28, 32] for the details of proof. It is worth emphasizing that this result states only for polytopic partitions of bounded sets. However, its extension to polyhedral partitions of an unbounded set can be performed along the same arguments. This observation can formally be stated as follows.

Lemma 2.2

For any polyhedral partition of a polyhedron, there always exists one subdivision such that the internal boundaries of this partition are preserved and the new partition is convexly liftable.

Proof

See the proof of Theorem IV.2 presented in [28].

Note that in practice a complete hyperplane arrangement is not necessary. One can find a particular case of refinement in [15].

5 Solution to Inverse Parametric Linear/Quadratic Programming Problems

Based on the above results, this section aims to put forward the solution to inverse optimality problem via convex liftings. This solution is viable with respect to the following standing assumption.

Assumption 2.2

The given cell complex $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_N}$ of a polyhedron $\mathcal {X}$ is convexly liftable.

Note that this assumption is not restrictive due to Lemma 2.2. Following this lemma, if a given polyhedral partition does not satisfy Assumption 2.2, it can be refined into a convexly liftable partition such that its internal boundaries are maintained.

We use z(x) to denote a convex lifting of $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_N},$ $z(x)=a^T_ix+b_i$ for $x \in \mathcal {X}_i.$ We want to recover a continuous PWA function, denoted by $f_{pwa}(x)$, i.e., $f_{pwa}(x)= H_ix+g_i$ for $x\in \mathcal {X}_i.$ Note that these results can be extended for discontinuous PWA functions; we refer to [31] for more details.

For ease of presentation, the following sets are also defined:

$$\begin{aligned} V_x&= \bigcup _{i \in \mathcal {I}_N} \mathcal {V}(\mathcal {X}_i), R_x = \bigcup _{i \in \mathcal {I}_N} \mathcal {R}(\mathcal {X}_i),\nonumber \\ V_{\left[ x^T \,z\,\,u^T\right] ^T}&= \left\{ \left[ x^T \,z(x)\,\,f^T_{pwa}(x)\right] ^T \mid x \in V_x \right\} , \nonumber \\ R_{\left[ x^T \,z\,\,u^T\right] ^T}&= \left\{ \left[ r^T \, \widehat{z}(r) \,\,\widehat{f}^{\,T}(r)\right] ^T \mid r \in R_x,\, \begin{aligned}&\widehat{z}(r)=a^T_ir \\&\widehat{f}(r) = H_ir \end{aligned} \,\, \text { if } \,\, r\in \mathcal {R}(\mathcal {X}_i) \right\} ,\\ \varPi _v&= \mathrm {conv}(V_{\left[ x^T \,z\,\,u^T\right] ^T}), \varPi _r = \mathrm {cone}(R_{\left[ x^T \,z\,\,u^T\right] ^T}), \nonumber \\ \varPi&= \varPi _v \oplus \varPi _r. \nonumber \end{aligned}$$

(2.7)

The main result of this manuscript is presented via the following theorem which generalizes the results in [32] to general polyhedra.

Theorem 2.3

Given a continuous PWA function $f_{pwa}(x),$ defined over a cell complex $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_N}$ satisfying Assumption 2.2, then $f_{pwa}(x)$ is the image via the orthogonal projection of the optimal solution to the following parametric linear programming problem:

$$\begin{aligned} \underset{\left[ z\,\,u^T\right] ^T}{\min }\, z \quad \text { subject to } \quad \left[ x^T \, z\,\, u^T\right] ^T \in \varPi . \end{aligned}$$

(2.8)

Proof

Consider $x \in \mathcal {X}_i,$ due to the Minkowski–Weyl theorem for polyhedra (Corollary 7.1b in [37]), x can be described as follows:

$$\begin{aligned} x = \sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v) v + \sum _{r \in \mathcal {R}(\mathcal {X}_i)} \beta (r)r, \nonumber \end{aligned}$$

where $\alpha (v),\beta (r) \in \mathbb {R}_+$ and $\sum _{v \in \mathcal {V}(\mathcal {X}_i)}\alpha (v)=1$. As a consequence, the convex lifting at x, i.e., z(x) can be described by

$$\begin{aligned} \begin{aligned} z(x)&= a^T_ix+b_i =a^T_i\left( \sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v) v + \sum _{r \in \mathcal {R}(\mathcal {X}_i)} \beta (r) r\right) +b_i, \\&=\sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v) \left( a^T_iv+b_i\right) + \sum _{r \in \mathcal {R}(\mathcal {X}_i)} \beta (r) \left( a^T_ir\right) . \end{aligned} \nonumber \end{aligned}$$

Similarly,

$$\begin{aligned} f_{pwa}(x) =\sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v) (H_iv+g_i) + \sum _{r \in \mathcal {R}(\mathcal {X}_i)} \beta (r) (H_ir). \nonumber \end{aligned}$$

It can be observed that if r is a ray of $\mathcal {X}_i$, then $\left[ r^T\,\,a^T_ir\right] ^T$ is a ray of the affinely equivalent polyhedron $\varPi _{\left[ x^T\,\,z\right] ^T}$ of $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_N},$ defined as follows:

$$\begin{aligned} \varPi _{\left[ x^T\,\,z\right] ^T}=\mathrm {conv}(V_{\left[ x^T \,z \right] ^T}) \oplus \mathrm {cone}(R_{\left[ x^T \,z \right] ^T}), \nonumber \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_{\left[ x^T \,z \right] ^T}&=\left\{ \left[ x^T \,\, z(x)\right] ^T \mid x \in V_x \right\} , \\ R_{\left[ x^T \,z \right] ^T}&=\left\{ \left[ r^T \,\, \widehat{z}(r)\right] ^T \mid r \in R_x,\,\,\widehat{z}(r)=a^T_ir \,\, \text { if } \,\, r\in \mathcal {R}(\mathcal {X}_i)\right\} . \end{aligned} \nonumber \end{aligned}$$

Therefore, for a region $\mathcal {X}_i$, there exists a facet of $\varPi _{\left[ x^T\,\,z\right] ^T}$, denoted by $F^{(i)}_{\left[ x^T\,\,z\right] ^T}$, such that

$$\begin{aligned} \begin{aligned}&\mathrm {Proj}_{\,\mathbb {R}^{n_x}}F^{(i)}_{\left[ x^T\,\,z\right] ^T}=\mathcal {X}_i, \\&\forall \left[ x^T \,z(x)\right] ^T \in F^{(i)}_{\left[ x^T\,\,z\right] ^T},\,\, z(x)= \underset{z}{\min } \,z \,\, \text { s.t. } \left[ x^T \,\,z\right] ^T \in \varPi _{\left[ x^T\,\,z\right] ^T}. \end{aligned} \end{aligned}$$

(2.9)

According to Proposition 5.1 in [27], every augmented point in $V_{\left[ x^T \,z \,\,u^T\right] ^T}$ is vertices of $\varPi _v$. Thus, lifting onto $\mathbb {R}^{n_x+n_u+1}$ leads to the existence of an $n_x-$face of $\varPi$, denoted by $F^{(i)}_{\left[ x^T\,\,z\,\,u^T\right] ^T}$ such that

$$\begin{aligned} \mathrm {Proj}_{\mathbb {R}^{n_x+1}}F^{(i)}_{\left[ x^T\,\,z\,\,u^T\right] ^T}=F^{(i)}_{\left[ x^T\,\,z\right] ^T}. \end{aligned}$$

(2.10)

Due to (2.9) and (2.10), the minimal value of z at a point $x \in \mathcal {X}_i$ happens when $\left[ x^T\,\,z\,\,u^T\right] ^T$ lies in $F^{(i)}_{\left[ x^T\,\,z\,\,u^T\right] ^T}.$ Therefore, optimal solution to (2.8) at x can be described by

$$\begin{aligned} \left[ \begin{matrix}x \\ z^{*}(x) \\ u^*(x)\end{matrix}\right] = \sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v) \left[ \begin{matrix}v\\ a^T_iv+b_i\\ H_iv+g_i\end{matrix}\right] + \sum _{r \in \mathcal {R}(\mathcal {X}_i)} \beta (r) \left[ \begin{matrix}r\\ a^T_ir \\ H_ir\end{matrix}\right] , \nonumber \end{aligned}$$

where $\alpha (v),\beta (r) \in \mathbb {R}_+$ and $\sum _{v \in \mathcal {V}(\mathcal {X}_i)} \alpha (v)=1$. It is clear that

$$\left[ \begin{matrix} z^{*}(x) \\ u^*(x)\end{matrix}\right] =\left[ \begin{matrix}a^T_ix+b_i \\ H_ix+g_i\end{matrix}\right] =\left[ \begin{matrix}z(x)\\ f_{pwa}(x) \end{matrix}\right] , \,\, \text { for } x\in \mathcal {X}_i.$$

To complete the proof, we now need to show that the optimal solution to (2.8) is unique. In fact, at a point $x \in \mathcal {X}_i$, suppose there exist two different optimal solutions to (2.8)

$$\begin{aligned} \begin{aligned} \left[ z_1(x) \,\,u^T_1(x)\right] ^T&=\mathrm {arg} \,\underset{\left[ z\,\,u^T\right] ^T}{\min } \,z \\ \left[ z_2(x) \,\,u^T_2(x)\right] ^T&=\mathrm {arg} \,\underset{\left[ z\,\,u^T\right] ^T}{\min } \,z \end{aligned} \quad \text { s.t. } \quad \left[ x^T \,\,z\,\,\,u^T\right] ^T \in \varPi . \nonumber \end{aligned}$$

It can be observed that $z_1(x) = z_2(x).$ If $u_1(x) \ne u_2(x),$ then there exist two different $n_x-$faces, denoted by $F_1, F_2,$ such that $\left[ x^T \,\,z_1(x) \,\,\,u^T_1(x)\right] ^T \in F_1$ and $\left[ x^T \,\,z_2(x) \,\,\,u^T_2(x)\right] ^T \in F_2.$ Therefore, $z_1(x) = z_2(x)$ leads to

$$\mathrm {Proj}_{\mathbb {R}^{n_x+1}}F_1=\mathrm {Proj}_{\mathbb {R}^{n_x+1}}F_2=F^{(i)}_{\left[ x^T\,\,z\right] ^T}.$$

Accordingly, $F_1, F_2$ lie in a hyperplane of dimension $n_x+1$ which is orthogonal to the space of $\left[ x^T \,\,z\right] ^T$. An illustration can be found in Fig. 2.6. This leads to the fact that $f_{pwa}(v)$ or $\widehat{f}(r)$ in (2.7) is not uniquely defined for some $v \in \mathcal {V}(\mathcal {X}_i)$ or some $r \in \mathcal {R}(\mathcal {X}_i).$ This contradicts with the construction of $\varPi$ in (2.7). Therefore, $F_1 = F_2$ meaning the optimal solution to (2.8) is unique. Further, such an $n_x-$face $F_1$ can be written in the following form:

$$\begin{aligned} \begin{aligned} F_1&= F^{\#}_1 \oplus F^{\#}_2 \\ F^{\#}_1&= \mathrm {conv}\left\{ \left[ v^T \,\,z(v)\,\,f^T_{pwa}(v)\right] ^T \mid v \in \mathcal {V}(\mathcal {X}_i)\right\} \\ F^{\#}_2&= \mathrm {cone}\left\{ \left[ r^T \,\,a^T_ir \,\,(H_ir)^T \right] ^T \mid r \in \mathcal {R}(\mathcal {X}_i) \right\} . \end{aligned} \nonumber \end{aligned}$$

The proof is complete.    $\square$

Based on this result, a procedure to construct an inverse optimization problem is summarized via the following algorithm.

Fig. 2.6

An illustration for the uniqueness of optimal solution to (2.8)

The complexity of Algorithm 2.3 depends almost on the complexity of convex lifting computation, carried out via Algorithm 2.1. Therefore, if Algorithm 2.1 is computationally tractable, so is Algorithm 2.3.

To conclude this section, the following theorem presents an important property of the convex lifting-based method.

Theorem 2.4

Any continuous PWA function, defined over a (not necessarily convexly liftable) polyhedral partition of a polyhedron, can be equivalently obtained via a parametric linear programming problem with at most one auxiliary 1-dimensional variable.

Proof

If the given polyhedral partition $\left\{ \mathcal {X}_i \right\} _{i\in \mathcal {I}_N}$ is convexly liftable, following Theorem 2.3, the given continuous PWA function $f_{pwa}(x)$, defined over $\mathcal {X}$ can be obtained through a parametric linear programming problem. This optimization problem is constructed via convex lifting. This convex lifting represents an auxiliary one-dimensional variable.

If the given polyhedral partition $\left\{ \mathcal {X}_i\right\} _{i\in \mathcal {I}_N}$ is not convexly liftable, Theorem 2.2 shows the existence of an equivalent cell complex $\left\{ \widetilde{\mathcal {X}}_i \right\} _{i\in \mathcal {I}_{\widetilde{N}}}$ such that $\left\{ \widetilde{\mathcal {X}}_i \right\} _{i\in \mathcal {I}_{\widetilde{N}}}$ is convexly liftable and the internal boundaries of $\left\{ \mathcal {X}_i \right\} _{i\in \mathcal {I}_N}$ are maintained. This refinement also leads to an equivalent PWA function $\widetilde{f}_{pwa}(x)$ of $f_{pwa}(x)$ defined over a convexly liftable cell complex $\left\{ \widetilde{\mathcal {X}}_i \right\} _{i\in \mathcal {I}_{\widetilde{N}}}$ of $\mathcal {X}$. Again, due to Theorem 2.3, $\widetilde{f}_{pwa}(x)$ can be obtained through a parametric linear programming problem with an auxiliary one-dimensional variable, this auxiliary variable being a convex lifting of $\left\{ \widetilde{\mathcal {X}}_i \right\} _{i\in \mathcal {I}_{\widetilde{N}}}$.    $\square$

Note that we can also find a parametric quadratic programming problem which equivalently recovers the given continuous PWA function defined over a polyhedral partition of a (possibly unbounded) polyhedron, as shown in [32].

Remark 2.2

It is well known that optimal solution to a parametric linear/quadratic programming problem is a PWA function defined over a polyhedral partition. For the parametric quadratic programming case, it is shown in [8] that the optimal solution is continuous and unique. However, for the parametric linear programming case, this continuity of optimal solution may not be guaranteed. Fortunately, a continuous solution can equivalently be selected, as shown in [34, 42]. Based on the arguments presented in this chapter, a continuous optimal solution, induced from a parametric linear/quadratic programming problem, can also be equivalently obtained via an alternative parametric linear programming problem with at most one auxiliary one-dimensional variable. This auxiliary variable represents the convex lifting.

Fig. 2.7

The given PWA function (2.11) to be recovered

Fig. 2.8

A convex lifting of the cell complex $\left\{ \mathcal {X}_i \right\} _{i \in \mathcal {I}_{6}}$

Fig. 2.9

Illustration for the optimal solution to IPL/QP via convex liftings

6 An Illustrative Example

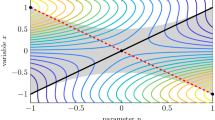
This section aims to illustrate the above results via a numerical example. Suppose we need to recover the PWA function (2.11), shown in Fig. 2.7. Note that this PWA function is continuous and is defined over the whole space $\mathbb {R}$. A box $B_1(3)$ is known to satisfy Assumption 2.1. The new partition $\left\{ \mathcal {X}_i \cap B_1(3)\right\} _{i \in \mathcal {I}_{6}}$ shown in Fig. 2.7 represents the multicolored segments along the x-axis. A convex lifting of the cell complex $\left\{ \mathcal {X}_i\right\} _{i \in \mathcal {I}_{6}}$ is analytically presented in (2.12) and is shown in Fig. 2.8. A set of constraints for the recovered optimization problem shown in (2.13) represents the pink polyhedron in Fig. 2.9. Therein, the multicolored segments along the x-axis denote the given partition covering $\mathbb {R},$ whereas the PWA function (2.11) represents the green curve above this partition. Also, the optimal solution to (2.8) represents the solid pink curve. It can be observed that the projection of this optimal solution to the space $\left[ x^T\,\,u^T\right] ^T$ coincides with the given PWA function. It is worth recalling that the proposed approach requires only one auxiliary one-dimensional variable, denoted by z, to recover (2.11). Finally, the numerical example in this chapter is carried out in the environment of MPT 3.0 [18].

$$\begin{aligned} f_{pwa}(x)= \left\{ \begin{aligned} -0.2447x - 0.2838 \,\,&\text { for } \,\, x \le -2 \\ 0.6940x + 1.5936 \,\,&\text { for } \,\, -2 \le x \le -1 \\ -0.1371x + 0.7626 \,\,&\text { for } \,\, -1 \le x \le 0 \\ 0.1199x + 0.7626 \,\,&\text { for } \,\, 0 \le x \le 1 \\ -0.5975x + 1.4800 \,\,&\text { for } \,\, 1 \le x \le 2 \\ 0.3883x - 0.4916 \,\,&\text { for } \,\, 2 \le x \end{aligned} \right. \end{aligned}$$

(2.11)

$$\begin{aligned} z(x)=\left\{ \begin{aligned} -2.5x - 2 \,\,&\text { for } \,\, x \le -2 \\ -1.5x \,\,&\text { for } \,\, -2 \le x \le -1 \\ -0.5x + 1 \,\,&\text { for } \,\, -1 \le x \le 0 \\ 0.5x + 1 \,\,&\text { for } \,\, 0 \le x \le 1 \\ 1.5x \,\,&\text { for } \,\, 1 \le x \le 2 \\ 2.5x - 2 \,\,&\text { for } \,\, 2 \le x \\ \end{aligned} \right. \end{aligned}$$

(2.12)

$$\begin{aligned} \varPi = \left\{ \left[ \begin{matrix}x \\ z\\ u \end{matrix}\right] \in \mathbb {R}^3 \mid \left[ \begin{array}{l@{\quad }l@{\quad }l} 1.0000 &{} -29.9413 &{} 116.5183 \\ 1.0000 &{} -18.4965 &{} 116.5183 \\ -2.2393 &{} -1.0000 &{} 1.0653 \\ -1.0000 &{} -1.7638 &{} 13.9320 \\ -1.0000 &{} -1.5039 &{} -1.8097 \\ 1.0000 &{} 1.7638 &{} -13.9320 \\ 1.0000 &{} 5.3390 &{} -50.4554 \\ 1.0000 &{} -13.0496 &{} -50.4554 \\ 2.1061 &{} -1.0000 &{} 1.0144 \\ 1.0000 &{} -1.4990 &{} -2.0893 \end{array} \right] \left[ \begin{matrix}x \\ z \\ u \end{matrix}\right] \le \left[ \begin{matrix} 58.9139 \\ 76.0811 \\ 1.6977 \\ 10.8883 \\ -2.8839 \\ 3.3214 \\ 3.6397 \\ -51.5262 \\ 1.5013 \\ -3.0923 \end{matrix}\right] \right\} \end{aligned}$$

(2.13)

7 Conclusions

This chapter presents recent results in inverse optimality and summarizes in a concise manner a procedure to recover a continuous PWA function defined over a polyhedral partition of a polyhedron. Based on convex lifting, the study covers the general case of continuous PWA functions, presenting a full construction for the inverse optimality problem. A numerical example is finally considered to illustrate this result.