Automata-Based Abstraction for Automated Verification of Higher-Order Tree-Processing Programs

Abstract

Higher-order model checking has been recently applied to automated verification of higher-order functional programs, but there have been difficulties in dealing with algebraic data types such as lists and trees. To remedy the problem, we propose an automata-based abstraction of tree data, and a counterexample-guided refinement of the abstraction. By combining them with higher-order model checking, we can construct a fully-automated verification tool for higher-order, tree-processing functional programs. We formalize the verification method, prove its correctness, and report experimental results.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Higher-order model checking [9, 15], or the model checking of higher-order recursion schemes (HORS), has been recently applied to automated verification of functional programs [9, 11, 16, 18, 19]. Since a HORS is essentially a simply-typed higher-order functional program with recursion and finite base types (such as Booleans, not integers), the control structure of a (higher-order) functional program can be precisely modeled and verified. Thus, with a suitable abstraction of data, we can verify functional programs fully automatically by using higher-order model checking. For example, Kobayashi et al. [11] used predicate abstraction and CEGAR (counterexample-guided abstraction refinement) for abstracting integers to Booleans, and constructed a fully automated verification tool MoCHi for simply-typed higher-order functional programs with recursion and integers.

There have, however, been limitations in the treatment of algebraic data types such as trees and lists. Sato et al. [18] extended MoCHi to deal with algebraic data types by encoding algebraic data into functions; for example, a list may be encoded as a function that maps an index to the corresponding element. That approach has not been so successful, because the encoding makes both programs and specifications complex. In another line of work, Kobayashi et al. [12] proposed a verification method for HMTT, a kind of higher-order tree transducers. The HMTT model is however much more restricted than the usual functional programs: there is a distinction between input and output trees, and input trees are read-only, and output trees are write-only. Unno et al. [19] later extended HMTT to allow conversion between input and output trees so that the model is as expressive as an ordinary functional language, but annotations are required for the conversion. Ong and Ramsay [16] introduced a verification method for an extension of HORS called pattern-matching recursion schemes (PMRS). PMRS supports pattern matching on tree-structured data, but the verification method, however, uses pattern-based abstraction, which is not powerful enough.

To remedy the situation above, we propose a new approach to using higher-order model checking for automated verification of higher-order tree-processing programs. As in [11], we apply abstraction to approximate a source program by a higher-order functional program over finite base types, so that the latter can be verified by higher-order model checking. Instead of using predicates on integers, however, we use an automaton for abstracting tree data: each tree is abstracted to a state of the automaton that accepts the tree. Using the automata-based abstraction, we can transform a higher-order tree-processing program to a higher-order functional program with finite data domains, so that the latter overapproximates the behavior of the source program. Thus, verification problems for the former can be reduced to those for the latter, which can further be reduced to higher-order model checking.

As an example, consider the following program.

Here, $\mathtt {Z}$ and $\mathtt {S}$ are tree constructors. The program consists of two functions $double$ and $add$. The main function $double$ takes a natural number $x$ (in the unary tree representation) and returns $x+x$. Suppose that we wish to verify that the output of $double$ is always even, i.e., a unary tree of the form $(\mathtt {S})^{2n}\mathtt {Z}$. We can use a tree automaton that distinguishes $(\mathtt {S})^{2n}\mathtt {Z}$ and $(\mathtt {S})^{2n+1}\mathtt {Z}$, consisting of two states $q_0$, from which trees of the form $(\mathtt {S})^{2n}\mathtt {Z}$ is accepted, and $q_1$, from which trees of the form $(\mathtt {S})^{2n+1}\mathtt {Z}$ is accepted. Using the automaton, the program above is abstracted to:

Here, $\mathrel {\square }$ represents a non-deterministic choice, and $\mathtt {s}$ is now a function on states. The new main function $\texttt {main}$ non-deterministically invokes double $q_{0}$ or double $q_{1}$; here, the argument of double is now a state of the automaton, instead of a tree. The call double $q_{0}$ (double $q_{1}$, resp.) simulates the case where the input is an even (odd, resp.) number. The case analysis on tree $x$ in function add has now been replaced by a case analysis on states. The case $x=q_0$ models the case where $x$ is of the form $(\mathtt {S})^{2n}$ z in the source program; since both of the branches are possible in the source program, the abstract program non-deterministically evaluates (the abstract version of) them. On the other hand, the case $x=q_1$ models the case where $x$ is of the form $(\mathtt {S})^{2n+1}$ Z; since only the second branch of the source program is possible, the abstract program evaluates add $q_0$ (s y) deterministically. To check that the return value of the source program is always even (given (S) $^n$ Z) as an input), it suffices to check that the return value of the abstract program is always $q_0$.

Fig. 1.

Our method

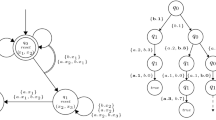
Figure 1 illustrates our overall method. As mentioned above, we apply an automata-based abstraction to reduce a given verification problem to that on a functional program with finite data domains. The latter problem can be decided by a reduction to higher-order model checking [9]. If the abstract program has no error path then we can conclude that the answer to the original verification problem is “yes”. Otherwise, we inspect an error path returned by a higher-order model checker. If a source program has a corresponding error path, we can conclude that the answer to the original verification problem is “no”. Otherwise, the abstraction was not precise enough, so the automaton used for abstraction is refined, and the cycle is repeated until the answer is found. (Since the verification problem is undecidable, the cycle may be repeated forever.)

A challenge arises on how to refine the automaton used for abstraction when a spurious error path is found. Unlike the case for predicate abstraction for integer values [11], we cannot use an interpolant-based method for predicate discovery. Given an initial automaton for abstraction, we split each state of the automaton to obtain a new automaton with an unknown transition function. From spurious error paths, we accumulate constraints on the transition function, which represent necessary conditions for eliminating spurious error paths. Then by using an SMT solver, we obtain a transition function that satisfies the constraints.This refinement procedure is relatively complete, in the sense that if there exists an automaton with which the abstract program can be proved to be safe, the procedure can eventually find such an automaton and the verification succeeds. The rest of this paper is organized as follows. Section 2 reviews the definitions of tree automata. Section 3 introduces our verification problem. Section 4 formalizes the automata-based abstraction. Section 5 describes an abstraction refinement method. Section 6 reports experimental results. Section 7 discusses related work, and Sect. 8 concludes this paper.

2 Preliminaries

In this section, we recall the standard notion of tree automata [4], which will be used for program specification and also for abstraction.

A ranked alphabet, written $\varSigma$, is a map from a finite set of symbols to the set of non-negative integers. An element $C$ of $dom (\varSigma )$ (the domain of $\varSigma$) may be considered a tree constructor of arity $\varSigma (C)$. The set $\mathbf {Trees}_{\varSigma }$ of finite trees is inductively defined by: $T_1,\ldots ,T_{\varSigma (C)}\in \mathbf {Trees}_{\varSigma } \Rightarrow C\,T_1\,\cdots \,T_{\varSigma (C)}\in \mathbf {Trees}_{\varSigma }$. Note that $\varSigma (C)$ may be $0$ above, so $C\in \mathbf {Trees}_{\varSigma }$ if $\varSigma (C)=0$.

Definition 1

(tree automata). A (bottom-up) tree automaton $\mathcal {M}$ is a quadruple $(\varSigma , Q, \varDelta , F)$ where (i) $\varSigma$ is a ranked alphabet. (ii) $Q$ is a set of states. (iii) $\varDelta$, called a transition function, is a subset of $dom (\varSigma ) \! \times \! Q^* \! \times \! Q$ such that $(C,q_1\cdots q_n,q)\in \varDelta$ implies $n=\varSigma (C)$. (iv) $F$ is a subset of $Q$. Elements of $F$ are called final states. We define the transition relation $T\longrightarrow _{\mathcal {M}}T'$ on $\mathbf {Trees}_{\varSigma \cup \{q\mapsto 0\mid q\in Q\}}$ by:

$$\begin{aligned} C\,q_1\,\cdots \,q_n \longrightarrow _{\mathcal {M}} q \qquad \text{ if } (C,q_1\cdots q_n,q)\in \varDelta . \end{aligned}$$

A tree $T\in \mathbf {Trees}_\varSigma$ is accepted by $\mathcal {M}$ if $T\longrightarrow _{\mathcal {M}}^{*} q\in F$ for some $q$. The language accepted by $\mathcal {M}$, written $\mathcal {L}(\mathcal {M})$, is the set of trees accepted by $\mathcal {M}$. We often write $\varSigma _\mathcal {M}, Q_\mathcal {M}, \varDelta _\mathcal {M}, F_\mathcal {M}$ for the four components of $\mathcal {M}$. We write $\mathcal {L}(\mathcal {M}, q)$ and $\mathcal {L}(\mathcal {M}, Q)$ for $\mathcal {L}((\varSigma _\mathcal {M}, Q_\mathcal {M}, \varDelta _\mathcal {M}, \{q\}))$ and $\mathcal {L}((\varSigma _\mathcal {M}, Q_\mathcal {M}, \varDelta _\mathcal {M}, Q))$ respectively. An automaton $(\varSigma , Q, \varDelta , F)$ is deterministic if for every $C\in dom (\varSigma )$ and $q_1\cdots q_{\varSigma (C)}\in Q^*$, there exists at most one $q$ such that $(C, q_1\cdots q_{\varSigma (C)}, q) \in \varDelta$. An automaton $(\varSigma , Q, \varDelta , F)$ is total if for every $C\in dom (\varSigma )$ and $q_1\cdots q_{\varSigma (C)}\in Q^*$, there exists at least one $q$ such that $(C, q_1\cdots q_{\varSigma (C)}, q) \in \varDelta$. When an automaton $\mathcal {M}$ is deterministic and total, we write $\varDelta _\mathcal {M}(C, q_1 \cdots q_{\varSigma _\mathcal {M}(C)})$ for the state $q$ such that $(C, q_1 \cdots q_{\varSigma _\mathcal {M}(C)}, q) \in \varDelta _\mathcal {M}$.

Example 1

Consider an automaton $\mathcal {M}= (\varSigma , \{q_1, q_2, q_3\}, \varDelta , \{q_1, q_2\})$ where $\varSigma = \{\mathtt {E} \mapsto 0, \mathtt {A}\mapsto 1, \mathtt {B}\mapsto 1\}$ and

$$\begin{aligned} \varDelta = \{ (\mathtt {E}, \epsilon , q_1), (\mathtt {A}, q_1, q_2), (\mathtt {A}, q_2, q_2), (\mathtt {A}, q_3, q_3), (\mathtt {B}, q_1, q_1), (\mathtt {B}, q_2, q_3), (\mathtt {B}, q_3, q_3) \} \end{aligned}$$

The automaton $\mathcal {M}$ is total and deterministic, and $\mathcal {L}(\mathcal {M}) = \mathtt {A}^*\mathtt {B}^*\mathtt {E}$. Here, we have identified unary trees with words, and used a regular expression for a set of unary trees. The regular expression $\mathtt {A}^*\mathtt {B}^*\mathtt {E}$ denotes

$$\begin{aligned} \{\underbrace{\mathtt {A}(\cdots (\mathtt {A}}_m(\underbrace{\mathtt {B}(\cdots (\mathtt {B}}_n\mathtt {E}))))) \mid m\ge 0, n\ge 0\}. \end{aligned}$$

We often use this kind of notation for a set of unary trees.

Henceforth, we consider only deterministic and total automata; this does not lose generality, as we are considering bottom-up automata.

3 The Verification Problem

This section introduces the language of tree processing programs, which is used as the target of our verification, and defines the verification problem. The target of verification is a higher-order, tree-processing functional program. We fix a ranked alphabet $\varSigma$. We sometimes write $\{e_i\}_{i=1}^n$ for $\{e_1,\ldots ,e_n\}$, and also write $\{f(x)\}_{x\in S}$ for $\{f(x) \mid x\in S\}$.

Definition 2

The set of expressions, ranged over by $e$, is given by:

$$\begin{aligned} e\, {:}{:}{=} \,C\mid x \mid \mathbf {fail}\mid e_1\ e_2 \mid \ \mathop {\mathrm {\mathbf {case}}}e \mathop {\mathrm {\mathbf {of}}}\{C_i\ \widetilde{y_i} \Rightarrow e_i\}_{i=1}^n. \end{aligned}$$

Here, $C$ ranges over $dom (\varSigma )$, and $x$ ranges over the set of variables and function symbols. A program $\mathcal {P}$ is a set of function definitions $\{f_1\ \widetilde{x_1} = e_1, \ldots f_m\ \widetilde{x_m} = e_m\}$ where $f_i$ is a function symbol, and $\widetilde{x_i}$ is a sequence of variables. The set of function symbols $\{f_1, \ldots , f_m\}$ must contain the main function symbol “main”. We write arity $(f_i)$ for the length of the sequence $\widetilde{x_i}$.

The expression $\mathbf {fail}$ aborts the execution. The expression $\mathop {\mathrm {\mathbf {case}}}e \mathop {\mathrm {\mathbf {of}}}\{C_i\ \widetilde{y_i} \Rightarrow e_i\}_{i=1}^n$ evaluates $e$ to a tree, and then evaluates $[\widetilde{T}/\widetilde{y_i}]e_i$ if the tree matches $C_i\ \widetilde{T}$. We assume that the patterns of every case expression are exhaustive; if not, we can insert a clause $C_i\ \widetilde{y_i} \Rightarrow \mathbf {fail}$. We consider only programs that are well-typed in the standard simple type system. The set of (simple) types, ranged over by $\kappa$, is given by: $\kappa \,{:}{:}{=}\, \mathtt {o}\mid \kappa _1 \rightarrow \kappa _2$. Here, $\mathtt {o}$ is the type of trees, and $\kappa _1 \rightarrow \kappa _2$ is the type of functions from $\kappa _1$ to $\kappa _2$. A type judgment is of the form $\mathcal {K}\vdash e:\kappa$, where $\mathcal {K}$ is a map from a finite set of variables (which may include function symbols) to the set of types. It is defined by the following rules.

We write $\vdash \mathcal {P}:\mathcal {K}$ if: (i) $\mathcal {P}= \{f_i\,x_{i,1}\,\cdots \,x_{i,k_i}=e_i\}_{i=1}^n$; (ii) $dom (\mathcal {K}) = \{f_1,\ldots ,f_{n}\}$; (iii) $\mathcal {K}(f_i)=\kappa _{i,1}\rightarrow \cdots \rightarrow \kappa _{i,k_i}\rightarrow \mathtt {o}$ and $\mathcal {K},x_{i,1}\mathbin {:}\kappa _{i,1},\ldots ,x_{i,k_i}\mathbin {:}\kappa _{i,k_i}\vdash e_i:\mathtt {o}$ for every $i\in \{1,\ldots ,n\}$; and (iv) $\mathcal {K}( main )=\mathtt {o}\rightarrow \mathtt {o}$. A program $\mathcal {P}$ is well-typed if $\vdash \mathcal {P}:\mathcal {K}$ for some $\mathcal {K}$. Henceforth, we consider only well-typed programs.

The sets of evaluation contexts and values are defined respectively by:

$$\begin{aligned}&\qquad E \text{(evaluation } \text{ contexts) } \,{:}{:}{=}\, [\ ] \mid E\ v \mid e\ E \mid \ \mathop {\mathrm {\mathbf {case}}}\ E\ \mathop {\mathrm {\mathbf {of}}}\ \{C_i\ \widetilde{y_i} \Rightarrow e_i\}_{i=1}^n\\&\qquad \qquad v \text{(values) } \,{:}{:}{=}\, f\ v_1 \cdots v_n\ (n < arity(f)) \mid C\ v_1 \cdots v_n\ (n \le \varSigma (C)) \end{aligned}$$

The reduction relation $e\longrightarrow _{\mathcal {P}} e'$ is defined by: (i) $E[\mathbf {fail}] \longrightarrow _{\mathcal {P}} \mathbf {fail}$; (ii) $E[f\ v_1 \cdots v_n] \longrightarrow _{\mathcal {P}} E[[v_1 \cdots v_n/x_1 \cdots x_n]e]$ if $f\ x_1 \cdots x_n =e\in \mathcal {P}$; and

(iii) $E[\mathop {\mathrm {\mathbf {case}}}a_k\ \widetilde{v} \mathop {\mathrm {\mathbf {of}}}{\{C_i\ \widetilde{y_i} \Rightarrow e_i\}_{i=1}^n}] \longrightarrow _{\mathcal {P}} E[[\widetilde{v}/\widetilde{y_k}]e_k]$. We often omit the subscript $\mathcal {P}$.

Example 2

The program in Sect. 1 is expressed as:

$$\begin{aligned} \begin{array}{l} \mathcal {P}_1{} = \{ main \ x = twice \,( add \ x)\,\mathtt {Z}{}, \ twice \ f\ x = f\,(f\,x),\\ \qquad \ add \ x\ y = \mathop {\mathrm {\mathbf {case}}}\; x\; \mathop {\mathrm {\mathbf {of}}}\mathtt {Z}{} \Rightarrow y \mid \mathtt {S}\ x' \Rightarrow add \ x'\ (\mathtt {S}\ y) \} \end{array} \end{aligned}$$

The expression $main \,(\mathtt {S}(\mathtt {Z}{}))$ is evaluated as follows.

$$\begin{aligned} \begin{array}{l} main \,(\mathtt {S}(\mathtt {Z}{})) \longrightarrow twice \,( add \ (\mathtt {S}(\mathtt {Z}{})))\,\mathtt {Z}{} \longrightarrow add \ (\mathtt {S}(\mathtt {Z}{})) ( add \ (\mathtt {S}(\mathtt {Z}{}))\,\mathtt {Z}{}) \longrightarrow ^*\mathtt {S}(\mathtt {S}(\mathtt {Z}{})). \end{array} \end{aligned}$$

Definition 3

(verification problem). Let $\mathcal {M}_I$ and $\mathcal {M}_O$ be tree automata. We write $\models (\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ if, for every $T\in \mathcal {L}(\mathcal {M}_I)$, $\textit{main}\;T\mathbin {\ \not \!\!\longrightarrow _{\mathcal {P}}^{*}}\mathbf {fail}$ and $\textit{main}\;T\longrightarrow _{\mathcal {P}}^{*}t'\in \mathbf {Trees}_{\varSigma }$ implies $t'\in \mathcal {L}(\mathcal {M}_O)$. The verification problem $(\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ is the problem of deciding whether $\models (\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ holds.

Intuitively, $\models (\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ means that given a tree accepted by $\mathcal {M}_I$ as an input, $P$ does not fail, and if it returns a (finite) tree, it is accepted by $\mathcal {M}_O$.

Example 3

Consider the verification problem $(\mathcal {P}_1{}, \mathcal {M}_1, \mathcal {M}_2)$ where $\mathcal {P}_1{}$ is the program given in Example 2, and

$$\begin{aligned} \begin{array}{ll} \mathcal {M}_1 = (\varSigma , \{q_1\}, \varDelta _1, \{q_1\}) &{} \varDelta _1 = \{(\mathtt {Z}{}, \epsilon , q_1), (\mathtt {S}, q_1, q_1)\}\\ \mathcal {M}_2 = (\varSigma , \{q_2, q_3\},\varDelta _2, \{q_2\}) &{} \varDelta _2 = \{(\mathtt {Z}{}, \epsilon , q_2), (\mathtt {S}, q_2, q_3), (\mathtt {S}, q_3, q_2)\} \end{array} \end{aligned}$$

The languages accepted by $\mathcal {M}_1$ and $\mathcal {M}_2$ are $(\mathtt {S})^*\mathtt {Z}{}$ and $(\mathtt {S}\ \mathtt {S})^*\mathtt {Z}{}$ respectively. The answer to the verification problem $(\mathcal {P}_1,\mathcal {M}_1, \mathcal {M}_2)$ is “yes”.

4 Automata-Based Abstraction

This section formalizes our automata-based abstraction method.

4.1 Abstract Programs

The target language of the automata-based abstraction has a finite enumeration type as the base type, instead of tree types. The enumeration type consists of the states of automata used for abstraction.

Definition 4

(abstract programs). The set of (abstract) expressions, ranged over by $t$, is given by: $t\,{:}{:}{=}\, q \mid x \mid t_1\ t_2 \mid \mathop {\mathrm {\mathbf {case}}}t\mathop {\mathrm {\mathbf {of}}}\{q_i \Rightarrow t_i\}_{i=1}^m \mid t_1 \mathrel {\square }t_2 \mid \mathbf {fail}$. Here, $q$ ranges over the set $\{q_1, \ldots , q_m\}$ of values of the finite enumeration type and $x$ ranges over a set of variables (including defined function symbols $f_i$’s). An abstract program $\mathcal {D}$ is a set of function definitions $\{f_1\ \widetilde{x_1} = t_1, \ldots , f_n\ \widetilde{x_n} = t_n\}$, where $main \in \{f_1, \ldots , f_n\}$.

The expression $\mathop {\mathrm {\mathbf {case}}}t\mathop {\mathrm {\mathbf {of}}}\{q_i \Rightarrow t_i\}_{i=1}^m$ is a case analysis on the finite enumeration type; it first evaluates $t$, and evaluates $t_i$ if the value is $q_i$. The expression $t_1 \mathrel {\square }t_2$ evaluates $t_1$ or $t_2$ in a non-deterministic manner. As for source programs, we require that abstract programs are simply-typed. The set of types is given by: $\tau \,{:}{:}{=}\, \mathtt {d}\mid \tau _1\rightarrow \tau _2$. Here, $\mathtt {d}$ is the finite enumeration type, consisting of values $q_1,\ldots ,q_m$. We show only the typing rules for $q$ and case-expressions; the other typing rules for expressions are essentially the same as those for source programs.

We write $\vdash \mathcal {D}:\varTheta$ if: (i) $\mathcal {D}= \{f_i\,x_{i,1}\,\cdots \,x_{i,k_i}=t_i\}_{i=1}^n$; (ii) $dom (\varTheta ) = \{f_1,\ldots ,f_{n}\}$; (iii) $\varTheta (f_i)=\tau _{i,1}\rightarrow \cdots \rightarrow \tau _{i,k_i}\rightarrow \mathtt {d}$ and $\varTheta ,x_{i,1}\mathbin {:}\tau _{i,1},\ldots ,x_{i,k_i}\mathbin {:}\tau _{i,k_i}\vdash t_i:\mathtt {d}$ for every $i\in \{1,\ldots ,n\}$; and (iv) $\varTheta ( main )=\mathtt {d}\rightarrow \mathtt {d}$.

We define the call-by-value, small-step reduction relation below. The sets of evaluation contexts and values, ranged over by $E$ and $v$, are defined by:

$$\begin{aligned} E \,{:}{:}{=}\, [\ ] \mid E\ v \mid t\ E \mid \mathop {\mathrm {\mathbf {case}}}E \mathop {\mathrm {\mathbf {of}}}{\{q_i \Rightarrow t_i\}_{i=1}^m} \quad v \,{:}{:}{=}\, f\ v_1 \cdots v_n\ (n < arity(f)) \mid q \end{aligned}$$

The relation $t_1 \longrightarrow _{\mathcal {D}} t_2$ is defined by: (i) $E[f\ v_1 \cdots v_n] \longrightarrow _{\mathcal {D}} E[[v_1 \cdots v_n/x_1 \cdots x_n]t]$ if $f\ x_1 \cdots x_n = t\in \mathcal {D}$; (ii) $E[\mathop {\mathrm {\mathbf {case}}}q_k \mathop {\mathrm {\mathbf {of}}}{\{q_i \Rightarrow t_i\}_{i = 1}^m}] \longrightarrow _{\mathcal {D}} E[t_k]$; (iii) $E[\mathbf {fail}] \longrightarrow _{\mathcal {D}} \mathbf {fail}$; and (iv) $E[t_1 \mathrel {\square }t_2] \longrightarrow _{\mathcal {D}} E[t_i]$ for $i\in \{1,2\}$.

Definition 5

(safety problem). Let $\mathcal {D}$ be an abstracted program and $F_I$ and $F_O$ be finite subsets of $\{q_1,\ldots ,q_m\}$. We write $\models (\mathcal {D}, F_I, F_O)$ if, for every $q\in F_I$, (i) $main \ q \mathbin {\ \not \!\!\longrightarrow _{\mathcal {D}}^{*}} \mathbf {fail}$; and (ii) $main \ q \longrightarrow _{\mathcal {D}}^{*} q'$ implies $q' \in F_O$. The safety problem $(\mathcal {D}, F_I, F_O)$ is the problem of deciding whether $\models (\mathcal {D}, F_I, F_O)$ holds.

The safety problem above is decidable by a reduction to higher-order model checking [9]. Furthermore, if $\models (\mathcal {D}, F_I, F_O)$ does not hold, we can obtain an error reduction sequence $main \ q \longrightarrow _{\mathcal {D}}^{*} \mathbf {fail}$ or $main \ q \longrightarrow _{\mathcal {D}}^{*} q'\not \in F_O$ by using a higher-order model checker [3, 8]. The knowledge of higher-order model checking and the reduction method is not required for understanding the rest of this paper; an interested reader may wish to consult [9].

4.2 Abstraction Method

We now formalize the automata-based abstraction. In order to allow a different automaton to be used for abstracting each expression of tree type, we use abstraction types, which specify how each expression should be abstracted.

The set of abstraction types is defined by: $\sigma \,{:}{:}{=}\, \mathtt {o}_{\mathcal {M}} \mid \sigma _1 \rightarrow \sigma _2$. Here, $\mathcal {M}$ is a (total, deterministic) automaton. Intuitively, $\mathtt {o}_{\mathcal {M}}$ describes trees that should be abstracted by using the automaton $\mathcal {M}$. The type $\sigma _1 \rightarrow \sigma _2$ describes functions whose argument should be abstracted according to $\sigma _1$, and return value should be abstracted according to $\sigma _2$. For example, consider the automata $\mathcal {M}_1$ and $\mathcal {M}_2$ in Example 3. The type $\mathtt {o}_{\mathcal {M}_1}\rightarrow \mathtt {o}_{\mathcal {M}_2}$ describes a function whose input tree should be abstracted using the automaton $\mathcal {M}_1$, and output tree should be abstracted using the automaton $\mathcal {M}_2$. Using this type, the identity function $\lambda x.x$ would be abstracted to $\lambda x.\mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}q_1 \Rightarrow (q_2\mathrel {\square }q_3)$; the argument is abstracted to $q_1$, and since there is no information about whether the original value of $x$ is even or not, the function returns $q_2$ (which is an abstraction of trees of the form $\mathtt {s}^{2n}\mathtt {Z}{}$) or $q_3$ (which is an abstraction of trees of the form $\mathtt {s}^{2n+1}\mathtt {Z}{}$) non-deterministically. If the abstraction type was $\mathtt {o}_{\mathcal {M}_2}\rightarrow \mathtt {o}_{\mathcal {M}_2}$, then $\lambda x.x$ would be abstracted to $\lambda x.x$.

The abstraction is formalized as a type-based program transformation relation $\varGamma \vdash e\mathbin {:}\sigma \leadsto t$, where $\varGamma$, called an abstraction type environment, is a map from a finite set of variables to the set of abstraction types. Intuitively, $\varGamma \vdash e\mathbin {:}\sigma \leadsto t$ means that assuming that each variable $x$ has been abstracted according to $\varGamma (x)$, the expression $e$ should be abstracted to $t$ according to the abstraction type $\sigma$. How to obtain an appropriate abstraction type environment is discussed in [13] The transformation relation is defined by the following rules.

Here, $\mathrel {\square }\{t_1,\ldots ,t_n\}$ is an abbreviation of $t_1 \mathrel {\square }(t_2 \mathrel {\square }\cdots \mathrel {\square }(t_{n-1} \mathrel {\square }t_n))$. In the rule for case-expressions, $\widetilde{y_i}\mathbin {:}\widetilde{\mathtt {o}_{\mathcal {M}}}$ abbreviates $y_{i,1}\mathbin {:}\mathtt {o}_{\mathcal {M}},\ldots ,y_{i,k}\mathbin {:}\mathtt {o}_{\mathcal {M}}$; note that the type of $y_{i,k}$ is the same as that of $e$.

A variable is abstracted to itself. A tree constructor is transformed to a function $f_{a,\mathcal {M}}$ defined below. A case expression is transformed to a case expression on the states of $\mathcal {M}$. If the value of $t$ matches $q$, then the value $T$ of the original expression $e$ is accepted by $\mathcal {M}$ from state $q$. So, $T$ must be of the form $a\,T_1\,\cdots \,T_k$ such that $(a,q_1\cdots q_k,q)\in \varDelta _M$ with $T_i\in \mathcal {L}(\mathcal {M},q_i)$. Thus, the body of the clause for $q$ is a non-deterministic branch on such cases. For example, consider the expression: $\mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}\{\mathtt {Z}{} \Rightarrow e_1, \mathtt {S}{}\,y \Rightarrow e_2\}$, with the abstraction type $x\mathbin {:}\mathtt {o}_{\mathcal {M}_2}$ (where $\mathcal {M}_2$ is that of Example 3). It is transformed to: $\mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}\{q_2 \Rightarrow (t_1 \mathrel {\square }[q_3/y]t_2),\quad q_3 \Rightarrow [q_2/y]t_2\}$, where $x\mathbin {:}\mathtt {o}_{\mathcal {M}_2}\vdash e_1:\sigma \leadsto t_1$ and $x\mathbin {:}\mathtt {o}_{\mathcal {M}_2},y\mathbin {:}\mathtt {o}_{\mathcal {M}_2}\vdash e_2:\sigma \leadsto t_2$. The rule for applications transforms $e_1$ and $e_2$ in a compositional manner, but it ensures that the argument abstraction type of $e_1$ is equal to the abstraction type of $e_2$, so that the abstraction is consistent.

A program is transformed by the following rule.

Here, $Automata (\varGamma )$ is the set of automata occurring in $\varGamma$, and $t_{C,\mathcal {M}}$ is:

$$\begin{aligned} \mathop {\mathrm {\mathbf {case}}}\; (x_1,\ldots ,x_{\varSigma (C)}) \mathop {\mathrm {\mathbf {of}}}\{(q_1,\ldots ,q_{\varSigma (C)}) \Rightarrow q\}_{(C,q_1\cdots q_{\varSigma (C)},q)\in \varDelta }. \end{aligned}$$

We have used a case expression on tuples for clarity; it can be easily flattened to case expressions on each of $x_1,\ldots ,x_{\varSigma (C)}$. In the rule A-Prog , $\widetilde{\sigma } \rightarrow \mathtt {o}_{\mathcal {M}}$ and $\widetilde{x}\mathbin {:}\widetilde{\sigma }$ abbreviate $\sigma _1\rightarrow \cdots \rightarrow \sigma _k\rightarrow \mathtt {o}_{\mathcal {M}}$ and $x_1\mathbin {:}\sigma _1,\ldots ,x_k\mathbin {:}\sigma _k$ respectively.

The soundness of the abstraction is stated as follows; see [13] for a proof.

Theorem 1

(soundness). Let $(\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ be a verification problem. If $\vdash \mathcal {P}:\varGamma \leadsto \mathcal {D}$ and $\varGamma (\textit{main})=\mathtt {o}_{\mathcal {M}_I'}\rightarrow \mathtt {o}_{\mathcal {M}_O'}$ with $\mathcal {L}(\mathcal {M}_I',F_I)=\mathcal {L}(\mathcal {M}_I)$ and $\mathcal {L}(\mathcal {M}_O',F_O)=\mathcal {L}(\mathcal {M}_O)$, then $\models (\mathcal {D}, F_I, F_O)$ implies $\models (\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$.

Example 4

Consider the verification problem $(\mathcal {P}_1, \mathcal {M}_1, \mathcal {M}_2)$ where $\mathcal {P}_1$ is defined in Example 2 and the automata $\mathcal {M}_1$ and $\mathcal {M}_2$ are given in Example 3. Let $\varGamma _1{}$ be:

$$\begin{aligned} \begin{array}{l} \{ main \mathbin {:}\mathtt {o}_{\mathcal {M}_1} \rightarrow \mathtt {o}_{\mathcal {M}_2}, \ add \mathbin {:}\mathtt {o}_{\mathcal {M}_1} \rightarrow \mathtt {o}_{\mathcal {M}_2} \rightarrow \mathtt {o}_{\mathcal {M}_2}, \\ \ \ twice \mathbin {:}(\mathtt {o}_{\mathcal {M}_2} \rightarrow \mathtt {o}_{\mathcal {M}_2})\rightarrow \mathtt {o}_{\mathcal {M}_2} \rightarrow \mathtt {o}_{\mathcal {M}_2}\}. \end{array} \end{aligned}$$

Then, $\vdash \mathcal {P}_1{}:\varGamma _1{}\leadsto \mathcal {D}_1$, where $\mathcal {D}_1$ consists of:

$$\begin{aligned} \begin{array}{l} main \ x = twice \ ( add \ x)\ q_2\qquad \qquad f_{\mathtt {S},\mathcal {M}_2}\ x = \mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}q_2 \Rightarrow q_3 \mid q_3 \Rightarrow q_2 \\ twice \ f\ x = f\ (f\ x) \qquad add \ x\ y = \mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}q_1 \Rightarrow y \mathrel {\square }( add \ q_1\ (f_{\mathtt {S},\mathcal {M}_2}\ y)).\\ \end{array} \end{aligned}$$

The verification problem has been reduced to the safety problem $(\mathcal {D}_1, \{q_1\}, \{q_2\})$. ($\models (\mathcal {D}_1, \{q_1\}, \{q_2\})$ does not hold, however, as shown in Sect. 5.1; we need to refine the abstraction using the method described in Sect. 5.2.) $\quad \square$

5 Abstraction Refinement

This section discusses how to refine the automata used for abstraction when they are not precise enough. The pseudo code of our verification method is shown in Fig. 2. Our method first infers the initial abstraction type environment, and performs some initialization (line 2). The verification problem is reduced to a safety problem as explained in Sect. 4.2 (line 4). The safety problem is solved by an existing higher-order model checker (line 5). If the answer to the problem is “no” (line 7), we inspect whether the abstract error path returned by the model checker is feasible, i.e., the source program has a corresponding error path (lines 8–9). If the error path is feasible, the answer to the verification problem is “no” (line 10). Otherwise, our method refines the abstraction by splitting each state of the automaton for abstraction so that the spurious error path is eliminated from the future abstraction (lines 12–17).

Fig. 2.

Pseudo code of our method

We explain below the feasibility checking (lines 8–9) and the abstraction refinement (lines 12–17) in Sects. 5.1 and 5.2 respectively. The inference of the initial abstraction type environment (line 2) is explained in the full version [13].

5.1 Feasibility Check

If the answer to a safety problem is “no”, a higher-order model checker [3, 8] outputs an error path of the abstract program. To check whether the source program has a corresponding error execution path, we evaluate the source program symbolically along the error path, and generate constraints on variables (line 8). We then check the satisfiability of constraints (line 9).

For example, recall the safety problem $(\mathcal {D}_1{}, \{q_1\}, \{q_2\})$ in Example 4. The answer to this safety problem is “no”, and one of the error paths output by a model checker is as follows.

$$\begin{aligned} \begin{array}{l} main \ q_1 \longrightarrow _{\mathcal {D}_1{}} twice \ ( add \ q_1)\ q_2 \longrightarrow _{\mathcal {D}_1{}} add \ q_1\ ( add \ q_1\ q_2)\\ \longrightarrow _{\mathcal {D}_1{}}^{*} add \ q_1\ (q_2 \mathrel {\square }( add \ q_1\ (f_{\mathtt {S}{},\mathcal {M}_2}\ q_2))) \longrightarrow _{\mathcal {D}_1{}} add \ q_1\ q_2\\ \longrightarrow _{\mathcal {D}_1{}}^{*} q_2 \mathrel {\square }( add \ q_1\ (f_{\mathtt {S}{},\mathcal {M}_2}\ q_2)) \longrightarrow _{\mathcal {D}_1{}} add \ q_1\ (f_{\mathtt {S}{},\mathcal {M}_2}\ q_2)\\ \longrightarrow _{\mathcal {D}_1{}}^{*} add \ q_1\ q_3 \longrightarrow _{\mathcal {D}_1{}}^{*} q_3 \mathrel {\square }( add \ q_1\ (f_{\mathtt {S}{},\mathcal {M}_2}\ q_3)) \longrightarrow _{\mathcal {D}_1{}} q_3 \end{array} \end{aligned}$$

We first prepare a concise version of the error path (of the abstract program), which is just a sequence $TR$ of the transition rules used for abstracting the values inspected by each case expression. Here, we ignore the case-expressions in the definition of $f_{C,\mathcal {M}}$, which have no corresponding case-expressions in the source program. For the example above, $TR = (\mathtt {Z}{}, \epsilon , q_1) (\mathtt {S}{}, q_1, q_1)(\mathtt {Z}{}, \epsilon , q_1)$. The $i$-th element ($i\in \{1,2,3\}$) corresponds to the evaluation of the $i$-th case expression evaluated in the error path above. For example, the first element corresponds to the first case expression; since the expression being evaluated to $q_1$ means that the corresponding value of the source program has been considered $\mathtt {Z}{}$, and it was abstracted to $q_1$ by using the transition rule $(\mathtt {Z}{}, \epsilon , q_1)$.

Given a concise error sequence $TR$, we replace $TR$ with a corresponding concise transition sequence $TR _0$ for the initial abstraction, which is obtained by replacing each transition rule $(C,\widetilde{q},q)$ with the corresponding transition rule $(C,\widetilde{q}',q')$ of the automata occurring in the initial abstraction type environment $\varGamma _0$. This is always possible by the construction of the refinement procedure described in Sect. 5.2; each state of an automaton in the current abstraction type environment is of the form $q^{(i)}$, and we just need to replace $q^{(i)}$ with $q$.

The symbolic evaluation of the original program is formalized as the relation $(e, Cnst , TR )\longrightarrow _{\mathcal {P}}(e', Cnst ', TR ')$, where $e$ is an expression of the original program, $Cnst$ is the set of constraints being accumulated, and $TR$ is a concise error sequence. The relation is defined by the following rules:

The first rule is for a function call, which is a deterministic evaluation that does not require information about the error path. The second rule is for case-expressions, where the first element of $TR$ is looked up (and consumed) to decide which branch should be taken. The premise $TR = (C_k, \widetilde{q}, q).~ TR '$ means that $v$ has been abstracted to $q$ using the transition rule $(C_k, \widetilde{q}, q)$. So, the constraints $v = C_k\ \widetilde{x}$, $v\mathbin {:}q$, and $\widetilde{x} \mathbin {:}\widetilde{q}$ are added. Here, $v$ is a tree expression consisting of variables and tree constructors; the latter constraint $\widetilde{x} \mathbin {:}\widetilde{q}$ is an abbreviation of $x_1\mathbin {:}q_1,\ldots ,x_k\mathbin {:}q_k$, which means that the value of $x_i$ should belong to $\mathcal {L}(\mathcal {M},q_i)$. (Here, the states of automata in $Automata (\varGamma )$ are disjoint from each other; so $\mathcal {M}$ is uniquely identified by $q_i$.) By applying the rules above, we obtain a symbolic execution sequence: $( main \,x,\emptyset , TR _0)\longrightarrow _{\mathcal {P}}^{*}(e, Cnst ,\epsilon )$. We let $Cnst$ be the output of gen_const on line 8 of Fig. 2. By the rules, it should be clear that if we instantiate each variable in the symbolic evaluation sequence so that $Cnst$ is satisfied, then we get an actual error path of the source program. Therefore, $Cnst$ is satisfiable if and only if the source program has an error path corresponding to the abstract error path $TR _0$. The satisfiability of $Cnst$ can be easily checked by first solving equality constraints using a standard unification algorithm, and then checking the remaining condition $v\mathbin {:}q$ based on the transition rules of the automaton.

Example 5

Recall the verification problem $(\mathcal {D}_1{}, \{q_1\}, \{q_2\})$ and the (concise) abstract error path $TR = (\mathtt {Z}{}, \epsilon , q_1) (\mathtt {S}{}, q_1, q_1) (\mathtt {Z}{}, \epsilon , q_1)$ considered above. We have the following symbolic execution sequence.

$$\begin{aligned}&\qquad \; ( main \ x_1, \emptyset , (\mathtt {Z}{}, \epsilon , q_1) (\mathtt {S}{}, q_1, q_1) (\mathtt {Z}{}, \epsilon , q_1))\\&\longrightarrow _{}^{*} \!\! ( add \,x_1\, (\mathop {\mathrm {\mathbf {case}}}x_1 \mathop {\mathrm {\mathbf {of}}}\mathtt {Z}{} \Rightarrow \mathtt {Z}{} \mid \mathtt {S}{}\, x' \Rightarrow add \, x' (\mathtt {S}{}\, \mathtt {Z}{})), \emptyset , (\mathtt {Z}{}, \epsilon , q_1) (\mathtt {S}{}, q_1, q_1) (\mathtt {Z}{}, \epsilon , q_1)) \\&\longrightarrow _{} ( add \ x_1\ \mathtt {Z}{}, \{x_1 \mathbin {:}q_1, x_1 = \mathtt {Z}{}\}, (\mathtt {S}{}, q_1, q_1) (\mathtt {Z}{}, \epsilon , q_1))\\&\longrightarrow _{} (\mathop {\mathrm {\mathbf {case}}}x_1 \mathop {\mathrm {\mathbf {of}}}\mathtt {Z}{} \Rightarrow \mathtt {Z}{} \mid \mathtt {S}{}\, x' \Rightarrow add \, x'\, (\mathtt {S}{}\, \mathtt {Z}{})), \{x_1 \mathbin {:}q_1, x_1 = \mathtt {Z}{}\}, (\mathtt {S}{}, q_1, q_1) (\mathtt {Z}{}, \epsilon , q_1))\\&\longrightarrow _{} ( add \ x_2\ (\mathtt {S}{}\ \mathtt {Z}{}), \{x_1 \mathbin {:}q_1, x_1 = \mathtt {Z}{}, x_1 = \mathtt {S}{}\ x_2, x_2 \mathbin {:}q_1\}, (\mathtt {Z}{}, \epsilon , q_1))\\&\longrightarrow _{} (\mathop {\mathrm {\mathbf {case}}}x_2 \mathop {\mathrm {\mathbf {of}}}\mathtt {Z}{} \Rightarrow \mathtt {S}{}\ \mathtt {Z}{} \mid \mathtt {S}{}\ x' \Rightarrow add \ x'\ (\mathtt {S}{}\ (\mathtt {S}{}\ \mathtt {Z}{})), \\&\qquad \qquad \{x_1 \mathbin {:}q_1, x_1 = \mathtt {Z}{}, x_1 = \mathtt {S}{}\ x_2, x_2 \mathbin {:}q_1\}, (\mathtt {Z}{}, \epsilon , q_1))\\&\longrightarrow _{} (\mathtt {S}{}\ \mathtt {Z}{}, \{x_1 \mathbin {:}q_1, x_1 = \mathtt {Z}{}, x_1 = \mathtt {S}{}\ x_2, x_2 \mathbin {:}q_1, x_2 = \mathtt {Z}{}\}, \epsilon ) \end{aligned}$$

We therefore get constraints $\{x_1 \mathbin {:}q_1, x_1= \mathtt {Z}{}, x_1 = \mathtt {S}{}\ x_2, x_2 \mathbin {:}q_1, x_2 = \mathtt {Z}{}\}$. Because the constraints are unsatisfiable (there are conflicting equalities $x_1= \mathtt {Z}{}$ and $x_1 = \mathtt {S}{}\ x_2$), the error path is infeasible. Note that the infeasible error path has been obtained because the variable $x_1$ has been copied as $add \ x_1\ ( add \ x_1\ \mathtt {Z}{})$ and instantiated differently (the first occurrence as $\mathtt {S}{}\ \mathtt {Z}{}$ and the second as $\mathtt {Z}{}$) due to the imprecise abstraction, which abstracts both $\mathtt {Z}{}$ and $\mathtt {S}{}\ \mathtt {Z}{}$ to the same state $q_1$. The procedure described in the next subsection refines the abstraction by splitting the state $q_1$ in order to avoid this confusion between $\mathtt {Z}{}$ and $\mathtt {S}{}\ \mathtt {Z}{}$.

5.2 Abstraction Refinement

As mentioned above, when the error path of the abstracted program is infeasible, our method refines the abstraction by splitting each automaton state $q$ to $q^{(1)},\ldots ,q^{(n)}$, where $n$, called the split number, is kept in variable $Split$ in Fig. 2. It is set to $1$ initially (line 2), and gradually increased.

We refine each automaton $\mathcal {M}\in Automata (\varGamma _0)$ to $\mathcal {M}'$, so that: (i) $\forall q\in Q_{\mathcal {M}}.\, \mathcal {L}(\mathcal {M}, q) = \mathcal {L}(\mathcal {M}', \{q^{(1)},\ldots ,q^{(n)}\})$; and (ii) the same error path ($TR _0$ in Sect. 5.1) never occurs again.

To guarantee the first condition, it suffices to guarantee that for each rule $(C, q_1 \cdots q_k, q) \in \varDelta _\mathcal {M}$,

$$\begin{aligned} \begin{array}{l} \forall i_1,\ldots ,i_k\in \{1,\ldots ,n\}. \exists i \in \{1,\ldots ,n\}. (C, q_1^{(i_1)} \cdots q_k^{(i_k)}, q^{(i)}) \in \varDelta _{\mathcal {M}'} \end{array} \end{aligned}$$

holds. Thus, $\mathcal {M}'$ is determined by a function $g_{(C, q_1 \cdots q_k, q)} \in \{1,\ldots , Split \}^k \rightarrow \{1,\ldots , Split \}$ for each $(C, q_1 \cdots q_k, q) \in \varDelta _\mathcal {M}$. We prepare an uninterpreted function symbol $g_{(C, q_1 \cdots q_k, q)}$ for representing the unknown function, and generate the constraints on $g_{(C, q_1 \cdots q_k, q)}$’s so that the second condition is guaranteed.

To guarantee the second condition, for each constraint $Cnst$ in $CnstSet$ (which accumulates the set of constraints generated from spurious error paths found so far), we generate the following SMT formula $F_{ Cnst }$.

$$\begin{aligned} \begin{array}{l} \forall x_1,\ldots ,x_\ell \in \{1,\ldots , Split \}. \bigvee _{v_1=v_2\in Cnst } ( state (v_1)\ne state (v_2)). \end{array} \end{aligned}$$

Here, $state (v)$ is defined by: (i) $state (x) = x$; and (ii) $state (C\,v_1\,\cdots \,v_k) = g_{(C,q_1\cdots \,q_k,q)}( state (v_1),\ldots , state (v_k))$ if $\varDelta '(v_1)=q_1,\ldots ,\varDelta '(v_k)=q_k$, and $\varDelta '(C\,v_1,\ldots \,v_k)=q$, where $\varDelta '(v)$ is defined by:

$$\begin{aligned} \begin{array}{l} \varDelta '(v) = {\left\{ \begin{array}{ll} q ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (\mathrm {if}\ v = x \wedge (x:q) \in Cnst )\\ \varDelta (C, \varDelta '(v_1) \cdots \varDelta '(v_{\varSigma (C)})) \ (\mathrm {if}\ v = C\ v_1 \cdots v_{\varSigma (C)}) \end{array}\right. } \end{array} \end{aligned}$$

with $\varDelta = \bigcup \{\varDelta _\mathcal {M}\mid \mathcal {M}\in Automata (\varGamma _0)\}$ for the initial abstraction type environment $\varGamma _0$. Then, gensmt outputs the conjunction of the above formula $\bigwedge _{ Cnst \in CnstSet } F_{ Cnst }$. If it is satisfiable, then we obtain a refined abstraction type environment $\varGamma$. Otherwise, we increase $Split$ until the SMT constraint becomes satisfiable.

Example 6

Recall the verification problem in Example 5 and suppose $Split = 2$. The generated SMT formula is:

$$\begin{aligned}&\forall x_1,x_2 \in \{1,2\}. x_1 \ne g_{(\mathtt {Z}{}, \epsilon ,q_1)}() \vee x_1 \ne g_{(\mathtt {S}{}, q_1,q_1)}(x_2) \vee x_2 \ne g_{(\mathtt {Z}{}, \epsilon ,q_1)}() \end{aligned}$$

One of the solutions is $g_{(\mathtt {Z}{}, \epsilon ,q_1)} = 1, g_{(\mathtt {S}{}, q_1,q_1)}(1) = 2, g_{(\mathtt {S}{}, q_1,q_1)}(2) = 1$. The transition function of the refined automaton is: $\{ (\mathtt {Z}{}, \epsilon , q_1^{(1)}), (\mathtt {S}{}, q_1^{(1)}, q_1^{(2)}), (\mathtt {S}{}, q_1^{(2)}, q_1^{(1)})\}$. Using this automaton, the verification succeeds.

The following theorem ensures that if there is an appropriate abstraction type environment with which the verification succeeds, then the algorithm eventually find such an abstraction type environment. See [13] for a proof.

Theorem 2

(relative completeness). Let $(\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ be a verification problem. Suppose there exists $\varGamma$ such that $\vdash \mathcal {P}:\varGamma \leadsto \mathcal {D}$, $\models (\mathcal {D},F_I,F_O)$, and $\varGamma ( main )=\mathtt {o}_{\mathcal {M}_I'}\rightarrow \mathtt {o}_{\mathcal {M}_O'}$ with $\mathcal {L}(\mathcal {M}_I)=\mathcal {L}(\mathcal {M}_I',F_I)$ and $\mathcal {L}(\mathcal {M}_O)=\mathcal {L}(\mathcal {M}_O',F_O)$. Then the algorithm eventually terminates and outputs “Yes”.

We say that check_reachability in Fig. 2 is fair if every concise error path is eventually generated; it is guaranteed if check_reachability always returns a shortest concise error path, for example. We can also guarantee:

Theorem 3

(completeness of refutation). Let $(\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$ be a verification problem such that $\not \models (\mathcal {P}, \mathcal {M}_I, \mathcal {M}_O)$. If check_reachability is fair, then the algorithm eventually terminates and outputs “No”.

6 Implementation and Experiments

We have implemented a verification tool based on our method, and evaluated it through experiments. The experiments were conducted on a machine with Intel(R) Xeon(R) CPU E5620 2.40 GHz and 3.73 GB memory. We used HorSat [3] as the higher-order model checker (except for the program “homrep-rev” for which we used [8] due to a problem of HorSat) and Z3 [5] as the SMT solver.

Table 1 shows the result of the experiments. The column “S” represents the size of the programs. The size of a program is the number of occurrences of constants and variables on the right side of the rules in the program. The column “O” represents the order of the programs. The order of a program is the largest order of the types of functions. Here, the order $order (\kappa )$ of the type $\kappa$ is defined by: $order (\mathtt {o}) = 0$, $order (\kappa _1 \rightarrow \kappa _2) = \max \{ order (\kappa _1) + 1, order (\kappa _2)\}$. The column “R” represents the number of refinements in the verification. The column “T” shows the running time (measured in seconds). We ran each program 3 times and show the average running time. “TO” in the column “T” means a time-out, where we set the time-out to 1000 seconds. For comparison, we have also run the verification tools for HMTT [12] and EHMTT [19] and show their running times in the columns “$\mathrm {T_H}$” and “$\mathrm {T_E}$” respectively. The “N/A” means that the tool is inapplicable; that is the case for the HMTT verification tool, when trees are repeatedly constructed and deconstructed inside the program. The EHMTT verification tool is inapplicable when there is no appropriate annotation; see the discussion below. We have also tried to compare our tool with the PMRS verification tool [16], but unfortunately we could not obtain its source code.

The benchmark programs consist of three categories (separated by lines in the table). The first category (the programs from “reverse” to “mincaml-k”) has been taken from the benchmark set for the EHMTT verification tool [19]. The original programs contain annotations required for EHMTT, and they have been removed for the experiments on our new tool. The second category has been taken from the benchmark set for the PMRS verification tool [16], available at http://mjolnir.cs.ox.ac.uk/cgi-bin/horsc/recheck-horsc/input. The third category contains a new benchmark set. The program “double” is the verification problem given in Example 3. The program “isort2” sorts a given list consisting of “A” and “B” by the insertion sort algorithm. The specification asserts that the result is a sorted list. The program “issorted” sorts a given list consisting of “A” and “B” by the insertion sort, and then (inside the program) checks that the result is a sorted list; if not, the program fails. The specification is that the program does not fail. The program “mergesort2” is the same as “insertionsort” except that the merge sort algorithm is used. The program “mapswsort” sorts a given list and maps a function that swaps “A” and “B” on the list. In the programs above, lists are encoded as trees constructed from $\mathtt {cons}$, $\mathtt {nil}$, $\mathtt {A}$, and $\mathtt {B}$. The program “remove0” takes a list of integers (in the unary representation) and removes 0 from the list.

Our tool could verify the benchmark programs, except “xmarkq1” and “gapid”. For the program “xmarkq1”, the tool failed to construct the initial abstraction. This is because the automata given as the specification of the program is large, and the current tool naively applies a product construction to make the automaton used for abstraction. For the program “gapid”, the abstraction refinement loop did not terminate within the given time limit. This is because the automaton required for abstracting intermediate trees is quite different from the automata given as the input/output specification.

As for the comparison with the HMTT/EHMTT verification tools, the HMTT tool is applicable to only a few of the benchmark programs. That is because HMTT [12] classifies trees into input trees and output trees, and pattern matching can be applied only to input trees, and tree constructors can be applied only to output trees. Most of the programs in the benchmark set repeatedly construct and deconstruct trees.

The EHMTT tool works for the first benchmark set, but it relies on user annotations. Like HMTT, EHMTT also distinguishes between input and output trees, but allows an explicit coercion of output trees to input trees. Each coercion must be annotated with an invariant on the shape of trees that are coerced, and that invariant is used for abstraction. Thus, since an appropriate abstraction is given by hand, EHMTT is faster than our tool when it is applicable. For the second and third categories, we have also added annotations for EHMTT, when applicable. For many of the benchmark programs in the second and third categories, however, there are no appropriate annotations that make the EHMTT verification succeed. There are two main reasons for this. One reason, which is somehow specific to the current implementation, is that the EHMTT tool allows only deterministic top-down automata as output specifications. Since the class of deterministic top-down tree automata is a strict subclass of deterministic bottom-up tree automata, some of the specifications cannot be handled by the EHMTT tool. The other reason is more fundamental. Consider the following function “iszero”.

$$\begin{aligned}&iszero \ x\ t\ f = \mathop {\mathrm {\mathbf {case}}}x \mathop {\mathrm {\mathbf {of}}}\mathtt {Z}{} \Rightarrow t \mid \mathtt {S}{}\,y \Rightarrow f. \end{aligned}$$

If the first argument of the function “iszero” is an output tree, the argument requires an annotation as follows.

$$\begin{aligned}&iszero \ (\mathtt {coerce}^\mathcal {L}e)\ e_t\ e_f \end{aligned}$$

Here, $\mathtt {coerce}^\mathcal {L}e$ converts an output tree constructed by $e$ to an input tree, so that pattern matching can be applied again. The annotation $\mathcal {L}$ is an invariant on the value of $e$; in this case, $\mathcal {L}$ would be typically $\mathtt {S}{}^*\mathtt {Z}{}$ (unless the value of $e$ can be statically determined). Given the annotation, the EHMTT converts the body of $iszero$ to a non-deterministic choice between $t$ and $f$, ignoring the actual value. Thus, if the property to be verified requires a case analysis on whether $x$ is $\mathtt {Z}{}$ or not, the EHMTT verification fails.

To summarize, compared with the HMTT/EHMTT verification tools, our new tool works for a larger set of programs, requiring no special annotations, although it may be slower when the previous tools are applicable. For the programs such as xmarkq1 and gapid, a compromise would be to allow users to provide abstraction types as annotations. Such annotations do not suffer from the problem of EHMTT annotations discussed above.

Table 1. Experimental results

7 Related Work

As mentioned in Sect. 1, several approaches have been proposed for automated verification of functional programs based on higher-order model checking. Kobayashi et al. [11] proposed predicate abstraction and CEGAR (counterexample-guided abstraction refinement) for higher-order model checking, but they used only predicates on integers for abstraction. They later supported some algebraic data structures by encoding them into functions on integers. That encoding approach, however, complicates both programs and specifications. For example, since a list is encoded into a pair consisting of its length and a function that maps an index to the corresponding element, the property of a list: “$1$ occurs in the list” would be converted to a refinement type specification:

$$\begin{aligned} n\mathbin {:}\mathtt {int}\times \{f\mathbin {:}\mathtt {int}\rightarrow \mathtt {int}\mid \exists x.(0\le x<n \wedge f(x)=1)\}, \end{aligned}$$

which would be simply represented by $\_^*1 \_^*$ with a regular language (or automaton) specification. The above specification involves function variables and existential quantifiers, which cannot be handled even by the recent extension of MoCHi [1]. Even if the encoding works, the resulting program and specification tends to become too complex and large, making automated verification difficult; in fact, the current implementation of MoCHi does not work for the benchmark programs in Sect. 6. That said, a limitation of our new approach is that we cannot verify some co-relation between arguments and return values, like “Function $f$ takes a list of length $n$, and returns a list of length $2\times n$.” This is because we use automata for abstracting information about each tree, which loses the relationship between multiple trees. A possible remedy to this problem would be to use tree automatic relations [2] for abstraction. Another approach would be to integrate our new approach with that of MoCHi.

We have already discussed HMTT [12] and EHMTT [19] in Sect. 6. Although HMTT also abstracts trees by using an automaton, the automaton used for the abstraction is fixed to the one specified as the input automaton. EHMTT decompose the verification problem to multiple HMTT verification problems, by using annotations. Again, the abstraction relies on the automata given as specifications or annotations. There was no abstraction refinement loop mechanism in the above work on HMTT/EHMTT verification. We have recently extended the HMTT verification with abstraction refinement loops [14], but it was restricted to HMTT (where there is a distinction between input/output trees), and the relative completeness (cf. Theorem 2) was not guaranteed. In short, our new method requires no annotations unlike EHMTT verification, and works (at least in theory) for a strictly larger set of verification problems than our previous work on HMTT/EHMTT verification.

Ong and Ramsay [16] introduced a verification method for tree-processing programs called PMRS. Their method abstracts trees based on finite patterns, so it cannot deal with general regular properties like “a tree contains an even number of $\mathtt {S}{}$”. For example, for the program $\mathcal {P}_1$ in Example 2: they abstract the argument $x$ of $add$ based on the information about whether $x$ matches $\mathtt {Z}{}$ or $\mathtt {S}{}\,x'$. If the verification fails, they expand patterns by unfolding functions; in the case of the above example, the new set of patterns would be $\{\mathtt {Z}{}, \mathtt {S}{}\,\mathtt {Z}{}, \mathtt {S}{}\,(\mathtt {S}{}\,x)\}$. Thus, their abstraction never captures properties like “$x$ is an even number” (i.e., $x$ is of the form $\mathtt {S}{}^{2n}\mathtt {Z}{}$). For the benchmark programs used in our experiments, PMRS works for the second category (because it has been taken from the benchmark of the PMRS tool), but it would not work for most of the benchmarks in the first and third categories.

Automata-based abstraction has also been recently used for $\mu$HORS model checking [10]. The $\mu$HORS model checking is an extension of higher-order model checking, where HORS has been extended with recursive types. They abstract the whole program configuration (which can be represented as applicative terms) by using a tree automaton, and gradually refines the abstraction using a similar technique utilizing an SMT solver. Since $\mu$HORS is Turing complete, their approach can in theory be applied to the verification problems considered in the present paper, but our approach would scale much better for tree-processing programs. They abstract both control and data structures using automata in a monolithic way, whereas we abstract only tree data using automata, and precisely analyze control structures thanks to the decidability of higher-order model checking.

Besides approaches based on higher-order model checking, there have been a few other approaches to (semi-)automated verification of higher-order functional programs that support algebraic data types. Liquid types [7, 17, 20] is a notable approach based on refinement types, but it requires a user’s hints on the predicates used in refinement types. Genet [6] applies a tree automata completion technique for term rewriting systems to static analysis of functional programs. His approach uses tree automata for modeling the whole program state (like in the $\mu$HORS model checking mentioned above), while our approach uses tree automata only for abstracting tree data. His method does not guarantee the relative completeness in the sense of ours.

8 Conclusion

In this paper, we have introduced a new method for fully automated verification of tree-processing, higher-order functional programs. We have introduced automata-based abstraction, and combined it with higher-order model checking. The automata-based abstraction is formalized as a type-based program transformation, and the abstraction is gradually refined based on counterexamples. Compared with the previous methods based on higher-order model checking, the new method is more automated (requires no annotations), and can deal with a larger class of programs. Future work includes improvement of the scalability of the verification method, and an integration of the proposed technique with the predicate abstraction approach of MoCHi [1, 11, 18].