The Theory of Transit Assignment: Basic Modelling Frameworks

Abstract

In this chapter, the different basic assumptions for the development of assignment models to transit networks (frequency-based, schedule-based) are presented together with the possible approaches to the simulation of the dynamic system (steady state, macroscopic flows, agent-based).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this chapter, the different basic assumptions for the development of assignment models to transit networks (frequency-based, schedule-based) are presented together with the possible approaches to the simulation of the dynamic system (steady state, macroscopic flows, agent-based). The main functional components of uncongested assignment and user equilibrium (route choice, flow propagation, arc performances) are also illustrated here in their general form, while the various demand and supply phenomena emerging in transit systems (regularity, congestion, information) are dealt with in the following Chap. 7.

1 Formulating and Solving Transit Assignment

• Guido Gentile 

In this section, a general mathematical framework for the formulation and solution of transit assignment is presented, which allows for different models, ranging from uncongested assignment to user equilibrium, from static to dynamic. The main functional components of assignment models (route choice, flow propagation, arc performances) are illustrated here with some specific reference to transit networks, but the simulation of public transport services is analysed with more proper detail in the sections that follow. The behavioural concept of strategy is introduced, together with its formulation through hyperarcs and hyperpaths.

1.1 Schedule-Based Versus Frequency-Based Services and Models

1.1.1 Information Provision and Passenger Decision-Making

A fundamental dichotomy in modelling transit services arises from the question whether or not passengers know or care about timetables. If service is so irregular or so frequent that passengers find no convenience in timing their arrival at a stop with that of a specific run, or simply the schedule is unavailable to them for whatever reason, then users perceive the line in terms of headways between subsequent run departures from that stop (often we refer to carrier arrivals instead of departures, ignoring dwell times).

Actually, while a timetable usually exists for management reasons (most transport companies do program the service in terms of runs in order to allocate vehicles and drivers), it is a specific choice of the operator to determine how much and which schedule information shall be provided to the public. Indeed, there might be issues of reliability and/or usefulness for such timetables. Due to road congestion (if transit carriers share the infrastructure with private vehicles), driver random behaviour, traffic signals, as well as passenger congestion (if dwell times depend on boarding and alighting loads), service regularity may be so poor that it turns out misleading to publish the programmed schedule. Moreover, when a service lags, some runs can be delayed or cancelled by the operator without the need of informing the public. On the other hand, it is not interesting to learn a published schedule by passengers when regularity is so poor that it is not really possible to identify which run of a same line is going to be served by an arriving carrier. Finally, it may be not useful nor possible to memorize the timetable if lines are very frequent (e.g., a metro passing every 3 min).

On the contrary, if actual arrivals are fairly regular with respect to the schedule (passengers are still able to associate a delayed carrier arrival with a specific run) and carrier arrivals are fairly infrequent (e.g., a regional bus passing every 30 min), then passengers perceive the service in terms of runs. This is particularly true for transit systems that require a seat reservation by users before boarding, as this clearly refers to a specific run.

In the following, this model dichotomy in passenger behaviour on the demand side is solved as an operator decision on the supply side.

In practice, we assume that if the operator publishes full information about the timetable, then the scheduled arrival and departure times of all runs at all stops are regular, and passengers are (at least in principle) able (and thus willing) to plan their complete trip before departure. This form of information provision/perception and consequent decision-making is called schedule-based.

Alternatively, scheduled times at stops remain unpublished and refer to a priori planned operations, i.e., without disturbances, but they may differ from actual arrival and departure times that occur in practice. Headways are then represented as random variables with a given distribution, while the frequency is equal to the inverse of the expected headway. The operator may publish only the stop sequence of each line (and possibly their frequency). Based on their travel experience, passengers figure out the (expected) running and dwell times, as well as the frequency and regularity of transit lines (but not the exact scheduled times). This form of information provision/perception and consequent decision-making is called headway-based or frequency-based services.

Clearly, in the same transit network, there can coexist services that are frequency-based and schedule-based. This requires non-trivial treatment from the modelling point of view; otherwise, we have to accept the limitations connected to one of the two main approaches.

1.1.2 Model Results for Design and Operation

In the above section, the differentiation between schedule-based and frequency-based services has been explained from the user point of view. On the other hand, the purpose of modelling travel behaviour in transit assignment is functional to obtaining passengers’ loads and service performances that are used for design and operation.

To this end, we can distinguish as follows:

• schedule-based models, which aim at determining passenger loads on each single run of the service, as well as the actual run trajectories (diagram in time and space along the line stops), since due to delays these may differ from the planned timetables;

• frequency-based models, which aim at determining the average loads on the lines and the possibly emerging phenomena of macroscopic congestion.

The first approach is more suitable for management in real time, because services are daily operated in terms of runs by public transport companies, and the second one is for planning offline, because services are usually yearly designed in terms of lines by mobility agencies. However, in the future, more attention shall be probably devoted to design the requirements of transit operations as an interconnected network of services, by also optimizing transfers in terms of total passenger delays; this objective clearly requires schedule-based assignment models.

Moreover, schedule-based models are in general richer than frequency-based models. Indeed, it is always possible to aggregate the results obtained for each run into results for each line. Clearly, more detailed output is obtained with a more detailed input, which might be unavailable or irrelevant during the preliminary phases of service planning, and with more complex models, which may require many parameters and high computing times. Therefore, the choice of the modelling approach shall be strictly linked to the actual need of the design task.

In the following, we will often refer to schedule-based and frequency-based assignment considering the above point of view of supply (model), rather than that of demand (service).

1.2 Multiclass Flows and Performances on Multimodal Networks

In this section, the topological (structural) relations among flows and among performances (separately) at the two different levels of arcs and routes are presented; no functional component is introduced here. We refer in general to ‘routes’ and not simply to ‘paths’ to later include (next section) the concept of ‘hyperpaths’ that is used in transit assignment to represent passenger strategic behaviour.

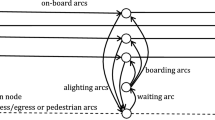
The topology of the transport network (supply) is represented through a directed graph (N, A), with nodes N and arcs A, on which a set of routes K (paths, for the moment) is defined to connect the different O–D pairs of trips made by users of various classes G (demand) with some modes M (see Sect. 5.1.2.8). In general, but even more notably in transit networks, each arc represents an atomic trip segment of a specific type (e.g., walking from one point to another, waiting for a given interval or for a given event, riding on-board a line from a stop to the subsequent one, driving from one intersection to the next) on a specific transport system (e.g., public transport, car, bike). The sequence of trip segments of the same type is called trip phase or trip leg. Different models may disarticulate trips in different ways and identify different arc types.

Arcs and routes are characterized with variables to quantify flows and performances for each class of users; arcs belong implicitly to one transport system network (one road link is represented by different arcs for pedestrians, cars and to support transit services), with the exception of those used for inter-modal changes (e.g., the stop arcs that connect the pedestrian network and the line network introduced in Sect. 6.2.2); routes belong explicitly to one (simple or combined) mode (for details see Sect. 5.1.1.2).

In static models and in space-time network models (such as in schedule-based models where a diachronic graph is used to represent the temporal dimension within the network topology, as in Sect. 6.3), the reference to time is usually omitted; this is the assumption adopted in the following, while extensions to other kind of dynamic models are presented in Sects. 6.4 and 6.5.

At the network level, flows and performances of arc a ∈ A for users of class g ∈ G are defined as follows:

q _ag :

class specific flow;

q _a :

volume (aggregation of all class flows);

t _a :

travel time (the same for all classes);

γ _ag :

value of time;

$c_{ag}^{nt}$ :

non-temporal cost;

c _ag :

generalized cost.

Flows and volumes express in general the number of users passing through a given section in a given time interval. But in space-time networks, where the arc topology embeds natively the simulation time, flows represent actually a number of users (loads); for example, the passengers travelling on a given run section.

The volume of arc a ∈ A is obtained by summing up the flows of each class g ∈ G, possibly multiplied by a specific equivalency coefficient ω _ag, which may differ by arc type, plus a base volume $q_{a}^{0}$, which represents flow components that are not modelled directly:

$$ q_{a} = q_{a}^{0} + \sum\limits_{g \in G} {q_{ag} } \cdot {\omega}_{ag}. $$

(6.1)

In case of passenger flows, the typical assumption is given as ω _ag  = 1 and q ⁰ _a  = 0.

The generalized cost of arc a ∈ A for users of class g ∈ G is obtained multiplying the travel time by the value of time plus the non-temporal cost:

$$ c_{ag} = c_{ag}^{nt} + {\gamma}_{ag} \cdot t_{a}. $$

(6.2)

The value of time of each class differs by arc type and may depend on volumes (discomfort) like the travel time itself (congestion); these phenomena are the subjects of later Sects. 7.2, 7.3 and 7.4 and are essential in transit equilibrium models. The non-temporal cost is in turn the sum of several disutility components, including monetary costs and user preferences with respect to a large variety of arc attributes (e.g., length, steepness, tortuosity, landscape, pollution, presence of economic activities).

At the trip level, flow and costs of route k ∈ K for users of class g ∈ G are defined as follows (recall that the notion of route k embeds its origin O _k  ∈ O, destination D _k  ∈ D and mode M _k  ∈ M):

$c_{kg}^{na}$ :

non-additive cost;

$c_{kg}$ :

generalized cost;

$q_{kg}$ :

class specific flow.

The generalized cost of route k ∈ K for users of class g ∈ G can be obtained by summing up the costs of the corresponding arcs plus a non-additive term, which may represent fares or any nonlinear component of disutility perceived by users (e.g., walking time):

$$ c_{kg} = c_{kg}^{na} + \sum\limits_{a \in A} {c_{ag} } \cdot\Delta _{ak} , $$

(6.3)

where Δ _ak is the number of times that a user travelling on route k ∈ K passes through arc a ∈ A. For acyclic paths, it is given as follows:

$$ {\Delta }_{ak} = \left\{ \begin{array}{l} 1{, }\quad {\text{if}}\;\; \, a \in A_{k} \hfill \\ 0{, }\quad {\text{otherwise}} \hfill \\ \end{array} \right.. $$

(6.4)

In case where the disutility associated with users to each route can be represented as a linear combination of its network element costs, then the supply model is said to be additive, i.e., the terms $c_{kg}^{na}$ are all null.

The flow on arc a ∈ A of class g ∈ G users is the sum of each route flow (of that same class) multiplied by the number of time it passes through that arc:

$$ q_{ag} = \sum\limits_{k \in K} {q_{kg} } \cdot\Delta _{ak}. $$

(6.5)

The flow q _kg on route k ∈ K _odm of class g ∈ G users results from the choice among all routes connecting origin o ∈ O to destination d ∈ D on mode m ∈ M, and is thus obtained as:

$$ q_{kg} = d_{odmg} \cdot p_{kg} , $$

(6.6)

i.e., by multiplying:

d _odmg :

is the demand flow of class g users travelling from o to d on mode m;

p _kg :

is the probability that user of class g choose route k.

1.3 Strategies and Hyperpaths

A strategy is in general a plan to achieve a goal under conditions of uncertainty. In game theory, a strategy refers to the rules that a player will use to choose among the available options. A strategy may recursively look ahead and consider what can happen in each contingent state of the game depending on the previous possible actions.

Applying this concept to route choice, the goal of the traveller was to reach the destination of his/her trip at a minimum expected (perceived and generalized) cost.

Travel strategies include diversion points (nodes), where users may exploit information acquired along the trip, about variables that are preventively seen as random unknowns, and on this base can make en-route decisions on how to proceed towards the destination. In most cases, the information is actually acquired at the diversion node, but modern information systems may change this circumstance.

This is for example the case of a passenger waiting at a stop for a subset of attractive lines (among all those available at the stop) that he/she wishes to board for reaching his/her destination. When he/she realizes which line is served by the vehicle that is approaching the stop, then he/she can decide whether to board it or keep waiting, depending on whether the line is attractive or not (line probabilities in Sect. 7.1).

In other cases, the outcome of the random variable that becomes known to the user at the diversion point directly determines the action undertaken without an actual decision made by the user. This is for example the case of a passenger boarding a line vehicle who may get, or not, a seat depending on the availability on-board and on how lucky he/she is with respect to the other boarding passengers (fail-to-sit probabilities in Sect. 7.2.2). A similar example is that of a passenger waiting for a line on a crowded platform who may get, or not, on the arriving vehicle depending on the available space on-board and on how lucky he/she is with respect to the other waiting passengers (fail-to-board probabilities in Sect. 7.3.3).

Strategic behaviour is thus connected with the presence of random variables which determine a probability for each one of the considered options among those available at a diversion point and the corresponding expected cost. A travel strategy is then described by a ‘complete’ iterative sequence of route diversions, starting from the origin, until the destination is reached for each possible combination of events, given the considered options (in this sense, complete).

From a topological point of view, a convenient way of formalizing this kind of strategies on a transit network (but not only) is to introduce hyperarcs and hyperpaths.

A hyperarc is a non-empty set of diversion arcs (also called its branches) exiting from a diversion node i ∈ N ^div ⊆ N; i.e., a subset of its forward star i ⁺. The set of diversion arcs is A ^div = {i ⁺: i ∈ N ^div}. Note that the number of hyperarcs that can be defined on a network may be very large, because each of them identifies a different combination of arcs exiting from a diversion node (the considered options among those available).

The generic hyperarc ă ⊆ i ⁺, with i ∈ N ^div, has a singleton tail, denoted ă ^– = i, while a set of nodes constitutes its head, denoted ă ⁺ = {a ⁺: a ∈ ă}. Let H be the set of hyperarcs defined on the transport network (not necessarily all combinations of diversion arcs exiting from a same diversion node make up a hyperarc of H). Each branch a ∈ ă of a hyperarc ă ∈ H is characterized by the following variables:

p _a|ă :

the diversion probability of using branch a among all branches ă of the hyperarc;

t _a|ă :

the conditional travel time connected using branch a as part of the hyperarc ă.

The (combined) travel time t _ă of the hyperarc is then given by:

$$ t_{\breve{a}} = \sum\limits_{{a \in {\breve{a}} }} {t_{{a|{\breve{a}} }} \cdot p_{{a|{\breve{a}} }} }. $$

(6.7)

The conditional cost c _a|ăg connected using branch a ∈ ă as part of the hyperarc ă ∈ H for users of class g ∈ G is proportional to its travel time through the value of time γ _ag :

$$ c_{{a|{\breve{a}} g}} = {\upgamma }_{ag} \cdot t_{{a|{\breve{a}} }} + c_{ag}^{nt}. $$

(6.8)

The (combined) cost c _ăg of the hyperarc is then given by:

$$ c_{{{\breve{a}} g}} = \sum\limits_{{a \in {\breve{a}} }} {c_{{a|{\breve{a}} \;g}} \cdot p_{{a|{\breve{a}} }} } = {\upgamma}_{{{\breve{a}}^{ - } g}} \cdot t_{{{\breve{a}} }}^{{}} + \sum\limits_{{a \in {\breve{a}} }} {c_{ag}^{nt} \cdot p_{{a|{\breve{a}} }} } ; $$

(6.9)

the latter assumes that the value of time γ _ig is equal to all diversion arcs exiting from the same tail node i = ă ⁻. This expression is useful because models often provide directly the combined travel time t _ă instead of the conditional travel time t _a|ă .

In the following, for notation consistency, it is intended that if a ∉ ă then p _a|ă  = 0, t _a|ă  = 0, c _{a|ă g}  = 0.

The generic hyperpath k is a ‘bush’ of arcs that connects its origin to its destination, i.e., an acyclic sub-graph (N _k , A _k ) with:

• |k ^–| = 1, i.e., one origin node;

• |k ⁺| = 1, i.e., one destination node;

• |i ⁺ _k | = 1, ∀i ∈ N _k  − k ⁺ − N ^div, i.e., one successor arc, except for the destination node which has none, and for diversion nodes which may have more than one;

• |i ⁺ _k | ≥ 1, ∀i ∈ N _k  ∩ N ^div, i.e., one or more successor arcs at diversion nodes, which make up one hyperarc, i.e., i ⁺ _k  ∈ H;

• |i ^– _k | ≥ 1, ∀i ∈ N _k  − k ^–, i.e., one or more predecessors, except for the origin node which has none;

• i _k  = ∅, ∀i ∉ N _k , just for notation consistency.

In the example of Fig. 6.1, there are 7 possible hyperarcs exiting from the diversion node i ∈ N ^div, i.e., all the possible combinations of diversion arcs a, b and c: {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}; but among them only one hyperarc, i.e., i ⁺ _k  = ă = {a, b}, can belong to a given hyperpath k.

Fig. 6.1

Example of a hyperpath k from origin o = k ⁻ to destination d = k ⁺. The hyperpath is depicted in dashed red lines. The diversion nodes are in red. The bold lines are diversion arcs

It is intended that exiting from a diversion node, no diversion arc can be used per se in a hyperpath but only hyperarcs can; clearly, it is possible to define a singleton hyperarc made of only one diversion arc.

A path can be seen as a hyperpath that does not include diversions. In the following, the term ‘route’ will then denote indifferently paths or hyperpaths; the proposed formulation is valid for both cases, unless otherwise specified.

In particular, a strategy can be formalized, from a topological point of view, as a hyperpath that connects the origin–destination pair of the trip. Each strategy has an expected cost which is considered by users to make their route choice before starting the trip.

The cost of a hyperpath (i.e., the cost of the underlined strategy) is defined as the sum of its arc costs and of its hyperarc branch costs, multiplied by the probability of using these arcs when following that route; in this sense, it may be additive (if the non-additive cost is null). Equation (6.3) becomes:

$$ c_{kg}^{{}} = c_{kg}^{na} + \sum\limits_{{a \in A - A^{div} }} {c_{ag}^{{}} } \cdot\Delta _{ak}^{{}} + \sum\limits_{{a \in A^{div} }} {c_{{a|\left( {a^{ - } } \right)_{k}^{ + } \;g}}^{{}} \cdot\Delta _{ak}^{{}} }, $$

(6.10)

where Δ _ak denotes now the probability of using arc a (possibly as a branch of a hyperarc) when travelling on route k, and (a ⁻) ⁺ _k  ∈ H is the one hyperarc made up by the successor arcs of the diversion node a ⁻ ∈ N ^div on hyperpath k.

Note that the conditional cost c _a|ăg may differ substantially from the cost c _ag ; it is usually lower, and from this derives the convenience of considering a hyperpath instead of a simple path (this is the case of attractive lines). In other cases (e.g., fail-to-sit or fail-to-board), there is no cost difference, but a hyperpath is actually the only available route.

The arc-route probabilities depend on the hyperarc diversion probabilities through the following recursive equation, which can be solved in topological order (from the origin to the destination of the route):

$$ \Delta_{ak}^{{}} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{if}} \; {a \in A_{k} - A^{div} } \hfill \\ {p_{{a|\left( {a^{ - } } \right)_{k}^{ + } }}^{{}} ,} \hfill & {\text{if}} \; {a \in A_{k} \cap A^{div} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} \cdot } \right.\left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{if}} \; {a^{ - } = k^{ - } } \hfill \\ {\sum\limits_{{b \in \left( {a^{ - } } \right)^{ - } }} {\Delta_{bk}^{{}} } ,} \hfill & {\text{otherwise};} \\ \end{array} } \right. $$

(6.11)

the first term is the conditional probability of using arc a from its initial node a ⁻ along hyperpath k, and the second term is the absolute probability of using its initial node.

The proper extension to hyperpaths of the structural cost Eq. (6.3) requires to formally change the network model from a graph to a hypergraph (N, Ă = A ∪ H), where hyperarcs are native elements:

$$ c_{kg}^{{}} = c_{kg}^{na} + \sum\limits_{{a \in A - A^{div} }} {c_{ag}^{{}} } \cdot\Delta_{ak}^{{}} + \sum\limits_{a \in H} {c_{{\check{a}}g}^{{}} \cdot\Delta_{{{\check{a}}k}}^{{}} }, $$

(6.12)

where Δ _ăk denotes the probability of using hyperarc ă when travelling on route k.

The structural flow equation, given by Eq. (6.5), can instead be extended immediately to hyperpaths under the new interpretation of Δ _ak as a arc-route probability.

However, in hyperpath-based models, the structural Eqs. (6.10) and (6.5) are not merely related to the network topology, but are rather the result of a functional model which describes en-route decisions and/or events connected with random variables yielding the diversion probabilities.

In more advanced models (see the case of information about next arrival for each line provided at stops presented in Sect. 7.1), the en-route diversions of a hyperarc reproduce indeed a strategic rerouting which depends on the destination, mode and class of the traveller; in this case, the diversion probabilities and the conditional travel times are denoted p _{a|ă dmg} and t _{a|ă dmg} , respectively. As a consequence, based on Eq. (6.11), the arc-route probabilities would depend also on the class (while destination and mode are intrinsic in the route). Clearly, p _{a|ă dmg}  = 0 and t _{a|ă dmg}  = ∞ if a ∉ A _m .

Finally, the number of hyperpaths defined on the network can be huge, although finite, because of the many possible combinations of diversion arcs each one represented by a different hyperarc.

Based on these considerations, although strategies can be formally represented by hyperpaths, their explicit enumeration is prohibitive. Thus, an implicit enumeration approach is usually adopted, as explained in the following Sect. 6.1.5.

1.4 Sequential Route Choice and Flow Propagation

The route probabilities of Eq. (6.6) depend in turn on the route costs, for example, through a random utility model (see Sects. 4.4 and 4.5):

$$ p_{kg}^{{}} = p_{kg}^{{}} \left( {c_{hg}^{{}},\quad \forall h \in K_{odm} } \right). $$

(6.13)

Route probabilities must satisfy the following consistency and non-negativity constraints:

$$ \sum\limits_{{k \in K_{odm} }} {p_{kg}^{{}} } = 1,\quad p_{kg}^{{}} \ge 0. $$

(6.14)

Equation (6.13) defines the route choice model in case of explicit enumeration of routes, while Eqs. (6.6) and (6.5) define the corresponding flow propagation model.

This basic model, where routes are chosen jointly, may be inadequate to describe passenger behaviour; as the number and complexity of paths increases, users can become unable to memorize and compare the available alternatives, as this would require too high cognitive faculties. Moreover, explicit path enumeration may be heavy from a computational point of view.

Decision-makers tend to simplify choice contexts that are too complex. A path, after all, is not an elementary concept, because it is constituted by a sequence of arcs.

In case of additive supply models, we can then assume that users reach their destination through a sequence of (more simple) choices at nodes, where the local alternatives are the arcs of the forward start. This approach is based on implicit enumeration of routes and requires to introduce the following variables, referred to users of class g ∈ G directed towards destination d ∈ D on mode m ∈ M:

• p _admg probability that users take arc a ∈ A conditional on being at its tail node;

• w _idmg expected cost perceived by users to reach the destination from node i ∈ N;

• q _idmg flow of users traversing node i ∈ N.

Sequential route choice models are generally referred to destinations, as this is the most natural way to address the problem from user’s perspective, and it is also the only possible way to proceed if one wants to introduce the concept of strategies (see Sect. 6.1.3). Travelling passengers aim to reach their destination and can take en-route decisions only in reaction to future events based on incoming information.

Consider the local choice at node i ∈ N − {d}, while for i = d it is: w _idmg  = 0, p _admg  = 0 ∀a ∈ i ⁺.

The cost of each alternative, also called remaining cost and denoted as w _bdmg , is obtained as the sum of the arc cost b ∈ i ⁺ ∩ A _m and the expected cost perceived by the user to reach the destination from its final node b ⁺:

$$ w_{bdmg} = c_{bg} + w_{{b^{ + } dmg}}. $$

(6.15)

These costs jointly determine the conditional probabilities of each arc a ∈ i ⁺ through a discrete choice model:

$$ p_{admg}^{{}} = \left\{ \begin{aligned} & p_{admg}^{{}} \left( {w_{bdmg}^{{}},\forall b \in i^{ + } \cap\,A_{m} } \right),\quad {\text{if }}a \in A_{m} \\ & 0,\quad {\text{otherwise}} \\ \end{aligned} \right.. $$

(6.16)

Note that users of mode m can take only arcs of this mode.

Arc conditional probabilities must satisfy the following consistency and non-negativity constraints:

$$ \sum\limits_{{a \in i^{ + } }} {p_{admg}} = 1,\quad p_{admg} \ge 0. $$

(6.17)

Any discrete choice model provides together with the probability of each alternative the so-called satisfaction, i.e., the expected value of the maximum utility resulting from the choice. We assume that the expected cost perceived by users coincides with the opposite of the satisfaction in the local choice at the node:

$$ w_{idmg} = w_{idmg}^{{}} \left( {w_{bdmg},\quad \forall b \in i^{ + } \cap\,A_{m} } \right). $$

(6.18)

Equation (6.18) for all nodes i ∈ N − {d} (given a triplet dmg) can be seen as a system of nonlinear equations, where unknowns are the node costs w _idmg . Under the assumption that only efficient routes are considered, i.e., paths getting closer to the destination with respect to some fixed cost or distance metric, which is typically acceptable in transit networks, the above system is triangular and can be easily solved by substitution, processing nodes in reversed topological order with respect to the chosen metric. Then, Eq. (6.16) can be computed in no particular order. It is interesting to recall that in case of Logit model, by introducing the concept of ‘weights’ as the negative exponential of costs scaled by the distribution parameter, the above system can be transformed in a system of linear equations (the first step of Dial’s algorithm).

The case of deterministic choices deserves particular attention. Equations (6.18) and (6.16) for each i ∈ N − {d} and a ∈ i ⁺ ∩ A _m , respectively, become the following:

$$ w_{idmg} = {Min}\left( {w_{admg}^{{}},\quad \forall a \in i^{ + } \cap\,A_{m} } \right), $$

(6.19)

$$ p_{admg} \cdot \left( {w_{admg}^{{}} - w_{idmg}} \right) = 0. $$

(6.20)

The complementarity condition represented by Eq. (6.20) is the formulation of Wardrop’s First Principle for the local choice. The result is a one-to-many mapping where multiple flow patterns may correspond to one cost pattern if there are alternatives of equal cost.

The probability of each path k ∈ K _odm from origin o ∈ O to destination d ∈ D on mode m ∈ M can be determined a posteriori as the product of all the arc conditional probabilities making up the route (this result does not apply to hyperpaths):

$$ p_{kg} = \prod\limits_{a \in A} {\left( {p_{admg}} \right)}^{{\Delta _{ak} }}. $$

(6.21)

This equation is not required in the assignment model itself; however, path information is necessary to undergo post-evaluation (see Sect. 5.2.3), because many result indicators are calculated on the basis of path flows, regardless the fact that a sequential or strategic approach (both yielding arc probabilities) has been used in the route choice model.

Indeed, in sequential models, the typical way of performing flow propagation avoids the need to introduce paths, by solving a system of linear equations for all nodes i ∈ N (given a triplet dmg), where unknowns are the node (exit) flows q _idmg . Each equation represents the following conservation of flows at the node.

$$ q_{idmg} = d_{idmg} + \sum\limits_{{a \in i^{ - } }} {q_{{a^{ - } dmg}} \cdot p_{admg}} , $$

(6.22)

where the exit flow is equal to the demand flow plus the entry flow. The latter is in turn given by the sum over the node backward star of each arc tail flow multiplied by the corresponding arc conditional probabilities. The demand flow d _idmg is null if i is not an origin. Under the assumptions of efficient routes, the above system is triangular and can be easily solved by substitution, processing nodes in direct topological order with respect to the chosen metric (such as in the second step of Dial’s algorithm). In the general (non-triangular) case, the coefficient matrix of system (6.22) is highly sparse, given that each equation involves only the adjacent arcs entering a node; this feature can be exploited by solution algorithms such as BiCGstab. Preconditioning by a triangularized solution (i.e., solving the problem without taking into account non-efficient arcs) has great advantages.

The arc flows of a specific user class can then be obtained as an aggregation of all contributions for each destination and mode:

$$ q_{ag}^{{}} = \sum\limits_{d \in D} {\sum\limits_{m \in M} {q_{admg}^{{}} } } , $$

(6.23)

where q _admg is the product of the node flow and the arc conditional probability:

$$ q_{admg}^{{}} = q_{{a^{ - } dmg}}^{{}} \cdot p_{admg}^{{}}. $$

(6.24)

It is worth warning that sequential models provide the same results (flows) of the corresponding route choice models only for some elementary case (e.g., deterministic, logit).

1.5 Sequential Model and Strategies

The proposed sequential model for route choice can be immediately extended to represent a strategy-based behaviour. In this case, the conditional probability p _admg of a diversion arc a ∈ A ^div is the result of two models:

• the local choice p _ădmg among the hyperarcs exiting from the diversion node a ⁻, and

• the hyperarc diversion probabilities p _{a|ă dmg} depending on random events.

$$ p_{admg}^{{}} = \sum\limits_{{{\breve{a}} \subseteq \left( {\left( {a^{ - } } \right)^{ + } \cap\,A_{m} } \right){: }{\breve{a}} \in H}} {p_{{{\breve{a}} dmg}}^{{}} } \cdot p_{{a|{\breve{a}} dmg}}^{{}}. $$

(6.25)

The local choice probabilities require to compute the remaining cost w _b̌dmg for reaching the destination using each hyperarc b̌ available at node i = a ⁻. This is equal to the average, weighted by the diversion probabilities p _{b|b̌ dmg} , among its branches b ∈ b̌, of the sum between the arc conditional cost c _{b|b̌ dmg} and the expected cost w _b+dmg from its final node b ⁺. Based on (6.9) and (6.15), it is given as follows:

$$ w_{{{\breve{b}} dmg}}^{{}} = \frac{{c_{{{\breve{b}} dmg}}^{{}} + \sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} \cdot w_{{b^{ + } dmg}}^{{}} } }}{{\sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} } }} = \frac{{\upgamma_{{{\breve{b}}^{ - } g}} \cdot t_{{{\breve{b}} dmg}}^{{}} + \sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} \cdot w_{bdmg}^{{}} } }}{{\sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} } }} ; $$

(6.26)

the latter assumes that the travel time of the arc branches per se is null as it is already included in that of the hyperarc.

The reason for rescaling the probabilities in Eq. (6.26) and not on Eq. (6.25) is to allow models, such as the fail-to-board probabilities of Sect. 7.3.3, where the sum of the hyperarc diversion probabilities is less than one, i.e., where some flow is eliminated from the network during the flow propagation.

The hyperarc diversion probabilities result from an adaptation strategy to circumstances rather than a choice among alternatives. They are strictly related to the particular stochastic process under consideration; on transit networks, en-route random events may depend on line frequencies and on remaining capacities, as well as on expected costs to destination (see Sects. 7.1, 7.2.2 and 7.3.3). Equations (6.16) and (6.18) become, respectively:

$$ p_{{{\breve{a}} dmg}}^{{}} = p_{{{\breve{a}} dmg}}^{{}} \left( {w_{{{\breve{b}} dmg}}^{{}},\forall {\breve{b}} \subseteq \left( {\left( {a^{ - } } \right)^{ + } \cap\,A_{m} } \right):{ }{\breve{b}} \in H} \right), $$

(6.27)

$$ w_{idmg}^{{}} = w_{idmg}^{{}} \left( {w_{{{\breve{b}} dmg}}^{{}},\forall {\breve{b}} \subseteq \left( {i^{ + } \cap\,A_{m} } \right):{ }{\breve{b}} \in H} \right). $$

(6.28)

It is worth noting again that there is a noticeable difference between the hyperarc choice probabilities p _ădmg and the arc diversion probabilities p _a|ădmg . The former are choice shares among possible route alternatives, the latter are the outcome percentages from random events. The arc conditional probabilities p _admg resulting from the route choice model are a combination of both, as evident from Eq. (6.25). Therefore, in the presence of hyperarcs and consequent strategy-based behaviour (in case of fail-to-sit and fail-to-board probabilities, there is no other option than strategies), the transit assignment model shall be extended to include the representation of physical phenomena providing, possibly congested, diversion probabilities.

1.6 Shortest Paths and All-or-Nothing Assignment

The computation of shortest trees rooted at zone centroids is at the base of most assignment algorithms, even when the route choice model is not deterministic but stochastic, and even when a sequential (arc-based) model is adopted instead of a path-based one. Therefore, in the following, we give some basic information about this problem.

In case of transit networks, the root of the tree is typically a destination and not an origin; this is a natural choice for strategic models.

Let us consider the problem for users of class g ∈ G directed towards destination d ∈ D on mode m ∈ M. Most shortest tree algorithms solve actually the dual problem of finding the minimum cost to reach the destination from each node i ∈ N by repeatedly applying to every arc a ∈ A _m the following Bellman update, until no further cost improvement is possible (Bellman 1958):

$$ w_{{a^{ - } dmg}} \leftarrow {Min}\left( {w_{{a^{ - } dmg}},w_{admg}^{{}} } \right). $$

(6.29)

The above minimization checks whether using arc a at a cost of w _admg  = c _ag  + w _a+dmg can improve the current cost w _a−dmg to reach the destination d from its initial node a ⁻.

The (expected) cost of each node (also called label) is initially set to infinity, except for the destination, whose cost is obviously zero.

Whenever a cost label is updated, that node is inserted in a list of nodes to be visited. The algorithm starts by initializing this list with the destination. Nodes are iteratively extracted from the list and Eq. (6.29) is applied to each arc of its backward star. If at each iteration a node with the least cost is extracted, then no node will be extracted twice, provided that all arc costs are non-negative. An effective way of (pseudo) ordering the nodes is by introducing a bucket list, where the space of expected costs is partitioned in (many small) n ^b buckets of equal span δ^b; identifying the proper bucket for the insertion of a node i with cost w _idmg in the list requires just an integer division: w _idmg \δ^b. The resulting algorithm of Dijkstra (1959) is particularly suited for transit networks, which are characterized by anisotropic costs and non-planar graphs, and provides also a topological order of the nodes given by the inverse order of their extraction from the list.

In case of acyclic graphs, the Bellman update can be applied in inverse topological order, without the need of handling a list of nodes to be visited.

At each successful (convenient) update, the algorithm records also a, as the successor arc of its tail node a ⁻ (or equivalently a ⁺ as its successor node); in other terms, p _admg is set to one, while for the other arcs of the node forward star the probability is set to zero. This information can be exploited in a so-called All-Or-Nothing assignment to shortest paths, where the travel demand is propagated by solving (6.22) in topological order. Then (6.24) is applied to obtain arc flows for each destination.

This yields one of the possible (extremal) outcomes of the deterministic model for route choice (6.19) and (6.20).

1.7 Extension to Shortest Hyperpaths

In principle, the computation of shortest hypertrees requires applying to every hyperarc ă ∈ H and the following revised version of the Bellman update, in addition of applying (6.29) to every arc a ∈ A _m , until no further cost improvement is possible:

$$ w_{{{\breve{a}}^{ - } dmg}} \leftarrow {Min}\left( {w_{{{\breve{a}}^{ - } dmg}},w_{{{\breve{a}} dmg}}^{{}} } \right). $$

(6.30)

However, the extension of the proposed Dijkstra algorithm to strategies is not trivial and some issues arise:

• to calculate in (6.30) the value of w _ădmg through (6.26), the algorithm has to wait for all the heads of hyperarc ă to be extracted (indeed, all such nodes must have a cost value and the head cost of the branch included in the backward star of the node currently visited is not enough);

• the resulting node cost of the hyperarc tail can be lower than those of (some of) its heads (such as when arcs with negative cost are considered), which prejudices the label setting approach of the Dijkstra algorithm (although nodes are extracted from the list in order of cost, a node with a lower cost will be extracted after a node with a higher cost, so that a node already extracted can be further optimized);

• this implies that the optimal strategy can involve so-called absorbing cycles (e.g., an unlucky boarding passenger unable to seat, who then alights at next stop and walks back to wait again for the line at the previous stop, thus gaining another chance of seating on-board);

• each further cycle would have a smaller probability to happen, but a label correcting approach (i.e., the node cost can be modified even if the node has been already extracted form the list, thus requiring its insertion again—so, nodes can be extracted more than once) would induce infinite updates; shortest hyperpath would then require to solve the problem as a system of nonlinear (the minimum function) equations.

However, a hyperpath is by definition an acyclic sub-graph; to avoid this kind of paradoxes requires some additional rules in the search. For example, a label setting approach (i.e., the cost is not updated if the node has already been extracted) can be forced, unless the node is a diversion (to allow waiting for hyperarcs to be processed), or unless the correction derives from the successor of the node. This allows to eliminate absorbing cycles (if no cycle of diversion nodes exists), which can be justified with a risk-adverse behaviour: passengers never take twice chances, even if on average this maybe convenient, because it can result sometime in a higher cost. A complete analysis of this heuristic goes beyond the scope of this short note, whose aim was rather to raise some concern on the implementation.

1.8 Uncongested Assignment Versus User Equilibrium

If no congestion phenomena are considered to be relevant, then transit assignment reduces to a simple chain of sub-models: a flow-independent performance model, a route choice model, a flow propagation model. This can be solved by computing the following sequence of equations that for given arc performances yield arc flows:

$$ {\text{with explicit path enumeration}}{:}\;{ }\left( {{6}.{2}} \right) \to \left( {{6}.{3}} \right) \to \left( {{6}.{13}} \right) \to \left( {{6}.{6}} \right) \to \left( {{6}.{5}} \right),{\text{ or }} $$

(6.31)

$$ {\text{with implicit path enumeration}}{:}\;{ }\left( {{6}.{2}} \right) \to \left( {{6}.{15}} \right) \to \left( {{6}.{18}} \right) \to \left( {{6}.{16}} \right) \to \left( {{6}.{22}} \right) \to \left( {{6}.{24}} \right) \to \left( {{6}.{23}} \right){ }. $$

(6.32)

In presence of congestion or discomfort, we have to replace (6.2) with proper arc performance functions:

$$ c_{ag} = c_{ag} \left( {q_{{bg^{\prime}}} ,\quad \forall b \in A,\;\;\forall g^{\prime} \in G} \right). $$

(6.33)

Using (6.33) and (6.5) in (6.3) as follows:

$$ c_{kg} = c_{kg}^{na} + \sum\limits_{a \in A} {c_{ag} \left( {\sum\limits_{h \in K} {q_{{hg^{\prime}}}} \cdot\Delta _{bh} ,\quad \forall b \in A,\;\;\forall g^{\prime} \in G} \right)} \cdot\Delta _{ak} , $$

(6.34)

yields the so-called supply function:

$$ c_{kg}^{{}} = c_{kg}^{{}} \left( {q_{{hg^{\prime}}}^{{}} ,\quad \forall h \in K,\;\;\forall g^{\prime} \in G} \right). $$

(6.35)

The relation represented by (6.33) closes an ‘internal’ loop in the model, because the arc flows provided by the uncongested assignment will change the arc costs, thus requiring to update route choice, and so on.

In case of recurrent congestion phenomena (discomfort and delay occurring every day at the same time), the most common paradigm adopted in the simulation of transit networks is the well-known User Equilibrium.

By definition, a User Equilibrium on a transit network is achieved when no passenger finds convenient to change route (as mentioned earlier, a route can be a single path connecting the O–D pair defining the trip of the passenger, or a hyperpath, in case of strategy modelling). This implies assuming that passengers are rational decision-makers, i.e., they minimize their (perceived) cost.

The introduction of arc performance functions that are able to reproduce the relevant congestion phenomena on transit networks makes the assignment problem more complex than the case of road networks. This is due to the non-separability of these phenomena: the cost of an arc depends on the flows of other adjacent arcs, and not only on the flow of the arc itself. Moreover, this dependency is in general not symmetric nor monotonic. The only noticeable exception is the case of overcrowding on-board discomfort.

In essence, the existence of an equilibrium is guaranteed (sufficient condition) by the continuity of the arc cost function, while the uniqueness of the equilibrium is guaranteed (sufficient condition) by the positive definiteness of the arc cost function Jacobian (in strict form, for deterministic choice models). As mentioned above, the latter does not hold in general; however, in standard situations, the non-uniqueness does not typically occur but counterexamples can be made.

In the particular case of separable (and monotone) arc cost functions, the equilibrium assignment can be formalized and solved through an (convex) optimization model where the objective function is the sum of cost integrals (see Sect. 7.2.3). Otherwise, more complex formulations are required, such as variational inequalities or fixed-point problems. The framework that follows is based on the latter paradigm.

In the two figures below, white boxes indicate variables, grey boxes indicate functions, green boxes indicate input, and red boxes denote post-evaluation.

In the case of transit assignment, the cost functions will also provide the hyperarc diversion probabilities, which are essential in strategic route choice models, through the computation of line probabilities and fail-to-board or fail-to-sit probabilities (see Chap. 7).

The above schemes describe how the outlined variables and their structural relations can be organized in a concatenation of models to yield different kinds of fixed-point problems that can be introduced to formulate transit equilibrium assignment.

In general, a fixed-point problem finds a point x in a given subset X of a multidimensional space. This point x is mapped by the fixed-point function ƒ(x) ∈ X on the point itself:

$$ {\text{find }}\mathbf{x} \in X{:}\;\mathbf{x} = f\left( \mathbf{x} \right). $$

(6.36)

In case of a one-to-many mapping ƒ(x) ⊆ X, we shall substitute in the problem defined by Eq. (6.36) the equality symbol ‘=’ with the belonging symbol ‘∈’; deterministic choice models are the examples of this modified instance.

In transport assignment, the space of search can be that of arc flows, arc costs, route flows or route costs, while the mapping results from the chain of models in the above schema that starting from the chosen fixed-point variable with a full round brings back to it. Figures 6.2 and 6.3 present in particular the case where x is the vector of arc flows, which is the typical modelling choice.

Fig. 6.2

Fixed-point formulation of equilibrium models on multimodal networks with explicit path enumeration

Fig. 6.3

Fixed-point formulation of equilibrium models on multimodal networks with implicit path enumeration. Path variables are obtained a posteriori for evaluation purposes

Fixed-point problems constitute thus a natural framework for equilibrium assignment. However, they present a drawback with respect to more classical optimization models: the lack of rapidly convergent algorithms prevents precise calculations of the equilibrium solutions which may be required when comparing scenarios.

In assignment models, the simple iteration of the fixed-point function does not converge in general (it is not a so-called contraction). Therefore, to solve the fixed-point problem, we typically use the method of successive averages (MSA), where at each iteration n = 1, 2, … the new equilibrium iterate is obtained as a convex combination between the current equilibrium flows and the application (to them) of the fixed-point function; in case of arc flows, the latter is also called Network Loading Map and the resulting flows are denoted q ^nlm _ag :

$$ q_{ag} \leftarrow q_{ag} + \frac{1}{n} \cdot \left( {q_{ag}^{nlm} - q_{ag}} \right). $$

(6.37)

The MSA (see Sect. 4.2) is presented above in its simpler form, where the coefficient of the convex combination is the inverse 1/n of the iteration number. This actually provides the average of all the flows resulting in the network loading maps obtained so far; thus, slow convergence is somehow intrinsic.

1.9 Fixed Versus Elastic Demand

Elastic demand is in general the dependence of O–D demand (flow) matrices from O–D skim (cost) matrices. This may involve different levels (stages) of the demand model (see Sect. 4.2.3.2), from generation rate, to distribution pattern and/or modal split (including departure time choice in case of dynamic models).

Elastic demand introduces a second ‘external’ loop in the model scheme of Figs. 6.2 and 6.3. But this can also be regarded as a fork and join, without the need of formulating a bi-level problem. Nevertheless, for traditional reasons, the (few) commercial software that allows for elastic demand modelling adopt a two-step iterative approach, solving the internal loop before updating the external loop; typically, the external loop is not solved with a high precision and no averaging process such as the MSA is applied to it.

1.10 User Equilibrium Versus Day-to-Day Evolution

As shown in the previous section, from an algorithmic point of view the computation of a user equilibrium consists of an iterative process. Each iteration corresponds to a single assignment on the transport network, which represents the interaction of supply and demand through route choice, flow propagation and performance functions. This process resembles also the chronological evolution of the system from non-equilibrium to a possible equilibrium state, with the single assignment time frame being one day; indeed, a day is the typical temporal horizon considered in cyclic travel decisions, as well as in most human activities. Hence, one fixed-point iteration can be regarded as a day and everything that happens in this time frame as within-day. The internal loop of the user equilibrium model therefore corresponds to a day-to-day dynamic process of route choice, while the external loop corresponds to longer term travel choices (e.g., mode, destination and trip frequency); however, if the fork and joint approach is considered in the analysis of elastic demand, then also these choices are seen as part of day-to-day dynamics.

While user equilibrium models define a priori the relevant state of the system as that in which average flows and costs (demand and supply) are mutually consistent, inter-period (or day-to-day) dynamic assignment models simulate the evolution of the system over a sequence of similar periods (days), and its possible convergence over time to a stable condition. Under some rather mild assumptions, the equilibrium configurations can be interpreted as attractors of the dynamic system. This allows us to analyse the stability of equilibria and provides a statistical description of transient states. Although the mathematical analysis of dynamic systems is out of the scope of this book, it must be clear that the existence of a unique equilibrium is just one of the possible cases; the day-to-day process does not necessarily lead to a steady state (static or within-day dynamic) and may oscillate among different equilibria or even show a chaotic pattern.

Each user may update the route choice made for the current day based on the information gathered on the route costs during the previous trips. Possibly, all previous experiences contribute to the knowledge of the network developed by the user, although the learning process typically privileges the relevance of latest trips. In this evolutionary interpretation of equilibrium, in general users would experience every day a different cost on the same route, because congestion may induce other users to change their route or because random events may affect loads and performances; whether the experienced costs or other information sources induce a considerable change in the expectations that motivated the current choice, then a user will consider changing route.

Thus, day-to-day dynamic assignment models require the explicit representation of two phenomena:

• users’ learning and forecasting mechanisms for utility updating; that is, how present route choices are influenced by experience on previous transport costs (memory);

• users’ choice updating behaviour; that is, how present route choices are influenced by the choices made on previous days (habit).

The utility updating model describes in which way expected (or predicted) utilities on day n are influenced by experienced utilities on previous days (and possibly by other sources of information). In principle, a disaggregate approach can describe the updating of the individual perceived utilities of each single user (agent); otherwise, the utility updating can be applied to their averages (systematic utilities) considered by several users (demand component), or directly to the generalized costs, which are the main drivers of route choice.

In the following, it is assumed that referring to the generic path k ∈ K _odm utilized by the travellers of class g ∈ G in day n, the expected costs $\tilde{c}_{kg}^{n + 1}$ of next day n + 1 are a convex combination (exponential filter) of the actual costs $c_{kg}^{n}$ incurred in day n resulting from the supply function given in Eq. (6.35) based on the actual flows $q_{kg}^{n}$ and the current expected costs ${\tilde{c}}_{kg}^{n}$:

$$ c_{kg}^{n} = c_{kg} \left( {q_{{hg^{\prime}}}^{n} ,\quad \forall h \in K,\;\;\forall g^{\prime} \in G} \right) , $$

(6.38)

$$ \tilde{c}_{kg}^{n + 1} = {\upalpha }_{g}^{learn} \cdot c_{kg}^{n} + \left( {1 - {\upalpha }_{g}^{learn} } \right) \cdot \tilde{c}_{kg}^{n} , $$

(6.39)

where the average weight $\upalpha_{g}^{learn} \in \left( {0,1} \right]$ attributed by the users of class g to the actual costs is usually assumed to be independent of the day. Note that given the structural linear relationship given by Eq. (6.3) between arc and (additive) path costs, the exponential filter can also be applied to arc costs; this would also have a physical interpretation, since during each trip on the network a traveller gathers experience on arc costs that are part of several paths.

The choice updating model describes in which way route choices on day n + 1 are influenced by choices made on previous days. In the following, it is assumed that each day some users repeat the choices made in the previous day, and others reconsider (although do not necessarily change) their choices. Then, the flows $q_{kg}^{n + 1}$ of next day n + 1 are a convex combination (exponential filter) of the flows ${\tilde{q}}_{kg}^{n + 1}$ that would result from the route choice model (6.13) based on the expected costs ${\tilde{c}}_{kg}^{n + 1}$ of next day n + 1 and the current flows $q_{kg}^{n}$:

$$ \tilde{q}_{kg}^{n + 1} = p_{kg} \left( {\tilde{c}_{hg}^{n + 1} ,\quad \forall h \in K_{odm} } \right) \cdot d_{odm} , $$

(6.40)

$$ q_{kg}^{n + 1} = \upalpha_{g}^{choup} \cdot \tilde{q}_{kg}^{n + 1} + \left( {1 - \upalpha_{g}^{choup} } \right) \cdot q_{kg}^{n} , $$

(6.41)

where the probability $\upalpha_{g}^{choup} \in \left( {0,1} \right]$ that a user of glass g reconsiders the choice made on the previous day is usually assumed to be independent of the day, while the complement 1 − α _g is the probability that the choice of the previous day is repeated. In some models, the choice updating is neglected assuming $\upalpha_{g}^{choup} = 1$.

Under this evolutionary interpretation of the equilibrium model, the main system variables are both the costs (utilities) and the flows (choice probabilities), which can be summarized in a state vector x = (c _KG , q _KG ), as in Fig. 6.4.

Fig. 6.4

Iterative flow propagation/congestion (within-day-dynamic) and cost learning/route choice updating process (day-to-day dynamic)

The within-day dynamic consists of a flow propagation procedure plus a new computation of performances; these may be possibly calculated at once (see 6.Dynamic Network Loading in Sect. 6.4). During the day, travellers execute their trip and accumulate experience concerning generalized costs.

Then, day-to-day dynamic takes place. The learning process filters the latest information about the network cost pattern gathered during the last day with the experience accumulated during all previous trips, updating the latter. The next day, the travellers can update their route choice on this basis in order to improve their objectives. But only a portion of them will actually reconsider the previous choice, probabilistically; the actual path flows that will load the network follow accordingly.

As travellers increase their experience with the system, their mental map extends and their expectations reflect more closely to the actual network performance. But a major issue in the application of the cost learning filter regards the update of path costs that have not been utilized by travellers in the previous day. In theory, only the cost of the utilized path should be actually revised by each single traveller. Instead, it is common practice to update the cost of all paths, independently from the fact that they have been used or not. To justify this approach, we can assume some form of collective awareness where information is shared among users; this is not far from reality in a changing world of social networks and travel information based on crowd sourcing. This is more credible in the context of probabilistic models where each path available to a demand component is travelled in a given day by at least a small proportion of users.

Clearly, this assumption accelerates the day-to-day process towards a possible equilibrium. If instead travel demand is represented through individual agents (see Sect. 6.5) with their own memory (in contrast to the collective memory of the above schema), the proposed process (possibly) leading towards equilibrium (which involves learning, choosing and congestion) is slower and must be guided necessarily by random perturbation of expected costs for each simulated day, as otherwise there is the risk of having individuals trapped on bad paths because of wrong estimation of their available alternatives.

1.11 Path-Based Versus Arc-Based

Similar to route choice and flow propagation, from a topological point of view, there are two main kinds of assignment models: path-based and arc-based.

In the first case, the relevant routes are explicitly enumerated; they can be identified in advance or generated during the assignment process (column generation). The route cost can include non-additive terms.

In the second case, the arc conditional probabilities result from a sequential model with implicit enumeration of routes, where users directed towards a given destination are recursively split among the arcs of the node forward star. Only additive cost structures are allowed.

Looking at route choices, path-based models are the most natural approach and are also richer in terms of modelling opportunities. In this case, for example, sophisticated stochastic models can be easily formulated using random utility theory, including correlation among alternatives (e.g., Probit, Cross Nested Logit, C-Logit). Moreover, route costs do not have to be necessarily additive with respect to arc cost, thus allowing to evaluate fancy fares structures and nonlinear disutilities (see Sect. 4.5.2).

However, path-based models usually require to preliminary identify and explicitly enumerate all the relevant route alternatives. Although on transit networks the number of good alternatives is definitely less than those emerging (due to congestion and grid topology) on an urban road network, this task may be cumbersome in terms of computation and hard in terms of modelling. Actually, explicit route enumeration requires a specific selection model, since the number of acyclic paths (and even more, hyperpaths) on a transport network is finite but can be extremely large, so much to make the problem with exhaustive enumeration practically unsolvable.

Column generation during equilibrium assignment (i.e., build up and store new paths at each iteration) is actually available only for deterministic models (in a stochastic framework the process would hardly converge) and provides a reduced set of used paths with respect to the whole set of possible equilibrium paths. Indeed, it is well known that the solution of deterministic equilibrium may be unique (under monotonicity conditions on the arc performance function) in terms of arc flows, but it is not in general unique in terms of path flows. Because equilibrium solutions in terms of paths obtained through column generation are rather poor, they are not suitable for post-processing procedures, such as O–D matrix estimation from traffic counts and critical link analysis (i.e., to identify all path flows using a given link).

Arc-based models are more robust with respect to these issues and are therefore often chosen for the implementation of commercial software. Moreover, it is always possible to retrieve a practical set of used paths starting from the arc conditional probabilities, using Eqs. (6.21) and (6.6), for example not considering paths whose probability is below a certain threshold. Finally, when considering strategies, arc-based models are almost a necessity.

1.12 Deterministic Versus Stochastic Route Choice

From a behavioural point of view, there are two main kinds of route choice models: deterministic and stochastic (or probabilistic). More details about route choice models are provided in Sect. 4.5; the purpose of this section is then to highlight some issues related to the assignment model.

Deterministic models assume homogeneity of attribute preferences for users of the same class and perfect information, i.e., passengers have a good knowledge of the network performance pattern (travel costs and speeds) in space and time for the current-day type. In this case, the rationality of the decision maker brings to the choice of minimum-cost alternatives.

The alternatives are routes connecting an O–D pair, in case of path-based models, or arcs exiting from a node, in case of arc-based models.

The most commonly applied paradigm for stochastic models is random utility theory, where it is assumed that users are rational decision-makers who associate a utility to each travel alternative of a (finite) choice set and choose the best among them. The modeller is not able to evaluate exactly these utilities for each user, due to several factors, among which:

• heterogeneity of preferences among users of a same class with respect to the same attributes of alternatives;

• subjective errors in the perception of objective attributes by users (incomplete information);

• measure errors in the evaluation of real attributes by the modeller.

Then, the modeller can represent the utility of these alternatives as a multivariate random variable with a joint distribution (if correlations among alternatives are relevant). As a result, it is only possible to calculate the probability that each alternative has to be chosen, i.e., to have the highest utility. If the variance of random utilities is null, the model reduces to the case of deterministic behaviour with perfectly informed users who choose (the) best alternatives.

Despite many years of research about stochastic assignment models, also for transit assignment, the fact is that still most of the methods implemented in commercial software and actually used in practice consider a deterministic behaviour. Clearly, stochastic models are much more flexible and realistic in reproducing passenger flow patterns. Nonetheless, advantages of deterministic model are given as follows:

• easier to understand from a theoretical point of view (not from the mathematical one);

• their results are easier to interpret and analyse;

• have no behavioural parameter to be calibrated; and

• are more reliable and robust from a computational point of view.

For these reasons, if the actual aim of the modeller is to analyse the sensitivity to design variables in a project and not to reproduce reality, deterministic models can represent a valid opportunity.

Another reason for opting to deterministic models is that the stochastic models which are able to suitably reproduce the correlations (e.g., due to path overlapping) among alternatives are not yet robust enough for scenario comparisons; in particular, the Probit model requires too many Monte carlo iterations of the main assignment loop to achieve a reasonable stability.

However, we shall be aware that deterministic models tend to transfer the motivation for a plurality of used paths serving a same O–D pair from behaviour heterogeneity in route choice to congestion.

Fig. 6.5

Probability density function of the Erlang headway distribution for different values of n ranging from 1 to 100 and f = 1/30. For n → ∞ the impulse function at h = 1/f = 30 is obtained

1.13 Static Versus Dynamic Assignment

Static models are based on the following assumptions of stationarity: the network can be described with constant flows and performances during the assignment period. This requires that travel demand as well as all supply features is constant for a sufficient period of time and that the network works in under-saturated conditions, i.e., no permanent queue is observed. Thus, queues at transit stops can be suitably modelled in a static framework only if each waiting passenger is able to board the next-arriving vehicle.

In dynamic models, the fact that travelling takes time and that network elements have a capacity is explicitly considered, not merely as a component of disutility. The following phenomena can be modelled:

• the route costs and the corresponding choices refer to specific departure times and shall be computed considering the concatenation of travel times, i.e., each arc cost shall be evaluated at the instant when a passenger following that route enters it (dynamic route choice);

• passenger flows move on the network consistently with travel times (dynamic propagation);

• exit flows on network elements satisfy the presence of capacity constraints (queues);

• entry flows on network elements satisfy the presence of occupancy constraints (spillback).

Five ways of incorporating dynamic aspects in transit assignment can be identified:

• space-time network models, where daytime is built-in the topological structure of a diachronic graph (see Sect. 6.3);

• quasi-dynamic models, where a layer sequence of static models is defined, each referred to a time interval, to reproduce some dynamic phenomena, such as queuing;

• macroscopic models, where passengers and vehicles are represented as a (semi) continuous fluid characterized by temporal profiles (see Sect. 6.4);

• microscopic models, where individual passengers and vehicles are represented as discrete particles;

• mesoscopic models, where in terms of travel behaviour passengers and vehicles are represented as individual agents or packets of agents, and moved accordingly on the network, while their interaction (congestion and travel times) is reproduced through aggregated traffic models (see Sect. 6.5.4).

Space-time network models consider the concatenation of dynamic route choice but adopt a graph-based representation of flow propagation, with no possibility of reproducing the effects of passenger congestion on run delays (dwell times) in a consistent way. Moreover, some limitations arise in the simulation of passenger queues at stops and their effects on travel times; for example, FIFO queues cannot be reproduced and only mingling is possible.

Quasi-dynamic models introduce a chronological sequence of static layers each representing a fairly long-time interval. Usually, this time discretization is such that passengers complete a relevant portion of their trip within a same interval (e.g., 15 min). The concatenation of times is neglected in the route choice, by assuming instantaneous route costs that are computed separately for each static layer; this holds true also for the dynamic flow propagation on the network as travel demand is loaded from origins to destinations during the same layer, without considering that the movement of passengers takes time. However, a proper congestion model can be adopted which allows for explicit reproduction of queues at stops, and the extra passengers who are not able to board during the current time interval due to capacity constraints can be shifted to the next temporal layer as additional demand components which behave according to current costs of the new layer.

Macro-, micro- and meso-models allow the simulation of all dynamic phenomena (dynamic route choice, dynamic propagation, queues and spillback).

1.14 Simulation-Based Versus Analytical Models

Public transport systems involve lots of complex relations among variables, many of which can be suitably described as random outcomes of erratic events that may change significantly from day-to-day (e.g., the actual number of passengers waiting at the stop, the actual arrival time of a vehicle and the actual travel time of a run). Most of the aspects regarding passenger information and service congestion that affect route choice on transit networks (see Chap. 7) are highly dependent on these unpredictable phenomena.

Random events involve both demand and supply. On the demand side, individual trip decisions are taken each day regarding the actual departure time or route choice. On the supply side, actual travel times of line vehicles are affected by road traffic and driver behaviour. Moreover, dwell times of vehicles at stops and queuing times of passengers at stops depend on the loads of passengers boarding, alighting and riding each line run (congestion), while the propagation of flows along passenger routes depend on the travel times on the transit network. The strategic behaviour of passengers at stops may amplify the effect of random events because in reaction en-route decisions are taken which further divert flows. On this basis, travel times and passenger flows become all correlated random variables.

A major distinction among the available approaches to transit assignment can then be made between:

• analytical formulations, where model results yield directly the expected values of the output variables (loads and performances),

• simulation tools, where model results yield one possible outcome of the output variables, so that (in theory) several repetitions of the model are necessary to obtain a stable average of each variable and (more interestingly) the shape of its distribution.

Simulation-based models for within-day transit assignment are highly flexible and more suitable to reproduce all such complex-correlated phenomena. This comes at the price of unstable results, which can be a serious drawback when the final aim is that of comparing design scenarios. However, this disadvantage may be alleviated if each within-day simulation is considered in the context of a day-to-day evolution framework (see Sect. 6.1.10), as this gives some justifications to the lack of (enough) repetitions.

However, also the design based on precise results in terms of expected values presents some limitations. For example, a robust project should be taken into consideration the random distribution of the output, rather than only the average values of the outcomes, so as to guarantee good performances in the majority of cases. In this respect, simulation-based models can effectively support robust design with the calculation of results in terms of percentiles based on the a priori definition of safety margins against unfavourable cases.

There are two main contexts of application for simulation-based models:

• in real-time applications, many of the variables can be retrieved directly from the field (e.g., the current estimation and forecast of vehicles arrival provided by an AVL system);

• in offline applications, the same information must instead be elaborated on the basis of synthetic values extracted from random variables with known distributions.

Different levels of aggregation are possible in simulation-based transit assignment and some models actually make use of relations among average variables, such as travel times and flows, instead of looking at individual passengers and vehicles (mesoscopic models). If individual passengers are simulated then also their preferences can be synthesized and the user classes are substituted by distribution of parameters.

Simulation models can really make a difference in reproducing the effect of information about random events and the reaction of travellers. We can define and distinguish the following types of events:

• minor events are perturbations of the cost pattern in which passengers incur while travelling without anticipated knowledge, whose relevance or frequency is not sufficient to induce a strategic or rerouting behaviour;

• recurrent events are outcomes of systematic phenomena on which passengers have expectations and may be informed at some point en-route, thus allowing a strategic behaviour;

• major events are relatively rare but serious accidents on which passengers do not have expectations because their frequency is low, but whose relevant impact may induce rerouting.

Minor events affect the distribution of the corresponding arc costs which are perceived by users. But without prior information, users will choose the best path on average, possibly associating an additional risk-adverse cost to variances. Analytical formulations, which are based directly on the averages, are still appropriate because the expected value of a sum of random variables (path cost) is the sum of the expected values (arc costs), and the same is true for variance.

Recurrent events induce a strategic behaviour where the cost and the probability of local alternatives depend recursively on the expected costs of the diversions possibly encountered later during the trip towards the destination (see Sect. 7.1). Only if the events are independent and are informed locally, then analytical formulations through the introduction of hyperarcs are actually suitable to reproduce average phenomena.

If the information is anticipated (which today is possible through mobile communication) and/or the random events are strongly correlated, then the simulation approach becomes unavoidable to reproduce the reaction of passenger in terms of en-trip route choices. Decision points are not anymore fixed (e.g., stops) as in the classical strategy representation based on hyperarcs, because the information can reach the passenger virtually anywhere and at any time. Upon each further injection of information, the passenger will reconsider all available alternatives to reach his/her destination and possibly update his/her route choice.

This usually requires the recomputation of attributes (in primis, travel and wait times) for a predetermined choice set of paths from that point to the destination. However, this practical approach (paths can be stored in computer memory) is not fully satisfactory because it does not take into account that the alternatives should be strategies with recursive diversions and not simple paths: this way only the first (current) diversion is properly considered. On the other hand, the explicit selection and storage of hyperpaths is prohibitive.

A possible alternative to path storage is the sequential route choice (see Sects. 6.1.4 and 6.1.5), where decisions are reconsidered locally by hypothesis; hyperpaths do not have to be explicitly enumerated but instead the expected cost of optimal strategies from nodes to destination is constantly updated. In this case, also the knowledge possibly acquired in a day-to-day learning process is stratified on node variables (expected cost to destination) and not on paths, by considering the cost actually suffered in the last within-day simulation from that node to the destination.

Major events and rerouting can be reproduced, not only with simulation models, but also through analytical models with a rolling horizon approach. This means that the analytical model is restarted every say 5 min to provide a prediction for the next say 60 min, by considering as a ‘warm’ initial state the result of the previous simulation; each iteration yields possibly different results from the previous one because new information and events are included in the simulation, affecting both supply characteristics and passenger behaviour.

1.15 Reference Notes and Concluding Remarks

The introduction of hyperarcs and hyperpaths for the representation of strategies on transit networks is due to work of Gallo et al. (1993).

A detailed presentation of stochastic (and deterministic) equilibrium models based on fixed-point problems for multiclass assignment on multimodal networks with elastic demand is provided in Cantarella (1997). With particular reference to transit networks, Nielsen (2000) uses a type of probit model to represent stochastic route choice.

Sequential route choice models have been proposed by many authors, among which Gentile and Papola (2006), who provide a general theoretical framework and several solution algorithms. Its consistent formalization with respect to multimodal transport networks and strategies, with the specific role of hyperarc diversion probabilities, can be considered an original contribution of this book.

Day-to-day dynamic processes in transport modelling were first proposed by Cascetta and Cantarella (1995) and by Watling (1999) in the framework of car assignment to road networks.

2 Frequency-Based Assignment on Transit Static Networks

• Guido Gentile &
• Michael Florian 

In this section, frequency-based (or headway based) models for static assignment on transit networks are presented in their basic version, without involving strategic behaviour of passengers with respect to common lines and information or congestion phenomena on the supply side, which will be analysed in Chap. 7.

Although the public transport service is organized with runs for each transit line and is thus actually available at stops only at discrete times, in frequency-based models the basic representation of supply is continuous (like that of cars on a road network) and the flow of vehicles can be seen as a moving walkway. The main issue is then the representation of the passenger wait times required at stops to access the available transit lines, which depend on the vehicle headways.

In this framework, the service is perceived by passengers in terms of probabilistic departure events of lines from the stops, because the timetable is not relevant in the route choice due to high frequency or low regularity. The line headway at any stop can be then represented as a random variable with given statistical distribution, and the frequency is defined as the inverse of its expected value.

The main characteristic of frequency-based models is thus their capability of reproducing discontinuous transit services by means of a continuous network representation. This implies to identify waiting as a separate trip phase through specific arcs. To this end it is necessary, on one side to calculate the expected wait time corresponding to a given headway distribution, on the other side to build up a proper topological representation of the transit graph.

2.1 Headway Distributions and Wait Times

Frequency-based models were originally based on the assumption that passengers arrive randomly at stops and service headways are deterministic (regular) and independent. In this case, the wait time has a uniform distribution equal to the frequency from zero to the inverse of the frequency (i.e., the given headway, which is also the maximum wait time); the expected wait time is simply equal to one half of the frequency inverse. However, these assumptions are inconsistent with statistical analysis of real-world data since constant headways can be obtained only under perfect service regularity (see Sect. 7.4).

On the other hand, instead of evenly spaced headways, one can consider the case where transit service is completely unpredictable (irregular) and can thus be described as a Poisson arrival process of rare events. This assumption results in a (negative) exponential distribution of the headways and of the wait times, which implies the ‘memory less’ property: the elapsed wait time gives no further indication about the remaining wait time (the conditional distribution of an exponential function is indeed that same exponential function). The expected wait time is equal to the inverse of the frequency; it is thus twice as long than the case with deterministic headways. This shows the relevance of the assumption regarding headway distributions.

In frequency-based assignment, the headway distribution is typically a characteristic of the whole line; but to represent service perturbation along the line (e.g., bouncing), it should be modelled as stop specific; the AVL systems today allow for such a more detailed input (see Sect. 5.1.2). In the following, we refer in general to a service headway h of a given line at a given stop during a given interval (thus the indices ℓst are omitted).

The headway is modelled as a random variable with an independent probabilistic distribution, i.e., a density function φ^h(h). As mentioned earlier, the inverse of its expected value f = 1/E(h) is called the frequency, which is the main parameter of the headway distribution.

A flexible representation of service regularity can be obtained under the assumption that headways adhere to an Erlang distribution, which describes the sum of n independent Poisson processes:

$$ \upvarphi^{h} \left( h \right) = \left\{ {\begin{array}{*{20}l} {\frac{{Exp\left( { - n \cdot f \cdot h} \right) \cdot \left( {n \cdot f} \right)^{n} \cdot h^{n - 1} }}{{\left( {n - 1} \right)!}},} \hfill & {\text{if}} \; {h \ge 0} \hfill \\ { 0 ,} \hfill & {\text{otherwise}.} \hfill \\ \end{array} } \right. $$

(6.42)

This distribution (see Fig. 6.5) can bridge the gap between the two above extreme cases, by letting the parameter n vary from 1 (exponential—perfect uncertainty) to ∞ (deterministic—perfect regularity). Note that in the above formula f · n is the frequency of the n independent Poisson processes, while f is the frequency of vehicle departures from the stop.

The minimum of independent exponential random variables is also distributed exponentially with a frequency parameter that equals the sum of the random variable parameters. Therefore, the expected wait time for the first vehicle serving a set of attractive lines equals the inverse of the cumulative frequency.

To obtain the analogous result in case of common lines with deterministic headways, i.e., to obtain an expected wait time which is half the inverse of the cumulative frequency, would require that departures from the same stop of different lines are equally spaced and in that sense perfectly coordinated, which is in contrast to the assumption of independent headways. But this would be theoretically possible only in case of identical line headways. Perfect correlation is thus practically impossible and assuming the above wait time expression for common lines with deterministic headways is just an optimistic approximation.

This justifies a more detailed analysis of independent headways and resulting wait times for the case of common lines that is developed in Sect. 7.1. Instead, in the following, we address the case of just one line for general headway distributions.

2.1.1 Mathematical Derivation

Because the headway h is random, then also the wait time (for a given line at a given stop) is random. Assuming that passengers arrive uniformly distributed at the stop, the probability density function φ^w(t) of the wait time is related to the headway distribution through the formula:

$$ \upvarphi_{{}}^{w} \left( t \right) = f \cdot \bar{\Phi }_{{}}^{h} \left( t \right), $$

(6.43)

where, by definition, it is:

$$ \bar{\Phi }_{{}}^{h} \left( h \right) = 1 -\Phi _{{}}^{h} \left( h \right) = \int\limits_{h}^{{h_{{}}^{max} }} {{\upvarphi }_{{}}^{h} \left( h \right)} \cdot {d}h, $$

(6.44)

and h ^max is the maximum headway (it can be h ^max = ∞).

Proof

We now prove the validity of Eq. (6.43).

To this end, we shall first show that:

$$ f = \frac{1}{{\int\nolimits_{0}^{{h_{{}}^{max} }} {\bar{\Phi }_{{}}^{h} \left( h \right) \cdot {d}h} }}. $$

(6.45)

Differentiating by parts, it is:

$$ \bar{\Phi }^{h} \left( h \right) \cdot {d}h = {d}\left( {\bar{\Phi }^{h} \left( h \right) \cdot h} \right) - h \cdot {d}\bar{\Phi }^{h} \left( h \right). $$

(6.46)

The following 3 statements hold true:

$$ \begin{aligned} & \left[ {\bar{{\Phi}}^{h} \left( h \right) \cdot h} \right]_{0}^{{h^{max} }} = \bar{{\Phi }}_{{}}^{h} \left( {h_{{}}^{max} } \right) \cdot h_{{}}^{max} - \bar{\Phi }_{{}}^{h} \left( 0 \right) \cdot 0 = 0 \cdot h_{{}}^{max} - 1 \cdot 0 = 0 \\ & - h \cdot {d}\bar{\Phi }_{{}}^{h} \left( h \right) = - h \cdot {d}\left( {1 - {\Phi }_{{}}^{h} \left( h \right)} \right) = h \cdot {d}{\Phi }^{h} \left( h \right) = h \cdot {\upvarphi }_{{}}^{h} \left( h \right) \cdot {d}h \\ & \int\limits_{0}^{{h_{{}}^{max} }} {h \cdot {\upvarphi }_{{}}^{h} \left( h \right) \cdot {d}h} = E\left[ h \right]\,. \\ \end{aligned} $$

(6.47)

Based on (6.47), taking the integral of (6.46) on both sides between h = 0 and h = h ^max yields:

$$ \int\limits_{0}^{{h^{max} }} {\bar{\Phi }_{{}}^{h} \left( h \right) \cdot {d}h} = E\left[ h \right]. $$

(6.48)

Because by definition it is: f = 1/E(h), then Eq. (6.48) is equivalent to (6.45), which shows the relation between the frequency and the integral of the distribution function; this is actually a general property of non-negative random variables.

Now, the fact that the wait time is exactly equal to t occurs for some value of headway h not lower than t (otherwise the passenger cannot have waited that long), if the passenger arrives at the stop h − t time units (e.g., minutes) after the previous vehicle departure. Given that passenger arrivals at stops are uniformly distributed, each one of these possible events has a probability that is proportional to φ^h(h), through a constant, say α. Therefore, summing up these probabilities yields the (density) of probability that the wait time is equal to t:

$$ {\upvarphi }_{{}}^{w} \left( t \right) = {\upalpha } \cdot \int\limits_{t}^{{h_{{}}^{max} }} {{\upvarphi }_{{}}^{h} \left( h \right) \cdot {d}h} = {\upalpha } \cdot \bar{\Phi }_{{}}^{h} \left( t \right). $$

(6.49)

Like any probability density function, the integral of φ^w(t) over all possible wait times is 1:

$$ \int\limits_{0}^{{h_{{}}^{max} }} {{\upvarphi }_{{}}^{w} \left( t \right) \cdot {d}t} = 1. $$

(6.50)

Then, substituting the right-hand side of Eq. (6.49) into to the integrand of Eq. (6.50), based on Eq. (6.45) gives:

$$ {\upalpha } = \frac{1}{{\int\nolimits_{0}^{{h^{max} }} {\bar{\Phi}^{h} \left( h \right) \cdot {d}h} }} = f. $$

(6.51)

Finally, based on Eqs. (6.51), (6.49) gives Eq. (6.43), which proves the assertion. ♦

In the case of Erlang headway distributions, based on formula (6.43), the probability density function of the wait time is given as:

$$ \upvarphi_{{}}^{w} \left( t \right) = \left\{ {\begin{array}{*{20}l} {f \cdot Exp\left( { - n \cdot f \cdot t} \right) \cdot \sum\limits_{i = 0}^{n - 1} {\frac{{\left( {n \cdot f \cdot t} \right)^{i} }}{i!}} ,} \hfill & {\text{if}} \; {t \ge 0} \hfill \\ { 0 ,} \hfill & {\text{otherwise},} \hfill \\ \end{array} } \right. $$

(6.52)

while the probability of waiting for more than t is:

$$ \bar{\Phi }_{{}}^{w} \left( t \right) = \left\{ {\begin{array}{*{20}l} {Exp\left( { - n \cdot f \cdot t} \right) \cdot \sum\limits_{i = 0}^{n - 1} {\left( {1 - \frac{i}{n}} \right) \cdot \frac{{\left( {n \cdot f \cdot t} \right)^{i} }}{i!}} ,} \hfill & {\text{if}} \; {t \ge 0} \hfill \\ { 1 ,} \hfill & {\text{otherwise}.} \hfill \\ \end{array} } \right. $$

(6.53)

In case of deterministic headways, we obtain a uniform distribution of wait times:

$$ \upvarphi_{{}}^{w} \left( t \right) = \left\{ {\begin{array}{*{20}l} {f ,} \hfill & {\text{if}} \; { 0\le t \le \frac{1}{f}} \hfill \\ {0 ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right., $$

(6.54)

while the probability of waiting for more than t is:

$$ \bar{\Phi }_{{}}^{w} \left( t \right) = \left\{ {\begin{array}{*{20}l} {1 - f \cdot t,} \hfill & {\text{if}} \; { 0\le t \le \frac{1}{f}} \hfill \\ {0,} \hfill & {\text{if}} \; {t > \frac{1}{f}} \hfill \\ {1,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.. $$

(6.55)

Based on Eq. (6.52) with n = 1, for exponential headways (irregular service), the expected wait time is given as:

$$ t_{{}}^{wait} = \int\limits_{0}^{\infty } {{\upvarphi }_{{}}^{w} \left( t \right) \cdot t \cdot dt} = \frac{1}{f}. $$

(6.56)

Based on Eq. (6.54), for deterministic headways (regular service), the expected wait time is given as:

$$ t_{{}}^{wait} = \int\limits_{0}^{{\frac{1}{f}}} {{\upvarphi }^{w} \left( t \right) \cdot t \cdot dt} = \frac{0.5}{f}. $$

(6.57)

The general formula for the expected wait time, under the assumption of uniform passengers’ arrivals at stops depends only on the first and second moments of the headway distribution and not on its pdf:

$$ t_{{}}^{wait} = 0.5 \cdot \frac{{E\left( {h^{2} } \right)}}{E\left( h \right)}. $$

(6.58)

Proof

We now prove the validity of Eq. (6.58).

Assume that a sequence of n independent random headways is given, which represent time intervals between two consecutive carrier arrivals at a stop, each of duration h _j , with j = 1, …, n. Let passengers’ arrivals at the stop be uniformly distributed.

The probability p _j that a passenger arrives during interval j is proportional to the headway h _j :

$$ p_{j} = \frac{{h_{j} }}{{\sum\nolimits_{i = 1}^{n} {h_{i} } }}. $$

(6.59)

The expected value of the wait time t, conditional to the above event is given as:

$$ E\left( {t|j} \right) = 0.5 \cdot h_{j}. $$

(6.60)

Based on the law of total probability, the expected wait time is obtained from the conditional expectations as follows:

$$ E\left( t \right) = \sum\limits_{j = 1}^{n} {E\left( {t|j} \right) \cdot p_{j} }. $$

(6.61)

Using Eqs. (6.59) and (6.60) in Eq. (6.61), we obtain:

$$ E\left( t \right) = \sum\limits_{j = 1}^{n} {0.5 \cdot h_{j} \cdot \left( {\frac{{h_{j} }}{{\sum\nolimits_{i = 1}^{n} {h_{i} } }}} \right)} = 0.5 \cdot \frac{{\sum\nolimits_{j = 1}^{n} {h_{j}^{2} } }}{{\sum\nolimits_{j = 1}^{n} {h_{j} } }} = 0.5 \cdot \frac{{\frac{{\sum\nolimits_{j = 1}^{n} {h_{j}^{2} } }}{n}}}{{\frac{{\sum\nolimits_{j = 1}^{n} {h_{j} } }}{n}}} = 0.5 \cdot \frac{{E\left( {h^{2} } \right)}}{E\left( h \right)}, $$

(6.62)

which proves the assertion.♦

2.1.2 Service Irregularity and Variation Coefficient

From an engineering point of view, the effect of service irregularity on the expected wait time can be reproduced through the variation coefficient σ ≥ 0, introduced in Sect. 5.1.2.4. Because in general it is:

$$ {Var}\left( h \right) = E\left( {\left( {h - E\left( h \right)} \right)^{2} } \right) = E\left( {h^{2} } \right) + E\left( h \right)^{2} - 2 \cdot E\left( h \right) \cdot E\left( h \right) = E\left( {h^{2} } \right) - E\left( h \right)^{2} , $$

(6.63)

and considering the definition σ = SD(h)/E(h), it is:

$$ 1 + \sigma^{2} = 1 + \left( {\frac{{{SD}\left( h \right)}}{E\left( h \right)}} \right)^{2} = 1 + \frac{{{Var}\left( h \right)}}{{E\left( h \right)^{2} }} = \frac{{E\left( {h^{2} } \right)}}{{E\left( h \right)^{2} }}. $$

(6.64)

Then, Eq. (6.58) can be rewritten as:

$$ t^{wait} = \frac{0.5}{f} \cdot \left( {1 + \sigma^{2} } \right) = \frac{1}{f} \cdot \sigma^{2} + \frac{0.5}{f} \cdot \left( {1 - \sigma^{2} } \right). $$

(6.65)

Again, for deterministic headway, it is: σ = 0; while, for exponential headway it is: σ = 1. Therefore, the above equation can be seen as the convex combination between the exponential wait time and the deterministic wait time through the square of the variation coefficient.

In case of Erlang headway distribution, where it is E(h) = 1/f and E(h ²) = (1 + 1/n)/f ², based on Eq. (6.58), the expected wait time is given as:

$$ t^{wait} = \frac{0.5}{f} \cdot \left( {1 + \frac{1}{n}} \right). $$

(6.66)

A simple comparison between Eqs. (6.65) and (6.66) shows how the second parameter of the Erlang distribution is related to the headway variation coefficient: n = 1/σ ².

The variation coefficient of the headway is the most common measure of service (ir)regularity and can be easily obtained from Automated Vehicle Location (AVL) data. Common values for different levels of transit right-of-way are available from transit planning guides (e.g., TCQSM, TRB 2013).

2.2 The Static Transit Network

In this section, the network topology for the static transit assignment with frequency-based services is derived starting from the input data (see Sect. 5.1).

A transit trip consists in general of several phases:

• accessing a transit stop from the origin, usually by walking;

• waiting at that stop for a transit vehicle;

• boarding a dwelling vehicle;

• travelling (or running, or riding) in the vehicle (on board) through a sequence of stops;

• alighting the vehicle at another stop;

• (possibly) transferring between two transit stops, usually by walking;

• (possibly) repeat the phases from waiting to transferring a certain number of times;

• and finally, egress from a transit stop to the destination, usually by walking.

Each trip phase is (possibly) represented by a sequence of arcs with a same type (which specifies the nature of the trip phase) on the transit network; the latter is composed by:

• the pedestrian network, including centroids and connectors, as well as access, egress, walking and transfer links;

• the line network, with a sub-network for each transit line articulated in boarding, running, dwelling and alighting arcs plus the stops shared by several lines;

• intermodal arcs at each stop to connect the pedestrian network with the line network.

In the frequency-based approach, to represent the topology of the transit network, several layers of nodes are then introduced, among which we can distinguish:

• the base nodes N ^base = B, coinciding with the vertices B, including

• the origin nodes $O = \{ B_{z}^{orig} :\forall z \in Z\} \subseteq N^{base}$ (each zone z ∈ Z is associated with an origin vertex, denoted $B_{z}^{orig} \in B$), and

• the destination nodes $D = \{ B_{z}^{dest} :\forall z \in Z\} \subseteq N^{base}$ (each zone z ∈ Z is associated with a destination vertex, denoted $B_{z}^{dest} \in B$);

• the stop nodes N ^stop = S, coinciding with the stops S (each stop s ∈ S is associated with a stop vertex, denoted $B_{s}^{stop} \in B$);

• the line nodes N _ℓ, with one layer for each line ℓ ∈ L.

A further specialization of line nodes is required by different models to represent specific phenomena. The key feature of frequency-based models is the representation of waiting as a separate trip phase. To this aim, when building-up the graph supporting the transit assignment model, the stop must be exploded into a set of arcs and nodes. There are several ways to do so; the scheme depicted in Fig. 6.6 allows to track most passenger flows and to reproduce (later on) the relevant congestion phenomena. Two nodes for each stop of line ℓ ∈ L are then introduced, so as to represent consistently dwelling and running:

Fig. 6.6

Typical topology of the public transport network for frequency-based models. Arcs and nodes of the sub-network for this specific line are depicted in red

• the arrival node $N_{\ell s}^{arr} \in N_{\ell } ,\forall s \in S_{\ell } - S_{\ell }^{ - }$;

• the departure node $N_{\ell s}^{dep} \in N_{\ell } ,\forall s \in S_{\ell } - S_{\ell }^{ + }$.

A typical way of building-up the transport network is to introduce the following types of arcs:

• the pedestrian arcs A ^walk = E ^walk;

• the stop arcs $A^{stop} = \left\{ {\left( {B_{s}^{stop} ,s} \right):\forall s \in S\}\,\cup\,\{ \left( {s,B_{s}^{stop} } \right):\forall s \in S} \right\}$;

• the running arcs $A^{run} = \{ (N_{\ell s}^{dep} ,N_{{\ell s\left[ { + \ell } \right]}}^{arr} ):\forall S \in S_{\ell } - S_{\ell }^{ + } ,\forall \ell \in L\}$;

• the dwelling arcs $A^{dwell} = \left\{ {\left( {N_{\ell s}^{arr} ,N_{\ell s}^{dep} } \right):\forall s \in S_{\ell } - S_{\ell }^{ - } - S_{\ell }^{ + } ,\forall \ell \in L} \right\}$;

• the waiting arcs $A^{wait} = \left\{ {\left( {s,N_{\ell s}^{dep} } \right):\forall s \in S_{\ell } - S_{\ell }^{ + } ,\forall \ell \in L} \right\}$;

• the alighting arcs $A^{alight} = \left\{ {\left( {N_{\ell s}^{arr} ,s} \right):\forall s \in S_{\ell } - S_{\ell }^{ - } ,\forall \ell \in L} \right\}$.

It is useful to denote L _a  ∈ L the line associated with arc a ∈ A, if any. It is also useful to distinguish stops from base nodes, as this allows us to separate the line network (to which the stop node belongs) from the base network, which includes pedestrian and support arcs; the two may even derive from two separate data source. Two dummy stop (inter-modal) arcs are, in this case, introduced to connect each stop s ∈ S to the associated base node $B_{s}^{stop} \in B$ (e.g., the closest one), from the latter to the former and vice versa. Note that the arcs describing the walking paths internal to a station are pedestrian arcs, and not stop arcs.

In some model, the stops S are directly a subset of vertices B, i.e., $B_{s}^{stop} = s$, in which case it is: N ^stop ⊆ N ^base and no stop arc is required.

In some model, the pedestrian network is not explicitly introduced. The stops are directly part of the base nodes, while two stops are possibly connected by a connection arc that represents the shortest path on the hidden/implicit pedestrian network between the two stops.

Each zone centroid is connected to one or several base nodes (and vice versa) via particular pedestrian arcs that are called connectors, which represent the average access (egress) time/cost from a location in the zone to that node (or stop). But connectors should not be used to cross a zone. This rule can be enforced on the network by splitting the centroid of each zone z ∈ Z into two different nodes, the origin vertex $B_{z}^{orig} \in B$ and the destination vertex $B_{z}^{dest} \in B$.

Support arcs represent the transport infrastructures used by line vehicles (e.g., road, reserved lanes, rail and tram tracks) and are not used by passengers directly. They are introduced for aggregating inputs and outputs, for plotting on maps the itineraries of the lines, and possibly to reproduce the mixed traffic congestion deriving from the concomitant use of roads between public and private transport means.

The proposed configuration has one major limitation: it does not allow us to identify the flow of passengers transferring from one line to another line within the same stop, based solely on the arc volumes. This can be obviated by introducing, as in Fig. 6.7, the following additional arc type:

Fig. 6.7

Alternative topology with transfer arcs. Arcs and nodes of the sub-network for each one of the two lines are depicted in red and blue, respectively

• the transfer arcs $A^{tran} = \{ (N_{\ell s}^{arr} ,N_{{\ell^{\prime} s}}^{dep} ):\forall s \in S_{\ell } ,\forall \ell \in L,\forall {\ell^{\prime}} \in L - \ell:s \in S_{{\ell^{\prime}}} \}$.

Transfer arcs have the same time/cost of the corresponding arcs for waiting the same line at that stop. A small cost is associated with the stop arcs, so that direct transfers are convenient when alighting and boarding at the same stop. More articulated topologies of stops can be defined to consolidate alighting and boarding flows including transfers on one single arc, which may be useful (but not necessary) to reproduce congestion phenomena.

In the following, we will refer to the more classical set-up of Fig. 6.6.

2.3 Arcs Travel Times and Costs

Once the topology of the transport network is defined, the relevant performance attributes for each arc are to be specified, with particular reference to the factors yielding the generalized costs of Eq. (6.2) that are travel time, value of time and non-temporal cost. The time associated with the different types of trip phases is typically perceived differently by passengers of a given user class g ∈ G; it is then transformed into costs multiplying a base value of time $\upgamma_{g}^{vot}$ by different weights; for example, walking and waiting are usually perceived as considerably more costly than riding.

For pedestrian arcs, the walking time, obtained as the ratio between the length of the arc l _a and the walking speed $s_{a}^{walk}$ (introduced in Sect. 5.1.2), is multiplied by:

• the base value of time $\upgamma_{g}^{vot}$;

• a walking discomfort coefficient $\upgamma_{g}^{walk}$ which differs for each user class g ∈ G (for example, elderly people suffer a higher discomfort for walking with respect to young people).

Monetary costs are assumed null. Thus, we have the following:

$$ t_{a}^{{}} = \frac{{l_{a}^{{}} }}{{s_{a}^{walk} }},\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{walk} ,\quad c_{ag}^{nt} = 0,\quad \forall a \in A^{walk}. $$

(6.67a)

Pedestrian arcs is one of the few noticeable cases in transit assignment where it would make some sense distinguishing the travel time per user class; but this would complicate the data structure unworthily.

Stop arcs are dummy; therefore, we assume a null cost and time:

$$ t_{a}^{{}} = 0,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = 0,\quad \forall a \in A^{stop}. $$

(6.67b)

For alighting arcs, the alighting time $t_{\ell }^{alight}$ (introduced in Sect. 5.1.2) is multiplied by the base value of time; monetary costs are assumed null, but a positive non-temporal cost associated with transfers is usually introduced:

$$ t_{a}^{{}} = t_{\ell }^{alight} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = c_{g}^{tran} ,\quad \forall a = \left( {N_{\ell s}^{arr} ,s} \right) \in A^{alight}. $$

(6.67c)

The transfer cost for each user class g ∈ G may represents a bundle of disutility components related to alighting and transferring, not necessarily connected with a measurable delay:

• the psychological stress of alighting (e.g., being aware of the current station);

• the psychological stress of possibly changing line;

• the additional travel time variance induced by the transfer.

For running arcs, the travel time $t_{{_{\ell s} }}^{tran}$ of the line segment (introduced in Sect. 5.1.2) is multiplied by:

• the base value of time $\upgamma_{g}^{vot}$;

• the line discomfort coefficient $\upgamma_{g}^{vot}$ (introduced in Sect. 5.1.2);

• the crowding discomfort coefficient $\upgamma_{{_{\ell g} }}^{crowd}$ of the line segment s ∈ S of line ℓ ∈ L for user class g ∈ G that possibly depends on (separable) congestion through the (same) arc volume (as detailed in Sect. 7.2.1).

Monetary costs of the line segment are given by the kilometric fee $c_{{_{\ell s} }}^{kfee}$ (introduced in Sect. 5.1.2) that is multiplied by a possible fee multiplier $\upgamma_{g}^{mfee}$ for user class g ∈ G. Thus, we have the following:

$$ \begin{aligned}t_{a}^{{}} &= t_{\ell s}^{run} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{\ell g}^{line} \cdot {\upgamma}_{\ell sg}^{crowd} \left( {q_{a} } \right),\\ c_{ag}^{nt} &= c_{\ell s}^{kfee} \cdot l_{\ell s}^{{}} \cdot {\upgamma}_{g}^{{{{mfee}}}} ,\forall a = \left( {N_{\ell s}^{dep} ,N_{{\ell s_{{}}^{ + \ell } }}^{{{{arr}}}} } \right) \in A^{run}. \end{aligned} $$

(6.67d)

For dwelling arcs, the travel time $t_{\ell s}^{dwell}$ (introduced in Sect. 5.1.2) that possibly depends on (non-separable) congestion through the volumes of the alighting and waiting arcs (as detailed in Sect. 7.4.4) is multiplied by the base value of time $\upgamma_{g}^{vot}$. Monetary costs are null. Thus, we have the following:

$$ t_{a} = t_{\ell s}^{dwell} \left( {{\mathbf{q}}_{A} } \right),\quad {\upgamma}_{ag} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = 0,\quad \forall a = \left( {N_{\ell s}^{arr} ,N_{\ell s}^{dep} } \right) \in A^{dwell}. $$

(6.67e)

The cost of waiting arcs and transfer arcs derives mainly from the service discontinuity in time. The expected wait time $t_{\ell s}^{wait}$ of line ℓ ∈ L at stop s ∈ S depends on the headway distribution through (6.58) or (6.65) and possibly depends on (non-separable) congestion (effective frequency) through the volume of the next running arc (as detailed in Sect. 7.3.2). This time is multiplied by:

• the base value of time $\upgamma_{g}^{vot}$;

• the waiting discomfort coefficient $\upgamma_{g}^{wait}$ which differs for each user class g ∈ G;

• the stop discomfort coefficient $\upgamma_{sg}^{stop}$ (introduced in Sect. 5.1.2);

• the crowding discomfort coefficient $\upgamma_{sg}^{crowd}$ of user class g ∈ G at stop s ∈ S that possibly depends on (non-separable) congestion through the volume of the waiting arcs (as detailed in Sect. 7.2.1).

The fixed fare of the line is applied here as a boarding fee c ^kfee_ℓs (introduced in Sect. 5.1.2). Thus, we have the following:

$$ \begin{array}{*{20}l} {t_{a}^{{}} = t_{\ell s}^{wait} \left( {{\mathbf{q}}_{A} } \right),} \hfill & {\gamma_{ag}^{{}} = \gamma_{g}^{vot} \cdot \gamma_{g}^{wait} \cdot \gamma_{sg}^{stop} \cdot \gamma_{sg}^{crowd} \left( {{\mathbf{q}}_{A} } \right),} \hfill \\ {c_{ag}^{nt} = c_{\ell s}^{bfee} \cdot \gamma_{g}^{mfee} ,} \hfill & {\begin{array}{*{20}l} {\forall a = \left( {s,N_{\ell s}^{dep} } \right) \in A^{wait} } \hfill \\ {\forall a = \left( {N_{{\ell^{\prime}s}}^{arr} ,N_{\ell s}^{dep} } \right) \in A^{trans}. } \hfill \\ \end{array} } \hfill \\ \end{array} $$

(6.67f)

The Eqs. (6.67)–(6.67f) allow to compute Eq. (6.2) and to obtain arc costs for the whole transit network.

As detailed in the following chapters, cost functions shall be associated with specific arc types to reproduce the effect of congestion on: crowding coefficients (Sect. 7.2.1), dwell times (Sect. 7.4.4) and wait times (Sect. 7.3).

The arc performance model proposed in this section includes many coefficients expressing the attitudes and preferences of the different user classes. The most effective way of determining their values is to calibrate a random utility model for route choice, based on an ad hoc survey with interviews to passengers of the study area including both revealed and stated preference questions (see Sect. 4.4.6).

2.4 Waiting Costs in the Case of Known Timetable and Regular Service

In case of lines with low frequency, the waiting cost resulting from Eqs. (6.67f) and (6.2) may be overestimated. Indeed, if the service is regular (i.e., σ_ℓs  = 0), we can assume that passengers have the possibility of knowing the timetable; then, they will adopt a schedule-based behaviour (see Sect. 6.1.1). At least for the first line used in their journey, passengers can stay at home (or at the office, in the case of a return trip), where (see Sect. 6.3.7) the value (disutility) of time $( {\upgamma_{g}^{del} \cdot \upgamma_{g}^{vot} })$ is lower than that of waiting at the stop [γ _ag in Eq. (6.67f)], as some more useful activity can be done there, until it is time to walk towards the stop (the user delays his/her desired departure time). In general, we can then assume that the passenger faces the following alternative:

• stay at home until possible for a time equal on average to half of the headway minus the boarding time $t_{\ell }^{board}$ (introduced in Sect. 5.1.2 as a safety margin), which implies a disutility related to the delay with respect to the desired departure time (see Sect. 6.3.7), and then wait at the stop only for time $t_{\ell }^{board}$;

• go directly at the stop and wait on average for half of the headway.

Of course, a rational passenger will choose the most convenient in terms of generalized costs of the above two options; then, the wait time at the stop and the additional cost due to departure delay are, respectively, as follows:

$$ \begin{array}{*{20}l} {t_{a}^{{}} = Min\left( {t_{\ell }^{board} ,\;\frac{0.5}{{f_{\ell s} }}} \right),} \hfill & {\begin{array}{*{20}l} {\forall a = \left( {s,N_{\ell s}^{dep} } \right) \in A^{wait} } \\ {\forall a = \left( {N_{{\ell^{\prime}s}}^{arr} ,N_{\ell s}^{dep} } \right) \in A^{trans} ,} \\ \end{array} } \hfill \\ \end{array} $$

(6.68)

$$ \begin{array}{*{20}l} {c_{ag}^{nt} = Min\left( {\left( {\frac{0.5}{{f_{\ell s} }} - t_{\ell }^{board} } \right) \cdot \gamma_{g}^{del} \cdot \gamma_{g}^{vot} ,\;0} \right) + c_{\ell s}^{bfee} \cdot \gamma_{g}^{mfee} } \hfill & {\begin{array}{*{20}c} {\forall a = \left( {s,N_{\ell s}^{dep} } \right) \in A^{wait} } \\ {\forall a = \left( {N_{{\ell^{\prime}s}}^{arr} ,N_{\ell s}^{dep} } \right) \in A^{trans} .} \\ \end{array} } \hfill \\ \end{array} $$

(6.69)

This model is typically applied to given lines on the whole network, without distinguishing between the first stop and additional transfers that are relative to a specific passenger trip. Thus, it can lead to some cost underestimation for transferring to regular lines with low frequency.

2.5 Route Choice and Uncongested Assignment

Any of the static methods for uncongested assignment presented in Sect. 6.1 can be used to analyse the transit network with a frequency-based model. In particular, we can adopt the path-based model of Eq. (6.31) or the arc-based model of Eq. (6.32), where arc performances given by Eq. (6.2) are specified by Eq. (6.67); route choice can be stochastic or deterministic, or a mixture for the different user classes.

In the following, an all-or-nothing assignment to shortest paths is illustrated for the example of Sect. 5.1.3. With respect to the network construction described in Sect. 6.2.2, the assignment graphs depicted in Fig. 6.8 simplify dwelling arcs and stop arcs. For the sake of simplicity, the only disutilities considered are the running times and the wait times (also depicted in the Figure). The latter are equal to the expected value of the headways assuming their exponential distribution. Demand flows to the destination stop 4 are reported below the origin stops. The colour of arcs is red for line 1, green for line 2, maroon for line 3 and black for line 4. The grey arc is a pedestrian connection.

Fig. 6.8

Input data and results of an AoN assignment to shortest paths are applied to the example network

The numerical computation presented in Table 6.1 results from the Dijkstra algorithm described in Sect. 6.1.6. The figures in brackets denote the Bellman updates of node costs and successors which are not convenient and/or are later replaced by a better solution.

Table 6.1 Shortest tree computation for destination node 4 following the Dijkstra algorithm

The shortest tree is identified recursively by following the successor nodes. The results of Table 6.1 show that all passengers take a direct route with no transfer. In particular, the shortest path from 1 to 4 is to use the red line; the shortest path from 2 to 4 is to use the maroon line, and the shortest path from 3 to 4 is to use the black line. The dashed arcs in Fig. 6.8 are not included in the shortest tree. The arc flows can be easily determined by propagating the demand flows along these paths; all flows are depicted in yellow in Fig. 6.8, where for simplicity only the running arcs are valorised.

2.6 Criticism of the Non-strategic Approach

The frequency-based model presented in this section ignores the possibility of combining transit lines that serve the same stop. At node 1, passengers have the choice between the red and the green line; at node 2 between the green line and the maroon line; and at node 3 between the maroon and the black line. But, a rational transit passenger could choose to board either lines, since he can actually reach the destination with both alternatives at a similar cost (see Table 6.1), while the wait time at the stop would decrease considerably since the resulting service frequency would combine that of two lines.

This leads to the notion of attractive lines at a stop, which is the set of transit lines at a given stop that a passenger may willing to board. These may be common lines that operate on the same corridor (a sequence of streets and stops) or transit lines that operate on different routes, but provide service with transfers to the same destination, which form a whole strategy formalized by a hyperpath (see Sect. 6.1.3).

More in general, the formulation of frequency-based model for choice route on transit networks depends on the assumptions made on the information that is available to passenger during the trip. If no information is available then the best choice would be the shortest (costliest) path.

The additional information that may become available during the trip is given as follows:

• departure of vehicles from the stop (visually obtained),

• some knowledge of transit timetables,

• estimated arrival time of vehicles at stops (also from remote via apps or vms),

• elapsed wait time at a stop,

• information on other transit lines by looking out the window once on board,

• vehicle occupancies.

On this basis, models of increasing complexity are formulated and solved in Sects. 6.3 and 7.1.

2.7 Reference Notes and Concluding Remarks

2.7.1 The Impact of ITS in Frequency-Based Models

The impact of ITS in frequency-based models emerges mainly through two indirect effects on variables:

• the reduction of headway variation coefficient that can be obtained by implementing a fleet control policy (e.g., holding vehicles at stops); this can lead up to halving the wait time (say from exponential headways with σ_ℓs  = 1 to deterministic headways σ_ℓs  = 0) obtaining the same effect of doubling the service frequency, especially for stops towards the end of the line;

• the reduction of waiting discomfort coefficient that can be obtained through better information to passengers at stops (e.g., displaying vehicle arrival times); also in combination with other measures (more comfortable stops), this can lead up to halving the cost of waiting, from say $\upgamma_{g}^{wait} = 2\;{\text{to}}\;\upgamma_{g}^{wait} = 1$.

These interventions can produce a relevant impact on the quality of public transport, acting specifically on its peculiar cost components due to service discontinuity (wait times) and thus greatly helping to bridge the performance gap with private transport.

2.7.2 The Evolution of Frequency-Based Models in the Literature

The development of transit assignment models can be traced to a contribution by Dial (1967), who proposed a variant on the shortest path algorithm, originally used for routing private vehicles on road networks that takes into account the wait time of passengers at stops, which is the main phenomenon characterizing public transport networks. The wait times at the transfer stops were computed as half of the inverse of the combined frequency of all the lines serving the stop, thus already embedding an embryonal idea of the common line dilemma (Chriqui and Robillard 1975). This concept was later developed into an efficient algorithm for large networks by De Cea and Fernandez (1989).

Other early contributions to the transit route choice literature are those of Fearnside and Draper (1971), Le Clercq (1972), Andreasson (1976) and Last and Leak (1976). Most of these initial methods employed heuristic approaches, where a behavioural assumption leads directly to an algorithm without stating a formal model that would be solved by the computational procedure. These were largely inspired from assignment algorithms used on car networks, such as the all-or-nothing assignment to shortest paths and the stochastic (logit) multipath assignment, modified to reflect the wait times at stops which are inherent to transit networks.

Since the 1980s, a significant body of research (references in Sect. 7.1.8) was contributed to the study of transit route choice models where passengers are assumed to know the frequency of the offered services but not the exact timetable. This assumption is reasonable for transit services in urban areas that operate with high line frequency; passengers arrive at a stop, either to start the trip or by transferring from another lines, and their wait time is related to the distribution of time intervals between successive vehicle arrivals, which is commonly referred to as the line headway. The typical hypothesis is that headways are independent with exponential (random) distribution (minimum regularity), or uniform (deterministic) distribution (maximum regularity), while the arrival of passenger at stops has a uniform distribution.

Another important stream of research is the theoretical analysis of headway distributions and their calibration with respect to real data. The proof of Eq. (6.58) is due to the seminal contribution of Osuna and Newell (1972). Further contributions were provided in the late 1970s and early 1980s (Jolliffe and Hutchinson 1975; Larson and Odoni 1981; Bowman and Turnquist 1981). A more general proof is given in Amin-Naseri and Baradaran (2014), who take also into account the correlation among subsequent arrivals. The formal derivation of wait time from the headway variation coefficient for Erlang distributions is an original contribution of this book.

3 Scheduled-Based Assignment on Transit Space-Time Networks

• Guido Gentile,
• Younes Hamdouch &
• Markus Friedrich 

In this section, schedule-based (or timetable based) models for transit assignment are presented in their basic version, without involving strategic behaviour and/or congestion phenomena.

The representation of supply shall take explicitly into account the fact that the public transport service is organized with runs for each transit line and is thus actually available not only at discrete places (the stops) but also at discrete times (the schedule). The main issue is then the representation of a discrete service, which can be accomplished through a suitable topological description of the transit network that incorporates timetables and other dynamic aspects of supply by introducing a diachronic graph.

There exist other approaches for the representation of schedule-based supply. One is to introduce a specific agent for the vehicle of each run in the context of a simulation model, as explained in Sect. 6.5.2. Another one can be achieved through a standard graph by macroscopic flow modelling with queuing; this requires the definition of proper temporal profiles of the exit time for waiting arcs and alighting arcs, to compress and decompress the passenger flows, respectively, as explained in Sect. 7.3.5. Considerations about such alternative frameworks will be provided in the referred sections, while this section is devoted to diachronic graphs.

In schedule-based assignment, the typical assumption is that passengers do consider the service timetable in their route choice, because this is available and reliable; they therefore select a path on the diachronic graph, which by construction embeds the departure time choice.

However, as already explained in Sect. 6.1.1, the schedule-based approach can be also confined to the description of the dynamic network loading, while a frequency-based perception of services, possibly including strategies, is considered for route choice. This can be simply achieved through a proper definition of arc costs on the diachronic graph, as shown in Sect. 6.3.3 (the cost of waiting arcs is null, while the cost of boarding will include the expected waiting).

Hyperpaths can be, explicitly or implicitly, defined on the diachronic graph to represent mingling queues of passengers at stops, as shown in Sect. 7.3.3 (the fail-to-board probability is associated with a hyperarc and a sequential route choice is considered, while iteration is required to reach equilibrium), or their strategic behaviour with respect to line arrivals at stop, as shown in Sect. 7.1.7 (the attractive set is built-up at stops in reverse chronological order and transmitted backward in time through waiting arcs on the diachronic graph).

3.1 The Diachronic Graph

The key feature of schedule-based transit services, from a modelling point of view, is that they can be easily represented through a space-time network, also called diachronic graph, where each single run has its own layer of topology.

In general, in a space–time network, each node has a specific time coordinate, beside space geo-coordinates. For the sake of simplicity, in the graphical representation, the x–y space is often reduced to one dimension, as depicted in Fig. 6.9; only in case of one transit line, it is easy to keep the metric of space consistent with the progressives of stops. Note that the same edge of the base network can have different travel times, for different entry times; but the FIFO rule is typically satisfied at the link (and path) level.

Fig. 6.9

Generic space-time network, or diachronic graph, and the corresponding base network. Waiting arcs are depicted in black, travel arcs are depicted in green

In particular, each node is defined here as a ordered couple of a vertex i ∈ B, which identifies its point in space, and a time index t ∈ T ∪ η + 1, which identifies its instant in time (see Sect. 5.1.1), thus adopting a discrete representation of both dimensions (space and time). Recall that the additional instant η + 1, with τ _η+1 = ∞ is introduced here to represent events occurring after the assignment period [τ ₀, τ _η ] or events not referred to a specific time.

To guarantee the consistency of the time-space network, we introduce the following index functions, which are used to shift any given instant τ ≥ τ ₀ to an instant of the predefined time discretization:

• t ⁺(τ) identifies the (next) time index t ∈ T ∪ η + 1 such that τ _t−1 < τ ≤ τ _t ; t ⁺(τ ₀) = 0;

• t ⁻(τ) identifies the (previous) time index t ∈ T such that τ _t  ≤ τ < τ _t+1.

In the following, the network topology of the diachronic graph for transit assignment with schedule-based services is derived starting from the input data (see Sect. 5.1).

Like in the frequency-based approach, each trip phase (refer to the list in Sect. 6.2.2) is (possibly) represented by a sequence of arcs with a same type on the transit network; the latter is composed by:

• the pedestrian network, including centroids and connectors, as well as access, egress, walking and transfer links;

• the line network, with a sub-network for each transit run (and not for each line, like it is in frequency-based models), plus the stops and the waiting arcs shared by different lines;

• intermodal arcs at each stop to connect the pedestrian network with the line network.

To represent the topology of public transport services through a space-time network, several layers of nodes are introduced, among which we can distinguish:

• the base nodes N ^base = {(i, t): ∀i ∈ B, ∀t ∈ T ∪ η +1}, including

• the origin nodes $O = \left\{ {\left( {B_{z}^{orig} ,t} \right):\forall z \in Z,\forall t \in T} \right\} \subseteq N^{base}$, and

• the destination nodes $D = \left\{ {\left( {B_{z}^{dest} ,\eta + {1}} \right):\forall z \in Z} \right\} \subseteq N^{base}$, without a specific time coordinate;

• the stop nodes $N^{stop} = \left\{ {\left( {s,t} \right):\forall s \in S,\forall t \in T\,\cup\,\eta + {1}} \right\}$;

• the run nodes N _r , with one layer for each run r ∈ R _ℓ of line ℓ ∈ L.

Figure 6.10 shows a typical structure of the diachronic graph with the different node layers.

Fig. 6.10

Typical topology of the diachronic graph for schedule-based models

A further specialization of run nodes is required by different models to represent specific phenomena. Like in frequency-based models, there are several ways to explode stops; the scheme depicted in Fig. 6.11 allows to track most passenger flows and to reproduce (later on) the relevant congestion phenomena. Two nodes for each stop of run r ∈ R _ℓ are introduced, so as to represent consistently dwelling (the idle vehicle at one stop) and running (the moving vehicle between two consecutive stops):

• the arrival node $N_{rs}^{arr} \in N_{r} ,\forall s \in S_{\ell } - S_{\ell }^{ - }$, with time coordinate t ⁺(τ _rs ) for a given scheduled time τ _rs ;

• the departure node $N_{rs}^{dep} \in N_{r} ,\forall s \in S_{\ell } - S_{\ell }^{ + }$, with time coordinate t ⁻(θ _rs ) for a given scheduled time θ _rs .

Fig. 6.11

Detail of the stop topology and of the connection with the pedestrian network

A typical way of building-up the diachronic graph is to introduce the following types of arcs:

• the pedestrian arcs $A^{walk} = \left\{ {\left( {\left( {a^{ - } ,t} \right),{ }\left( {a^{ + } ,t^{ + } (\tau_{t} + l_{a} /s_{a}^{walk} )} \right)} \right):\forall a \in E^{walk} ,\forall t \in T} \right\}$;

• the destination arcs $A^{dest} = \left\{ {\left( {\left( {B_{z}^{dest} ,t} \right),{ }\left( {B_{z}^{dest} ,\eta + {1}} \right)} \right):\forall z \in Z,\forall t \in T} \right\}$;

• the running arcs $A^{run} = \left\{ {\left( {N_{rs}^{dep} ,N_{rs[ + \ell ]}^{arr} } \right):\forall s \in S_{\ell } - S_{\ell }^{ + } ,\forall r \in R_{\ell } ,\forall \ell \in L} \right\}$;

• the stop arcs $A^{stop} = \left\{ {(\left( {B_{s}^{stop} ,t} \right),{ }(s,t + {1})):\forall s \in S,\forall t \in T\}\,\cup\,\{ (\left( {s,t} \right),{ }(B_{s}^{stop} ,t + {1})):\forall s \in S,\forall t \in T} \right\}$

• the waiting arcs $A^{wait} = \{ (\left( {s,t} \right),{ }(s,t + {1})):\forall s \in S,\forall t \in T$;

• the dwelling arcs $A^{dwell} = \{ \left( {N_{rs}^{arr} ,N_{rs}^{dep} } \right):\forall s \in S_{\ell } - S_{\ell }^{ - } - S_{\ell }^{ + } ,\forall r \in R_{\ell } ,\forall \ell \in L\} \}$;

• the boarding arcs $A^{board} = \{ ((s,t^{ - } (\theta_{rs} - t_{\ell }^{\text{board}} )),N_{rs}^{\text{dep}} ):\forall s \in S_{\ell } - S_{\ell }^{ + } ,\forall r \in R_{\ell } ,\forall \ell \in L\}$;

• the alighting arcs $A^{alight} = \{ (N_{rs}^{\text{arr}} , \, (s,t^{ + } (\tau_{rs} + t_{\ell }^{alight} ))):\forall s \in S_{\ell } - S_{\ell }^{ - } ,\forall r \in R_{\ell } ,\forall \ell \in L\}$.

In this configuration, the intermodal arcs are only the stop arcs, while the boarding and alighting arcs are part of the line network. Note that running arcs connect two consecutive stops; they do not represent a trip leg that in some other models is introduced to jointly identify a sequence of stops between possible boarding and alighting.

Base and stop nodes are replicated for each instant of the predefined time discretization, while any arc shall connect two existing nodes by construction. For this purpose, the index function has been introduced, so that the instants which are used in the dynamic computation of route choice (concatenation) and flow propagation are fictitiously shifted to keep the time-space network consistent and acyclic. However, the travel time associated with each arc which is used in the computation of costs can be evaluated precisely. The typical time discretization in schedule-based model for transit assignment has one-minute intervals; but shorter intervals shall be adopted to properly describe pedestrian networks with short edges, such as the connections inside a station (e.g., l _a  < 80 m). Clearly, larger time intervals imply bigger approximations in the concatenation of costs and propagation of flows, while shortest time intervals imply more precise calculations at the price of higher computational costs due to the presence of many pedestrian and waiting arcs (ram and run-time are proportional to the number of arcs).

Acyclicity is a key feature of the diachronic graph topology, which turns very useful in the computation of shortest paths and flow propagation; in particular, the chronological order is in this case a topological order.

Arcs and nodes of the sub-network for this specific run are depicted in green; the bold arcs (including waiting at stops) make up the line network. Horizontal lines represent the instants of the predefined time discretization. The grey vertical line entails that a complex pedestrian network may be introduced to ensure the connection between origin, destinations and the base nodes of stops (i.e., access, egress and transfer).

3.2 Travel Costs in the Case of Run Choices

Once the space-time network is defined, the arcs can be characterized with exactly the same performance variables introduced for the frequency-based static model, since the representation of dynamics is here intrinsic in the topology of the diachronic graph. However, the travel times are to be here interpreted as a cost component used for route choice, while the speed of movements used in flow propagation and cost concatenation, as well as for the construction of paths/trajectories on the space-time network, are those connected with the temporal dimension of the diachronic graph.

If passengers make their route choice using the run schedule, the arc performance model developed in Sect. 6.2.3 for frequency-based services is still valid, with two noticeable differences:

• the travel time of boarding arcs includes only the constant value $t_{\ell }^{board}$ that is related to a safety margin compared to the departure, while the waiting phase is represented with a specific arc type;

• the running times and the dwell times are provided by the timetable, respectively, as τ _rs+ℓ − θ _rs and θ _rs  − τ _rs .

The Eqs. (6.70a)–(6.70h) presented below allow us to compute (6.2) and obtain arc costs for the whole space-time network.

$$ t_{a}^{{}} = \frac{{l_{a}^{{}} }}{{s_{a}^{walk} }},\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{walk} ,\quad c_{ag}^{nt} = 0,\quad \forall a \in A^{walk} {;} $$

(6.70a)

$$ t_{a}^{{}} = 0,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = 0,\quad \forall a \in A^{stop} {;} $$

(6.70b)

$$ t_{a}^{{}} = t_{\ell }^{alight} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = c_{g}^{tran} ,\quad \forall a = \left( {N_{rs}^{arr} ,\left( {s,t^{ + } \left( {\tau_{rs}^{{}} + t_{\ell }^{alight} } \right)} \right)} \right) \in A^{alight} {;} $$

(6.70c)

$$ \begin{aligned} t_{a}^{{}} &= {\tau }_{{rs_{{}}^{ + \ell } }}^{{}} - {\theta }_{rs}^{{}} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{\ell g}^{line} \cdot {\upgamma}_{rsg}^{crowd} \left( {q_{a} } \right),\\ c_{ag}^{nt} &= c_{\ell s}^{kfee} \cdot l_{\ell s}^{{}} \cdot \upgamma_{g}^{mfee} ,\quad \forall a = \left( {N_{rs}^{dep} ,N_{{rs_{{}}^{ + \ell } }}^{arr} } \right) \in A^{run} {;} \end{aligned} $$

(6.70d)

$$ t_{a}^{{}} = {\theta }_{rs}^{{}} - {\tau }_{rs}^{{}} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{\ell g}^{line} ,\quad c_{ag}^{nt} = 0,\quad \forall a = \left( {N_{rs}^{arr} ,N_{rs}^{dep} } \right) \in A^{{{dwel}l}} {;} $$

(6.70e)

$$ \begin{aligned} t_{a}^{{}} &= t_{\ell }^{board} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{wait} ,\quad c_{ag}^{nt} = c_{\ell s}^{bfee} \cdot {\upgamma}_{g}^{mfee} ,\\&\quad \forall a = \left( {\left( {s,t^{ - } \left( {{\theta }_{rs} - t_{\ell }^{board} } \right)} \right),N_{rs}^{dep} } \right) \in A^{board}. \end{aligned} $$

(6.70f)

The crowding discomfort coefficient $\upgamma_{sgt}^{crowd} > {1}$ of the segment s ∈ S of run r ∈ R _ℓ of line ℓ ∈ L for user class g ∈ G possibly depends on (separable) congestion through the number of passengers on-board given by the volume on the (same) arc (as detailed in Sect. 7.2.1).

For waiting arcs, the duration of the interval τ _t+1 − τ _t is multiplied by:

• the base value of time $\upgamma_{g}^{vot}$;

• the waiting discomfort coefficient $\upgamma_{g}^{wait}$;

• the stop discomfort coefficient $\upgamma_{sg}^{stop}$;

• the crowding discomfort coefficient $\upgamma_{sgt}^{crowd}$ of stop s ∈ S for class g ∈ G users entering the waiting arc at instant t ∈ T that possibly depends on (separable) congestion through the (load) number of waiting passengers given by the volume on the (same) arc (as detailed in Sect. 7.2.1).

Monetary costs are assumed null. Thus, we have the following:

$$ t_{a}^{{}} = {\tau }_{t + 1} - {\tau }_{t} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{wait} \cdot {\upgamma}_{sg}^{stop} \cdot {\upgamma}_{sgt}^{crowd} \left( {q_{a} } \right),\quad c_{ag}^{nt} = 0,\quad \forall a = \left( {\left( {s,t} \right),\left( {s,t + 1} \right)} \right) \in A^{wait}. $$

(6.70g)

Note that given the possibility offered by longer waits, for scheduled services the stop discomfort coefficient $\upgamma_{sg}^{stop}$ (introduced in Sect. 5.1.2), besides ergonomy, depends also on the activities (e.g., shopping) that can be developed by the passenger at the specific stop.

Destination arcs are dummy; therefore, we assume a null cost and time:

$$ t_{a}^{{}} = 0,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} ,\quad c_{ag}^{nt} = 0,\quad \forall a \in A^{dest}. $$

(6.70h)

3.3 Travel Costs in the Case of Line Choices

The cost model presented in the previous section is to be considered the reference one for schedule-based assignment. However, there are cases where the assignment of the diachronic graph is aimed to determine the load on each run, while passenger behaviour is still connected with the perception of service in terms of line frequencies.

In this case, the arc performance model developed in Sect. 6.2.3 for frequency-based services can be still applied, with few exceptions:

• the cost of boarding arcs shall include the expected waiting time and its disutility, but not the cost due to the crowding discomfort, as each coefficient $\upgamma_{sgt}^{crowd}$ is arc specific and depends on the load of waiting passengers at the stop entering at that specific instant;

• the cost of waiting arcs (that would in this case be null in principle) shall thus include only the crowding discomfort.

In this case, Eqs. (6.71a)–(6.71e) and (6.71h) are identical to Eqs. (6.70a)–(6.70e) and (6.70h), while for boarding and waiting arcs it is, respectively:

$$ \begin{aligned} t_{a}^{{}} &= t_{\ell }^{board} + t_{\ell st}^{wait} \left( {{\mathbf{q}}_{A} } \right),\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{wait} \cdot {\upgamma}_{sg}^{stop} ,\\ c_{ag}^{nt} &= c_{\ell s}^{bfee} \cdot {\upgamma}_{g}^{mfee} ,\begin{array}{*{20}c} {\forall a = \left( {\left( {s,t} \right),N_{rs}^{dep} } \right) \in A^{board} } \\ {t = t^{ - } \left( {\theta_{rs} - t_{\ell }^{board} } \right)} \\ \end{array} {;} \end{aligned} $$

(6.71f)

$$ \begin{aligned} t_{a}^{{}} &= {\tau }_{t + 1} - {\tau }_{t} ,\quad {\upgamma}_{ag}^{{}} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{wait} \cdot {\upgamma}_{sg}^{stop} \cdot \left( {{\upgamma}_{sgt}^{crowd} \left( {q_{a} } \right) - 1} \right),\\ c_{ag}^{nt} &= 0,\quad \forall a = \left( {\left( {s,t} \right),\left( {s,t + 1} \right)} \right) \in A^{wait}.\end{aligned} $$

(6.71g)

This way, the cost of waiting is arbitrarily separated in two discomfort components that are associated with two different arc types, i.e., boarding and waiting, respectively. This modelling choice is justified by several facts:

• the perceived wait time (6.71f) preventively estimated by passengers to make their route choice is linked with the headway distribution and primarily with the line frequency;

• the actual wait time (6.71g) suffered by passengers is that accumulated during the wait, under the assumption that the timetable embedded in the diachronic graph is a possible instance of what will actually occur in reality;

• by perceiving some cost also on the waiting arcs, passengers are induced boarding the first available run(s) of each line (under the typical assumption that $\upgamma_{sgt}^{crowd} > {1}$);

• the crowding discomfort coefficient at the stop depends on the number of waiting passengers, which may grow during the wait and is thus well represented by the load on the waiting arc.

Once again, be aware that the travel times evaluated by the above arc performance model are functional to the route choice model through perceived costs. The correct computation of an output indicator such as the total travel time is properly accomplished by taking into consideration the temporal coordinates embedded into the diachronic graph; indeed, by considering (6.71f) and (6.71g) wait times would be counted twice.

The expected wait time $t_{\ell st}^{wait}$ at stop s ∈ S for line ℓ ∈ L at instant t ∈ T depends on the headway distribution through (6.65), where the frequency f _ℓst and the irregularity σ _ℓst shall be evaluated through Eqs. (5.12) and (5.13), respectively, starting from the schedule. This can be done by considering fairly long-time intervals (say 1 h), which would be feasible with the memory ability of passengers in recalling temporal profiles of attributes. As an alternative, the frequency can be calculated as the inverse of the (departure) headway between the current run and the previous one. In case of queuing, the perceived wait time can also possibly depend on (non-separable) congestion (effective frequency) through the load of the next running arc (as detailed in Sect. 7.3.2).

As already mentioned, the crowding discomfort coefficient $\upgamma_{sgt}^{crowd}$ of stop s ∈ S for user class g ∈ G at instant t ∈ T possibly depends on (separable) congestion through the number of waiting passengers given by the load on the corresponding arc (as detailed in Sect. 7.2.1).

The disutility connected with the possible difference between the desired departure time and the actual one is discussed in Sect. 6.3.7.

3.4 Route Choice and Uncongested Assignment

Any of the static methods for uncongested assignment presented in Sect. 6.1 can be used to analyse the transit network with a schedule-based model. In particular, we can adopt the path-based model given in Eq. (6.31) or the arc-based model given in Eq. (6.32), where arc performances in Eq. (6.2) are specified by Eq. (6.70) or by Eq. (6.71); route choice can be stochastic or deterministic, or a mixture for the different user classes.

Although there is no technical drawback in adopting an arc-based model, the traditional approach to the schedule-based assignment on the diachronic graph is path-based, because this allows to better represent some important attributes, such as fares and walking distance, that may be modelled as nonlinear components in the passengers disutility, as well as other behavioural aspects of route choice, such as the correlation among alternatives.

The different preferences of users on the many relevant attributes (e.g., walking time, wait time, on-board time, transfers, monetary cost, stop ergonomy and comfort) are not easy to synthesize in the deterministic coefficients of a given class segmentation. Hence, a random utility model can be used which incorporates passenger heterogeneity in a stochastic framework.

The correlation among route alternatives is a relevant aspect to take into account in stochastic assignment when the model is conceived to distinguish the service provided by each run of a same line. On the other hand, the number of non-dominated routes available on the space-time network and practical to consider for each O–D pair is usually limited.

In Sect. 4.5.2, some methods are presented to generate a ‘good’ set of paths, which is a critical step in this kind of assignment procedure; moreover, in the next section, the multi-path algorithm is presented as a route generation method specifically conceived for schedule-based models of long distance trips.

Under these considerations, path-based models allow for more opportunities than arc-based models:

• a proper selection of usable routes, which comes at the price of introducing rules for their identification;

• a proper representation of their correlation, which comes at the price of a more complex route choice model;

• the possibility of introducing non-additive costs, such as fares, which comes at the price of a more complex supply model.

A connector exiting from the origin node represents the access to the pedestrian network, which allows us to reach the first stop. The passenger waits at the platform a specific run for a certain number of time intervals and then boards the vehicle at the end of its dwell time, which instead occurs on the track (thinking of a railway example). The run departs from the stop (with the passenger on-board) at the scheduled time and arrives at the next stop again on schedule. The passenger travels along a sequence of line segments on such run until he/she alights upon vehicle arrival at the planned stop. The passenger may transfer to a new stop using the pedestrian network, or stay in the same stop, and the waiting–boarding–alighting sequence is repeated, until the last stop is reached. Finally, the passenger walks towards the destination and egresses there from the transit network via a connector; the trip on the diachronic graph actually ends with a dummy destination arc.

Each one of the above trip phases is represented through a sequence of arcs on the diachronic graph. Thus, the route costs c _kg can be obtained by summing up all the arc costs of the path, plus possibly a non-additive term, as in Eq. (6.3). Route probabilities p _kg can then be reproduced through any discrete choice model (e.g., based on random utility), as in Eq. (6.13).

In the schedule-based approach with space-time network, a trip starting at instant t ∈ T from origin zone z ∈ Z to destination zone z′ ∈ Z is represented as an (acyclic) path k ∈ K _od from origin node $o = (B_{z}^{orig} ,t) \in O$ to destination node $d = (B_{{z^{\prime }}}^{dest} ,\eta + {1}) \in D$ on the diachronic graph; thus, the notion of departure time is embedded in the origin.

Travel demand d _odg represents here trips from origin node $o = (B_{z}^{orig} ,t)$ to destination d, i.e., the number of passengers of class g who (wish to) depart from origin zone z during a time interval (τ _t-1, τ _t ] to reach d at a later time. It is assumed that all such passengers will behave like the one departing in the final instant of the interval, who will consider the costs c _kg of the paths k ∈ K _od . The resulting path flows q _kg are consistent with the route probabilities p _kg as in (6.6). Finally, the arc flows and volumes are computed as in Eqs. (6.5) and (6.1).

Most of the existing models for schedule-based assignment adopt the above path-based approach, which can support also the simulation of real-time information about vehicle arrivals and the consequent en-route adaptation of the path choice. In that case, random utility models are though forced to represent also the events occurring at stop relative to the service departure time, in a context of imperfect regularity, while actually the two phenomena (random utility and random headways) follow in general quite different statistical laws. Moreover, service irregularity leads passengers to a strategic behaviour, which cannot be represented satisfactorily by stratifying the network knowledge, possibly acquired through a day-to-day learning process, in terms of path costs. Instead, strategies are well formalized through hyperpaths, which given their awkward explicit representation require de facto an implicit modelling of sequential arc choice towards the destination. For this reason, as already explained in Sect. 6.1.3, despite the advantages of path-based models in reproducing nonlinear attributes, arc-based models can better provide a suitable support for the future development of schedule-based algorithms, where:

• the assumption of perfectly reliable timetables is abandoned,

• the representation of supply variability becomes a key aspect of the simulation, and

• the diachronic graph reduces to a technical tool for the analysis of the loads resulting from the assignment on each run and is not anymore meant to reflect the mental map of the passenger.

3.5 Branch and Bound Algorithm for Choice-Set Generation

The multi-path algorithm (Friedrich et al. 2001) is here presented as a method for generating the set K _od of all potential routes from origin node $o = (B_{z}^{orig} ,t) \in O$ to any destination node $d = (B_{{z^{\prime}}}^{dest} ,\eta + {1}) \in D$ on the diachronic graph that are compliant with a set of given rules.

The construction algorithm builds-up iteratively a connection tree which may provide several paths from an origin (at a given time) to possibly every destination, as depicted in Fig. 6.12. The root of the tree is the origin node; a walk leg (i.e., a sequence of pedestrian arcs) is added to the tree to reach each stop of public transport in the vicinity (a proper distance threshold is to be defined) and the corresponding node (stop and arrival time) is added to a list of nodes to examine.

Fig. 6.12

Structure of the connection tree

Then, for each one of the reached stops (contained in the list), a branch and bound approach is applied to visit and possibly add to the connection tree all transit legs (i.e., a sequence of line network arcs, such as board, run, dwell, run, dwell, alight) that bring from the current stop at the current time (current node) to another stop and satisfy a set of rules (to be specified in the following). When this happens, the final stop of the visited leg (at the arrival time) is added to the list of nodes to be further examined. Once all stops of one level are visited, the depth of the tree is increased to the next level. Moreover, additional walk legs are added to the tree if destinations are reachable in the vicinity.

The use of entire connection legs as tree edges simplifies and accelerates the search for new routes on the diachronic graph to a great extent; the combinatorial explosion of connections is primarily limited by the maximum number of transfers.

The construction of the connection tree includes the definition of a search impedance c ^imp _k for each route k:

$$ c_{k}^{imp} = {\upbeta }^{time} \cdot t_{k}^{tot} + {\upbeta }^{trans} \cdot n_{k}^{trans} + {\upbeta }^{fare} \cdot c_{k}^{fare} , $$

(6.72)

where:

• $t_{k}^{tot}$ is the total travel time of the path (undistinguished for trip phase),

• $n_{k}^{trans}$ is the number of transfers and

• $\begin{aligned} \hfill \\ c_{k}^{fare} \hfill \\ \end{aligned}$ is the fare, while

• β ^time, β ^trans and β ^fare are global search parameters.

The functional form of this search impedance is thus similar but usually simpler than that of the systematic utility. Indeed, while the utility should reflect at best the perception of the travellers in the route choice, the impedance is used only to generate an appropriate choice set of paths. This can justify some somewhat different parameter values.

Now, we present the set of rules that can be applied in the branch and bound constructive search to determine if a given transit leg (i, u) → (j, v) from the stop of the currently examined node (i, t) to another stop j reachable at a later time with no transfer from i should be added to the connection or not:

• Rule 1. Temporal suitability. The run of the transit leg under consideration shall depart after the arrival time at stop i: u > t.

• Rule 2. Dominance. No other connection k ∈ K _oj should already exist on the tree from origin o to stop j that dominates in all relevant aspects the one h created by adding the transit leg under consideration, i.e., such that $t_{k}^{tot} <_{{}}^{{}} t_{h}^{tot}$ and $n_{k}^{trans} < n_{h}^{trans}$ and $c_{k}^{fare} < c_{h}^{fare}$.

• Rule 3. Tolerance. The following constraints are satisfied: $c_{h}^{imp} \le \upalpha^{imp} \cdot {Min}(c_{k}^{imp} :k \in K_{oj} ) + \chi^{imp} \;{and}\;n_{h}^{trans} \le \chi^{trans} n$, where α ^imp > 1 is the relative tolerance with respect to the least impedance path, χ ^imp is an additive absolute tolerance with respect to the least impedance path, and χ ^trans is the maximum number of transfers allowed within a connection.

When a connection is added, then its final stop is added to the list of nodes with the resulting arrival time. A tree level is explored completely before connection legs of the next level are considered. The procedure terminates when the list of nodes is empty or the maximum number of transfers (levels) is reached. Finally, for each destination d, one additional connection is added directly to the origin o, which contains a walking leg using the shortest path on the pedestrian network.

3.6 Computation of Shortest Tree on the Space-Time Network

A practical alternative to the preliminary explicit generation of all relevant paths is their iterative construction through the computation (and storage, if needed) of minimum-cost trees on the diachronic graph.

In space-time networks, each node has a specific time coordinate, with the exception of destination nodes, which have none. This way, with one shortest tree rooted at the destination node the minimum-cost path starting from every origin node (each one representing an origin centroid and a departure time) is obtained; let us see why this is convenient.

Usually, in a dynamic assignment problem, we are faced with the computation of the costless path to reach the destination centroid $B_{d}^{dest} \in B$ of zone d ∈ Z (at any time) starting from the origin centroid $B_{o}^{orig} \in B$ of zone o ∈ Z at a given instant t ∈ T, because the demand is specified and stratified for departure time. This can be achieved at once for all possible origin zones o ∈ Z and departure times t ∈ T with one single visit in reverse chronological order of the diachronic graph by initializing to zero the labels of the base nodes ($B_{d}^{dest} \in B,\forall e \in T$) corresponding to the destination centroid at all possible arrival times (these are not the destination node); the result of the algorithm would be therefore a forest and not a tree. However, the introduction of dummy destination arcs allows to initialize only the label of the destination node ($B_{d}^{dest} ,\eta + {1}$) to zero.

Moreover, the computation of a shortest tree on the diachronic graph is trivial, since the graph is acyclic and has a natural topological order that is the chronological order (we can assume destination nodes have an infinite time). Under such conditions, a shortest tree can be easily computed by processing all nodes with Eq. (6.19), i.e., by applying the Bellman relation given in Eq. (6.29) to each arc of the forward star, in reverse chronological order starting from the destination, without the need of introducing a list of nodes to be visited. This approach is here referred to as the Pallottino algorithm (1998), who proposed and analysed several variants of this problem.

The example below presents the computation of the shortest tree to destination 4 by considering (Fig. 6.13) a simplified version of the diachronic graph topology with respect to that proposed in Sect. 6.3.1 applied to our test case of Sect. 5.1.3. In particular, for the sake of simplicity, the stop is here represented as a single node; thus, while the feasible connections among possible runs are correctly represented, the resulting arc loads are not capable of explaining boarding, alighting and transfer flows.

Fig. 6.13

Results of an AoN assignment to shortest paths on the diachronic graph applied to the example network

The colour of running arc is that associated with the line: red for line 1, green for line 2, maroon for line 3 and black for line 4. The grey time boxes represent the base nodes replicated for each instant of the time discretization, while the white time boxes represent departure and arrivals of runs. The grey lines between stops 1 and 2 represent the pedestrian arcs. The dashed arrows at stop 1 represent the departure options (red for delay and green for anticipation) as explained in Sect. 6.3.7.

In Table 6.2, each line shows the solution for a node of the diachronic graph. Nodes are visited in reverse chronological order from the destination and the best local alternative of the forward star (such that the arc cost plus its head cost is minimum) is identified, thus providing expected cost and successor stop for the node under analyses.

Table 6.2 Shortest tree computation for destination 4 following the Pallottino algorithm

At the end of the process, it is possible to reconstruct the shortest path starting from any origin node by following on the table the sequence of successor nodes. For example (see dark cells of the table), starting from stop 1 at 7:30, the sequence is: (board and ride the green line) stop 2 at 7:37, (ride the green line) stop 3 at 7:43, (alight from the green line and wait) stop 3 at 7:45, (board and ride the black line) stop 4 at 7:55, (reach the destination node) stop 4 at time η + 1.

The numbers at the left of the node and on the arcs in yellow depicted in Fig. 6.13 identify the passenger loads resulting from an AoN assignment to shortest paths on the diachronic graph; in red (stop 2 at 8:30) is depicted a demand load that is unable to reach the destination.

3.7 Departure Time Choice

The results obtained with the simulation of route choice only are not particularly satisfactory in the case of schedule-based models, because the departure time choice is not properly taken into account in a context where the availability of service is scarce in time.

For example, passengers who desire to depart at 8:30 from stop 2 do not have an available travel alternative if they must necessarily start their trip at 8:30; but, they may be willing to anticipate their trip, and this allows to have more travel alternatives. Passengers who desire to depart at 7:30 from stop 3 have a cost of 25 min by starting their trip exactly at 7:30; but they may be willing to postpone their trip at 8:00 when the cost to destination is only 4 min. Passenger who desire to depart at 8:00 from stop 1 have a cost of 33 min by starting their trip exactly at 8:00; but they may be willing to anticipate their trip at 7:30 when the cost to destination is only 25 min.

However, the shift from the desired departure time to the actual departure time conveys a cost (disutility) for anticipation or delay; therefore, the final trip decision will result from the combination of route opportunities available at different departure times and the above shift disutility.

In the framework of diachronic graphs, it is fairly easy to couple the route choice with the departure time choice. To this end, after the computation of the shortest tree to destination d ∈ D and before performing the flow propagation, the demand d _odg of class g ∈ G users directed to d that desire to depart form origin zone z ∈ Z at instant t ∈ T shall not be (necessarily) loaded on origin node $o = (B_{z}^{orig} ,t) \in O$, but instead on the origin node $i = (B_{z}^{orig} ,e) \in O$, with actual departure instant e ∈ T, which shows the best utility. The latter is given by the combination of the route (expected) cost w _idg from node i to destination d and of the cost (disutility) for anticipation τ _t  − τ _e (if e ≤ t) or delay τ _e  − τ _t (if e ≥ t) due to the shift of the actual departure time τ _e with respect to the desired departure time τ _t . Usually, the choice set of actual departure times that users of class g ∈ G take into consideration is identified by considering a maximum anticipation $t_{g}^{ant}$ and a maximum delay $t_{g}^{del}$.

Typically, a linear expression of the above disutilities for users of class g ∈ G is assumed with different coefficients for anticipation $t_{g}^{ant}$ and delay $t_{g}^{del}$; because the demand is specified for desired departure times, then usually $\upgamma_{g}^{ant} > \upgamma_{g}^{del}$; indeed, in this case users are doing some activity at the origin which ends at a given time. The total cost w _odge to reach destination d for users of class g that desire to depart at instant t from node $o = (B_{z}^{orig} ,t)$ but instead depart at instant e from node $i = (B_{z}^{orig} ,e)$ is then given by:

$$ w_{odge} = w_{idg} + \left\{ {\begin{array}{*{20}l} {{\upgamma}_{g}^{ant} \cdot {\upgamma}_{g}^{vot} \cdot \left( {{\tau }_{t} - {\tau }_{e} } \right){,}\quad {\text{if}}\;\;{ }{\tau }_{t} - t_{g}^{ant} \le {\tau }_{e} \le {\tau }_{t} } \\ \begin{array} {l} {\upgamma}_{g}^{del} \cdot {\upgamma}_{g}^{vot} \cdot \left( {{\tau }_{e} - {\tau }_{t} } \right){,}\quad {\text{if}}\;\; \, {\tau }_{t} < {\tau }_{e} \le {\tau }_{t} + t_{g}^{del} \hfill \\ \infty {,}\quad {\text{otherwise}} \hfill \\ \end{array} \\ \end{array} } \right.. $$

(6.73)

On the contrary, if the demand is specified for desired arrival times, then the user is going to undertake an activity at the destination which will start at a given time. However, in this case, the shortest paths shall be computed from the origin, basically inverting the described approach.

A probabilistic model based on random utility (see Sect. 4.4) can also be used to split the demand on the alternative departure times, where the opposite of the above cost combination works as a systematic utility.

In an equilibrium assignment including departure time choice, some commuters will travel before the desired departure time and some after, so as to avoid the congestion of the peak period.

Below an example of departure time choice from origin 1 is presented, under the assumption of a disutility for delay equal to 6 min/h and for anticipation equal to 10 min/h. Passengers who desire to depart at 8:00 find more convenient to depart at 7:30 (Fig. 6.14).

Fig. 6.14

Departure time choice for passengers leaving from origin stop 1 destination stop 4

In the case where the departure time choice can be considered as part of the route choice like if anticipation or departure delay are an additional phase of the trip, then the departure time choice can be simulated within the assignment model simply by extending the network into a super-network with departure arcs that connect the origin node (with its desired departure time) and any other feasible departure time. The cost associated with these arcs is the disutility of anticipation or delay which can take any form (e.g., linear or quadratic) as a function of the above-mentioned difference; interestingly in this particular case, the anticipation arcs will travel back in time.

3.8 Networks with Mixed Schedule-Based and Frequency-Based Services

This section shortly addresses the problem of modelling in transit assignment the case of networks where both schedule-based (SB) and frequency-based (FB) services are present.

When do passengers refer to timetables or not? This depends mainly on headways and on their regularity. Typical threshold for regular headways is around 10–20 min. But what if the network contains lines with both high and low headways? The structures of FB models with static network and SB models with space-time network are quite different and do not fit well together, so they cannot be combined simply in a same model. Alternative solutions are then:

• use the FB approach for the whole model and approximate the passenger behaviour for lines with low frequency, as proposed in Sect. 6.2.4;

• use the SB approach for the whole model and approximate the passenger behaviour for lines with high frequency, as proposed in Sect. 6.3.3.

One way is then to introduce in a static transit network a proper limit to the maximum wait time, so as to represent the convenience expected by passengers of timing their arrival at the stop with that of vehicles, and wait at home instead of at the stop, as in Eq. (6.69).

Another way of dealing with networks with mixed services is to apply the two cost functions (6.70) and (6.71) on the diachronic graph of the same model where appropriate. In this case, we shall assume that stops are dedicated either to SB or to FB services.

Finally, note that dynamic models (macroscopic assignment and simulation) can instead support natively the presence of both high and low-frequency services, as explained in Sects. 6.4 and 6.5.

3.9 Reference Notes and Concluding Remarks

Schedule-based model has been widely developed from the beginning of the new millennium exploiting the conceptual framework of space-time networks, which allow for the explicit representation of each single run, in contrast to the aggregated representation of service in terms of lines used in frequency-based modes.

The most natural and well-established approach to model run-based assignment involves the representation of transit supply, which is intrinsically discrete in time, as a diachronic graph (Nuzzolo and Russo 1998; Nguyen et al. 2001), where each run is modelled through a specific sub-graph whose nodes have space and time coordinates according to the timetable. As an alternative, it is possible to define a dual graph (Nielsen and Jovicic 1999; Moller-Pedersen 1999), where each run section is a node, while the arcs represent the connections at stops satisfying temporal consistency. A third approach is to explicitly generate a number of alternative paths that constitute the passenger choice set and then assign on them the demand by means of a random utility model (Tong and Wong 1999; Friedrich et al. 2001). In general, stochastic models are often considered to simulate route choice on dynamic transit networks with timetables (Hickman and Bernstein 1997; Nuzzolo et al. 2001; Nielsen 2004).

The use of super networks to explicitly represent the departure time choice in the assignment model is an original contribution of this book, as Sheffi (1984) exploited this approach to reproduce different forms of elastic demand (mode choice, destination choice) in the context of static assignment algorithms.

The presentation of a consistent approach to reproduce a frequency-based behaviour on a schedule-based supply and a schedule-based behaviour on a frequency-based supply (see Sect. 6.2.4), both obtained by introducing proper arc costs, which paves the way to simulate networks with mixed services, is an original contribution of this book.

4 Macroscopic Models for Dynamic Transit Assignment

• Guido Gentile 

Macroscopic models for dynamic assignment have been developed in the last 30 years, mostly for private traffic. Their aim was to reproduce road congestion and more specifically how travel times are affected by the forming and vanishing of vehicle queues. This gives rise to the so-called Dynamic Network Loading (DNL) problem, where the flow propagation is performed using fixed route choices (not to be confused with the Network Loading Map of Sect. 6.1.8, which includes elastic route choice). A second use case of DTA involves, indeed, elastic route choice and the focus is on how the flow pattern is affected by congestion, giving rise to the so-called Dynamic User Equilibrium (DUE) problem.

In transit assignment, the interest for macroscopic dynamic models derives essentially from the possibility to describe FIFO queues at bus stops formed by passengers that are not able to board the first arriving carrier due to a lack of remaining capacity on the vehicle; these oversaturation queues are not to be confused with the under saturation queues that are due to the discontinuity of the service. Another relevant phenomenon that can be well captured by macroscopic models is the variation of service frequencies along the line due to the impact of boarding and alighting flows on dwelling times, which can even lead to bouncing (see Sect. 7.4). On the contrary, the scheduled-based models based on space-time networks presented in Sect. 6.3, which are the most common form of dynamic models for transit networks, are not suited to represent congestion phenomena that affect travel times.

In macroscopic models, vehicles are represented as a partially compressible fluid, whose physical law in stationary flow states is fully described by the so-called fundamental diagram. It is an experimental relation between flow density and its speed; the assumption that this holds true also in transition states results in the kinematic wave theory, which supports a number of (first order) traffic flow models.

In dynamic macroscopic models for transit networks, private vehicles are replaced by passengers. In this case, though, the progression of the user fluid is not affected by its density, as the speed of carriers is practically independent of on-board passenger loads, if the vehicle has sufficient engine power. However, this is not true for pedestrian arcs, where the congestion among walking passengers may resemble vehicle congestion, as well as for boarding and alighting arcs, whose flows influence the dwell times as explained in Sect. 7.4.4. In some model, indeed, transit line vehicles are represented as another flow component which follows a fixed path; in this case, the progression of the two flow components is strongly interdependent, thus adding a degree of complexity (non-separability) to the assignment problem.

Congestion is the focus of dynamic models. On the supply side of the DUE problem, the attention is thus essentially devoted to the passenger queuing at stops and to the seating mechanism, with emphasis on the node models with capacities and priorities, rather than on the arc model. On the demand side of the DUE problem, however, other congestion phenomena play a relevant role affecting costs through the value of time, rather than the travel time; these are primarily connected through discomfort for overcrowding, as explained in Sect. 7.2.1.

In the following, we focus on the mathematical framework of the approach and on the demand side of the DUE problem, leaving the description of congestion phenomena to Chap. 7. Section 6.4.1 extends the equilibrium formulation for transit assignment as a fixed-point problem to the dynamic case. Sections 6.4.2 and 6.4.3 illustrate how the concatenation of travel times influences the flow propagation and route choice, respectively, in a dynamic model. Section 6.4.5 shows how dynamic flow propagation applies to service frequency. Finally, Sect. 6.4.6 presents some references.

While the general ideas embedded in macroscopic modelling for network dynamics (presented in Sect. 6.4.1) are relevant for transit assignment as soon as there are congestion phenomena affecting travel times (e.g., queues of passengers at stops), the specific formulation of each component (presented in Sects. 6.4.2 and 6.4.3) can be considered an advanced material that is not necessary to understand the reminder of the book, with the exception of Sects. 7.3.4 and 7.3.5.

4.1 Fixed-Point Formulations of Arc-Based Dynamic Assignment

In this section, the fixed-point scheme of Fig. 6.3, introduced to formulate User Equilibrium problems on static transit networks, is extended to macroscopic models for dynamic assignment, yielding Fig. 6.15; moreover, some details on the resulting functional components are provided.

Fig. 6.15

Fixed-point formulation of DUE and DNL for arc-based macroscopic models

An arc-based (see Sect. 6.1.11) macroscopic model for dynamic transit assignment consists of the four sub-models presented below, where the variables are temporal profiles, i.e., (semi) continuous functions of the daytime τ. Here, in contrast to the case of diachronic graph, the network is just a spatial and functional representation of the transport system with no embedded time dimension. The reference network element is the generic arc a ∈ A; variables are referred to users of class g ∈ G directed towards destination d ∈ D on mode m ∈ M.

Network congestion model (NCM) takes as input the arc volumes q _a (τ) that are typically aggregated from destination-specific flows q _admg (τ), and the arc characteristics δ _a (τ). It yields as output the arc exit times θ _a (τ) for a given entry time τ and the corresponding value of time γ _ag (τ). This sub-model aims at reproducing various congestion phenomena, from discomfort to queuing, which introduce an increasing level of complexity; discomfort affects only costs, whereas queuing affects also times. Moreover, in transit assignment, some conditional probabilities derive from hyperarc diversion probabilities p _a|ădmg (τ) (see Sect. 6.1.5); they are not the result of route choices, but are rather related to random events on the supply side, such as the attractive line probabilities (see Sect. 7.1) and the fail-to-board probabilities (see Sect. 7.3.3). The NCM shall also represent these physical phenomena.

Arc cost model (ACM) takes as input the arc travel times θ _a (τ) − τ, the value of times γ _ag (τ) and the arc characteristics δ _a (τ). It yields as output the arc costs c _ag (τ) perceived by each user class, considering their different values of time and preferences. The need of handling the value of time as a separate variable from travel times and not directly in the ACM (as usual for traffic models) derives from the relevance of comfort in transit assignment, which can be heavily affected by overcrowding congestion, on-board and at stops (see Sect. 7.2.1).

Route choice model (RCM) takes as input the arc costs, as well as the arc travel times that allow for the dynamic concatenation of perceived utilities (see Sect. 6.1.13). It yields as output the expected costs (un-satisfactions, if route choice is based on a random utility model) to reach the destination from each node w _idmg (τ) that are then used to compute the arc conditional probabilities p _admg (τ) (the node costs can be seen as the dual variables of the arc probabilities). Interestingly, from an algorithmic point of view, it can be convenient to perform the computation of the latter directly in the FPM.

Flow propagation model (FPM) takes as input the travel demand d _odmg (τ) and the local choices, as well as the travel times that allow for the dynamic propagation of flows (see Sect. 6.1.13). It yields as output the arc flows of each class directed towards each destination, which are then aggregated into arc volumes. Arc flows by destination are needed as such by the more advanced NCM based on macro-, micro- or meso-simulations, as well as to apply gradient projection algorithms instead of MSA.

In the figure above, the rounded grey boxes are functionals; sharp white boxes are variables; and sharp green boxes are input. The bold box denotes the pivot variable of the fixed-point problem. The bold arrow closes the equilibrium loop and recalls that an algorithmic transformation of the pivot (e.g., through MSA or Gradient Projection) is required to ensure convergence. The dotted bold arrows highlight the crucial role of travel times in dynamic models. The dashed elements represent the extension to the case of strategic behaviour.

Two main cycles can be identified in the scheme of Fig. 6.15: inner and outer. The whole outer cycle is the DUE problem, while the inner cycle between FPM and NCM in the DNL problem. More specifically, the DUE can be then formalized as a fixed-point problem in terms of the arc flows:

$$ {\text{DUE}} = {\text{NCM}} \to {\text{ACM}} \to {\text{RCM}} \to {\text{FPM}} \to \left[ {\text{MSA}} \right] \to {\text{NCM}}. $$

(6.74)

The DNL is a sub-problem of DUE, which consists of seeking, for given route choices, an arc flow pattern consistent with the travel times through the arc performance model. DNL can be seen as a simplified DUE, without route choice. However, it still has a circular dependency to be solved iteratively in order to guarantee temporal consistency (not more than few iterations in practice). Arc flows can be again considered as pivot variables of this fixed-point problem:

$$ {\text{DNL}} = {\text{NCM}} \to {\text{FPM}} \to \left[ {\text{MSA}} \right] \to {\text{NCM }}. $$

(6.75)

Both fixed-point problems, DUE and DNL, can be solved through the method of successive averages (MSA) considering as pivot variable the arc flows by destination q _admg (τ).

As an alternative, the DNL can also be solved in chronological order as a one-shot procedure (such as the link transmission models) without iteration by exploiting the acyclicity of causalities in time (i.e., an event occurring on an arc during a given time interval may have an effect on other arcs only in future time intervals), although this requires in practice a fine time discretization for short arcs. In general, the choice probabilities that are the input of DNL can be given in different forms: path probabilities (which requires their explicit enumeration), arc conditional probabilities per destination (which implies a sequential route choice model, as in the proposed framework), or non-destination-specific arc splitting rates (which does not guarantee the consistency of the loading with a given O–D matrix).

Note that in case of strategies, the DNL problem includes the update of the hyperarc probabilities through the NCM and their consequent use in the FPM. To correctly express this circumstance, in the scheme of Fig. 6.15 with respect to that of Figs. 6.2 and 6.3, the arc conditional probabilities p _admg (τ) derive explicitly from the hyperarc probabilities p _ădmg (τ) and the diversion probabilities p _a|ădmg (τ) as illustrated in Eq. (6.25). Clearly, if no strategic behaviour is considered, then all the dashed components of the scheme are discarded.

4.2 Propagation of Continuous Flows

To cope with the complexity of dynamic assignment, the concept of travel time is to be extended accordingly, as shown in Fig. 6.16. Let θ _a (τ) be the exit time from arc a of a passenger who enters it at time τ. The inverse θ ⁻¹ _a (τ) of the exit time profile yields the entry time of a passenger who exits it at time τ. The travel time t _a (τ) for a given entry time τ is then:

$$ t_{a}^{{}} \left( {\tau } \right) = {\theta }_{a}^{{}} \left( {\tau } \right) - {\tau }. $$

(6.76)

Fig. 6.16

The dynamic extension of the travel time variable: exit and entry time

As the travel time of any arc of non-null length is positive, the exit time profile θ _a (τ) is always above the bisection with derivative 1. When travel times are increasing, its derivative is higher than 1; when travel times are decreasing, its derivative is lower than 1. If (strict) FIFO rule holds true, i.e., no overtaking is possible among passengers, then the derivative is always non-negative (positive).

In macroscopic models, passengers are represented as a partially compressible fluid. The flow is the amount of fluid traversing a given section at a given instant. It is then not possible to talk generically of the passenger flow on a given network element, path or arc; instead, instantaneous inflows and outflows are to be defined and analysed, as well as entry and exit capacities. Indeed, at a solution of a DNL problem, the flow shall be consistent with the available capacities.

If the FIFO rule holds true, the cumulative outflow $q_{ag}^{\text{count}}$ at time θ = θ _a (τ) when the passenger exits arc a ∈ A is equal to the cumulative inflow $q_{ag}^{cin}$ at the time τ = θ ⁻¹ _a (θ) when the passenger entered it:

$$ q_{ag}^{cout} \left( \theta \right) = q_{ag}^{cin} \left( \tau \right). $$

(6.77)

Figure 6.17 shows how these dynamic variables are intrinsically connected: the horizontal distance between the cumulative outflow and inflow temporal profiles is the travel time, while their vertical distance is the number of passengers on the arc.

Fig. 6.17

Relation among the profiles of travel time, entry flow and exit flow, according to FIFO rule, in the space of cumulative flows

By taking the derivative of Eq. (6.77) with respect to τ while considering θ = θ _a (τ), the following result for instantaneous flows is obtained (cumulative flows are the integral in time of instantaneous flows):

$$ q_{ag}^{out} \left( {\theta } \right) = \frac{{q_{ag}^{in} \left( {\tau } \right)}}{{\frac{{\partial {\theta }_{a} \left( {\tau } \right)}}{{\partial {\tau }}}}}, $$

(6.78)

showing that the outflow $q_{ag}^{out}$ at time θ when the passenger exits arc a ∈ A is equal to the inflow $q_{ag}^{in}$ at time τ when the passenger entered it, divided by the derivative of the exit time at τ.

When the travel time is increasing (e.g., due to a growing queue), the outflow is smaller than the corresponding inflow; the opposite is true when the travel time is decreasing. Figure 6.19 shows how an arc speed v _a decreasing in time implies an arc flow q _a decreasing in space x, as the area of the two rectangles is equal.

Based on Eq. (6.78), the dynamic propagation of flows can be obtained by extending Eq. (6.22) expressing the flow balance of the node (see Fig. 6.18), as follows:

$$ q_{idmg} \left( \theta \right) = d_{idmg}^{{}} \left( \theta \right) + \sum\limits_{{a \in i^{ - } }} {\frac{{q_{{a^{ - } dmg}}^{{}} \left( {\tau_{a} } \right)}}{{\frac{{\partial \theta_{a} \left( {\tau_{a} } \right)}}{\partial \tau }}} \, \cdot p_{admg}^{{}} \left( {\tau_{a} } \right)} ,\quad \tau_{a} = \theta_{a}^{ - 1} \left( \theta \right),\forall a \in i^{ - } . $$

(6.79)

Fig. 6.18

Flow balance of node i at time θ for passengers directed towards destination d

The above time continuous model for network flow propagation can be transformed into a time discrete model by introducing the entry–exit map m _aet which denotes the share of users that enter arc a during interval e and exit it during interval t. Figure 6.19 shows how this share can be obtained from the exit time functional θ _a (τ), as follows:

Fig. 6.19

Relation among the profiles of travel time, entry flow and exit flow, according to FIFO rule, in the case of discrete time intervals

$$ m_{aet} = \frac{{{Min}\left( {{Min}\left( {{\theta }_{a}^{ - 1} \left( {{\tau }_{t + 1} } \right),{\tau }_{e + 1} } \right) - {Max}\left( {{\theta }_{a}^{ - 1} \left( {{\tau }_{t} } \right),{\tau }_{e} } \right),0} \right)}}{{{\tau }_{e + 1} - {\tau }_{e} }}. $$

(6.80)

In this case, the dynamic flow propagation, given in Eq. (6.79), becomes a series of systems, one for each interval t of duration h _t , which can be solved in chronological order, so that the node flows of previous time intervals are always known:

$$ q_{idmgt} = d_{idmgt}^{{}} + \sum\limits_{{a \in i^{ - } }} {\sum\limits_{e < t} {q_{{a^{ - } dmge}}^{{}} \cdot \frac{{h_{e} }}{{h_{t} }} \cdot m_{aet} \cdot p_{admge}^{{}} } } + \sum\limits_{{a \in i^{ - } }} {q_{{a^{ - } dmgt}}^{{}} \cdot m_{att} \cdot p_{admgt}^{{}} } $$

(6.81)

For sufficiently short-time intervals such that no user enters and exists any arc during the same interval (i.e., the aciclicity of causalities holds) it is: m _att  = 0; the above systems become diagonal and their solution is trivial (nodes can be processed in any order). Otherwise, the solution algorithms proposed in Sect. 6.1.4 can be applied.

4.3 Temporal Layer Formulation of Route Choice

The concatenation of time in dynamic route choices (see Fig. 6.20) can be ensured for arc-based models by substituting in Eqs. (6.18) and (6.16) the cost of each local alternative b ∈ i ⁺, denoted w _bdmg , with the cost of arc b for users entering it at time τ plus the expected cost to reach the destination from its final node evaluated at exit time θ _b (τ):

Fig. 6.20

Concatenation of travel times and local alternative cost

$$ w_{bdmg}^{{}} \left( {\tau } \right) = c_{bg}^{{}} \left( {\tau } \right) + w_{{b^{ + } dmg}}^{{}} \left( {{\theta }_{b} \left( {\tau } \right)} \right). $$

(6.82)

When time is discretized, Eq. (6.82) becomes the following:

$$ w_{bdmgt} = c_{bgt} + w_{{b^{ + } dmge}} + \left( {{\theta }_{bt} - {\tau }_{e} } \right) \cdot \frac{{w_{{b^{ + } dmg\;e + 1}} - w_{{b^{ + } dmge}} }}{{h_{e} }}{;} $$

(6.83)

the temporal profile of the head expected cost is interpolated at the exit time τ _t  + t _bt as a piecewise linear function between times τ _e and τ _e+1, where time index e is such that the corresponding interval of duration h _e  = τ _e+1 − τ _e contains the exit time: τ _e  ≤ τ _t  + t _bt  ≤ τ _e+1, as shown in Fig. 6.21.

Fig. 6.21

Linear interpolation of cost label profile

For what concerns the computation of local probabilities it is worth mentioning that to ensure the stability of equilibrium it is assumed that everybody behaves like the last passenger of the interval, otherwise some passenger would not suffer the effect of the congestion he/she generates.

For a suitable extension of the shortest paths problem to macroscopic dynamic models, temporal layers can be solved in reverse chronological order by setting the cost labels for passengers directed towards the current destination and leaving the node at the current time. If the largest interval of the adopted time discretization is smaller than the smallest arc travel time, then the dynamic shortest tree can be obtained by applying the Bellman update to all arcs in no particular order, otherwise the shortest path shall be processed in reverse topological order from destination to the furthest node, possibly adopting a Dijkstra algorithm as explained in Sect. 6.1.6.

4.4 Extension to Dynamic Hyperarcs

The extension of (6.82) and (6.26) to dynamic hyperarcs yields the following:

$$ w_{{{\breve{b}} dmg}}^{{}} \left( {\tau } \right) = \frac{{{\upgamma}_{{{\breve{b}}^{ - } g}} \cdot t_{{{\breve{b}} dmg}}^{{}} \left( {\tau } \right) + \sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} \left( {\tau } \right) \cdot \left( {c_{bg}^{nt} \left( {\tau } \right) + w_{{b^{ + } dmg}}^{{}} \left( {{\theta }_{{b|{\breve{b}} \;dmg}} \left( {\tau } \right)} \right)} \right)} }}{{\sum\nolimits_{{b \in {\breve{b}} }} {p_{{b|{\breve{b}} \;dmg}}^{{}} \left( {\tau } \right)} }}{,} $$

(6.84)

where the combined exit time θ _{b|b̌ dmg} (τ) = τ + t _{b|b̌ dmg} (τ) conditional to taking branch b ∈ b̌ is introduced to represent correctly the concatenation of travel times. This requires to modify also the flow propagation model by explicitly taking into account the hyperarcs and their branches as in (6.25):

$$ q_{idmg} \left( {\theta} \right) = d_{idmg}^{{}} \left( {\theta} \right) + \sum\limits_{{a \in i^{ - } }} {\left\{ \begin{array}{l} \sum\limits_{{{\breve{a}} \subseteq \left( {\left( {a^{ - } } \right)^{ + } \cap A_{m} } \right){: }{\breve{a}} \in H}} {\frac{{q_{{a^{ - } dmg}}^{{}} \left( {{\tau}_{a} } \right)}}{{\frac{{\partial {\theta}_{{a|{\check{a}}{\kern 1pt} dmg}} \left( {{\tau}_{a} } \right)}}{{\partial {\tau} }}}} \cdot p_{{{\breve{a}} dmg}}^{{}} \left( {{\tau}_{a} } \right) \cdot p_{{a|{\breve{a}} \;dmg}}^{{}} \left( {{\tau}_{a} } \right),} \quad {\text{if }}a \in A^{div} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\tau}_{{a|{\check{a}}}} = {\theta}_{{a|{\check{a}}\; dmg}}^{ - 1} \left( {\theta} \right),\forall a \in i^{ - } \hfill \\ \frac{{q_{{a^{ - } dmg}}^{{}} \left( {{\tau}_{a} } \right)}}{{\frac{{\partial {\theta}_{a} \left( {{\tau}_{a} } \right)}}{{\partial {\tau} }}}} \cdot p_{admg}^{{}} \left( {{\tau}_{a} } \right),\quad {\text{otherwise}},\quad {\tau}_{a} = {\theta}_{a}^{ - 1} \left( {\theta} \right),\forall a \in i^{ - } \hfill \\ \end{array} \right.}. $$

(6.85)

4.5 Representation of Service Frequency as a Continuous Vehicle Flow

Line frequencies are among the most important features of a transit network. In a within-day, dynamic context frequencies are not a constant input but rather the result of a propagation process, as shown in this section.

It is possible to represent frequencies as a flow of vehicles, for example, as an additional class of users who travel from the first stop of the line to the last one with disabled boarding and alighting arcs; the demand of this particular class is the frequency profile f _ℓ(τ) from the first stop. By construction, this flow has no route choice and shall follow exactly the line route.

From a formulation point of view, nothing changes with respect to the fixed-point scheme of Fig. 6.15 as frequencies can then be treated as an additional flow variable. Frequencies are processed by the FPM based on the current travel times and in turn influence, jointly with passenger flows, the travel times of both passenger and line-vehicle flows through the NCM. Thus, they become part of the DNL problem, which includes the averaging process.

More specifically, this particular flow can be propagated according to Eq. (6.78) along the sequence of line stops. The arrival and departure frequency of the generic line ℓ ∈ L at each stop can then be obtained by applying recursively the following equation starting from the first stop:

$$ \begin{aligned} f_{\ell s}^{dep} \left( {\theta } \right) &= \left\{ {\begin{array}{*{20}l} {f_{\ell }^{{}} \left( {\theta } \right){,}\quad {\text{if }}s = S_{\ell }^{ - } } \\ {\frac{{f_{\ell s}^{arr} \left( {\tau } \right)}}{{\frac{{\partial t_{\ell s}^{dwell} \left( {\tau } \right)}}{{\partial {\tau }}} + 1}},\quad {\tau }{ : }t_{\ell s}^{dwell} \left( {\theta } \right) + {\tau } = {\theta }{,}\quad {\text{otherwise}}} \\ \end{array} } \right. \hfill \\ f_{\ell s}^{arr} \left( {\theta } \right) &= \frac{{f_{{\ell s^{ - \ell } }}^{dep} \left( {\tau } \right)}}{{\frac{{\partial t_{{\ell s^{ - \ell } }}^{run} \left( {\tau } \right)}}{{\partial {\tau }}} + 1}},\quad {\tau }{ : }t_{{\ell s^{ - \ell } }}^{run} \left( {\tau } \right) + {\tau } = {\theta } \hfill \\ \end{aligned} $$

(6.86)

The result is a frequency which varies in time and is different from stop to stop depending on the travel time variation on running arcs and dwelling arcs. The latter is more relevant because it is an internal congestion and will be specifically addressed in Sect. 7.4.4.

4.6 Reference Notes and Concluding Remarks

As mentioned earlier, the development of macroscopic models for dynamic assignment has been casted mainly in the context of road networks; in particular, the proposed approach has been proposed in Bellei et al. (2005) and further developed in Gentile et al. (2005), Bellei et al. (2006), Gentile and Papola (2006) and Gentile (2015). Thus, the proposition of the framework presented in this section for transit networks, which introduces also sequential route choice through hyperarcs to reproduce passenger strategic behaviour, is to be considered an original contribution of this book.

Over the past few decades, many models were developed to solve dynamic transit assignment problems. Sumi et al. (1990) proposed a stochastic approach to jointly model departure times and route choices of passengers on a mass transit system. Alfa and Chen (1995) developed a transit assignment model for forecasting the temporal demand distribution along a corridor under a random assumption of passenger boarding. But more recently, the introduction of schedule-based models diverted most of the attention from macroscopic models for dynamic transit assignment.

An exception to this trend is provided in Meschini et al. (2007), who proposed a macroscopic DTA model based on continuous temporal profiles with variable frequencies and passenger queues; this work will be further analysed in Sect. 7.3.4. In the future, the link transmission models, developed by Yperman (2007) and by Gentile (2010) for road networks, will be likely adapted to reproduce transit networks by introducing a suitable node model describing the stop, thus further pushing the proposing approach.

5 Simulation-Based Models for Transit Assignment

• Oded Cats,
• Umberto Crisalli &
• Agostino Nuzzolo 

Computer simulations have become a useful framework for numerical modelling and the analysis of complex systems in various domains. In particular, simulations provide a powerful and attractive tool for representing system dynamics. This is especially true for large-scale systems that involve several interrelated stochastic processes that could not be solved analytically.

Agent-based simulations, in particular, allow to model complex systems that involve numerous autonomous and responsive elements. The agent-based modelling approach is used in a wide range of disciplines where the system dynamics emerge from the execution of individual strategies and the interactions among agents, as well as between each agent and the environment.

How can the simulation approach be used in the context of transit assignment modelling? Can transit system performance be represented as an emerging rather than a derived process? This section addresses these questions, exploring the development of simulation-based models for transit assignment by focussing on their potential capabilities, rather than on the formulation detail.

5.1 The Simulation Approach and Its Advantages

The transit assignment problem is concerned with finding the passenger flows and the corresponding travel times on the public transport network for a given travel demand. This is typically solved by the iterative loading of an origin–destination matrix consistently with a route choice model and the subsequent update of network conditions that may be required due to congestion phenomena (see Chap. 7). Simulation models enable to mimic the development of a global spontaneous order from numerous inter-dependent local and/or individual decisions. This modelling approach implies that the emerging equilibrium conditions are the results of complex interactions among numerous agents and the transit network dynamics.

The simulation-based approach has intrinsic advantages in obtaining a realistic representation of transit dynamics and in supporting the development of models that are practical for large-scale networks. Moreover, simulation models natively incorporate multiple classes through the synthesis of individual agents that are extracted from any distribution of user attributes. A great flexibility is allowed in the representation of agent interactions on the transport network (e.g., queuing, mingling, discomfort, seating), as well as of information provision and the consequent decision processes. In particular, simulation models are intended to mimic the adaptive response of travellers to changing system conditions and the incorporation of en-trip information in rerouting choices, thus making them a proper tool to support real-time traffic forecast and fleet management.

The main drawbacks of simulation models are the inability to derive mathematical functions that describe the system properties and the intrinsic randomness of the results, which actually represent a possible outcome of the system rather than the expected value of the desired output.

The combination of event-based mesoscopic modelling where passengers are aggregated in flows or packets on the supply side (congestion), along with a disaggregate modelling of individual decision-makers on the demand side (behaviour), yields better conditions for analysing large-scale systems with respect to fully microscopic models. This is particularly true when considering applications to advanced traffic management systems and advanced traveller information systems, where algorithm performance is an issue.

The more mature developments in the field of (road) traffic assignment models point to the potential role that simulation models can play in the context of transit assignment models. Coupling dynamic network loading (for the supply) and multi-agent simulation (for the demand) has been identified as a promising approach for modelling transit systems along with performance uncertainties and adaptive user decisions. However, the evolution of transit simulation models into dynamic transit assignment tools is at its early stages.

The mesoscopic approach in transit assignment consists of a dynamic disaggregated representation of both demand and supply, while their interaction is achieved through more aggregated models (e.g., discomfort functions, instead of pedestrian microsimulation). Assignment results are obtained from the iterative loading of individual passengers to individual-vehicles serving the runs of public transport. This stands in strike difference to both frequency-based assignment models on static network and schedule-based assignment models on diachronic graph which consider travellers in terms of aggregate flows or loads. In contrast, the simulation approach applied to transit assignment aims at reproducing traveller behaviour at a microscopic level where each autonomous unit is considered an agent. The progress of vehicles and passengers on the transit system yields the temporal and spatial distribution of demand over supply.

Each iteration of the simulation is usually regarded, not as a repetition of a same random outcome, but as the representation of a single day in the context of an evolutionary day-to-day process which may be continued until the system possibly reaches stable conditions (see Sect. 6.1.10). In this sense, the system performances at equilibrium (if any) emerge in a ‘bottom-up’ rather than a ‘top-down’ fashion.

The simulation-based approach is especially appropriate in cases where the design problem at hand is concerned with travel demand attributes and their distribution, such as the provision of information, possibly in real time and the consequent adaptive behaviour of passengers, where the resulting travel strategies differ considerably depending on heterogeneous preferences and socio-demographic characteristics.

Simulation is also useful when various travel decisions, such as trip departure time and mode choice, are jointly considered as part of the assignment model together with route choice.

The disaggregated representation of supply and demand dynamics (vehicles and passenger trajectories), but, on the other side, the aggregated representation of interaction between vehicles and passengers (e.g., dwell time, discomfort), facilitate the explicit modelling of service uncertainties. In particular, simulation is well suited for capturing the dynamic evolution of network performances under oversaturation conditions due to queuing and crowding on vehicles and at stops. Service reliability and passenger congestion are therefore endogenous variables which emerge from system dynamics and their impact on individual travellers can be explicitly modelled.

5.2 Agent-Based Models

Agent-based models have been first developed in the domains of computer science, artificial intelligence and cognitive science. The iterative process is therefore often presented as either a computational method for optimization problem or a learning algorithm. The former considers the assignment procedure in terms of an iterative convergent method that seeks to obtain travellers’ flows under stable steady conditions, while the latter formulates the iterative loading in terms of a cognitive process. While these different perspectives may be associated with a different interpretation and even implementation of modelling components, the simulation framework can be ultimately summarized in the following agent-based assignment algorithm, which adopts a day-to-day evolutionary approach, rather than an equilibrium approach (see Sect. 6.1.10):

• Step 0 Initialization: generate traveller population U; select K _u ∀u ∈ U; reset c̃ ¹ _KU ; n ← 0

• Step 1 New day: n ← n + 1

• Step 2 Network Loading: perform within-day assignment $p_{ku}^{n} \leftarrow p_{ku} ({\tilde{\mathbf{c}}}_{hu}^{n} ,\forall h \in K_{u} );$ obtain c ⁿ _KU for p ⁿ _KU

• Step 4 Stop criteria: check steady condition, e.g., $\left\| {\tilde{\mathbf{c}}_{KU}^{n} - {\mathbf{c}}_{KU}^{n} } \right\| < \varepsilon$

• Step 5 Update: perform day-to-day learning $\tilde{c}_{{ku}} ^{{n + 1}} \leftarrow \alpha _{u} ^{{learn}} \cdot c_{{ku}} ^{n} + (1 - \alpha _{u} ^{{learn}} ) \cdot \tilde{c}_{{ku}} ^{n}$

• Step 6 Return to Step 1

where

• n is the generic day

• U is the set of travellers

• u ∈ U is the generic traveller

• K _u is the set of paths considered by traveller u ∈ U

• K ∈ K _u is the generic path considered by traveller u ∈ U

• ${\tilde{\mathbf{c}}}_{ku}^{n}$ is the forecasted cost of path k ∈ K _u for traveller u ∈ U on day n

• $p_{ku}^{n}$ is the probability of path k ∈ K _u for traveller u ∈ U on day n (route choice)

• $c_{ku}^{n}$ is the actual cost of path k ∈ K _u for traveller u ∈ U on day n (congestion)

• $\upalpha_{u}^{learn}$ is the coefficient of the exponential learning filter for traveller u ∈ U

• ε is a small positive number

Note that in this scheme, the choice updating filter presented in Sect. 6.1.10 to reproduce the tendency of users to conform to habits is not explicitly introduced, but is indeed present is some of the implementations presented in the following.

Network loading (this is not the DNL of Sect. 6.4.1, but the NLM of Sect. 6.1.8) is hence performed in Step 2 iteratively at the individual level for the entire travellers’ population at once, so that congestion phenomena can emerge and affect passenger advancement. If the assignment results have not reached stable steady conditions, then the experienced travel attributes are incorporated into traveller cost anticipations for the following day/iteration.

The steps of the above algorithm are discussed in the remainder of this section, starting with a description of how supply and demand are represented in the simulation-based assignment model of transit networks, followed by the presentation of within-day and day-to-day dynamics. The discussion will refer to the following models which share the overarching schematic algorithm described above but vary with respect to their development context and objectives:

• MATSim, where the transit assignment model is part of an activity-based model;

• MILATRAS, which is tool for long-term planning of the transit system;

• BusMezzo, which is a joint traffic and transit assignment model oriented to operations.

These differences are clearly reflected in how supply and demand are represented in each one of these models as well as their overall design.

5.2.1 Demand Representation

The conventional origin–destination matrix considers demand in terms of aggregate traveller flows. However, travellers vary in their travel knowledge and preferences. For example, some travellers are extremely familiar with service supply and network prevailing conditions, such as the timetable and typical travel times, while others may have a limited knowledge on potential connections. Individuals also vary with respect to their travel preferences concerning alternative modes of transport, departure time and the importance of various trip attributes. For example, some travellers are very reluctant to transfer between transit services due to the uncertainty as well as physical and mental effort it induces, while others may be willing to transfer whenever it results with time savings.

The simulation of individual travellers enables, not only the representation of various user groups or classes with heterogeneous characteristics and preferences, but also the modelling of utility perception, strategy and experience at the individual level.

The first initialization step of an agent-based model for transit assignment involves the generation of a synthetic population of travellers. Initial conditions matter in case the learning and evolution processes are of interest, rather than only the (possible) steady conditions obtained at the end of the iterative process. MILATRAS was developed with the latter approach as it considers agents to have perfect knowledge on network topology but lack prior knowledge on performance attributes.

The generation process converts the O–D matrix into a population of agents, based on conditional probability functions for various user attributes. In case of transit travellers, origins and destinations may correspond to any location in the study area that is within walking distance to a transit stop. In the context of transit assignment, system initial conditions correspond to the planned service and individuals’ prior-perception of its performances. Agents could be distinguished with respect to attribute preferences, prior knowledge (e.g., commuter vs. occasional users), learning patterns (e.g., bounded rationality) or explorative versus habitual attitude. This determines the initially anticipated path attributes of each traveller. We can assume that all relevant attributes of paths are synthetized by a generalized cost. Cognitive science approach will imply that the initial conditions reflect agents’ mental map which is then progressively articulated.

BusMezzo is a joint traffic and transit assignment model where public transport passengers and private cars are generated based on separate time-dependent origin–destination matrices. Each traveller is assigned with inherited attributes such as trip departure time, walking speed, access to personal mobile device (e.g., real-time updates on instantaneous journey time), travel preferences (e.g., disutility associated with in-vehicle time versus wait time, walking time and transferring) and decision protocols (e.g., non-compensatory filtering rules, level of adaptation). These inherited attributes are maintained throughout the day-to-day simulation.

MILATRAS transforms a given O–D demand matrix into random geographical origin and destination locations based on residential and employment proportions through a GIS platform. Similarly, the synthetic population generated by MATSIM could also be obtained based on a probability function which reflects the distribution of various socio-demographic characteristics in the target population. For example, the population could be derived from the conditional probabilities that describe the relationships between fundamental travel decision determinants such as age, household composition and car availability. The activity-based simulation can hence link socio-demographic attributes to travel experience and guarantee the internal consistency of trip chains.

5.2.2 Supply Representation

Simulation-based models for transit assignment can vary with respect to the level of representation of the fundamental supply elements, namely stops and vehicles, as well as the movements associated with them. However, the disaggregate representation of travellers does not necessarily imply a microscopic simulation of transit vehicles and traffic dynamics.

Traffic simulation models are commonly classified based on their level of representation detail. Macroscopic models represent traffic as a continuous flow based on flow-density functions without the explicit modelling of lanes or vehicles. In contrast, microscopic models represent traffic at the most detailed level: individual-vehicle movements are represented and their driving behaviour depends on interactions with other vehicles, on the road geometry, on lane usage, etc. As a result of computational constraints, there is an inverse proportionality between the level of details and the possible size of networks under study. Mesoscopic models are an intermediate category, where individual vehicles are represented but detailed modelling of their second-by-second movement and interaction is avoided. Travel times on links are indeed determined by speed-density functions, while delays at intersections are calculated by using queue models.

Simulation-based model for transit assignment can conceptually use any of these levels of representation for passenger and carriers flow dynamics. A multi-agent transit assignment approach would typically imply the representation of individual transit vehicles and their movement would be governed by either microscopic or mesoscopic traffic flow principles. Occupancy on-board each vehicle can then be updated throughout the simulation and capacity constraints can be explicitly enforced. Moreover, passenger movements at stops and on-board can be represented in order to capture the impacts of crowding discomfort and queuing delays.

The available agent-based models for transit assignment differ considerably with respect to the level of integration they exercise with road traffic simulation models. MATSim is integrated into a larger transport model on the demand side, but transit supply is simulated separately from private traffic and a deterministic representation is adopted. MILATRAS is an advanced programming interface that allows the enhancement of PARAMICS, a mesoscopic traffic model. This implies certain restrictions on the extent to which transit dynamics could be explicitly modelled. BusMezzo is completely integrated into Mezzo, a traffic simulation model.

The progress of transit vehicles between one stop and the other is affected by the interaction with other vehicles. Even though MATSim includes a mesoscopic modelling of multimodal traffic flows, total traveller door-to-door journey time is deterministically assumed to be twice the corresponding free-flow times of cars. Transit travel times between stops are instead extracted in MILATRAS from link speeds that are modelled in a mesoscopic way by PARAMICS. Transit vehicles are thus propagated based on exogenous traffic conditions. BusMezzo also models traffic flows at a mesoscopic level where travel times of cars and transit vehicles depend on general (equivalent) traffic conditions. The explicit representation of background traffic allows capturing the impacts of congestion on transit operations. The level of interaction between transit vehicles and other vehicles depends on the right-of-way (e.g., buses running in mixed traffic, dedicated lanes, underground).

The explicit simulation of transit vehicles enables a rich and stochastic representation of public transport supply and its dynamics. Dwell times at stops are modelled in MILATRAS and BusMezzo as a function of passenger activity at stops. Trip dispatching times are modelled as a random variable in MILATRAS. Vehicle scheduling is modelled explicitly in BusMezzo which enables the propagation of delays through trip chaining. Different transit lines may be assigned to various vehicle types, running speeds and are operated with different control strategies. The explicit modelling of these processes and their inter-relations can facilitate a more realistic reproduction of the underlying sources of uncertainty and their joint impacts on reliability, compared with their generation based on independent statistical distributions. Specifically, emulating these dynamics allows modelling their impact on travellers’ route choice decisions. Moreover, it allows mimicking the generation and provision of passenger information.

5.2.3 Within-Day Dynamics

Route attributes may include travel time components (walking, waiting, riding, etc.), travel costs, number of transfers, as well as quality of service measures such as punctuality, crowding level and probability of denied boarding. Anticipated route attributes evolve iteratively through the incorporation of realized travel attributes from assignment results.

The within-day activity corresponds to a dynamic network loading procedure with travellers’ flow pattern determined by the decisions passengers make in reaction to transit conditions, such as vehicle arrivals at stops, experienced travel conditions and information provision. Throughout the day, travellers execute their trips and accumulate experience concerning various route attributes. For example, travellers gain experience on wait times for different lines, in-vehicle time between different locations using different routes or modes or even assess the reliability and crowding conditions on alternative services. This within-day learning allows travellers to exercise adaptive (or strategic) travel behaviour. At the same time, travellers’ decisions affect transit performances through the effect of passenger loads and flows on crowding, dwell times at stops and their secondary implications on service reliability. The dynamic interaction between supply and demand lies in the core of the within-day assignment.

The modelling of day-to-day dynamics allows both service users and service providers to adapt their strategy in order to optimize or improve their objectives. This occurs in the day-to-day update phase, where travellers integrate the experience of the previous days into their perception of the network cost pattern and choose the strategy that they will carry out in the following day. As travellers increase their experience with the transit system, their mental map extends and their expectations reflect more closely the actual performances. This day-to-day learning process can result in steady conditions that are equivalent under certain conditions to user equilibrium.

The interaction between network supply and passenger demand takes place in the within-day dynamic network loading. This is the core of the day-to-day iterative process, where system dynamics are simulated and transit performance is determined.

The other fundamental building block is the way in which individual agents decide how to travel towards their destination. This highlights an important difference from conventional models for transit assignment, as the choice probability is referred to individual decisions rather than to travellers flow. Here, choice probabilities determine therefore the likelihood that a certain travel alternative will be used by a single individual depending on his/her specific attributes, instead of the passenger flow share that is distributed over a certain path set. A choice-set generation model composes first the paths that will be further considered in the route choice phase based on a combination of various path search methods and heuristic filtering rules.

Various route choice models can be formulated and embed into simulation-based transit assignment, which may differ with respect to each of the above components. In particular, the linkage between these components could be based on alternative theoretical grounds, from rule-based computational processes to utility maximization econometric models. In general, we can apply Eq. (6.40) to the single traveller:

$$ p_{ku}^{n} = p_{ku}^{{}} \left( {\tilde{c}_{hu}^{n} ,\forall h \in K_{u} } \right). $$

(6.87)

The within-day network loading in MATSim is the result of choices among alternative travel plans rather than paths per se. The utility function of transit alternatives is composed of static and deterministic door-to-door travel time. Hence, the utility value is uniform across the population. Probabilities are assigned to alternative travel plans based on a multinomial Logit. Paths are chosen at the O–D level with no within-day learning.

MILATRAS assigns at the origin a tentative travel plan to each passenger that will be followed unless the travel experience differs substantially from the expectations. Expected travel time components are based on previous experience (day-to-day learning) and real-time information provision; in case that no information is available, travellers’ expectations depend solely on their experience. MILATRAS is a bounded rationality model with a deterministic utility function: there is a rule that allows to decide between an exploitation option (a deterministic choice of the alternative with the maximum utility) and an exploration option (a random choice over the set of considered alternatives). This can potentially capture the process of habit formation and occasional deviations.

Route decisions in BusMezzo are based on agent’s current expectations on future travel attributes. The anticipated travel attributes incorporate prior knowledge, previous experience (day-to-day learning) and real-time information provision. The model includes a phase of non-compensatory choice-set generation followed by a probabilistic path choice process. The progress of travellers in the transit network is considered as a sequential process of successive arc decisions; thus passengers do not choose at any point between door-to-door paths. The adaptive path choice model was developed within the framework of random utility.

More specifically, for each local choice, such as boarding versus waiting at the stop or alighting versus staying-on-board, the passenger evaluates alternative actions by assessing the joint (or expected) utility to reach the destination conditional on taking that arc using the logsum term for all the available paths, as follows:

$$ w_{au}^{n} = Log\left( {\sum\limits_{{k \in K_{ua} }} {{Exp}\left( { - \tilde{c}_{ku}^{n} } \right)} } \right){,} $$

(6.88)

where

• a is the travel action (e.g., ‘walk to given stop’, ‘board a given line’) associated with an arc

• K _ua is the subset of sub-paths of K _u from arc a to the destination of traveller u ∈ U

• $w_{au}^{n}$ is the composite utility of the local action a for traveller u ∈ U in day n.

Thus, the upper level of the choice model refers to travel actions rather than path, while the used path is merely an outcome of individual’s successive decisions; again, passengers do not choose a path per se at any given point along their trip.

The generalized cost ${\tilde{\mathbf{c}}}_{ku}^{n}$ may synthesize in a linear form several attributes c ∈ C of path k, whose expected values anticipated by the passenger for day n are denoted $\tilde{a}_{{kcu}}^{n}$; these are differently perceived by each user u who associates to them a specific weight β _cu , so that it is:

$$ \tilde{c}_{ku}^{n} = \sum\limits_{c \in C} {{\upbeta }_{cu}^{{}} \cdot \tilde{a}_{kcu}^{n} } . $$

(6.89)

As an example, the set of attributes C may include the number of transfers, in-vehicle time, wait time and walking time. This path utility function can be extended by accounting for service reliability and on-board crowdedness. The attribute values are determined by the integration of various information sources.

The within-day dynamic network loading yields passenger flows on each arc for that day. In addition, the values of the attributes experienced by the passengers on the utilized paths are obtained and are used to update the anticipated values for next day.

5.2.4 Day-to-Day Dynamics

The day-to-day learning process updates system states between successive network loadings. This process continues as long as the stopping criteria are not satisfied. The stopping criteria typically refer to the marginal change in key assignment outputs. For example, the stopping criterion can be defined as the share of travellers that changed their path from the previous day. If passengers cannot improve their travel costs by choosing an alternative path, then equilibrium conditions have been obtained. A probabilistic path choice, such as in MATSim and BusMezzo, could also be conceived in terms of a strategy repeated game and the Nash equilibrium. The convergence of assignment results can also be defined as a stopping criterion by considering changes in obtained arc flows. From a behavioural perspective, this indicates that travellers’ perceptions are consistent with their experience, so that they have not gained new information from their most recent trips. This can also be explicitly assessed by checking whether the vector of travel attributes (costs) experienced by each single passenger is significantly different from its estimation before travelling.

The day-to-day learning process updates traveller perception by integrating the experience c ⁿ _ku obtained on the path that was followed on day n, denoted k, to the accumulated passenger memory c̃ ⁿ _ku . Then, we can apply Eq. (6.39) to the single traveller:

$$ \tilde{c}_{ku}^{n + 1} = {\upalpha }_{u}^{learn} \cdot c_{ku}^{n} + \left( {1 - {\upalpha }_{u}^{learn} } \right) \cdot \tilde{c}_{ku}^{n} {,} $$

(6.90)

where $\upalpha_{u}^{learn}$ is the step size assigned to the most recent experience. Various learning functions can be specified for different segments of the traveller population to determine how the step size evolves over time. For example, in the method of successive averages, (MSA) the step size is a function of the number of days/iterations, but not of their corresponding performances, with the weight of new solutions gradually decreasing throughout the solution process. In contrast, a more behavioural approach may assign larger weights to latter experiences.

The updating process in MILATRAS is formulated as a Markov decision. Each possible departure time and path decision combination is expressed as a state-action pair, where passengers’ current state contains sufficient information for determining the next state. The Markov process is a non-equilibrium framework; however, the decision process may fulfil the conditions for convergence to a unique and optimal solution in terms of passenger state-action choices.

The day-to-day learning in MILATRAS and BusMezzo includes also the update of real-time information credibility. The information provided is evaluated against the experienced performance and influences the weight given to real-time information in future decisions.

5.3 Traveller Cognitive Process

In simulation-based models for transit assignment, the route choice probabilities lie at the individual level, as shown in Eq. (6.87), and result in passenger flows only after aggregation.

The disaggregated agent-based representation of transit demand is well suited to represent a population of travellers that is not uniformly informed about transit supply. Moreover, the representation of traveller learning behaviour, with an emerging mental map representation, enables the incorporation of various information sources and their integration into the path choice that changes dynamically from day-to-day.

These notions are elaborated in the following while referring to their implementation in MILATRAS and BusMezzo. In contrast, MATSim performs a joint modal split and route choice assuming that all travellers have perfect knowledge and information of the transit system; this approach is inspired by co-evolutionary theories. Moreover, this model does not distinguish between anticipated and experienced travel attributes. MATSim is therefore currently not suitable for modelling information scenarios and rerouting.

The strategies of travellers in a simulation-based model for transit assignment could be determined as the outcome of three sources of information:

• prior knowledge—the static information for passengers has on the planned service (e.g., schedule, frequencies);

• past experience—the accumulated first-hand experience with service performance, and

• real-time information—with respect to the arrival times expected today, in case available.

The reminder of this section describes how each of the above information sources is modelled in the context of a simulation-based framework, as well as how these information sources are integrated in the within-day assignment model and evolve from day to day.

5.3.1 Prior Knowledge on the Transit Network

A synthetic population U of users is generated based on probability functions that reflect the distribution of travellers’ characteristics in the population. Expectations for day 1 on costs ${\tilde{\mathbf{c}}}_{ku}^{1}$ for each user u ∈ U and each path k ∈ K _u are static sources of information that travellers inherit upon initialization.

This prior knowledge can be limited to network topology, as in MILATRAS, without any information on travel attributes; e.g., a fully optimistic null cost c̃ ¹ _ku  = 0 ∀ k ∈ K _u is assumed. This implies that the first simulation will result with randomly chosen paths. This is equivalent to starting an optimization process with a randomly sampled solution and then progressively improving it using an iterative update process. Note that this is nevertheless different from models that generate travellers that are ‘tabula rasa’ and let them explore the network by applying random walk methods.

Alternatively, travellers can be assumed to have certain expectations on alternative path costs based on their prior knowledge. This information can be derived from planned headways, travel distances, travel times between stops or even timetables, as in BusMezzo.

In any case, travellers have no prior knowledge concerning other path attributes, such as service reliability or crowding levels.

For example, the prior knowledge may imply that the anticipated wait time at a given stop is half of the expected headway of the considered line, while actual wait times are the outcomes of the dynamic progress of individual travellers and vehicles in the simulation; the anticipated in-vehicle time may reflect the schedule or the expected speeds of road links during the relevant time period, which may vary due to traffic conditions on different times of day.

5.3.2 Accumulated Experience

The travel experience of each passenger u ∈ U is however accumulated at the level of each single attribute c ∈ C of the path k ⁿ ∈ K _u used in each day n, whose value is denoted ${{a}}_{kcu}^{n}$. The way in which this continuously updated source of information is compressed into a single value ${\tilde{{a}}}_{kcu}^{n}$ anticipated by the passenger for day n is defined by the day-to-day learning function. This function can, for example, allocate a greater value to more recent experience or specify a limited memory horizon.

The experienced attributes are calculated based on simulation dynamics. In particular, the experienced wait times are calculated directly as the time difference between traveller arrival time at stop and the time at which the passenger boarded a vehicle. The latter is also used as the reference value for calculating the experienced in-vehicle time until the passenger alighted the vehicle. BusMezzo and MILATRAS also represent access, egress and transfer links and account for their experienced travel times in a similar fashion.

The experience in the same day made earlier during the trip can also influence in traveller path choice. If the perceived path attributes deviate substantially from those anticipated, then passengers may revise their choice. For example, if a passenger experiences a wait time that exceeds considerably from that anticipated, then the connection decision is reconsidered and the traveller may choose to walk to another nearby stop.

5.3.3 Real-Time Information Provision

The dissemination of real-time information (RTI) may influence travellers’ attribute perception and ultimately passenger flows. The RTI that is available to a traveller when making a certain route decision is determined by the dissemination means and their locations, as well as by individual characteristics, such as the availability of a personal mobile device. The rapid increase in the penetration rate of smart phones may considerably change the dissemination pattern, since passengers are possibly provided with instantaneous access to RTI during their entire trip.

Agent-based models for transit assignment enable the generation of RTI for the single passenger, based on individual-vehicle progress and arrival prediction schemes, which are embedded into the simulation engine. The explicit modelling of real-time predictions and information generation as a function of dynamic supply conditions enables the analysis of alternative dissemination strategies. In particular, the impact of various information provision schemes on travellers’ decisions and ultimately on travellers’ flows can be assessed. Note that RTI is therefore not equivalent to modelling the impact of perfect information.

Information availability is uniform across the population in MILATRAS, which represents the impacts of RTI on vehicle arrival times, when available pre-trip or through public displays at stops or on-board. The RTI concerning wait times is calculated based on the average conditions during the previous 45 min.

The dissemination of passenger information simulated in BusMezzo is classified according to the following aspects:

• Type—wait times, in-vehicle travel times, crowding levels, service disruptions;

• trip stage—pre-trip, at stops, on-board;

• comprehensiveness—concerning the local stop, cluster of connected stops (i.e., transit hub), the entire system.

The share of individuals that have access to RTI by using a personal mobile device can be specified in the population generation phase. The combination of the above aspects determines the level of information that is available to a specific passenger at each trip stage regarding downstream travel conditions.

The approach adopted in the BusMezzo implementation is to generate RTI based on historical data as expressed in timetables and on real-time data as resulting from the vehicle propagation. For example, RTI concerning wait time is calculated based on the current schedule deviation of the next vehicle arriving vehicle and the remaining travel time to reach the stop based on historical average. This scheme is aimed to replicate the method that is commonly used by transit agencies for generating real-time information.

Given the above information sources, traveller decisions are modelled in the probabilistic framework of random utility choice models. The evaluation of local alternative actions, as in Eq. (6.88), depends on passenger preferences and expectations with respect to forecasted travel attributes. The individual decision protocol specifies the forecasted attributes â ⁿ _kcu as convex combination of the following information sources:

• ${\varvec{\hat{a}}}_{kcu}^{n}$, the prior knowledge,

• ${\varvec{\hat{a}}}_{kcu}^{n}$, the value anticipated by the passenger based on the accumulated experience,

• ${\varvec{\hat{a}}}_{kcu}^{RTI}$, the value resulting from real-time information.

We have then:

$$ \hat{a}_{kcu}^{n} = {\upalpha }_{u}^{{{PK}n}} \cdot \tilde{a}_{kcu}^{1} + {\upalpha }_{u}^{{{TE}\;n}} \cdot \tilde{a}_{kcu}^{n} + {\upalpha }_{u}^{{{RTI}\;n}} \cdot \tilde{a}_{kcu}^{RTI} {,} $$

(6.91)

where $\upalpha_{u}^{{{PK}n}}$, $\upalpha_{u}^{{{TE}n}}$ and $\upalpha_{u}^{{{RTI}n}}$ are the weights (that sum up to one) associated with prior knowledge (PK), travel experience (TE) and real-time information (RTI), respectively, in day n. These weights could be interpreted in terms of the credibility associated with each information source. Therefore, in presence of information Eq. (6.89) becomes:

$$ \tilde{c}_{ku}^{n} = \sum\limits_{c \in C} {{\upbeta }_{cu}^{{}} \cdot \hat{a}_{kcu}^{n} } . $$

(6.92)

5.3.4 Day-to-Day Evolution of Information Credibility

The weights associated with the various information sources are determined through a day-to-day learning process and thus vary with day n. Hence, day-to-day dynamics influence not only the experienced travel attributes, but also the credibility assigned to various information sources. As the day-to-day assignment progresses, the weight given to prior knowledge is expected to decrease while the impact of experience increases. Moreover, the credibility associated with various information sources vary among travellers. However, the extent to which the memory of passenger u with respect to path k ⁿ ∈ K _u extends over time is determined endogenously as it depends on how relevant is the path that was followed in day n in that network loading iteration and cannot be defined a priori as a function of n.

Moreover, the weight given to RTI reflects its perceived credibility which is a function of the extent to which the information provided in advance accurately predicted the corresponding travel attributes actually experienced. For example, the day-to-day update function of the RTI weight can take the following form:

$$ {\upalpha }_{u3}^{{{RTI}\;n + 1}} = \upalpha_{u}^{cred} \cdot \frac{{\left\| {\tilde{a}_{kcu}^{RTI} - a_{kcu}^{n} } \right\|}}{{a_{kcu}^{n} }} + \left( {1 - {\upalpha }_{u}^{cred} } \right) \cdot {\upalpha }_{u3}^{{{RTI}\;n}}, $$

(6.93)

where $\upalpha_{u}^{cred}$ is the step size assigned to the most recent experience and the attributes refer to k ⁿ that is the path used in day n.

5.4 Mesoscopic Models for Schedule-Based Simulation

In Sect. 6.3, the schedule-based assignment is presented for uncongested networks with regular services (that perfectly adhere to the timetable) assuming that passengers make a fully preventive route choice. This approach is very limiting to model urban transit networks, especially when we need to take into account the effects of:

• vehicle capacity, with queue formation and fail-to-board events;

• service irregularity, with path attributes that change over time;

• passenger’s en-route choices, due for example to the arrival of a run at a stop later than expected or the arrival of overcrowded vehicles.

In particular, the basic schedule-based models reported in Sect. 6.3 do not allow for the simulation of real-time conditions and short-term prediction.

Therefore, in the following another class of schedule-based models for transit assignment is reported. It uses a simulation approach, which allows to overcome the above-mentioned limits.

In particular, schedule-based assignment can be casted as an event-based simulation, in which events represent instants when passengers depart from origins or transit vehicles arrive and depart at stops.

Passengers depart from origins with a preventive path choice in mind. Once arrived at stops, the simulation of fail-to-board probabilities due to possible formation of queues induces rerouting choices, thus providing a better estimation of vehicle loads for each run. Note that rerouting (especially if queues are not a recurrent event) does not necessarily imply a strategic behaviour, where passenger would choose a hyperpath (and not a path) fully including expectations on the real-time events and their costs.

Moreover, the use of schedule-based simulation models allows to reduce the computational complexity of large networks. It can be defined in the context of a mesoscopic approach similar to that described in Sect. 6.5.2, which presents an aggregate representation of individual-vehicle performances, allowing to avoid the simulation of second-by-second vehicle movements and interactions. Specifically, while the mesoscopic models of Sect. 6.5.2 are characterized by a disaggregate representation of the demand at single passenger level, the simulation approach to the schedule-based assignment here presented considers also in aggregate way the demand as group of travellers with homogeneous features, called ‘packets’, i.e., passengers moving over the transit network and experiencing the same trip. Therefore, the demand–supply interaction of this class of models is based on a within-day dynamic network loading in which packets of passengers are propagated along the chosen transit routes.

5.4.1 Supply Variance

The network model is made of transit services represented by runs moving between stops with travel times that are external inputs. Therefore, the representation of transit services uses the run-based approach and the diachronic graph described in Sect. 6.3. In case of real-time simulation, each time a transit vehicle departs from a stop; the diachronic network is updated with the new forecasted travel times that are used for the next step of the simulation. Such travel times can be obtained through an Automated Vehicle Location (AVL) system in case of real-time and short-term modelling or they can be the result of realisations of multidimensional random variables with parameters and dispersion matrix obtained from experimental data (e.g., using Automated Vehicle Monitoring data). If experimental data are not available, departure times from the terminals can be assumed equal to the scheduled times and travel times (summing up, running and dwell times) as multivariate normal variables with the average equal to the scheduled times plus a given quantity and variance–covariance matrix Σ defined, considering correlation among running and dwell times of the same and different sections.

Starting from the vector of scheduled arrival/departure run-times at stops, we obtain the vector of scheduled run and dwell times θ, according to which vector θ ⁿ of actual run and dwell times in day n is generated by extracting values from multivariate normal random variable, MVN(θ, Σ).

The obtained vector θ ⁿ must satisfy some feasibility rules including the congruence of generated times with the allowed speeds for transit vehicles and the congruence of possible bunching phenomena, for which runs passing on the same sections cannot pass one another, so the quickest vehicles must slow down and follow the slowest ones. The vector that satisfies the above feasibility criteria is used to update the diachronic graph for the next simulation step.

5.4.2 Hierarchic, Sequential and Adaptive Route Choice

In the framework of the simulation-based mesoscopic approach, instead of individual passengers, the model considers packets of passengers with homogeneous characteristics (at least, origin, destination and desired departure time from origin or desired arrival time at destination) moving on the transit network.

The segmentation over time of the demand can be represented by dynamic O–D trip matrices, from which packets of passengers can be generated for each minute of the simulation period.

The typical approach in modelling trip choices is based on random utility, where a set of alternatives is identified and each one is associated with a systematic utility plus a random residual with a given joint distribution (see Sect. 4.5). In this case, the path choice probabilities (6.87) apply to the packet of travellers, allowing thus to estimate the average number of passengers using a given run, and then their contribution to its on-board load.

As introduced in the previous section, the preventive joint (one shot) approach to modelling route choice, where the passenger decides the whole path from the origin to the destination before starting his/her journey, based on historic information obtained from previous trip experiences or supplied by a travel planning system, can be questioned from a behavioural point of view.

A different interpretation of user behaviour assumes that the actual route used by the passenger results from a hierarchic sequence of stop choice and run choice, until the destination is reached. Moreover, these choices can be based, not only on past experience, but also on the information regarding the current conditions of the transport system, possibly improved by real-time updates.

For the choice of the first boarding stop s ∈ S where to access the next service starting from vertex i ∈ B at instant t ∈ T, we can assume a pre-trip choice behaviour, based on the comparison of possible alternative considering expected characteristics, or attributes, which also include variables such as the inclusive utility. The choice set is defined by the stops that are reachable within a maximum walking time t ^wmax _g on the pedestrian network, which differs for each user class g ∈ G.

The opposite of the systematic utility v ^idgt _s of each stop s ∈ S for passengers of class g ∈ G directed towards destination d ∈ D can be given as follows:

$$ - v_{s}^{idgt} = {\upgamma}_{sg}^{stop} \cdot t_{g}^{stop} + {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{walk} \cdot t_{is}^{walk} + w_{jdg}^{{}} {,} $$

(6.94)

taking into account:

• the characteristics of the stop (e.g., ergonomy, presence of shops) which can be synthetized by the stop discomfort coefficient $\upgamma_{sg}^{stop}$ (introduced in Sect. 5.1.2) that multiplies in this case a reference stop time $t_{sg}^{stop}$;

• the walking time $t_{is}^{walk}$ on the shortest path from i to $B_{s}^{stop}$ on the pedestrian network;

• the set of connection opportunities that can be found at stop s, synthetized by the inclusive utility (also called satisfaction) w _jdg of node j = (s, e), which represents the attractiveness of the stop in terms of runs useful to reach the destination at the time when s is reached, $e = t^{ + } (\tau_{t} + t_{is}^{walk} )$.

The probability $p_{s}^{idgt}$ of choosing stop s starting from vertex i ∈ B at instant t ∈ T is formally given by (Fig. 6.22):

$$ p_{s}^{idgt} = p_{s}^{idgt} \left( {v_{{s^{\prime}}}^{idgt} ,\forall s^{\prime}{: }t_{{is^{\prime}}}^{walk} \le t_{g}^{wmax} } \right). $$

(6.95)

Fig. 6.22

Example of hierarchic approach to the subsequent choice of first stop and route

Once arrived at stop, transit vehicle boarding (e.g., run choice) is simulated through an at-stop choice behaviour, which describes how users respond to unknown or unpredictable events, such as the transit vehicle arrivals in a different sequence with respect to the expected one due to service irregularity.

The overall choice set for a passenger arriving at stop s at instant t includes each run that directly or indirectly allows to reach to destination d and satisfies some predefined rules, such as the following:

• it is the first run of its line departing from the stop after the user arrival (this shall be removed in case of oversaturation queues when passengers may not be able to board the next-arriving run of each line);

• it is not dominated by another run leaving after arriving before with a lesser generalized cost;

• it implies less that a maximum number of transfers.

The choice of the run r ∈ R to board at stop s ∈ S for a user that reached it at instant t ∈ T can be interpreted as the result of a sequential dynamic decision, where the passengers waiting at the stop probabilistically reject or accepts to board each arriving run r ∈ R depending on their performance estimation of the run alternatives r′ that are still available to reach the destination d ∈ D.

The estimation may take into account also the current conditions of the service (possibly provided by a real-time information system). Indeed, frequent users, who know from previous experience how the system operates, can react to en-route events (or to their information) to optimize their journey cost by adapting their route choice (the same result can be obtained through personal information provided by a real-time journey planner). However, this goes in the direction of a strategic behaviour which is treated in the next chapter (see Sect. 7.1); therefore, in the following, the role of information is simply included in the random errors associated with each run of the choice set.

The opposite of the systematic utility $v_{{r|r^{\prime}}}^{sdgt}$ associated with each run r of the choice-set conditional upon arrival of run r′ for passengers of class g ∈ G directed towards destination d ∈ D can be given as follows:

$$ - v_{{r|r^{\prime}}}^{sdgt} = {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{wait} \cdot {\upgamma}_{sg}^{stop} \cdot {\upgamma}_{sgt}^{crowd} \cdot \left( {{\theta }_{rs}^{{}} - {\theta }_{{r^{\prime}s}}^{{}} } \right) - {\upgamma}_{g}^{vot} \cdot {\upgamma}_{g}^{loss} \cdot \left( {{\theta }_{{r^{\prime}s}}^{{}} - {\tau }_{t}^{{}} } \right) + c_{{L_{r} s}}^{bfee} \cdot {\upgamma}_{g}^{mfee} + w_{jdg}^{{}} {,} $$

(6.96)

taking into account:

• the wait time for run r given by θ _rs  − θ _r′s ;

• the time already waited θ _r′s  − τ _t , where the value of time γ ^vot _g is further multiplied by a new discomfort coefficient $\upgamma_{{_{g} }}^{loss}$ that weights the regret of the passenger on the past lost opportunities and the consequent ‘loss of hope’ in the future opportunities;

• the monetary cost $c_{\ell s}^{bfee}$ of boarding line ℓ = L _r at stop s;

• the expected cost to reach the destination once the passenger is on-board of the run r, which includes travel time, comfort and number of transfers, which is synthetized by the inclusive utility (also called satisfaction) w _jdg of node $j = N_{rs}^{dep}$.

The attributes composing Eq. (6.96), including those making up the inclusive disutility w _rsdg , can be differently estimated according to the information sources through Eq. (6.91).

It is worth noting that the choice set is modified over time during the wait because after each arrival, the corresponding run is eliminated (and possibly the next run of the line is added).

When a run r arrives at the stop a passenger may choose to board it if its perceived utility (given by the systematic utility plus a random residual) is greater than that of each other run r′ > r of the choice set that has not passed yet (with some abuse of notation). The resulting (conditional) probability of choosing to board the arriving run r′ is denoted p ^sdgt _r′|r′ and depends on the systematic utilities v _r′′|r′ of each run r′′ ≥ r′. If the passenger does not choose run r, the choice is reconsidered when the next run r′ arrives and so on.

Thus, a run r is boarded if it is chosen when it arrives at the stop while the runs r′ < r of each previous arrival where not chosen. If such events are assumed independent from each other, it is possible to evaluate the unconditional probability $p_{r}^{sdgt}$ of boarding run r by a passenger of class g directed to destination d who arrives at stop s at instant t as follows:

$$ p_{r}^{sdgt} = p_{r|r}^{sdgt} \left( {v_{{r^{\prime\prime}|r}}^{sdgt} ,\forall r^{\prime\prime} \ge r^{\prime}} \right) \cdot \prod\limits_{{r^{\prime} < r}} {\left( {1 - p_{{r^{\prime}|r^{\prime}}}^{sdgt} \left( {v_{{r^{\prime\prime}|r^{\prime}}}^{sdgt} ,\forall r^{\prime\prime} \ge r^{\prime}} \right)} \right)} . $$

(6.97)

The above model can be particularly difficult to solve. To reduce the computational effort of this approach, the following further assumptions can be made:

• only the choice of the first stop from the origin is considered as a separate hierarchic level, while the choice of intermediate stops is included in the run choice of a joint route to reach the destination;

• the choice-set restriction mechanism is not considered, while instead a new run of the line that just passed is added;

• the loss discomfort coefficient is assumed null.

In this case, the proposed sequential framework reduces to a stochastic arc-based model on the diachronic graph which can be solved easily through the equations and algorithms provided in the previous sections. Indeed, for each run departure from a stop, the diversion on the diachronic graph between boarding arc and (keep) waiting arc represents a binary probabilistic choice, in which all passengers have the same behaviour independently from their arrival time at the stop.

5.4.3 Dynamic Network Loading

The dynamic network loading allows to simulate the propagation of travellers on the diachronic graph and to obtain run on-board loads. It can be divided into several steps considering the simulation framework in which the previous choices of travellers moving on the network are updated at stops.

The first step consists of loading the pedestrian network from origins to access stops on the basis of traveller pre-trip choices consistently with Eq. (6.95). The second step allows defining the contribution to the on-board load of each run consistently with Eq. (6.97).

The loading process is carried out in discrete times, considering only the instants in which a run of transit services arrives at any of the stops and hence on-board loads could change. Passenger boarding a given run is obtained by summing up all contributions due to all paths of all O–D pairs.

If the loads of passengers willing to board a given run at a given stop exceeds the residual capacity, this implies a redistribution of this share to next-arriving runs and updating the path choice for the passengers who failed-to-board, using in a recursive way the loading process defined by Eqs. (6.96)–(6.97), and assuming a FIFO rule or a mingling rule at the stops (see Sect. 7.3).

5.5 Reference Notes and Concluding Remarks

The application of day-to-day dynamic assignment to transit networks for schedule-based models on diachronic graphs (see Sect. 40) is today further employed in most simulation-based approaches (e.g., Toledo et al. 2010).

Among simulation-based models for transit networks we can mention: MATSim (Balmer et al. 2008), where the transit assignment model is part of an activity-based model; MILATRAS (Wahba and Shalaby 2005), which is tool for long-term planning of the transit systems; BusMezzo (Cats 2013), which is a joint traffic and transit assignment model oriented to operations. In addition to the above models, an agent-based bus model was developed by Meignan et al. (2007). However, it is not a simulation-based as passengers’ decision is limited to choosing between the shortest path by alternative travel modes.

In any case, the reader should know that the development of simulation-based models for transit assignment is still in its early stage. Their development is inspired by a range of theoretical domains and their implementation is often part of a larger laboratory environment development.

The dynamic and disaggregate modelling of both transit supply and demand could potentially yield more realistic assignment results. The validation of simulation-based transit assignment model is a prerequisite for them to become more operational. The representation of traffic dynamics is already at a mature stage with sufficient validation studies. Transit vehicle trajectories and service variations were validated for BusMezzo (Cats et al. 2010, 2011). Moreover, MATSim traffic assignment and MILATRAS transit assignment were validated against standard assignment tools (Gao et al. 2010; Wang et al. 2010). These validation results provided positive indications. However, there is a need to further validate assignment results against actual time-dependent passenger flows at the individual-vehicle run level.

The performance of agent-based transit assignment model in terms of running times and convergence properties has not been carefully analysed yet. The availability of prior knowledge for example may provide a first feasible solution, which will improve the assignment solution process in terms of both quality and speed compared with starting with a random solution. The learning function parameters also presumably have important implications on the converging process. Further developments of dynamic path choice models and the underlying behavioural determinants will require a more extensive framework for representing memory construction as well as habit formation and risk assessment.

Until agent-based models will not reach acceptable calculation times, the use of schedule-based simulation models allows us to reduce the computational complexity, particularly in large network applications. The use of the schedule-based assignment approach can be very useful for real-time and short-term modelling, and today, it represents one of the frontiers of modelling and applications in this field, especially when effects of traveller information on short-term predictions about on-board loads should be deployed.

Simulation-based assignment models provide a natural common modelling platform for analysing complex urban transport dynamics. The co-evolutionary process which drives the assignment and the modular simulation environment could potentially accommodate additional travellers’ adaptation strategies such as modal shift, trip departure time adjustments and even destination choice. Existing models already combine several decisions layers. This development is in line with the development of activity-based demand models and agent-based urban planning tools such as ILUTE (Salvini and Miller 2005) and PUMA (Ettema et al. 2007).