The Perspective Face Shape Ambiguity

Abstract

When a face is viewed under perspective projection, its shape (i.e. the 2D position of features) changes dramatically as the distance between face and camera varies. This causes substantial variation in appearance which is significant enough to disrupt human recognition of unfamiliar faces. However, a face viewed at any distance is still perceived as natural and humans are bad at interpreting the subject-camera distance given only a face image. We show that perspective viewing of faces leads to an ambiguity. Namely, that observed configurational information (position of projected vertices) and shading can be explained by a continuous class of possible faces. To demonstrate the ambiguity, we propose a novel method for efficiently fitting a 3D morphable model to 2D vertex positions when the subject-camera distance is known. By varying this distance, we obtain a subspace of faces, all of which are consistent with the observed data. We additionally show that faces within this subspace can all produce approximately the same shading pattern via a spherical harmonic lighting model.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

When a human face is viewed under perspective projection, its projected shape varies with the distance between the camera and subject. The change in the relative distances between facial features can be quite dramatic. When a face is close to the camera, it appears taller and slimmer with the features closest to the camera (nose and mouth) appearing relatively larger and the ears appearing smaller and partially occluded. As distance increases and the shape converges towards the orthographic projection, faces appear broader and rounder with ears that protrude further and the internal features more concentrated towards the centre of the face. We show some examples of this effect in Fig. 14.1. Images from the Caltech Multi-Distance Portraits database [10] are shown in which subjects are viewed at a distance of 60 cm and 490 cm. Each face is cropped and rescaled such that the interocular distance is the same. The distortion caused by perspective transformation is clearly visible. When the faces are unfamiliar, it is difficult to believe that the identity of the faces in the first row are the same as those in the second.

Fig. 14.1

Perspective transformation of real faces (From [10]). The subject is the same in each column but the change in viewing distance induces a significant change in projected shape

The change in face appearance under perspective projection has been widely noted before, for example in art history [20] and psychology [22, 23]. However, the vast majority of 2D face analysis methods that involve estimation of 3D face shape or fitting of a 3D face model neglect this effect and assume an affine camera (e.g. scaled orthographic or “weak perspective”). Such a camera does not introduce any perspective transformation. While this assumption is justified in applications where the subject-camera distance is likely to be large, any situation where a face may be viewed from a small distance must account for the effects of perspective.

While such close viewing conditions may appear contrived, there are many examples of scenarios where this occurs in both machine and human vision. In the former case, so-called “selfies” are an example of a widely popular picture format in which the subject-camera distance is small. Another example would be secure door entry systems where a subject presents themselves directly in front of the camera. The latter case includes security peepholes or even a mother nursing a child (where, presumably, crucial learning of the mother’s face is occurring).

We do not believe that the perspective effect has previously been viewed as an ambiguity. Namely that, two different faces viewed at different distances could give rise to the same (or very similar) configuration and appearance. We call this the perspective face shape ambiguity. This ambiguity has implications for face recognition, 3D face shape estimation, forensic image analysis and establishing model-image dense correspondence.

Variation in face shape and appearance over a population is highly amenable to description using a linear statistical model. In particular, a 3D morphable model has been shown to accurately capture 3D face shape and generalise well to novel, unseen faces. We use such a model to represent prior knowledge about the space of face shapes. We address the face shape ambiguity by presenting a novel method for fitting a 3D morphable model to projected 2D vertex positions under perspective projection and with a specified subject-camera distance. Hence, observed 2D vertex positions provide a continuous class of solutions as the subject-camera distance is varied. We verify that, indeed, multiple explanations of observed 2D shape data is possible. We show that two faces with significantly different 3D shape can produce almost identical 2D projected shapes. We then go further by showing that a change in illumination (using a diffuse spherical harmonic model) can produce almost identical shading and hence appearance. This suggests that the ambiguity is not only geometric but also photometric.

2 Related Work

Faces under perspective projection

The effect of perspective transformation on face appearance has been studied from both a computational and psychological perspective previously.

In art history, Latto and Harper [20] discuss how uncertainty regarding subject-artist distance when viewing a painting results in distorted perception. To investigate this further, they conducted a study which showed that perceptions of body weight from face images are influenced by subject-camera distance. Perona et al. [9, 27] investigated a different effect, noting that perspective distortion influences social judgements of faces. In psychology, Liu et al. [22, 23] show that human face recognition performance is degraded by perspective transformation.

There have been two recent attempts to address the problem of estimating subject-camera distance from monocular, perspective views of a face [10, 12]. The idea is that the configuration of projected 2D face features conveys something about the degree of perspective transformation. Flores et al. [12] approach the problem using exemplar 3D face models. They fit the models to 2D landmarks using the EPnP algorithm [21] and use the mean of the estimated distances as the estimated subject-camera distance. Burgos-Artizzu et al. [10] on the other hand work entirely in 2D. Their idea is to describe 2D landmarks in terms of their offset from mean positions, with the mean calculated either across views at different distances of the same face, or across multiple identities at the same distance. They can then perform regression to relate offsets to distance.

Our results highlight the difficulty that both of these approaches face. Namely that many interpretations of 2D facial landmarks are possible, all with varying subject-camera distance. We approach the problem in a different way by showing how to solve for shape parameters when the subject-camera distance is known. We can then show that multiple explanations are possible.

3D face shape from 2D geometric features

  Facial landmarks, i.e. points with well defined correspondence between identities, are used in a number of ways in face processing. Most commonly, they are used for registration and normalisation, as is done in training an Active Appearance Model [11]. For this reason, there has been sustained interest in building feature detectors capable of accurately labelling face landmarks in uncontrolled images [29].

The robustness and efficiency of 2D facial feature detectors has improved significantly in recent years. This has motivated the use of 2D facial landmarks as a cue for the recovery of 3D face shape. In particular, by fitting a 3D morphable model to these detected landmarks [2, 6, 19, 25]. All of these methods assume an affine camera and hence the problem reduces to a multilinear problem in the unknown shape and camera parameters.

Some work has considered other 2D shape features besides landmark points. Keller et al. [17] fit a 3D morphable model to contours (both silhouettes and inner contours due to texture, shape and shadowing). A related problem is to describe the remaining flexibility in a statistical shape model that is partially fixed. In other words, if the position of some points, curves or subset of the surface is known, the goal is to characterise the space of shapes that approximately fit these observations. Albrecht et al. [1] show how to compute the subspace of faces with the same profile. Lüthi et al. [24] extended this approach into a probabilistic setting.

We emphasise that the ambiguity occurs only in monocular, uncalibrated images. For example, Amberg et al. [3] describe an algorithm for fitting a 3D morphable model to stereo face images. In this case, the stereo disparity cue used in their objective function conveys depth information which helps to resolve the ambiguity. However, note that even here, their solution is unstable when camera parameters are unknown. They introduce an additional heuristic constraint on the focal length, namely they restrict it to be between 1 and 5 times the sensor size.

Other ambiguities

  There are other known ambiguities in the perception of 3D shape, some of which have been studied in the context of faces.

The bas relief ambiguity [5] shows that certain transformations of a surface can yield identical images when the lighting and albedo are also appropriately transformed. Specifically, a Generalised Bas Relief (GBR) transformation applied to a surface represented as an orthographic depth map yields ambiguous images (under the assumption of Lambertian reflectance). The GBR is a linear transformation and the bas relief ambiguity is exact (two different surfaces can produce identical appearance).

On the other hand, the perspective face ambiguity is nonlinear (perspective transformation has a nonlinear effect on projected shape) and approximate (we minimise error between observed and fitted vertex positions). It is also predominantly a geometric ambiguity – it is concerned with the projection of vertex positions to 2D, rather than appearance (although we show that shading can be approximately recreated). However, most importantly, the perspective face ambiguity is statistically constrained. The transformed faces stay within the span of a statistical model and, hence, remain plausible face shapes. A GBR transformation of a face surface will inevitably produce shapes that are not plausible faces.

Exploiting this fact, Georghiades et al. [13] resolve the bas-relief ambiguity by exploiting the symmetries and similarities in faces. Specifically they assume: bilateral symmetry; that the forehead and chin should be at approximately the same depth; and that the range of facial depths is about twice the distance between the eyes. Such assumptions would not resolve the perspective face ambiguity that we describe as all fitted faces lie within the span of a statistical model and hence are plausible.

In the hollow face illusion [16], shaded images of concave faces are interpreted as convex faces with inverted illumination. The illusion even holds when hollow face is moving, with rotations being interpreted as reversed. This illusion is nothing other than the convex/concave ambiguity encountered in single image shape-from-shading. In human vision, this is always resolved for faces using a convex interpretation since experience of face shape makes the concave interpretation extremely unlikely. Again, the convex/concave ambiguity is not related to the perspective face ambiguity since a concave face would be impossible in the context of a statistical face model.

3 Preliminaries

Our approach is based on fitting a 3DMM to observations under perspective projection. Hence, we begin by describing the 3D morphable model and pinhole camera model.

3.1 3D Morphable Model

A 3D morphable model is a deformable mesh $\mathcal{M}(\boldsymbol{\alpha }) = (\mathcal{K},\mathbf{s}(\boldsymbol{\alpha }))$, whose shape is determined by the shape parameters $\boldsymbol{\alpha } \in \mathbb{R}^{S}$. Shape is described by a linear model learnt from data using Principal Components Analysis (PCA) [7]. So, the shape of any object from the same class as the training data can be approximated as:

$$\displaystyle{ \mathbf{s}(\boldsymbol{\alpha }) = \mathbf{P}\boldsymbol{\alpha } +\bar{ \mathbf{s}}, }$$

(14.1)

where $\mathbf{P} \in \mathbb{R}^{3N\times S}$ contains the S principal components, $\bar{\mathbf{s}} \in \mathbb{R}^{3N}$ is the mean shape and the vector $\mathbf{s}(\boldsymbol{\alpha }) \in \mathbb{R}^{3N}$ contains the coordinates of the N vertices, stacked to form a long vector: $\mathbf{s} = \left [u_{1}\ v_{1}\ w_{1}\ \ldots \ u_{N}\ v_{N}\ w_{N}\right ]^{\text{T}}$. Hence, the ith vertex is given by: $\mathbf{v}_{i} = \left [s_{3i-2}\ s_{3i-1}\ s_{3i}\right ]^{\text{T}}$.

The connectivity or topology of the deformable mesh is fixed and is given by the simplicial complex $\mathcal{K}$, which is a set whose elements can be vertices {i}, edges {i, j} or triangles {i, j, k} with the indices i, j, k ∈ [1. . N].

For convenience, we denote the sub-matrix corresponding to the ith vertex as $\mathbf{P}_{i} \in \mathbb{R}^{3\times S}$ and the corresponding vertex in the mean face shape as $\bar{\mathbf{s}}_{i} \in \mathbb{R}^{3}$, such that the ith vertex is given by: $\mathbf{v}_{i} = \mathbf{P}_{i}\boldsymbol{\alpha } +\bar{ \mathbf{s}}_{i}.$ Similarly, we define the row corresponding to the u component of the ith vertex as P _iu (similarly for v and w) and define the u component of the ith mean shape vertex as $\bar{s}_{iu}$ (similarly for v and w).

3.2 Pinhole Camera Model

The perspective projection of the 3D point v = [u v w]^T onto the 2D point x = [x y]^T is given by the pinhole camera model $\mathbf{x} = \mathbf{pinhole}[\mathbf{v},\boldsymbol{\varLambda },\boldsymbol{\varOmega },\boldsymbol{\tau }]$ where

$$\displaystyle{ \mathbf{pinhole}[\mathbf{v},\boldsymbol{\varLambda },\boldsymbol{\varOmega },\boldsymbol{\tau }] = \left [\begin{array}{c} \frac{\phi (\omega _{11}u+\omega _{12}v+\omega _{13}w+\tau _{x})} {\omega _{31}u+\omega _{32}v+\omega _{33}w+\tau _{z}} +\delta _{x} \\ \frac{\phi (\omega _{21}u+\omega _{22}v+\omega _{23}w+\tau _{y})} {\omega _{31}u+\omega _{32}v+\omega _{33}w+\tau _{z}} +\delta _{y} \end{array} \right ] }$$

(14.2)

where

$$\displaystyle{\boldsymbol{\varOmega } = \left [\begin{array}{ccc} \omega _{11} & \omega _{12} & \omega _{13}\\ \omega _{ 21} & \omega _{22} & \omega _{23}\\ \omega _{31 } & \omega _{32 } & \omega _{33} \end{array} \right ]}$$

is a rotation matrix and $\boldsymbol{\tau } = \left [\tau _{x}\ \tau _{y}\ \tau _{z}\right ]^{T}$ is a translation vector which relate model and camera coordinates (the extrinsic parameters). The matrix:

$$\displaystyle{\boldsymbol{\varLambda } = \left [\begin{array}{ccc} \phi &0&\delta _{x} \\ 0& \phi &\delta _{y} \\ 0&0&1 \end{array} \right ]}$$

contains the intrinsic parameters of the camera, namely the focal length ϕ and the principal point (δ _x , δ _y ).

This nonlinear projection can be written in linear terms by using homogeneous representations $\tilde{\mathbf{v}} = \left [u\ v\ w\ 1\right ]^{T}$ and $\tilde{\mathbf{x}} = \left [x\ y\ 1\right ]^{T}$:

$$\displaystyle{ \lambda \tilde{\mathbf{x}} = \boldsymbol{\varLambda }\left [\begin{array}{cc} \boldsymbol{\varOmega }&\boldsymbol{\tau } \end{array} \right ]\tilde{\mathbf{v}}, }$$

(14.3)

where λ is an arbitrary scaling factor. Without loss of generality, we work with a zero-centred image (i.e. δ _x  = δ _y  = 0).

4 Perspective Fitting to 2D Projections

In this section we present an algorithm for fitting a 3D morphable model to the 2D positions of the projected model vertices under perspective projection with an uncalibrated camera. As we will show, this process is ambiguous so we solve the problem for the case when the subject-camera distance is known. We do not consider the problem of computing correspondence between the model and observed data, since this is unnecessary for the demonstration of the ambiguity. Unknown correspondences could only increase the space of solutions consistent with the observations. Our approach is based on a linear approximation to the underlying objective function which we derive based on the direct linear transform method.

Our observations are the projected 2D positions $\mathbf{x}_{i} = \left [x_{i}\ y_{i}\right ]^{T}$ (i = 1… L) of the L vertices that are visible (unoccluded). Without loss of generality, we assume that the ith 2D position corresponds to the ith vertex in the morphable model. The objective of fitting a morphable model to these observations is to obtain the shape parameters that minimise the reprojection error between observed and predicted 2D positions:

$$\displaystyle{ \boldsymbol{\alpha }^{{\ast}} =\mathop{ \mathrm{arg\,min}}\limits _{\boldsymbol{\alpha }}\sum _{ i=1}^{L}\|\mathbf{x}_{ i} -\mathbf{pinhole}\left [\mathbf{P}_{i}\boldsymbol{\alpha } +\bar{ \mathbf{s}}_{i},\boldsymbol{\varLambda },\boldsymbol{\varOmega },\boldsymbol{\tau }\right ]\|^{2}. }$$

(14.4)

This optimisation is non-convex due to the nonlinearity of perspective projection. Moreover, the intrinsic and extrinsic parameters may also be unknown. Nevertheless, a good approximate solution can be found using linear methods. This initial estimate provides a suitable initialisation for local nonlinear optimisation to further refine the shape parameters.

4.1 Direct Linear Transform

From Equations 14.1 and 14.3 we can relate each model vertex and observed 2D position via a linear similarity relation:

$$\displaystyle{ \left [\begin{array}{c} \mathbf{x}_{i} \\ 1 \end{array} \right ] \sim \boldsymbol{\varLambda }\left [\begin{array}{cc} \boldsymbol{\varOmega }&\boldsymbol{\tau } \end{array} \right ]\left [\begin{array}{c} \mathbf{P}_{i}\boldsymbol{\alpha } +\bar{ \mathbf{s}}_{i} \\ 1 \end{array} \right ], }$$

(14.5)

where ∼ denotes equality up to a non-zero scalar multiplication. Such sets of relations can be solved using the direct linear transformation (DLT) algorithm [15]. Accordingly, we write

$$\displaystyle{ \left [\begin{array}{c} \mathbf{x}_{i} \\ 1 \end{array} \right ]_{\times }\boldsymbol{\varLambda }\left [\begin{array}{cc} \boldsymbol{\varOmega }&\boldsymbol{\tau } \end{array} \right ]\left [\begin{array}{c} \mathbf{P}_{i}\boldsymbol{\alpha } +\bar{ \mathbf{s}}_{i}\\ 1 \end{array} \right ] = \mathbf{0} }$$

(14.6)

where 0 = [0 0 0]^T and $\left [.\right ]_{\times }$ is the cross product matrix:

$$\displaystyle{ \left [\mathbf{x}\right ]_{\times } = \left [\begin{array}{ccc} 0 & - x_{3} & x_{2} \\ x_{3} & 0 & - x_{1} \\ - x_{2} & x_{1} & 0\\ \end{array} \right ]. }$$

(14.7)

This means that each vertex yields three linear equations in the unknown shape parameters $\boldsymbol{\alpha }$ (although only two are linearly independent). However, the intrinsic and extrinsic parameters are, in general, also unknown.

To simplify our consideration, we ignore the effects of rotation (i.e. $\boldsymbol{\varOmega } = \mathbf{I}_{3}$). Note that introducing rotations would only increase the ambiguity since it would allow the model to explain a broader set of observations.

Since we are interested in the effect of varying subject-camera distance, we limit translations to the z direction, hence $\boldsymbol{\tau } = [0\ 0\ \tau _{z}]^{T}$. It has been shown previously that translating a face away from the centre of projection (i.e. in the x and y directions) does not affect human recognition performance [23]. We believe that this is because the relatively small field of view in a typical camera means that the change in perspective appearance has only a small dependence on such translations. For this reason, we do not study its effect here and concentrate only on subject-camera distance.

Substituting these simplifications yields:

$$\displaystyle{ \left [\begin{array}{cccc} 0 & -\phi & y_{i} & \tau _{z}y_{i} \\ \phi & 0 & - x_{i}& -\tau _{z}x_{i} \\ -\phi y_{i}&\phi x_{i}& 0 & 0 \end{array} \right ]\left [\begin{array}{c} \mathbf{P}_{i}\boldsymbol{\alpha } +\bar{ \mathbf{s}}_{i}\\ 1 \end{array} \right ] = \mathbf{0}. }$$

(14.8)

The only remaining unknown besides the shape parameters $\boldsymbol{\alpha }$ is the focal length of the camera ϕ. Recall that changing the focal length amounts only to a uniform scaling of the projected points in 2D. Note that this corresponds exactly to the scenario in Fig. 14.1. There, subject-camera distance was varied before each image was rescaled such that the interocular distance was constant. We now seek to explore the ambiguity by varying subject-camera distance, solving for the best shape parameters whilst choosing the 2D scaling that minimises distance between observed and predicted 2D vertex positions.

4.2 Alternating Least Squares Solution

This problem is bilinear in the unknown shape and focal length parameters. We solve this problem using alternating linear least squares . Hence, we begin by writing the linear equations for each vertex in terms of the shape parameters, leading to a system of linear equations for all visible vertices:

$$\displaystyle{ \mathop{\underbrace{\left [\begin{array}{c} y_{1}\mathbf{P}_{1w} -\phi \mathbf{P}_{1v} \\ \phi \mathbf{P}_{1u} - x_{1}\mathbf{P}_{1w} \\ x_{1}\mathbf{P}_{1v} - y_{1}\mathbf{P}_{1u}\\ \vdots \\ y_{L}\mathbf{P}_{Lw} -\phi \mathbf{P}_{Lv} \\ \phi \mathbf{P}_{Lu} - x_{n}\mathbf{P}_{Lw} \\ x_{L}\mathbf{P}_{Lv} - y_{n}\mathbf{P}_{Lu}\\ \end{array} \right ]}}\limits _{\mathbf{C}}\boldsymbol{\alpha } =\mathop{\underbrace{ \left [\begin{array}{c} \phi \bar{s}_{1v} - y_{1}\bar{s}_{1w} -\tau _{z}y_{1} \\ x_{1}\bar{s}_{1w} -\phi \bar{ s}_{1u} +\tau _{z}x_{1} \\ y_{1}\bar{s}_{1u} - x_{1}\bar{s}_{1v}\\ \vdots \\ \phi \bar{s}_{Lv} - y_{n}\bar{s}_{Lw} -\tau _{z}y_{L} \\ x_{L}\bar{s}_{Lw} -\phi \bar{ s}_{Lu} +\tau _{z}x_{L} \\ y_{L}\bar{s}_{Lu} - x_{L}\bar{s}_{Lv}\\ \end{array} \right ]}}\limits _{\mathbf{d}}. }$$

(14.9)

Hence, we have a linear system of the form $\mathbf{C}\boldsymbol{\alpha } = \mathbf{d}$. Since the number of vertices is much larger than the number of model dimensions, the problem is over constrained. Hence, we solve in a least squares sense subject to an additional constraint to ensure plausibility of the solution. We follow Brunton et al. [8] and use a hyperbox constraint on the shape parameters. This ensures that each parameter lies within k standard deviations of the mean by introducing a linear inequality constraint on the shape parameters. We use a hard hyperbox constraint in preference to a soft elliptical prior as it avoids mean-shape bias and having to choose a regularisation weight.

To solve for focal length, we again form a linear system of equations which leads to a simple linear regression problem with a straightforward closed form solution:

$$\displaystyle{ \phi ^{{\ast}} = \frac{\sum _{i=1}^{L}\left [(x_{ i}(\mathbf{P}_{iu}\boldsymbol{\alpha } +\bar{ s}_{iu}) + y_{i}(\mathbf{P}_{iv}\boldsymbol{\alpha } +\bar{ s}_{iv})\right ]\left [\tau _{z} + \mathbf{P}_{iw}\boldsymbol{\alpha } +\bar{ s}_{iw}\right ]} {\sum _{i=1}^{L}(\mathbf{P}_{iv}\boldsymbol{\alpha } +\bar{ s}_{iv})^{2} + (\mathbf{P}_{iu}\boldsymbol{\alpha } +\bar{ s}_{iu})^{2}} }$$

(14.10)

We alternate between solving Equations 14.9 and 14.10, alternately fixing $\boldsymbol{\alpha }$ and ϕ. This process converges rapidly and usually 5 iterations are sufficient. We initialise by using the mean shape from the morphable model to solve for focal length first, i.e. we substitute the zero vector $\boldsymbol{\alpha } = \mathbf{0}$ into Equation 14.10. The overall approach can be viewed as solving the following minimisation problem:

$$\displaystyle{ \boldsymbol{\alpha }(\tau _{z}) =\mathop{ \mathrm{arg\,min}}\limits _{\boldsymbol{\alpha }}\min _{\phi }\left \|\mathbf{C}\boldsymbol{\alpha } -\mathbf{d}\right \|^{2},\ \text{s.t. }\left [\begin{array}{cc} \mathbf{I}_{m} \\ -\mathbf{I}_{m} \end{array} \right ]\boldsymbol{\alpha } \leq \left [\begin{array}{c} k\sigma _{1}\\ \vdots \\ k\sigma _{m} \\ k\sigma _{1}\\ \vdots \\ k\sigma _{m} \end{array} \right ] }$$

(14.11)

where σ _i is the standard deviation of the ith shape parameter. Note that solving this minimisation is not equivalent to solving the original objective in Equation 14.4. Hence, we can further refine the solution by applying nonlinear optimisation over $\boldsymbol{\alpha }$ and ϕ, using the original objective function. In practice, the improvement obtained by doing this is very small – typically the fitting energy is reduced by less than 1 % with no visible difference in the fitted model. So in our experimental results we simply use the alternating least squares solution with 5 iterations.

4.3 The Perspective Face Shape Ambiguity

Given 2D observations x _i , we therefore have a continuous space of solutions $\boldsymbol{\alpha }(\tau _{z})$ as a function of subject-camera distance. This is the perspective face shape ambiguity .

Note that this can be viewed as a transformation within the shape parameter space of the morphable model. If the target observations x _i are provided by projecting a 3D face obtained from Equation 14.1 with shape parameters $\boldsymbol{\alpha }_{1}$ and distance τ _z  = d ₁, then solutions $\boldsymbol{\alpha }(d_{2})$ can be seen as a nonlinear transformation within parameter space, yielding a new set of shape parameters $\boldsymbol{\alpha }_{2}$, as a function of the fitted distance τ _z  = d ₂. When d ₁ = d ₂ the fitted face will be approximately equal to the target face.

5 Fitting Lighting to Diffuse Shading

The fitting process described in the previous section aims to minimise the distance between the 2D projected positions of target and fitted vertices. In other words, it recreates the 2D configuration of features present in the target face. However, this does not mean that the two faces will have the same appearance. Since the 3D shape of the faces is different (as will be shown in the experimental results), the surface normals at corresponding points will be different. Under the same illumination, this will lead to different shading and hence appearance.

We now show how the shape obtained using the method in the previous section can be shaded so as to minimise the difference in appearance between the target and fitted face. We do not consider the effect of surface texture (i.e. diffuse albedo). The effect of albedo on appearance is to simply scale the diffuse shading. Hence, it plays no role in the perspective shape ambiguity. In fact, if albedo is also allowed to vary between target and fitted face, it may be able to improve the approximation of the observed appearance and hence enhance the ambiguity. We show here simply how to make the diffuse shading pattern approximately equal.

If $\mathbf{n}_{i} \in \mathbb{R}^{3}$ is the surface normal at vertex i, with ∥ n _i  ∥  = 1, the order 2 spherical harmonic lighting basis vector for that vertex (ignoring constant factors) is given by [4]:

$$\displaystyle{ \mathbf{b}_{i} = \left [1\ \ n_{i,x}\ \ n_{i,y}\ \ n_{i,z}\ \ 2n_{i,z}^{2}\! -\! n_{ i,x}^{2}\! -\! n_{ i,y}^{2}\ \ n_{ i,x}n_{i,y}\ \ n_{i,x}n_{i,z}\ \ n_{i,y}n_{i,z}\ \ n_{i,x}^{2}\! -\! n_{ i,y}^{2}\right ]. }$$

(14.12)

Hence, the matrix of basis vectors for the L observed vertices is given by:

$$\displaystyle{ \mathbf{B} = \left [\begin{array}{c} \mathbf{b}_{1}\\ \vdots \\ \mathbf{b}_{L}\\ \end{array} \right ]. }$$

(14.13)

We compute basis matrices B _T and B _F for the target and fitted faces respectively. If the target face is illuminated by known spherical harmonic lighting vector l _T then the diffuse shading for the mesh is given by: B _T l _T . The lighting vector that minimises the difference in appearance of the fitted face to the target is given by solving the linear system of equations:

$$\displaystyle{ \mathbf{l}_{F}^{{\ast}} =\mathop{ \mathrm{arg\,min}}\limits _{\mathbf{ l}_{F}}\|\mathbf{B}_{T}\mathbf{l}_{T} -\mathbf{B}_{F}\mathbf{l}_{F}\|^{2}. }$$

(14.14)

This provides the optimal transformation of lighting for the fitted face.

6 Experimental Results

We use the Basel Face Model [26] (BFM) which is a 3D morphable model comprising 53,490 vertices and which is trained on 200 faces. We use the shape component of the model only. The model is supplied with 10 out-of-sample faces which are scans of real faces that are in correspondence with the model. Unusually, the model does not factor out scale, i.e. faces are only aligned via translation and rotation. This means that the vertex positions are in absolute units of distance. This allows us to specify camera-subject distance in physically meaningful units.

We begin with a target face. For this purpose, we either use the BFM out-of-sample faces or we randomly generate a face. We do this by sampling randomly from the multivariate normal distribution with zero mean and covariance matrix $\boldsymbol{\varSigma } = \text{diag}(\sigma _{1}^{2},\ldots,\sigma _{n}^{2})$ to yield a shape parameter vector and hence shape. We arbitrarily set the focal length ϕ = 1 and choose the subject-camera distance. We then project every vertex of the target face to provide 2D observations. We use all S = 199 model dimensions and constrain parameters to be within k = 3 standard deviations of the mean.

Fig. 14.2

Target (column 1) and fitted results (columns 2–5) shown under orthographic projection. When the target is viewed under perspective projection at distance d ₁ and the fitted faces at distances d ₂, they give almost identical 2D projections

Fig. 14.3

An illustration of the nonlinearity of the perspective face ambiguity. We plot the fitted parameter vectors in a 2D MDS space as the subject-camera distance is varied. The target face is the same as in Fig. 14.2, again with d ₁ = 60 cm

6.1 Subspace of Ambiguity

We begin by visualising the subspace associated with the perspective face shape ambiguity for a single target face. We randomly generate shape parameters, yielding the target face shown in column 1 of Fig. 14.2. Note that in the figure the face is shown in orthographic projection. For our observations, we project the face under perspective projection at a distance of d ₁ = 60 cm. We then solve for the optimal fit at distances ranging from d ₂ = 35 to 390 cm. We show a sample of these fitted results, again under orthographic projection, in columns 2–5 of Fig. 14.2. There is significant variation in the shape of the face, yet all produce the same projected 2D positions when viewed at different distances.

To verify that the transformation is indeed nonlinear, in Fig. 14.3 we perform multidimensional scaling (MDS) on the fitted parameter vectors. We then plot the trajectory of the fitted faces through the space formed by the first two MDS dimensions. We highlight the positions in MDS space associated with the fitting results from Fig. 14.2. It is clear that the trajectory, and hence the perspective ambiguity, is highly nonlinear.

6.2 Shape Fitting

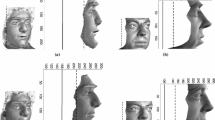
In Figs. 14.4 and 14.5 we show the result of fitting to 4 of the BFM scans (i.e. the targets are real, out-of-sample faces). We experiment with two subject-camera distances for either extreme (τ _z  = 30 cm) or moderate (τ _z  = 90 cm) perspective distortion. In Fig. 14.4, the target face is close to the camera (τ _z  = 30 cm) and we fit the model at a far distance (τ _z  = 90 cm). This configuration is reversed in Fig. 14.5. For visualisation we show the results both as shaded surfaces and with the texture of the real target face.

The target face is shown under perspective and orthographic projection in the first and third columns respectively. The fitted face is similarly shown in the second and fourth columns. Hence, the observations are provided by column 1 and the fitted result in column 2. The orthographic views in columns 3 and 4 enable comparison between the target and fitted shape under the same projection. This demonstrates clearly that two faces with significantly different 3D shape can give rise to almost identical 2D landmark positions under perspective projection.

Quantitatively, d _S is the mean Euclidian distance between the target and fitted surface. In all cases, d _S is significant, sometimes as much as 1 cm. On the other hand, in all cases, the mean distance between fitted and target landmarks is less than a pixel (and less than 1 % of the interocular distance). Note that Burgos-Artizzu et al. [10] found that the difference between landmarks on the same face placed by two different humans was typically 3 % of the interocular distance. Similarly, the 300 faces in the wild challenge [29] found that even the best methods did not obtain better than 5 % accuracy for more than 50 % of the landmarks. Hence, the vertex fitting error is substantially smaller than the accuracy of either human or machine placed landmarks.

There are clear differences in shading with the fittings in Fig. 14.4 exhibiting sharper features and hence more dramatic shading and in Fig. 14.5, flatter features and hence flatter shading. This is seen more clearly in Fig. 14.6 where we show rotated views of the target and two fitted surfaces.

Fig. 14.4

Fitting results (near target): target at 30 cm, fitted result at 90 cm

Fig. 14.5

Fitting results (distant target): target at 90 cm, fitted result at 30 cm

Fig. 14.6

Rotated views of target (left), fitting to distant target (middle) and fitting to near target (right). The faces in each row can produce almost identical projected 2D shapes

Fig. 14.7

Illumination fitting results (close target): target at 30 cm, fitted result at 90 cm. RMS errors are computed for intensity of foreground pixels

Fig. 14.8

Illumination fitting results (distant target): target at 90 cm, fitted result at 30 cm. RMS errors are computed for intensity of foreground pixels

6.3 Illumination Fitting

We now show how a change in illumination can enable the fitted face to produce almost identical shading to the target, despite the large difference in 3D shape. For this experiment, we render the target face under perspective projection with frontal illumination and Lambertian shading. We then solve for the spherical harmonic lighting parameters that minimise the error between this target shading and that of the fitted face. In Figs. 14.7 and 14.8 we show the results of this experiment, again for two scenarios of near and distant target.

In the top row we show the fitted face rendered with the same illumination as the target. In the middle row we show the target face. It is clear that there is a significant difference in shading. In the bottom row, we show the target face rendered with fitted spherical harmonic lighting. Notice that the shading is now much closer to that of the target face. This perceptual improvement is corroborated quantitatively where it can be seen that the RMS error in the image intensity reduces in all cases.

7 Discussion

In this paper we have introduced a new ambiguity which arises when faces are viewed under perspective projection. We have shown that 2D shape and shading can be explained by a space of possible faces which vary significantly in 3D shape. There are a number of interesting implications of this ambiguity. First, any attempt to recover 3D facial shape from 2D shape or shading observations is ill-posed under perspective projection, even with a statistical constraint. Second, metric distances between landmark points in 2D images are not unique. We have shown that faces with very different shapes can give rise to almost identical projected 2D shapes (with mean differences less than 1 % of interocular distance in all cases). This casts doubt on the use of metric distances between features as a way of comparing the identity of two face photographs. This has previously been used in forensic imaging [28]. The perspective face shape ambiguity perhaps partially explains the studies that have demonstrated the weakness of these approaches [18].

We consider it surprising that the natural variability in face shape (at least as far as is captured by a morphable model) should include variations consistent with perspective transformation. An intuitive interpretation of this is that there are faces which look like they have been subjected to perspective transformation when they have not. There must be a limit to this. For example, to fit to a target face that is distant requires the close fitted face to have large protruding ears (see Fig. 14.5). If this fitted face was then used as a distant target, the ears would need to increase in size again for a close fitting. Clearly, repeating this process would quickly take the fitted result outside the span of the model (or the hyper box constraint would simply limit the ability of the model to explain the observations).

7.1 Generality of Assumptions

The perspective face ambiguity applies in an uncalibrated scenario, i.e. when camera focal length or pixel size is unknown and therefore the subject-camera distance cannot be estimated from the size of the face in the image. Images taken by digital cameras usually contain meta data including the focal length and camera model. The pixel size is fixed for a particular camera model and so could, in principle, be stored in a database. Hence, it appears that in practice some calibration information is likely to be available and the ambiguity resolved. In fact, there are two reasons why this is not the case:

• 1. In a fully calibrated situation (i.e. when camera focal length and pixel size is known) then the size of a face in the image does give some indication as to the subject-camera distance. However, head size varies significantly across the population: e.g. the bitragion breadth (i.e. face width) ranges from 12.51 cm to 15.87 cm for males and females [14] – a variation of over 25 %. With an uncertainty in the distance estimate of ∼ 25 %, the perspective ambiguity remains significant, particularly when the face is close to camera. Moreover, in statistical shape modelling, the scale of each sample is often factored out when generalised Procrustes analysis is used to register the training data. This means that the statistical shape model has no explicit scale, rendering the size cue even less accurate for distance estimation.

• 2. Images that have been modified in any way, e.g. cropped, resized or compressed, will often no longer contain meta data or the meta data will incorrectly describe the effective camera geometry. This is likely to be the case for a large proportion of the images on the web (and the images in Fig. 14.1 are perfect examples: these files contain no metadata). In this case, no calibration information is available and the ambiguity is exactly as described in this paper.

7.2 Future Work

There are many ways in which the work can be extended. First, there are a number of simplifications that we made which could be relaxed and their effect investigated. This includes allowing rotations and hence considering the ambiguity in non-frontal poses. There appears to be very little work investigating the effect of perspective transformation on non-frontal faces. Intuitively, the effects may be less dramatic since it is the large (relative) depth variation between nose tip and ears that makes the effect so noticeable. We also ignored the effect of the skew parameter and translations in x and y away from the centre of projection. A more complex camera model could even be used, for example considering radial distortion.

Next, our shape estimation approach could be cast in probabilistic terms. We take a rather simplistic approach, simply seeking to minimise the 2D vertex error in a least squares sense. As has been shown previously [1, 24], partially fixing a statistical shape model still leaves flexibility. Hence, our fitting algorithm could return the subspace of faces that is approximately consistent with the observed vertices. Shape fitting could also be extended to edge features such as silhouettes. These are interesting because there is no longer a one-to-one correspondence between 2D shape features and model vertices. This suggests that the ambiguity would be even more significant in this case. An interesting follow-up to the work of Amberg et al. [3] would be to investigate whether there is an ambiguity in uncalibrated stereo face images.

Our consideration of appearance was limited to diffuse shading under a spherical harmonic illumination model. It is known that light source attenuation is a useful cue for the interpretation of shading under perspective projection so this may be an interesting avenue for future work. Similarly, cast shadows and specular reflections may also help resolve the ambiguity.