New Formulas for Dyck Paths in a Rectangle

Abstract

We consider the problem of counting the set of $\mathscr {D}_{a,b}$ of Dyck paths inscribed in a rectangle of size $a\times b$. They are a natural generalization of the classical Dyck words enumerated by the Catalan numbers. By using Ferrers diagrams associated to Dyck paths, we derive formulas for the enumeration of $\mathscr {D}_{a,b}$ with a and b non relatively prime, in terms of Catalan numbers.

1 Introduction

The study of Dyck paths is a central topic in combinatorics as they provide one of the many interpretations of Catalan numbers. A partial overview can be found for instance in Stanley’s comprehensive presentation of enumerative combinatorics [1] (see also [2]). As a language generated by an algebraic grammar is characterized in terms of a Dyck language, they are important in theoretical computer science as well [3]. On a two-letter alphabet they correspond to well parenthesized expressions and can be interpreted in terms of paths in a square. Among the many possible generalizations, it is natural to consider paths in a rectangle, see for instance Labelle and Yeh [4], and more recently Duchon [5] or Fukukawa [6]. In algebraic combinatorics Dyck paths are related to parking functions and the representation theory of the symmetric group [7]. The motivation for studying these objects stems from this field in an attempt to better understand the links between these combinatorial objects.

In this work, we obtain a new formula for $|\mathscr {D}_{a,b}|$, when a and b are not relatively prime, in terms of the Catalan numbers using the notion of Christoffel path. More precisely, the main results of this article (diagrams decomposition method in Sect. 3, Theorems 1 and 2 in Sect. 4) are formulas for the case where $a=2k$ :

$$\begin{aligned} |\mathscr {D}_{a,b}| = \left\{ \begin{array}{ll} \mathbf{Cat}_{(a,n)}^{(-)}- \displaystyle \sum \limits _{j=1}^{k-1} { \mathbf{Cat}_{(a-j,n)}^{(-)}\mathbf{Cat}_{(j,n)}^{(-)} } , \quad &{}\text {if}\, b=a(n+1)-2,\\ \mathbf{Cat}_{(a,n)}^{(+)}+ \displaystyle \sum \limits _{j=1}^{k} { \mathbf{Cat}_{(a-j,n)}^{(+)}\mathbf{Cat}_{(j,n)}^{(+)} } , &{}\text {if}\, b=an+2, \end{array}\right. \end{aligned}$$

where $k,n \in \mathbb {N}$, $\mathbf{Cat}_{(a,n)}^{(-)}:=\mathbf{Cat}_{(a,a(n+1)-1)},$ and $\mathbf{Cat}_{(a,n)}^{(+)}:=\mathbf{Cat}_{(a,an+1)}$.

The paper is organized as follows. In Sect. 2 we fix the notation for Dyck and Christoffel paths, and present their encoding by Ferrers diagrams. Then, in Sect. 3, we develop the “Ferrers diagram comparison method” and “diagrams decomposition method”. Section 4 contains several technical results in order to prove the main results, and in Sect. 5 we present the examples.

2 Definitions and Notation

We borrow the notation from Lothaire [8]. An alphabet is a finite set $\varSigma$, whose elements are called letters. The set of finite words over $\varSigma$ is denoted $\varSigma ^*$ and $\varSigma ^+ = \varSigma ^*\setminus \{\varepsilon \}$ is the set of nonempty words where $\varepsilon \in \varSigma ^*$ is the empty word. The number of occurrences of a given letter $\alpha$ in the word w is denoted $|w|_\alpha$ and $|w|=\sum _{\alpha \in \varSigma }|w|_\alpha$ is the length of the word. A language is a subset $L\subseteq \varSigma ^*$. The language of a word w is $\mathcal {L}(w) = \{f \in \varSigma ^* \mid w = pfs,\ p,s\in \varSigma ^*\}$, and its elements are called the factors of w.

Dyck words and paths. It is well-known that the language of Dyck words on $\varSigma =\{{\mathbf{0}},{\mathbf{1}}\}$ is the language generated by the algebraic grammar $D\rightarrow {\mathbf{0}}D{\mathbf{1}}D +\varepsilon$. They are enumerated by the Catalan numbers (see [9]),

$$\begin{aligned} \mathbf{Cat}_{n}= \frac{1}{n+1}{2n \atopwithdelims ()n}, \end{aligned}$$

and can be interpreted as lattice paths inscribed in a square of size $n\times n$ using down and right unit steps (see Fig. 1 (a)).

Fig. 1.

Dyck path and Ferrers diagram.

More precisely an (a, b)-Dyck path is a south-east lattice path, going from (0, a) to (b, 0), which stays below the (a, b)-diagonal, that is the line segment joining (0, a) to (b, 0). In Fig. 1, the paths are respectively ${\mathbf{0}}{\mathbf{1}}{\mathbf{0}}{\mathbf{1}}{\mathbf{0}}{\mathbf{1}}$ and ${\mathbf{0}}{\mathbf{1}}{\mathbf{0}}{\mathbf{1}}{\mathbf{1}}{\mathbf{0}}{\mathbf{1}}{\mathbf{1}}$.

Alternatively such word may be encoded as a Ferrers diagram corresponding to the set of boxes to left (under) the path. As usual, Ferrers diagrams are identified by the number of boxes on each line, thus corresponding to partitions:

$$\begin{aligned} \lambda&=(\lambda _{a-1},\lambda _{a-2},\ldots ,\lambda _{1}),&\text { with}\, \lambda _{a-l}\le \left\lfloor \dfrac{bl}{a} \right\rfloor \text {where}\, 1\le l\le a-1. \end{aligned}$$

(1)

In the examples of Fig. 1, the paths are respectively encoded by the sequences (2, 1, 0) and (3, 1, 0). The cases where (a, b) are relatively prime, or $b=ak$ are of particular interest. For the case $b=ak$ with $k\ge 1$ we have the well-know formula of Fuss-Catalan (see [9]).

$$\begin{aligned} \mathbf{Cat}_{(a,k)}=\dfrac{1}{ak+1} \left( {\begin{array}{c} ak+a\\ a\end{array}}\right) . \end{aligned}$$

For $a\times b$ rectangles, with a and b are relatively prime, we also have the “classical” formula:

$$\begin{aligned} \mathbf{Cat}_{(a,b)}=\dfrac{1}{a+b+1} \left( {\begin{array}{c} a+b+1\\ a\end{array}}\right) . \end{aligned}$$

In particular, when $a=p$ is prime, either b and p are relatively prime, or b is a multiple of p. Hence the relevant number of Dyck paths is:

$$\begin{aligned} |\mathscr {D}_{p,b}|={\left\{ \begin{array}{ll} \frac{1}{p+b} \left( {\begin{array}{c} p+b\\ p\end{array}}\right) &{} \text{ if } \mathbf{gcd}(p,b)=1, \\ \frac{1}{p+b+1} \left( {\begin{array}{c} p+b+1\\ p\end{array}}\right)&\text{ if } b=kp. \end{array}\right. } \end{aligned}$$

The generalized ballot problem is related with the number of lattice paths form (0, 0) to (a, b) that never go below the line $y=kx$ (see [10]):

$$\begin{aligned} \dfrac{b-ka+1}{b} \left( {\begin{array}{c} a+b\\ a\end{array}}\right)&\text {where}\, k\ge 1, \text {and}\, b>ak\ge 0. \end{aligned}$$

And the number of lattice paths of length $2(k+1)n+1$ that start at (0, 0) and that avoid touching or crossing the line $y=kx$ (see [11]) has the formula:

$$\begin{aligned} \left( {\begin{array}{c} 2(k+1)n\\ 2n\end{array}}\right) -(k-1) \displaystyle \sum \limits _{2n-1}^{i=0} { \left( {\begin{array}{c} 2(k+1)n\\ i\end{array}}\right) } ,&\text {where}\, n\ge 1 \text {and}\, k\ge 0. \end{aligned}$$

In the more general case we have a formula due to Bizley (see [12]) expressed as follows. Let $m=da$, $n=db$ and $d=\mathbf{gcd}(m,n)$, then:

$$\begin{aligned} \mathcal {B}_{k}^{(a,b)}&:=\dfrac{1}{a+b} \left( {\begin{array}{c} ka+kb\\ ka\end{array}}\right)&\text {for}\, k\in \mathbb {N}, \\ \mathcal {B}_{\lambda }^{a,b}&:=\mathcal {B}_{\lambda _{1}}^{(a,b)}\mathcal {B}_{\lambda _{2}}^{(a,b)}\cdots \mathcal {B}_{\lambda _{l}}^{(a,b)}&\text {if}\, \lambda =(\lambda _1,\lambda _2,\dots ,\lambda _l), \end{aligned}$$

It is straightforward to show that the number of Dyck paths in $m\times n$ is:

$$\begin{aligned} |\mathscr {D}_{m,n}|&:= \displaystyle \sum \limits _{\lambda \vdash d}^{} { \frac{1}{z_{\lambda }}\mathcal {B}_{\lambda }^{(a,b)}}&\text {where}\, n\ge 1 \text {and}\, k\ge 0. \end{aligned}$$

Christoffel Paths and Words. A Christoffel path between two distinct points $P=(0,k)$ and $P'=(0,l)$ on a rectangular grid $a\times b$ is the closest lattice path that stays strictly below the segment $PP'$ (see [13]). For instance, the Dyck path of Fig. 1(b) is also Christoffel, and the associated word is called a Christoffel word. The Christoffel path of a rectangular grid $a\times b$ is the Christoffel path associated to the line segment going from the north-west corner to the south-east corner of the rectangle of size $a\times b$. As in the case of Dyck paths, every Christoffel path in a fixed rectangular grid $a\times b$ is identified by a Ferrers diagram of shape $(\lambda _{a-1},\lambda _{a-2},\ldots ,\lambda _{1})$ given by Equation (1).

For later use, we define two functions associated to Ferrers diagram. Let $Q_{a, b}$ to be the total number of boxes in the Ferrers diagram associated to the Christoffel path of $a\times b$ (see [14]):

$$\begin{aligned} Q_{a,b}&=\dfrac{(a-1)(b-1)+\mathbf{gcd}(a,b)-1}{2}. \end{aligned}$$

(2)

Also, let $\varDelta _ {a, b} (l)$ be the difference between the boxes of the Ferrers diagrams associated to the Christoffel paths of $a\times b$ and $a \times (b-1)$, respectively:

$$\begin{aligned} \varDelta _{a,b}(l):=\left\lfloor \dfrac{bl}{a} \right\rfloor -\left\lfloor \dfrac{(b-1)l}{a} \right\rfloor , \end{aligned}$$

where $a<b\in \mathbb {N}$ and $1\le l \le a-1$.

In the next section we give an alternate method to calculate the number of (a, b)-Dyck paths when a and b are not relatively prime, and satisfying certain conditions in terms of the Catalan numbers.

Isosceles Diagrams. An isosceles diagram $\mathscr {I}_{n}$ is a Ferrers diagram associated to a Christoffel path in a square having side length n. Given a Ferrers diagram $\mathscr {T}_{a,b}$, we call maximum isosceles diagram the largest isosceles diagram included in $\mathscr {T}_{a,b}$.

Ferrers Set. Let $\mathscr {T}_{a,b}$ be a Ferrers diagram. The Ferrers set of $\mathscr {T}_{a,b}$ is the set of all Dyck paths contained in $\mathscr {T}_{a,b}$.

Fig. 2.

Rule 1.

3 Ferrers Diagrams Comparison Method

Let $\mathscr {T}_{a,b}$ be the Ferrers diagram associated to a Christoffel path of $a\times b$. In order to establish the main results we need to count the boxes in excess between the Christoffel paths in rectangles $a\times b$ and $a\times c$, for any $c>b$. We develop a method to do this by removing exceeding boxes between $\mathscr {T}_{a,b}$ and $\mathscr {T}_{a,c}$, for $c>b$. Using the functions $Q_{a,b}$ and $\varDelta _{a,b}(l)$, our comparison method gives the following rules:

• Rule 1: If $Q_{a,b}=1$ and $\varDelta _{a,b}(i)=1$, there is only one corner in $\mathscr {T}_{a,c}$ which does not belong to the $\mathscr {T}_{a,b}$. Let $\mathscr {T}_{a_1,b_1}$ and $\mathscr {T}_{a'_1,b'_1}$ be the Ferrers diagram obtained by erasing from $\mathscr {T}_{a,c}$ the row and the column that contain (see Fig. 2(b)). These Ferrers diagrams are not associated to a Christoffel path in general. Let

  $$\begin{aligned} \mathcal {J}_{a_1,b_1}\subseteq \mathscr {D}_{a_1,b_1}, \text { and } \mathcal {J}_{a'_1,b'_1}\subseteq \mathscr {D}_{a'_1,b'_1} \end{aligned}$$

  be the sets of Dyck paths contained in the Ferrers diagrams $\mathscr {T}_{a_1,b_1}$ and $\mathscr {T}_{a'_1,b'_1}$, respectively. We have:

  $$\begin{aligned} |\mathscr {D}_{a,c}|-|\mathscr {D}_{a,b}|=-|\mathcal {J}_{a_1,b_1}|\cdot |\mathcal {J}_{a_1',b_1'}|, \end{aligned}$$

  It is clear that if the box $\alpha$ is located on the bottom line ($l=a-1$), the equation is reduced to:

  $$\begin{aligned} |\mathscr {D}_{a,c}|-|\mathscr {D}_{a,b}|=-|\mathcal {J}_{a_1,b_1}|. \end{aligned}$$

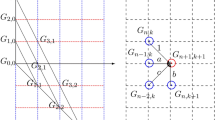
• Rule 2: When $Q_{a,b}=k$ and there are exactly k rows with a difference of one box we need to calculate how many paths contain these boxes (see Fig. 3), so we construct a sequence of disjoint sets as follows. Let $A_j$ be the set of all paths that do not contain the boxes for each $i> j$, where $1\le j\le k$. Also, let $B_j$ be the set of all paths that do not contain the boxes $\alpha _i$ for each $i <j$, where $1 \le j \le k$. This strategy gives us disjoint sets that preserve the total union, so using Rule 1 for every $A_j$ or $B_j$ we get:

  $$\begin{aligned} |\mathscr {D}_{a,c}|-|\mathscr {D}_{a,b}|=- \displaystyle \sum \limits _{j=1}^{k} { (|\mathcal {J}_{a_j,b_j}|\cdot |\mathcal {J}_{a_j',b_j'}|)} , \end{aligned}$$

  where $\mathcal {J}_{a_j,b_j}\subseteq \mathscr {D}_{a_j,b_j}$, and $\mathcal {J}_{a'_j,b'_j}\subseteq \mathscr {D}_{a'_j,b'_j}$.

Fig. 3.

More one box.

3.1 Diagrams Decomposition Method

Using the diagrams comparison method we make an iterative process erasing boxes in excess between the diagram $\mathscr {T}_{a,b}$ and its respective maximum isosceles diagram $\mathscr {I}_{n}$. It begins at the right upper box as shown in Fig. 5. The decomposition is give in sums and products of diagrams. The sum operation $+$ is given by the union of disjoint Ferrers sets. We can consider a red box in the border of the diagram. Any path contained in a diagrams having the red box is written as one of the two cases in Fig. 4.

Fig. 4.

Separation of diagrams.

The products of diagrams $\mathscr {T}\times \mathscr {T}'$ is a diagram containing all possible concatenation of a Dyck path of $\mathscr {T}$ with a Dyck path of $\mathscr {T}'$. For example, the diagram corresponding to $\mathscr {D}_{4,6}$ is [4, 3, 1]

includes the isosceles diagram [3, 2, 1]

. When we remove the box the diagram splits into two pairs associated with operations that simplify the computation of paths (see Fig. 5).

Fig. 5.

First diagram decomposition.

In Fig. 5, $\mathbbm {1}$ is an empty diagram. We repeat this method until all the diagrams are isosceles (the operation $\times$ distributes the operation $+$) (Fig 6).

Fig. 6.

Full diagram decomposition.

Clearly, we can count the Dyck paths in an isosceles diagram with a classical Catalan formula because there is a relation between the decomposition and the number of Dyck paths. This relation, denoted $\mathcal {H}$, between the isosceles diagrams and Catalan numbers is such as:

$$ \begin{array}{c c} \mathcal {H}(\mathbbm {1}):=1,&{} \mathcal {H}(\mathscr {I}_n+\mathscr {I}_m):=\mathcal {H}(\mathscr {I}_n)+\mathcal {H}(\mathscr {I}_m),\\ \mathcal {H}(\mathscr {I}_n):=\mathbf{Cat}_{n},&{} \mathcal {H}(\mathscr {I}_n\times \mathscr {I}_m):=\mathcal {H}(\mathscr {I}_n)\cdot \mathcal {H}(\mathscr {I}_m). \end{array} $$

3.2 Technical Results

The following technical formulas are needed in the sequel (see [14]).

• i) Let $a=2k$, $b=2k(n+1)-1$, and $1\le l \le 2k-1$. Then,

  $$\begin{aligned} \varDelta _{2k,2k(n+1)-1}(l)={\left\{ \begin{array}{ll} 0 &{}\text{ if } 1\le l\le k,\\ 1&{}\text{ if } k+1\le l\le 2k-1. \end{array}\right. } \end{aligned}$$

  (3)

• ii) Let $a=2k$, $b=2kn+2$, and $1\le l \le 2k-1$. Then,

  $$\begin{aligned} \varDelta _{2k,2kn+2}(l)={\left\{ \begin{array}{ll} 0 &{}\text{ if } 1\le l\le k-1,\\ 1&{}\text{ if } k\le l\le 2k-1. \end{array}\right. } \end{aligned}$$

  (4)

• iii) Let $a,k\in \mathbb {N}$, and $k<a$ . There exists a unique $r\in \mathbb {N}$ such as for $k=1,\ldots , a-1$ :

  $$\begin{aligned} \left\lfloor \dfrac{kr}{a} \right\rfloor =k-1&\text { or } \left\lfloor \dfrac{kr}{a} \right\rfloor =k, \end{aligned}$$

  (5)

  and $\mathbf{gcd}(r,a)=1$. The solution is given by $r=a-1$

4 Theorems

Now we are ready to prove the two main results of this article. The formulas are obtained by studying the “Ferrers diagram comparison method” (see Sect. 3), in the cases where every Ferrers diagram obtained by subdivisions of $\mathscr {T}_{a,c }$ is associated to a Christoffel path inscribed in a rectangular box of co-prime dimension.

Theorem 1

(see [14]). Let $a=2k$, $b=a(n+1)-2$, and $k,n \in \mathbb {N}$, then the number of Dyck paths is:

$$\begin{aligned} |\mathscr {D}_{a,b}| = \mathbf{Cat}_{(a,n)}^{(-)}- \displaystyle \sum \limits _{j=1}^{k-1} { \mathbf{Cat}_{(a-j,n)}^{(-)}\mathbf{Cat}_{j,n}^{(-)} } , \end{aligned}$$

where $\mathbf{Cat}_{a,n}^{(-)}:=\mathbf{Cat}_{(a,a(n+1)-1)}.$

Proof

From Eqs. 2 and 3, we get that there are $k-1$ total difference between the Ferrers diagram associated to the Christoffel path of $a\times b$ and $a\times (b+1)$. We easily obtain that the Ferrers diagram associated to $\mathscr {D}_{c,cn+c-1}$ is $\lambda =((c-1)n+c-2,\dots ,2n+1,n)$.

By definition of $A_j$, the rectangles $j \times b_1$ and $(2k-j)\times b'_1$ are such that their maximal underlying diagrams are:

$$\begin{aligned} \lambda&=((j-1)n+j-2,\dots ,3n+2,2n+1,n),&\\ \lambda '&=((2k-j-1)n+2k-j-2,\dots ,2n+1,n), \end{aligned}$$

respectively. So,

$$\begin{aligned} |A_j|=|\mathscr {D}_{2k-j,(2k-j)n+2k-j-1}||\mathscr {D}_{j,jn+j-1}|. \end{aligned}$$

Since all rectangles are relatively prime, we have:

$$\begin{aligned} |\mathscr {D}_{a,b}|-|\mathscr {D}_{a,b+1}|=- \displaystyle \sum \limits _{j=1}^{k-1} { (|\mathscr {D}_{a-j,(a-j)(n+1)-1}|\cdot |\mathscr {D}_{j,j(n+1)-1}|)} . \end{aligned}$$

then

$$\begin{aligned} |\mathscr {D}_{a,b}| = \mathbf{Cat}_{(a,n)}^{(-)}- \displaystyle \sum \limits _{j=1}^{k-1} { \mathbf{Cat}_{(a-j,n)}^{(-)}\mathbf{Cat}_{j,n}^{(-)}} . \end{aligned}$$

where .   $\square$

Theorem 2

(see [14]). Let $a=2k$, $b=an+2$ and $k,n \in \mathbb {N}$, then the number of Dyck paths is:

$$\begin{aligned} |\mathscr {D}_{a,b}| = \mathbf{Cat}_{(a,n)}^{(+)}+ \displaystyle \sum \limits _{j=1}^{k} { \mathbf{Cat}_{(a-j,n)}^{(+)}\mathbf{Cat}_{j,n}^{(+)} } . \end{aligned}$$

where $\mathbf{Cat}_{a,n}^{(+)}:=\mathbf{Cat}_{a,an+1}$.

Proof

From Eqs. 2 and 4, we get that there are k total difference between the Ferrers diagram associated to the Christoffel path of $a\times b$ and $a\times (b+1)$. We easily get that the Ferrers diagram associated to $\mathscr {D}_{c,cn+1}$ is $\lambda =((c-1)n,\dots ,2n,n)$. By definition of $B_j$, the rectangles $j \times b_1$ et $(2k-j)\times b'_1$ are such as that their maximal underlying diagram are:

$$\begin{aligned} \lambda&=((j-1)n,\dots ,3n,2n,n),&\\ \lambda '&=((2k-j-1)n,\dots ,2n,n), \end{aligned}$$

respectively. So,

$$\begin{aligned} |B_j|=|\mathscr {D}_{2k-j,(2k-j)n+1}||\mathscr {D}_{j,jn+1}|. \end{aligned}$$

Since all rectangles are relatively prime, we have:

$$\begin{aligned} |\mathscr {D}_{a,b}|-|\mathscr {D}_{a,b-1}|=- \displaystyle \sum \limits _{j=1}^{k-1} { (|\mathscr {D}_{a-j,(a-j)n-1}|\cdot |\mathscr {D}_{j,jn+1}|)} . \end{aligned}$$

then

$$\begin{aligned} |\mathscr {D}_{a,b}| = \mathbf{Cat}_{(a,n)}^{(+)}+ \displaystyle \sum \limits _{j=1}^{k} { \mathbf{Cat}_{(a-j,n)}^{(+)}\mathbf{Cat}_{j,n}^{(+)} } . \end{aligned}$$

where $\mathbf{Cat}_{t,n}^{(+)}:=\mathbf{Cat}_{(t,tn+1)}$, of course $\mathbf{Cat}_{(1,n)}^{(+)}=1$.   $\square$

5 Examples

In order to illustrate the main results, we consider the cases $\mathscr {D}_{8,8n + 6}$, to generalize the case of discrepancies with a larger diagram. Then we study $\mathscr {D}_{6,6n + 2}$ to generalize the case of discrepancies for shorter diagram. These cases corresponding to rectangles having relatively prime dimensions such that $\mathcal {J}_{a_j, b_j} = \mathscr {D}_{a_j, b_j}$ and $\mathcal {J}_{a'_j, b'_j} = \mathscr {D}_{a'_j, b'_j}$. Finally, we give some examples of the diagrams decomposition method.

5.1 Example $\mathscr {D}_{8,8n+6}$

We apply the comparison method to $\mathscr {D}_{8,8n + 6}$ and $\mathscr {D}_{8,8n + 7}$. Using Eq. 2, we get that the difference in total number of sub-diagonal boxes is $Q_{8,8n + 7} -Q_{8,8n + 6} = 3$. To find the lines where they are located we use the Eq. 3. In this cases $\varDelta (l)$ is zero except for $l=5,6,7$ (see Fig. 7).

Fig. 7.

$\mathscr {D}_{8,8n+6}$ and $\mathscr {D}_{8,8n+7}$

Applying Rule 2, we have that $A_1=\{$ paths containing the box $\alpha _1\text { and not} (\alpha _2 \text { or } \alpha _3)\}$, $A_2 =\{$ paths containing the box $\alpha _2 \text { and not }\alpha _3\}$, and $A_3 =\{ \text {paths containing the box } \alpha _3 \}$.

Applying the rule 1 to these sets, we have:

• Case 1: for $A_1$, we must find the rectangles $5 \times b_1$ and $3\times b'_1$ with underlying diagram $\lambda =(5n+4,4n+3,3n+2,2n+1,n)$ and $\lambda '=(n)$, then

  $$\begin{aligned} |A_1|=|\mathscr {D}_{5,5n+4}||\mathscr {D}_{3,3n+2}|. \end{aligned}$$

• Case 2: for $A_2$, we must find the rectangles $6 \times b_2$ and $2\times b'_2$ with underlying diagram $\lambda =(5n+4,4n+3,3n+2,2n+1,n)$ and $\lambda '=(n)$, then

  $$\begin{aligned} |A_2|=|\mathscr {D}_{6,6n+5}||\mathscr {D}_{2,2n+1}|. \end{aligned}$$

• Case 3: for $A_3$, we must find the rectangle $7 \times b_3$ with underlying diagram $\lambda =(6n+5,5n+4,4n+3,3n+2,2n+1,n)$, then,

  $$\begin{aligned} |A_3|=|\mathscr {D}_{7,7n+6}|. \end{aligned}$$

Finally, we obtain:

$$\begin{aligned} |\mathscr {D}_{8,8n+6}| = \mathbf{Cat}_{(8,8n+7)}&-\mathbf{Cat}_{(7,7n+6)}\\&-\mathbf{Cat}_{(6,6n+5)}\mathbf{Cat}_{(2,2n+1)} - \mathbf{Cat}_{(5,5n+4)}\mathbf{Cat}_{(3,3n+2)}. \end{aligned}$$

5.2 Example $\mathscr {D}_{6,6n+2}$

Similarly to the previous example, comparing $\mathscr {D}_{6,6n + 2}$ and $\mathscr {D}_{6,6n + 1}$ from Eq. 2, we get that the total difference is $Q_{6,6n + 2}-Q_{6,6n + 1} = 3$. From Eq. 4, in this cases $\varDelta (l)$ is zero except for $l = 3,4,5$ (see Fig. 8).

Fig. 8.

$\mathscr {D}_{6,6n+1}$ et $\mathscr {D}_{6,6n+2}$

We consider the sets:

$$\begin{aligned} B_1&=\{ \text {paths containing the box } \alpha _1 \},&\\ B_2&=\{ \text {paths containing the box } \alpha _2 \text { and not } \alpha _1\},&\\ B_3&=\{ \text {paths containing the box } \alpha _3 \text { and not }( \alpha _1 \text { or } \alpha _2)\}.&\end{aligned}$$

We have the following cases :

• Case 1: For $B_1$, we find $3 \times b_1$ and $3\times b'_1$ with underlying diagram $\lambda =(2n,n)$ and $\lambda '=(2n,n)$, respectively (see Eq. 5). Then,

  $$\begin{aligned} |B_1|=|\mathscr {D}_{3,3n+1}||\mathscr {D}_{3,3n+1}|. \end{aligned}$$

• Case 2: For $B_2$, the rectangles $4 \times b_2$ and $2\times b'_2$ such as $\lambda =(3n,2n,n)$ et $\lambda '=(n)$ (see Eq. 5). Then,

  $$\begin{aligned} |B_2|=|\mathscr {D}_{4,4n+1}||\mathscr {D}_{2,2n+1}|. \end{aligned}$$

• Case 3: for $B_3$, the rectangle $5 \times b_3$ such as $\lambda =(4n,3n,2n,n)$ (see Eq. 5). Then,

  $$\begin{aligned} |B_3|=|\mathscr {D}_{5,5n+1}|. \end{aligned}$$

Finally, we obtain:

$$\begin{aligned} |\mathscr {D}_{6,6n+2}| = \mathbf{Cat}_{(6,6n+1)}&+\mathbf{Cat}_{(5,5n+1)} \\&+\mathbf{Cat}_{(4,4n+1)}\mathbf{Cat}_{(2,2n+1)} + \mathbf{Cat}_{(3,3n+1)}\mathbf{Cat}_{(3,3n+1)}. \end{aligned}$$

5.3 Example $\mathscr {D}_{6,9}$.

For $\mathscr {D}_{6,9}$ the Ferrers diagram is (Fig. 9):

Fig. 9.

Ferrers diagram $\mathscr {D}_{6,9}$ and $\mathscr {D}_{6}$

and the diagrams decomposition method. After six iterations the decomposition is:

then,

We can also decompose (see Fig. 10), and after four iterations the decomposition is:

Fig. 10.

Ferrers diagram $\mathscr {D}_{6,9}$ and $\mathscr {D}_{6,8}$

then,

As they are many possible decomposition, finding the shortest one is an open problem.