Security Aspects of Compressed Sensing

Abstract

In this chapter, we will consider the security achievable by the compressed sensing (CS) framework under different constructions of the sensing matrix. CS can provide a form of data confidentiality when the signals are sensed by a random matrix composed of i.i.d. Gaussian variables. However, alternative constructions, based either on different distribution or on circulant matrices, which have similar CS recovery performance as Gaussian random matrices and admit faster implementations, are more suitable for practical CS systems. Compared to Gaussian matrices, which leak only the energy of the sensed signal, we show that generic matrices leak also some information about the structure of the sensed signal. In order to characterize this information leakage, we propose an operational definition of security linked to the difficulty of distinguishing equal energy signals and we propose practical attacks to test this definition. The results provide interesting insights on the security of generic sensing matrices, showing that a properly randomized partial circulant matrix can provide a weak encryption layer irrespective of the signal sparsity and the sensing domain.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

9.1 Introduction

Compressed sensing (CS) has recently been proposed as an efficient framework for acquiring sparse signals represented by few nonzero coefficients in a suitable basis [8]. CS relies on the fact that linear measurements of a sparse signal enable signal recovery with high probability when the measurements satisfy certain incoherence properties with respect to the signal basis. Interestingly, measurements acquired using linear projections generated according to a random sensing matrix have such properties [3]. The low complexity acquisition and reduced energy consumption offered by CS can be beneficial to several applications, as shown by recent works on spectrum sensing [9], wireless sensor networks [11], network anomaly detection [15]. Hence, assessing whether the randomness in the acquisition process implicitly provides some kind of confidentiality is an important open problem.

In the literature, the security of CS has been analyzed following two main paradigms. A first approach is to argue that CS provides computational secrecy if viewed as a cryptosystem, since looking for the correct sensing matrix over the key space is a computationally intractable problem [16, 17]. However, this approach does not provide any formal security proof regarding CS. The second approach is to consider the security of random linear measurements according to an information theoretic framework [19]. As correctly pointed out in [17], CS does not provide information theoretic secrecy, since the mutual information between the measurements and the sensed signal is always greater than zero. However, it is possible to prove that CS measurements asymptotically reveal only the energy of the signal [2] and that normalizing the measurements can provide a perfectly secure channel in the case of Gaussian sensing matrices [1].

The results in the previous works are based on the central limit theorem and the properties of the Gaussian distribution and are valid when the elements of the sensing matrix are i.i.d. random variables. Moreover, they consider a scenario in which the sensing matrix is continually updated, implementing a sort of one time pad. Such requirements are usually too demanding for practical CS systems. Using fully random matrices requires either storing or generating on the fly a great amount of random values. Moreover, the generation of Gaussian distributed values may be difficult in low complexity systems.

The above problems can be solved in practice by resorting to structured matrices [7, 12] and generating the sensing matrix according to simpler distributions, like the Bernoulli one. However, even if such constructions guarantee similar recovery properties as fully random matrices made of Gaussian i.i.d. values, their security properties are still not fully understood. In this chapter, we will analyze the security of practical sensing matrices according to an alternative security definition based on the performance of a detector which tries to distinguish different signals from their measurements. We will also provide useful bounds to characterize the security of CS according to this definition and validate such bounds in simple scenarios through simulations.

9.2 Background

9.2.1 Compressed Sensing

A signal $x \in \mathbb {R}^n$ is called k-sparse if there exists a basis $\varPhi$ such that $x = \varPhi \vartheta$ and $\vartheta$ has at most k nonzero entries, i.e., $||\vartheta ||_0 \le k$. According to the compressed sensing framework, a k-sparse signal can be exactly recovered from $m < n$ linear measurements

$$\begin{aligned} y = A x \end{aligned}$$

(9.1)

by solving a non-convex minimization problem [4, 8].

In practice, if the entries of A are i.i.d. variables from a sub-Gaussian distribution, then exact recovery of k-sparse signals can be achieved with very high probability by solving the convex minimization problem

$$\begin{aligned} \hat{\vartheta } = \arg \min _\vartheta ||\vartheta ||_1,\ \ \text {subject to}\,A\varPhi \vartheta = y \end{aligned}$$

(9.2)

as long as $m = O(k\log (n/k))$ [3].

9.2.2 Security Definitions

Let us call the set of possible plaintexts $\mathscr {P}$, the set of cipher texts $\mathscr {C}$ and a key K. A private key cryptosystem is a pair of functions $e_{K} : \mathscr {P} \rightarrow \mathscr {C}, d_{K} : \mathscr {C} \rightarrow \mathscr {P}$ such that, given a plain text $p \in \mathscr {P}$, and a ciphertext $c \in \mathscr {C}$, we have that $d_{K}(e_{K}(p))=p$ and that it is unfeasible, without knowing the key K, to determine p such that $e_{K}(p)=c$.

A cryptosystem is said to be perfectly secure [19] if the posterior probability of the ciphertext given the plaintext p is independent of p, i.e., if

$$\begin{aligned} \mathbb {P}(c | p) = \mathbb {P}(c). \end{aligned}$$

(9.3)

Given a perfectly secure cryptosystem, an attack cannot be more successful than guessing the plaintext at random.

Following the approach in [1], we define a CS-based cryptosystem where the signal x is the plain text p, the sensing matrix A is the secret key K and the measurement vector y is the cipher text c. The encryption function $e_A$ is the matrix multiplication between the sensing matrix A and the signal x; the decryption is achieved by solving the problem in (9.2). We assume that each sensing matrix is used only once (one-time sensing matrix (OTS) scenario), and that different sensing matrices are statistically independent. Under this scenario, we can assume that the adversary has only knowledge of the measurements y (ciphertext-only attack (COA) scenario), since the knowledge of plaintext/ciphertext pairs (x, y) does not reveal anything about the unknown plaintexts. CS-based cryptosystems cannot achieve in general perfect secrecy [1, 17]. However, weaker security notions may apply, as we will show in the next sections.

9.3 Security of the Measurements

In this section, we summarize the main results regarding the security of CS measurements. In the first subsection, we review the security of fully random sensing matrices, i.e., when the matrix entries are i.i.d. random variables. In the second subsection, we address the security of partial circulant random sensing matrices, which have an important role in the deployment of practical CS systems.

9.3.1 Fully Random Matrices

Let us consider the OTS cryptosystem defined by $y = A x$. Let us denote with I(x, y) the mutual information between x and y [5], and define $\mathscr {E}_x = ||x||_2^2$. We have the following important result [1]:

Theorem 9.1

If $[A]_{i,j}$ are i.i.d. zero-mean Gaussian variables, then the OTS cryptosystem satisfies $I(x;y) = I(\mathscr {E}_x;y)$.

The above result says that an OTS cryptosystem using an i.i.d. Gaussian sensing matrix does not reveal anything more about x than its energy and what can be inferred by knowing its energy. It is worth noting that this is true irrespective of the sparsity degree of x, that is, x does not necessarily have to be sparse. In the following, we will denote such a cryptosystem as Gaussian-OTS (G-OTS) cryptosystem.

The special properties of Gaussian sensing matrices can be exploited to obtain a perfectly “secured” version of the G-OTS cryptosystem. Let us modify the G-OTS cryptosystem so that only normalized measurements are transmitted, i.e., using as ciphertext the vector

$$\begin{aligned} u_y = {\left\{ \begin{array}{ll} y/\sqrt{\mathscr {E}_y} &{} \mathscr {E}_y > 0\\ U &{} \mathscr {E}_y = 0 \end{array}\right. } \end{aligned}$$

(9.4)

where U is a random vector uniformly distributed on a unit radius m-sphere. We denote it as SG-OTS.

Theorem 9.2

The SG-OTS cryptosystem is perfectly secure, i.e., $\mathbb {P}(u_y|x) = \mathbb {P}(u_y)$.

Proof

It is easy to verify that for a Gaussian A the vector y is spherically distributed, i.e., $u_y$ is uniformly distributed on the unit radius m-sphere irrespective of x. ${\square }$

9.3.2 Circulant Matrices

Due to the complexity of performing the product Ax when A is a fully random matrix, some authors have suggested to use partial circulant matrices generated from a row of i.i.d. variables [12, 18, 21]. Such matrices have the following form

$$\begin{aligned} A = \left[ \begin{array}{ccccc} a_1 &{} a_2 &{} a_3 &{} \ldots &{} a_n \\ a_n &{} a_1 &{} a_2 &{} \ldots &{} a_{n-1} \\ \vdots &{} &{} &{} &{} \vdots \\ a_{n-m+2} &{} a_{n-m+3} &{} a_{n-m+4} &{} \dots &{} a_{n-m+1} \end{array} \right] \end{aligned}$$

(9.5)

where the first row $a^T = [a_1, a_2,\ldots ,a_n]$ is a vector of i.i.d. variables from a Gaussian or sub-Gaussian (e.g., Bernoulli) distribution. Partial circulant matrices have similar recovery performance as fully random matrices [21]. Moreover, they can be diagonalized using a discrete Fourier transform (DFT) as

$$\begin{aligned} A = P W^H \Lambda W \end{aligned}$$

(9.6)

where W is the unitary DFT matrix, $\Lambda$ is a diagonal matrix whose nonzero elements are the DFT of the sequence $[a_1, a_n,a_{n-1},\ldots , a_2]$, i.e., the first column of the $n\times n$ fully circulant matrix generated from $a^T$, and P is a $m\times n$ matrix that selects the first m entries of a vector of n elements. Thanks to the above decomposition, the product Ax can be efficiently implemented using a fast Fourier transform (FFT). Moreover, the cost of transmitting or generating the sensing matrix is also sensibly reduced, since only n random values are required.

In order to generalize the concept of partial circulant matrix, in the following we will consider sensing matrices that can be expressed as

$$\begin{aligned} A = P W^H \Lambda W R. \end{aligned}$$

(9.7)

In the above notation, we assume that P select a generic subset of m indexes [21], whereas R is a generic scrambling matrix. The above construction is somewhat similar to the structurally random matrices proposed in [7].

Let us consider the OTS cryptosystem defined by $y = A x$, where A can be expressed as in (9.7) and the matrices P and R are public. We will denote such a cryptosystem as OTS-circulant (OTS-C). Let us define $C_v$ as the circular autocorrelation matrix of vector v, that is, $[C_v]_{ij} = \sum _{r=1}^n v_r v_{r+i-j \mod n}$, for $i,j = 1,\ldots ,n$, where $[A]_{ij}$ denotes the element in the ith row and jth column of matrix A. It is easy to verify that $C_v$ is a Toeplitz matrix and that its diagonal elements are equal to $\mathscr {E}_v = v^T v$. We have the following result:

Theorem 9.3

If $a_i$, $i=1,\ldots ,n$, are i.i.d. zero-mean Gaussian variables, then the OTS-C cryptosystem satisfies $\mathbb {P}(y|x) = \mathbb {P}(y|PC_{Rx}P^T)$.

Proof

Let us consider the probability distribution function $\mathbb {P}(y|x)$ for a given x. Since $a_i$ are Gaussian, we have that $\mathbb {P}(y|x)$ is a multivariate Gaussian distribution with mean $\mu _{y|x}$ and covariance matrix $C_{y|x}$. It is immediate to find $\mu _{y|x} = E[y|x] = E[A] x = 0$, whereas we have

$$\begin{aligned} \begin{array}{ll} C_{y|x} &{} = E[A x x^T A^T] = E[PW^H \Lambda (WRx)(WRx)^H \Lambda ^H WP^T]\\ &{} = n PW^H \mathrm {diag}\{WRx\}E[(W^H a)(W^H a)^H]\\ &{} \quad \times \mathrm {diag}\{WRx\}^H WP^T \\ &{} = n PW^H \mathrm {diag}\{WRx\}W^H E[aa^T] W\mathrm {diag}\{WRx\}^H WP^T\\ &{} = n\sigma _A^2 PW^H \mathrm {diag}\{WRx\}\mathrm {diag}\{WRx\}^H WP^T = \sigma _A^2 PC_{Rx}P^T \end{array} \end{aligned}$$

(9.8)

where $\mathrm {diag}\{v\}$ denotes a diagonal matrix defined by vector v, we use $\Lambda = \sqrt{n}\cdot \mathrm {diag}\{W^H a\}$ and the fact that $\mathrm {diag}\{u\}v = \mathrm {diag}\{v\}u$, and we assume that $a_i$ have variance $\sigma _A^2$. It follows that y depends on x only through the autocorrelation $PC_{Rx}P^T$, i.e., $\mathbb {P}(y|x) = \mathbb {P}(y|PC_{Rx}P^T)$. ${\square }$

The above result says that an OTS-C cryptosystem using i.i.d. Gaussian variables reveals only some elements of the circular autocorrelation matrix of Rx, according to the particular selection matrix P. It is worth noting that this is true irrespective of the sparsity degree of x, that is, x does not necessarily have to be sparse.

In the following, we will consider three variants of the OTS-C cryptosystem:

• 1. Gaussian-OTS-C (G-OTS-C) cryptosystem, where P is fixed and public and R is the identity matrix, implying $\mathbb {P}(y|x) = \mathbb {P}(y|PC_{x}P^T)$;

• 2. Gaussian-OTS-singly randomized circulant (G-OTS-R1), where the selection matrix P is randomly drawn, with uniform distribution, over all the possible choices of m indexes out of n and kept secret whereas R is the identity matrix. In this case, it is easy to derive

  $$\mathbb {P}(y|x) = \frac{1}{N_P}\sum _{r=1}^{N_P}\mathscr {N}(0, \sigma _A^2 P_r C_x P_r^T)$$

  where $P_r$ denotes the rth possible selection matrix, $N_P = n!/(n-m)!$, and $\mathscr {N}(\mu ,C)$ denotes a multivariate Gaussian distribution with mean $\mu$ and covariance matrix C.

• 3. Gaussian-OTS-doubly randomized circulant (G-OTS-R2), where P is chosen as above and R is a diagonal matrix introducing a random sign flip on the elements of x, i.e., its diagonal elements are i.i.d. Rademacher variables. In this case, we obtain

  $$\mathbb {P}(y|x) = \frac{1}{N_P}\frac{1}{N_R}\sum _{r=1}^{N_P}\sum _{s=1}^{N_R}\mathscr {N}(0, \sigma _A^2 P_r C_{R_s x} P_r^T)$$

  where $R_s$ denotes the sth possible sign randomization matrix and $N_R = 2^n$.

9.4 Security Metrics

Measurements taken with a non-Gaussian or a circulant sensing matrix in general are not distributed according to a spherically symmetric distribution. As a result, this kind of sensing matrices provide a weaker security than Gaussian sensing matrices, since their information leakage is not limited to the energy of x [1]. In order to characterize this additional leakage, we introduce a security metric based on the problem of distinguishing whether the measurements y comes from one of two known signals $x_1$ and $x_2$. This security definition is inspired to indistinguishability definitions commonly used in cryptography [10]. Let us consider a signal x that belongs to a two-element set $\{x_1,x_2\}$; a detector is a function that given the measurements y outputs one of two possible signals $x_1$, $x_2$. Formally, this can be defined as $\mathscr {D}: \mathbb {R}^m \rightarrow \{x_1,x_2\}$. Given a certain detector, we define the probability of detection with respect to signal $x_i$ as $P_{d,i} = \mathrm {Pr}\{\mathscr {D}(y) = x_i|x = x_i\}$ and the respective probability of false alarm as $P_{f,i} = \mathrm {Pr}\{\mathscr {D}(y) = x_i|x \ne x_i\}$. It is immediate to verify $P_{d,2} = 1 - P_{f,1}$ and $P_{f,2} = 1 - P_{d,1}$, so that $P_{d,1}-P_{f,1} = P_{d,2}-P_{f,2} \triangleq P_d - P_f$.

Definition 1

A cryptosystem is $\vartheta$-indistinguishable with respect to two signals $x_1$ and $x_2$ if for every possible detector $\mathscr {D}(y)$ we have

$$\begin{aligned} P_d - P_f \le \vartheta . \end{aligned}$$

(9.9)

According to the above definition, lower values of $\vartheta$ correspond to higher security, with $\vartheta = 0$ being equivalent to perfect secrecy.

Given an OTS cryptosystem defined by a sensing matrix A with a certain distribution, we can link the $\vartheta$-indistinguishability of the cryptosystem to $\mathbb {P}(y|x_1)$ and $\mathbb {P}(y|x_2)$. Let us define the total variation (TV) distance between the probability distributions $\mathbb {P}_A(a)$ and $\mathbb {P}_B(b)$ as $\delta (\mathbb {P}_A(a),\mathbb {P}_B(b)) = \frac{1}{2}\int {|\mathbb {P}_A(t) - \mathbb {P}_B(t)|dt}$. Let us also denote in short $\delta (\mathbb {P}(y|x_1),\mathbb {P}(y|x_2)) = \delta (\mathbb {P}_1,\mathbb {P}_2)$. We have the following:

Theorem 9.4

An OTS cryptosystem is at least $\delta (\mathbb {P}_1,\mathbb {P}_2)$-indistinguishable with respect to two signals $x_1$ and $x_2$.

Proof

The sum of error probabilities in a statistical hypothesis test can be lower bounded as [14]

$$\begin{aligned} \mathrm {Pr}\{\mathscr {D}(y) = x_2|x_1\} + \mathrm {Pr}\{\mathscr {D}(y) = x_1|x_2\}&= 1 - P_d + P_f \nonumber \\&\ge 1 - \delta (\mathbb {P}(y|x_1),\mathbb {P}(y|x_2)) \end{aligned}$$

(9.10)

from which it is immediate to derive $P_d - P_f \le \delta (\mathbb {P}_1,\mathbb {P}_2)$. ${\square }$

In general, it is difficult to find a closed form expression for the TV distance in the case of arbitrary distributions and/or structured matrices. However, a useful upper bound on the TV distance can be evaluated thanks to the Pinsker’s inequality, which states $\delta (\mathbb {P}_1,\mathbb {P}_2) \le \sqrt{D(\mathbb {P}_1||\mathbb {P}_2)/2}$, where $D(\mathbb {P}_1||\mathbb {P}_2)$ denotes the Kullback-Leibler (KL) divergence between the distributions $\mathbb {P}_1$ and $\mathbb {P}_2$.¹

9.4.1 Bounds for Fully Random Matrices

Under the assumption that the elements of y are i.i.d., it is possible to find an upper bound for $P_d-P_f$ by numerically evaluating the KL divergence between $\mathbb {P}([y]_i|x_1)$ and $\mathbb {P}([y]_i|x_2)$, where $[y]_i$ denotes the ith element of vector y. Namely, we can estimate

$$\begin{aligned} P_d-P_f \le \vartheta _{\mathrm {KL}}(x_1,x_2) \triangleq \sqrt{\frac{m}{2}D(\mathbb {P}([y]_i|x_1)||\mathbb {P}([y]_i|x_2))} \end{aligned}$$

(9.11)

where KL divergences can be computed numerically. In order to compute numerical approximations of the probability density functions $\mathbb {P}([y]_i|x_1)$ and $\mathbb {P}([y]_i|x_2)$, we can consider the characteristic function of the random variable $a = [A]_{ij}$, defined as $\varphi _a(t) = E[e^{jta}]$. It is well known that the pdf of a random variable a can be obtained as $\mathbb {P}(a) = \frac{1}{2\pi }\int _{-\infty }^{\infty } \varphi _a(t)e^{-jta}dt$, i.e., that the characteristic function and the corresponding pdf form a Fourier transform pair. We have that the characteristic function of $[y]_i$ given a generic signal x can be computed as

$$\begin{aligned} \varphi _{[y]_i|x}(t) = \prod _{j=1}^{n}\varphi _a([x]_j t) \end{aligned}$$

(9.12)

where $\varphi _a(t)$ is the characteristic function of a generic element of the sensing matrix A. Hence, given $x_1$ and $x_2$, we can use (9.12) to evaluate the characteristic functions $\varphi _{[y]_i|x_1}$ and $\varphi _{[y]_i|x_2}$, find the corresponding $\mathbb {P}([y]_i|x_1)$ and $\mathbb {P}([y]_i|x_2)$ through a Fourier transform.

9.4.2 Bounds for Circulant Matrices

In the case of circulant sensing matrices composed by Gaussian random variables, it is possible to exploit the fact that the KL divergence of two multivariate Gaussian distributions has a nice closed form. Given any two different signals $x_1$ and $x_2$, we have the following result:

Theorem 9.5

A G-OTS-C cryptosystem is at least $\vartheta _C(x_1,x_2)$-indistinguishable w.r.t. $x_1$, $x_2$, where

$$\begin{aligned} \vartheta _C(x_1,x_2) = \frac{1}{2}\sqrt{\log \frac{|C_{2}|}{|C_{1}|} + \mathrm {Tr}(C_{2}^{-1}C_{1}) - m} \end{aligned}$$

(9.13)

and $C_h = PC_{x_h}P^T$, for $h = 1,2$.

Proof

Thanks to Proposition 9.3, we have that $\mathbb {P}(y|x_h) = \mathscr {N}(0,\sigma _A^2 C_{h})$. Hence, the Kullback-Leibler (KL) divergence between $\mathbb {P}(y|x_1)$ and $\mathbb {P}(y|x_2)$ can be expressed as [6]

$$\begin{aligned} D(\mathbb {P}_1||\mathbb {P}_2) = \frac{1}{2}\left[ \log \frac{|C_{2}|}{|C_{1}|} + \mathrm {Tr}(C_{2}^{-1}C_{1}) - m\right] . \end{aligned}$$

(9.14)

The result then follows from Pinsker’s inequality. ${\square }$

Theorem 9.6

A G-OTS-R1 cryptosystem is at least $\vartheta _{R1}(x_1,x_2)$-indistinguishable w.r.t. $x_1$, $x_2$, where

$$\begin{aligned} \vartheta _{R1}(x_1,x_2) = \sqrt{\frac{1}{4N_P^2}\sum _{r1=1}^{N_P}\sum _{r2=1}^{N_P}\left[ \log \frac{|C_{2,r2}|}{|C_{1,r1}|} + \mathrm {Tr}(C_{2,r2}^{-1}C_{1,r1})\right] - \frac{m}{4}} \end{aligned}$$

(9.15)

and $C_{h,r} = P_r C_{x_h}P_r^T$, for $h = 1,2$. A G-OTS-R2 cryptosystem is at least $\vartheta _{R2}(x_1,x_2)$-indistinguishable w.r.t. $x_1$, $x_2$, where

$$\begin{aligned} \vartheta _{R2}(x_1,x_2) = \sqrt{\frac{1}{4N_P^2 N_R^2}\sum _{r1=1}^{N_P}\sum _{r2=1}^{N_P}\sum _{s1=1}^{N_R}\sum _{s2=1}^{N_R}\left[ \log \frac{|C_{2,r2,s2}|}{|C_{1,r1,s1}|} + \mathrm {Tr}(C_{2,r2,s2}^{-1}C_{1,r1,s1})\right] - \frac{m}{4}} \end{aligned}$$

(9.16)

and $C_{h,r,s} = P_r C_{R_s x_h}P_r^T$, for $h = 1,2$.

Proof

For G-OTS-R1 and G-OTS-R2, we have that $\mathbb {P}(y|x_h)$ can be expressed as a mixture of Gaussian distributions. The KL divergence between two mixture distributions $\mathbb {P}_i = \sum _r w_{h,r}\mathbb {P}_{h,r}$, $h = 1,2$, can be upper bounded using the following convexity bound [13]

$$\begin{aligned} D(\mathbb {P}_1||\mathbb {P}_2) \le \sum _{r1,r2} w_{1,r1}w_{2,r2}D(\mathbb {P}_{1,r1}||\mathbb {P}_{2,r2}). \end{aligned}$$

(9.17)

Hence, the result can be easily obtained by considering that $w_{1,r} = w_{2,r} = \frac{1}{N_P}$, for G-OTS-R1, or $w_{1,r} = w_{2,r} = \frac{1}{N_P N_R}$, for G-OTS-R2, and then applying Pinsker’s inequality to the upper bound on the KL divergence. ${\square }$

For relatively large values of n and m, the exact computation of the bounds in (9.15) and (9.16) can become prohibitively expensive. A possible approach is to estimate the bound using Monte Carlo integration. Alternatively, following the suggestion in [13], we can approximate the KL divergence between the two mixture distributions using the KL divergence of two multivariate Gaussian distributions having the same mean and covariance matrix. For the G-OTS-R1 cryptosystem, the covariance matrix of the involved mixture distributions has a very peculiar form, since

$$\begin{aligned}{}[C_h]_{ij} = \sum _{r=1}^{N_P}\frac{1}{N_P}[C_{h,r}]_{ij} = {\left\{ \begin{array}{ll} \sigma _A^2\mathscr {E}_{x_h} &{} i = j \\ \sigma _A^2\sum _{s\ne t} x_{h,s}x_{h,t} &{} i\ne j \end{array}\right. } \end{aligned}$$

(9.18)

for $h = 1,2$. The above covariance matrix can be expressed in a compact form as $C_h = \alpha _h I_m + \beta _h\mathbbm {1}\mathbbm {1}^T$, where we define $\alpha _h = \frac{\sigma _A^2}{n-1}(n\mathscr {E}_{x_h} - (\mathbbm {1}^T x_h)^2)$ and $\beta _h = \frac{\sigma _A^2}{n-1}((\mathbbm {1}^T x_h)^2 - \mathscr {E}_{x_h})$. According to the above representation, the KL divergence between $\mathbb {P}(y|x_1)$ and $\mathbb {P}(y|x_2)$ can be approximated as

$$\begin{aligned} D(\mathbb {P}_1||\mathbb {P}_2) \approx&\frac{1}{2}\left[ \log \frac{\alpha _2^{m-1}(\alpha _2 + m\beta _2)}{\alpha _1^{m-1}(\alpha _1 + m\beta _1)} + \frac{m\alpha _2(\alpha _1 + \beta _1) + m(m-1)\alpha _1\beta _2}{\alpha _2(\alpha _2 + m\beta _2)} - m\right] \\ \triangleq&\tilde{D}(x_1,x_2).\nonumber \end{aligned}$$

(9.19)

Thanks to the above equation, an approximate security metric can be defined as

$$ \vartheta '_{R1}(x_1,x_2) = \sqrt{\frac{\tilde{D}(x_1,x_2)}{2}}. $$

However, since (9.19) is not an upper bound on KL divergence, $\vartheta '_{R1}(x_1,x_2)$ does not provide a strict security bound for the G-OTS-R1 cryptosystem.

Unfortunately, the above approach cannot be used to provide a meaningful bound for the G-OTS-R2 cryptosystem, since in this case we have

$$\begin{aligned} C_h = \sum _{r=1}^{N_P}\sum _{s=1}^{N_R}\frac{1}{N_P N_R}C_{h,r,s} = \mathscr {E}_{x_h}I_m, \end{aligned}$$

meaning that for equal-energy signals the approximated KL divergence is zero. Nevertheless, by using the convexity bound approach, an approximate security metric for the G-OTS-R2 cryptosystem can be obtained as

$$ \vartheta '_{R2}(x_1,x_2) = \sqrt{\frac{1}{2N_R^2}\sum _{s1=1}^{N_R}\sum _{s2=1}^{N_R}\tilde{D}(R_{s1}x_1,R_{s2}x_2)}. $$

Again, the exact computation of the above metric may become too expensive for large values of n. In those cases, we can resort to Monte Carlo integration.

9.4.3 Bounds for Normalized Measurements

The normalization strategy described in Sect. 9.3 does not provide a perfectly secure channel in the case of arbitrary sensing matrices. However, we can provide an upper bound on the security of normalized measurements by using the above bounds that holds for equal energy signals. Let us define $u_{x_h} = x_h/\sqrt{\mathscr {E}_{x_h}}$ and $u_{y_h} = y_h/\sqrt{\mathscr {E}_{y_h}}$, where $y_h = Ax_h$, $h = 1,2$. Then we have the following

Theorem 9.7

The upper bounds given in (9.13), (9.15), and (9.16) computed for equal-energy signals $u_{x_1},u_{x_2}$ holds also in the case of normalized measurements of generic signals $x_1,x_2$.

Proof

Let us define $y'_i = Au_{x_i}$. It is easy to verify that $u_{y'_i} = y'_i/\sqrt{\mathscr {E}_{y'_i}} = u_{y_i}$. Then, we have the following inequalities involving the KL divergence

$$\begin{aligned} \begin{array}{ll} D(y'_1 || y'_2) &{} = D(\mathbb {P}(u_{y_1},\mathscr {E}_{y'_1}) || \mathbb {P}(u_{y_2},\mathscr {E}_{y'_2}) ) \\ &{} = D(u_{y_1}||u_{y_2}) + D(\mathbb {P}(\mathscr {E}_{y'_1}|u_{y_1}) || \mathbb {P}(\mathscr {E}_{y'_1}|u_{y_1}) ) \\ &{} \ge D(u_{y_1}||u_{y_2}) \end{array} \end{aligned}$$

(9.20)

where we exploited the chain rule for KL divergence [5] and the fact that KL divergence is always nonnegative. Hence, the proof follows from the following chain of inequalities

$$\begin{aligned} \delta (\mathbb {P}(u_{y_1}),\mathbb {P}(u_{y_2})) \le \sqrt{\frac{1}{2}D(u_{y_1}||u_{y_2})} \le \sqrt{\frac{1}{2}D(y'_1 || y'_2)} \end{aligned}$$

(9.21)

where it is easy to verify that the right hand side of (9.21) evaluates to the upper bound on the distinguishability of equal energy signals. ${\square }$

9.5 Attacks to CS Cryptosystems

The bounds introduced in the previous Section hold for any possible attack under the COA scenario. However, it is interesting to evaluate the performance of practical attacks with respect to those bounds. We consider an hypothetical scenario in which an OTS cryptosystem is used to sense two distinct signals $x_1$ and $x_2$ having equal energy. Without loss of generality, we can assume that $\mathscr {E}_{x_1} = \mathscr {E}_{x_2} = 1$. The aim of the attacker is to guess whether the measurements conceal the signal $x_1$ or the signal $x_2$. This is a classical detection problem, where the aim is to distinguish whether the measurements y come from the probability distribution $\mathbb {P}(y|x_1)$ or from the probability distribution $\mathbb {P}(y|x_2)$.

Let us consider a detector $\mathscr {D}$. The Neyman-Pearson (NP) lemma states that for $P_f = \alpha$, the probability of detection is maximized by letting $\mathscr {D}(y) = x_1$ whenever

$$\begin{aligned} \Lambda (y) = \frac{\mathbb {P}(y|x_1)}{\mathbb {P}(y|x_2)} \ge \tau \end{aligned}$$

(9.22)

where $\tau$ satisfies $\mathrm {Pr}\{\Lambda (y) \ge \tau | x_2\} = P_f$.

When the sensing matrix is made up of i.i.d. elements, it turns out that the elements of y are i.i.d. as well. This permits to rewrite the optimal NP test as

$$\begin{aligned} \Lambda '(y) = \sum _{i=1}^{m}\left( \log (\mathbb {P}([y]_i|x_1)) - \log (\mathbb {P}([y]_i|x_2))\right) \ge \tau '. \end{aligned}$$

(9.23)

Moreover, since each element of y is given by the sum of independent variables, the distributions $\mathbb {P}([y]_i|x_1)$ and $\mathbb {P}([y]_i|x_2)$ can be numerically computed as detailed in Sect. 9.4.

In the case of the G-OTS-C cryptosystem, the optimal NP test can be easily obtained as

$$\begin{aligned} \Lambda _C(y) = y^T(C_2^{-1} - C_1^{-1})y \ge \tau '. \end{aligned}$$

(9.24)

In the case of the G-OTS-R1 cryptosystem, the optimal NP test would be obtained as the ratio of two mixture distributions. Since the computation of the NP test is not practical in this case, we consider a simpler test obtained by approximating the two mixture distributions using two multivariate Gaussian distributions with the same mean and covariance matrix. By using the expressions of the covariance matrices found in Sect. 9.3, the test can be expressed as

$$\begin{aligned} \Lambda _{R}(y) = \left( \frac{1}{\alpha _2}-\frac{1}{\alpha _1}\right) y^T y - \left( \frac{\beta _2}{\alpha _2(\alpha _2 + m\beta _2)} - \frac{\beta _1}{\alpha _1(\alpha _1 + m\beta _1)}\right) (\mathbbm {1}^T y)^2 \ge \tau ''. \end{aligned}$$

(9.25)

It is worth noting that the above test is not able to distinguish equal-energy signals sensed with the G-OTS-R2 cryptosystem, since equal energy signals yields measurements with the same covariance matrix.

9.6 Simulation Results

In this section, we evaluate the distinguishability of equal-energy signals in different scenarios. In each experiment, for the numerical evaluation of $\vartheta _{\mathrm {KL}}$ and the NP test (9.23), the involved pdfs have been sampled on 10000 equispaced bins between $-8$ and 8, whereas $\vartheta _{R1}$, $\vartheta _{R2}$, and $\vartheta '_{R2}$ have been estimated via a Monte Carlo integration using $10^{5}$ random samples.

9.6.1 Upper Bound Validation

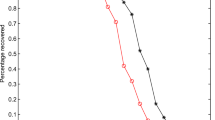
The first experiment has been carried out with the aim of assessing the different upper bounds on the distinguishability of unit energy signals: thanks to Theorem 9.7, similar results also apply to arbitrary signals if we consider normalized measurements. In the case of fully random matrices, the signals have been defined as $[x_1]_i = 1/\sqrt{n}$ and $[x_2]_i = Z(\alpha )e^{-\alpha (i-1)}$, for $i = 1,\ldots ,n$, where $Z(\alpha )$ is a suitable normalizing constant such that $\mathscr {E}_{x_2} = 1$. In Fig. 9.1 we show the numerically evaluated upper bound $\vartheta _{\mathrm {KL}}$ when the entries of A are i.i.d. uniform variables with unit variance (uniform sensing matrix), for $n = 1000$ and different combinations of $\alpha$ and m parameters. In the same plots, we also show the maximum value of $P_d-P_f$ achieved by the optimal NP test (9.23), evaluated over $10^6$ independent realizations. As can be seen, the performance of the detection attack is predicted quite well by the numerical upper bound.

Fig. 9.1

Distinguishability of unit energy vectors using a uniform sensing matrix: a $m=1$, $n = 1000$; b $\alpha = 0.1$, $n = 1000$

In the case of G-OTS cryptosystems based on circulant matrices, the signals have been defined as $x_1 = [1,0,\ldots ,0]$ and $[x_2]_i = Z(\alpha )e^{-4\alpha (i-1)}$, for $i = 1,\ldots ,n$, where $Z(\alpha )$ is a suitable normalizing constant such that $\mathscr {E}_{x_2} = 1$. For the G-OTS-C cryptosystem, we consider the matrix P that selects the first m rows of the $n\times n$ circulant matrix $W^H\Lambda W$: an advantage of this construction is that the resulting sensing matrix enables several processing tasks directly on the measurements [20]. In Fig. 9.2, we compared the theoretical upper bounds $\vartheta _C$, $\vartheta _{R1}$, and $\vartheta _{R2}$ with the performance obtained by the optimal test $\Lambda _C$ and the suboptimal test $\Lambda _{R}$, respectively, for $n = 100$ and different combinations of $\alpha$ and m parameters. The approximated bounds $\vartheta '_{R1}$, and $\vartheta '_{R2}$ are shown as well. The performance of the detection attack $\Lambda _C$ is predicted quite well by the theoretical upper bound $\vartheta _C$, whereas the upper bounds $\vartheta _{R1}$ and $\vartheta _{R2}$ appear quite loose. Interestingly, the approximation $\vartheta '_{R1}$ is quite close to the simulated performance of the detection attack $\Lambda _{R}$, especially for higher values of $\vartheta$.

Fig. 9.2

Distinguishability of unit energy vectors using circulant matrices: a $m=2$, $n = 100$; b $\alpha = 1$, $n = 100$

9.6.2 Expected Security

In the second experiment, we computed the numerical upper bounds and the approximated bounds for different realizations of equal-energy signals $x_1$ and $x_2$ and different scenarios. Namely, we considered 1000 pairs $\vartheta _1,\vartheta _2$ of independent vectors with k nonzero entries uniformly distributed on a unit norm n-sphere, where the respective k-sparse signals were obtained by multiplying those vectors by a unitary matrix $\varPhi$. The first scenario considered as $\varPhi$ the identity matrix, i.e., the signals were sparse in the sensing domain. The second scenario considered as $\varPhi$ the discrete cosine transform (DCT) matrix. It can be noticed that for equal energy signals a sensing matrix with Gaussian i.i.d. entries achieves perfect secrecy [1], i.e., $\vartheta = 0$. Hence, the proposed experiment permits to immediately evaluate the security loss incurred when using more structured sensing matrices.

In both scenarios we computed $\vartheta _{\mathrm {KL}}$ for $m=1$, since for $m > 1$ $\vartheta _{\mathrm {KL}}$ can be easily obtained by multiplying the distinguishability calculated previously by a factor $\sqrt{m}$, whereas $\vartheta _{C}$, $\vartheta '_{R1}$, and $\vartheta '_{R2}$ were computed for $m=2$.

In Fig. 9.3a, we show the 0.95 percentile of $\vartheta _{\mathrm {KL}}$ when $n = 1000$ and k varies in the interval [1, 500]. As expected, if the signals are sparse in the sensing domain the distinguishability decreases when k increases, whereas if the signal are sparse in a different domain the distinguishability is almost constant with respect to k. In Fig. 9.3b, we show the 0.95 percentile of $\vartheta _{\mathrm {KL}}$ when $k = 10$ and n varies in the interval [20, 1000]. As expected, the distinguishability of signals that are sparse in the DCT domain decreases when n increases, whereas if the signals are sparse in the sensing domain the distinguishability does not depend on n.

Fig. 9.3

Distinguishability of k-sparse unit energy signals when using different fully random sensing matrix: a $n = 1000$; b $k = 10$

In Fig. 9.4a, we show the 0.95 percentile of $\vartheta _{C}$, $\vartheta '_{R1}$, and $\vartheta '_{R2}$ when $n = 1000$ and k varies in the interval [1, 500]. The results show that for the two considered classes of sparse signals the security of G-OTS-C and G-OTS-R1 has a similar behavior: the security of both cryptosystems is independent of k when the signal is sparse in the sensing domain, whereas there is a strong dependence on the signal sparsity when the signal is sparse in the DCT domain, since sparser signals are more difficult to conceal. An intuitive explanation is that a very sparse signal in the DCT domain is heavily correlated in the sensing domain and a circulant matrix leaks a lot of information on this correlation. For G-OTS-R2, the security is independent of both k and the sparsity domain, indicating that the prerandomization improves the confidentiality of measurements.

In Fig. 9.4b, we show the 0.95 percentile of $\vartheta _{C}$, $\vartheta '_{R1}$, and $\vartheta '_{R2}$ when $k = 10$ and n varies in the interval [20, 1000]. The security of the G-OTS-C cryptosystem increases for large values of n when the signal is sparse in the sensing domain, whereas it decreases for large values of n when the signal is sparse in the DCT domain. This can be explained by the fact that a signal having a fixed sparsity in the DCT domain becomes extremely correlated when n increases. In the case of the G-OTS-R1 cryptosystem, the security is independent of n when the signal is sparse in the DCT domain, whereas it significantly increases for large values of n when the signal is sparse in the sensing domain. In the case of the G-OTS-R2 cryptosystem, the security always increases for large values of n, showing that this second acquisition strategy guarantees the same level of confidentiality irrespective of the sparsity domain.

Fig. 9.4

Distinguishability of k-sparse unit energy signals when using different random circulant sensing matrices: a $n = 1000$; b $k = 10$

9.7 Conclusions

In this chapter, we have analyzed the security of CS measurements when the sensing matrix is either a fully random non-Gaussian matrix or a partial circulant random matrix. Unlike the case of fully random Gaussian matrices, which reveal only the energy of the sensed signal, we find that more general constructions also reveal some partial information on the structure of the signal. This fact implies that normalizing the measurements cannot achieve a perfectly secure channel for this kind of matrices. In order to measure this loss of security, we introduce an operational definition of security based on the problem of distinguishing different signals and we provide useful bounds for evaluating the security of various types of sensing matrices according to this definition.

The above definition has been applied considering two classes of sparse signals. The results indicate that non-Gaussian sensing matrices can provide a certain level of confidentiality when signals are sparse in a DFT-like domain, however they are not able to conceal signals that are very sparse in the sensing domain. For what concerns circulant sensing matrices, the results indicate that partial circulant matrices obtained by taking the first rows of a circulant matrix, which are interesting in practical settings since they enable processing directly on the measurements, provide a very poor encryption layer. The security of circulant sensing matrices can be improved by using a proper randomization. If the sensing matrix is obtained by choosing the rows at random, this construction provides a weak encryption layer if the signals are sparse in the sensing domain, but is not very secure if the signal is sparse in a DFT-like domain. If, in addition, the signs of the signal samples are randomly scrambled before acquisition, this second construction is shown to provide a weak encryption layer irrespective of the sparsity of the signal and the sparsity domain. It is worth noting that the above randomized constructions, even if they do not permit direct processing of the measurements, still retain the computational advantages of standard circulant matrices.