On Time Discretizations of Fluid-Structure Interactions

Abstract

In this contribution, time discretizations of fluid-structure interactions are considered. We explore two specific complexities: first, the stiffness of the coupled system including different scales of the Navier-Stokes equations of parabolic type and the structure equation of hyperbolic type and second, the problem of moving domains that is inherent to fluid-structure interactions.

Typical moving mesh approaches, such as the arbitrary Lagrangian-Eulerian framework, give rise to nonlinearities and time-derivatives with respect to the mesh-deformation. We derive different time-stepping techniques of Crank-Nicolson type and analyse their stability and approximation properties. Further, we closely look at the dominant time-scales that must be resolved to capture the global dynamics. Moreover, our discussion is supplemented with an analysis of the temporal discretization of Eulerian fixed-mesh approaches for fluid-structure interactions, where the interface between fluid and solid will change from time-step to time-step. Finally, a formulation of parallel multiple shooting methods for fluid-structure interaction is presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fluid-structure interactions (fsi) are part of many application problems and appear in mechanical engineering, aeroelasticity, hemodynamics, or as pore-scale modeling in porous media flow. Concretely in this work, we consider the interaction of a laminar, incompressible fluid with an elastic solid governed by the Saint Venant Kirchhoff material law. While the simulation of both single sub-processes is already a difficult task, covering their interaction is further complicated by the two-way coupling between both systems. In this contribution, we will focus on issues concerning the time-discretization of fully-coupled fluid-structure interactions by means of time-stepping schemes. In every time-step, an approximation to the fully coupled system at a new time-step is to be found. The fully coupled approach is called monolithic compared to partitioned approaches, where the fluid- and solid-problem are solved separately and coupled via outer iterations. Monolithic schemes always belong to strongly coupled methods whereas partitioned schemes can be either strongly or loosely coupled depending on the number of inner iterations and the desired accuracy of force balance at the interface. For instance, strongly coupled schemes are necessary when the added mass effect takes place as in applications in hemodynamics. On the other hand, partitioned solution schemes are very efficient for problems with a less stiff coupling, as they are common in aeroelasticity.

Time discretization of fluid-structure interactions is mainly governed by two specific complexities. First, the overall stiffness of the coupled problem is by far greater than that of the sub-problems. This is mainly due to the coupling of parabolic-type fluid equations with hyperbolic-type solid equations. Second, using a (most common) moving-mesh approach, time derivatives do not appear separated from spatial differential operators, but they depend nonlinearly on other solution variables and their spatial derivatives, giving rise to terms like

$$\displaystyle{\mathop{\mathrm{det}}\nolimits (I + \nabla \mathbf{u})[I + \nabla \mathbf{u}]^{-1}\nabla \mathbf{v}\partial _{ t}\mathbf{u},}$$

where v is the unknown velocity and u is the unknown deformation determining the domain motion. Detailed analysis for fluid flows on moving domains has been performed by Formaggia and Nobile [15, 16]. These studies already tackle several important aspects such as stability, order of convergence and the geometric conservation law. In fluid-structure interaction, the fluid-domain movement is caused by the solid deformation. Hence, the analysis of fully coupled fluid-structure interaction is similar but must also include detailed consideration of the solid discretization. This analysis is not present in literature.

In the following section, we will shortly introduce the governing equations for the fully coupled fluid-structure interaction problem in Arbitrary Lagrangian Eulerian (ALE) coordinates. Then, in the central third section, we analyze time-dependent dynamics of a typical fluid-structure interaction benchmark. In Sect. 4 we present and discuss different time-stepping technique and closely analyze their accuracy and stability properties. In Sect. 5, we recapitulate the current state-of-the-art of an alternative (to the ALE approach) monolithic formulation, the fully Eulerian framework and discuss special aspects with respect to its time-discretization. The prospective of applying parallel multiple shooting methods to enhance stability and efficiency is discussed in Sect. 6. Finally, we conclude in Sect. 7.

2 Fluid-Structure Interactions

By $\varOmega \subset \mathbb{R}^{d}$ we denote a two or three-dimensional domain that is split into a fluid-part $\mathcal{F}$ and a solid-part $\mathcal{S}$. The splitting is such, that $\mathcal{F}$ and $\mathcal{S}$ are d-dimensional domains with a common interface $\mathcal{I} = \partial \mathcal{F}\cap \partial \mathcal{S}$. Figure 1 shows a possible configuration of fluid-structure interactions, where the fluid encloses an obstacle with elastic beam. By the arising dynamics, the beam will deform and hence, solid and fluid domain will change such that at time t > 0 it holds $\varOmega (t) = \mathcal{F}(t) \cup \mathcal{S}(t)$ with interface $\mathcal{I}(t) = \partial \mathcal{F}(t) \cap \partial \mathcal{S}(t)$. In $\mathcal{F}(t)$, fluid’s velocity v _f and pressure p _f are governed by the incompressible Navier-Stokes equations, where in $\mathcal{S}(t)$ the elastic beam’s deformation u _s and velocity v _s is controlled by a St. Venant Kirchhoff material, see [28].

Fig. 1

Configuration of the fsi3-benchmark problem. Flow around obstacle with elastic beam. Inflow boundary Γ _in, outflow boundary Γ _out and fluid-solid interface $\mathcal{I}$. The cfd-benchmark is recovered by omitting the beam

The coupling between these two sub-problems is controlled by the kinematic condition that calls for continuity of the velocities on the common interface $\mathcal{I}(t)$ and the dynamic condition that asks for continuity of normal stresses on $\mathcal{I}(t)$.

To cope with the moving fluid-domain, we introduce the Arbitrary Lagrangian Eulerian (ALE) formulation that maps the domains $\mathcal{F}(t)$ back to the fixed reference domain $\mathcal{F}$ at time t = 0. We introduce by u _f the deformation field of the fluid-domain, that maps every reference point $\hat{x} \in \mathcal{F}$ to a point in the current configuration $x \in \mathcal{F}(t)$ via

$$\displaystyle{x \in \mathcal{F}: \quad T(x,t) = x + \mathbf{u}_{f}(x,t) \in \mathcal{F}(t).}$$

This mapping is not the physically motivated mapping between Lagrangian and Eulerian coordinates that follows the path of a particle, but a mapping between a completely arbitrary reference domain and the current configuration, see [8, 27, 32]. In both subdomains $\mathcal{F}$ and $\mathcal{S}$, we denote by $\mathbf{F}:= I + \nabla \mathbf{u}$ the deformation gradient and by $J:=\mathop{ \mathrm{det}}\nolimits (\mathbf{F})$ its determinant.

On Ω, $\mathcal{F}$ and $\mathcal{S}$ we introduce the function spaces

$$\displaystyle{\mathcal{V}:= H_{0}^{1}(\varOmega;\varGamma ^{D})^{d},\quad \mathcal{L}_{ f}:= L^{2}(\mathcal{F}),\quad \mathcal{V}_{ f}:= H_{0}^{1}(\mathcal{F};\partial \mathcal{F})^{d},\quad \mathcal{V}_{ s}:= L^{2}(\mathcal{S})^{d},}$$

where by H ¹(Ω; Γ) we denote the Sobolev space of Lebesgue integrable functions with the first weak derivative in L ² and trace zero on the boundary Γ. The full system of coupled fluid-structure interactions in variational formulation is to find

$$\displaystyle{v = (\mathbf{v}_{f},\mathbf{v}_{s}) \in \mathcal{V},\quad \mathbf{u} = (\mathbf{u}_{f},\mathbf{u}_{s}) \in \mathcal{V},\quad p_{f} \in \mathcal{L}_{f},}$$

such that

$$\displaystyle\begin{array}{rcl} \Big(\rho _{f}J(\partial _{t}\mathbf{v} + \nabla \mathbf{v}\mathbf{F}^{-1}(v - \partial _{ t}\mathbf{u})),\phi \Big)_{\mathcal{F}} +\Big (J\hat{\pmb{\sigma }}_{f}\mathbf{F}^{-T},\nabla \phi \Big)_{ \mathcal{F}}\quad & & \\ +\Big(\rho _{s}d_{t}\mathbf{v},\phi \Big)_{\mathcal{S}} +\Big (\mathbf{F}\pmb{\varSigma }_{s},\nabla \phi \Big)_{\mathcal{S}}\quad & & \\ +\Big(\mathop{\mathrm{det}}\nolimits (J\mathbf{F}^{-1}\mathbf{v}),\xi _{ f}\Big)_{\mathcal{F}} +\Big (\nabla \pmb{\sigma }_{\text{mesh}},\nabla \psi _{f}\Big)_{\mathcal{F}} +\Big (d_{t}\mathbf{u} - v,\psi _{s}\Big)_{\mathcal{S}}& & = (f,\phi )_{\varOmega },{}\end{array}$$

(1)

for all

$$\displaystyle{\phi \in \mathcal{V},\quad \xi _{f} \in \mathcal{L}_{f},\quad \psi _{f} \in \mathcal{V}_{f},\quad \psi _{s} \in \mathcal{V}_{s}.}$$

Here, by f we denote a given volume force, by $\pmb{\varSigma }_{s}$ the 2nd Piola Kirchhoff stress tensor, which for the St. Venant Kirchhoff material takes the form

$$\displaystyle{\pmb{\varSigma }_{s} = 2\mu \mathbf{E}_{s} +\lambda _{s}\mathop{ \mathrm{trace}}\nolimits (\mathbf{E}_{s})I,\quad \mathbf{E}_{s}:= \frac{1} {2}(\mathbf{F}^{T}\mathbf{F} - I),}$$

where by μ _s and $\lambda _{s}$ we indicate the two material parameters. By $\pmb{\sigma }_{f}$ we denote the fluid’s Cauchy stresses expressed in the reference coordinate system

$$\displaystyle{\pmb{\sigma }_{f} =\rho _{f}\nu _{f}(\mathbf{F}^{-1}\nabla \mathbf{v}_{ f} + \nabla \mathbf{v}_{f}^{T}\mathbf{F}^{-T}) - p_{ f}I,}$$

and finally, by $\pmb{\sigma }_{\text{mesh}}$ we denote the mesh-moving operator of harmonic, linear-elastic, or biharmonic type [23, 49, 57].

Kinematic

$$\displaystyle{\mathbf{v}_{f} = \mathbf{v}_{s}\quad \text{on }\mathcal{I}(t),}$$

and dynamic coupling conditions

$$\displaystyle{J\pmb{\sigma }_{f}\mathbf{F}^{-T}n_{ f} = \mathbf{F}\pmb{\varSigma }_{s}n_{s}\quad \text{on }\mathcal{I}(t),}$$

are embedded in this formulation, as the velocities $v \in \mathcal{V}$ and test-functions $\phi \in \mathcal{V}$ have a well-defined continuous trace on the interface $\mathcal{I}$.

Spatial discretization of this coupled system will be accomplished with conforming finite elements. For details, we refer to [12, 41–43, 45, 57].

3 Analysis of Two Benchmark Problems: cfd and fsi

We start the discussion on time-discretizations of fluid-structure interaction with a literature survey on published results for two benchmark problems in fluid-dynamics: first, the cfd-benchmark Laminar Flow Around a Cylinder as published in 1995 by Schäfer and Turek [46] and called cfd-benchmark in the following. Second an extension of this benchmark to fluid-structure interactions, the fsi3-benchmark problem, published in 2006 by Hron and Turek [30] and called fsi3 in the following. Both problems feature the flow around a circular obstacle. In the fsi3 configuration, an elastic beam is attached to the rear of the circular obstacle. See Fig. 1 for a sketch of the configuration. The cfd benchmark is obtained by completely omitting the beam. Both problems are driven by a time-dependent inflow data v = v ^D on Γ _in. The full set of parameters for both problems is given by

$$\displaystyle{\rho _{f}^{\text{cfd}} = 1,\quad \rho _{ f}^{\text{fsi}} = 10^{3},\quad \nu _{ f}^{\text{cfd/fsi}} = 10^{-3},\quad \mathbf{v}^{D}(0,y) = 1.5\omega (t)\frac{y(H - y)} {(H/2)^{2}} \bar{\mathbf{v}},}$$

where $\omega (t) = (1 -\cos (\pi t/2))/2$ for t < 2 and ω(t) = 1 for t ≥ 2 is used for regularizing the initial data. As average velocity, $\bar{\mathbf{v}} = 2$ for the fsi3-benchmark and $\bar{\mathbf{v}} = 1$ for the cfd benchmark was considered. With the radius of the circular obstacle D = 0. 1, the Reynolds number is given by

$$\displaystyle{Re_{\text{cfd}} = \frac{\bar{\mathbf{v}}D} {\nu } = 100,\quad Re_{\text{fsi}} = \frac{\bar{\mathbf{v}}D} {\nu } = 200.}$$

The description of the problem is closed by providing the material parameters of the elastic solid

$$\displaystyle{\rho _{s}^{\text{fsi}} = 10^{3},\quad \mu _{ s} = 2 \cdot 10^{6},\quad \lambda _{ s} = 8 \cdot 10^{6}.}$$

As quantity of interest, we consider principal boundary stresses in x- and y-direction on the obstacle with boundary Γ _obs:

$$\displaystyle{J_{\text{drag}}(v,p) = \frac{2} {\bar{\mathbf{v}}^{2}\rho _{f}L}\int _{\varGamma _{\text{obs}}}\pmb{\sigma }_{f}\mathbf{n}\mathbf{e}_{x}\,\text{d}o,\quad J_{\text{lift}}(v,p) = \frac{2} {\bar{\mathbf{v}}^{2}\rho _{f}L}\int _{\varGamma _{\text{obs}}}\pmb{\sigma }_{f}\mathbf{n}\mathbf{e}_{y}\,\text{d}o.}$$

By Γ _obs we denote the boundary of the circle with diameter in the case of the cfd-benchmark and the circle with attached beam in the case of the fsi-benchmark problem. Efficient ways for evaluating these functionals are shown in ([5]) and ([43]).

Figure 2 shows the drag-coefficient as function over time I = [0, 5] for the two benchmark problems. To avoid confusion, we note, that Hron and Turek [30] also published a new fluid dynamics benchmark, the cfd3-benchmark problem, where the beam was considered as rigid part of the obstacle and the flow was driven with Reynolds number Re = 200. Here however, we compare the fsi3-benchmark problem with the published results of the original cfd-benchmark taken from [46]. Both configurations show a similar behavior with a transient initial phase leading to a periodic oscillation with dominant frequencies f _cfd = 13 Hz for the cfd-benchmark and f _fsi ≈ 11 Hz for the fsi problem. The first obvious difference is the longer transient phase for the fsi-benchmark problem. An insight look into the subinterval I′ = [2. 5, 3] reveals high frequent oscillations f _high ≈ 100 Hz in the drag-coefficient with a small amplitude a ≈ 10⁻⁴ that is not visible on the large scale. These high frequent oscillations are no numerical artefacts but remain stable under temporal and spatial mesh refinement.

Fig. 2

Comparison of the two benchmark problems, original cfd [46] and fsi3 [30]. We plot the drag coefficient as function over time. For the fsi-problem we show a detailed view of the transient oscillations revealing high frequent modes

Reviewing the results published by many research groups in the two surveys on the cfd benchmark problem [46] and the fsi3-benchmark [30, 31] a first surprising observation is the choice of discretization parameters that have been necessary to obtain approximations with appropriate accuracy: even though more than a decade lies between both benchmark problems, the dimension of the spatial discretization is very similar. In both cases, different research groups had to use 20.000 to 200.000 spatial degrees of freedom to generate output values with at least 1 % accuracy. The large margin stems from different discretization schemes (lowest order finite element or finite volume schemes, higher order methods) but also from different triangulations of the geometry. The increased difficulty of the fsi3-benchmark problem has been accounted for by a general use of higher order finite elements.

However, observing the temporal discretization, it is found, that the fsi benchmark asks for significantly finer resolution in time. While less than 10 time-steps per period of the oscillation were sufficient in the cfd case, accurate results to the fsi benchmark problem required up to 100 time-steps per period of oscillation resulting in time-steps as small as 10⁻³. One explanation for this difference in temporal discretization can be found in the high frequent oscillations that are present with small amplitude, see Fig. 2.

Further insight is given by a discrete Fourier analysis of the output functional J _drag(t) as function over time. At very fine temporal resolution (down to $k = 10^{-5}$), some complete periods of the fully developed oscillation are analyzed in detail. Figure 3 reveals several dominant frequencies, at about 100 Hz (see also Fig. 2, 500 and 800 Hz. These modes are stable under mesh refinement and further decrease of the time step. The results in Fig. 3 are scaled. The modes belonging to higher frequencies carry less energy. But even though the high frequent contributions take place on a much smaller scale as the dominant oscillation f _fsi ≈ 11 Hz, they must be carefully resolved to capture the overall dynamics of the coupled benchmark problem. The key question in this respect is the origin of these micro-oscillations. They are not present in pure fluid-dynamical simulations. Further, they are no numerical artifact, but stable under discretization of both spatial and temporal discretization. Instead they stem from the coupling to the hyperbolic structure equations.

Fig. 3

Discrete Fourier analysis of the output functional (drag) shows the dominant frequency f _fsi ≈ 11 Hz and further important sub-frequencies at about f ≈ 100 and 500 Hz as well as 800 Hz. These modes are stable under temporal and spatial mesh refinement

4 Time-Stepping Schemes for Fluid-Structure Interactions

There is little theoretical background to monolithic time-discretizations of fluid-structure interactions. The main difficulty stems from the motion of the subdomains, that must either be modeled explicitly in partitioned approaches or that must be taken care of by implicit transformations of either the fluid-domain or the solid-domain. Concentrating first on pure fluid problems on moving domains, some crucial aspects with respect to stability and order of convergence are already identified [15, 16]. The equations presented therein can be directly employed in an implementation. In addition, [14] provided stability analysis of fluid-structure interaction problems. Several studies with qualitative comparisons of different time-stepping schemes and their long-time behavior has been reported in [56, 62]. In the primer study and additionally [57, 61], we provide many details for the practical realization and implementation of time-stepping schemes for ALE fluid-structure interaction.

In the following, we focus the attention to the well-established ALE-approach that results from transformation of the moving fluid-domain to a fixed reference domain. The domain motion is hidden in the ALE-map T _f (x, t) and calls for the discretization of non-standard space-time coupled terms like [see ( 1)]

$$\displaystyle{ (J(\mathbf{u})\nabla \mathbf{v}\mathbf{F}^{-1}(\mathbf{u})\partial _{ t}\mathbf{u},\phi )_{\mathcal{F}}. }$$

(2)

Most approaches for the temporal discretization of this term are ad hoc and based on the experience with other types of equations as Navier-Stokes of multiphase fluids, see [29].

Remark 1

An alternative approach to the monolithic formulation of fluid-structure interactions is given by an implicit transformation of the solid-domain to Eulerian coordinates resulting in the Fully Eulerian approach [11, 45]. This method of interface-capturing type must deal with subdomains that move freely through a fixed background mesh from time-step to time-step. We come back to this procedure in Sect. 5.

4.1 Derivation of Second Order Time-Stepping Schemes

The derivation of a second order stable time-stepping scheme is not obvious. Specifically, regarding (2), two immediate reasonable choices for are given by the secant version

$$\displaystyle{\left (\left [\frac{J(\mathbf{u}^{m-1})\nabla \mathbf{v}^{m-1}\mathbf{F}^{-1}(\mathbf{u}^{m-1})} {2} + \frac{J(\mathbf{u}^{m})\nabla \mathbf{v}^{m}\mathbf{F}^{-1}(\mathbf{u}^{m})} {2} \right ]\frac{\mathbf{u}^{m} -\mathbf{u}^{m-1}} {k_{m}},\phi \right ),}$$

and the midpoint-tangent version

$$\displaystyle{\left (\left [J(\bar{\mathbf{u}})\nabla \bar{\mathbf{v}}\mathbf{F}^{-1}(\bar{\mathbf{u}})\right ]\frac{\mathbf{u}^{m} -\mathbf{u}^{m-1}} {k_{m}},\phi \right ),\quad \bar{\mathbf{u}}:= \frac{\mathbf{u}^{m-1} + \mathbf{u}^{m}} {2},\quad \bar{\mathbf{v}}:= \frac{\mathbf{v}^{m-1} + \mathbf{v}^{m}} {2},}$$

of the trapezoidal rule. This idea is explored in [56, 62]. A third version of a time-stepping scheme can be derived by using a temporal cG(1)∕dG(0)-Galerkin approach on ( 2) (see [44]):

$$\displaystyle\begin{array}{rcl} & & \left (\left [\frac{1} {6}J(\mathbf{u}^{m-1})\nabla \mathbf{v}^{m-1}\mathbf{F}^{-1}(\mathbf{u}^{m-1}) + \frac{2} {3}J(\bar{\mathbf{u}})\nabla \bar{\mathbf{v}}\mathbf{F}^{-1}(\bar{\mathbf{u}})\right.\right. {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left.\left.+\frac{1} {6}J(\mathbf{u}^{m})\nabla \mathbf{v}^{m}\mathbf{F}^{-1}(\mathbf{u}^{m})\right ]\frac{\mathbf{u}^{m} -\mathbf{u}^{m-1}} {k_{m}},\phi \right ), {}\\ \end{array}$$

where again by $\bar{\mathbf{u}}$ and $\bar{\mathbf{v}}$ we denote the average of old and new approximation. Such a Galerkin-derivation is also possible for more advanced time-stepping schemes like the fractional step theta method, see [37, 38].

Simple truncation error analysis shows second order convergence for k → 0 in all three cases. The leading error constants slightly differ:

$$\displaystyle{C_{1} \approx \frac{11} {8},\quad C_{2} \approx \frac{3} {8},\quad C_{3} \approx \frac{3} {4}.}$$

In numerical experiments, it is found, that all these variants show a very similar performance. Significant differences in temporal accuracy could not be found.

Finally, we point out, that the Crank-Nicolson scheme applied to the elastic structure equation in mixed formulation is closely related to the Newmark scheme [3], which is one of the most prominent time-discretization techniques in solid mechanics.

4.2 Temporal Stability

Issues of numerical stability are of utter importance for fluid-structure interaction problems, as they consist of the coupled consideration of two different types of equations: the incompressible Navier-Stokes equations which is of parabolic type and that comes with smoothing properties and the hyperelastic solid equation of hyperbolic type, that calls for good conservation properties with very little numerical dissipation. By these considerations, the Crank-Nicolson scheme and its variants like shifted versions [34, 40] or the fractional step theta scheme [7, 54], appear to be ideal candidates that further show second order accuracy.

Motivated by [16, 26, 34], it is reported in [14, 62], that the discretization of the domain-motion term ( 2) introduces further stability issues. To investigate this stability problem, we again consult the fsi3-benchmark problem introduced in the previous sections. Figure 4 shows the drag as functional over time for an unstable pair of spatial and temporal discretization parameters. Further, we also show the stable simulation using a damped version of the time-stepping scheme, see Sect. 4.3.

Fig. 4

Simulation for k = 0. 005. Top: undamped Crank-Nicolson scheme develops an instability after T = 8. 5. Bottom: implicitly shifted scheme produces a stable solution on I = [0, 10]

In a first test, we aim at obtaining a stable solution up to T = 10. On a sequence of uniform meshes, we identify the largest timestep k that is suited to generate a stable solution. The left part of Table 1 shows the results. Here, we see, that on the coarsest mesh, the large step size k = 0. 02 is sufficient, while on finer meshes k < 0. 004 is required. We however cannot identify a further relationship between mesh size and time step if we go to an even finer spatial mesh resolution.

Table 1 Long-term stability of the Crank-Nicolson scheme

In a second test-case, we consider the (relatively large) step size k = 0. 005 and $k = 0.00\bar{3}$ and determine the point in time T _max, where the solution gets unstable. Again, we carry out this test-case on different meshes. At first glance, the results in the right part of Table 1 for k = 0. 005 suggest a stability relationship between time step and mesh size. The results concerning the second configuration with $k = 0.00\bar{3}$ however does not confirm this conjecture. Here, we can even reach a larger final point in time T _max on finer meshes. Further, the simulations on the finest mesh do not cease due to stability problems but due to early failure of the Newton scheme. Altogether, it is not possible to numerically certify a strict time-step restriction. Instead, we find general stability problems for long-term simulation, if we consider the Crank-Nicolson scheme.

4.3 Stable Time-Discretization and Damping

By analyzing the fsi3-benchmark problem, it seems, that time-step restrictions due to stability issues are too restrictive and not justified by the needs of approximation accuracy, see Sects. 4.2 and 4.1. It is therefore nearby to search for accurate time-discretization schemes with better stability properties. Different possibilities are either to resort to A stable time-discretization schemes, or to apply modifications to the Crank-Nicolson schemes. Here, two possibilities are often discussed in literature: by slight implicit shifting of the discretization

$$\displaystyle{(u^{m} - u^{m-1},\phi ) + \left (\frac{1} {2} + O(k)\right )a(u^{m},\phi ) + \left (\frac{1} {2} - O(k)\right )a(u^{m-1},\phi ) = 0,}$$

global stability is recovered, see [25, 26, 34]. This is just sufficient for the damping of accumulated errors by truncation, quadrature or inexact solution of the algebraic systems. If the shift depends on the time-step size, the resulting scheme is still second order accurate in time. Similar results are recovered by applying some initial time-steps with the A-stable backward Euler method, see [40]. If these few (usually two are sufficient) backward Euler steps are introduced after every fixed time-interval, e.g. at every t = j for $j = 0,1,\ldots$, we also recover sufficient stability for long term calculations. This scheme, also referred to as Rannacher time-marching, is second order accurate.

Higher stability, that is also able to cover non-smooth initial data is reached by applying strongly A-stable time-integration techniques. Here, the fractional-step theta method appears to be an optimal choice [7]. This time-stepping scheme consists of three sub-steps, that results in a second order, strongly A-stable scheme that further has very good dissipation properties. It is highly preferable for flow problems [54] and also frequently used in the analysis of fluid-structure interactions problems [29, 55, 56].

An analysis of different damping strategies applied to the fsi-2 benchmark problem (a slightly more difficult test-case) is given in [62], which we briefly summarize in the following: There are only minor differences in the drag evaluation computed with the unstabilized Crank-Nicolson scheme using the different ALE convection term discretizations. Specifically, unstable behavior (blow-up) for computations over long-term intervals is observed. As expected, the shifted Crank-Nicolson scheme and the Fractional-Step-$\theta$ scheme do not show any stability problems in long-term computations, even for large time steps k = 0. 01. This result indicates that the instabilities induced by the ALE convection term have minor consequences, and our observation is in agreement with the statement in [16].

In the following, we compare the three possibilities of a non-damped Crank-Nicolson scheme, with an implicitly shifted version using $\frac{1} {2} + k$ and the Rannacher time-marching algorithm with two steps of the backward Euler method at times t = 0, t = 1, t = 2 and so on. In Fig. 5 we compare these three damping strategies. We show the drag-coefficient (see Figs. 2 or 4 for a global view) in the sub-intervals t ∈ [3. 5, 4. 2], t ∈ [7. 95, 8. 15] and t ∈ [9. 3, 9. 6]. While all three versions are stable at initial time, Rannacher time-marching develops a first instability after two steps of backward Euler at time t = 4, see the left sketch in Fig. 5. This instability will stay during the simulation, but it will not be further developed, as can be seen in the middle and right sketch of the figure. The undamped version of the Crank-Nicolson scheme delivers stable solutions up to a moderate time of about t = 5 but develops a strong instability that fill finally lead to a break-down of the scheme, as can be seen in the middle and right sketch. Finally, the implicitly shifted version of the Crank-Nicolson scheme gives stable and good result globally in time.

Fig. 5

Comparison of different damping strategies: undamped Crank-Nicolson, shifted version $\frac{1} {2} + k$ and Rannacher time-marching with two backward Euler steps at every time-unit

5 Alternative Formulation in Fully Eulerian Coordinates

As previously mentioned, an interesting alternative to ALE formulations is the fully Eulerian framework [11, 45]. Specific extensions are reported in [43, 58] and combinations with ALE in [59, 60]. Apart from monolithic formulations, other recent studies (but not tested with the fsi-benchmarks) on fully Eulerian formulations are known [9, 22, 50, 51, 64]. As discussed in the previous sections, the ALE formulation of the fluid problems introduced several difficulties for the analysis as well as the implementation. In fact, all kinds of transformation in the fluid equations are avoided in a fully Eulerian description of the equations.

Here, the idea is to have fluid- and solid-problem on the moving domains $\mathcal{F}(t)$ and $\mathcal{S}(t)$. While fluid-system is simply let in Eulerian coordinates, we now need to transform the solid problem to match the Eulerian coordinate system. An illustration is given in Fig. 6.

Fig. 6

Comparison of cell occupation and computational domains for two time steps between the ALE (top and middle) and Eulerian (bottom) method. In ALE, all computations are done in the same fixed reference domain Ω (top). In particular, a specific cell remains all times the same material (here, an elastic structure in red), i.e., Ω _f and Ω _s are time-independent. The mesh movement is hidden in the transformation F and J. The physical ALE domain Ω(t) including the mesh movement is displayed in the middle. In contrast, the computation with the Eulerian approach is performed on a fixed (time-independent) mesh Ω _E (bottom). However, the two sub-domains for the structure and the fluid Ω _s, E and Ω _f, E change in each time step because the material id of a cell might change since the elastic structure (red) moves freely through the mesh. Figures partially taken from [59]

By the simple observation, that the deformation $\hat{\mathbf{u}}_{s}(\hat{x},t) = x(\hat{x},t) -\hat{ x}$ just maps between Lagrangian points $\hat{x} \in \hat{\mathcal{S}}$ and their Eulerian coordinates $x = x(\hat{x},t) \in \mathcal{S}(t)$, we can defined Eulerian counterparts for deformation $\mathbf{u}_{s}(x,t) =\hat{ \mathbf{u}}_{s}(\hat{x},t)$ and velocity $\mathbf{v}_{s}(x,t) =\hat{ \mathbf{v}}_{s}(\hat{x},t)$. Then, following [11, 45], the Eulerian system is similar to a multiphase flow

$$\displaystyle{ \begin{array}{lllll} \rho _{f}(\partial _{t}\mathbf{v}_{f} + \mathbf{v}_{f} \cdot \nabla \mathbf{v}_{f}) -\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{f} & =\rho _{f}f &&\text{in} &\mathcal{F}(t), \\ \phantom{\rho _{f}(\partial _{t}\mathbf{v}_{f} + \mathbf{v}_{f} \cdot \nabla \mathbf{v}_{f}) -}\mathop{\mathrm{div}}\nolimits \,\mathbf{v}_{f} & = 0 &&\text{in} &\mathcal{F}(t), \\ J_{s}\rho _{s}(\partial _{t}\mathbf{v}_{s} + \mathbf{v}_{s} \cdot \nabla \mathbf{v}_{s}) -\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{s} & = J_{s}\rho _{s}f &&\text{in} &\mathcal{S}(t), \\ \phantom{J_{s}\rho _{s}(\partial _{t}\mathbf{v}_{s} + \mathbf{v}_{s}}\partial _{t}\mathbf{u}_{s} + \mathbf{v}_{s} \cdot \nabla \mathbf{u}_{s}& = \mathbf{v}_{s} &&\text{in} &\mathcal{S}(t), \\ \phantom{J_{s}\rho _{s}(\partial _{t}\mathbf{v}_{s} + a}\mathbf{v}_{f} = \mathbf{v}_{s},\quad n \cdot \pmb{\sigma }_{f} & = n \cdot \pmb{\sigma }_{s} &&\text{on}&\mathcal{I}(t).\end{array} }$$

(3)

For the exact form of modeling structural stresses $\pmb{\sigma }_{s}$ in Eulerian coordinates, we refer to the literature [45]. The big advantage of this Eulerian framework is the avoidance of any kind of unphysical (hence arbitrary) mapping of the systems. The transformation between Lagrangian and Eulerian coordinates of the structure system motivated by physical principles and will not be cause for break-down of the scheme, see e.g. [43]. The obvious drawback of an Eulerian model is the front-capturing type of this formulation, where the interface $\mathcal{I}(t)$ will move freely in the domain and through the mesh elements. The ALE technique has a front-tracking character that allows to resolve the interface at all times with a finite element mesh.

To capture the interface, we need to constantly keep record of its location. One classical approach is the Level Set techniques [39, 47], where a scalar function ψ is introduces, that indicates the signed distance to the interface and that is transported with the velocity of the interface. Here, we instead use the Initial Point Set [11, 43, 58], a vector field, that transports the complete reference coordinate system. In the context of fluid-structure interactions, this Initial Point Set is exactly the structure’s deformation and its extension to the fluid-domain. Another benefit of the Initial Point Set technique is its ability to depict sharp edges.

As a front-capturing technique, the fully Eulerian formulation is an interface problem, where some mesh elements are cut by the interface and where different equations live on the two sides of the interface. Solutions to such interface problems are usually not regular and standard finite element schemes only give sub-optimal convergence $O(\sqrt{h})$ independent of the approximation degree, see the early works of Babuška [1] or MacKinnon and Carey [35]. Modern techniques to enhance the interface accuracy are to locally fit the mesh in order to recover the optimal approximation order [4, 6, 18, 63] or to enhance the finite element space with special basis functions that can resolve irregularities [2, 20, 21, 36].

All these techniques are suited to accomplish the problems of limited spatial accuracy. It then remains to derive efficient time-stepping schemes. This problem is still not sufficiently solved. To illustrate this problem, we step back from the coupled fluid-structure interaction problem and instead discuss a simple parabolic equation

$$\displaystyle{(\partial _{t}u,\phi )+\mathcal{A}(u,\phi ) = 0,\quad \mathcal{A}(u,\phi ) = \left \{\begin{array}{@{}l@{\quad }l@{}} \mathcal{A}_{1}(u,\phi )\quad &\text{in }\mathcal{S}(t) \\ \mathcal{A}_{2}(u,\phi )\quad &\text{in }\mathcal{F}(t) \end{array} \right.,}$$

where $\mathcal{A}_{1}$ and $\mathcal{A}_{2}$ represent two different differential operators and where the interface between the two subdomains moves from one time-step to the other. Direct time-stepping approaches result in iterative schemes of the type

$$\displaystyle{ (u^{m} - u^{m-1},\phi ) +\theta k\mathcal{A}(u^{m},\phi ) + (1-\theta )k\mathcal{A}(u^{m-1},\phi ) = 0. }$$

(4)

It is now possible, that for a given point x ∈ Ω it holds $x \in \varOmega _{1}(t_{m-1})$ but $x \in \varOmega _{2}(t_{m})$, i.e., that one points belongs to the fluid domain at the old time-step and the solid-domain at the new time. For such a configuration, the expression $u^{m}(x) - u^{m-1}(x)$ lacks any physical relevance, as there is not immediate relation between the two different phases. This problem also appears in the discretization of multiphase flows, here however it is justifiable to replace the sharp interface by a smoothed one using harmonic averages of the different parameters, see [48, 53]. Smoothing of two entirely different phases like fluid and solid is however no option.

If problem ( 4) is to be discretized with fitted finite elements, where the mesh locally resolves the interface, or by the extended finite element technique, different time-steps require difference finite element spaces $V _{h}^{m-1}$ and $V _{h}^{m}$. Then, evaluation of terms like

$$\displaystyle{\mathcal{A}(u^{m-1},\phi ^{m}),}$$

with $u^{m-1} \in V _{h}^{m-1}$ and $\phi ^{m} \in V _{h}^{m}$ requires the projection of basis functions from one mesh to the other and numerical quadrature that carefully resolves all possible areas of non-smoothness.

The difficulties of deriving adequate time-discretizations for the Fully Eulerian scheme are even more articulate, if we simply discuss the discretization of the elastic structure equation in Eulerian coordinates. This relates to solving a partial differential equation on a moving domain. For simplicity, we simply consider the parabolic problem:

$$\displaystyle{(\partial _{t}u,\phi )_{\varOmega (t)} + (\nabla u,\nabla \phi )_{\varOmega (t)} = 0.}$$

Here, ad hoc time-discretization with the backward Euler method using changing finite element spaces would results in

$$\displaystyle{(u^{m} - u^{m-1},\phi ^{m})_{\varOmega (t_{m})} + k(\nabla u^{m},\nabla \phi ^{m})_{\varOmega (t_{m})} = 0.}$$

The expression $u^{m} - u^{m-1}$ is not valid, as the two functions live on different domains. Averaging techniques that may work for multiphase flow problem will not be applicable here.

Efficient and accurate time-discretization schemes for the Eulerian approach will have to consider the motion of the domain. In the following, we will outline two basic ideas. For details, we refer to [17]. The first idea is closely related to the ALE approach flow problems on moving domains and based on old ideas on the method of characteristics [10]. We start by formulating the problem on the time-dependent domain

$$\displaystyle{ (\partial _{t}u,\phi )_{\varOmega (t)} + (\nabla u,\nabla \phi )_{\varOmega (t)} = 0,\quad t \in (t_{m-1},t_{m}). }$$

(5)

Then, by $T_{m}(t):\varOmega (t_{m}) \rightarrow \varOmega (t)$ we denote the transformation between the domains at time t _m and back at time $t \in (t_{m-1},t_{m})$. In the context of fluid-structure interaction or solid problems in Eulerian coordinates, such a mapping is implicitly given by the deformation. By this transformation, we can map Eq. ( 5) onto the fixed domain Ω(t _m ) similar to the ALE approach:

$$\displaystyle{ \big(\mathop{\mathrm{det}}\nolimits (\nabla T_{m})(\partial _{t}u-\partial _{t}T_{m}\cdot \nabla u),\phi \big)_{\varOmega (t_{m})}+\big(\mathop{\mathrm{det}}\nolimits (\nabla T_{m})\nabla T_{m}^{-1}\nabla u\nabla T_{ m}^{-T},\nabla \phi \big)_{\varOmega (t_{m})} = 0. }$$

(6)

Nonlinearities are introduced, we however shift the motion of the domain into this implicit mapping such that standard time-stepping schemes can be applied.

An alternative approach is given by formulating ( 5) as a space-time Galerkin approach, based on

$$\displaystyle{\int _{t_{m-1}}^{t_{m} }\Big\{(\partial _{t}u(t),\phi (t))_{\varOmega (t)} + (\nabla u(t),\nabla \phi (t))_{\varOmega (t)}\Big\}\,\text{d}t = 0.}$$

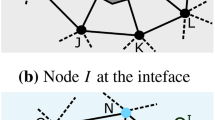
Then, following the concepts introduced by Eriksson, Estep, Hansbo, and Johnson [13] and Thomée [52], discrete space-time functions are used to approximate this equation. We know for instance, that by combining piece-wise linear (in time) trial functions with piece-wise constant test-functions, we result in a variant of the Crank-Nicolson scheme. To apply this technique to problems with moving interface, we must consider space-time meshes that fit to the interface, see Fig. 7. A space-time Galerkin approach must now resolve the interface location. To derive a Crank-Nicolson like scheme, the piece-wise linear trial functions must be linear along the interface and not necessarily linear in straight t-direction. This causes an implicit coupling of space- and time-variables. On the element K _kh the space-time Galerkin approach is simply the space of bilinear elements in space and time $\mathop{\mathrm{span}}\nolimits \{1,x,t,xt\}$. This coupling of spacial and temporal variables again leads to an implicit mapping of the space-time slice onto a fixed domain with straight edges which is equivalent to the mapping-approach described in ( 6). In [17] this technique is analyzed for parabolic problems with moving interfaces. By a proper projection of the old solution to the new finite element space and by applying suitable mapping between the domains at different time-steps, second order schemes in space and time can be derived. First results show however, that the error is not clearly separated into a spatial and a temporal part, but that for elements cut by the interface, simultaneous refinement in space and time is required.

Fig. 7

Triangulation in space and time. The triangulation fits the interface $\mathcal{I}(t)$ in space and time. By K _kh we denote one space-time element

6 Multiple Shooting as Time-Parallel Time-Integration for Fluid-Structure Interaction: Concepts and an Outlook

A further possibility to enhance the stability of time-discretization schemes is to realize them in a time-domain decomposition fashion [19, 33]. Stability issues in the context of fluid-structure interactions mostly appear due to long-time accumulated error contributions. The small time-steps that are necessary to efficiently resolve all these modes are not required for obtaining an adequate accuracy. Here, it might be an option to employ the multiple shooting method for time-discretization. By keeping the sub-intervals small, stability will be under control.

In the following, we briefly explain conceptional issues related to fluid-structure interaction. Once we have set up the basis of a consistent semi-linear form, the solution of the multiple shooting problem follows standard techniques. Specifically, a consistent semi-linear form is provided by a monolithic formulation of the ALE system (1) or the fully Eulerian system (3), respectively.

Find $\mathbf{U} =\{ \mathbf{v}_{f},\mathbf{v}_{s},\mathbf{u}_{f},\mathbf{u}_{s},p_{f}\} \in X:= \mathcal{V}\times \mathcal{V}\times \mathcal{L}$ such that

$$\displaystyle{\int _{I}A(\mathbf{U})(\varPhi ) = 0\quad \forall \varPhi \in X}$$

with $\varPhi =\{\phi,\xi _{f},\psi _{f},\psi _{s}\} \in \mathcal{V}\times \mathcal{L}\times \mathcal{V}_{f} \times \mathcal{V}_{s}$ and

$$\displaystyle\begin{array}{rcl} A(\mathbf{U})(\varPhi ) =\Big (\rho _{f}J(\partial _{t}\mathbf{v} + \nabla \mathbf{v}\mathbf{F}^{-1}(v - \partial _{ t}\mathbf{u})),\phi \Big)_{\mathcal{F}} +\Big (J\hat{\pmb{\sigma }}_{f}\mathbf{F}^{-T},\nabla \phi \Big)_{ \mathcal{F}}\quad & & \\ +\Big(\rho _{s}d_{t}\mathbf{v},\phi \Big)_{\mathcal{S}} +\Big (\mathbf{F}\pmb{\varSigma }_{s},\nabla \phi \Big)_{\mathcal{S}}- (f,\phi )_{\varOmega }\quad & & \\ +\Big(\mathop{\mathrm{det}}\nolimits (J\mathbf{F}^{-1}\mathbf{v}),\xi _{ f}\Big)_{\mathcal{F}} +\Big (\nabla \pmb{\sigma }_{\text{mesh}},\nabla \psi _{f}\Big)_{\mathcal{F}} +\Big (d_{t}\mathbf{u} - v,\psi _{s}\Big)_{\mathcal{S}}.\quad & &{}\end{array}$$

(7)

In fully Eulerian coordinates we have: Find $\mathbf{U} =\{ \mathbf{v}_{f},\mathbf{v}_{s},\mathbf{u}_{s},p_{f}\} \in X:= \mathcal{V}\times \mathcal{V}_{s} \times \mathcal{L}$ such that

$$\displaystyle{\int _{I}A(U)(\varPhi ) = 0\quad \forall \varPhi \in X}$$

with $\varPhi =\{\phi,\xi _{f},\psi _{f},\psi _{s}\} \in \mathcal{V}\times \mathcal{L}\times \mathcal{V}_{f} \times \mathcal{V}_{s}$ and

$$\displaystyle\begin{array}{rcl} A(\mathbf{U})(\varPhi ) = (\rho _{f}(\partial _{t}\mathbf{v}_{f} + \mathbf{v}_{f} \cdot \nabla \mathbf{v}_{f}),\phi ) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{f},\nabla \phi ) - (\rho _{f}f_{f},\phi )& & \\ +(\mathop{\mathrm{div}}\nolimits \,\mathbf{v}_{f},\xi )& & \\ +(J_{s}\rho _{s}(\partial _{t}\mathbf{v}_{s} + \mathbf{v}_{s} \cdot \nabla \mathbf{v}_{s}),\psi _{f}) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{s},\nabla \psi _{f}) - (J_{s}\rho _{s}f_{s},\psi _{f})& & \\ +(\partial _{t}\mathbf{u}_{s} + \mathbf{v}_{s} \cdot \nabla \mathbf{u}_{s} -\mathbf{v}_{s},\psi _{s})& & \\ = (\rho _{f}(\partial _{t}\mathbf{v}_{f},\phi ) + (J_{s}\rho _{s}(\partial _{t}\mathbf{v}_{s},\psi _{f}) + (\partial _{t}\mathbf{u}_{s},\psi _{s})& & \\ (\rho _{f}\mathbf{v}_{f} \cdot \nabla \mathbf{v}_{f},\phi ) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{f},\nabla \phi ) - (\rho _{f}f_{f},\phi )& & \\ +(\mathop{\mathrm{div}}\nolimits \,\mathbf{v}_{f},\xi )& & \\ +(J_{s}\rho _{s}\mathbf{v}_{s} \cdot \nabla \mathbf{v}_{s},\psi _{f}) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{s},\nabla \psi _{f}) - (J_{s}\rho _{s}f_{s},\psi _{f})& & \\ +(\mathbf{v}_{s} \cdot \nabla \mathbf{u}_{s} -\mathbf{v}_{s},\psi _{s}).& &{}\end{array}$$

(8)

In order to obtain a standard setting for multiple shooting for PDEs [24], we re-arranged and separated the time derivatives from the spatial operators in the previous equation.

In the following, we describe the algorithm for the fully Eulerian case. The formal description (apart from the specific difficulties as described in the previous sections) of the ALE system is analogous. Let I = (0, T) be a decomposition of the time interval into m (not necessarily of the same length) multiple shooting intervals $I_{j}:= (t_{j},t_{j+1})$ with

$$\displaystyle{0 = t_{0} < t_{1} <\ldots < t_{m-1} < t_{m} = T.}$$

The multiple shooting formulation asks now for the solution of the matching conditions at the multiple shooting nodes $t_{j},j = 0,\ldots,m$ in which we introduce the multiple shooting variables $q^{\,j},r^{\,j},s^{\,j}$ (in some Hilbert space) for $v_{f},v_{s},u_{s}$. The variables $q^{\,j},r^{\,j},s^{\,j}$ serve as initial value for $v_{f}^{\,j},v_{s}^{\,j},u_{s}^{\,j}$ in t _j . Then, the multiple shooting system for the m (separate) interval-wise boundary value problems of fluid-structure interaction read:

$$\displaystyle\begin{array}{rcl} \int _{I_{j}}& & \Bigl ((\rho _{f}\partial _{t}\mathbf{v}_{f}^{\,j},\phi ) + (J_{ s}\rho _{s}\partial _{t}\mathbf{v}_{s}^{\,j},\psi _{ f}) + (\partial _{t}\mathbf{u}_{s}^{\,j},\psi _{ s}) + A(\mathbf{U}^{\,j})(\varPhi ) + {}\\ \quad & & (\mathbf{v}_{f}^{\,j}(t_{ j}) - q^{\,j},\phi (t_{ j})) + (\mathbf{v}_{s}^{\,j}(t_{ j}) - r^{\,j},\psi _{ f}(t_{j})) + (\mathbf{u}_{s}^{\,j}(t_{ j}) - s^{\,j},\psi _{ s}(t_{j}))\Bigr ) {}\\ \end{array}$$

where the semi-linear form of all ‘stationary’ terms is given by

$$\displaystyle\begin{array}{rcl} A(\mathbf{U}^{\,j})(\varPhi ) = (\rho _{ f}\mathbf{v}_{f} \cdot \nabla \mathbf{v}_{f},\phi ) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{f},\nabla \phi ) - (\rho _{f}f_{f},\phi )& & \\ +(\mathop{\mathrm{div}}\nolimits \,\mathbf{v}_{f},\xi )& & \\ +(J_{s}\rho _{s}\mathbf{v}_{s} \cdot \nabla \mathbf{v}_{s},\psi _{f}) + (\mathop{\mathrm{div}}\nolimits \,\pmb{\sigma }_{s},\nabla \psi _{f}) - (J_{s}\rho _{s}f_{s},\psi _{f})& & \\ +(\mathbf{v}_{s} \cdot \nabla \mathbf{u}_{s} -\mathbf{v}_{s},\psi _{s}).& &{}\end{array}$$

(9)

Now, the multiple shooting system is solved by finding $q^{0},\ldots,q^{m},r^{0},\ldots,r^{m},s^{0},\ldots,s^{m}$ such that the matching conditions hold true:

$$\displaystyle\begin{array}{rcl} (q^{0} -\mathbf{v}_{ f}^{0},\psi )& =& 0\quad \forall \text{ admissible }\phi, {}\\ (s^{\,j+1} -\mathbf{v}_{ f}^{\,j}(t_{ j+1}),\psi )& =& 0\quad \forall \text{ admissible }\phi,\quad j = 0,\ldots,m - 1, {}\\ (r^{0} -\mathbf{v}_{ s}^{0},\psi _{ f})& =& 0\quad \forall \text{ admissible }\psi _{f}, {}\\ (r^{\,j+1} -\mathbf{v}_{ s}^{\,j}(t_{ j+1}),\psi _{f})& =& 0\quad \forall \text{ admissible }\psi _{f},\quad j = 0,\ldots,m - 1, {}\\ (s^{0} -\mathbf{u}_{ s}^{0},\psi )& =& 0\quad \forall \text{ admissible }\psi _{ s}, {}\\ (s^{\,j+1} -\mathbf{u}_{ s}^{\,j}(t_{ j+1}),\psi _{s})& =& 0\quad \forall \text{ admissible }\psi _{s},\quad j = 0,\ldots,m - 1, {}\\ \end{array}$$

These matching conditions form a nonlinear system

$$\displaystyle{F(X) = 0\quad \text{with }X = (q^{0},\ldots,q^{m},r^{0},\ldots,r^{m},s^{0},\ldots,s^{m}),}$$

which can be solved with Newton’s method. Details for the general solution algorithm are found in [19]. The implementation and analysis for our fluid-structure interaction systems is planned as next task in our future work. We are specifically interested in the parallel solution capabilities (the link to the parallel algorithm [19, 33]) of this approach because we have to solve for, let us say, ten shooting time intervals for the fsi2-benchmark and m = 100 in the case of fsi3-benchmark. This leads to a huge Newton system to solve.

7 Conclusion

We have analyzed implicit time-discretizations of fully coupled monolithic fluid-structure interactions. The difficulties connected to this special application field is two-fold: first, the implicit handling of the mesh motion, captured by the ALE-map, leads to non-standard coupling of temporal and spatial derivatives. For such nonlinear couplings, time discretizations schemes have not been investigated so far. Further, the motion of the mesh, and the coupling of the incompressible Navier-Stokes equations with hyperelastic materials gives rise to stability problems that play an important role for long-time simulations. By analyzing the fsi benchmark problems published by Hron & Turek, these difficulties have been investigated in detail. For running stable long-time simulations, one must either resort to strongly A-stable time-discretization schemes like the fractional step theta method or one must modify standard schemes to improve the stability. A further promising approach to run long-time fluid-structure interaction simulations is the use of the multiple shooting method as a time domain decomposition scheme. Such an approach would allow to use efficient standard schemes like the Crank-Nicolson method by keeping the sub-intervals short.