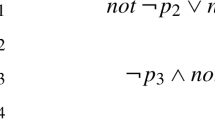Characterising and Explaining Inconsistency in Logic Programs

Abstract

A logic program under the answer set semantics can be inconsistent because its only answer set is the set of all literals, or because it does not have any answer sets. In both cases, the reason for the inconsistency may be (1) only explicit negation, (2) only negation as failure, or (3) the interplay between these two kinds of negation. Overall, we identify four different inconsistency cases, and show how the respective reason can be further characterised by a set of culprits using semantics which are weaker than the answer set semantics. We also provide a technique for explaining the set of culprits in terms of trees whose nodes are derivations. This can be seen as an important first step towards debugging inconsistent logic programs.

1 Introduction

A logic program represents knowledge in the form of rules made of statements which can be negated in two ways: using explicit negation, expressing that the statement does not hold, or negation as failure (NAF), expressing that the statement cannot be proven to hold. If no negation of either kind is present, a logic program will always be consistent under the answer set semantics [8]. However, if negation is used in a logic program, inconsistency may arise in one of two different ways: either the only answer set of the logic program is the set of all literals, or the logic program has no answer sets at all.

Efficient solvers have been developed for computing the answer sets of a given logic program [6, 10, 11]. However, in the case of an inconsistent logic program these solvers do not provide any classification of the inconsistency, or explanation thereof. Especially when dealing with a large inconsistent logic program or if the inconsistency is unexpected, understanding why the inconsistency arises and which part of the logic program is responsible for it is an important first step towards debugging the logic program in order to restore consistency. Various approaches have been developed for finding the source of inconsistency and even for suggesting ways of debugging the logic program. In particular, [7, 12, 17] feed the inconsistent logic program into a meta logic program whose answer set describes the structure of and potential mistakes in the original logic program. In another recent approach [13], the user assigns truth values to literals in the inconsistent logic program step-by-step until encountering a conflict.

These debugging approaches assume explicitly or implicitly the existence of an intended answer set. We propose a new method for identifying the reason of inconsistency in a logic program without the need of an intended answer set, based on the well-founded [19] and M-stable [3] model semantics. These semantics are “weaker” than answer sets in that they are 3-valued rather than 2-valued. In contrast to some previous approaches [1, 7, 17], we consider logic programs that may comprise both explicit negation and NAF. We prove that the two ways in which a logic program may be inconsistent are further divided into four inconsistency cases which have different reasons for the inconsistency: one where only explicit negation is responsible and the only answer set is the set of all literals, one where only NAF is responsible and the logic program has no answer sets, and two where an interplay of explicit negation and NAF is responsible and the logic program has no answer sets. We show how in each of these inconsistency cases the reason of the inconsistency can be refined to a characteristic set of “culprits”. These “culprits” can then be used to construct trees whose nodes hold derivations. These trees explain why the inconsistency arises and which part of the logic program is responsible. Furthermore, we show how the inconsistency case and the respective set of culprits can be determined using the aforementioned “weaker” semantics.

2 Background

A logic program $\mathcal {P}$ is a (finite) set of ground clauses¹ of the form $l_0 \leftarrow l_1, \ldots , l_m,$ $not ~ l_{m+1},\ldots , not ~ l_{m+n}$ with $m,n \ge 0$. All $l_i$ ($1 \le i \le m$) and all $l_j$ ($m+1 \le j \le m+n$) are classical literals, i.e. atoms a or explicitly negated atoms $\lnot a$, and $not~ l_j$ are negation as failure (NAF) literals. We will use the following notion of dependency inspired by [20]: $l_0$ is positively dependent on $l_i$ and negatively dependent on $l_j$. A dependency path is a chain of positively or negatively dependent literals. A negative dependency path is obtained from a dependency path by deleting all literals l in the path such that some k in the path is positively dependent on l, e.g. if p, q, r is a dependency path where p is positively dependent on q, and q is negatively dependent on r then p, r is a negative dependency path.

$\mathcal {HB}_{\mathcal {P}}$ is the Herbrand Base of $\mathcal {P}$, i.e. the set of all ground atoms of $\mathcal {P}$, and $Lit_{\mathcal {P}} = \mathcal {HB}_{\mathcal {P}} \cup \{\lnot a \,|\, a \in \mathcal {HB}_{\mathcal {P}}\}$ consists of all classical literals of $\mathcal {P}$. $\textit{NAF}_{\mathcal {HB}_{\mathcal {P}}} = \{ not~ a \,|\, a \in \mathcal {HB}_{\mathcal {P}} \}$ consists of all NAF literals of atoms of $\mathcal {P}$ and $\textit{NAF}_{Lit_{\mathcal {P}}} = \{ not~ l \,|\, l \in Lit_{\mathcal {P}} \}$ of all NAF literals of classical literals of $\mathcal {P}$. An atom a and the explicitly negated atom $\lnot a$ are called complementary literals.

$\vdash _{MP}$ denotes derivability using modus ponens on $\leftarrow$ as the only inference rule, treating $l\! \leftarrow \,$ as $l\! \leftarrow true$, where $\mathcal {P} \vdash _{MP} true$ for any $\mathcal {P}$. For a logic program $\mathcal {P}$ and $\varDelta \subseteq \textit{NAF}_{Lit_{\mathcal {P}}}$, $\mathcal {P} \cup \varDelta$ denotes $\mathcal {P} \cup \{not~l \leftarrow | not~l \in \varDelta \}$. When used on such $\mathcal {P}\! \cup \varDelta$, $\vdash _{MP}$ treats NAF literals syntactically as in [4] and thus $\mathcal {P}\! \cup \! \varDelta$ can be seen as a logic program. $l \in Lit_{\mathcal {P}}$ is strictly derivable from $\mathcal {P}$ iff $\mathcal {P} \vdash _{MP} l$, and defeasibly derivable from $\mathcal {P}$ iff $\mathcal {P} \nvdash _{MP} l$ and $\exists \varDelta \subseteq \textit{NAF}_{Lit_{\mathcal {P}}}$ such that $\mathcal {P}\! \cup \! \varDelta \vdash _{MP} l$. l is derivable from $\mathcal {P}$ iff l is strictly or defeasibly derivable from $\mathcal {P}$.

Answer Sets [8]. Let $\mathcal {P}$ be a logic program without NAF literals. The answer set of $\mathcal {P}$, denoted $\mathcal {AS}(\mathcal {P})$, is the smallest set $S \subseteq Lit_{\mathcal {P}}$ such that:

• (1) for any clause $l_0 \leftarrow l_1,\ldots ,l_m$ in $\mathcal {P}$: if $l_1,\ldots ,l_m \in S$ then $l_0 \in S$; and

• (2) $S = Lit_{\mathcal {P}}$ if S contains complementary literals.

For a logic program $\mathcal {P}$, possibly with NAF literals, and any $S \subseteq Lit_{\mathcal {P}}$, the reduct $\mathcal {P}^S$ is obtained from $\mathcal {P}$ by deleting:

• all clauses containing not  l where $l \in S$, and

• all NAF literals in the remaining clauses.

Then S is an answer set of $\mathcal {P}$ if it is the answer set of the reduct $\mathcal {P}^S$, i.e. if $S = \mathcal {AS}(\mathcal {P}^S)$. $\mathcal {P}$ is inconsistent if it has no answer sets or if its only answer set is $Lit_{\mathcal {P}}$, else it is consistent.

3-Valued Models[15]. Let $\mathcal {P}$ be a logic program with no explicitly negated atoms. A 3-valued interpretation of $\mathcal {P}$ is a pair $\langle \mathcal {T}, \mathcal {F} \rangle$, where $\mathcal {T}, \mathcal {F} \subseteq \mathcal {HB}_{\mathcal {P}}$, $\mathcal {T} \, \cap \, \mathcal {F} = \emptyset$, and $\mathcal {U} = \mathcal {HB}_{\mathcal {P}} \backslash (\mathcal {T} \cup \mathcal {F})$. The truth value of $a \in \mathcal {HB}_{\mathcal {P}}$ and $not~a \in \textit{NAF}_{\mathcal {HB}_{\mathcal {P}}}$ with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$ is:

$val(a) = T$, if $a \in \mathcal {T}$;    $val(not~a) = T$, if $a \in \mathcal {F}$;

$val(a) = F$, if $a \in \mathcal {F}$;    $val(not~a) = F$, if $a \in \mathcal {T}$;

$val(a) = U$, if $a \in \mathcal {U}$;    $val(not~a) = U$, if $a \in \mathcal {U}$;

The truth values are ordered by $T>U>F$ and naturally $val(T) = T$, $val(F) = F$, and $val(U) = U$. A 3-valued interpretation $\langle \mathcal {T}, \mathcal {F} \rangle$ satisfies a clause $a_0 \leftarrow a_1, \ldots , a_m, not~a_{m+1},\ldots , not~a_{m+n}$ if $val(a_0) \ge min \{val(a_1),\ldots , val(a_{m+n})\}$. $\langle \mathcal {T}, \mathcal {F} \rangle$ satisfies $a_0 \leftarrow \;$ if $val(a_0) = T$. The partial reduct $\frac{\mathcal {P}}{\langle \mathcal {T}, \mathcal {F} \rangle }$ of $\mathcal {P}$ with respect to a 3-valued interpretation $\langle \mathcal {T}, \mathcal {F} \rangle$ is obtained by replacing each NAF literal in every clause of $\mathcal {P}$ by its respective truth value.

• A 3-valued interpretation $\langle \mathcal {T}, \mathcal {F} \rangle$ of $\mathcal {P}$ is a 3-valued model of $\mathcal {P}$ iff $\langle \mathcal {T}, \mathcal {F} \rangle$ satisfies every clause in $\mathcal {P}$.

• A 3-valued model $\langle \mathcal {T}, \mathcal {F} \rangle$ of $\mathcal {P}$ is a 3-valued stable model of $\mathcal {P}$ iff it is a minimal 3-valued model of $\frac{\mathcal {P}}{\langle \mathcal {T}, \mathcal {F} \rangle }$, i.e. if $\not \exists \langle \mathcal {T}_1, \mathcal {F}_1 \rangle$ which is a 3-valued model of $\frac{\mathcal {P}}{\langle \mathcal {T}, \mathcal {F} \rangle }$ such that $\mathcal {T}_1 \subseteq \mathcal {T}$ and $\mathcal {F}_1 \supseteq \mathcal {F}$ and $\mathcal {T} \ne \mathcal {T}_1$ or $\mathcal {F} \ne \mathcal {F}_1$.

• A 3-valued stable model $\langle \mathcal {T}, \mathcal {F} \rangle$ of $\mathcal {P}$ is the well-founded model of $\mathcal {P}$ if $\mathcal {U}$ is maximal (w.r.t. $\subseteq$) among all 3-valued stable models of $\mathcal {P}$. The well-founded model always exists for logic programs without explicitly negated atoms.

• A 3-valued stable model $\langle \mathcal {T}, \mathcal {F} \rangle$ of $\mathcal {P}$ is a 3-valued M-stable model (Maximal-stable) of $\mathcal {P}$ if $\not \exists \langle \mathcal {T}_1, \mathcal {F}_1 \rangle$ which is a 3-valued stable model of $\mathcal {P}$ such that $\mathcal {T} \subseteq \mathcal {T}_1$ and $\mathcal {F} \subseteq \mathcal {F}_1$ and $\mathcal {T} \ne \mathcal {T}_1$ or $\mathcal {F} \ne \mathcal {F}_1$ [3].

The translated logic program $\mathcal {P}'$ of a logic program $\mathcal {P}$ is obtained by substituting every explicitly negated atom $\lnot a$ in $\mathcal {P}$ with a new atom $a' \notin \mathcal {HB}_{\mathcal {P}}$ [8, 15]. Then $a'$ (resp. a) is the translated literal of the original literal $\lnot a$ (resp. a). The 3-valued stable models of a logic program $\mathcal {P}$, possibly containing explicitly negated atoms, are defined in terms of the 3-valued stable models of $\mathcal {P}'$ [15]. For every 3-valued stable model $\langle \mathcal {T}', \mathcal {F}' \rangle$ of $\mathcal {P}'$ the corresponding 3-valued stable model $\langle \mathcal {T}, \mathcal {F} \rangle$ of $\mathcal {P}$ is obtained from $\langle \mathcal {T}', \mathcal {F}' \rangle$ by replacing every translated literal by its original literal. The 3-valued stable models of $\mathcal {P}$ are those corresponding 3-valued stable models where $\mathcal {T}$ does not contain complementary literals. Note that $\mathcal {P}'$ always has a well-founded model but that $\mathcal {P}$ might not have a well-founded model. Furthermore, note that a 3-valued stable model of $\mathcal {P}$ is an answer set of $\mathcal {P}$ iff $\mathcal {U} = \emptyset$.

From here onwards, and if not stated otherwise, we assume as given an inconsistent logic program $\mathcal {P}$ and the translated logic program $\mathcal {P}'$, where $a'$, $a_i'$, a are the translated literals of $\lnot a$, $\lnot a_i$, and a, respectively.

3 Characterising the Type of Inconsistency

We first show how to identify in which way a logic program is inconsistent, i.e. if its only answer set is the set of all literals or if it has no answer sets at all, assuming that we only know what an answer set solver gives us, i.e. that the logic program is inconsistent. This identification is based on whether or not the logic program has a well-founded model, which can be computed in polynomial time [19]. Our results show that even though a logic program can only be inconsistent in two ways, in fact there are three different inconsistency cases which arise due to different reasons (see Sect. 4). The three inconsistency cases are:

• $\mathcal {P}$ has no well-founded model and:

• (1) the only answer set of $\mathcal {P}$ is $Lit_{\mathcal {P}}$;

• (2) $\mathcal {P}$ has no answer sets.

• $\mathcal {P}$ has a well-founded model and

• (3) $\mathcal {P}$ has no answer sets.

In the following, we prove that these three cases are the only ones, and characterise them in more detail.

Example 1

Let $\mathcal {P}_1$ be the following logic program:

$\mathcal {P}_1$ has no well-founded model and its only answer set is $Lit_{\mathcal {P}_1}$, so $\mathcal {P}_1$ falls into inconsistency case 1. The reason that the only answer set is $Lit_{\mathcal {P}_1}$ is that for any $S \subseteq Lit_{\mathcal {P}_1}$ satisfying the conditions of an answer set, $s, r, \lnot p \in S$, then $q, p \in S$, and thus S contains the complementary literals p and $\lnot p$. Note that NAF literals do not play any role in the inconsistency of $\mathcal {P}_1$; an atom and its explicitly negated atom, both strictly derivable, are responsible for the inconsistency.

The observations in Example 1 agree with a well-known result about logic programs whose only answer set it the set of all literals (Proposition 6.7 in [9]).

Lemma 1

The only answer set of $\mathcal {P}$ is $Lit_{\mathcal {P}}$ iff $\exists a \in \mathcal {HB}_{\mathcal {P}}$ such that $\mathcal {P} \vdash _{MP} a$ and $\mathcal {P} \vdash _{MP} \lnot a$.

Example 2

Let $\mathcal {P}_2$ be the following logic program:

$\mathcal {P}_2$ has no well-founded model and no answer sets, so $\mathcal {P}_2$ falls into inconsistency case 2. The reason that $\mathcal {P}_2$ has no answer sets is an interplay of explicit negation and NAF: for any $S \subseteq Lit_{\mathcal {P}_2}$ satisfying the conditions of an answer set, $\lnot t, \lnot s \in S$, and thus $r \leftarrow not~\lnot t$ is always deleted in ${\mathcal {P}_2}^S$ and both $q \leftarrow$ and $\lnot q \leftarrow \lnot s$ are always part of ${\mathcal {P}_2}^S$. Consequently, for any such S it holds that $q, \lnot q \in \mathcal {AS}({\mathcal {P}_2}^S)$, meaning that the only possible answer set is $Lit_{\mathcal {P}_2}$. However, since $r, p, \lnot t \in Lit_{\mathcal {P}_2}$ the reduct will only consist of $\lnot t \leftarrow$ and $\lnot s \leftarrow$, so that $\mathcal {AS}({\mathcal {P}_2}^{Lit_{\mathcal {P}_2}}) = \{\lnot t, \lnot s\}$ which does not contain complementary literals. Consequently, $\mathcal {P}_2$ has no answer sets at all. Even though both here and in $\mathcal {P}_1$ the inconsistency arises due to complementary literals, the difference lies in their derivations: here the complementary literals are defeasibly derivable, i.e. not only explicit negation but also NAF involved in the derivation is responsible for the inconsistency.

The following Theorem characterises inconsistency cases 1 and 2 illustrated in Examples 1 and 2.

Theorem 1

If $\mathcal {P}$ has no well-founded model then

• 1. the only answer set of $\mathcal {P}$ is $Lit_{\mathcal {P}}$ iff $\exists a \in \mathcal {HB}_{\mathcal {P}}$ such that $\mathcal {P} \vdash _{MP} a$ and $\mathcal {P} \vdash _{MP} \lnot a$;

• 2. $\mathcal {P}$ has no answer sets iff $\not \exists a \in \mathcal {HB}_{\mathcal {P}}$ such that $\mathcal {P} \vdash _{MP} a$ and $\mathcal {P} \vdash _{MP} \lnot a$.

Proof

From Lemma 1.

Example 3

Let $\mathcal {P}_3$ be the following logic program:

The well-founded model of $\mathcal {P}_3$ is $\langle \emptyset , \emptyset \rangle$ but $\mathcal {P}_3$ has no answer sets, so it falls into inconsistency case 3. The reason that $\mathcal {P}_3$ has no answer sets is an interplay of explicit negation and NAF similar to Example 2. From the first two clauses, it follows that any potential answer set $S \subseteq Lit_{\mathcal {P}_3}$ cannot contain both s and r. If $r \notin S$ then $p, \lnot p \in S$; if $s \notin S$ then $q, \lnot q \in S$, and thus the only possible answer set is $Lit_{\mathcal {P}_3}$. However, ${\mathcal {P}_3}^{Lit_{\mathcal {P}_3}}$ is empty, so $\mathcal {AS}({\mathcal {P}_3}^{Lit_{\mathcal {P}_3}}) = \emptyset$, which does not contain complementary literals. Thus, $\mathcal {P}_3$ has no answer sets. As in Example 2, the inconsistency is due to an atom and its explicitly negated atom being defeasibly derivable, but in contrast to $\mathcal {P}_2$ here the derivations of the complementary literals involve NAF literals which form an even-length negative dependency loop, namely s and r.

Theorem 2 characterises inconsistency case 3, illustrated in Example 3.

Theorem 2

If $\mathcal {P}$ has a well-founded model then $\mathcal {P}$ has no answer sets.

Proof

Assume that $\exists a \in \mathcal {HB}_{\mathcal {P}}$ s.t. $\mathcal {P} \vdash _{MP} a$ and $\mathcal {P} \vdash _{MP} \lnot a$. Then a and $a'$ are in the well-founded model of $\mathcal {P}'$ (by the alternating fixpoint definition of well-founded models [18]) and thus a and $\lnot a$ are contained in the corresponding well-founded model of $\mathcal {P}$, so $\mathcal {P}$ has no well-founded model (contradiction). Thus, $\not \exists a \in \mathcal {HB}_{\mathcal {P}}$ s.t. $\mathcal {P} \vdash _{MP} a$ and $\mathcal {P} \vdash _{MP} \lnot a$, so by Lemma 1 it is not the case that the only answer set of $\mathcal {P}$ is $Lit_{\mathcal {P}}$. Consequently, $\mathcal {P}$ has no answer sets.

In summary, if $\mathcal {P}$ has no well-founded model then its only answer set is $Lit_{\mathcal {P}}$ – caused by explicit negation – or it has no answer sets – caused by the interplay of explicit negation and NAF. If $\mathcal {P}$ has a well-founded model then it definitely has no answer sets – caused by the interplay of explicit negation and NAF.

4 Characterising Culprits

In the examples in Sect. 3, we already briefly discussed that the reasons for the inconsistency are different in the three inconsistency cases: either only explicit negation or the interplay of explicit negation and NAF. In this section, we show that inconsistency case 3 can in fact be further split into two sub-cases: one where the interplay of explicit negation and NAF is responsible as seen in Example 3 (case 3a), and one where only NAF is responsible for the inconsistency (case 3b). Furthermore, we characterise the different reasons of inconsistency in more detail in terms of “culprit” sets, which are sets of literals included in the well-founded (cases 1,2) or 3-valued M-stable (case 3b) model of $\mathcal {P}$, or in the answer sets of $\mathcal {P}'$ (case 3a). In other words, culprits can be found in “weaker” models.

Definition 1

(culprit sets). Let $\mathcal {P}$, $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$ be the well-founded model of $\mathcal {P}'$, $S_1', \ldots , S_n'$ ($n \ge 0$) its answer sets, and $\langle \mathcal {T}_M', \mathcal {F}_M' \rangle$ one of its 3-valued M-stable models with $\mathcal {U}_M'$ the set of undefined atoms.

• If $\mathcal {P}$ has no well-founded model then

  • $\{a, \lnot a\}$ is a culprit set of $\mathcal {P}$ iff $a, a' \in \mathcal {T}_w'$ and a and $a'$ are strictly derivable from $\mathcal {P}'$ (case 1).

  • $\{a, \lnot a\}$ is a culprit set of $\mathcal {P}$ iff $a, a' \in \mathcal {T}_w'$ and one of them is defeasibly derivable from $\mathcal {P}'$ and the other one is derivable from $\mathcal {P}'$ (case 2).

• If $\mathcal {P}$ has a well-founded model and

  • $\mathcal {P}'$ has n answer sets ($n \ge 1$), then $\{a_1, \lnot a_1, \ldots , a_n, \lnot a_n\}$ is a culprit set of $\mathcal {P}$ iff $\forall a_i, \lnot a_i$ ($1 \le i \le n$): $a_i, a_i' \in S_i'$ and one of them is defeasibly derivable from $\mathcal {P}'$ and the other one is derivable from $\mathcal {P}'$ (case 3a).

  • $\mathcal {P}'$ has no answer sets, then C is a culprit set of $\mathcal {P}$ iff for some $a_1 \in \mathcal {U}_M'$ there exists a negative dependency path $a_1, \ldots , a_m, b_1, \ldots , b_o$ ($m,o \ge 1$), in $\mathcal {P}'$ such that all $a_h$ ($1 \le h \le m$) and $b_j$ ($1 \le j \le o$) are in $\mathcal {U}_M'$, o is odd, $a_m = b_o$, and C consists of the original literals of the translated literals $b_1, \ldots , b_o$ (case 3b).

We now show that for every inconsistency case at least one culprit set exists.

Example 4

The well-founded model of the translated logic program ${\mathcal {P}_1}'$ (see $\mathcal {P}_1$ in Example 1) is $\langle \{p, p', q, r, s\},\emptyset \rangle$. $p, p' \in \mathcal {T}_w'$ and both of them are strictly derivable from $\mathcal {P}'$. Thus, $\{p, \lnot p\}$ is a culprit set of $\mathcal {P}_1$, which confirms our observation that $Lit_{\mathcal {P}_1}$ is the only answer set of $\mathcal {P}_1$ because every potential answer set contains both p and $\lnot p$ (see Example 1). Note that it is not only the literals in the culprit set which characterise this inconsistency case, it is the derivation of the literals, i.e. that both are strictly derivable.

Theorem 3 states the existence of a culprit set in inconsistency case 1.

Theorem 3

Let $\mathcal {P}$ have no well-founded model and let its only answer set be $Lit_{\mathcal {P}}$. Then $\mathcal {P}$ has a case 1 culprit set $\{a, \lnot a\}$.

Proof

By Lemma 1, $\exists a, a' \in \mathcal {HB}_{\mathcal {P}'}$ s.t. $\mathcal {P}' \vdash _{MP} a$ and $\mathcal {P}' \vdash _{MP} a'$. By definition of well-founded model (as an alternating fixpoint [18]), $a, a' \in \mathcal {T}_w'$ where $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$ is the well-founded model of $\mathcal {P}'$. By Definition 1, $\{a, \lnot a\}$ is a case 1 culprit set.

Example 5

The well-founded model of $\mathcal {P}_2'$ (see $\mathcal {P}_2$ in Example 2) is $\langle \{q, q', s',$ $t'\}, \{p, r\} \rangle$. $q, q' \in \mathcal {T}_w'$ and here even both of them are defeasibly derivable. Thus, $\{q, \lnot q\}$ is a culprit set of $\mathcal {P}_2$ which confirms our observation that the reason for the inconsistency of $\mathcal {P}_2$ is that every potential answer set contains both q and $\lnot q$, but $Lit_{\mathcal {P}_2}$ is not an answer set due to the NAF literals involved in the derivations of q and $\lnot q$. Note that even though the culprit sets of $\mathcal {P}_1$ and $\mathcal {P}_2$ are very similar – both consist of complementary literals – the difference lies in the derivations of the literals in the culprit set: here the literals are not both strictly derivable, so the reason of the inconsistency is both that complementary literals are derivable (explicit negation) and that their derivations involve NAF literals.

Theorem 4 proves the existence of a culprit set in inconsistency case 2.

Theorem 4

Let $\mathcal {P}$ have no well-founded model and no answer sets. Then $\mathcal {P}$ has a case 2 culprit set $\{a, \lnot a\}$.

Proof

Let $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$ be the well-founded model of $\mathcal {P}'$. Since $\mathcal {P}$ has no well-founded model, $\mathcal {T}_w'$ must contain some $a, a'$. Since every answer set is a superset of the well-founded model (Corollary 5.7 in [19]), every potential answer set of $\mathcal {P}$ contains a and $\lnot a$, meaning that the only possible answer set is $Lit_{\mathcal {P}}$. From the assumption that $\mathcal {P}$ has no answer sets, we can conclude that $\mathcal {AS}(\mathcal {P}^{Lit_{\mathcal {P}}})$ does not contain a and $\lnot a$. Thus, all of the rules needed for the derivation of either a or $\lnot a$ are deleted in $\mathcal {P}^{Lit_{\mathcal {P}}}$, meaning that a or $\lnot a$ is defeasibly derivable. Trivially, the other literal is also derivable as $a, a' \in \mathcal {T}_w'$. Then by Definition 1, $\{a, \lnot a\}$ is a case 2 culprit set of $\mathcal {P}$.

Example 6

$\mathcal {P}_3'$ (see $\mathcal {P}_3$ in Example 3) has two answer sets $S_1' = \{q, q', r\}$ and $S_2' = \{p, p', s\}$, so $\mathcal {P}_3$ falls into inconsistency case 3a. $q,q',p, p'$ are all defeasibly derivable from ${\mathcal {P}_3}'$ and thus $\{q, \lnot q, p, \lnot p\}$ is a culprit set of $\mathcal {P}_3$. This confirms our observation that the reason for the inconsistency of $\mathcal {P}_3$ is that the two potential answer sets both contain complementary literals but that $Lit_{\mathcal {P}_3}$ is not an answer set due to the NAF literals involved in the derivations of the complementary literals. Thus, as in Example 5 the inconsistency is due to the interplay of explicit negation and NAF with the difference of the even-length loop described in Example 2. Due to this difference in the derivations, here the well-founded model of the translated logic program does not provide any information about culprits, but the answer sets do.

Theorem 5 states the existence of a culprit set in inconsistency case 3a.

Theorem 5

Let $\mathcal {P}$ have a well-founded model and let $\mathcal {P}'$ have $n \ge 1$ answer sets. Then, $\mathcal {P}$ has a case 3a culprit set $\{a_1, \lnot a_1, \ldots , a_n, \lnot a_n\}$.

Proof

By Theorem 2, $\mathcal {P}$ has no answer sets, so all $S_i \subseteq Lit_{\mathcal {P}}$ with $S_i = \mathcal {AS}(\mathcal {P}^{S_i})$ contain complementary literals $a_i$ and $\lnot a_i$, but $\mathcal {AS}(\mathcal {P}^{Lit_{\mathcal {P}}})$ does not contain complementary literals. Thus, all $S_i'$ with $S_i' = \mathcal {AS}(\mathcal {P}'^{{S_i}'})$ contain $a_i$ and $a_i'$, so $a_i$ and $a_i'$ must be derivable from $\mathcal {P}'$. Assume that $\mathcal {P}' \vdash _{MP} a_i$ and $\mathcal {P}' \vdash _{MP} a_i'$. Then by Lemma 1 the only answer set of $\mathcal {P}$ is $Lit_{\mathcal {P}}$ (contradiction). Thus, at least one of $a_i$ and $a_i'$ is defeasibly derivable from $\mathcal {P}'$. Then by Definition 1, $\{a_1, \lnot a_1, \ldots , a_n, \lnot a_n\}$ is a case 3a culprit set of $\mathcal {P}$.

Example 7

Let $\mathcal {P}_4$ be the following logic program:

$\mathcal {P}_4$ has a well-founded model and $\mathcal {P}_4'$ has no answer sets, so $\mathcal {P}_4$ falls into inconsistency case 3b. The only 3-valued M-stable model of $\mathcal {P}_4'$ is $\langle \{x\}, \{y\} \rangle$, where $\mathcal {U}_M' = \{s, t, u', v, w, x'\}$. For $s \in \mathcal {U}_M'$ there exists a negative dependency path $s, t, u', v, t$ of atoms in $\mathcal {U}_M'$, where $u',v,t$ is an odd-length loop. Thus, $C = \{\lnot u, v, t\}$ is a culprit set of $\mathcal {P}_4$. Note that this culprit set is found no matter with which atom in $\mathcal {U}_M'$ the negative dependency path is started. This example shows that in inconsistency case 3b the inconsistency is due to NAF on its own; explicit negation plays no role.

Theorem 6 states not only the existence of a culprit set in inconsistency case 3b, but also characterises how to find a culprit set. This extends the results of [20] about odd-length loops.

Theorem 6

Let $\mathcal {P}$ have a well-founded model and let $\mathcal {P}'$ have no answer sets. Let $\langle \mathcal {T}_M', \mathcal {F}_M' \rangle$ be a 3-valued M-stable model of $\mathcal {P}'$ with $\mathcal {U}_M'$ the set of undefined atoms. Then, for any $a_1 \in \mathcal {U}_M'$ there exists a negative dependency path $a_1, \ldots , a_n, b_1, \ldots , b_m$ such that the set C consisting of the original literals of the translated literals $b_1, \ldots , b_m$ is a case 3b culprit set of $\mathcal {P}$.

Proof

(Sketch). By definition of 3-valued stable models any undefined atom is negatively dependent on an undefined atom. Thus, there is a negative dependency path of undefined atoms $a_1, \ldots , a_n$, which must lead to a negative dependency loop $a_n, b_1, \ldots , b_m$ ($a_n = b_m$) where no $b_j$ is part of another negative-dependency path containing literals other than the ones in the loop. Assuming that the negative-dependency loop and all sub-loops are of even length, the loop on its own has a 2-valued stable model. We can show (omitted for lack of space) that it is possible to change the truth values of atoms not in the loop and in $\mathcal {U}_M'$ to T or F in such a way that if combined with the new truth values of the loop, a 3-valued stable model $\langle \mathcal {T}', \mathcal {F}' \rangle$ of $\mathcal {P}'$ is created. Clearly $\mathcal {T}_M' \subset \mathcal {T}'$ and $\mathcal {F}_M' \subset \mathcal {F}'$, so $\langle \mathcal {T}_M', \mathcal {F}_M' \rangle$ is not a 3-valued M-stable model. Contradiction.

Note that in each of the three inconsistency cases discussed in Sect. 3, the translated logic program $\mathcal {P}'$ might or might not have answer sets. However, regarding culprit sets this distinction only makes a difference in inconsistency case 3.

It follows directly from the previous theorems that the culprit sets we identified are indeed responsible for the inconsistency, i.e. if no culprit sets exist then the logic program is not inconsistent, which is an essential first step for a user to understand what causes the inconsistency in a logic program.

Corollary 1

Let $\mathcal {P}$ be a (possibly consistent) logic program. If there exists no culprit set of inconsistency cases 1, 2, 3a, or 3b of $\mathcal {P}$, then $\mathcal {P}$ is consistent.

5 Explaining Culprits

As pointed out in the previous sections, even though we identify culprits as sets of literals, the reason of the inconsistency is mostly the way in which these literals are derivable from the logic program. In order to make the reason of the inconsistency more understandable for the user, we now show how explanations of the inconsistency can be constructed in terms of trees whose nodes are derivations. For this purpose, we define derivations with respect to a 3-valued interpretation $\langle \mathcal {T}, \mathcal {F} \rangle$. We call a derivation true with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$ if all NAF literals not k used in the derivation are true with respect to the interpretation, i.e. the literals k are false in the interpretation. We call a derivation false with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$ if there exists a NAF literal not k used in the derivation which is false with respect to the interpretation, i.e. k is true in the interpretation.

Definition 2

(true/false derivation). Let $\langle \mathcal {T}, \mathcal {F} \rangle$ be a 3-valued interpretation of $\mathcal {P}$, $l \in Lit_{\mathcal {P}}$, and $\varDelta \subseteq \textit{NAF}_{Lit_{\mathcal {P}}}$.

• 1. $\mathcal {P} \cup \varDelta \vdash _{MP} l$ is a true derivation of l w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ if $\forall not\, k \in \varDelta : k \in \mathcal {F}$.

• 2. $\mathcal {P} \cup \varDelta \vdash _{MP} l$ is a false derivation of l w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ if $\exists not\, k \in \varDelta : k \in \mathcal {T}$.

Example 8

Consider $\mathcal {P}_4$ from Example 7. $\mathcal {P}_4 \cup \{not~t, not~x\} \vdash _{MP} v$ is a true derivation w.r.t. $\langle \{s\}, \{t, x\} \rangle$, a false derivation w.r.t $\langle \{s, t\}, \{x\} \rangle$, and neither a true nor a false derivation w.r.t. $\langle \{s\}, \{x\} \rangle$.

An explanation of inconsistency cases 1–3a illustrates why the literals in a culprit set are contained in the respective 3-valued stable model $\langle \mathcal {T}, \mathcal {F} \rangle$ used to identify this culprit set, which is due to the literals’ derivations. Thus, an explanation starts with a true derivation of a literal in the culprit set with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$. The explanation then indicates why this derivation is true, i.e. why all NAF literals not k are true with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$. The reason why not k is true is that some derivation of k is false, i.e. a NAF literal $not\, m$ in a derivation of k is false with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$. This in turn is explained in terms of why m is the true with respect to $\langle \mathcal {T}, \mathcal {F} \rangle$, and so on.

Definition 3

(explanation). Let $\langle \mathcal {T}, \mathcal {F} \rangle$ be a 3-valued stable model of $\mathcal {P}$ and let $l \in Lit_{\mathcal {P}}$. An explanation of l w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ is a tree such that:

• 1. Every node holds either a true or a false derivation w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$.

• 2. The root holds a true derivation of l w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$.

• 3. For every node N holding a true derivation $\mathcal {P} \cup \varDelta \vdash _{MP} k$ w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ and for every $not\, m \in \varDelta$: every false derivation of m w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ is held by a child of N.

• 4. For every node N holding a false derivation $\mathcal {P} \cup \varDelta \vdash _{MP} k$ w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$: N has exactly one child holding a true derivation of some m w.r.t. $\langle \mathcal {T}, \mathcal {F} \rangle$ such that $not\, m \in \varDelta$.

• 5. There are no other nodes except those given in 1–4.

Since culprit sets are determined with respect to different 3-valued stable models in the different inconsistency cases, explanations are constructed with respect to these different models, too.

Definition 4

(inconsistency explanation - cases 1,2). Let $\mathcal {P}$ have no well-founded model and let $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$ be the well-founded model of $\mathcal {P}'$. Let $\{a, \lnot a\}$ be a culprit set of $\mathcal {P}$. A translated inconsistency explanation of $\mathcal {P}$ consists of an explanation of a w.r.t. $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$ and an explanation of $a'$ w.r.t. $\langle \mathcal {T}_w', \mathcal {F}_w' \rangle$. An inconsistency explanation of $\mathcal {P}$ is derived by replacing every translated literal in the translated inconsistency explanation by its respective original literal.

Since explanations are trees, they can be easily visualised, as shown for $\mathcal {P}_2$ (see Examples 2 and 5) in Fig. 1.

Fig. 1.

The inconsistency explanation of $\mathcal {P}_2$ (Examples 2, 5).

Definition 5

(inconsistency explanation - case 3a). Let $\mathcal {P}$ have a well-founded model and let $S_1', \ldots , S_n'$ ($n \ge 1$) be the answer sets of $\mathcal {P}'$. Let $\{a_1, \lnot a_1,$ $\ldots , a_n, \lnot a_n\}$ be a culprit set of $\mathcal {P}$. A translated inconsistency explanation of $\mathcal {P}$ consists of an explanation of all $a_i$ and $a_i'$ ($1 \le i \le n$) w.r.t. $\langle S_i', (\mathcal {HB}_{\mathcal {P}'} \backslash S_i') \rangle$. An inconsistency explanation of $\mathcal {P}$ is derived by replacing every translated literal in the translated inconsistency explanation by its respective original literal.

Figure 2 shows part of the inconsistency explanation of $\mathcal {P}_3$ (see Examples 3 and 6). It also illustrates the difference between the reasons of inconsistency in $\mathcal {P}_2$ and $\mathcal {P}_3$, namely the negative dependency loop of s and r in $\mathcal {P}_3$.

Fig. 2.

Part of the inconsistency explanation of $\mathcal {P}_3$ explaining q and $\lnot q$. The full inconsistency explanation also comprises similar explanations for p and $\lnot p$.

For inconsistency case 3b, where the literals in a culprit set form an odd-length negative dependency loop, the inconsistency explanation is a tree whose nodes hold derivations. However, since all literals in a culprit set are undefined with respect to a 3-valued M-stable model, an explanation is constructed with respect to the set of undefined atoms $\mathcal {U}$ rather than $\mathcal {T}$ and $\mathcal {F}$. In particular, the reason that a literal is undefined is that its derivation contains a NAF literal not k which is undefined. Then $k \in \mathcal {U}$ which again is due to the derivation containing some undefined NAF literal, and so on. Thus, an explanation of inconsistency case 3b is a tree of negative derivations with respect to $\mathcal {U}$.

Definition 6

(inconsistency explanation - case 3b) . Let $\mathcal {P}$ have a well-founded model and let $\mathcal {P}'$ have no answer sets. Let $\langle \mathcal {T}_M', \mathcal {F}_M' \rangle$ be a 3-valued M-stable model of $\mathcal {P}'$ with $\mathcal {U}_M'$ the set of undefined atoms. Let C be a culprit set of $\mathcal {P}$ and $a \in C$. A translated inconsistency explanation of $\mathcal {P}$ is a tree such that:

• 1. Every node holds a false derivation w.r.t. $\langle \mathcal {U}_M', \emptyset \rangle$.

• 2. The root holds a false derivation of a w.r.t. $\langle \mathcal {U}_M', \emptyset \rangle$.

• 3. For every node N holding a false derivation $\mathcal {P} \cup \varDelta \vdash _{MP} b$ w.r.t. $\langle \mathcal {U}_M', \emptyset \rangle$: N has exactly one child node holding a false derivation of some m w.r.t. $\langle \mathcal {U}_M', \emptyset \rangle$ such that $not\, m \in \varDelta$ and $m \in C$.

• 4. There are no other nodes except those given in 1–3.

An inconsistency explanation of $\mathcal {P}$ is derived by replacing every translated literal in the translated inconsistency explanation by its respective original literal.

Figure 3 illustrates the inconsistency explanation of $\mathcal {P}_4$ (see Example 7), showing the responsible odd-length loop. It also illustrates how the derivations in an inconsistency explanation can be expanded to derivation trees, which can also be done for cases 1–3a.

Fig. 3.

The inconsistency explanation of $\mathcal {P}_4$ (left) and the version where derivations are expanded to trees (right).

Note that in all our examples, the culprit set is unique. However, in general a logic program may have various culprit sets (from the same inconsistency case) resulting in various inconsistency explanations. Moreover, there may be various inconsistency explanations for a given culprit set.

6 Conclusion

We showed that the two ways in which a logic program may be inconsistent – it has no answer sets or its only answer set is the set of all literals – can be determined using the well-founded model semantics and further divided into four inconsistency cases: one where only explicit negation is responsible, one where only NAF is responsible, and two where the interplay of explicit negation and NAF is responsible for the inconsistency. Each of these cases is characterised by a different type of culprit set, containing literals which are responsible for the inconsistency due to the way in which they are derivable. These culprit sets can be identified using “weaker” semantics than answer sets and can be used to explain the inconsistency in terms of trees whose nodes are derivations.

Our approach is related to early work on characterising logic programs with respect to the existence of answer sets [2, 5, 20]. However, none of these considers the properties of explicit negation in addition to NAF. It should also be pointed out that our explanations are related to the graphs used in [14, 16] for explaining answer sets. In comparison to debugging approaches [1, 7, 12, 13, 17], our approach detects reasons for the inconsistency in terms of culprit sets, which is independent of an intended answer set. This naturally leads to the questions how to perform debugging based on the culprit sets, as well as how to deal with of multiple culprit sets for a logic program, which will be addressed in the future.

Since answer set programming for real-world applications often involves more complicated language constructs, e.g. constraints or aggregates, future work involves the extension of our approach to characterising inconsistency in logic programs using these constructs.