Rayleigh and Raman Spectra

Abstract

Unlike absorption and emission, Rayleigh and Raman spectroscopy are based on how a molecule scatters photons. One key difference to keep in mind as we explore scattering processes further is that while absorption requires that the molecule have energy-level spacings (for allowed transitions) corresponding to the energy of the interacting photon, scattering can occur with an incident photon of almost any energy. That is, for a molecule to absorb light, the light must generally be at specific wavelengths or frequencies. Scattering, on the other hand, can occur at almost any wavelength.

Unlike absorption and emission, Rayleigh and Raman spectroscopy are based on how a molecule scatters photons. One key difference to keep in mind as we explore scattering processes further is that while absorption requires that the molecule have energy-level spacings (for allowed transitions) corresponding to the energy of the interacting photon, scattering can occur with an incident photon of almost any energy. That is, for a molecule to absorb light, the light must generally be at specific wavelengths or frequencies. Scattering, on the other hand, can occur at almost any wavelength.

6.1 Light Scattering

For the light scattering experimental schematic in Fig. 6.1, the incident laser power, P _i , becomes scattered (Rayleigh or Raman) when it interacts with molecules inside the volume element δ V = δ A × L. The scattered laser power, P _s , is determined by the product of incident laser power, number density of molecules inside the volume element, length L, scattering cross-section, and collection angle of the optics.

Fig. 6.1

Schematic of a light scattering experiment

Incident Laser Power :

$P_{i} =\dot{ N}_{p}h\nu$ [W]

$\dot{N}_{p}$ = incident photons/s

Scattered Laser Power :

$P_{s} =\dot{ N}_{s}h\nu$ [W]

$\dot{N}_{s}$ = scattered photons/s into collection angle

$\dot{N}_{s} =\mathop{\underbrace{ \frac{\dot{N}_{p}} {\delta A} }}\limits _{\begin{array}{c} \text{photons}\\ \text{per area} \\ \text{per second}\end{array} }\times \mathop{\underbrace{N \frac{\partial \sigma } {\partial \Omega }\Omega }}\limits _{\begin{array}{c} \text{projected}\\ \text{scattering} \\ \mbox{ area, cm$^{2}$} \end{array} }$

$N = n \cdot \delta A \cdot L = \mbox{ the number of molecules in $\delta V $}$; n is the molecular density [molec∕cm³]

$\frac{\partial \sigma } {\partial \Omega } = \mbox{ differential scattering cross-section [$\mathrm{cm^{2}/molec\,Sr}$]}$

$\Omega = \mbox{ solid angle of collection [Steradians, Sr]}$

so that

$$\displaystyle{\fbox{ $P_{s} = P_{i}nL \frac{\partial \sigma } {\partial \Omega }\Omega $} }$$

(6.1)

Since scattering is essentially instantaneous, the above relation applies at any instant, when the incident power varies with time. For pulsed light, often employed for Rayleigh and Raman scattering, P _i and P _s can be reinterpreted as the total number of incident and scattered (collected) photons.

6.1.1 Cross-Sections

Rayleigh Cross-Sections

The differential Rayleigh cross-section is a property of a molecule that describes its propensity to scatter light. In general, this cross-section depends on the angle between the detection beam and the incident beam as well as the polarization. One can derive the differential Rayleigh cross-section as a function of laser and scattering geometry by modelling a molecule as an infinitesimally small oscillating dipole interacting with an imposed electric field. While a thorough discussion can be found in Miles et al. [1] or in Banwell [2], some key results are given here.

A spherically symmetric molecule’s differential cross-section at 90^∘ relative to the plane of incident polarization (formed by the E-field vector of the propagating wave and the direction of propagation) is

$$\displaystyle{ \left ( \frac{\partial \sigma _{\mathrm{ss}}} {\partial \Omega }\right )_{\mathrm{Rayleigh}}\mathop{\cong}\frac{4\pi ^{2}\left (n_{i} - 1\right )^{2}} {N^{2}\lambda ^{4}} }$$

(6.2)

where n _i is the refractive index and N is the number density of the scattering molecules (written here as a capital N to distinguish number density from the refractive index). Note the strong inverse dependence on wavelength. Also, since the quantity (n _i − 1) of a gas is proportional to its density, the quantity $(n_{i} - 1)^{2}/N^{2}$ is independent of density, and hence the Rayleigh cross-section (per molecule) is an intrinsic property (actually, this property is proportional to something called the polarizability of the molecule). The total cross-section is the differential cross-section integrated over the surface of a sphere enclosing the scatterer. It is given by

$$\displaystyle{ \sigma _{\mathrm{ss}}\mathop{\cong}\frac{32\pi ^{3}} {3\lambda ^{4}} \left (\frac{n_{i} - 1} {N} \right )^{2} = \frac{8\pi } {3}\ \left ( \frac{\partial \sigma _{\mathrm{ss}}} {\partial \Omega }\right )_{\mathrm{Rayleigh}} }$$

(6.3)

This formula will generally allow one to calculate the scattering cross-section to within a few percent for most molecules. If more accuracy is required, particles with some spherical asymmetry (e.g., diatomics) also have a King factor, F _K , that describes their anisotropy:

$$\displaystyle{ \sigma \mathop{\cong}F_{K}\sigma _{\mathrm{ss}} }$$

(6.4)

Typical values of the total cross-section in the visible region are on the order of 10⁻²⁷ cm²∕molec for small molecules. A few examples are given in Table 6.1.

Table 6.1 Rayleigh scattering parameters for selected molecules, taken from [1] and [3]

Raman Cross-Sections

The cross-section for Raman scattering is much smaller than for Rayleigh scattering (Table 6.2).

$$\displaystyle{\left ( \frac{\partial \sigma } {\partial \Omega }\right )_{\mathrm{Raman}} \approx 10^{-3}\left ( \frac{\partial \sigma } {\partial \Omega }\right )_{\mathrm{Rayleigh}}}$$

Table 6.2 Vibrational Raman cross-sections for common molecules at 532 nm (in units of 10⁻³⁰ cm²∕molec∕Sr)

Example: Rayleigh and Raman Scattering by N₂

at STP For a laser source with P _i  = 1 W at λ = 500 nm, the incident photon rate is $\dot{N}_{p} = 2.5 \times 10^{18}$ photons/s. The approximate differential scattering cross-section for Rayleigh scattering is

$$\displaystyle{\left ( \frac{\partial \sigma } {\partial \Omega }\right )_{\mathrm{Rayleigh}} \approx 8.1 \times 10^{-28}\ [\mathrm{cm^{2}/molec\,Sr}]}$$

For a system with 4 W of incident laser power at this wavelength, a measurement length L = 1 mm and $\Omega \approx 10^{-2}$ Sr,

$$\displaystyle\begin{array}{rcl} & & \dot{N}_{s} =\mathop{\underbrace{ \left (10^{19}\ \frac{\mathrm{photons}} {\mathrm{s}} \right )}}\limits _{\dot{N}_{p}}\mathop{\underbrace{ \left (2.7 \times 10^{19}\ \frac{\mathrm{molec}} {\mathrm{cc}} \right )}}\limits _{n=n_{L}\ \mathrm{at\ STP}}\mathop{\underbrace{ (0.1\,\mathrm{cm})}}\limits _{L}\mathop{\underbrace{ \left (8.1 \times 10^{-28}\ \frac{\mathrm{cm^{2}}} {\mathrm{molec\,Sr}}\right )}}\limits _{\partial \sigma /\partial \Omega }\mathop{\underbrace{ (10^{-2}\ \mathrm{Sr})}}\limits _{ \Omega } {}\\ & & \qquad \qquad \qquad \qquad \qquad \qquad \quad \dot{N}_{s} = 22 \times 10^{7}\,\text{photons/s} {}\\ & & \qquad \qquad \qquad \qquad \quad \qquad \qquad P_{s} \approx 88\,\text{pW} {}\\ \end{array}$$

For Raman scattering, however,

$$\displaystyle\begin{array}{rcl} \dot{N}_{s}& =& 22 \times 10^{4}\,\text{photons/s, and} {}\\ P_{s}& \approx & 0.088\,\text{pW} = 88\,\text{fW (small!)} {}\\ \end{array}$$

6.2 Quantum Model

Consider radiation to be composed of discrete photons that exchange energy with molecules (see Fig. 6.2). There are three different scattering possibilities: elastic (incident and scattered energy/wavelength are the same), and inelastic with either increased or decreased energy. Rayleigh scattering corresponds to elastic interactions, and Raman scattering corresponds to the two inelastic interaction possibilities.

Fig. 6.2

Photon scattering due to interaction with a molecule

Rayleigh :

E (elastic); ν = ν′

Anti-Stokes Raman :

$E + \Delta E$ (inelastic); $\nu =\nu ' + \Delta E/h$

Stokes Raman :

$E - \Delta E$ (inelastic); $\nu =\nu ' - \Delta E/h$

where

$$\displaystyle{\Delta E = \Delta E_{\mathrm{rot}}\ \mathrm{or}\ \Delta E_{\mathrm{rot,vib}},}$$

with new selection rules for allowed transitions. Scattering is a weak process, and thus requires a sensitive apparatus for making measurements.

6.3 Classical Theory

Classical theory for scattering is based on the polarizability of molecules. Whereas absorption and emission require an intrinsic dipole to be resonant with the interacting photon, scattering occurs when an externally applied electric field (the photon in classical terms) induces a dipole in the molecule. The induced dipole strength, μ, is given by

$$\displaystyle{ \mu =\alpha E }$$

(6.5)

where α is the polarizability and E is the E-field of the light wave. The E-field is oscillatory in nature (e.g., E = E _o sin(2π ν t)) and induces an oscillation in the molecule. The induced oscillation can occur:

• 1. at the same frequency of the incident field, resulting in “emission” at ν (Rayleigh), or

• 2. at beat frequencies based on the interaction of the incident field and the molecule’s rotational/vibrational frequencies, i.e. with “emission” at ν ±ν _vib∕rot

These beat frequencies are the Raman sidebands. This occurs because the polarizability may oscillate with the rotational and/or vibrational frequencies of the molecule, e.g.

$$\displaystyle{\alpha =\alpha _{o} +\beta \sin (2\pi \nu _{\mathrm{vib}}t),}$$

where β is the rate of change of polarizability with the rotation/vibration. From Eq. (6.5), the induced dipole strength becomes

$$\displaystyle{\mu =\mathop{\underbrace{ \alpha _{o}E_{o}\sin (2\pi \nu t)}}\limits _{\mathrm{Rayleigh}} + \frac{1} {2}\beta E_{o}[\mathop{\underbrace{\cos (2\pi (\nu -\nu _{\mathrm{vib}})t)}}\limits _{\mathrm{Stokes}} -\mathop{\underbrace{\cos (2\pi (\nu +\nu _{\mathrm{vib}})t)}}\limits _{\text{Anti-Stokes}}]}$$

Therefore, for molecules with β ≠ 0, molecular motion leads to sidebands. That is, in order to be Raman active a molecular rotation or vibration must cause a change in a component of the molecular polarizability. The electron motion and response is a primary factor in polarizability, as nuclei might not move much in the short times of applied field oscillations.

6.4 Rotational Raman Spectra

For now, consider only pure rotational interactions for Raman scattering. Two pertinent cases are linear and symmetric top molecules.

6.4.1 Linear Molecules

The energy for a linear molecule is

$$\displaystyle{ F(J) = BJ(J + 1) -\mathop{\underbrace{ DJ^{2}(J + 1)^{2}}}\limits _{\text{neglect for Raman}} }$$

(6.6)

The scattering rotational selection rules for linear rigid rotor molecules are

$$\displaystyle{ \mathbf{Selection\ Rules}\ \ \Delta J = 0,\ +2 }$$

(6.7)

$\Delta J = 0$ :

corresponds to Rayleigh scattering

$\Delta J = +2$ :

corresponds for pure rotations to the S branch; pure rotations cannot have $\Delta J = -2$ since, by definition, $\Delta J = J' - J''$

Why do the selection rules allow transitions with $\Delta J = +2$ instead of + 1? This difference emerges from the symmetry arguments of polarizability (see Banwell [2, p. 105]). The branch associated with increments of 2 in the rotational quantum number J is the S branch (Fig. 6.3). The expression for the transition energy in the S branch as a function of the lower-level value of J (i.e., J″) is given below.

$$\displaystyle\begin{array}{rcl} \Delta E(J)& =& E_{J'} - E_{J''} \\ & =& B[(J + 2)(J + 3) - J(J + 1)] \\ & =& B(4J + 6) \\ S(J)& =& B(4J + 6),\ \ J = 0,1,2,\ldots {}\end{array}$$

(6.8)

Therefore,

$$\displaystyle{\fbox{ $\overline{\nu } = \overline{\nu }_{\mathrm{ex}} \pm B(4J + 6)$}, }$$

(6.9)

where J refers to J″. For anti-Stokes Raman transitions, the photon gains energy (the molecule loses energy), and Eq. (6.9) becomes

$$\displaystyle{ \overline{\nu } = \overline{\nu }_{\mathrm{ex}} + B(4J + 6) }$$

(6.10)

Similarly, the photon loses energy for Stokes Raman transitions, producing

$$\displaystyle{ \overline{\nu } = \overline{\nu }_{\mathrm{ex}} - B(4J + 6) }$$

(6.11)

Fig. 6.3

Sample energy levels for rotational Raman transitions

Figure 6.4 illustrates the equal transition spacings and unequal transition strengths associated with the Stokes and anti-Stokes branches in rotational Raman spectra. Rayleigh scattering, which occurs at $\overline{\nu } = \overline{\nu }_{\mathrm{ex}}$, is shown in the plot as a strong transition halfway between the two branches. Note that IR and μwave inactive molecules, such as N₂ and O₂, have Raman spectra.

Fig. 6.4

Two branches of Raman spectra. Note that the signal strength is proportional to the population of molecules in the initial state (N _J-initial)

Nuclear spin effects alter the rotational Raman spectra in a similar fashion to the rotational absorption spectra discussed earlier.

O₂ :

even J lines are missing

CO₂ :

odd J lines are missing

N₂ :

alternating line intensities 2:1 (even J: odd J)

6.4.2 Symmetric Top Molecules

Recall that the rotational energy for a symmetric top molecule is

$$\displaystyle{ E_{J,K},\mathrm{cm^{-1}} = F(J,K) = BJ(J + 1) + (A - B)K^{2} }$$

(6.12)

The scattering selection rules are:

$$\displaystyle\begin{array}{rcl} \Delta K& =& 0 {}\\ \Delta J& =& 0,+1,+2 {}\\ \end{array}$$

except,

$$\displaystyle{\Delta J = +2\ \text{when}\ K = 0}$$

Molecules with K = 0 are essentially linear, so the selection rule for a linear molecule applies, namely $\Delta J = +2$. The R branch is for transitions in which $\Delta J = 1$ and the S branch is for transitions with $\Delta J = 2$. The transition spacing as a function of J for the two branches is given by the following equations.

R branch::

$\Delta J = 1$, spacing = 2B

$$\displaystyle{ \Delta E_{R} = R(J) = 2B(J + 1)\ \ \ J = 1,2,3,\ldots }$$

(6.13)

S branch::

$\Delta J = 2$, spacing = 4B

$$\displaystyle{ \Delta E_{S} = S(J) = B(4J + 6)\ \ \ J = 0,1,2,\ldots }$$

(6.14)

Applying these two branches for the Stokes and anti-Stokes conditions gives

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{R}& =& \overline{\nu }_{\mathrm{ex}} \pm 2B(J + 1){}\end{array}$$

(6.15)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{S}& =& \overline{\nu }_{\mathrm{ex}} \pm B(4J + 6){}\end{array}$$

(6.16)

where the + sign applies to the anti-Stokes lines and the − sign is for the Stokes lines.

Figure 6.5 shows the alternating intensities in the Stokes and anti-Stokes regimes due to the additive and overlapping nature of the R and S branches. These alternating intensities are evidence of the two branches, and thus, symmetric top structure. The spacing of 4B instead of 2B from the null gap is a clue that the spectra are from Raman transitions, rather than emission or absorption. For spherical tops, all rotational modes are Raman inactive. For asymmetric rotors, all rotational modes are Raman active.

Fig. 6.5

Sample energy levels for symmetric top rotational Raman transitions

6.5 Vibrational Raman Spectra

The Raman-activity of a molecule’s vibrational modes generally follows a pattern. For asymmetric molecules, all vibrational modes are usually Raman-active. For symmetric molecules:

symmetric stretch vibrations::

very strong

asymmetric stretch vibrations::

usually weak (sometimes unobservable)

bending vibrations::

usually weak

The reader may notice that Raman-activity tends to be strong when infrared-activity is weak or non-existent. Because of this, infrared and Raman spectroscopy are often considered complementary. The relationship between infrared- and Raman-activity can be summarized by the Rule of Mutual Exclusion.

Rule of Mutual Exclusion

$\fbox{If a molecule has a center of symmetry, then Raman-active modes are IR-inactive, and vice versa. If no center of symmetry exists, then some modes may be both IR- and Raman-active.}$

For a definition and discussion of the center of symmetry, see Appendix E.

6.5.1 Polarization

Polarization information of Raman-scattered light can help in interpreting spectra and molecular structure.

• 1. symmetric vibration → partially/fully polarized scattering

• 2. asymmetric vibration → depolarized scattering

The usefulness of combining IR and Raman techniques is illustrated in the following example.

Example: N ₂ O

IR and Raman spectra can be used to investigate the symmetry and linearity of N₂O’s molecular structure. For example, using Table 6.3 below can we answer the following questions:

Linearity :

Linear or nonlinear?

Symmetry :

N–N–O or N–O–N?

Table 6.3 Raman and IR spectra information for N₂O

• some bands with only P, R branches → hence a linear molecule

• Raman and IR in the same band → hence no center of symmetry, must be N–N–O

• symmetric modes are polarized → hence the 1285 cm⁻¹ band is the symmetric stretch (ν ₁)

• asymmetric modes are depolarized → hence the 2224 cm⁻¹ band is the asymmetric stretch vibrational mode (ν ₃)

• the 589 cm⁻¹ band has P, Q, and R lines → hence it must be the perpendicular bending mode (ν ₂)

6.5.2 Selection Rules

The selection rules for vibrational Raman spectra permit the following vibrational quantum number change for a harmonic oscillator:

$$\displaystyle{\Delta v = v' - v'' = +1}$$

and for an anharmonic oscillator:

$$\displaystyle{\Delta v = v' - v'' = +1,+2,+3,\ldots }$$

Note that $\Delta v = 0$ corresponds to pure rotational Raman, and that transitions corresponding to changes greater than 1 in the vibrational quantum number v are generally much weaker than for $\Delta v = 1$.

6.5.3 Diatomics

The selection rules for a diatomic harmonic oscillator are

$$\displaystyle\begin{array}{rcl} & & \Delta v = v' - v'' = +1 {}\\ & & \Delta J = J' - J'' = 0,\pm 2 {}\\ \end{array}$$

The changes in rotational quantum number J are what produce the different branches (Fig. 6.6).

$$\displaystyle{\Delta J = \left \{\begin{array}{@{}l@{\quad }l@{}} 0 \quad &\mbox{ corresponds to the $Q$ branch} \\ +2\quad &\mbox{ corresponds to the $S$ branch} \\ -2\quad &\mbox{ corresponds to the $O$ branch} \end{array} \right.}$$

Fig. 6.6

S, Q, and O branches for Stokes and anti-Stokes vibrational and rotational Raman spectra. Note that the signal strength is dependent on the population of molecules in the initial state (N _v-initial)

The general expressions for the transition frequencies in the three branches are

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{Q} = \overline{\nu }_{\mathrm{ex}} \pm \overline{\nu }_{0}\qquad \overline{\nu }_{0} = \omega _{e}(1 - 2x_{e})& &{}\end{array}$$

(6.17)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{S} = \overline{\nu }_{\mathrm{ex}} \pm (\overline{\nu }_{0} + B(4J + 6))\qquad J = 0,1,2,\ldots & &{}\end{array}$$

(6.18)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{O} = \overline{\nu }_{\mathrm{ex}} \pm (\overline{\nu }_{0} - B(4J - 2))\qquad J = 2,3,4,\ldots & &{}\end{array}$$

(6.19)

where J denotes the rotational state in the lower vibrational level. Thus, the anti-Stokes lines are at

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{Q}& =& \overline{\nu }_{\mathrm{ex}} + \overline{\nu }_{0}{}\end{array}$$

(6.20)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{S}& =& \overline{\nu }_{\mathrm{ex}} + \overline{\nu }_{0} + B(4J + 6){}\end{array}$$

(6.21)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{O}& =& \overline{\nu }_{\mathrm{ex}} + \overline{\nu }_{0} - B(4J - 2){}\end{array}$$

(6.22)

and the Stokes lines are at

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{Q}& =& \overline{\nu }_{\mathrm{ex}} -\overline{\nu }_{0}{}\end{array}$$

(6.23)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{S}& =& \overline{\nu }_{\mathrm{ex}} - [\overline{\nu }_{0} + B(4J + 6)]{}\end{array}$$

(6.24)

$$\displaystyle\begin{array}{rcl} \overline{\nu }_{O}& =& \overline{\nu }_{\mathrm{ex}} - [\overline{\nu }_{0} - B(4J - 2)]{}\end{array}$$

(6.25)

6.5.4 Temperature

The ratio of anti-Stokes and Stokes signals can be used for temperature measurements. The anti-Stokes signals are proportional to the initial population in the v = 1 state, while the Stokes signals are proportional to the initial population in the v = 0 vibrational state. This ratio can be related to temperature through the Boltzmann relation for vibrational levels.

$$\displaystyle{\frac{\text{anti-Stokes}} {\text{Stokes}} \propto \frac{N_{v=1}} {N_{v=0}} \rightarrow T}$$

6.5.5 Typical Raman Shift

A typical excitation wavelength is the second harmonic of the output of an Nd:YAG laser,

$$\displaystyle{\lambda _{\mathrm{ex}} = 532\,\text{nm} \rightarrow \overline{\nu }_{\mathrm{ex}} = 18,797\,\mathrm{cm^{-1}}}$$

A representative vibrational frequency of 1880 cm⁻¹  would thus correspond to a Raman shift of 10 % in frequency, shifting the Stokes scattered signal to a longer wavelength, λ = 591 nm, where the light can be readily separated from that at the excitation wavelength. Also, the efficiency of photo-detection at λ = 591 nm can be larger than that at λ = 532 nm.

6.6 Summary of Rayleigh and Raman Scattering

• 1. Raman is complementary to IR and μwave absorption and emission

• 2. Techniques are linear (signal is proportional to I _illum)

• 3. Observable signals made possible by the availability of intense laser sources (high photons/cm² s)

• 4. Rayleigh ≫ Raman and $\sigma _{\mathrm{abs}} \gg \sigma _{\mathrm{Rayleigh}} \gg \sigma _{\mathrm{Raman}}$

• 5. Scattering is instantaneous; fluorescence takes time

• 6. Raman spectrum can be observed in the visible (where detector responsivities are generally high)

• 7. Rayleigh/Raman cross-sections generally scale with 1∕λ ⁴

6.7 Exercises

• 1.

  • (a) Which type of spectroscopy would one observe the pure rotational spectrum of H₂?

  • (b) If the characteristic rotational temperature of H₂, θ _r , is 87.59 K, and it is a rigid rotor, what is the spacing of the lines in the pure rotational spectrum?

  • (c) The spin of the hydrogen nucleus is 1/2. How would that affect your answer to part (b)?

• 2. You are asked to measure the temperature at a point along the centerline of a high-temperature stream of N₂ gas. You elect to infer the temperature from the ratio of the anti-Stokes and Stokes branches of the vibrational Raman spectrum of N₂. A pulsed laser at 500 nm is used to generate the Raman spectrum. Spectral filters are used to separate the anti-Stokes and Stokes signals so that they can be recorded on separate detectors. The individual features of the anti-Stokes and Stokes are not resolved, just the total signal of each branch is recorded. Assume ω _e  = 2354 cm⁻¹ and $\omega _{e}x_{e} = 0$.

  • (a) Calculate the temperature of the gas if the ratio of the anti-Stokes and Stokes signals is 1/e (i.e., 0.368).

  • (b) What is the center wavelength of the anti-Stokes signal?

• 3.

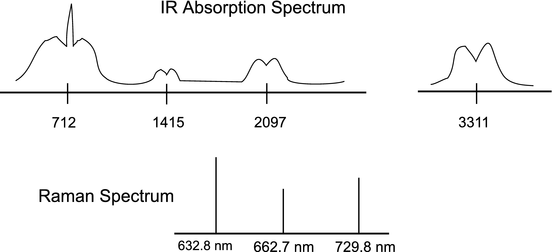
  • (a) A cell contains an unknown gas. Probing of the infrared region has revealed absorption features centered at 712 (VS), 1415 (VW), 2097 (W), and 3311 (S) cm⁻¹, as shown in the sketch below. The first feature can be resolved into three distinct, but unresolved branches, while the others contain only two branches, also unresolved. In addition, Raman scattering from a HeNe laser (632.8 nm) has been measured at 662.7 and 729.8 nm (see sketch). Determine the origin of each of these features and the geometry of the molecule contained in the cell. Try to identify the molecule.

  • (b) Upon further examination, the separation between the tallest peaks of the two outer branches of the 712 cm⁻¹  IR feature has been found to be 93.6 cm⁻¹ at 1000 K. Use this fact to determine the shift in the purely rotational Raman spectrum for the 18th stokes line and the 14th anti-stokes line.

  • (c) A second cell containing another gaseous molecule has qualitatively similar IR and Raman spectra, except the IR absorption bands are now centered at 569, 2630, and 1925 cm⁻¹ and the Raman scattering of the HeNe laser is now found to be at 656.4 and 720.6 nm. Suggest the identity of this new molecule.

  
• 4.

  • (a) A 500 nm laser is used to record the Raman spectrum of CO. Use the following constants for CO: ω _e  = 2000 cm⁻¹, $\omega _{e}x_{e} = 0\,\mathrm{cm^{-1}}$, B _e  = 2 cm⁻¹, and α _e  = 0 cm⁻¹.

    • (i) What is the frequency of the Rayleigh scattering, in cm⁻¹?

    • (ii) What is the frequency (in cm⁻¹) of the Q branch of the anti-Stokes ($\Delta v = 1$) Raman spectrum?

    • (iii) What is the frequency (in cm⁻¹) of the first S branch transition in the anti-Stokes ($\Delta v = 1$) Raman spectrum?

    • (iv) Calculate the frequency of the O(2) line in the same band.

    • (v) What is the frequency (in cm⁻¹) of the Q branch of the anti-Stokes ($\Delta v = 2$) Raman scattering?

  • (b) The above experiment is repeated for O₂ which has a ground state configuration of $X^{3}\Sigma _{g}^{-}$ and the following spectroscopic parameters: $\omega _{e} = 1500\,\mathrm{cm^{-1}}$, $\omega _{e}x_{e} = 15\,\mathrm{cm^{-1}}$, B _e  = 1. 5 cm⁻¹, and α _e  = 0 cm⁻¹.

    • (i) What is the frequency (in cm⁻¹) of the first S branch transition in the anti-Stokes ($\Delta v = 1$) Raman spectrum?

    • (ii) What is the frequency (in cm⁻¹) of the Q branch of the anti-Stokes ($\Delta v = 2$) Raman scattering?