Abstract
The mechanism for electromagnetic radiation to interact with polyatomic molecules is similar to the process discussed previously for diatomics. Molecular vibrations and rotations cause changes in electric dipole moments that occur at resonant frequencies. At these frequencies, molecules can interact with radiation (via emission, absorption, or scattering). The difference is that polyatomic molecules have more rotational and vibrational modes, and each of these modes gives rise to additional possible resonances.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
The mechanism for electromagnetic radiation to interact with polyatomic molecules is similar to the process discussed previously for diatomics. Molecular vibrations and rotations cause changes in electric dipole moments that occur at resonant frequencies. At these frequencies, molecules can interact with radiation (via emission, absorption, or scattering). The difference is that polyatomic molecules have more rotational and vibrational modes, and each of these modes gives rise to additional possible resonances.
This chapter will introduce the fundamental concepts necessary to understand the spectra of various groups of polyatomic molecules. In so doing, we will also present how groups of molecules are classified by their geometry, e.g. linear molecules, symmetric tops, spherical tops, and asymmetric rotors. Similar to our presentation of the material on diatomics, we will first present the aspects of rotational lines and vibrational bands separately before combining them into rovibrational spectra.
4.1 Rotational Spectra of Polyatomic Molecules
A body or molecule is characterized by three principal axes of molecular rotation, about which the three principal moments of inertia, I A , I B , and I C , are defined. These axes pass through the center of mass and are orthogonal to each other (see Fig. 4.1). Molecules are classified in terms of the relative values of I A , I B , and I C . There is more than one convention for assigning the A-axis, but we will say that the A-axis is the “unique” or “figure” axis, along which lies the molecule’s defining symmetry.
4.1.1 Linear Molecules
Linear molecules are those for which all the atoms are “on a line,” including diatomics. The principal moments of inertia are I B = I C and I A ≈ 0, where the A-axis passes through each atom. I A is actually finite, but quantized momentum means that the molecule will remain in the lowest state of rotation about the A-axis, so that effectively, I A = 0. Examples of linear molecules include OCS, HCN, and HC2Cl.
Linear polyatomic molecules must be asymmetric to have a permanent electric dipole moment and resulting rotational spectra. Linear molecules that do not have a permanent dipole moment (i.e., molecules that are both linear and symmetric), such as CO2 and C2H2, are not microwave active. Isotopic substitution in symmetric molecules does not alter bond lengths or charge distributions, and thus does not yield dipole moments.
Linear polyatomics can be treated the same as diatomics, with one value of I. Therefore, the linear polyatomic rotational constant, rotational energy levels, and transition frequencies are the same as for diatomics.
Compared to diatomics, polyatomic molecules typically have a larger moment of inertia, I, and thus have smaller rotational constants, B, and smaller line spacing.
For linear molecules with N atoms, there are N − 1 bond lengths that can be found with spectroscopy. Absorption/emission spectra yield the rotational constant, B, and its associated moment of inertia, I B . Using N − 1 isotopes yields measurements of N − 1 different values for I B ; the resulting N − 1 equations can be solved for the N − 1 bond lengths. Carbon oxysulfide provides one such example (Fig. 4.2).
Example:OCS, Carbon Oxysulfide
There are two bond lengths, r CO, and r CS, which can be determined from the measured moment of inertia I from two isotopes, e.g.
4.1.2 Symmetric Top
Molecules with symmetric top structure are those that have two equivalent moments or inertia, both of which are different from the third moment. Molecules such as boron trichloride (BCl3) and ammonia (NH3) are symmetric tops. The A-axis corresponds to the figure axis of a symmetric top, and thus is also the main axis of symmetry. For symmetric tops, I A ≠ I B = I C , and I A ≠ 0 (Fig. 4.3). Similar to the description for linear molecules, the rotational constants are related to the moments of inertia by
Typically, the equivalent moments of inertia for symmetric top molecules are described simply as I B , and the main axis moment is I A . The relative magnitudes of the inertial moments or rotational constants can be used to further distinguish the tops as Prolate or Oblate:
Prolate: | I A < I B = I C | |
A > B = C | Example: CH3F | |
Oblate: | I A > I B = I C | |
A < B = C | Example: BCl3 |
Since symmetric tops have two main directions of rotation, they have two quantum numbers to describe rotational energy, J and K, where J represents the total angular momentum (0, 1, 2, …), and K represents the angular momentum about the A-axis. There are 2J + 1 possible values of K for each value of J, with K restricted to \(J,J - 1,\ldots,1,0,-1,\ldots,-J\). All non-zero values of K are doubly degenerate since states, that differ only by the sign of K, have different directions of motion but the same energy.
- J :
-
Total angular momentum: 0, 1, 2, …
- K :
-
Angular momentum about the A-axis: \(J,J - 1,\ldots,1,0,-1,\ldots,-J\)
There are 2J + 1 possibilities of K for each J. Positive and negative values of K are allowed, without a change in energy.
As before, the quantized total angular momentum is (see Eq. (2.5))
Here ω i is the rotational angular velocity. In addition, the angular momentum about the A-axis is quantized.
Energy Levels
The energy levels, assuming rigid rotation, from Eqs. (4.5) and (4.6) are given by
which leads, after some algebra, to
Note that the sign of K has no effect on the rotational energy, i.e., the direction of rotation does not affect the rotational energy.
Selection Rules
The selection rules that result from quantum mechanics are:
-
\(\Delta J = +1\) As before for pure rotation
-
\(\Delta K = 0\)
The interpretation is that since there is no dipole moment for rotation about the A-axis, no changes in K will occur with absorption or emission.
Line Positions
The transition frequencies for the polyatomic rigid rotor are
Again, since the line positions are differences in energy levels, they are independent of K for a rigid rotor. K-dependency is introduced for non-rigid rotation.
Non-rigid Rotation
Energy level descriptions for non-rigid rotation include higher-order correction terms with centrifugal distortion constants that are J-dependent (D J ), K-dependent (D K ), and J–K dependent (D JK ).
Note that there are 2J + 1 components (K values) for each total angular momentum quantum number J but only J + 1 frequencies, since − K and K are degenerate. The last two terms in Eq. (4.11) are small except at very high J and K values. The reader should gain some idea of the magnitude of these corrections from the following example.
Example:CH3F, Methyl Fluoride
-
B = 0. 851 cm−1
-
\(D_{J} = 2 \times 10^{-6}\) cm−1
-
\(D_{JK} = 1.47 \times 10^{-5}\) cm−1
4.1.3 Spherical Top
Spherical tops are characterized by three equal moments of inertia.
Molecules such as CH4 are spherically symmetric (Fig. 4.4). There is no permanent electric dipole moment along any of the principal axes; therefore, spherical tops have no rotational spectra.
4.1.4 Asymmetric Rotor
Asymmetric rotors (also known as asymmetric tops) are characterized by three moments of inertia, none of which are equal to each other.
This category is the most complex and will not be addressed here. Examples of asymmetric rotors include H2O and NO2 (Fig. 4.5).
4.1.5 Rotational Partition Function
The classical expressions for polyatomic rotational partition functions are different for the various molecular structures. Linear polyatomics can be treated as diatomics, and thus, from before,
where \(\sigma\) is the molecule-dependent symmetry factor (defined in Sect. 2.2.7) (Table 4.1). For symmetric top molecules, where B = C,
For spherical top molecules, the rotational partition function simplifies even further to
Similarly, for an asymmetric rotor:
4.2 Vibrational Bands of Polyatomic Molecules
Polyatomic molecules have multiple and different vibrational modes depending on their structure and number of atoms. The existence and nature of these modes affect the vibrational bands in the spectra of these molecules.
4.2.1 Number of Vibrational Modes
For polyatomic molecules with N atoms, a total of 3N dynamical coordinates are needed to specify the instantaneous location and orientation of the molecule (i.e., the nuclei). This total corresponds to the sum of coordinates needed to specify the molecular center of mass, the angular rotation of the molecule, and vibrational motion (bond lengths), and hence provides an easy accounting method for identifying the number of vibrational modes, as follows:
- Center of Mass: :
-
requires 3 coordinates (has 3 translational modes)
- Rotation: :
-
2 angular coordinates (hence rotational modes) for linear molecules
3 angular coordinates (rotational modes) for nonlinear molecules
- Vibrations: :
-
the remaining number of vibrational coordinates/ modes is:
3N − 5 for linear molecules
3N − 6 for nonlinear molecules
4.2.2 Parallel and Perpendicular Modes
H2O and CO2 are good examples of triatomic molecules with different vibrational modes. The numbering (i.e., identification) convention for the vibrational modes (and their resultant bands in a spectrum) is based first on symmetry, and second on decreasing energy [1]. That is, ν 1 is the highest-frequency symmetric vibrational mode, ν 2 the next highest symmetric mode, and so on, followed by the asymmetric modes in order of declining frequency. (See [1, p. 272] for an exception to this rule.) There are two types of vibrational modes:
-
1.
Parallel ( ║ ), where the vibrations are those that occur parallel to the main axis of symmetry
-
2.
Perpendicular ( ⊥ ), where the vibrations are those that occur perpendicular to the main axis of symmetry
In order for vibrational motion of a molecule to result in an absorption/emission spectrum, some change must occur in the electric dipole of the molecule during this motion (i.e., a difference must exist in the dipole moment between vibrational quantum states). If this change in dipole occurs along the axis of symmetry of the molecule, the absorption/emission spectrum is termed a “parallel ( ║ ) band,” while if the change in dipole moment occurs perpendicular to the axis of symmetry, a “perpendicular ( ⊥ ) band” will occur. It follows that for a symmetric molecule, such as CO2, the symmetric stretch vibration will not produce a change in dipole moment, and hence there will be no active parallel band for this mode of vibration (see the discussion below).
4.2.2.1 Water, H2O
H2O is a nonlinear triatomic molecule, so it has three vibrational modes. The C 2 notation in Fig. 4.6 means that there is a twofold symmetry of rotation about this axis (which is the unique A-axis of H2O ). The symmetric stretch vibration, known as ν 1 (as it is the highest-frequency symmetric motion), results in a ║ band, as does the symmetric bending vibration, ν 2. The remaining vibrational mode, ν 3, involves asymmetric stretching, and produces dipole variations perpendicular to the axis of symmetry. Hence ν 3 is a ⊥ band.
Carbon Dioxide, CO2
For a linear molecule, such as CO2, there are two stretching modes: symmetric and asymmetric. The stretching and compression of these bonds are illustrated in the following figure with exaggerated amplitude (Fig. 4.7).
Symmetric stretching of carbon dioxide (Fig. 1.6, Banwell)
For the “symmetric stretch” vibrational mode, the two C–O bonds are stretched or compressed simultaneously, preventing formation of a dipole moment. Since the dipole moment remains zero for this mode, no direct light interaction (i.e., absorption or emission) is possible. Thus, the “symmetric stretch” vibration for CO2 is “infra-red inactive.” For anti-symmetric stretching (see Fig. 4.8), one bond is stretched while the other is compressed, giving rise to a changing dipole moment. This vibrational mode is “infra-red active,” and there will be an absorption band at the characteristic frequency of vibration. Since CO2 is a linear triatomic molecule, it has 4 vibrational modes, two of which are degenerate. Only a single absorption band will appear at the degenerate frequency. Hence there are three fundamental frequencies (ν 1, ν 2, and ν 3) as shown in Fig. 4.9.
Interestingly, for symmetric molecules we will find (Chap. 6) that vibrational modes are either IR-active or Raman-active (see Table 4.2) for symmetric molecules.
Ammonia, NH3
A listing of the fundamental vibrational modes of ammonia is given in Table 4.3. Note that ammonia has six vibrational modes, but two (ν 1 and ν 2) are doubly degenerate.
4.2.3 Types of Bands
There are various types of bands that appear in a spectrum; they are all based on the vibrational modes discussed above. The terminology for these different types of bands is as follows:
- Fundamental Bands :
-
ν i , the ith vibrational mode
\(\Delta v = v' - v'' = 1\) for the ith mode
- First Overtone :
-
2ν i
\(\Delta v = v' - v'' = 2\) for the ith mode
- Second Overtone :
-
3ν i
\(\Delta v = v' - v'' = 3\) for the ith mode
- Combination Bands :
-
Changes in multiple quantum numbers, e.g.
- ν 1 + ν 2 :
-
\(\Delta v_{1} = \Delta v_{2} = 1\); i.e. v 1 and v 2 both increase by 1 for absorption or decrease by one for emission.
- 2ν 1 + ν 2 :
-
\(\Delta v_{1} = +2\) and \(\Delta v_{2} = +1\)
- Difference Bands :
-
Quantum number changes with mixed sign
- ν 1 −ν 2 :
-
This means that \(v_{1\mathrm{final}} - v_{1\mathrm{initial}} = \pm 1\) and \(v_{2\mathrm{final}} - v_{2\mathrm{initial}} = \mp 1\), i.e., a unit increase in v 1 is accompanied by a unit decrease in v 2, and vice versa.
4.2.4 Relative Strengths
The fundamental bands are generally much stronger than the combination, difference, and overtone bands. For fairly harmonic molecules such as CO, the difference in relative strengths between the fundamental and overtone bands is approximately two orders of magnitude. However, for very anharmonic molecules such as NH3, the difference between the fundamental and overtone or combination bands is often just one order of magnitude or less. Nearly harmonic molecules have much weaker overtones and combination bands because they closely approximate the SHO model that was presented earlier, namely that overtone bands are forbidden. In reality, these bands are not forbidden, but rather have low transition probabilities (that is, they are nearly forbidden). For highly anharmonic molecules, the bands are much more likely to occur (that is, they are less forbidden because the SHO solutions are bad approximations), and thus have strengths that are closer to the fundamental bands.
Relative Strengths Exception
Accidental degeneracies (i.e., near resonances) can strengthen weak processes: e.g.,
Since the first overtone of the ν 2 band is nearly resonant with the fundamental of the ν 1 band, the two vibrational modes are strongly coupled by radiative and collisional exchanges. This case is called Fermi resonance.
4.2.5 Vibrational Partition Function
For polyatomics whose vibrational potential energy can be approximated by the SHO model [see Eqs. (2.41) and (2.42) and note the choice of zero-point energy], the vibrational partition function, Q vib, can be written as the product of the harmonic partition function for each vibrational mode
where ω e, i is the harmonic frequency of the ith vibrational mode, and g i is the degeneracy of that mode. For example, ammonia’s molecular formula is NH3, and thus it has \(3N - 6 = 6\) possible vibrations. However, two vibrations are degenerate, so the molecule has four different vibrational frequencies (see Table 4.3). Thus, ammonia’s vibrational partition function is
4.3 Rovibrational Spectra of Polyatomic Molecules
4.3.1 Linear Polyatomic Molecules
There are two types of vibrational bands, parallel and perpendicular, defined in terms of the orientation of the electric dipole moment associated with a specific vibrational mode, as discussed in Sect. 4.2.2. Here we limit consideration to fundamental transitions within that mode (i.e., we exclude overtone and combination bands).
Case I: Parallel Bands
There are two types of parallel band vibrations: symmetric and asymmetric stretch. For fundamental transitions, we consider only the vibrational energy stored in mode i and rotational energy.
- Energy :
-
\(T(v_{i},J) = G(v_{i}) + F(J)\)
- Selection Rules :
-
\(\Delta v_{i} = 1\)
\(\Delta J = \pm 1\) (R and P branches)
\(\Delta v_{j} = 0,\ j\neq i\)
- Absorption Spectrum :
-
P and R branches only (see Fig. 2.12)
- Examples :
-
CO2 (ν 3), HCN (ν 1, ν 3)
i.e., the ν 3 mode of CO2 (asymmetric stretch), and the ν 1 (symmetric stretch) and ν 3 (asymmetric stretch) modes of HCN are all parallel bands.
- Note: :
-
The ν 1 mode of CO2 is not IR-active, since symmetric stretching of a symmetric molecule causes no oscillating electric dipole moment. Hence, there is no ν 1 parallel band.
Case II: Perpendicular Bands
- Selection Rules :
-
\(\Delta v_{i} = 1\)
\(\Delta J = \pm 1,\ 0\) (R, P and Q branches)
\(\Delta v_{j} = 0,\ j\neq i\)
-
1.
If B′ = B″, all Q branch lines occur at the same frequency.
-
2.
If B′ ≠ B″, then \(Q(J'') =\omega _{o} + (B' - B'')J''(J'' + 1)\)
Since \(B' - B'' = -\alpha\), the Q branch “degrades” to lower frequencies (i.e., to the “red” in wavelength) (Fig. 4.10).
Table 4.4 summarizes the bands and relative strengths for the moles of HCN.
4.3.2 Symmetric Top Molecules
A symmetric top molecule has two, equal, principal moments of inertia, i.e. I B = I C ≠ I A . Example molecules include CH3F and BCl3. The total energy for symmetric top molecules is simply a summation of the vibrational and rotational energies.
Recall that K is the quantum number for angular momentum around axis A. Again we limit consideration to fundamental transitions within a single vibrational mode i.
Case I: Parallel Bands
- Selection Rules :
-
\(\Delta v_{i} = 1\)
- a. if K ≠ 0:
-
\(\Delta K = 0\), \(\Delta J = \pm 1,\ 0\) (P, Q, R branches)
- b. if K = 0:
-
\(\Delta K = 0\), \(\Delta J = \pm 1\) (no Q-branch), except \(\Delta J = +1\) for J = 0
Since K is the same in the upper and lower states, we have P, Q, and R branches for each value of K. That is to say, there are 2J + 1 values of K (\(K = J,J - 1,\ldots,0,\ldots,-J\)), each of which produces a P, Q, and R branch. The resultant absorption spectrum can become somewhat complex, although the general features are recognizable, as shown in Fig. 4.11. The intensity of the Q branch is a function of (I A /I B ). As (I A /I B ) approaches zero, the symmetric top approaches the structure of a linear molecule, and the strength of the Q branch approaches zero.
The resolved components of a parallel band showing the contributions from each of the K levels of the v = 0 state. The small but discernible splitting evident in the superposed P- and R-branch spectra (bottom row of this figure) is due to a difference in the magnitude of (A − B) in the upper and lower vibrational levels; see Eq. (4.20). The discernible splitting in the superposed Q-branch is due mostly to the difference in B in the upper and lower vibrational levels (B′ < B″, so spectra degrade to lower frequencies)
Referring to Fig. 4.11, the following observations can be made:
-
1.
For K = 0, the spectrum reduces to that of a linear molecule, i.e. there is no Q-branch.
-
2.
For each value of K, the minimum value of J in the P-branch is K + 1, since \(J' = J'' - 1\), and K (unchanged in the transition) cannot exceed J.
Case II: Perpendicular Bands
- Selection Rules :
-
\(\Delta v_{i} = 1\)
\(\Delta J = \pm 1,\ 0\)
\(\Delta K = \pm 1\)
- \(\boldsymbol{R}\) Branch :
-
\(\Delta J = +1,\Delta K = \pm 1\)
\(\overline{\nu }_{R} =\omega _{o} + 2B(J + 1) + (A - B)(1 \pm 2K)\)
- \(\boldsymbol{P}\) Branch :
-
\(\Delta J = -1,\Delta K = \pm 1\)
\(\overline{\nu }_{P} =\omega _{o} - 2BJ + (A - B)(1 \pm 2K)\)
- \(\boldsymbol{Q}\) Branch :
-
\(\Delta J = 0,\Delta K = \pm 1\)
\(\overline{\nu }_{Q} =\omega _{o} + (A - B)(1 \pm 2K)\)
Thus, we have two sets of R, P, and Q branches for each lower-state value of K. The result is generally a very complex spectrum, which is simplest at low temperatures (fewer J levels are populated) and low pressures (individual lines are narrow—more on this in Chap. 8).
An example of the J, K energy levels for a symmetric top molecule and the allowed transitions for a perpendicular band are shown in Fig. 4.12. The complete band can be understood in terms of a summation of sub-bands. These sub-bands consist of all the \(\Delta J = 0,\pm 1\) that occur for a given change in K [1]. A resulting spectrum, decomposed to illustrate the component sub-bands, is given in Fig. 4.13. These two figures are from Barrow [2, pp. 151–152].
The energy levels of a symmetric top molecule showing the transitions that are allowed for a perpendicular band. Figure from Barrow [2, p. 151]
The components of a perpendicular band of a symmetric top molecule. Note that the lines with \(\Delta J = \Delta K\) have greater intensity than those with \(\Delta J = -\Delta K\), i.e., R-branch lines with \(\Delta J = \Delta K = +1\) are stronger than the P-branch lines of \(\Delta J = -1\), when \(\Delta K = +1\). See Herzberg [1, pp. 424–426], for the selection rules that characterize this effect. Figure from Barrow [2, p. 152]
4.4 Exercises
-
1.
List the vibrational modes of the following molecules, and indicate which of the modes are IR active, and/or Raman active? (Note: the molecular structure can be found in [1])
-
(a)
HBr
-
(b)
OCS (linear)
-
(c)
SO2 (bent)
-
(d)
C2H4 (only determine the IR- and Raman-activity of the modes: C–C stretch, C–H symmetric stretch)
-
(a)
-
2.
Calculate the vibrational partition function of CO and CO2 from 300 to 3000 K. Explain the trends and differences you observe.
-
3.
What is the ratio of NH3’s rotational energy for the J = 1, K = 0, and J = 4, K = 0 levels?
-
4.
Absorption spectra of three species (CO2, H2O, and CO) important to combustion and atmospheric science are shown below. By visual inspection of the spectra and knowledge of bond structure, address the following:
-
(a)
How many vibrational modes exist for each species?
-
(b)
What type of absorption spectra are shown (rotational, rovibrational, rovibronic)? Why?
-
(c)
Label the spectra by species name.
-
(d)
Which types of bands exist within each spectra (hint: this should help you with part iii)?
-
(e)
Identify and label the fundamental bands of CO and CO2.
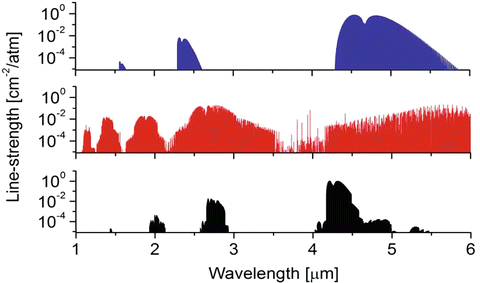
-
(a)
-
5.
A student measured the absorption spectrum (2280–2400 cm−1) of a mixture of 0.2 % CO2 in argon, at 1 atm and 296 K in a gas cell of length 10 cm using an equipment with very poor resolution. The absorption band was known to be centered at 2349 cm−1. Having a strong background in mathematics, this student is able to describe the absorption profile as:
$$\displaystyle{\alpha (\nu ) = \frac{0.93} {1 + 0.005(\nu -2333)^{2}} + \frac{1.5} {1 + 0.0152(\nu -2362)^{2}}}$$where ν is the wavenumber.
-
(a)
Draw the graph of α(ν). Label P, Q, and R branches, if they exist. What are the allowed and forbidden transitions of this band?
-
(b)
Now we will perform a simple calculation of CO2 spectrum based on what we learned in class. Assume a simple harmonic oscillator model. All the transitions are known to be in the CO2 fundamental band with lower-state v″ = 0.
- Step 1::
-
Given the moment of inertia 7. 175 × 10−46 kg m2, calculate the rotational constant B of CO2 and give expressions for the transitions in each branch of the band. What is the highest energy transition of P branch? What is the lowest energy transition of R branch?
- Step 2::
-
The probability of each transition is nearly proportional to the lower-state population, which we assume to be given by a Boltzman distribution with a degeneracy of (2J + 1). Here we approximate the probability as:
$$\displaystyle{\text{transition probability} \propto (2J + 1)\exp \left (\frac{-S(0,J)hc} {kT} \right )}$$where S(0, J) is the energy of the (0, J) state. What is the rotational level that has the maximum transition population, J max? With J max, you can normalize the predicted structure by examining the transition probability ratio. Give the expression for the normalized probability.
- Step 3::
-
Plot the above ratio as a function of wavenumber and compare your calculation with the ratio α(ν)∕α max, where α max is the maximum value of α(ν).
-
(a)
References
G. Herzberg, Molecular Spectra and Molecular Structure, Volume II. Infrared and Raman Spectra of Polyatomic Molecules, 2nd edn. (Krieger Publishing Company, Malabar, FL, 1945)
G.M. Barrow, Introduction to Molecular Spectroscopy, 1st edn. (McGraw-Hill International (UK) Limited, New York, 1962)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hanson, R.K., Spearrin, R.M., Goldenstein, C.S. (2016). Polyatomic Molecular Spectra. In: Spectroscopy and Optical Diagnostics for Gases. Springer, Cham. https://doi.org/10.1007/978-3-319-23252-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-23252-2_4
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-23251-5
Online ISBN: 978-3-319-23252-2
eBook Packages: EngineeringEngineering (R0)















