The SIR Model and Identification of Spreaders

Abstract

In this chapter, we review the classic susceptible-infected-recovered (SIR) model for disease spread as applied to a social network. In particular, we look at the problem of identifying nodes that are “spreaders” which cause a large part of the population to become infected under this model. To do so, we survey a variety of nodal measures based on centrality (degree, betweenness, etc.) and other methods (shell decomposition, nearest neighbor analysis, etc.). We then present a set of experiments that illustrate the relation of these nodal measures to spreading under the SIR model.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

In this chapter, we study one of the most ubiquitous diffusion models: the susceptible-infected-recovered (SIR) model. Considering a network structure, a key problem relating to SIR model is how to identify the nodes that, if initially infected, will result in the greatest expected infected population. These nodes are often referred to as “spreaders”. Unfortunately, exactly computing the expected number of infected individuals in a network-structured population given a single initial infectee is # P-hard (we shall discuss this complexity result further in Chap. 4). This implies that solving this problem exactly is likely beyond the ability of today’s computer systems. However, the literature on complex networks has provided various nodal measures that can be used as heuristics. In this chapter, we review various nodal measures and examine the utility of these measures as heuristics to find spreaders under the SIR model. These experiments show that the ability of nodal measures to identify spreaders in the SIR Model.

With these experiments, we carefully selected the parameter β based on β′, the epidemic threshold of the network. We can be sure that a contagion can spread to a significant portion of the network for β > β′, and we studied a variety of different values for β above this threshold.

The rest of this chapter is organized as follows. In Sect. 2.2, we review the SIR model and describe how we calculate the epidemic threshold of a given complex network. This is followed by a review of the various centrality and other nodal measures we will study in Sect. 2.3 along with a recap of the description of the “imprecision function” [17] used to measure the effectiveness of a nodal measure in identifying the top spreaders in a network. We give a description and discussion of the experimental results in Sect. 2.4.

2.2 The SIR Model

As in [17], we consider the classic susceptible-infected-recovered (SIR) model of disease spread introduced in [2]. In this model, all nodes in the network are in one of three states: susceptible (able to be infected), infected, or recovered (no longer able to infect or be infected). At each time step, only node infected in the last time step can infect any of its neighbors who are in a susceptible state with a probability β. After that time step, the node previously in an infected state moves into a recovered state and is no longer able to infect or be infected.

2.2.1 Selecting the Infection Probability

We note that for scale-free networks, having degree distribution P(k) ∼ k ^−γ, the literature shows that for γ ≤ 3, the epidemic threshold of β approaches 0 as the number of nodes goes to infinity [10, 14]. However, the networks we examine are of finite size and have various levels of “scale-freeness”, based on the R ² value of the linear correlation of a log-log plot of the degree distribution (see Sect. 2.4.1 for details). Instead, we explored β values based on the epidemic threshold calculation in [20]. Using this method, the SIR model is mapped onto a bond percolation process. Assuming a randomly connected network, the average number of influenced neighbors, $\langle n\rangle$ can be written

$$\displaystyle{ \langle n\rangle =\beta \cdot \sum \limits _{k}\frac{P(k) \cdot k \cdot (k - 1)} {\langle k\rangle }, }$$

(2.1)

where k is the degree of a node, P(k) is the probability of a node having degree k, and $\langle k\rangle$ is the average degree. Since an epidemic state can only be reached when $\langle n\rangle> 1$, and from (2.1) we have

$$\displaystyle{ \beta> \left (\sum \limits _{k}\frac{P(k) \cdot k \cdot (k - 1)} {\langle k\rangle } \right )^{-1} =\beta '. }$$

(2.2)

We note that there is some work discussing the effect of different infection probabilities on spreading in [17] and more recent and comprehensive study on the topic in [12]. These works consider the effect of this parameter with respect to degree and shell decomposition (and betweenness in [17]). Here we consider these and many other nodal measures, and find that some of them, such as eigenvector centrality, outperform those in these previous works.

2.3 Centrality and Other Nodal Measures

We now describe the centrality measures that we examine in our experiments. We note that the major centrality measures in the literature can be classified as either radial (the quantity of certain paths originating from the node) or medial (the quantity of certain paths passing through the node) as done in Borgatti and Everett [6]. Based on the negative result concerning betweenness of Kitsak et al. [17] and the intuitive association between high-radial nodes and spreading, we focused our efforts on radial measures. While the work of Kitsak et al. [17] compares shell number to degree and betweenness, we consider several other well-known radial measures in addition to degree, including closeness and eigenvector centrality. As done in [17], we also develop “imprecision functions” for these centrality measures.

2.3.1 Degree Centrality

Of all the measures that we are examining, degree is perhaps the most simplistic measure—simply the total of incident edges for a given node. As noted throughout the literature, such as [24], it is perhaps the easiest centrality measure to compute. Further, in other diffusion processes, such as the voter model on undirected networks in [1], it has been shown to be proportional to the expected number of individuals becoming infected¹ (we discuss these results in detail in Chap. 6). As pointed out in [6], degree is a radial measure as it is the number of paths starting from a node of length 1. Degree is one of three measures considered in [17].

2.3.2 Shell Number

The other radial measure considered in [17], shell number, or “k-shell number”, is determined using shell decomposition [23]. High shell-number nodes in the network are often referred to as the “core” and are regarded by Kitsak et al. [17] as influential spreaders under the SIR model. Our results described later in this chapter confirm this finding, although we also show that shell number was generally outperformed by eigenvector centrality. There have also been some more practical applications of this technique to find key nodes in a network. For instance, Borge-Holthoefer and Moreno [7, 8] uses shell-decomposition to find individuals likely to initiate information cascades in an online social network while [11] uses it to identify key nodes in a subset of autonomous systems on the Internet.

An example of this process is shown in Fig. 2.1. Given graph G = (V, E), shell decomposition partitions a graph into shells and is described in the algorithm below.

Fig. 2.1

Consider the progression of the graph above, where the elimination of nodes with degree 1 occurs in B and C. D represents the first iteration for the second shell, and E represents the complete second shell (as well as the first). F finalizes the decomposition with the third shell

2.3.3 Betweenness Centrality

The intuition behind high betweenness centrality nodes is that they function as “bottlenecks” as many paths in the network pass through them. Hence, betweenness is a medial centrality measure. Let σ _st be the number of shortest paths between nodes s and t and σ _st (v) be the number of shortest paths between s and t containing node v. In [15], betweenness centrality for node v is defined as $\sum _{s\neq v\neq t}\frac{\sigma _{st}(v)} {\sigma _{st}}$. In most implementations, including the ones used in this chapter, the algorithm of Brandes [9] is used to calculate betweenness centrality.

2.3.4 Closeness Centrality

Another common measure from the literature that we examined is closeness [16]. Given node i, its closeness C _c (i) is the inverse of the average shortest path length from node i to all other nodes in the graph. Intuitively, closeness measures how “close” it is to all other nodes in a graph.

Formally, if we define the shortest path between nodes i to j as function d _G (i, j), we can express the average path length from i to all other nodes as

$$\displaystyle{ L_{i} = \frac{\sum _{j\in V \setminus i}d_{G}(i,j)} {\vert V \vert - 1}. }$$

(2.3)

Hence, the closeness of a node can be formally written as

$$\displaystyle{ C_{c}(i) = \frac{1} {L_{i}} = \frac{\vert V \vert - 1} {\sum _{j\in V \setminus i}d_{G}(i,j)}. }$$

(2.4)

2.3.5 Eigenvector Centrality

The use of the principle eigenvector of the adjacency matrix of a network was first proposed as a centrality measure in [5]. Hence, the intuition behind eigenvector centrality is that it measures the influence of a node based on the sum of the influences of its adjacent nodes. Given a network V = (G, E) with adjacency matrix A = (a _ij ), where a _ij  = 1 if an edge exists between nodes i and j, the eigenvector centrality of node i satisfies

$$\displaystyle{ x_{i} = \frac{1} {\lambda } \sum \limits _{j\in V }a_{ij}x_{j}, }$$

(2.5)

for some λ. If we define x to be the vector of x _i ’s, this relationship can be expressed as

$$\displaystyle\begin{array}{rcl} x = \frac{1} {\lambda } Ax,\,\text{ or }\,\,Ax =\lambda x,& &{}\end{array}$$

(2.6)

which is the familiar equation relating A with its eigenvalues and eigenvector. The eigenvector centralities for the network are the entries of the eigenvector corresponding to the largest real eigenvalue.

2.3.6 PageRank

PageRank, introduced in [22], is computed for each node based on the PageRank of its neighbors. Where E is the set of undirected edges, R _v , d _v is the PageRank and degree of v, and c is a normalization constant, we have the relationship

$$\displaystyle{R_{v} = c \cdot \sum _{v'\vert (v,v')\in E}\frac{R_{v'}} {d_{v'}}.}$$

An initial value for rank is entered for each node and the relationship is then computed iteratively until convergence is reached. Intuitively, PageRank can be thought of as the importance of a node based on the importance of its neighbors.

2.3.7 Neighborhood

The next nodal measure we consider is the “neighborhood.” Given a natural number q, the q-neighborhood of vertex i is the number of nodes in the network that are distance q or closer from node i. For example, for q = 0, this metric is 1 for every node. For q = 1, this metric is identical to degree centrality of node i, since it is the number of nodes within a distance 1 of i. For q = 2, this metric counts the number of nodes within a distance 2 of i, so it counts i’s neighbors along with its neighbors’ neighbors. In our work, we computed neighborhoods using q = 2, 3, 5, 10, and denoted these measures by nghd2, nghd3, nghd5, and nghd10, respectively. We note that the work of Chen et al. [13] develops a centrality measure with a similar intuition to the neighborhood and show it performs well in identifying influential spreaders.

2.3.8 The Imprecision Functions

We now define the imprecision functions from [17] that are used to measure the effectiveness of a nodal measure in identifying influential spreaders. We also extend their definition for all nodal measures explored in this chapter. Let N denote the number of nodes, and let p be a real number between 0 and 100. The pN∕100 highest efficiency spreaders, Υ _eff (p), are chosen based on number of nodes infected M _i per node. Similarly, a set $\varUpsilon _{k_{s}}(p)$ is defined as the pN∕100 predicted most efficient spreaders, chosen with priority to highest k _s valued nodes. Let

$$\displaystyle\begin{array}{rcl} M_{eff}(p) =\sum \limits _{i\in \varUpsilon _{eff}(p)}\frac{M_{i}} {pN},\mathit{and}& &{}\end{array}$$

(2.7)

$$\displaystyle\begin{array}{rcl} M_{k_{s}}(p) =\sum \limits _{i\in \varUpsilon _{k_{ s}}(p)}\frac{M_{i}} {pN}.& &{}\end{array}$$

(2.8)

The imprecision function of k _s , $\epsilon _{k_{s}}(p)$, is defined as

$$\displaystyle{ \epsilon _{k_{s}}(p) = 1 - \frac{M_{k_{s}}(p)} {M_{eff}(p)} }$$

(2.9)

Similarly, ε _eig (p) and ε _deg (p) are defined as

$$\displaystyle\begin{array}{rcl} \epsilon _{eig}(p) = 1 - \frac{M_{eig}(p)} {M_{eff}(p)},& &{}\end{array}$$

(2.10)

$$\displaystyle\begin{array}{rcl} \epsilon _{deg}(p) = 1 - \frac{M_{deg}(p)} {M_{eff}(p)}& &{}\end{array}$$

(2.11)

In general, for any nodal measure c, the imprecision function ε _c (p) is defined as

$$\displaystyle{ \epsilon _{c}(p) = 1 - \frac{M_{c}(p)} {M_{eff}(p)} }$$

(2.12)

2.4 Experimental Findings

In this section, we will briefly recap some of our previous experiments involving the identification of spreaders under the SIR model using nodal measures. Please refer to [3] for the complete technical report.

2.4.1 Datasets

We obtained our datasets from a variety of sources. Brief descriptions of these networks are as follows:

• cond-mat-GCC is an academic collaboration network from the e-print arXiv and covers scientific collaborations between authors’ papers submitted to Condensed Matter category from 1999 [21].

• ca-GrQc-GCC is an academic collaboration network from the e-print arXiv and covers scientific collaborations between authors’ papers submitted to the General Relativity and Quantum Cosmology category from Jan. 1993 to Apr. 2003 [18].

• urv-email is an e-mail network based on communications of members of the University Rovira i Virgili (Tarragona) [4]. It was extracted in 2003.

• 1-edges-GCC is a network formed from YouTube, the video-sharing website that allows users to establish friendship links [25]. The sample was extracted in Dec. 2008. Links represent two individuals sharing one or more subscriptions to channels on YouTube.

• std-GCC is an online sex community in Brazil in which links represent that one of the individuals posted online about a sexual experience with the other individual, resulting in a bipartite graph. The data was extracted from September of 2002 to October of 2008 [19].

• as20000102 is a one day snapshot of Internet routers as constructed from the border gateway protocol logs [18]. It was extracted on Jan 2nd, 2000.

• oregon_010331 is a network of Internet routers over a one week period as inferred from Oregon route-views, looking glass data, and routing registry from covering the week of March 3rd, 2001 [18].

• ca-HepTh-GCC is a collaboration network from the e-print arXiv and covers scientific collaborations between authors’ papers submitted to the High Energy Physics—Theory category. It covers paper from Jan 1993 to Apr 2003 [18].

• as-22July06 is a snapshot of the Internet on 22 July 2006 at the autonomous systems level compiled by Mark Newman [21].

• netscience-GCC is a network of coauthorship of scientists working on network theory and experiments compiled by Mark Newman in May 2006 [21].

All datasets used for this chapter were obtained from one of four sources: the ASU Social Computing Data Repository [25], the Stanford Network Analysis Project [18], Mark Newman’s data repository at the University of Michigan [21], and Universitat Rovira i Virgili [4]. All networks considered were symmetric; i.e., if a directed edge from vertex v to v′ exists, there is also an edge from vertex v′ to v. Summary statistics for these networks can be found in Table 2.1.

Table 2.1 Network summary statistics

In the cases where the network had more than one connected component, we used only the greatest one. We append the suffix “-GCC” when referring to those networks. For example, the cond-mat network had more than one component, so we will use the greatest connected component and refer to this network as “cond-mat-GCC”.

As seen in the Table 2.1, all networks used are approximately scale free. This does not infer that they were generated using a preferential attachment model, as many mechanisms can be responsible for generating scale free networks. If they were generated using a preferential attachment model then we would see a correlation between shell number and degree. This would also mean that degree centrality and shell number would have little difference in predicting spreaders, but our simulations show otherwise. Figure 2.2 shows an example in which degree and shell number are not correlated.

Fig. 2.2

In the higher shells of these two examples, degree and shell number are not correlated, indicating these can not be assumed to be generated by preferential attachment models. The red line shows the average degree of each shell. Note that log scales are being used on both axes

2.4.2 Sensitivity to β

The experiments revealed that (1) the relative performance of degree, shell number and other nodal measures can depend on the β parameter of the SIR model, and (2) eigenvector centrality performs very well in general regardless of the value of β used, typically outperforming all of the other measures that we tried. Here we present more results illustrating these two points. Unless otherwise specified, the β values that we used when plotting the imprecision function versus β are 1. 1β′, 1. 2β′, …, 2. 0β′, where β′ is the epidemic threshold for the network in question.

In Fig. 2.3a, b, we give an example of a network where shell number outperforms degree for one value of β, but degree outperforms shell number for another value of β. In Sect. 2.4, we give additional examples illustrating that the imprecision functions of other measures, as well as the choice of the “best” nodal measure, can be sensitive to β as well.

Fig. 2.3

Imprecision plots vs. p for the cond-mat network with different β. (a) Imprecision versus p for the cond-mat network with β = 11. 17. Notice that for this β, k-shell has a lower imprecision, meaning that shell number outperforms degree. See Sect. 2.3 for the definitions of imprecision function and p. (b) Imprecision plots vs. p for the cond-mat network with β = 15. 95. Notice that for this β, degree has a lower imprecision, meaning that degree outperforms shell number, the opposite of what we saw in Fig. 2.3a

Figure 2.3a, b show that the performance of degree relative to shell number changes with β for the cond-mat network. For β = 11. 17, shell number is a better indicator of spreading, but for β = 15. 95, degree is better. Another way that we could depict this dependence on β is to fix p and plot the imprecision versus β, instead of fixing β and plotting the imprecision versus p. In Fig. 2.4a, we fix p = 5 and plot the imprecision function of degree, shell number, and eigenvector centrality versus β, for β between 11. 17 and 15. 95. As it shows, degree outperforms shell number after β gets large enough.

Fig. 2.4

Imprecision vs. β for the cond-mat network and ca-GrQc-GCC network. (a) Imprecision vs. β for the cond-mat network. The relative performance of degree and shell number changes near β = 14. (b) Imprecision vs. β for the ca-GrQc-GCC network

The relative performance of other centrality measures can change as well. In Fig. 2.4b, we plot the imprecision functions of degree, shell number, eigenvector, and closeness centrality versus β for p = 5.

In this network, for β near β′, degree and shell number perform very well. However, as β increases, the imprecision functions of those measures increase, and other measures, like closeness and eigenvector, outperform degree and shell number.

2.4.3 Eigenvector Centrality for Spreader Identification

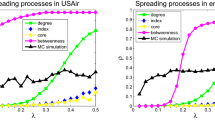
The experiments show that eigenvector centrality consistently outperforms all other measures considered, including both shell number and degree (which were considered by Kitsak et al.), in all but one of the networks examined. See Fig. 2.5 for a comparison of shell number (the best performing measure of Kitsak et al.) with eigenvector centrality. Also, if we average over all of our networks, including the one where eigenvector was not the best, we find that, on average, eigenvector centrality outperforms the other measures.

Fig. 2.5

Imprecision of k-shell minus the imprecision of eigenvector centrality. Positive values indicate that shell number has a higher imprecision than eigenvector centrality, which means that eigenvector centrality typically outperforms shell number

As we saw in Fig. 2.5, eigenvector centrality outperforms shell number for all but one of the networks we examined. Eigenvector centrality also typically outperforms all of the other measures that we tried. In Fig. 2.6a, we plot the imprecision functions of several different measures for the cond-mat network. We see that eigenvector centrality performs best for this network. In Figs. 2.6b and 2.7a–c, we give examples of a collaboration network, an online network, a STD network and an email network in which eigenvector performs best.

Fig. 2.6

Imprecision vs. p for the cond-mat-GCC network and netscience-GCC network. (a) Imprecision vs. p for the cond-mat-GCC network with $\beta = 1.1\beta ' = 8.77$. We see that eigenvalue centrality performs best for this network. (b) Imprecision vs. p for the netscience-GCC network with $\beta = 1.1\beta ' = 15.67$. We see that eigenvalue centrality performs best for this network

Fig. 2.7

Imprecision vs. p for 1-edges-GCC, std-GCC and urv-email network. (a) Imprecision vs. p for the 1-edges-GCC network with $\beta = 1.1\beta ' = 2.50$. We see that eigenvalue centrality performs best for this network. (b) Imprecision vs. p for the std-GCC network with $\beta = 1.1\beta ' = 4.01$. We see that eigenvalue centrality performs best for this network. (c) Imprecision vs. p for the urv-email network with $\beta = 1.1\beta ' = 6.22$. We see that eigenvalue centrality performs best for this network

Eigenvector centrality does not outperform shell number for the ca-HepTh network, so we can not conclude that eigenvector centrality performs best for every network that we tried. However, it does seem that, on average, for the networks we considered, eigenvector centrality performs best for $\beta = 1.1\beta ',1.2\beta ',\ldots,2.0\beta '.$ Suppose we take the imprecision functions for β = 1. 1β′ for each network, and we average these imprecision functions over all of our networks, including the ca-HepTh network. This would be one way to check how well each measure performs on average. In Fig. 2.8, we plot this the average imprecision versus p for β = 1. 1β′. We see that, on average, eigenvector centrality outperforms the other measures. The measure nghd2 performs well also. We show similar results for β = 1. 5β′ and β = 2. 0β′ in Fig. 2.9a, b. In both cases, eigenvector centrality outperforms all of the other measures.

Fig. 2.8

Average imprecision vs. p with β = 1. 1β′, where the average is taken over all networks that we considered

Fig. 2.9

Average imprecision vs. p with different β. (a) Average imprecision vs. p with β = 1. 5β′, where the average is taken over all networks that we considered. We see that, on average, eigenvector performs best. (b) Average imprecision vs. p with β = 2. 0β′, where the average is taken over all networks that we considered. We see that, on average, eigenvector performs best. (c) Average imprecision vs. p with β = 5β′, where the average is taken over all networks that we considered. We see that, on average, eigenvector performs best

We believe that eigenvector centrality performs well for some of the same reasons that shell number performs well. A node has high eigenvector centrality when the node and its neighbors have high degree. Nghd2, nghd3, and the closely related measure of Chen et al. [13] also perform well for this reason. A hub, or a node with high degree, in the periphery of a network, which does not have many neighbors with high degree, will not typically be as good of a spreader as a node with high eigenvector centrality.

2.4.4 Large Values of β

In [17], only relatively small values for β were explored as it was noted that larger values of β would likely cause spreading to a large portion of the population regardless of the location of the initially infected node. However, in the networks we studied, we found a difference in the ability of the starting node to spread even at seven times the epidemic threshold. Further, the result that eigenvector centrality performs best, based on average imprecision over all the networks, still holds for these large values of β. We display our imprecision functions for large values of β in Fig. 2.10. We also show that for five times the epidemic threshold, eigenvector centrality still outperforms the other centrality measures for different values of p (Fig. 2.9c).

Fig. 2.10

Average imprecision vs. β with p = 5. We see that, on average, eigenvector performs best

2.5 Conclusions

In this chapter we studied the SIR model and looked at identifying nodes that cause diffusion to spread to a large extent based on various nodal measures. However, we made two assumptions—that the infection probability was the same amongst all edges and that we only looked for single “spreaders”. In the Chap. 4, we make efforts to find sets of nodes and extend the model to allow for different infection probabilities amongst the edges.