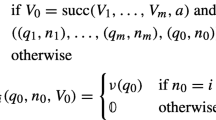On the Disambiguation of Weighted Automata

Abstract

We present a disambiguation algorithm for weighted automata. The algorithm admits two main stages: a pre-disambiguation stage followed by a transition removal stage. We give a detailed description of the algorithm and the proof of its correctness. The algorithm is not applicable to all weighted automata but we prove sufficient conditions for its applicability in the case of the tropical semiring by introducing the weak twins property. In particular, the algorithm can be used with all acyclic weighted automata and more generally any determinizable weighted automata. While disambiguation can sometimes be achieved using determinization, our disambiguation algorithm in some cases can return a result that is exponentially smaller than any equivalent deterministic automaton. We also present some empirical evidence of the space benefits of disambiguation over determinization in speech recognition and machine translation applications.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Weighted finite automata and transducers are widely used in applications. Most modern speech recognition systems used for hand-held devices or spoken-dialog applications use weighted automata and their corresponding algorithms for the representation of their models and their efficient combination and search [2, 18]. Similarly, weighted automata are commonly used for a variety of tasks in machine translation [9] and other natural language processing applications [10], computational biology [6], image processing [1], optical character recognition [5], and many other areas.

A problem that arises in several applications is that of disambiguation of weighted automata: given an input weighted automaton, the problem consists of computing an equivalent weighted automaton that is unambiguous, that is one with no two accepting paths labeled with the same string. The need for disambiguation is often motivated by the computation of the marginals given a weighted transducer, or the common problem of determining the most probable string or more generally the n most likely strings, $n \ge 1$, of a lattice, an acyclic weighted automaton generated by a complex model, such as those used in machine translation, speech recognition, information extraction, and many other natural language processing and computational biology systems. A lattice compactly represents the model’s most likely hypotheses. It defines a probability distribution over the strings and is used as follows: the weight of an accepting path is obtained by multiplying the weights of its component transitions and the weight of a string obtained by summing up the weights of accepting paths labeled with that string. In general, there may be many accepting paths labeled with a given string. Clearly, if the lattice were unambiguous, a standard shortest-paths or n-shortest-paths algorithm [8] could be used to efficiently determine the n most likely strings. When the lattice is not unambiguous, the problem is more complex and can be solved using weighted determinization [19]. An alternative solution, which we will show has benefits, consists of first finding an unambiguous weighted automaton equivalent to the lattice and then running an n-shortest-paths algorithm on the resulting weighted automaton.

In general, one way to determine an equivalent unambiguous weighted automaton is to use the weighted determinization algorithm [16]. This, however, admits several drawbacks. First, weighted determinization cannot be applied to all weighted automata. This is both because not all weighted automata admit an equivalent deterministic weighted automaton but also because even for some that do, the weighted determinization algorithm may not halt. Sufficient conditions for the application of the algorithm have been given [3, 16]. In particular the algorithm can be applied to all acyclic weighted automata. Nevertheless, a second issue is that in some cases where weighted determinization can be used, the size of the resulting deterministic automaton is prohibitively large.

This paper presents a new disambiguation algorithm for weighted automata extending to the weighted case the algorithm of [17] – the weighted case is significantly more complex and this extension non-trivial. As we shall see, our disambiguation algorithm applies to a broader family of weighted automata than determinization: we show that, for the tropical semiring, if a weighted automaton can be determinized using the algorithm of [16], then it can also be disambiguated using the algorithm presented in this paper. Furthermore, for some weighted automata, the size of the unambiguous weighted automaton returned by our algorithm is exponentially smaller than that of any equivalent deterministic weighted automata. In particular, our algorithm leaves the input unchanged if it is unambiguous, while the size of the automaton returned by determinization for some unambiguous weighted automata is exponentially larger. We also present empirical evidence that shows the benefits of weighted disambiguation over determinization in applications. Our algorithm applies in particular to unweighted finite automata. Note that it is known that for some non-deterministic finite automata of size n the size of an equivalent unambiguous automaton is at least $\varOmega (2^{\sqrt{n}})$ [22], which gives a lower bound on the time and space complexity of any disambiguation algorithm for finite automata.

Our disambiguation algorithm for weighted automata is presented in a general way and for a broad class of semirings. Nevertheless, the algorithm is limited in several ways. First, not all weighted automata admit an equivalent unambiguous weighted automaton. But, even for some that do, our algorithm may not succeed. The situation is thus similar to that of weighted determinization. However, we present sufficient conditions based on a new notion of weak twins property under which our algorithm can be used. In particular, our algorithm applies to all acyclic weighted automata and more generally to all determinizable weighted automata. Our algorithm admits two stages. The first stage called pre-disambiguation constructs a weighted automaton with several key properties, including the property that paths leaving the initial state and labeled with the same string have the same weight. The second stage consists of removing some transitions to make the result unambiguous. Our disambiguation algorithm can be applied whenever pre-disambiguation terminates.

We refer to [17] for an extensive discussion of disambiguation algorithms for unweighted automata and finite-state transducers, in particular the algorithm of Schützenberger. In the weighted case, we already mentioned and discussed weighted determinization [16] as a possible disambiguation algorithm in some cases. A procedure was described by [14] for the special case of the disambiguation of finitely ambiguous min-plus automata, which is a straightforward application of Schützenberger’s algorithm for the disambiguation of functional transducers. That procedure does not extend to the general case of weighted automata we are considering because in the general case, the removal of transitions causing ambiguity cannot be executed correctly in that way.¹ An alternative procedure was also described by [13][pp. 598–599] for constructing an unambiguous weighted automaton (when it exists) in the specific case of polynomially ambiguous min-plus weighted automata. The construction is rather intricate and further relies on the prior determination of a threshold value Y. The authors do not give an explicit algorithm for computing Y but state that it can be inferred from [13, Proposition 5.1]. However, the corresponding procedure seems intractable. In fact, as indicated by the authors, the cost of determining Y using that property is super-exponential. The authors of [13] do not give the running-time complexity of their procedure and do not detail various aspects, which makes a comparison difficult. But, our algorithm is much simpler and seems to be significantly more efficient. Our algorithm is also more general since it applies in particular to weighted automata over the tropical semirings that verify the weak twins property and that may be exponentially ambiguous. It is also given for a broader family of semirings. While we are not presenting guarantees for its applicability for semirings different from the tropical semiring, its applicability for at least acyclic weighted automata for those semirings is clear. One advantage of the procedures described by [13] is that the existence of an unambiguous weighted automaton is first tested, though that test procedure appears also to be very costly. Finally, let us mention that an algorithm of Eilenberg [7] bears the same name, disambiguation, but it is in fact designed for an entirely different problem.

The paper is organized as follows. In Sect. 2, we introduce some preliminary definitions and notation relevant to the description of our algorithm. Section 3 describes our pre-disambiguation algorithm and proves some key properties of its result. We describe in fact a family of pre-disambiguation algorithms parameterized by a relation R over the set of pairs of states. A simple instance of that relation is for two states to be equivalent when they admit a path labeled by the same string leading to a final state. In Sect. 4, we describe the second stage, which consists of transition removal, and prove the correctness of our disambiguation algorithm. In Sect. 5, we introduce the notion of weak twins property which we use to prove the sufficient conditions for the application of pre-disambiguation and thus the full disambiguation algorithm. The proofs for this section are given in the case of weighted automata over the tropical semiring. Finally, in Sect. 6, we present experiments that compare weighted disambiguation to determinization in speech recognition and machine translation applications. Our implementation of these algorithms used in these experiments is available through a freely available OpenFst library [4]. Detailed proofs for most of our results are given in the [20].

2 Preliminaries

Given an alphabet $\varSigma$, we will denote by |x| the length of a string $x \in \varSigma ^*$ and by $\epsilon$ the empty string for which $|\epsilon | = 0$.

The weighted automata we consider are defined over a broad class of semirings. A semiring is a system $(\mathbb {S}, \oplus , \otimes , \overline{0}, \overline{1})$ where $(\mathbb {S}, \oplus , \overline{0})$ is a commutative monoid with $\overline{0}$ as the identity element for $\oplus$, $(\mathbb {S}, \otimes , \overline{1})$ is a monoid with $\overline{1}$ as the identity element for $\otimes$, $\otimes$ distributes over $\oplus$, and $\overline{0}$ is an annihilator for $\otimes$.

A semiring is said to be commutative when $\otimes$ is commutative. Some familiar examples of (commutative) semirings are the tropical semiring $(\mathbb {R}_+ \!\cup \! \{+\infty \}, \min , +, +\infty , 0)$ or the semiring of non-negative integers $(\mathbb {N}, +, \times , 0, 1)$. The multiplicative operation of a semiring $(\mathbb {S}, \oplus , \otimes , \overline{0}, \overline{1})$ is said to be cancellative if for any x, $x'$ and z in $\mathbb {S}$ with $z \ne \overline{0}$, $x \otimes z = x' \otimes z$ implies $x = x'$. When that property holds, the semiring $(\mathbb {S}, \oplus , \otimes , \overline{0}, \overline{1})$ is also said to be cancellative.

A semiring $(\mathbb {S}, \oplus , \otimes , \overline{0}, \overline{1})$ is said to be left divisible if any element $x \in \mathbb {S}-\{ {\overline{0}} \}$ admits a left inverse $x' \in \mathbb {S}$, that is $x' \otimes x = \overline{1}$. $(\mathbb {S}, \oplus , \otimes , \overline{0}, \overline{1})$ is said to be weakly left divisible if for any x and $x'$ in $\mathbb {S}$ such that $x \oplus x' \ne \overline{0}$, there exists at least one z such that $x = (x \oplus x') \otimes z$. When the $\otimes$ operation is cancellative, z is unique and we can then write: $z = (x \oplus x')^{-1} \otimes x$.

Weighted finite automata (WFAs) are automata in which the transitions are labeled with weights in addition to the usual alphabet symbols which are elements of a semiring [15]. A WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$ over $\mathbb {S}$ is a 7-tuple where: $\varSigma$ is the finite alphabet of the automaton, Q is a finite set of states, $I \subseteq Q$ the set of initial states, $F \subseteq Q$ the set of final states, E a finite multiset of transitions which are elements of $Q \times \varSigma \times \mathbb {S}\times Q$, $\lambda {:}I \rightarrow \mathbb {S}$ an initial weight function, and $\rho {:}F \rightarrow \mathbb {S}$ the final weight function mapping F to $\mathbb {S}$.

A path $\pi$ of a WFA is an element of $E^*$ with consecutive transitions. We denote by ${{\mathrm{orig}}}[\pi ]$ the origin state and by ${{\mathrm{dest}}}[\pi ]$ the destination state of the path. A path is said to be accepting or successful when ${{\mathrm{orig}}}[\pi ] \in I$ and ${{\mathrm{dest}}}[\pi ] \in F$.

We denote by w[e] the weight of a transition e and similarly by $w[\pi ]$ the weight of path $\pi = e_1 \cdots e_n$ obtained by $\otimes$-multiplying the weights of its constituent transitions: $w[\pi ] = w[e_1] \otimes \cdots \otimes w[e_n]$. When ${{\mathrm{orig}}}[\pi ]$ is in I, we denote by ${w_{\mathcal I}}[\pi ] = \lambda ({{\mathrm{orig}}}[\pi ]) \otimes w[\pi ]$ the weight of the path including the initial weight of the origin state. For any two subsets $U, V \subseteq Q$ and any string $x \in \varSigma ^*$, we denote by P(U, x, V) the set of paths labeled with x from a state in U to a state in V and by W(U, x, V) the $\oplus$-sum of their weights:

$$\begin{aligned} W(U, x, V) = \bigoplus _{\pi \in P(U, x, V)} w[\pi ]. \end{aligned}$$

When U is reduced to a singleton, $U = \{ {p} \}$, we will simply write W(p, x, V) instead of $W(\{ {p} \}, x, V)$ and similarly for V. To include initial weights, we denote:

$$\begin{aligned} {W_{\mathcal I}}(x, V) = \bigoplus _{\pi \in P(I, x, V)} {w_{\mathcal I}}[\pi ]. \end{aligned}$$

We also denote by $\delta (U, x)$ the set of states reached by paths starting in U and labeled with $x \in \varSigma ^*$. The weight associated by A to a string $x \in \varSigma ^*$ is defined by

$$\begin{aligned} A(x) = \bigoplus _{\pi \in P(I, x, F)} {w_{\mathcal I}}[\pi ] \otimes \rho ({{\mathrm{dest}}}[\pi ]), \end{aligned}$$

(1)

when $P(I, x, F) \ne \emptyset$. A(x) is defined to be $\overline{0}$ when $P(I, x, F) = \emptyset$.

A state q of a WFA A is said to be accessible if q can be reached by a path originating in I. It is coaccessible if a final state can be reached by a path from  q. Two states q and $q'$ are co-reachable if they each can be reached by a path from I labeled with a common string $x \in \varSigma ^*$. A WFA A is trim if all states of A are both accessible and coaccessible. A is unambiguous if any string $x \in \varSigma ^*$ labels at most one accepting path. The intersection of two WFAs is a WFA that satisfies $(A_1 \cap A_2) (x) = A_1(x) \otimes A_2(x)$.

In all that follows, we will consider weighted automata over a weakly left divisible cancellative semiring.²

3 $\mathsf R$-Pre-disambiguation of Weighted Automata

3.1 Relation $\mathsf R$ over $Q \times Q$

Two states $q, q' \in Q$ are said to share a common future if there exists a string $x \in \varSigma ^*$ such that P(q, x, F) and $P(q', x, F)$ are not empty. Let $\mathsf R^*$ be the relation defined over $Q \times Q$ by $q \, \mathsf R^* \, q'$ iff $q = q'$ or q and $q'$ share a common future in A. Clearly, $\mathsf R^*$ is reflexive and symmetric, but in general it is not transitive. Observe that $\mathsf R^*$ is compatible with the inverse transition function, that is, if $q \, \mathsf R^* \, q'$, $q \in \delta (p, x)$ and $q' \in \delta (p', x)$ for some $x \in \varSigma ^*$ with $(p, p') \in Q^2$, then $p \, \mathsf R^* \, p'$. We will also denote by $\mathsf R_0$ the complete relation defined by $q \, \mathsf R_0 \, q'$ for all $(q, q') \in Q^2$. Clearly, $R_0$ is also compatible with the inverse transition function.

The construction we will define holds for any relation $\mathsf R$ out of the set of admissible relations $\mathcal{R}$ defined as the reflexive relations over $Q \times Q$ that are compatible with the inverse transition function and coarser than $\mathsf R^*$. Thus, $\mathcal{R}$ includes $\mathsf R^*$ and $\mathsf R_0$, as well as any reflexive relation $\mathsf R$ compatible with the inverse transition function that is coarser than $\mathsf R^*$, that is, for all $(q, q') \in Q^2$, $q \, \mathsf R^* \, q' \implies q \, \mathsf R\, q'$. Thus, for a relation $\mathsf R$ in $\mathcal{R}$, two states q and $q'$ that share the same future are necessarily in relation, but they may also be in relation without sharing the same future. Note in particular that $\mathsf R$ is always reflexive.

3.2 Construction

Fix a relation $\mathsf R\in \mathcal{R}$. For any $x \in \varSigma ^*$, and $q \in \delta (U, x)$, we also denote by $\delta _q(U, x)$ the set of states in $\delta (U, x)$ that are in relation with q:

$$\begin{aligned} \delta _q(U, x) = \delta (U, x) \cap \{ {p{:}p \, \mathsf R\, q} \}. \end{aligned}$$

Note that, since $\mathsf R$ is reflexive, by definition, $\delta _q(I, x)$ contains q. We will assume that ${W_{\mathcal I}}(x, \{ {p_1, \ldots , p_t} \}) \ne \overline{0}$ for any $x \in \varSigma ^*$, otherwise the subset corresponding to x needs not be constructed. For any $x \in \varSigma ^*$ and $q \in \delta (I, x)$, we define the weighted subset s(x, q) by

$$\begin{aligned} s(x, q) =&\Big \{(p_1, w_1), \ldots , (p_t, w_t){:}\big ( \{ {p_1, \ldots , p_t} \} = \delta _q(I, x) \big )\\&\ \wedge \big ( \forall i \in [1, t], w_i = {W_{\mathcal I}}(x, \{ {p_1, \ldots , p_t} \})^{-1} \otimes {W_{\mathcal I}}(x, p_i)\big ) \Big \}. \end{aligned}$$

For a weighted subset s, define ${{\mathrm{set}}}(s) = \{ {p_1, \ldots , p_t} \}$. For any automaton A define $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ as follows:

$$\begin{aligned}&Q' = \{ {(q, s(x, q)) {:}x \in \varSigma ^*, q \in \delta (I, x)} \}\\&I' = \{ {(q, s(\epsilon , q)) {:}q \in I} \} \quad \text {and} \quad F' = \{ {(q, s(x, q)) {:}x \in \varSigma ^*, q \in \delta (I, x) \cap F} \}\\&E' = \bigg \{((q, s), a, w, (q', s')) {:}(q, s), (q', s') \in Q', a \in \varSigma ,\\[-.15cm]&\qquad \quad \exists x \in \varSigma ^*\mid s = s(x, q) = \{ {(p_1, w_1), \ldots , (p_t, w_t)} \}, \\&\qquad \qquad \qquad \quad s'= s(xa, q') = \{ {(p'_1, w'_1), \ldots , (p'_{t'}, w'_{t'})} \},\\[-.15cm]&\qquad \qquad \qquad \quad q' \in \delta (q, a), w = \bigoplus _{i = 1}^t \Big (w_i \otimes W(p_i, a, {{\mathrm{set}}}(s')) \Big ),\\[-.4cm]&\qquad \qquad \qquad \quad \forall j \in [1, t'], w'_j = w^{-1} \otimes \Big ( \bigoplus _{i = 1}^{t} w_i \otimes W(p_i, a, p'_j \Big ) \bigg \} \end{aligned}$$

$$\begin{aligned} \text {and} \quad&\forall (q, s) \in I', s = \{ {(p_1, w_1), \ldots , (p_t, w_t)} \}, \, \lambda '((q, s)) = \bigoplus _{\begin{array}{c} i \in [1, t] \end{array}} \lambda (p_i).\\&\forall (q, s) \in F', s = \{ {(p_1, w_1), \ldots , (p_t, w_t)} \}, \, \rho '((q, s)) = \bigoplus _{\begin{array}{c} p_i \in F\\ i \in [1, t] \end{array}} (w_i \otimes \rho (p_i)). \end{aligned}$$

Note that in definition of the transition set $E'$ above, the property ${{\mathrm{set}}}(s') = \delta _{q'}({{\mathrm{set}}}(s), a)$ always holds. In particular, if $p'$ is in $\delta _{q'}({{\mathrm{set}}}(s), a)$, then there is a path from I to some $p \in {{\mathrm{set}}}(s)$ labeled x and a transition from p to $p'$ labeled with a and $p'\, R \, q'$ so $p'$ is in ${{\mathrm{set}}}(s')$. Conversely, if $p'$ is in ${{\mathrm{set}}}(s')$ then there exists p reachable by x with a transition labeled with a from p to $p'$. Since $p'$ is in ${{\mathrm{set}}}(s')$, $p'$ is in $\delta _{q'}(I, xa)$, thus $p' \, R \, q'$. Since there exists a transition labeled with a from q to $q'$ and from p to $p'$, this implies that $p \, R \, q$. Since $p \, R \, q$ and p is reachable via x, p is $\delta _q(I, x)$.

When the set of states $Q'$ is finite, $A'$ is a WFA with a finite set of states and transitions and is defined as the result of the R -pre-disambiguation of A. In general, $\mathsf R$-pre-disambiguation is thus defined only for a subset of weighted automata, which we will refer to as the set of R -pre-disambiguable weighted automata. We will show later sufficient conditions for an automaton A to be R -pre-disambiguable in the case of the tropical semiring. Figure 1 illustrates the $\mathsf R$-pre-disambiguation construction.

3.3 Properties of the Resulting WFA

In this section, we assume that the input WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$ is $\mathsf R$-pre-disambiguable. In general, the WFA $A'$ constructed by $\mathsf R$-pre-disambiguation is not equivalent to A, but the weight of each path from an initial state equals the $\oplus$-sum of the weights of all paths with the same label in the input automaton starting at an initial state.

Proposition 1

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. Then, the following equalities hold for any path $\pi \in P(I', x, (q, s))$ in $A'$, with $x \in \varSigma ^*$ and $s = \{ {(p_1, w_1), \ldots , (p_t, w_t)} \}$:

$$\begin{aligned} {w_{\mathcal I}}[\pi ] = {W_{\mathcal I}}(x, {{\mathrm{set}}}(s)) \quad \text { and } \quad \forall i \in [1, t], \ {w_{\mathcal I}}[\pi ] \otimes w_i&= {W_{\mathcal I}}(x, p_i). \end{aligned}$$

The proof of this proposition, as well as others not included here due to space limitations, can be found in the full version of this paper [20].

Proposition 2

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. Then, for any accepting path $\pi \in P(I', x, (q, s))$ in $A'$, with $x \in \varSigma ^*$ and $(q, s) \in F'$, the following equality holds:

$$\begin{aligned} {w_{\mathcal I}}[\pi ] \otimes \rho '((q, s)) = A(x). \end{aligned}$$

Proof

Let $s = \{ {(p_1, w_1), \ldots , (p_t, w_t)} \}$. By definition of $\rho '$, we can write

$$\begin{aligned} {w_{\mathcal I}}[\pi ] \otimes \rho '((q, s))&= {w_{\mathcal I}}[\pi ] \otimes \mathop {\bigoplus }\limits _{\begin{array}{c} p_i \in F\\ i \in [1, t] \end{array}} (w_i \otimes \rho (p_i)) = \mathop {\bigoplus }\limits _{\begin{array}{c} p_i \in F\\ i \in [1, t] \end{array}} ({w_{\mathcal I}}[\pi ] \otimes w_i \otimes \rho (p_i)). \end{aligned}$$

Plugging in the expression of $({w_{\mathcal I}}[\pi ] \otimes w_i)$ given by Proposition 1 yields

$$\begin{aligned} {w_{\mathcal I}}[\pi ] \otimes \rho '((q, s)) = \mathop {\bigoplus }\limits _{\begin{array}{c} p_i \in F \\ i \in [1, t] \end{array}} ( {W_{\mathcal I}}(x, p_i) \otimes \rho (p_i)). \end{aligned}$$

(2)

By definition of $\mathsf R$-pre-disambiguation, q is a final state. Any state $p \in \delta (I, x) \cap F$ shares a common future with q since both p and q are final states, thus we must have $p \, R \, q$, which implies $p \in {{\mathrm{set}}}(s)$. Thus, the $\oplus$-sum in (2) is exactly over the set of states $\delta (I, x) \cap F$, which proves that ${w_{\mathcal I}}[\pi ] \otimes \rho '((q, s)) = A(x)$.    $\square$

Proposition 3

Let $A' = (\varSigma , Q', I', F', E', \lambda ' \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. Then, any string $x \in \varSigma ^*$ accepted by A is accepted by $A'$.

Proof

Let $(q_0, a_1, w_1, q_1) \cdots (q_{n - 1}, a_n, w_n, q_n)$ be an accepting path in A with $a_1 \cdots a_n = x$. By construction, $((q_0, s_0), a_1, w'_1, (q_1, s_1)) \cdots ((q_{n - 1}, s_{n - 1}), a_n, w'_n,$ $(q_n, s_n))$ is a path in $A'$ for some $w'_i \in \mathbb {S}$ and with $s_i = s(a_1 \cdots a_i, q_i)$ for all $i \in [1, n]$ and $s_0 = \epsilon$ and by definition of finality in $\mathsf R$-pre-disambiguation, $(q_n, s_n)$ is final. Thus, x is accepted by $A'$.    $\square$

Fig. 1.

Illustration of the $\mathsf R$-pre-disambiguation construction in the semiring $(\mathbb {R}_+, +, \times , 0, 1)$. Initial states are depicted by a bold circle (always with initial weight $\overline{1}$ in figures here) and final states by double circles. For each state (q, s) of the result, the subset s is explicitly shown. q is the state of the first pair in s shown. The weights are rational numbers, for example $\frac{1}{11} \approx .091$.

4 Disambiguation Algorithm

Propositions 1, 2 and 3 show that the strings accepted by $A'$ are exactly those accepted by A and that the weight of any path in $A'$ accepting $x \in \varSigma ^*$ is A(x). Thus, if for any x, we could eliminate from $A'$ all but one of the paths labeled with x, the resulting WFA would be unambiguous and equivalent to A. Removing transitions to achieve this objective without changing the function represented by the WFA turns out not to be straightforward. The following two lemmas (Lemmas 1 and 2) and their proofs are the critical technical ingredients helping us define the transition removal and prove its correctness. This first lemma provides a useful tool for the proof of the second.

Fig. 2.

Illustration of the proof of Lemma 1. The lemma proves the existence of the dashed transitions and the dashed state when $(q, s) \ne (q', s')$ and $x \ne x'$.

Lemma 1

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. Let (q, s) and $(q', s')$ be two distinct states of $A'$ both admitting a transition labeled with $a \in \varSigma$ to the same state $(q_0, s_0)$ (or both final states), and such that $(q, s) \in \delta (I', x)$ and $(q', s') \in \delta (I', x)$ for some $x \in \varSigma ^*$. Then, if $(q, s) \in \delta (I', x')$ for some $x' \ne x$, $x' \in \varSigma ^*$, there exists a state $(q', s'') \in \delta (I', x')$ with $(q', s'') \ne (q, s)$ and such that $(q', s'')$ admits a transition labeled with a to $(q_0, s_0)$ (resp. is a final state).

Proof

Figure 2 illustrates the proof of the lemma. First, note that since $s = s(q, x)$ and $s' = s(q', x)$, $q = q'$ implies $(q, s) = (q', s')$. By contraposition, since $(q, s) \ne (q', s')$, we must have $q \ne q'$. Since both $q_0 \in \delta (q, a)$ and $q_0 \in \delta (q', a)$ in A (or both q and $q'$ are final states), q and $q'$ share a common future, which implies $q \, \mathsf R\, q'$. Since $(q', s')$ is reachable by x in $A'$ from $I'$, $q'$ must be reachable by x from I in A. This, combined with $q \, \mathsf R\, q'$, implies that $q'$ must be in ${{\mathrm{set}}}(s)$. Since $(q, s) \in \delta (I', x')$, all states in ${{\mathrm{set}}}(s)$ must be reachable by $x'$ from I in A, in particular $q'$. Thus, by definition of the $\mathsf R$-pre-disambiguation construction, $A'$ admits a state $(q', s(q', x'))$, which is distinct from (q, s) since $q \ne q'$. If (q, s) admits a transition labeled with a to $(q_0, s_0)$, then we have $s_0 = s(q_0, x'a)$. If $(q', s')$ also admits a transition labeled with a to $(q_0, s_0)$, then $q'$ admits a transition labeled with a to $q_0$ and by definition of the $\mathsf R$-pre-disambiguation construction, $(q', s(q', x'))$ must admit a transition by a to $(q_0, s(q_0, x'a)) = (q_0, s_0)$. Finally, in the case where both (q, s) and $(q', s')$ are final states, then $q'$ is final in A and thus $(q', s(q', x'))$ is a final state in $A'$.    $\square$

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. For any state $(q_0, s_0)$ of $A'$ and label $a \in \varSigma$, let $\mathcal{L}(q_0, s_0, a) = ((q_1, s_1), \ldots , (q_n, s_n))$, $n \ge 1$, be the list of all distinct states of $A'$ admitting a transition labeled with $a \in \varSigma$ to $(q_0, s_0)$, with $q_1 \le \cdots \le q_n$. We define the processing of the list $\mathcal{L}(q_0, s_0, a)$ as follows: the states of the list are processed in order; for each state $(q_j, s_j)$, $j \ge 2$, this consists of removing its a-transition to $(q_0, s_0)$ if and only if there exists a co-reachable state $(q_i, s_i)$ with $1 \le i < j$ whose a-transition to $(q_0, s_0)$ has not been removed.³ Note that, by definition, the a-transition to $(q_0, s_0)$ of the first state $(q_1, s_1)$ is kept.

We define in a similar way the processing of the list $\mathcal{F}= ((q_1, s_1), \ldots , (q_n, s_n))$, $n \ge 1$, of all distinct final states of $A'$, with an arbitrary order $q_1 \le \cdots \le q_n$ as follows: the states of the list are processed in order; for each state $(q_j, s_j)$, $j \ge 1$, this consists of making it non-final if and only if there exists a co-reachable state $(q_i, s_i)$ with $i < j$ whose finality has been maintained. By definition, the finality of state $(q_1, s_1)$ is maintained.

Lemma 2

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the finite automaton returned by the $\mathsf R$-pre-disambiguation of the WFA $A = (\varSigma , Q, I, F, E, \lambda , \rho )$. Let $(q_0, s_0)$ be a state of $A'$ and $a \in \varSigma$, then, the automaton $A''$ resulting from processing the list $\mathcal{L}(q_0, s_0, a)$ accepts the same strings as $A'$. Similarly, the processing of the list of final states $\mathcal{F}$ of $A'$ does not affect the set of strings accepted by $A'$.

Assume that A is $\mathsf R$-pre-disambiguable. Then, this helps us define a disambiguation algorithm Disambiguation for A defined as follows:

• 1. construct $A'$, the result of the $\mathsf R$-pre-disambiguation of A;

• 2. for any state $(q_0, s_0)$ of $A'$ and label $a \in \varSigma$, process $\mathcal{L}(q_0, s_0, a)$; process the list of final states $\mathcal{F}$.

Theorem 1

Let $A = (\varSigma , Q, I, F, E, \lambda , \rho )$ be a $\mathsf R$-pre-disambiguable weighted automaton. Then, algorithm Disambiguation run on input A generates an unambiguous WFA B equivalent to A.

Proof

Let $A' = (\varSigma , Q', I', F', E', \lambda ', \rho ')$ be the WFA returned by $\mathsf R$-pre-disambiguation run with input A. By Lemma 2, the set of strings accepted after processing the lists $\mathcal{L}(q_0, s_0, a)$ and $\mathcal{F}$ remains the same⁴. Furthermore, in view of the Propositions 1, 2 and 3, the weight of the unique path labeled with an accepted string x in B $\otimes$-multiplied by its final weight is exactly A(x). Finally, by definition of the processing operations, the resulting WFA is unambiguous, thus B is an unambiguous WFA equivalent to A.    $\square$

Differing numberings of the states can lead to different orderings in each list and thus to different transition or finality removals, thereby resulting in different weighted automata, with potentially different sizes after trimming. Nevertheless, all such resulting weighted automata are equivalent.

Figure 3 gives an example illustrating the pre-disambiguation and transition-removal stages of our disambiguation algorithm and also shows the result of determinization.

Fig. 3.

Example illustrating the full disambiguation algorithm applied to a non-acyclic WFA. (a) WFA A over the tropical semiring. (b) WFA $A'$ obtained from A by application of pre-disambiguation. (c) WFA $A''$ result of our disambiguation algorithm applied to A. $A''$ is obtained from $A'$ by removal of the transition from state 2 labeled with c / 2 and trimming. (d) WFA obtained from A by application of determinization.

5 Sufficient Conditions

The definition of siblings and that of twins property for weighted automata were previously given by [16] (see also [3]). We will use a weaker (sufficient) condition for $\mathsf R$-pre-disambiguability.

Definition 1

Two states p and q of a WFA A are said to be siblings if there exist two strings $x, y \in \varSigma ^*$ such that both p and q can be reached from an initial state by paths labeled with x and there are cycles at both p and q labeled with y.

Two sibling states p and q are said to be twins if for any such x and y, $W(p, y, p) = W(q, y, q)$. A is said to have the twins property when any two siblings are twins. It is said to have the $\mathsf R$-weak twins property when any two siblings that are in $\mathsf R$ relation are twins. When A admits the $\mathsf R^*$-weak twins property, we will also say in short that it admits the weak twins property.

The results given in the remainder of this section are presented in the specific case of the tropical semiring. To show the following theorem we partly use a proof technique from [16] for showing that the twins property is a sufficient condition for weighted determinizability.

Theorem 2

Let A be a WFA over the tropical semiring that admits the $\mathsf R$-weak twins property. Then, A is $\mathsf R$-pre-disambiguable.

The theorem implies in particular that if A has the twins property then A is $\mathsf R$-pre-disambiguable. In particular, any acyclic weighted automaton is $\mathsf R$-pre-disambiguable.

Fig. 4.

(a) Weighted automaton A that cannot be determinized by the weighted determinization algorithm of [16]. (b) A has the weak twins property and can be disambiguated by Disambiguationas shown by the figure. One of the two states in dashed style is not made final by the algorithm. The head state for each of these states, is the state appearing in the first pair listed.

A WFA A is said to be determinizable when the weighted determinization algorithm of [16] terminates with input A (see also [3]). In that case, the output of the algorithm is a deterministic automaton equivalent to A.

Theorem 3

Let A be a determinizable WFA over the tropical semiring, then A is $\mathsf R$-pre-disambiguable.

By the results of [11], this also implies that any polynomially ambiguous WFA that has the clones property is $\mathsf R$-pre-disambiguable and can be disambiguated using Disambiguation. There are however weighted automata that are $\mathsf R$-pre-disambiguable and thus can be disambiguated using Disambiguation but that cannot be determinized using the algorithm of [16]. Figure 4 gives an example of such a WFA. To see that the WFA A of Fig. 4 cannot be determinized, consider instead B obtained from A by removing the transition from state 3 to 5. B is unambiguous and does not admit the twins property (cycles at states 1 and 2 have distinct weights), thus it is not determinizable by theorem 12 of [16]. Weighted determinization creates infinitely many subsets of the form $\{ {(1, 0), (2, n)} \}$, $n \in \mathbb {N}$, for paths from the initial state labeled with $ab^n$. Precisely the same subets are created when applying determinization to A.

On the tropical semiring, define $-A$ as the WFA in which each non-infinite weight in A is replaced by its negation. The following result can be proven in a way that is similar to the proof of the analogous result for the twins property given by [3].⁵

Theorem 4

Let A be a trim polynomially ambiguous WFA over the tropical semiring. Then, A has the weak twins property iff the weight of any cycle in $B = \text {Trim}(A \cap (-A))$ is 0.

This leads to an algorithm for testing the weak twins property for polynomially ambiguous automata in time $O(|Q|^2 + |E|^2)$. It was recently shown that the twins property is a decidable property that is PSPACE-complete for WFAs over the tropical semiring [12]. It would be interesting to determine if the weak twins property we just introduced is also decidable.

6 Experiments

In order to experiment with weighted disambiguation, we implemented the algorithm (using the $\mathsf R^*$ relation) in the OpenFst C++ library [4]. For comparison, an implementation of weighted determinization is also available in that library [16].

For a first test corpus, we generated 500 speech lattices drawn from a randomized, anonymized utterance sampling of voice searches on the Google Android platform [21]. Each lattice is a weighted acyclic automaton over spoken words that contains many weighted paths. Each path represents a hypothesis of what was uttered along with the automatic speech recognizer’s (ASR) estimate of the probability of that path. Such lattices are useful for passing compact hypothesis sets to subsequent processing without commitment to, say, just one solution at the current stage.

The size of a lattice is determined by a probability threshold with respect to the most likely estimated path in the lattice; hypotheses within the threshold are retained in the lattice. Using $|A| = |Q| + |E|$ to measure automata size, the mean size for these lattices was 2384 and the standard deviation was 3241.

The ASR lattices are typically non-deterministic and ambiguous due to both the models and the decoding strategies used. Determinization can be applied to reduce redundant computation in subsequent stages; disambiguation can be applied to determine the combined probability estimate of a string that may be distributed among several otherwise identically-labels paths.

Disambiguation has a mean expansion of 1.23 and a standard deviation of 0.59. Determinization has a mean expansion of 1.31 and a standard deviation of 1.35. For this data, disambiguation has a slightly less mean expansion compared to determinization but a very substantially less standard deviation.

As a second test corpus, we used 100 automata that are the compact representation of hypothesized Chinese-to-English translations from the DARPA Gale task [9]. These automata may contain cycles due to details of the particular translation system, which provides an interesting contrast to the acyclic speech case. Some fail to determinize within the allotted memory (1 GB) and about two-thirds of those also fail to disambiguate, possible when cycles are present.

Considering only those which are both determinizable and disambiguable, disambiguation has a mean expansion of 4.53 and a standard deviation of 6.0. Determinization has a mean expansion of 54.5 and a standard deviation of 90.5. For this data, disambiguation has a much smaller mean and standard deviation of expansion compared to determinization.

As a final example, Fig. 5 shows an acyclic unambiguous (unweighted) automaton whose size is in $O(n^2)$. No equivalent deterministic automaton can have less than $2^n$ states since such an automaton must have a distinct state for each of the prefixes of the strings $\{ {(a + b)^{k - 1} b (a + b)^{n - k} {:}1 \le k \le n} \}$, which are prefixes of L. Thus, while our disambiguation algorithm leaves the automaton of Fig. 5 unchanged, determinization would result in this case in an automaton with more than $2^n$ states.

Fig. 5.

Unambiguous automaton over the alphabet $\{ {a, b, c} \}$ accepting the language $L = \{ {(a + b)^{k - 1} b (a + b)^{n - k} c a^k {:}1 \le k \le n} \}$. For any $k \ge 0$, $U^k$ serves as a shorthand for $(a + b)^k$.

7 Conclusion

We presented an algorithm for the disambiguation of WFAs. The algorithm applies to a family of WFAs defined over the tropical semiring verifying a sufficient condition that we described, which includes all acyclic and, more generally, all determinizable WFAs. Our experiments showed the favorable properties of this algorithm in applications related to speech recognition and machine translation. The algorithm is likely to admit a large number of applications in areas such as natural language processing, speech processing, computational biology, and many other areas where WFAs are commonly used. The study of the theoretical properties we initiated raises a number of novel questions which include the following: the decidability of the weak twins property for arbitrary WFAs, the characterization of WFAs that admit an equivalent unambiguous WFA, the characterization of WFAs to which our algorithm can apply and perhaps an extension of our algorithm to a wider domain, and finally the proof and study of these questions for other semirings than the tropical semiring.