Abstract
We introduce techniques for proving uniform termination of graph transformation systems, based on matrix interpretations for string rewriting. We generalize this technique by adapting it to graph rewriting instead of string rewriting and by generalizing to ordered semirings. In this way we obtain a framework which includes the tropical and arctic type graphs of [6] and a new variant of arithmetic type graphs. These type graphs can be used to assign weights to graphs and to show that these weights decrease in every rewriting step in order to prove termination. We present an example involving counters and discuss the implementation in the tool Grez.
Research partially supported by DFG project GaReV.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
For every computational formalism, the question of termination is one of the most fundamental problems, consider for instance the halting problem for Turing machines. For graph transformation systems there has been some work on termination, but this problem has received less attention than, e.g., confluence or reachability analysis. There are several applications where termination analysis is essential: one scenario is termination of graph programs, especially for programs operating on complex data structures. Furthermore, model transformations, for instance of UML models, usually require functional behaviour, i.e., every source model should be translated into a unique target model. This requires termination and confluence of the model transformation rules.
There is a huge body of termination results in string and term rewriting [2] from which one can draw inspiration. Still, adapting these techniques to graph transformation is often non-trivial. A helpful first step is often to modify these techniques to work with cycle rewriting [16, 20], which imagines the two ends of a string to be glued together, so that rewriting is indeed performed on a cycle.
In this paper we focus exclusively on uniform termination, i.e., there is only a set of graph transformation rules, but no fixed initial graph, and the question is whether the rules terminate on all graphs. All variants of the termination problem, termination on all graphs as well as termination on a fixed set of initial graphs, are undecidable [15].
In [6] we have shown how to adapt methods from string rewriting [13, 18] and to develop a technique based on weighted type graphs, which was implemented in the tool Grez. Despite its simplicity the method is quite powerful and finds termination arguments also in cases which are difficult for human intuition. However, there are some examples (see for instance the example discussed in Sect. 5) where this technique fails. The corresponding techniques in string rewriting can be seen as matrix interpretations of strings in certain semirings, more specifically in the tropical and arctic semiring. Those semirings can be replaced by the arithmetic semiring (the natural numbers with addition and multiplication) in order to obtain a powerful termination analysis method for string rewriting [10, 12].
Here we generalize this method to graphs. Due to their non-linear nature, we have to abandon matrices and instead state a different termination criterion that is based on weights of morphisms of the left-hand and right-hand sides of rules into a type graph. Type graphs [7] are a standard tool for typing graph transformation systems, but we are not aware of any case where they have been used for termination analysis before [6].
By introducing weighted type graphs we generalize matrix interpretations for string rewriting in two ways: first, we transform graphs instead of strings and second, we consider general semirings. Our techniques work for so-called strictly and strongly ordered semirings, which have to be treated in a slightly different way. After introducing the theory we will discuss an extended example, followed by a presentation of the implementation in the termination tool Grez.Footnote 1 All proofs can be found in [4].
2 Preliminaries
2.1 Graphs and Graph Transformation
We first introduce graphs, morphisms, and graph transformation, in particular the double pushout approach [8]. In the context of this paper we use edge-labeled, directed graphs, but it is straightforward to generalize the results to hypergraphs.
Definition 1
(Graph). Let \(\varLambda \) be a fixed set of edge labels. A \(\varLambda \) -labeled graph is a tuple \(G = \langle V,E,\, { src }{},\,{ tgt }{}, \, { lab }{}\rangle \), where V is a finite set of nodes, E is a finite set of edges, \(\, { src }{},\,{ tgt }{}:E\rightarrow V\) assign to each edge a source and a target, and \( \, { lab }{}:E\rightarrow \varLambda \) is a labeling function.
As a notational convention, we will denote, for a given graph G, its components by \(V_G\), \(E_G\), \(\, { src }{G}\), \(\,{ tgt }{G}\) and \( \, { lab }{G}\), unless otherwise indicated.
Definition 2
(Graph morphism). Let \(G,G'\) be two \(\varLambda \)-labeled graphs. A graph morphism \(\varphi :G\rightarrow G'\) consists of two functions \(\varphi _V:V_G\rightarrow V_{G'}\) and \(\varphi _E:E_G\rightarrow E_{G'}\), such that for each edge \(e\in E_G\) it holds that \(\, { src }{_{G'}}(\varphi _E(e)) = \varphi _V(\, { src }{_{G}}(e))\), \(\,{ tgt }{_{G'}}(\varphi _E(e)) = \varphi _V(\,{ tgt }{_{G}}(e))\) and \( \, { lab }{_{G'}}(\varphi _E(e)) = \, { lab }{_{G}}(e)\).
We will often drop the subscripts V, E and simply write \(\varphi \) instead of \(\varphi _V\), \(\varphi _E\). We work with standard double-pushout (DPO) graph transformation [8]. Note that our termination results would still hold if we restricted to injective matches.

Definition 3
(Graph transformation). A graph transformation rule \(\rho \) consists of two morphisms  , consisting of the left-hand side L, the right-hand side R and the interface I. We require that I is discrete.
, consisting of the left-hand side L, the right-hand side R and the interface I. We require that I is discrete.
A match of a left-hand side in a graph G is a morphism \(m:L\rightarrow G\). Given a rule \(\rho \) and a match \(m:L\rightarrow G\), a graph H is the result of applying the rule at the match, written \(G \Rightarrow _{m,\rho } H\) (or \(G \Rightarrow _\rho H\) if m is arbitrary or clear from the context), if there exists a graph C and morphisms such that the two squares in the diagram on the right are pushouts in the category of graphs and graph morphisms.
A graph transformation system \(\mathcal {R}\) is a finite set of graph transformation rules. For a graph transformation system \(\mathcal {R}\), \(\Rightarrow _{\mathcal {R}}\) is the rewriting relation on graphs induced by those rules.
Intuitely in a graph transformation step from G to H, the images of all elements of the left-hand side L, which are not present in the interface I are deleted, and the right-hand side R is added, by gluing it to the interface.
Although the graph transformation systems themselves are untyped, our method for termination analysis is based on type graphs [7]. For given graphs G, T, where T is considered as a type graph, we say that G is typed over T whenever there is a morphism \(t:G\rightarrow T\). The morphism t will also be called typing morphism. We need a way to compose and decompose typing morphisms.
Lemma 1
Let a pushout \( PO \) consisting of objects \(G_0,G_1,G_2,G\) be given. Then there exists a bijection between pairs of commuting morphisms \(t_1:G_1\rightarrow T\), \(t_2:G_2\rightarrow T\) and morphisms \(t:G\rightarrow T\) (see diagram below).

For each t we obtain a unique pair of morphisms \(t_1,t_2\) by composing with \(\varphi _1\) and \(\varphi _2\), respectively. Conversely, for each pair \(t_1,t_2\) of morphisms with \(t_1\circ \psi _1 = t_2\circ \psi _2\) we obtain a unique \(t:G\rightarrow T\) as mediating morphism. In this case we will write \( med _{ PO }(t_1,t_2) = t\) and \( med ^{-1}_{ PO }(t) = \langle t_1,t_2 \rangle \).
2.2 Matrix Interpretations for String Rewriting
Our technique is strongly influenced by matrix interpretations for proving termination in string, cycle and term rewriting systems [10, 12, 16]. We will generalize this technique, resulting in a technique for graph transformation systems that has a distinctly different flavour than the original method. In order to point out the differences later and motivate our choices, we will introduce matrix interpretations first.
We are working in the context of string rewrite systems, where a rule is of the form \(\ell \rightarrow r\), where \(\ell ,r\) are both strings over a given alphabet \(\varSigma \). For instance, consider the rule \(aa\rightarrow aba\), which rewrites \(aaa \Rightarrow abaa \Rightarrow ababa \not \Rightarrow \).
We first start with some preliminaries: let A, B be two square matrices A, B over \(\mathbb {N}_0\) of equal dimension n. We write \(A > B\) if \(A_{1,1} > B_{1,1}\) and \(A_{i,j} \ge B_{i,j}\) for all indices i, j with \(1\le i,j \le n\), i.e., we require that the entries in the upper left corner are strictly ordered, whereas the remaining entries may also be equal. It holds that \(A>B\) implies \(A\cdot C > B\cdot C\) and \(C\cdot A> C\cdot B\) for a matrixFootnote 2 \(C > 0\) of appropriate dimension.
As always in termination analysis strings are assigned to elements in a well-founded set and it has to be shown that each rule application leads to a decrease within this order.
Here, every letter of the alphabet \(a\in \varSigma \) is associated with a square matrix \(A = [a] > 0\) (where all matrices have the same dimension n). Similarly every word \(w = a_1\dots a_n\) is mapped to a matrix \([w] = [a_1]\cdot \dots \cdot [a_n]\), which is obtained by taking the matrices of the single letters and multiplying them. If we can show \([\ell ] > [r]\) for every rule \(\ell \rightarrow r\), then termination is implied by the considerations above and by the fact that the order \(\le \) on \(\mathbb {N}_0\) is well-founded, i.e., there are no infinite strictly decreasing chains.
For the example above take the following matrices (as in [12]):
For cycle rewriting a similar argument can be given, which is based on the idea that the trace, i.e., the sum of the diagonal, of a matrix decreases [16].
A natural question to ask is how such matrices can be obtained. We will later discuss how SMT solvers can be employed to automatically generate the required weights.
In the following, we will generalize this method in two ways: we will replace the natural numbers by an arbitrary semiring – an observation that has already been made in the context of string rewriting – and we will make the step from string to graph rewriting.
2.3 Ordered Semirings
We continue by defining semirings, the algebraic structures in which we will evaluate the graphs occurring in transformation sequences, and orders on them.
A (partial) order is a reflexive, transitive and antisymmetric relation. If \(\le \) is an order, then we denote by \(<\) its strict subrelation e.g. \(x<y\) if and only if \(x \le y \wedge x \ne y\). An order is well-founded if it does not allow infinite, strictly decreasing sequences \(x_0 > x_1 > x_2 > \cdots \).
Definition 4
A semiring is a tuple \(\langle S,\oplus ,\otimes ,0,1 \rangle \), where S is the (finite or infinite) carrier set, \(\langle S,\oplus ,0 \rangle \) is a commutative monoid, \(\langle S,\otimes ,1 \rangle \) is a monoid, \(\otimes \) distributes over \(\oplus \) and 0 is an annihilator for \(\otimes \). That is, the following laws hold for all \(x,y,z\in S\):
A semiring \(\langle S,\oplus ,\otimes ,0,1 \rangle \) is commutative if \(\otimes \) is commutative (that is, if \(x \otimes y = y \otimes x\), for all \(x,y\in S\)).
We will often confuse a semiring with its carrier set, that is, S can refer to both the semiring \(\langle S,\oplus ,\otimes ,0,1 \rangle \) and the carrier set S.
In order to come up with termination arguments, we need a partial order on the semirings that has to be compatible with its operations.
Definition 5
A structure \(\langle S,\oplus ,\otimes ,0,1,\le \rangle \) is an ordered semiring if \(\langle S,\oplus ,\otimes ,0,1 \rangle \) is a semiring and \({\le }\in S\times S\) is a partial order on S such that for all \(x,y,u,z\in S\):
-
\(x\le y\) implies \(x \oplus u \le y \oplus u\), \(x \otimes z \le y \otimes z\) and \(z \otimes x \le z \otimes y\) for \(z\ge 0\).
The ordered semiring S is strongly ordered, if
-
\(x < y\), \(z < u\) implies \(x \oplus z < y \oplus u\); and
-
\(z > 0\), \(x < y\) implies \(x \otimes z < y \otimes z\) and \(z \otimes x < z \otimes y\).
The ordered semiring S is strictly ordered, if in addition \(x < y\) implies \(x \oplus z < y \oplus z\).
Example 1
Examples of semirings which play a role in termination proving are:
-
The natural numbers form a semiring \(\langle \mathbb {N}_0,+,\cdot ,0,1,\le \rangle \), where \(\le \) is the standard ordering of the natural numbers. We will call this semiring the arithmetic semiring (on the natural numbers). This is a strictly ordered semiring because both \(<\) and \(\le \) are monotone in \(+\) and \(\cdot \)
-
The tropical semiring (on the natural numbers) is:
$$\begin{aligned} T_{\mathbb {N}_0}=\langle \mathbb {N}_0\cup \{\infty \},\mathrm {min},+,\infty ,0,\le \rangle , \end{aligned}$$where \(\le \) is the usual ordering of the natural numbers. The tropical semiring is not strictly ordered, because, for example, \(2 < 3\) but \(\min (1,2) \not < \min (1,3)\). It is however still strongly ordered.
-
The arctic semiring (on the natural numbers) is
$$\begin{aligned} T_{\mathbb {N}_0}=\langle \mathbb {N}_0\cup \{-\infty \},\mathrm {max},+,-\infty ,0,\le \rangle , \end{aligned}$$where \(\le \) is the normal ordering of the natural numbers. Like the tropical semiring, the arctic semiring is not strictly ordered, but strongly ordered.
All semirings above are commutative. We will in the following restrict ourselves to commutative semirings, since we are assigning weights to graphs by multiplying weights of nodes and edges, and nodes and edges are typically unordered.
3 Weighted Type Graphs
Similarly to mapping a word to a matrix, we will associate weights to graphs, by typing them over a type graph with weights from a semiring.
Definition 6
Let an ordered semiring S be given. A weighted type graph T over S is a graph with a weight function \(w_T:E_T\rightarrow S\) and a designated flower node  , such that for each label \(A\in \varLambda \) there exists a designated edge \(e_A\) with
, such that for each label \(A\in \varLambda \) there exists a designated edge \(e_A\) with  ,
,  , \( \, { lab }{_{T}}(e_A) = A\) and \(w_T(e_A) > 0\).
, \( \, { lab }{_{T}}(e_A) = A\) and \(w_T(e_A) > 0\).
For a graph G, we denote with  (or just
(or just  if T is clear from the context) the unique morphism from G to T that maps each node \(v\in V_G\) of G to the flower node
if T is clear from the context) the unique morphism from G to T that maps each node \(v\in V_G\) of G to the flower node  and each edge \(e\in E_G\), with \( \, { lab }{_{T}}(e)=A\), to \(e_A\). Note that, for a morphism \(c:G\rightarrow H\), it is always the case that
and each edge \(e\in E_G\), with \( \, { lab }{_{T}}(e)=A\), to \(e_A\). Note that, for a morphism \(c:G\rightarrow H\), it is always the case that  .
.
Note that every matrix A of dimension n can be associated with an (unlabelled) type graph with n nodes, where an edge from node i to j is assigned weight \(A_{i,j}\) (or does not exist if \(A_{i,j} = 0\)). Hence our idea of weighted type graphs is strongly related with the matrices of Sect. 2.2.
The node  is also called the flower node, since the loops attached to it look like a flower. Those loops correspond to the matrix entries at position (1, 1) and similar to those entries they play a specific role. Note that the flower structure also ensures that every graph can be typed over T (compare with the terminal object in the category of graphs, which is exactly such a flower).
is also called the flower node, since the loops attached to it look like a flower. Those loops correspond to the matrix entries at position (1, 1) and similar to those entries they play a specific role. Note that the flower structure also ensures that every graph can be typed over T (compare with the terminal object in the category of graphs, which is exactly such a flower).
With a bit of notation overloading, we assign a weight to each morphism \(t:D\rightarrow T\) with codomain T and arbitrary domain D as follows:
That is, we multiply the weights of all edges in the image of t with respect to \(\otimes \).
Finally, the weight of a graph G with respect to T is defined by summing up the weights of all morphisms from G to T with respect to \(\oplus \):
The subscript T of \(w_T\) will be omitted if clear from the context.

Example 2
We give a small example for the weight of a graph.
Consider for instance the type graph T. Edges are labelled a, b and the weights, in this case natural numbers, are given as superscripts. Consider also the left-hand side L of rule \(\rho \) below, consisting of two a-edges (the graph rewriting analogue of the string rewriting rule \(aa\rightarrow aba\) considered in Sect. 2.2). There are five morphisms \(L\rightarrow T\), each having weight 1, as they are calculated by multiplying the weights of two a-edges which also have weight 1. Hence the weight of L with respect to T is \(w_T(L) = 1+1+1+1+1=5\). More details on this are given in Example 3.

If we glue two graphs \(G_1,G_2\) in order to obtain G, the weight of G can be obtained from the weights of \(G_1,G_2\).

Lemma 2
(Properties of weighted type graphs). Let S be an ordered commutative semiring and T a weighted type graph over S.
-
(i)
Whenever S is strongly ordered, for all graphs G,
 exists and
exists and  .
. -
(ii)
Given the following diagram, where the square is a pushout and \(G_0\) is discrete, it holds that \(w_T(t) = w_T(t\circ \varphi _1) \otimes w_T(t\circ \varphi _2)\).
Since property (ii) above only holds if \(G_0\) is discrete we restrict to discrete graphs I in the rule interface.Footnote 3
While the process of obtaining the weight of a graph corresponds to calculating the matrix of a word and summing up all its entries, we also require a way to be more discriminating, i.e., to access separate matrix entries. Evaluating a string-like graph would mean to fix its entry and exit node within the type graph (similarly to fixing two matrix indices). However, in graph rewriting, we have interfaces of arbitrary size. Hence, we do not index over pairs of nodes, but over arbitrary interface graphs, and compute the weight of a graph L with respect to a typed interface I.

Definition 7
Let \(\varphi :I\rightarrow L\) and \(t:I\rightarrow T\) be graph morphisms, where T is a weighted type graph. We define:
Finally, we can define what it means that a rule is decreasing, analogous to the condition \([\ell ] > [r]\) introduced in Sect. 2.2. In addition we also introduce non-increasingness, a concept that will be needed in the following for so-called relative termination arguments.
Definition 8
Let a rule  , an ordered commutative semiring S and a weighted type graph T over S be given.
, an ordered commutative semiring S and a weighted type graph T over S be given.
-
(i)
The rule \(\rho \) is non-increasing if for all \(t_I:I\rightarrow T\) it holds that \(w_{t_I}(\varphi _L) \ge w_{t_I}(\varphi _R)\).
-
(ii)
The rule \(\rho \) is decreasing if it is non-increasing, and
 .
.
Example 3
We come back to Example 2 and check whether rule \(\rho \) is decreasing. For this we have to consider the following four morphisms \(t:I\rightarrow T\) from the two-node interface into the weighted type graph T:
-
The flower morphism
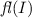 which maps both interface nodes to the left node of T. In this case we have
which maps both interface nodes to the left node of T. In this case we have  .
. -
Furthermore there are three other morphisms \(t_1,t_2,t_3:I\rightarrow T\) mapping the two interface nodes either both to the right node of T, or the first interface node to the left and the second interface node to the right node of T, or vice versa. In all these cases we have \(w_{t_i}(\varphi _L) = 1 = w_{t_i}(\varphi _R)\).
Hence, the rule is decreasing. Note also that these weights correspond exactly to the weights of the multiplied matrices in Sect. 2.2.
Finally, we have to show that applying a decreasing rule also decreases the overall weight of a graph. For a non-increasing rule the weight might also remain the same.
Lemma 3
Let S be a strictly ordered commutative semiring and T a weighted type graph over S. Furthermore, let \(\rho \) be a rule such that \(G \Rightarrow _\rho H\).
-
(i)
If \(\rho \) is non-increasing, then \(w_T(G) \ge w_T(H)\).
-
(i)
If \(\rho \) is decreasing, then \(w_T(G) > w_T(H)\).
From this lemma we can prove our main theorem that is based on the well-known concept of relative termination [11, 19]: if we can find a type graph for which some rules are decreasing and the rest is non-increasing, we can remove the decreasing rules without affecting termination. We are then left with a smaller set of rules for which termination can either be shown with a different type graph or with some other technique entirely.
Theorem 1
Let S be a strictly ordered commutative semiring with a well-founded order \(\le \) and T a weighted type graph over S. Let R be a set of graph transformation rules, partitioned in two sets \(R^{<}\) and \(R^{=}\). Assume that all rules of \(R^{<}\) are decreasing and all rules of \(R^{=}\) are non-increasing. Then R is terminating if and only if \(R^{=}\) is terminating.
A special case of the theorem is when \(R^{=}=\varnothing \). Then the statement of the theorem is that a graph transformation system R is terminating if all its rules are decreasing with respect to a strictly ordered commutative semiring S and type graph T over S.
4 Using Strongly Ordered Semirings
In the last section the semirings were required to be strictly ordered. In this section we consider what happens when we weaken this requirement and also allow non-strictly ordered semirings, which must however be strongly ordered. This allows us to work with the tropical and arctic semiring. It turns out that we obtain similar results to above if we strengthen the notion of decreasing.
Definition 9
Let a rule  , an ordered commutative semiring S and a weighted type graph T over S be given. The rule \(\rho \) is strongly decreasing (with respect to T) if for all \(t_I:I\rightarrow T\) it holds that \(w_{t_I}(\varphi _L) > w_{t_I}(\varphi _R)\).
, an ordered commutative semiring S and a weighted type graph T over S be given. The rule \(\rho \) is strongly decreasing (with respect to T) if for all \(t_I:I\rightarrow T\) it holds that \(w_{t_I}(\varphi _L) > w_{t_I}(\varphi _R)\).
Using this new notion of decreasingness we can also formulate a termination argument, which is basically equivalent to the termination argument we presented in [6].
Lemma 4
Let S be a strongly ordered commutative semiring and T a weighted type graph over S. Furthermore, let \(\rho \) be a rule such that \(G \Rightarrow _\rho H\).
-
(i)
If \(\rho \) is non-increasing, then \(w_T(G) \ge w_T(H)\).
-
(ii)
If \(\rho \) is strongly decreasing, then \(w_T(G) > w_T(H)\).
Now it is easy to prove a theorem analogous to Theorem 1, using Lemma 4 instead of Lemma 3.
Theorem 2
Let S be a strongly ordered commutative semiring with a well-founded order \(\le \) and T a weighted type graph over S. Let R be a set of graph transformation rules, partitioned in two sets \(R^{<}\) and \(R^{=}\). Assume that all rules of \(R^{<}\) are strongly decreasing and all rules of \(R^{=}\) are non-increasing. Then R is terminating if and only if \(R^{=}\) is terminating.
In this way we have recovered the termination analysis from one of our earlier papers [6], however spelt out differently. In order to explain the connection, let us consider what it means for a rule  to be non-increasing in the tropical semiring where \(\oplus \) is \(\min \) and \(\otimes \) is \(+\): for each \(t:I\rightarrow T\) into a weighted type graph T it must hold that
to be non-increasing in the tropical semiring where \(\oplus \) is \(\min \) and \(\otimes \) is \(+\): for each \(t:I\rightarrow T\) into a weighted type graph T it must hold that
where \(w_T(t_L)\) is the weight of the morphism \(t_L\), obtained by summing up (via \(+\)) the weights of all edges in the image of \(t_L\).
A different way of expressing that the minimum of the first set is larger or equal than the minimum of the second set, is to say that for each morphism \(t_L:L\rightarrow T\) with \(t_L\circ \varphi _L = t\) there exists a morphism \(t_R:R\rightarrow T\) with \(t_R\circ \varphi _R = t\) and \(w_T(t_L) \ge w_T(t_R)\). And this is exactly the notion of tropically non-increasing of [6].
Comparing the results of Theorems 1 and 2 we notice the following: as underlying semiring S we can take either a strictly ordered or a strongly ordered one, but if we choose a strongly ordered semiring, the termination argument becomes slightly weaker because for every morphism from the left-hand side to the type graph there must exist a compatible, strictly smaller morphism from the right-hand side to the type graph.
5 Examples
We give examples to show that with a weighted type graph over a strictly ordered semiring (such as the arithmetic semiring), we can prove termination on some graph transformation systems where strongly ordered semirings fail. We start with a graph transformation system for which a termination argument can be found using both variants. Then we will modify some rules and explain why weighted type graphs over strongly ordered semirings can not find a termination argument for the modified system.
Example 4
As an example we take a system consisting of several counters, which represent their current value by a finite number of bits. Each counter may possess an incr marker, that can be consumed to increment the counter by 1.

One possible graph describing a state of such a system is given by G. This is just one possible initial graph, since we really show uniform termination, i.e., termination on all initial graphs, even those that do not conform to the schema indicated by G.
We consider the graph transformation system \(\{\rho _1, \rho _2, \rho _3, \rho _4\}\), adapted from [16], consisting of the following four rules:

Each counter may increment at most once. Rules \(\rho _1\) and \(\rho _2\) specify that a counter (represented by a count-labelled edge) may increment its least significant bit by 1 if an incr marker was not consumed yet. If the least significant bit is 1, the bit is marked by a label c, to remember that a carry bit has to be passed to the following bit. Rule \(\rho _3\) increments the next bit of the counter by 1 (if it was 0 before), while rule \(\rho _4\) shifts the carry bit marker over the next 1.

The fact that this graph transformation system is uniformly terminating can be shown using a weighted type graph over either a strictly or strongly ordered semiring. For example, using a non-relative termination argument, we evaluate the rules with respect to the weighted type graph \(T_{trop}\) over the tropical semiring.
A relative termination argument is even easier: the rules \(\rho _1\) and \(\rho _2\) can be removed due to the decreasing number of incr-labelled edges. Then we can remove \(\rho _3\) due to the decreasing number of c-labelled edges (which remain constant in \(\rho _4\)) and afterwards remove \(\rho _4\) since it decreases 1-labelled edges. With all rules removed, the graph transformation system has been shown to terminate uniformly.

We now consider the arithmetic semiring and again use a non-relative termination argument: we evaluate the rules with respect to the weighted type graph \(T_{arit}\), where all weights are just increased by one with respect to \(T_{trop}\). That is due to the fact, that we are working in the arithmetic semiring and hence have to make sure that all weights of flower edges are strictly larger than 0.
Example 5
We will now modify rules \(\rho _1\) and \(\rho _2\) in order to give an example where weighted type graphs over tropical and arctic semirings fail to find a termination argument.
Consider the graph transformation system \(\{\rho _{1}', \rho _{2}', \rho _{3}', \rho _{4}'\}\) consisting of rules \(\rho _3\) and \(\rho _4\) from Example 4 with two additional new rules:

With respect to Example 4, the counter may increment its value not only once but several times, until the least significant bit is permanently marked by the carrier bit label c. This will eventually happen, since counters are never extended by additional digits and carry bits finally accumulate and can not be processed.
We now give a relative termination argument, to show uniform termination of this graph transformation system. The termination of this system is not obvious as the numbers of the labels c, 0 and 1 increase and decrease depending on the rules used for the derivation.

First, we evaluate the rules with respect to the following weighted type graph \(T'\) over the arithmetic semiring. Consider for instance rule \(\rho '_1\) and the following four interface morphisms:
-
 is the flower morphisms and maps both interface node to the left node of \(T'\). In this situation we have \(w_{t_0}(\varphi _L) = 1\cdot 1 + 1\cdot 2 = 3 > 2 = 1\cdot 1 + 1\cdot 1 = w_{t_0}(\varphi _R)\) (there are two ways to map the left-hand side in such a way that both interface nodes are mapped to the left node, resulting in weight 3; similar for the right-hand side, where we obtain weight 2).
is the flower morphisms and maps both interface node to the left node of \(T'\). In this situation we have \(w_{t_0}(\varphi _L) = 1\cdot 1 + 1\cdot 2 = 3 > 2 = 1\cdot 1 + 1\cdot 1 = w_{t_0}(\varphi _R)\) (there are two ways to map the left-hand side in such a way that both interface nodes are mapped to the left node, resulting in weight 3; similar for the right-hand side, where we obtain weight 2). -
\(t_1:I\rightarrow T'\) is the morphism that maps the first interface node to the right node of \(T'\) and the second interface node to the left node of \(T'\). In this case we have \(w_{t_1}(\varphi _L) = 1\cdot 2 = 2\ge 2 = 1\cdot 2 = w_{t_1}(\varphi _R)\).
-
\(t_2:I\rightarrow T'\) is the morphism that maps the first interface node to the left node of \(T'\) and the second interface node to the right node of \(T'\). In this case we have \(w_{t_2}(\varphi _L) = 0 \ge 0 = w_{t_2}(\varphi _R)\), since there are no possibilities to map either the left-hand or the right-hand side.
-
\(t_3:I\rightarrow T'\) is the morphisms that maps both interface node to the right node of \(T'\). Here we have \(w_{t_3}(\varphi _L) = 0 \ge 0 = w_{t_3}(\varphi _R)\) (again, there are no fitting matches of the left-hand and right-hand side).
Hence \(\rho '_1\) is decreasing. Similarly we can prove that \(\rho '_2\) is decreasing and \(\rho '_3,\rho '_4\) are non-increasing, which means that \(\rho '_1,\rho '_2\) can be removed. To show termination of the remaining rules \(\rho _{3}',\rho _{4}'\) we can simply use the weighted type graph \(T_{arit}\) from Example 4 again.
We found a relative termination argument for Example 5 using a weighted type graph over the arithmetic semiring. However, there is no way to obtain a termination argument with a weighted type graph over either tropical or arctic semirings: in these cases the weight of any graph is linear in the size of the graph (since we use only addition and minimum/maximum to determine the weight of a graph). If we have an interpretation where at least one rule is decreasing, and the other rules are non-increasing, then in any derivation, the number of applications of the decreasing rules is at most linear in the size of the initial graph. However, if we start with a counter which consists of n bits (all set to 0), we obtain a derivation in which \(all \) of the rules are applied at least \(2^n\) times.
This means that it is principally impossible to find a proof with weighted type graphs over the tropical or arctic semiring, even using relative termination.
The last two examples were inspired by string rewriting and the example rules could easily be encoded into a string grammar. We give another final example and prove termination using a weighted type graph over the arithmetic semiring. We now switch from strings to trees, staying with a scenario where reductions of exponential length are possible. In addition we discard the \( count \)-label as each counter will be represented by a node with no incoming edge and we will exploit the dangling edge condition.
Example 6
In the next example we interweave our counters into a single treelike structure. Each path from a root node to a leaf can be interpreted as a counter.

One possible graph describing a state of the modified system is given by \(\widehat{G}\). Each counter shares a number of bits with other counters, where the least significant bit is shared by all counters. Again this is just one possible initial graph, since we prove uniform termination.
Let the following graph transformation system \(\{\widehat{\rho _{1}}, \widehat{\rho _{2}}, \widehat{\rho _{3}}, \widehat{\rho _{4}}, \widehat{\rho _{5}}, \widehat{\rho _{6}}\}\) be given:

The rules \(\widehat{\rho _{1}}\) and \(\widehat{\rho _{2}}\) increment the shared least significant bit by 1. These two rules can only be applied at the root of the tree (due to the dangling edge condition of the DPO approach), as long as the edge is either labelled 0 or 1. By applying the rules \(\widehat{\rho _{3}},\dots ,\widehat{\rho _{6}}\), a carrier bit can be passed to the next bit. Proving termination of this graph transformation system is non-trivial. By applying for instance \(\widehat{\rho _{6}}\), the value of the counters containing interface node 1 does not change, while other counter values decrease.
We evaluate the rules with respect to the following weighted type graph \(\widehat{T}\) over the arithmetic semiring. We can prove that \(\widehat{\rho _{1}}\) and \(\widehat{\rho _{2}}\) are decreasing and \(\widehat{\rho _{3}},\dots ,\widehat{\rho _{6}}\) are non-increasing, which means that \(\widehat{\rho _{1}}\), \(\widehat{\rho _{2}}\) can be removed using a relative termination argument.

The rules \(\widehat{\rho _{3}}\) and \(\widehat{\rho _{4}}\) can be removed due to the decreasing number of c-labelled edges, which remain constant in \(\widehat{\rho _{5}}\) and \(\widehat{\rho _{6}}\). Afterwards we can remove \(\widehat{\rho _{5}}\), \(\widehat{\rho _{6}}\) since they decrease the number of 1-labelled edges. The graph transformation system has been shown to terminate uniformly, since there are no rules left.
6 Finding Weighted Type Graphs and Implementation
The question of how to find suitable weighted type graphs has been left open so far. Instead of manually searching for a suitable type graph we employ a satisfiable modulo theories (SMT) solver (in this case Z3) that can solve inequations over the natural numbers.
We fix a number n of nodes in the type graph and proceed as follows: take a complete graph T with n nodes, i.e., a graph with an edge for every pair \(i,j\in \{1,\dots ,n\}\) of nodes and every edge label \(a\in \varLambda \). Every edge e in this graph is associated with a variable \(x_e\). The task is to assign weights to those variables such that rules can be shown as either decreasing or non-increasing.
Now, for every rule  and every map \(t:I\rightarrow T\) we obtain an inequation:
and every map \(t:I\rightarrow T\) we obtain an inequation:
If we want to show that \(\rho \) is decreasing and t is the flower morphism \(\ge \) has to be replaced by \(>\).
Doing this for each rule and every map t gives us equations that can be used as input for an SMT-solver. We consider the weights as natural numbers only up to a given bound by restricting the length of the corresponding bit-vectors. Note that we would be outside the decidable fragment of arithmetics otherwise since the equations would contain multiplication of variables (as opposed to multiplication of constants and variables). By using a bit-vector encoding the SMT-solver Z3 can reliably find a solution (if it exists) and especially such solutions are found for the examples discussed in Sect. 5. Any solution gives us a valid weighted type graph.
A prototype Java-based tool, called Grez, has been written and was introduced in [6]. Given a graph transformation system \(\mathcal {R}\), the tool tries to automatically find a proof for the uniform termination of \(\mathcal {R}\). The tool supports relative termination and runs different algorithms (which are chosen by the user) concurrently to search a proof. If one algorithm succeeds in finding a termination argument for at least one of the rules, all processes are interrupted and the corresponding rule(s) will be removed from \(\mathcal {R}\). The algorithms are then executed on the smaller set of rules and this procedure is repeated until all rules have been removed. Afterwards Grez generates the full proof which can be saved as a PDF-file.
Grez provides both a command-line interface and a graphical user interface. The tool supports the integration of external tools, such as other termination tools or SMT-solvers. Grez can use any SMT-solver which supports the SMT-LIB2 format [1]. Grez generates the inequation described above in this format and passes it, either through a temporary file or via direct output stream, to the SMT-solver. The results are parsed back into the termination proof, as soon as the SMT-solver terminates and produces a model for the formula.
We ran the tool on all examples of this paper using a Windows workstation with a 2, 67 Ghz, 4-core CPU and 8 GB RAM. All proofs were generated in less than 1 second. The tool, a user manual [5] and the examples from this paper can be downloaded from the Grez webpage: www.ti.inf.uni-due.de/research/tools/grez.
7 Conclusion
We have shown how to generalize the tropical and arctic weighted type graphs of [6] to weighted type graphs over general semirings and their application to the termination analysis of graph transformation systems. This enables us to work in the arithmetic semiring and to prove termination of systems that could not be handled with previous approaches. Note that arithmetic type graphs do not subsume previous termination analysis methods, but rather complement them. In practice one should always try several methods in parallel threads, as it is done in our termination tool Grez.
Related Work. As already mentioned in the introduction, there is some work on termination analysis for graph transformation systems, often using rather straightforward counting arguments. Some work is specifically geared to the analysis of model transformations, taking for instance layers into account.
The paper [3] considers high-level replacement units (hlru), which are transformation systems with external control expressions. The paper introduces a general framework for proving termination of such hlrus, but the only concrete termination criteria considered are node and edge counting, which are subsumed by the weighted type graph method (for more details see [6]).
In [9] layered graph transformation systems are considered, which are graph transformation systems where interleaving creation and deletion of edges with the same label is prohibited and creation of nodes is bounded. The paper shows such graph transformation systems are terminating.
Another interesting approach encodes graph transformation systems into Petri nets [17] by introducing one place for every edge label and transforming rules into transitions. Whenever the Petri net terminates on all markings, we can conclude uniform termination of the original graph transformation rules. Note that the second example of Sect. 5 can not be handled in this way by Petri nets.Footnote 4 On the other hand [17] can handle negative application conditions in a limited way, a feature we did not consider here.
Another termination technique via forward closures is presented in [14]. Note that the example discussed in this paper (termination of a graph transformation system based on the string rewriting rules \(ab\rightarrow ac, cd\rightarrow db\)) can be handled by our tool via tropical type graphs.
Future Work. Naturally, integration of (negative) application condition is an interesting direction for future work. Furthermore we have already started to work on techniques for pattern counting. Here we are interested in deciding, whether a given rule \(\rho \) always decreases the number of occurrences of a given subgraph P.
Another area of future research that might be of great interest is non-uniform termination analysis, i.e., to analyse whether the rules terminate only on a restricted set of graphs. In applications it is often the case that rules do not always terminate, but they terminate on all input graphs of interest (lists, cycles, trees, etc.). For this, it will be necessary to find a suitable way to characterize graph languages that is useful for the application areas and integrates well with termination analysis.
Notes
- 1.
- 2.
Here 0 denotes the matrix with all entries zero.
- 3.
Compare also with the “stable under pushouts” property of [6].
- 4.
Starting with three edges labelled \(0,1, count \), rule \(\rho '_2\) transforms them into three labels \(0,c, count \), which, via rule \(\rho '_3\), are again transformed into \(0,1, count \).
References
Barrett, C., Stump, A., Tinelli, C.: The SMT-LIB standard - version 2.0. In: Proceedings of the 8th International Workshop on Satisfiability Modulo Theories (SMT 2010), Edinburgh, Scotland, July 2010
Bezem, M., Klop, J.W., de Vrijer, R. (eds.): Term Rewriting Systems. Cambridge University Press, London (2003)
Bottoni, P., Hoffman, K., Presicce, F.P., Taentzer, G.: High-level replacement units and their termination properties. J. Vis. Lang. Comput. 16(6), 485–507 (2005)
Bruggink, H.J.S., König, B., Nolte, D., Zantema, H.: Proving termination of graph transformation systems using weighted type graphs over semirings (2015). arXiv:1505.01695
Bruggink, H.J.S.: Grez user manual (2015). www.ti.inf.uni-due.de/research/tools/grez
Bruggink, H.J.S., König, B., Zantema, H.: Termination analysis for graph transformation systems. In: Diaz, J., Lanese, I., Sangiorgi, D. (eds.) TCS 2014. LNCS, vol. 8705, pp. 179–194. Springer, Heidelberg (2014)
Corradini, A., Montanari, U., Rossi, F.: Graph processes. Fundam. Informaticae 26(3/4), 241–265 (1996)
Corradini, A., Montanari, U., Rossi, F., Ehrig, H., Heckel, R., Löwe, M.: Algebraic approaches to graph transformation-part I: basic concepts and double pushout approach. In: Rozenberg, G. (ed.) Handbook of Graph Grammars and Computing by Graph Transformation. Foundations, vol. 1, pp. 163–245. World Scientific, Singapore (1997)
Ehrig, H., Ehrig, K., de Lara, J., Taentzer, G., Varró, D., Varró-Gyapay, S.: Termination criteria for model transformation. In: Cerioli, M. (ed.) FASE 2005. LNCS, vol. 3442, pp. 49–63. Springer, Heidelberg (2005)
Endrullis, J., Waldmann, J., Zantema, H.: Matrix interpretations for proving termination of term rewriting. J. Autom. Reasoning 40(2–3), 195–220 (2008)
Geser, A.: Relative termination. Ph.D. thesis, Universität Passau (1990)
Hofbauer, D., Waldmann, J.: Termination of string rewriting with matrix interpretations. In: Pfenning, F. (ed.) RTA 2006. LNCS, vol. 4098, pp. 328–342. Springer, Heidelberg (2006)
Koprowski, A., Waldmann, J.: Arctic termination..below zero. In: Voronkov, A. (ed.) RTA 2008. LNCS, vol. 5117, pp. 202–216. Springer, Heidelberg (2008)
Plump, D.: On termination of graph rewriting. In: Nagl, M. (ed.) WG 1995. LNCS, vol. 1017, pp. 88–100. Springer, Heidelberg (1995)
Plump, D.: Termination of graph rewriting is undecidable. Fundam. Informaticae 33(2), 201–209 (1998)
Sabel, D., Zantema, H.: Transforming cycle rewriting into string rewriting. In: Proceedings of RTA 2015, LIPIcs. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2015)
Varró, D., Varró–Gyapay, S., Ehrig, H., Prange, U., Taentzer, G.: Termination analysis of model transformations by petri nets. In: Corradini, A., Ehrig, H., Montanari, U., Ribeiro, L., Rozenberg, G. (eds.) ICGT 2006. LNCS, vol. 4178, pp. 260–274. Springer, Heidelberg (2006)
Zantema, H.: Termination of term rewriting by semantic labelling. Fundam. Informaticae 24(1/2), 89–105 (1995)
Zantema, H.: Termination. In: Bezem, M., Klop, J.W., de Vrijer, R. (eds.) Term Rewriting Systems, Chap. 6, pp. 181–259. Cambridge University Press, London (2003)
Zantema, H., König, B., Bruggink, H.J.S.: Termination of cycle rewriting. In: Dowek, G. (ed.) RTA-TLCA 2014. LNCS, vol. 8560, pp. 476–490. Springer, Heidelberg (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Bruggink, H.J.S., König, B., Nolte, D., Zantema, H. (2015). Proving Termination of Graph Transformation Systems Using Weighted Type Graphs over Semirings. In: Parisi-Presicce, F., Westfechtel, B. (eds) Graph Transformation. ICGT 2015. Lecture Notes in Computer Science(), vol 9151. Springer, Cham. https://doi.org/10.1007/978-3-319-21145-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-21145-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-21144-2
Online ISBN: 978-3-319-21145-9
eBook Packages: Computer ScienceComputer Science (R0)





 exists and
exists and  .
. .
.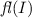 which maps both interface nodes to the left node of T. In this case we have
which maps both interface nodes to the left node of T. In this case we have  .
. is the flower morphisms and maps both interface node to the left node of
is the flower morphisms and maps both interface node to the left node of