Time-Varying Phasors and Their Application to Power Analysis

Abstract

The classical complex phasor representation of sinusoidal voltages and currents is generalized to arbitrary waveforms. The method relies on the so-called analytic signal using the Hilbert transform. This naturally leads to the notion of a time-varying power triangle and its associated instantaneous power factor. Additionally, it is shown for linear systems that Budeanu’s reactive power can be related to energy oscillations, but only in an average sense. Furthermore, Budeanu’s distortion power is decomposed into a part representing a measure of the fluctuation of power around the active power and a part that represents the fluctuation of power around Budeanu’s reactive power. The results are presented for single-phase systems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Introduction

I first met Arjan when I was a Ph.D. student during his notorious course on nonlinear systems. In the last lecture of the course, Arjan treated a relatively new subject: port-Hamiltonian systems. Port-Hamiltonian systems theory is the result of combining network theory with classical (Hamiltonian) mechanics and nowadays provides the basis for many interesting and novel control methodologies. Port-Hamiltonian systems and related concepts, such as power and energy, remained among my main topics of interest and during the past decade we collaborated on several papers, research projects, national and international courses, and recently we finalized the book “Port-Hamiltonian Systems Theory: An Introductory Overview” [23].

Three years ago, I retrieved my interest in power analysis under nonsinusoidal conditions and during the preparations of our book we had several discussions about this subject and the possibilities to approach the problem from a port-Hamiltonian perspective and Dirac structures in particular. During these discussions, Arjan always came up with the same but very important and fundamental questions: what is this reactive power, what are its origins, and does it have any physical meaning? With this contribution, I consider it as an honor, on the occasion of the 60th birthday of my scientific collaborator, colleague, and dear friend, to dedicate a chapter to our fruitful quests for interesting and open problems, and to recollect some thoughts and interpretations of reactive power and related concepts.

Happy birthday Arjan and enjoy reading!

4.1.1 Motivation and Background

The usage of alternative sources of power has caused that the problem of energy transfer optimization is increasingly involved with nonsinusoidal signals and nonlinear loads. The power factor (PF) is used as a measure of the effectiveness of the transfer of energy between an electrical source and a load. It is defined as the ratio between the power consumed by a load (real or active power), denoted as P, and the power delivered by a source (apparent power), denoted as S, i.e.,

$$\begin{aligned} \lambda := \frac{P}{S}. \end{aligned}$$

(4.1)

The active power is defined as the average of the instantaneous power and apparent power as the product of the root-mean-square norms of the source current and voltage. The standard approach to improve the PF is to place a passive compensator, such as a capacitor or an inductor, parallel to the load. Conceptually, the design of the compensator typically assumes that the source is ideal, i.e., the internal (Thevenin) impedance is negligible, producing a fixed sinusoidal voltage.

If the load is linear and time-invariant (LTI) and the source voltage is sinusoidal, the resulting stationary current generally is a shifted sinusoid, and the PF is the cosine of the phase-shift angle between the source voltage and current. Classically, the remaining part of the power is called reactive power, and is denoted as Q. The relationship between the three types of power is given by

$$\begin{aligned} S^2=P^2+Q^2. \end{aligned}$$

(4.2)

Thus, any improvement of the PF is accomplished by the reduction of the absolute value of the reactive power, hence reducing the phase shift between the current and the voltage.

For nonsinusoidal voltages and currents, the problem of decomposing the apparent power into active and reactive components is much more involved. Starting from the work of Steinmetz [21], Iliovici [14] and Budeanu [2], many authors have aimed to improve the concept of reactive power in the most general case; see e.g., [1, 8, 11], and the references therein. Every year dozens of articles are published on this subject and most of these contributions aim at decompositions of the load current into physical meaningful orthogonal quantities. The methods and ways of describing the power phenomena and to increase the effectiveness of the energy flow between the source and the load under nonsinusoidal conditions have not been standardized so far and the definition of reactive power has been changed several times [12, 13]. Why is this important? Apart from the economical reasons as electricity is a commodity, one of the main reasons is to reduce the operating costs of the power grid and to protect its reliability.

4.1.2 Contribution and Outline

In this chapter, a different approach is presented that generalizes the classical complex phasor representation of the port voltages and currents. The method relies on the so-called analytic signal using the Hilbert transform. This enables one to translate the power flows proposed in [9, 16] for three-phase systems to single-phase systems and naturally leads to the notion of a time-varying power triangle and its associated instantaneous PF. From an instrumentation and measurement perspective, the introduction of the time-varying power triangle offers interesting properties as it reveals an instantaneous view into the power flows in the system.

A major advantage of the proposed framework is that it is applicable to general loads (e.g., nonlinear and time-varying) as well as to general voltage and current waveforms (e.g., nonsinusoidal, non-periodical, interharmonics, etc.). Additionally, it is shown for LTI systems that Budeanu’s reactive power can be related to energy oscillations, but only in an average sense. Furthermore, Budeanu’s distortion power is decomposed into a part representing a measure of the fluctuation of power around the active power and a part that represents the fluctuation of power around Budeanu’s reactive power. This relaxes some of the assertions in [5].

The remainder of the chapter is organized as follows. In Sect. 4.2, the classical power model for systems operating under sinusoidal conditions is reviewed and an interpretation of the associated active and reactive power is provided from both a time- and frequency-domain perspective. The extension of the classical phasor approach is generalized to time-varying phasors in Sect. 4.3. Section 4.4 revisits the infamous Budeanu power model and provides some novel insights using the time-varying phasor approach. Finally, in Sect. 4.5, some examples are provided to illustrate the theory.

4.1.3 Notation

Given two square integrable T-periodic signals u(t) and i(t), we define the inner product as

$$\begin{aligned} \langle u,i \rangle := \frac{1}{T}\int \limits _0^T u(t)i(t)\mathrm{{d}}t, \end{aligned}$$

(4.3)

and by $||u||:=\sqrt{\langle u,u \rangle }$ the rms (root-mean-square) value. Time differentiation is denoted by $u'(t)=\frac{\mathrm{{d}}u}{\mathrm{{d}}t}(t)$. Voltages are represented in volts [V] and currents are represented in Ampère [A]. However, these units will be omitted in the text.

To simplify the presentation, all voltage and current waveforms are assumed to have zero mean values.

4.2 The Classical Sinusoidal Power Model

Consider the well-known classical case of a single-phase sinusoidal source (power system) transmitting power to a LTI load; see Fig. 4.1. Let the voltage at the load terminals be given by

$$\begin{aligned} u(t)=U\sqrt{2}\cos (\omega t + \alpha ), \end{aligned}$$

(4.4)

where $\omega = 2 \pi /T$. Under the assumption that the voltage at the terminals does not depend on the transmitted current (infinitely strong power system), the associated current reads

$$\begin{aligned} i(t)=I\sqrt{2}\cos (\omega t + \beta ). \end{aligned}$$

(4.5)

The instantaneous power delivered to the load is given by

$$\begin{aligned} p(t)=u(t)i(t) = \underbrace{P\big [1+\cos (2\omega t +2\alpha )\big ]}_{p_a(t)} + \underbrace{Q\sin (2\omega t+2\alpha )}_{p_r(t)}, \end{aligned}$$

(4.6)

where P and Q represent the active power and the reactive power defined by

$$\begin{aligned} \begin{aligned} P:=UI\cos (\varphi ),\\ Q:=UI\sin (\varphi ), \end{aligned} \end{aligned}$$

(4.7)

respectively, with $\varphi :=\alpha - \beta$ representing the phase shift between u(t) and i(t).

Fig. 4.1

The classical scenario of a single-phase power system transmitting power to a LTI load

4.2.1 On the Meaning of Active and Reactive Power

The term $p_a(t)$ in (4.6) describes the nonnegative component of the instantaneous power, with an average value equal to load’s active power P, i.e.,

$$\begin{aligned} P = \frac{1}{T}\int \limits _0^T p(t) \mathrm{{d}}t = \frac{1}{T}\int \limits _0^T p_a(t) \mathrm{{d}}t = UI\cos (\varphi ), \end{aligned}$$

(4.8)

and represents the one-directional flow of energy from the source to the load.

The alternating term $p_r(t)$ in (4.6) is characterized by an amplitude equal to load’s reactive power Q and average value equal to zero. This component characterizes the bidirectional flow of the transmitted energy from the source to the load. It is not present if load phase angle is equal to zero. Therefore, in case of a purely resistive load or if the load exhibits phase resonance, bidirectional oscillations in the energy flow between source and load do not exist. For example, if the load in Fig. 4.1 solely consists of a resistor, with resistance R, and is driven by a sinusoidal voltage of the form (4.4), then the associated current reads as in (4.5), with $\beta = \alpha$. Hence, there is no phase shift as $\varphi = 0$, and, according to (4.7), the active power equals $P_R= RI^2$, whereas the reactive power equals $Q_R =0$.

The alternating component $p_r(t)$ may thus be interpreted as the measure of the backward flow of energy between load’s reactance elements and the source. Indeed, if the load in Fig. 4.1 solely consists of an inductor, with inductance L, and is driven by a sinusoidal voltage of the form (4.4), with $\alpha =0$, then the associated current reads

$$\begin{aligned} i(t) = \frac{1}{L} \int \limits _0^t u(\tau ) \mathrm{{d}}\tau = \frac{U}{\omega L}\sqrt{2} \sin (\omega t) = I \sqrt{2} \cos \left( \omega t - \tfrac{\pi }{2}\right) . \end{aligned}$$

(4.9)

Hence, the inductor causes a phase shift $\varphi = \frac{\pi }{2}$ and stores a magnetic (co-)energy

$$\begin{aligned} e_L(t)=\frac{1}{2}Li^2(t) = E_{L}^{\text {max}} \sin ^2(\omega t), \end{aligned}$$

(4.10)

where $E_{L}^{\text {max}} = LI^2$. This suggests that the (inductive) reactive power equals

$$\begin{aligned} Q_L = UI\sin \left( \tfrac{\pi }{2}\right) = UI = \omega L I^2 = \omega E_{L}^{\text {max}}. \end{aligned}$$

(4.11)

Alternatively, the (inductive) reactive power can also be expressed in terms of the average stored magnetic (co-)energy as

$$\begin{aligned} Q_L = 2\omega E_L, \end{aligned}$$

(4.12)

with $E_L = \frac{1}{2}LI^2$. Obviously, the active power of an inductor equals $P_L=0$.

Similarly, if the load in Fig. 4.1 solely consists of a capacitor, with capacitance C, and is driven by a sinusoidal current of the form (4.5), with $\beta =0$, then the associated voltage reads

$$\begin{aligned} u(t) = \frac{1}{C} \int \limits _0^t i(\tau ) d \tau = \frac{I}{\omega C}\sqrt{2} \sin (\omega t) = U \sqrt{2} \cos \left( \omega t - \tfrac{\pi }{2}\right) . \end{aligned}$$

(4.13)

Hence, the capacitor causes a phase shift $\varphi = -\frac{\pi }{2}$ and stores an electric (co-)energy

$$\begin{aligned} e_C(t)=\frac{1}{2}Cu^2(t) = E_{C}^{\text {max}} \sin ^2(\omega t), \end{aligned}$$

(4.14)

where $E_{C}^{\text {max}} = CU^2$. This suggests that the (capacitive) reactive power equals

$$\begin{aligned} Q_C = UI\sin \left( -\tfrac{\pi }{2}\right) = -UI = -\omega C U^2 = -\omega E_{C}^{\text {max}}. \end{aligned}$$

(4.15)

Alternatively, the (capacitive) reactive power can also be expressed in terms of the average stored electric (co-)energy as

$$\begin{aligned} Q_C = -2\omega E_C, \end{aligned}$$

(4.16)

with $E_C = \frac{1}{2}CU^2$. Again, note that $P_C=0$.

Generally, in case of a load network consisting of LTI resistors, inductors and capacitors, the active power associated to each branch of the network may be expressed as

$$\begin{aligned} P_b = P_{R_b}, \end{aligned}$$

(4.17)

where $P_{R_b}$ represents the active power associated to the resistance in the bth branch. Note that $P_{L_b}=P_{C_b}=0$. The reactive power for each branch is then expressed as

$$\begin{aligned} Q_b = Q_{L_b} + Q_{C_b} = \omega \left( E_{L_b}^{\text {max}} - E_{C_b}^{\text {max}}\right) = 2 \omega \left( E_{L_b} - E_{C_b}\right) . \end{aligned}$$

(4.18)

Then, by Boucherot’s theorem [4], the total active power and the total reactive power are obtained by summing over all the branches, i.e.,

$$\begin{aligned} \begin{aligned} P&= \sum _b P_b,\\ Q&= \sum _b Q_b. \end{aligned} \end{aligned}$$

(4.19)

Remark 4.1

Note that compensation (reduction) of the reactive power naturally boils down to minimizing the difference between the total (average) magnetic and electric energies stored in the load network. Such perspective on reactive power compensation is known as energy equalization [11].

Remark 4.2

It is important to emphasize that the previous interpretations of reactive only apply to LTI systems driven by a purely sinusoidal voltage. If the load is nonlinear and/or time-varying, then it may be proven that reactive power does not uniquely relate to energy accumulation and it may be present in a purely resistive load. This will be exemplified in Sect. 4.5.

4.2.2 The Classical Phasor Representation

Alternatively, a standard method in electrical engineering is to represent the sinusoidal time functions of the voltages and currents by their complex phasor representation [7]

$$\begin{aligned} \underline{U}=U\sqrt{2}e^{j\alpha }, \ \underline{I}=I\sqrt{2}e^{j\beta }, \end{aligned}$$

(4.20)

where $j:=\sqrt{-1}$. This enables one to define the complex power

$$\begin{aligned} \underline{S}:=\frac{1}{2}\underline{U}\,\underline{I}^* = UIe^{j\varphi } = UI\cos (\varphi ) + jUI\sin (\varphi ) = P+jQ, \end{aligned}$$

(4.21)

the well-known power triangle (see Fig. 4.2), the PF as $\lambda = \cos (\varphi )$, and the notion of complex impedance [7]

$$\begin{aligned} \underline{Z}=\frac{\underline{U}}{\underline{I}} = \frac{U}{I} e^{j\varphi } = \frac{P+2j\omega \left( E_L - E_C\right) }{\frac{1}{2}\underline{I}\,\underline{I}^*}, \end{aligned}$$

(4.22)

where $E_L$ and $E_C$ now represent the total mean magnetic and electric energies, respectively. In the same way, the complex admittance reads

$$\begin{aligned} \underline{Y}=\frac{\underline{I}}{\underline{U}} =\frac{I}{U} e^{-j\varphi } = \frac{P+2j\omega \left( E_C - E_L\right) }{\frac{1}{2}\underline{U}\,\underline{U}^*}. \end{aligned}$$

(4.23)

Fig. 4.2

The classical power triangle with $S=|\underline{S}|$

The underlying mathematical principle behind the transition from the sinusoidal time functions of the voltages and currents to their complex phasor representation is the so-called analytical signal widely used in telecommunication applications [22]. The analytic signal corresponding to the voltage (4.4) is given by

$$\begin{aligned} \underline{u}(t) = U\sqrt{2}\cos (\omega t + \alpha ) + j U\sqrt{2} \sin (\omega t + \alpha ) = U\sqrt{2}e^{j(\omega t + \alpha )}, \end{aligned}$$

(4.24)

and, similarly, the analytic signal corresponding to (4.5) is given by

$$\begin{aligned} \underline{i}(t) = I\sqrt{2}\cos (\omega t + \beta ) + j I \sqrt{2}\sin (\omega t + \beta )= I\sqrt{2}e^{j(\omega t + \beta )}. \end{aligned}$$

(4.25)

Hence, the transition from the analytical signal representations (4.24)–(4.25) to the phasors (4.20) is accomplished by multiplying the latter with $e^{-j\omega t}$, which defines a linear (coordinate) transformation.

Fig. 4.3

Series RL circuit driven by a sinusoidal voltage: uncompensated ($C=0$) and compensated ($C>0$)

Furthermore, a straightforward computation shows that

$$ \frac{1}{T} \int \limits _0^{T} \underline{u}(t)\underline{i}^*(t) \mathrm{{d}}t = \underline{U} \, \underline{I}^*. $$

Thus, the correspondence between sinusoidal signals and their phasor representation is power-preserving once the real voltage and current signals are extended toward their analytic signal representations. This demonstrates that both P and Q are, in fact, average quantities.

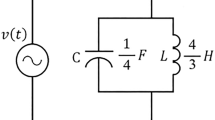
4.2.3 RL Circuit Example

Consider the uncompensated RL circuit shown in Fig. 4.3 driven by a sinusoidal voltage

$$\begin{aligned} u(t)=10\sqrt{2}\cos {(t)} \ \Rightarrow \ \underline{U} = 10\sqrt{2}. \end{aligned}$$

The load admittance is given by

$$\begin{aligned} \underline{Y}=\frac{1}{1+2j}=\frac{1}{5}\sqrt{5}e^{-j \arctan (2)} \ \Rightarrow \ \underline{I}=\underline{Y}\,\underline{U} = 2\sqrt{10}e^{-j\arctan (2)}. \end{aligned}$$

The complex power is then easily computed as $\underline{S} = 20+j40$. Hence, the active power is $P=20$ [W], the reactive power $Q=40$ [VAr], and the apparent power $S=|\underline{S}|=20\sqrt{5}$ [VA]. The results in a PF $\lambda =0.447$. If a shunt capacitor is placed to compensate Q, then it is clear that a capacitance of $C=0.4$ [F] is necessary to compensate the effect of the inductance and to drive the PF to unity.

4.3 Time-Varying Phasors

Note that the relationship between the real voltage and current signals and their imaginary counterparts in (4.24)–(4.25) is a $90^{\circ }$ backshift operation. For arbitrary waveforms this operation is generalized by the Hilbert transform [22]. Indeed, denoting by $\hat{u}(t):=\mathcal {H}\{u(t)\}$ the Hilbert transform

$$\begin{aligned} \mathcal {H}\{u(t)\} = \frac{\text {PV}}{\pi } \int \limits _{-\infty }^\infty \frac{u(\tau )}{t-\tau }\mathrm{{d}}\tau , \end{aligned}$$

(4.26)

with PV the Cauchy principal value, of the real voltage u(t), then from standard complex analysis we know that

$$\begin{aligned} \underline{u}(t) = U(t)\sqrt{2}e^{j\alpha (t)}, \end{aligned}$$

(4.27)

where

$$\begin{aligned} U(t)&= \sqrt{\frac{u^2(t)+\hat{u}^2(t)}{2}} = |\underline{u}(t)|,\\ \alpha (t)&= \arctan \left\{ \frac{\hat{u}(t)}{u(t)}\right\} = \mathrm {Im}\{\ln \underline{u}(t)\} = \mathrm {arg}\{\underline{u}(t)\},\\ \omega _\alpha (t)&= \alpha '(t) = \frac{\hat{u}'(t)u(t)-u'(t)\hat{u}(t)}{u^2(t)+\hat{u}^2(t)} = \mathrm {Im}\left\{ \frac{\underline{u}'(t)}{\underline{u}(t)}\right\} , \end{aligned}$$

represent the instantaneous amplitude, phase, and frequency, respectively. In a similar fashion, the complex port current can be written as

$$\begin{aligned} \underline{i}(t) = I(t)\sqrt{2}e^{j\beta (t)}. \end{aligned}$$

(4.28)

Remark 4.3

It is important to emphasize that in spite of both being measured in radians per second, harmonic and instantaneous radial frequencies are different concepts, which only coincide in the sinusoidal case. Indeed, for a voltage of the form (4.4), we have $\underline{u}(t) = \underline{U}$ and $\alpha (t)= \omega t + \alpha$, and thus $\omega _\alpha (t) = \omega$. See, e.g., [22] for further information. In [16], the representation (4.27) was justified based on Fourier transform. However, as argued in [22], the only way to unambiguously associate U(t) and $\alpha (t)$ with amplitude, phase, and frequency is via the Hilbert transform. Additionally, note that (4.27) allows to removing the fundamental phase $\omega t$, i.e., $\underline{U}(t) = U(t)\sqrt{2}e^{j\tilde{\alpha }(t)}$, where $\tilde{\alpha }(t):=\alpha (t) - \omega t$.

Remark 4.4

The use of analytic signals, or the voltage and current representations (4.27) and (4.28), is not new in power systems analyses and control. See, for instance, the work of [15]. The Hilbert transform is also successfully used in [19] to derive a single-phase version of the well-known instantaneous p-q theory [8].

4.3.1 Kirchhoff Operators and Tellegen’s Theorem

In the time domain, starting from the instantaneous power delivered at the port, i.e., $p(t)=u(t)i(t)$, Tellegen’s theorem in generalized form can be stated as [18]

$$\begin{aligned} \mathcal {A}\{u(t)\}\mathcal {B}\{i(t)\} = \sum _b \mathcal {A}\{u_b(t)\}\mathcal {B}\{i_b(t)\}, \end{aligned}$$

(4.29)

where $\mathcal {A}$ and $\mathcal {B}$ are so-called Kirchhoff voltage and current operators, respectively. A Kirchhoff voltage (current) operator is defined as an operation that if applied to a set of voltages (currents) that satisfy KVL (KCL) generates a new set of numbers or functions that also satisfy KVL (KCL). These quantities need not have the units of voltages (currents) and may depend on other parameters or variables introduced by the operator. All linear operations that operate in the same way on all branches and ports of the network are Kirchhoff operators. Well-known examples of linear operators are: differentiation, integration, averaging, complex conjugation, and time-shifting.

Since the Hilbert transform is also a linear operator, i.e.,

$$\begin{aligned} \mathcal {H}\left\{ \sum _n c_n f_n \right\} = \sum _n c_n\mathcal {H}\left\{ f_n \right\} , \end{aligned}$$

(4.30)

where $c_n$ are arbitrary numbers and $f_n$ are arbitrary functions for which the Hilbert transform is defined, we may select the Kirchhoff operators in (4.29) as $\mathcal {A}=\mathcal {I} + j \mathcal {H}$ and $\mathcal {B}=\mathcal {I} - j \mathcal {H}$, where $\mathcal {I}$ is the identity operator, i.e., $\mathcal {I}\{f_n\} = f_n$. This yields the complex power balance

$$\begin{aligned} \big (u(t)+j\hat{u}(t)\big )\big (i(t)-j\hat{i}(t)\big )= \sum _b \big (u_b(t)+j{\hat{u}_b(t)}\big )\big (i_b(t)-j{\hat{i}}_b(t)\big ). \end{aligned}$$

(4.31)

This motivates and justifies the developments in the next section.

4.3.2 Time-Varying Complex Power

Starting from the analytical port voltage and current, (4.27) and (4.28), the time-domain nonsinusoidal equivalent of the complex power is defined by the time-varying complex power (compare with (4.31))

$$\begin{aligned} \underline{S}(t) := \frac{1}{2}\underline{u}(t)\underline{i}^*(t) =U(t)I(t)e^{j\varphi (t)} =P(t) + jQ(t), \end{aligned}$$

(4.32)

where $\varphi (t):=\alpha (t)-\beta (t)$ denotes the instantaneous phase shift between $\underline{u}(t)$ and $\underline{i}(t)$, and

$$\begin{aligned} P(t)&:= \frac{1}{2}\big (u(t)i(t) + \hat{u}(t)\hat{i}(t)\big ),\end{aligned}$$

(4.33)

$$\begin{aligned} Q(t)&:= \frac{1}{2}\big (\hat{u}(t)i(t) - u(t)\hat{i}(t)\big ), \end{aligned}$$

(4.34)

or, equivalently,

$$\begin{aligned} P(t) := \frac{1}{2}\mathrm {Re}\big \{\underline{u}(t)\underline{i}^*(t)\big \},\quad Q(t) := \frac{1}{2}\mathrm {Im}\big \{\underline{u}(t)\underline{i}^*(t)\big \}, \end{aligned}$$

represent the time-varying real and imaginary powers, respectively. Furthermore, the time-varying apparent power equals

$$\begin{aligned} S(t)=|\underline{S}(t)| = U(t)I(t) = \sqrt{P^2(t)+Q^2(t)}, \end{aligned}$$

(4.35)

which naturally suggests the definition of a time-varying PF

$$\begin{aligned} \lambda (t):=\frac{P(t)}{S(t)} = \cos \big (\varphi (t)\big ), \end{aligned}$$

(4.36)

and a time-varying power triangle as shown in Fig. 4.4.

Fig. 4.4

The time-varying power triangle

Another feature of the analytical representation of the port voltage and current is that the real parts of (4.27) and (4.28) are representing the real port voltage and current, which, in turn, are expressed in a very familiar form:

$$\begin{aligned} u(t)&= \mathrm {Re}\{\underline{u}(t)\} = U(t)\sqrt{2}\cos \big (\alpha (t)\big ),\\ i(t)&= \mathrm {Re}\{\underline{i}(t)\} = I(t)\sqrt{2}\cos \big (\beta (t)\big ). \end{aligned}$$

This means that the instantaneous power (4.6) generalizes to

$$\begin{aligned} p(t) = P(t)\left[ 1+\cos \big (2\alpha (t)\big ) \right] + Q(t)\sin \big (2\alpha (t)\big ), \end{aligned}$$

(4.37)

where P(t) and Q(t) are now rather expressed as

$$\begin{aligned} P(t)&=U(t)I(t)\cos \big (\varphi (t)\big ),\\ Q(t)&= U(t)I(t)\sin \big (\varphi (t)\big ). \end{aligned}$$

Expression (4.37) is extremely general and also holds for non-periodic waveforms (provided (4.26) exists as a principal value). For that reason, we propose to refer to (4.37) as the ‘universal power template (UPT).’ In Sect. 4.4, one particular application of the UPT is highlighted.

4.3.3 Resistors, Inductors, and Capacitors

Let us next study the time-varying real and imaginary powers associated to the resistor, inductor, and capacitor. Interestingly, these powers bear a marked similarity in form as the powers derived for three-phase systems from the Poynting vector in [9] (see also [16]).

The Resistor

Consider an LTI resistor R driven by a nonsinusoidal voltage u(t). Using Ohm’s law $u(t)=Ri(t)$, the associated time-varying real power (4.33) takes the form

$$\begin{aligned} P_R(t)&= \frac{1}{2}\big (Ri^2(t) + R\hat{i}^2(t)\big )=RI^2(t), \end{aligned}$$

whereas the imaginary power (4.34) is zero, i.e., $Q_R(t)=0$, since $\mathcal {H}\{u(t)\} = R\,\mathcal {H}\{i(t)\}$.

The Inductor

For an LTI inductor $u(t)=Li'(t)$. Using the time stationarity of the Hilbert transform [22], we have that $\mathcal {H}\{i'(t)\} = (\mathcal {H}\{i(t)\})'$. Hence, the real power (4.33) reads

$$\begin{aligned} P_L(t) = \frac{1}{2}\left( Li'(t)i(t) + L\hat{i}'(t)\hat{i}(t)\right) = LI_L'(t)I_L(t) = E'_L(t), \end{aligned}$$

where $E_L(t)=\frac{1}{2}LI^2(t)$ represents the envelope of the oscillation of the inductor’s magnetic energy storage. The imaginary power (4.34) now takes the form

$$\begin{aligned} Q_L(t) = \frac{1}{2}\big (L\hat{i}'(t)i(t) - Li'(t)\hat{i}(t)\big ), \end{aligned}$$

which, after multiplication of the numerator and denominator with $i^2(t)+\hat{i}^2(t)$, yields

$$\begin{aligned} Q_L(t) = \frac{1}{2}L\frac{\hat{i}'(t)i(t) - i'(t)\hat{i}(t)}{i^2(t)+\hat{i}^2(t)}\big (i^2(t)+\hat{i}^2(t)\big ) = \beta '(t)LI^2(t) = 2\omega _\beta (t)E_L(t). \end{aligned}$$

Note that if i(t) is of the form (4.5), we have $\omega _\beta (t)=\omega$ and $I(t)=I$, and thus that $Q_L=2\omega E_L$, as established in (4.12).

The Capacitor

In a similar fashion, for an LTI capacitor $i(t)=Cu'(t)$, the real power (4.33) reads

$$\begin{aligned} P_C(t) = \frac{1}{2}\big (u(t)Cu'(t) + \hat{u}(t)C\hat{u}'(t)\big ) = CU(t)U'(t) = E'_C(t), \end{aligned}$$

where $E_C(t)=\frac{1}{2}CU^2(t)$ represents the envelope of the oscillation of the capacitor’s electric energy storage. The imaginary power (4.34) now takes the form

$$\begin{aligned} Q_C(t) = \frac{1}{2}\big (\hat{u}(t)Cu'(t) - u(t)C\hat{u}'(t)\big ), \end{aligned}$$

which, after multiplication of the numerator and denominator with $u^2(t)+\hat{u}^2(t)$, yields

$$\begin{aligned} Q_C(t)&= \frac{1}{2}C\frac{\hat{u}(t)u'(t) - u(t)\hat{u}'(t)}{u^2(t)+\hat{u}^2(t)}\big (u^2(t)+\hat{u}^2(t)\big ) = -\alpha '(t)CU^2(t)\\ {}&= -2\omega _\alpha (t)E_C(t). \end{aligned}$$

Under sinusoidal conditions, i.e., if u(t) is of the form (4.4), then $\omega _\alpha (t)=\omega$ and $U(t)=U$, and thus $Q_C=-2\omega E_{C}$, as in (4.16).

4.4 Budeanu’s Concept of Reactive and Distortion Power Revisited

Consider a single-phase LTI power system with distorted voltage and current waveforms of the form

$$\begin{aligned} u(t)&= \sum _k U_k\sqrt{2} \cos (k\omega t + \alpha _k),\end{aligned}$$

(4.38)

$$\begin{aligned} i(t)&= \sum _k I_k\sqrt{2} \cos (k\omega t + \beta _k), \end{aligned}$$

(4.39)

with $\varphi _k=\alpha _k - \beta _k$. It is readily checked that the active power (from here on denoted by $P_A$) is straightforwardly obtained from the instantaneous power $p(t)=u(t)i(t)$ after averaging over a period, i.e.,

$$\begin{aligned} P_A := \frac{1}{T}\int \limits _0^T p(t)\mathrm{{d}}t = \sum _{k} U_kI_k \cos (\varphi _k). \end{aligned}$$

(4.40)

However, how to define and generalize the reactive power?

Inspired by, e.g., Bunet [3] and Boucherot’s theorem [4], Budeanu [2] was among the first who tried to find an answer to this question and proposed to define reactive power as

$$\begin{aligned} Q_B := \sum _{k} U_kI_k \sin (\varphi _k). \end{aligned}$$

(4.41)

He also observed that for nonsinusoidal voltages and currents the quadratic sum of the active and reactive power is not equal to the apparent power S as in the sinusoidal case, and ended up with $S^2=P_A^2+Q_B^2+(\mathrm {REST})^2$. To fill in this gap, a new concept

$$\begin{aligned} D_B := \sqrt{S^2 -P_A^2 -Q_B^2}, \end{aligned}$$

(4.42)

called distortion (or deformation) power was proposed.

For decades, Budeanu’s power model has enjoyed a lot of support and is set down in many publications and academic textbooks on power phenomena in systems with periodical and distorted waveforms, and for a long time has been part of the IEEE Standard [12]. Nevertheless, from the very beginning it has also been criticized by various opponents. Apart from the fact that it took almost 50 years before the first instruments where developed to measure Budeanu’s reactive and distortion powers [10], critical questions where raised due to the apparent lack of physical meaning of the distortion power as it does not represent a conserved quantity and the (unauthorized) summing up of amplitudes of oscillating components of different harmonics [20], see also [1] and the references therein. Budeanu’s power model was finally vigorously challenged by Czarnecki, and, although the arguments in [5] did not convince adherents of Budeanu’s power model instantaneously [8], it was finally abandoned from the latest IEEE Standard [13].

In the following subsections it is shown, using the notion of time-varying phasors and the UPT, that the assertions against Budeanu’s power model are either wrong, misinterpreted, or overstressed.

4.4.1 Budeanu’s Reactive Power Represents an Average

First of all, we note that Budeanu’s reactive power (4.41) can be expressed in the time domain using the Hilbert transform as [17]

$$\begin{aligned} Q_B := \langle \hat{u},i\rangle = \frac{1}{T}\int \limits _0^T \hat{u}(t)i(t)\mathrm{{d}}t, \end{aligned}$$

(4.43)

where we recall that $\hat{u}(t)=\mathcal {H}\{u(t)\}$ denotes the Hilbert transform. Interestingly, using the fact that $\langle \hat{u},i\rangle = -\langle u,\hat{i}\rangle$, it is readily observed that (4.43) is equivalent to averaging (4.34) over a period, i.e.,

$$\begin{aligned} Q_B := \frac{1}{T}\int \limits _0^T Q(t)\mathrm{{d}}t. \end{aligned}$$

(4.44)

Hence, Budeanu’s reactive power $Q_B$ does not represent a magnitude or an absolute quantity, but an average; the average of the imaginary power Q(t) in a fashion similar to the active power $P_A$ which represents the average of the real power P(t). Furthermore, this means that Budeanu’s reactive power represents the average of the difference between the envelopes of the oscillation of the magnetic and electric energies.

4.4.2 Power Fluctuations

It is correctly observed in [5] that Budeanu’s concept of distortion power is not directly related to waveform distortion of the port voltages and currents itself. It may, however, be related to the fluctuations of the real and imaginary powers around their averages, i.e., the active and reactive powers. In this subsection, it is shown that the norms of these fluctuations can be naturally interpreted as distortion powers.

Let ${D_P(t):=P(t)-P_A}$ and ${D_Q(t):=Q(t)-Q_B}$ represent the power fluctuations around the active and reactive powers $P_A$ and $Q_B$, respectively. Furthermore, let $I_P(t):=I(t)\cos (\varphi (t))$ and $I_Q(t):=I(t)\sin (\varphi (t))$, then it is easily shown that $\langle I_P,I_Q\rangle =0$, i.e., the currents $I_P(t)$ and $I_Q(t)$ are mutually orthogonal. Hence, the ‘normed’ apparent power can be decomposed into two components:

$$ ||U||^2||I||^2 = ||U||^2||I_P||^2 + ||U||^2||I_Q||^2, $$

which, in turn, suggest

$$\begin{aligned} ||U||\,||I_P||&\ge |\langle U,I_P\rangle | \equiv |P_A|,\\ ||U||\,||I_Q||&\ge |\langle U,I_Q\rangle | \equiv |Q_B|. \end{aligned}$$

If $||U||\,||I_P|| > |\langle U,I_P\rangle |$, the residual is given by

$$\begin{aligned} D_{P_U}^2 :=||U||^2 ||I_P||^2 - \langle U,I_P\rangle ^2 = \frac{1}{2T^2}\int \limits _0^T\int \limits _0^T \big (U(s)I_P(t) - U(t)I_P(s)\big )^2\mathrm{{d}}s\mathrm{{d}}t. \end{aligned}$$

Similarly, if $||U||\,||I_Q|| > |\langle U,I_Q\rangle |$, we have

$$\begin{aligned} D_{Q_U}^2 :=||U||^2 ||I_Q||^2 - \langle U,I_Q\rangle ^2= \frac{1}{2T^2}\int \limits _0^T\int \limits _0^T \big (U(s)I_Q(t) - U(t)I_Q(s)\big )^2\mathrm{{d}}s\mathrm{{d}}t. \end{aligned}$$

This naturally suggest the decomposition of distortion power into two components:

$$\begin{aligned} D_B^2 := D_{P_U}^2 + D_{Q_U}^2, \end{aligned}$$

(4.45)

where $D_{P_U}$ and $D_{Q_U}$ can be considered as a measure of the fluctuation (distortion) around the active power and Budeanu’s reactive power, respectively, relative to the voltage amplitude. Hence, we have

$$\begin{aligned} S^2 = P_A^2+Q_B^2 + D_B^2 = P_A^2 + D_{P_U}^2 + Q_B^2 + D_{Q_U}^2. \end{aligned}$$

(4.46)

In the sinusoidal case, $D_{P_U}=D_{Q_U}=0$, and (4.46) reduces to the well-known standard (static) power triangle.

On the other hand, an equally valid starting point would be by selecting instead of $I_P(t)$ and $I_Q(t)$, the voltages $U_P(t):=U(t)\cos (\varphi (t))$ and $U_Q(t):=U(t)\sin (\varphi (t))$. This suggest to decompose the ‘normed’ apparent power as

$$ ||U||^2||I||^2 = ||U_P||^2||I||^2 + ||U_Q||^2||I||^2, $$

and, in a similar fashion as before, gives rise to the distortion powers, $D_{P_I}$ and $D_{Q_I}$, relative to the current amplitude, and satisfying

$$\begin{aligned} D_B^2 := D_{P_I}^2 + D_{Q_I}^2. \end{aligned}$$

(4.47)

Note that, in general, $D_{P_U} \ne D_{P_I}$ and $D_{Q_U} \ne D_{Q_I}$.

4.5 Examples

In this section, two examples are provided to illustrate the previous developments. First, a simple LTI circuit operating under nonsinusoidal conditions is discussed. The second example consists of a periodically switched resistive (triac) circuit.

Fig. 4.5

Fluctuation of the time-varying real and imaginary powers around the active power and Budeanu’s reactive power for the uncompensated circuit of Fig. 4.3 driven by the nonsinusoidal voltage (4.48)

4.5.1 RL Circuit Example (Cont’d)

Consider again the (uncompensated) series RL circuit as shown in Fig. 4.3, but now supplied by a nonsinusoidal voltage

$$\begin{aligned} u(t)=10\sqrt{2}\cos {(t)}+5\sqrt{2}\cos {(5t)}. \end{aligned}$$

(4.48)

In terms of the current amplitude, the complex power reads

$$\begin{aligned} \underline{S}(t)&= P_R(t) + P_L(t) + j Q_L(t) = RI^2(t) + LI'(t)I(t)+ j\omega _\beta (t)LI^2(t). \end{aligned}$$

The waveforms for $P(t)=P_R(t)+P_L(t)$ and $Q(t)=Q_L(t)$, and their average values $P_A = 20.248$ [W] and $Q_B=42.475$ [VAr] are depicted in Fig. 4.5. Note that the Budeanu reactive power is clearly related with energy oscillation, but only in an average sense, i.e.,

$$\begin{aligned} Q_B = \frac{2}{T} \int \limits _0^T \omega _\beta (t)E_L(t)\mathrm{{d}}t, \end{aligned}$$

with $E_L(t)=\frac{1}{2}LI^2(t)$ represents the envelope of the magnetic energy. The power fluctuations $D_P(t)$ and $D_Q(t)$ are also indicated in Fig. 4.5. Furthermore, Fig. 4.6 shows the time-varying power triangle associated to (4.35), which is expanding and contracting at the speed ${\omega _\varphi (t)=\varphi '(t)}$. Since for this particular example the same current is flowing through both the resistor and the inductor, the ‘normed’ apparent power can be written as

$$\begin{aligned} ||U||^2||I||^2 = ||RI+LI'||^2||I||^2 + ||\omega _\beta L I||^2||I||^2. \end{aligned}$$

It seems therefore most natural to consider the distortion power relative to the port current amplitude. Indeed, the fluctuation around the active power $P_A=R||I||^2$ is caused by the rate of change of $E_L(t)$, i.e., $E'_L(t)=LI'(t)I(t)$. This change of stored energy is due to the variation of the voltage and the current amplitudes and must come from real power. This causes the fluctuation of $D_P(t)$ for which the distortion power $D_{P_I} = ||U_P||\,||I||$ applies, with $||U_P|| = ||LI'||$. The distortion power associated with the fluctuation $D_Q(t)$ equals $D_{Q_I}=||U_Q||\,||I||$, with $||U_Q||=||\omega _\beta L I||$. The values of the distortion power, including the alternative decomposition relative to the voltage amplitude, are computed (in [VAd]) as follows:

$D_B$	$D_{P_U}$	$D_{Q_U}$	$D_{P_I}$	$D_{Q_I}$
17.799	13.245	11.891	12.664	12.508

Fig. 4.6

The time-varying power triangle for the uncompensated circuit of Fig. 4.3 driven by the nonsinusoidal voltage (4.48)

The question that remains is how to improve the PF? It is known [5] that the addition of a shunt capacitor $C=0.189$ [F] renders $Q_B=0$. However, the PF then becomes even worse than in the uncompensated case (from $\lambda = 0.403$ to $\lambda = 0.353$) as the distortion power increases to $D_B = 53.654$ [VAd]. Hence, the compensation of Budeanu’s reactive power in this way is indeed useless for PF improvement and this was one of the main motivation behind the assertions in [5] against Budeanu’s power model.

However, as explained in [24], the main reason why in the above example the compensator current, which renders Budeanu’s reactive power to zero, does not reduce the source current—and even increases the distortion power—is that this particular compensator current and the nonactive part of the load current are not mutually orthogonal. The appropriate choice of the current that needs to be compensated is the co-called Budeanu current:

$$\begin{aligned} i_B(t) := \frac{Q_B}{||\hat{u}||^2}\hat{u}(t). \end{aligned}$$

(4.49)

Consequently, if the compensator is supplying the Budeanu reactive current to the load, the Budeanu reactive power seen by the source will be zero and the distortion power remains unaltered. As a result, the apparent power decreases. This shows that by choosing the appropriate compensation current the PF increases and that the Budeanu reactive power concept, in general, does lead to a compensation scheme that reduces the line losses, except for systems in which $Q_B=0$ already before compensation.

Fig. 4.7

Series RL circuit driven by a nonsinusoidal voltage with compensation network to render $Q_B=0$ without altering the distortion power

The compensation results for the RL circuit of Fig. 4.3, supplied with (4.48) and based on compensation of the Budeanu current (4.49), are shown in Fig. 4.7. It should be emphasized that, in general, the compensator supplying the Budeanu current cannot be realized by a single lossless shunt element. In fact, for the given example, it is composed of the same capacitor $C=0.189$ [F] as before, but in series with a parallel connection of a capacitor $C_x=0.128$ [F] and an inductor $L_x=1.805$ [H]. This compensator increases the PF to $\lambda = 0.751$.

Remark 4.5

Although this example demonstrates that, in spite the fact that compensation based on the Budeanu current (if it exists), always leads to an improvement of the PF without altering the distortion power, it may not lead to optimal results as power fluctuations around the average powers may still exist and their compensation using passive filters seems so far not trivial from a time-domain perspective. On the other hand, based on the approach of [19], the power fluctuations can be compensated using an active filter.

4.5.2 Triac Circuit

Consider the uncompensated (i.e., $C=0$) triac circuit shown in Fig. 4.8 [6]. Under the assumption that $u(t)=220\sqrt{2}\sin (t)$, $R=1$ $\varOmega$, and a switching angle $\alpha = 135^\circ$, the apparent power equals

$$\begin{aligned} S=\Vert u\Vert \,\Vert i\Vert = 14.588~[\text {kVA}], \end{aligned}$$

(4.50)

whereas the active power $P_A=4.397$ [kW]. This means that the PF is far less than unity, i.e., $\lambda \approx 0.3$. The Budeanu reactive power equals $Q_B = 7.703$ [kVAr], whereas the distortion power and its associated decomposition reads (in [kVAd]):

$D_B$	$D_{P_U}$	$D_{Q_U}$	$D_{P_I}$	$D_{Q_I}$
11.582	8.190	8.190	8.671	7.678

Fig. 4.8

Triac circuit and its associated Lissjous plot. Although there is no energy storage, the circuit exhibits a reactive power that is equal to the sum of the areas $A_1+A_2$. The reactive power can be fully compensated using a capacitor

It is important to realize that the uncompensated circuit does not store any energy. The reason why no energy is accumulated in the circuit becomes apparent when we consider the Lissajous plot of Fig. 4.8. Here it is observed that, although there is a phase shift between the current and voltage caused by the moments that the triac is switching ON, there is no energy accumulation as $i(t) \equiv 0$ whenever $u(t) \equiv 0$, and vice versa. From a frequency-domain perspective, the presence of reactive power can be explained as follows. The fundamental harmonic of the supply current reads

$$\begin{aligned} \begin{aligned} i_1(t)&= 40.317 \sqrt{2} \sin (t - 0.334\pi ), \end{aligned} \end{aligned}$$

which is subsequently decomposed into an active component, $i_{1_a}(t)$, that is directly proportional (collinear) with the supply voltage and a quadrature component $i_{1_r}(t)$ as

$$\begin{aligned} i_1(t) = i_{1_a}(t) + i_{1_r}(t) = 19.987 \sqrt{2} \sin (t) - 35.014 \sqrt{2} \cos (t). \end{aligned}$$

Now, $P_A = \Vert u\Vert \,\Vert i_{1_a}\Vert$ and $Q_B = \Vert u\Vert \,\Vert i_{1_r}\Vert$. Thus, the active power is related to the part of the current that is in-phase with the voltage, whereas the reactive power is related to the part that is exactly $90^{\circ }$ out-of-phase. The remaining part of the current, $i_d(t)=i(t)-i_1(t)$, represents the harmonics that are due to the triac invoked distortion of the supply voltage and is responsible for the distortion power.

Although there is no energy accumulation, we may conclude that the triac circuit exhibits an inductive-like character since ${Q_B>0}$. Hence, it is natural to compensate this behavior by placing a shunt capacitor. The value of the capacitor that fully compensates the reactive power equals $C = 0.159$ [F]. See [6] for more details.