Heat and Mass Transfer in Rotating Cone-and-Disk Systems for Laminar Flows

Abstract

This chapter focuses on laminar flow, heat and mass transfer between a disk and a cone that touches the disk with its apex. It comprises such geometries as “rotating cone—stationary disk”, “rotating disk—stationary cone”, “co-rotating or contra-rotating disk and cone” and “non-rotating conical diffuser”. The influence of the boundary conditions and various Prandtl/Schmidt numbers on the pressure, velocity and temperature profiles, as well as on the Nusselt/Sherwood numbers was revealed. Novel is the section describing effects of the Prandtl and Schmidt numbers, as well as a review of the relevant recently published works. In Chap. 6, results of different authors for the problems of convective heat and mass transfer for the Prandtl and Schmidt numbers larger than unity are critically analysed and generalized. Chapter 6 presents original theoretical models of the author developed for naphthalene sublimation in air and electrochemical problems. In the integral method of the author, effects of large Prandtl and Schmidt numbers are taken into account.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 General Characterization of the Problem

In the past, non-rotating conical diffusers (Fig. 5.1) were modeled using simplified Navier–Stokes equations without flow pre-swirl at the inlet [1]. Flow pre-swirl effects on the heat transfer were for the first time studied by the author of this work [2].

Fig. 5.1

Schematic of swirling flow in a stationary conical diffuser [9]

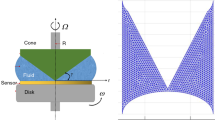
Cone-and-plate devices, where flow develops in a gap with small angles γ = 1…0.5° between a rotating cone and a stationary plate (Fig. 5.2), are used in viscosimetry [3–5]. Medicine employs such devices for nurturing endothelial cells that grow as a monolayer on the non-rotating plate, whereas a cone rotates slowly to renew the feeding fluid and simultaneously not to damage the cells [6–8].

Fig. 5.2

Schematic of fluid flow in a gap with a rotating cone and a stationary disk [9]

Flow regimes in cone-and-plate devices were studied experimentally [8], simulated using CFD codes [3, 8] and using perturbation techniques [5–7]. Self-similar Navier–Stokes and energy equations were derived and solved by the author of this work [2, 9–11].

Convective heat transfer in cone-and-disk configurations, with one of them rotating or both co-rotating/contra-rotating, along with a stationary conical diffuser, depends strongly on the radial temperature distribution on the disk [2, 9, 10]. Simulations were done mostly for air (Pr = 0.71); new phenomena in heat and mass transfer for other values of the Prandtl and Schmidt numbers were first investigated by the author in [11].

For the small angle γ, the Navier–Stokes Eqs. (2.1)–(2.3) can be simplified [5–7] for the considered laminar flow

$$- \frac{{v_{\varphi }^{ 2} }}{r} = - \frac{1}{\rho }\frac{{{\partial }p}}{{{\partial }r}} + \nu \frac{{{\partial }^{2} {{v}}_{r} }}{{{\partial }z^{2} }},$$

(5.1)

$$v_{r} \frac{{{\partial }v_{\varphi } }}{{{\partial }r}} + v_{z} \frac{{{\partial }v_{\varphi } }}{{{\partial }z}} + \frac{{v_{r} v_{\varphi } }}{r} = \nu \frac{{{\partial }^{2} v_{\varphi } }}{{\partial z^{2} }},$$

(5.2)

$$- \frac{1}{\rho }\frac{{{\partial }p}}{{{\partial }z}} + \nu \frac{{{\partial }^{2} {{v}}_{z} }}{{{\partial }z^{2} }} = 0.$$

(5.3)

A perturbation solution of Eqs. (5.1)–(5.3) by the method of expansion in the small parameter $Re = Re_{\Omega } {\eta }_{1}^{2} /12$ (where $\eta_{1} = {h \mathord{\left/ {\vphantom {h r}} \right. \kern-0pt} r}$) yields [5]

$${{v_{r} } \mathord{\left/ {\vphantom {{v_{r} } {(\Omega r)}}} \right. \kern-0pt} {(\Omega r)}} = Re(1.8\tilde{z}^{2} - \tilde{z}^{4} - 0.8\tilde{z}),$$

(5.4)

$${{v_{\varphi } } \mathord{\left/ {\vphantom {{v_{{\varphi }} } {(\Omega r)}}} \right. \kern-0pt} {(\Omega r)}} = \tilde{z} + Re^{2} ( - 83\tilde{z} + 70\tilde{z}^{4} + 63\tilde{z}^{5} - 50\tilde{z}^{7} )/175,$$

(5.5)

$${{v_{z} } \mathord{\left/ {\vphantom {{v_{z} } {(\Omega r)}}} \right. \kern-0pt} {(\Omega r)}} = Re{\eta }_{1} (\tilde{z}^{2} - \tilde{z}^{3} ).$$

(5.6)

Based on Eqs. (5.4) and (5.5), one can derive expressions for the flow swirl angle on the surface of a stationary disk φ _w , whereas a cone is rotating

$${\varphi }_{{w}} = {\text{arctan[}}{{0.8{{Re}}} \mathord{\left/ {\vphantom {{0.8{{Re}}} {(1 - 83{Re}^{2} /175)}}} \right. \kern-0pt} {(1 - 83{Re}^{2} /175)}} ]\quad {\text{for}}\,Re = 0 - 1. 4 5 2,$$

(5.7)

$${\varphi }_{{w}} = { \arctan }(0.8{Re})\quad{\text{for}}\,{Re} \ll 1.$$

(5.8)

Equation (5.7) agrees well with measurements [5] and Eq. (5.8) just for Re ≤ 0.5 (Fig. 5.3). Equation (5.8) that formally holds just for $Re \ll 1$ correlates nevertheless with the measurements up to Re = 2. Authors [5] deduced only Eq. (5.8), whereas Eq. (5.7) automatically stemming from Eqs. (5.4) and (5.5) was ignored in [5]. At Re = 1.452, Eq. (5.7) predicts the value φ _w  = 90°, whereas the expression in brackets of the function arctan tends effectively to infinity; this contradicts to the physics of the problem.

Fig. 5.3

Flow swirl angle on the surface of a stationary disk with a rotating cone [9]. Computations: 1—Eq. (5.7); 2—Eq. (5.8) [5]; 3—self-similar Eqs. (5.19)–(5.22) [10]; 4—self-similar Eqs. (5.24)–(5.26) [10]. Data 5—experiments [5]

A series expansion in the small parameter Re, with up to 70 terms, were used also in the works [6, 7] to solve Eqs. (5.1)–(5.3). However, the parameter φ _w predicted by the authors [6, 7] deviated from experiments [5] at Re = 0.5–1 more noticeably than Eq. (5.8). In addition, the parameter φ _w predicted in [6, 7] at Re = 1.2928 exhibits an asymptotical trend to infinity contradictive to the physics of the problem.

This chapter summarizes results of simulations of convective heat transfer in the geometries “stationary conical diffuser” (Fig. 5.1) and “rotating cone-and-disk” without initial flow swirl (Fig. 5.2). Such pioneering studies based on full self-similar forms of the Navier–Stokes equations together with the thermal boundary layer equation have been for the first time performed by the author of the present work [2, 9–11].

5.2 Self-similar Navier–Stokes and Energy Equations

Considering a steady-state axisymmetric laminar flow and heat transfer, we will solve the Navier–Stokes Eqs. (2.1)–(2.3) and the reduced Eqs. (5.1)–(5.3) together with the energy Eq. (2.12) for laminar flow. For the configurations “rotating cone-and-disk” without initial swirl, the boundary conditions are given by

$$z = 0{:}\quad v_{r} = 0,\quad v_{z} = 0,\quad v_{\varphi } = {\omega } r,\quad T_{{w}} - T_{{\infty }} = c_{0} r^{{n_{\text{ * }} }} ,$$

(5.9)

$$z = h{:}\quad v_{r} = 0,\quad v_{z} = 0,\quad v_{\varphi } =\Omega r,\quad T = T_{{\infty }} .$$

(5.10)

For the geometry “stationary conical diffuser,” the boundary conditions are given by

$$z = 0{:}\quad v_{r} = v_{\varphi } = v_{z} = 0,\quad T_{{w}} - T_{{\infty }} = c_{0} r^{{n_{*} }} ,$$

(5.11)

$$z = z_{1} = h/2{:}\quad v_{r} = v_{r1} ,\quad v_{\varphi } = v_{\varphi 1} ,\quad {\text{d}}v_{r} /{\text{d}}z = 0,\quad T = T_{{\infty }} .$$

(5.12)

Here, c ₀ and n _* are the constants, while the conditions at $z = z_{1} = h/2$ are denoted with a subscript “1.” We will study convective heat transfer of a disk (but not a cone) under the wall boundary conditions (5.9) and (5.11) that match with Eq. (2.30) for a single disk.

The exponent n _* in Eqs. (5.9) and (5.11) takes negative, zero, or positive values −2 ≤ n _* ≤ 4. Cone heat/mass transfer is unimportant for the current study; therefore, the temperature T _∞ and the concentration C _∞ on the surface of the cone are assumed to be constant and equal to those of the fluid at infinity. In case of convective diffusion in bioengineering applications, the boundary concentration on the plate/disk C _w is lower than that on the cone/infinity C _∞, because endothelial cells digest feeding culture from the fluid.

The boundary layer equation for the temperature is used instead of the full energy equation; this model assumption is justified above in Chaps. 2–4.

Self-similar variables and functions enable simplifying partial differential Eqs. (2.1)–(2.3), (5.1)–(5.3) and (2.12) and translating them to ordinary non-linear differential equations to be solved numerically with the help of the software like Mathcad [1, 12–17].

Self-similar variables and functions can be derived with the help of group theory [2, 9, 10]. Let us enter a linear transformation of differential equations

$$\begin{aligned} r & = A^{{\alpha_{1} }} \overline{r} ,\quad z = A^{{\alpha_{2} }} \overline{z} ,\quad v_{r} = A^{{\alpha_{3} }} \overline{{v}}_{r} , \\ v_{{\varphi }} & = A^{{\alpha_{4} }} \overline{v}_{{\varphi }} ,\quad v_{z} = A^{{\alpha_{5} }} \overline{v}_{z} ,\quad p = A^{{\alpha_{6} }} \overline{p} , \\ \end{aligned}$$

(5.13)

with α _k (k = 1, …, 6) and the parameter of transformation A being constants [12]. Transformations (5.13) are substituted into Eqs. (2.1)–(2.3), (5.1)–(5.3) and (2.12). If the exponents at the constant A are identical for every summand, this means that the non-transformed and transformed equations are invariant, which yields

$$\alpha_{1} = \alpha_{2} = \alpha ,\quad \alpha_{3} = \alpha_{4} = \alpha_{5} = - \alpha ,\quad \alpha_{6} = - 2\alpha ,$$

(5.14)

$$\begin{aligned} A & = \left( {\frac{r}{{\overline{r} }}} \right)^{1/\alpha } = \left( {\frac{z}{{\overline{z} }}} \right)^{1/\alpha } = \left( {\frac{{\overline{v}_{r} }}{{v_{r} }}} \right)^{1/\alpha } \\ & = \left( {\frac{{\overline{v}_{\varphi } }}{{v_{\varphi } }}} \right)^{1/\alpha } = \left( {\frac{{\overline{v}_{z} }}{{v_{z} }}} \right)^{1/\alpha } = \left( {\frac{{\overline{p} }}{p}} \right)^{1/(2\alpha )} , \\ \end{aligned}$$

(5.15)

$${{\overline{z} } \mathord{\left/ {\vphantom {{\overline{z} } z}} \right. \kern-0pt} z} = {{\overline{r} } \mathord{\left/ {\vphantom {{\overline{r} } r}} \right. \kern-0pt} r},\quad\overline{v}_{r} \overline{r} = v_{r} r,\quad\overline{v}_{\varphi } \overline{r} = v_{\varphi } r,\quad\overline{v}_{z} \overline{r} = v_{z} r,\quad\overline{p} \cdot \overline{r}^{2} = p \cdot r^{2} .$$

(5.16)

Morgan’s theorem states [12] that Eq. (5.16) serve as similarity variables, if the boundary conditions are independent of the coordinate r.

The self-similar variables and functions were formulated using Eqs. (5.15) and (5.16)

$$\eta = {z \mathord{\left/ {\vphantom {z r}} \right. \kern-0pt} r},\quad F = {{v_{r} r} \mathord{\left/ {\vphantom {{v_{r} r} \nu }} \right. \kern-0pt} \nu },\quad G = {{v_{\varphi } r} \mathord{\left/ {\vphantom {{v_{\varphi } r} \nu }} \right. \kern-0pt} \nu },\quad H = {{v_{z} r} \mathord{\left/ {\vphantom {{v_{z} r} \nu }} \right. \kern-0pt} \nu },$$

(5.17)

$$P = {{pr^{2} } \mathord{\left/ {\vphantom {{pr^{2} } {(\rho \nu^{2} )}}} \right. \kern-0pt} {(\rho \nu^{2} )}},\theta = (T - T_{{\infty }} )/(T_{{w}} - T_{{\infty }} ).$$

(5.18)

Function θ does not change its form because of the linearity of the energy equation. Substituting Eqs. (5.17) and (5.18) into Eqs. (2.1)–(2.3) and (2.12), one can deduce

$$F^{2} + G^{2} + 2P + F^{\prime } L + {\eta} P^{\prime } + F^{\prime\prime} M = 0,$$

(5.19)

$$G^{\prime}L + G^{\prime\prime}M = 0,$$

(5.20)

$$P^{\prime} - H(1 + F) - H^{\prime}L - H^{\prime\prime}M = 0,$$

(5.21)

$$H^{\prime} - {\eta } F^{\prime\prime} = 0,$$

(5.22)

$${\theta^{\prime\prime}} = \Pr \left[ {n_{*} F{\theta } + {\theta^{\prime}}(H - {\eta } F)} \right].$$

(5.23)

Here, $M = 1 + \eta^{2}$ and $L = 3{\eta } + {\eta }F - H$. In ordinary differential Eqs. (5.19)–(5.23), primes denote derivatives with respect to the η-coordinate.

A substitution of Eqs. (5.17) and (5.18) into Eqs. (5.1)–(5.3) gives

$$G^{2} + 2P + {\eta }P^{\prime } + F^{\prime \prime } = 0,$$

(5.24)

$$G^{{\prime }} \left( {{\eta }F - H} \right) + G^{\prime\prime } = 0,$$

(5.25)

$$P^{{\prime }} = H^{{\prime \prime }} .$$

(5.26)

Boundary conditions (5.9) and (5.10) can be rewritten as

$$\eta = 0{:}\quad F = H = 0,\quad G = G_{0} ,\quad\theta = 1,$$

(5.27)

$$\eta = \eta_{1}{:}\quad F = H = 0,\quad G = G_{1} ,\quad\theta = 0,$$

(5.28)

with ${\eta }_{1} = {h \mathord{\left/ {\vphantom {h r}} \right. \kern-0pt} r},\,G_{0} = {{Re}}_{\omega } = {\omega }r^{2} /\nu ,\,G_{1} = {{Re}}_{\Omega } =\Omega r^{2} /\nu$.

Boundary conditions (5.11) and (5.12) can be rearranged as

$$\eta = 0{:}\quad F = G = H = 0,\quad\theta = 1,$$

(5.29)

$$\eta = \eta_{1}{:}\quad G = G_{1} ,\quad F = F_{1} ,\quad F^{{\prime }} = 0,\quad\theta = 0.$$

(5.30)

Here, $\eta_{1} = {{0.5h} \mathord{\left/ {\vphantom {{0.5h} r}} \right. \kern-0pt} r}$, and subscripts “0” and “1” denote functions at η = 0 and η = η ₁, accordingly.

Boundary conditions (5.27) and (5.28) for the functions $G_{0} = {Re}_{\omega }$ and $G_{1} = {Re}_{\Omega }$ are r-dependent and do not comply with the self-similarity requirements that the self-similar functions must be constant at the boundaries. Self-similar fuctions are Eq. (5.29) (G ₀ = 0) for a stationary disk and Eq. (5.30) with G ₁ = const., F ₁ = const., which imply the free vortex laws for the velocity components v _r and v _φ in the middle of the stationary conical diffuser

$$(v_{\varphi } )_{{\eta = \eta_{1} }} = {{G_{1} \nu } \mathord{\left/ {\vphantom {{G_{1} \nu } r}} \right. \kern-0pt} r},\quad ({{v}}_{r} )_{{\eta = \eta_{1} }} = {{F_{1} \nu } \mathord{\left/ {\vphantom {{F_{1} \nu } r}} \right. \kern-0pt} r}.$$

(5.31)

We treat here Eqs. (5.27) and (5.28) as locally self-similar, with G ₀ and G ₁ being parameters at each specific r-coordinate [2, 10]. As demonstrated beneath, this model yields the results that are in good agreement with experiments and theoretical predictions.

5.3 Rotating Disk and/or Cone

5.3.1 Numerical Values of Parameters in the Computations

The Mathcad software has been used to obtain a numerical solution of Eqs. (5.19)–(5.26). Angles of conicity for the simulations were γ = 4° (small η ₁ = 0.0698) and γ = 45° (relatively large η ₁ = 1). The value of η ₁ varying over the span of γ = 1–5° was shown to have no influence on the results of simulations.

Values of the Prandtl and Schmidt numbers were Pr = Sc = 0.1–100 for a configuration with a rotating cone and a stationary disk, Pr = Sc = 0.1–800 for a stationary cone and a rotating disk, and Pr = Sc = 0.71 for the rest of the geometries. In the simulations, the value of ${Re} = {Re}_{\omega } {\eta }_{1}^{2} /12$ (or ${Re} = {Re}_{\Omega } \eta_{1}^{2} /12$) was set to be unity, which yields Re _Ω = 12, Re _ω  = 12 at η ₁ = 1, and Re _ω  = 2463, Re _Ω = 2463 at η ₁ = 0.0698. The exponent n _* in Eq. (5.23) took negative, zero, or positive values −2 ≤ n _* ≤ 4 that enable modeling different radially decreasing, constant, or increasing distributions of T _w on the disk surface.

5.3.2 Rotating Cone and Stationary Disk

Figures 5.4, 5.5, and 5.6 depict velocity profiles predicted in [9] for Re = 1 (Re _ω  = 2463) by Eqs. (5.19)–(5.22), (5.24)–(5.26) and those computed in the work [5] with a help of the method of expansion in the small parameter Re.

Fig. 5.4

Profiles of the radial velocity component in a gap between a rotating cone and a stationary disk [9]. 1—Eqs. (5.19)–(5.22); 2—Eqs. (5.24)–(5.26); 3—Eq. (5.4) [5]

Fig. 5.5

Profiles of the axial velocity component in a gap between a rotating cone and a stationary disk [9]. 1—Eqs. (5.19)–(5.22); 2—Eqs. (5.24)–(5.26); 3—Eq. (5.6) [5]

Fig. 5.6

Profiles of the tangential velocity component (1, 2) and temperature θ (3–5) in a gap between a rotating cone and a stationary disk [9]. 1—Eqs. (5.19)–(5.22) and (5.24)–(5.26); 2—Eq. (5.5) [5]; 3—Eqs. (5.19)–(5.23) at n _* = 2; 4—(5.19)–(5.23) at n _* = 0; 5—(5.19)–(5.23) at n _* = −1

The axial velocity component (Fig. 5.5) is an order of magnitude smaller than the radial velocity component (Fig. 5.4), which, in turn, is an order of magnitude smaller than the tangential velocity component (Fig. 5.6). Curves predicted by Eqs. (5.19)–(5.22) and (5.24)–(5.26) practically merge, which certifies validity of the simplified Eqs. (5.24)–(5.26) for small angles of conicity γ. Data of [5] for the radial velocity v _r agree well with the simulations in Fig. 5.4; however, discrepancies between the data of [5] and the simulations for components v _z and v _φ are more distinct (Figs. 5.5 and 5.6).

To validate the accuracy of the simulations of the tangential velocity, experimental data [5] and predictions [9] for the flow swirl angle on the disk surface $\varphi {}_{{w}} = {\text{arctan[}}{{v_{r} } \mathord{\left/ {\vphantom {{v_{r} } {(\Omega r - v_{\varphi } )}}} \right. \kern-0pt} {(\Omega r - v_{\varphi } )}} ]_{z = 0} = { \arctan }( - {{F_{{w}}^{{\prime }} } \mathord{\left/ {\vphantom {{F_{{w}}^{{\prime }} } {G_{{w}}^{{\prime }} }}} \right. \kern-0pt} {G_{{w}}^{{\prime }} }})$ were compared. Predictions and experiments correlate for the Reynolds number depicted in Fig. 5.3. It can be also concluded that the velocity profiles in Figs. 5.4, 5.5, and 5.6 predicted by Eqs. (5.19)–(5.22) and (5.24)–(5.28) model the flow in the gap more realistically than those by Eqs. (5.4)–(5.8) [5].

Figure 5.6 shows temperature profiles in the gap computed at for Pr = 0.71. The temperature curves demonstrate the decreasing trend from unity at the disk surface to zero at the cone wall. The form of the curves is affected by the value of n _*. Near the disk, derivatives of the θ profiles diminish with increasing n _*.

To compute the local Nusselt number, the following expression was used:

$$Nu = \frac{{q_{{w}} r}}{{\lambda (T_{{w}} - T_{{\infty }} )}} = -\theta_{\eta = 0}^{{\prime }} .$$

(5.32)

To enable comparisons with Eqs. (3.4) and (3.5) for the rotating disks, the Nusselt number may be rearranged using a derivative with respect to the variable $\zeta = z\sqrt {\Omega /\nu }$

$$Nu = K_{1} {Re}_{\Omega }^{1/2}$$

(5.33)

$$K_{1} = \frac{{ - ({\text{d}}\theta /{\text{d}}\eta )_{\eta = 0} }}{{Re_{\Omega }^{1/2} }} = - \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\zeta }}} \right)_{\zeta = 0} .$$

(5.34)

Based on these expressions, it was calculated at η ₁ = 0.0698 (or Re _Ω = 2463) that Nu = 15.28, 13.40, 9.35 and K ₁ = 0.308, 0.270, 0.188 at n _* = −1, 0, 2, accordingly. These values of the coefficient K ₁ match fairly well with those for a single rotating disk (see Table 3.8). For larger values of n _*, the coefficient K ₁ diminishes, which is observed in centripetal flow over a stationary disk imposed by a rotating cone (to compare, an increase in the coefficient K ₁ together with n _* occurs in centrifugal flow over a rotating disk, see Chaps. 3 and 4).

Given η ₁ = 1 and Re = 1 (or Re _Ω = 12), the Nusselt numbers are Nu = 1.047, 0.954, 0.760 with K ₁ = 0.302, 0.275, 0.219 for the same exponents n _*. One can conclude that the coefficient K ₁ is conservative and only weakly dependent on the conicity angle γ.

5.3.3 Rotating Disk and Stationary Cone

Radial flow pattern here is opposite to that considered above: the flow is centripetal over the cone, and centrifugal over the disk (Fig. 5.7).

Fig. 5.7

Velocity and temperature profiles in the gap between a rotating disk and a stationary cone at Re = 1 (Re _ω  = 2463) and η ₁ = 0.0698 [9]. 1—v _r /(ωr); 2—v _φ /(ωr); 3—20v _z /(ωr); 4—θ(Pr = 0.71, n _* = 0)

The tangential velocity v _φ demonstrates a trend linearly subsiding from a disk toward a cone, while the profile of axial velocity component v _z looks mirror-symmetrical as compared to the v _z profile in Fig. 5.5. The temperature profile θ in Fig. 5.7 for Pr = 0.71 almost merges with the v _φ /(ωr) curve.

To compute the Nusselt number at the disk, Eqs. (5.32)–(5.34) are again employed; as Ω = 0, it must be replaced with ω while defining the Re number and coordinate ζ. Based on this, the calculated Nusselt numbers for η ₁ = 0.0698, Re = 1 (Re _ω  = 2463) are Nu = 13.33, 15.35, 19.13 and K ₁ = 0.269, 0.309, 0.386 at Pr = 0.71, and n _* = −1, 0, 2, accordingly. It is evident that the coefficient K ₁ is an increasing function of n _*. However, the rate of increase is lower than that for a single rotating disk, where K ₁ = 0.189, 0.326, 0.519 for the identical values n _* (Table 3.1). Given η ₁ = 1 and Re = 1 (Re _ω  = 12), the computed Nusselt numbers are Nu = 0.96, 1.041, 1.197 and K ₁ = 0.277, 0.301, 0.345 for identical exponents n _* and Pr = 0.71. Thus, the coefficient K ₁ is again very weakly dependent on the conicity angle γ.

5.3.4 Effects of Prandtl and Schmidt Numbers

Effects of the Prandtl or Schmidt numbers are considered for the geometries with a rotating disk and stationary cone or a stationary disk and a rotating cone [11].

Rotating disk and stationary cone. As the Pr numbers increase, curves of the temperature profiles θ for n _* = 0 and n _* = −1 shift downward exhibiting a non-linear trend of variation due to diminished heat conduction, whereas the function θ at Pr ≥ 100 becomes zero inside the gap between the cone and the disk (Figs. 5.8 and 5.9). For n _* ≥ 0, curves of θ demonstrate qualitatively analogous trend. With respect to the profiles of θ for n _* = −1, the condition dθ/dη → 0 in the vicinity of the cone is attained already at Pr ≥ 20 (Fig. 5.9).

Fig. 5.8

Temperature profiles θ in the gap for n _* = 0 [11]. Solid lines rotating disk and stationary cone. Dash-dot lines stationary disk and rotating cone. 1—Pr = 0.71; 2—Pr = 10; 3—Pr = 100

Fig. 5.9

Temperature profiles θ in the gap for n _* = −1 [11]. Dashed lines rotating disk and stationary cone. Solid lines stationary disk and rotating cone. 1—Pr = 0.71; 2—Pr = 10; 3—Pr = 100

Over the range 0 ≤ n _* ≤ 4, the constant K ₁ increases with the Prandtl number (Table 5.1); the trend persists also at n _* = −0.5, i.e., when negative gradient dT _w /dr is weak.

Table 5.1 Coefficient K ₁, for rotating disk and stationary cone [11]

As seen from Table 5.1, signs of v _r and dT _w /dr become different and coefficient K ₁ diminishes for larger Prandtl numbers, when the wall temperature gradient dT _w /dr is strongly negative (n _* = −1). Let us write the coefficient K ₁ at n _* = 0 as follows:

$$K_{1} = K_{1,Pr = 1} {Pr}^{{m_{p} }} ,$$

(5.35)

where K _1,Pr=1 = 0.318. This enables determining a function for the exponent m _p (Pr) presented in Table 5.2, whose asymptotic limit is m _p  = 0.372 for high Prandtl numbers. To compare, this limit for a single rotating disk is m _p  = 1/3 at Pr → ∞ [9] (see Chap. 6).

Table 5.2 Exponent m _p in Eq. (5.35) at T _w  = const., rotating disk, and stationary cone [11]

Rotating cone and stationary disk. Profiles of θ for n _* = 0 and n _* = −1 at Pr = 0.71 span practically linear between unity on the disk surface and zero on the cone wall; further, for larger Prandtl numbers, profiles of θ shift upward demonstrating a non-linear trend of variation owing to reduced heat conduction (Figs. 5.8 and 5.9). For Pr ≥ 100, the derivative dθ/dη in the vicinity of the disk exhibits zero values.

For n _* > 0, Pr ≤ 1 and n _* = −1, Pr ≤ 1, curves of θ practically merge with the profile predicted for Pr = 0.71, n _* = 0. Curves of θ demonstrate a S-shape at n _* = −1 and Pr = 1–10 (Fig. 5.9). Profiles of θ become non-physical at Pr > 1, n _* > 0 and Pr > 10, n _* = −1.

For larger Pr numbers and n _* < 0, the constant K ₁ increases (because signs of v _r and dT _w /dr are the same); at n _* ≥ 0, the coefficient K ₁ diminishes due to the opposite signs of v _r and dT _w /dr (Table 5.3).

Table 5.3 Coefficient K ₁, rotating cone, and stationary disk [11]

Application to the cone - and - plate devices. The results described in Sect. 5.3.4 become applicable to mass transfer upon replacement of T, Pr, Nu with C, Sc, Sh, respectively. Here, data for K ₁ at n _* = 0 from Tables 5.1, 5.2, and 5.3 are to be used, since the wall boundary condition for mass transfer is C _w  = const. [9]. It is evident that the coefficients K ₁ for a stationary disk and a rotating cone are always smaller than the K ₁ values for a rotating disk and a stationary cone. This difference becomes more pronounced at larger Schmidt numbers and is equal to 14.6 % at Sc = 0.71; 2.6 times at Sc = 5; 46.1 times at Sc = 20, and asymptotically tends to infinity in the limit at infinite Schmidt numbers.

Thus, one can enhance efficiency of a cone-and-plate device used in bioengineering for nurturing endothelial cells spread on the plate via assigning the disk to rotate and fixing the cone instead of the currently used devices “rotating cone—stationary plate.”

5.3.5 Co-rotating Disk and Cone

Here, the ratio between the Re _Ω and Re _ω numbers makes a crucial influence on the flow pattern. If Re _Ω > Re _ω (cone revolves faster), fluid flow over the cone is centrifugal, and centripetal over the disk. If Re _Ω < Re _ω (disk revolves faster), a reverse flow pattern emerges. Equations (5.32)–(5.34) (reference angular speed Ω) were used to compute the Nusselt number for Pr = 0.71. A situation with approximately the same angular speeds of a disk and a cone was considered. Given Re _ω  = 1.01Re _Ω, Eqs. (5.32)–(5.34) yield Nu = 14.31, 14.35, 14.43 and K ₁ = 0.288, 0.289, 0.291; given Re _ω  = 0.99Re _ω , one can obtain Nu = 14.35, 14.31, 14.23 and K ₁ = 0.289, 0.288, 0.287 at n _* = −1, 0, 2, accordingly. In both cases, we pre-set Re = 1 and η ₁ = 0.0698 (Re _Ω = 2463). The computed Nusselt numbers were Nu = 0.999, 1.001, 1.004 and K ₁ = 0.288, 0.289, 0.290 at Re _ω  = 1.01Re _Ω, Re = 1 and η ₁ = 1 (Re _Ω = 12).

The coefficient K ₁ is practically the same for all considered cases. For larger values of n _*, Nusselt numbers increase in centrifugal flow over the disk and decrease in centripetal flow. Variation of the conical spacing practically does not affect the coefficient K ₁.

5.3.6 Counter-Rotating Disk and Cone

The most complex flow pattern emerges here with centrifugal flow over a disk and a cone and centripetal flow in the center of the conical cavity (Fig. 5.10). The axial velocity v _z is negative in the vicinity of the walls and positive in the center of the gap; the tangential velocity v _φ /(Ωr) behaves as a linear function increasing between −1 and 1, whereas the temperature function θ at Pr = 0.71 monotonically diminishes from unity to zero.

Fig. 5.10

Counter-rotating disk and a cone at Re = 1 [9]: 1—v _φ /(ωr); 2, 4—10v _r /(ωr); 3—100v _z /(ωr); 5—θ (Pr = 0.71, n _* = 0). Here 1–3—Re _ω  = −Re _Ω = 2463 and η ₁ = 0.0698; 4—Re _ω  = −Re _Ω = 12 and $\eta_{1} = 1$

Given η ₁ = 0.0698, Re = 1, and Re _ω  = −Re _Ω = 2463, profile of v _r is symmetrical relative to the center of the gap (curve 2, Fig. 5.10).

Equations (5.32)–(5.34) (reference velocity Ω) were used to compute the Nusselt number for Pr = 0.71. Nusselt number increases with n _* over the disk surface: Nu = 14.21, 14.44, 14.85 and K ₁ = 0.286, 0.201, 0.299 at n _* = −1, 0, 2. The conditions η ₁ = 1, Re = 1, Re _ω  = 12, and Re _Ω = −12 yield a non-symmetrical radial velocity profile v _r , since the radial flow is stronger near the cone (curve 4, Fig. 5.8). As a result, increasing n _* is accompanied with a decreasing Nusselt number on the disk: Nu = 1.011, 0.989, 0.942 and K ₁ = 0.292, 0.285, 0.272, given the same set of the n _* values as that used above.

Thus, here heat transfer is almost insensitive to the value and sign of dT _w /dr on the disk surface. Variation of the conical gap spacing and revolution speeds of a cone and a disk influence on the v _r profile and qualitative trend of the dependence of Nu on n _*.

5.4 Radially Outward Swirling Flow in a Stationary Conical Diffuser

A non-rotating diffuser with conicity of γ = 35° or η ₁ = 0.35 was studied here (Fig. 5.2). The physical interpretation of Eqs. (5.30) and (5.31) is that they describe a free vortex expanding along the centerline of the gap. In practice, potential flow in the form of a free vortex spans over a significant height of the conical gap pushing the boundary layers toward the walls. Hence, Eqs. (5.30) and (5.31) describe a somewhat idealized vortex flow pattern.

Simulations demonstrated that non-swirling purely radial flow (G ₁ = 0) does not undergo separation from the walls at F ₁ < 63. Separation starts at F ₁  ≈ 63, whereas at F ₁ > 63, a pronounced recirculation flow region is visible over the disk (Fig. 5.11).

Fig. 5.11

Profiles of the radial velocity F/F ₁ (1–4) or F/|F|_max (5, 6) in a gap between a disk and a cone [9]. G ₁  = 0: 1—F ₁ = 2; 2—F ₁ = 63; 3—F ₁ = 90. G ₁  = 97.96: 4—F ₁ = 20; 5—F ₁ = 10, |F|_max = 20.66; 6—F ₁ = 0, |F|_max = 24.28

Responsible for the onset of separation is the large conicity of the diffuser: a reduced conicity η ₁ = 0.035 shifts the separation value of F ₁ to about 7500. Flow swirl (G ₁ = 97.96, $Re = G_{1} \eta_{1}^{2} /12 = 1$) causes accentuated recirculation region over the disk (Fig. 5.11).

Given a zero radial velocity F ₁ = 0 at the inlet to the diffuser, the radial velocity v _r becomes negative over the entire gap height excluding the point η = η ₁ (curve 6 in Fig. 5.11; |F|_max relates to the minimum point of the plot of F/|F|_max at η/η ₁ ≈ 0.4, i.e., F _max = −24.28). For larger values of F ₁, the recirculation area reduces, whereas the centrifugal flow area near the center of the conical gap grows up. The tangential velocity G/G ₁ shows a linear distribution between 0 at η = 0 (disk) and 1 (cone) for η = η ₁ (curve 1 in Fig. 5.12).

Fig. 5.12

Profiles of the tangential velocity component G/G ₁ and temperature θ in the gap between a cone and a disk [9]. 1—G/G ₁ for F ₁ = 30, G ₁ = 97.96; 2—θ for G ₁ = 97.96 and F ₁ = 10; 3—θ for G ₁ = 97.96 and F ₁ = 30; 4—θ for G ₁ = 97.96 and F ₁ = 60 (Pr = 0.71, n _* = 2)

The diffuser is used to restore the static pressure, which grows with r as the velocity components $(v_{r} )_{{\eta = \eta_{1} }}$ and $(v_{{\varphi }} )_{{\eta = \eta_{1} }}$ decrease. To ensure self-similarity of the function P in Eq. (5.18), the quantity P must denote the excess pressure p–p _∞, where p = p _∞ = const. for r → r _∞. Thus, the parameter P shows the pressure recovery level; in non-swirling flow (G ₁ = 0), P increases with F ₁ (Fig. 5.13).

Fig. 5.13

Static pressure drop in the gap for G ₁ = 0 (curves 1–4) and G ₁ = 97.96 (curves 5, 6) [9]. 1, 6—F ₁ = 20; 2—F ₁ = 45; 3—F ₁ = 63; 4—F ₁ = 90; 5—F ₁ = 10

Flow swirl G ₁ = 97.96 entails noticeable additional augmentation of the pressure recovery parameter P, whereas the contribution of F ₁ in the range F ₁ = 0–20 is rather insignificant. As can be seen from Fig. 5.14, curves Nu(F ₁) computed by Eq. (5.32) for F ₁ = 50–63 demonstrate maxima at n _* = 2 and 0 and minima at n _* = −1.

Fig. 5.14

Nusselt numbers in the gap for G ₁ = 0 (curves 1–3) and G ₁ = 97.96 (curves 4–6) [9]. 1, 4—n _* = 2; 2, 5—n _* = 0; 3, 6—n _* = −1

For non-swirling flow (G ₁ = 0) and non-zero inlet radial velocity F ₁, the Nusselt numbers increase together with the exponent n _* (curves 1–3, Fig. 5.14).

If the exponent n _* remains within the range n _* = 0–2 and the radial velocity F ₁ increases, the Nusselt numbers (a) demonstrate a trend of augmentation under the conditions of non-separating centrifugal flow, (b) stay practically constant, if the function F ₁ approaches the onset of separation, and (c) show a reduction for centripetal secondary flow over the disk (curves 1 and 2 in Fig. 5.14). These trends become rather insignificant at n _* = 0.

Flow with initial swirl G ₁ = 97.96 demonstrates different signs of v _r and dT _w /dr accompanied with reduced Nusselt numbers at n _* = 2 and 0 (curves 4 and 5 in Fig. 5.14) as compared to the flow without swirl. Given n _* = −1, signs of v _r and dT _w /dr become the same, accompanied with increased Nusselt numbers (curve 6 in Fig. 5.14) as compared to non-swirling fluid. Although, for G ₁ = 97.96 and increasing F ₁, the radially inward flow persists in the vicinity of the disk, the shapes of the curves 4, 5, and 6 for Nu(F ₁) are analogous to curves 1, 2, and 3 plotted for non-swirling flow for the same values of n _* (see Fig. 5.14).

Temperature profiles 2 and 3 in Fig. 5.12 for swirling flow (G ₁ = 97.96) and n _* = 2 show a decreasing behavior at F ₁ > 21. For F ₁ ≤ 21, the temperature curve 4 in Fig. 5.11 exhibits a maximum near the wall, if fluid flows centripetally in the direction of the decrease in T _w . This causes the Nusselt number curve 4 in Fig. 5.14 to become negative: the disk is heated by the fluid (whereas positive Nu numbers mean fluid heated by a disk).

To conclude, in this chapter, self-similar solutions of the Navier–Stokes and energy equations were derived for fluid flow in a conical gap depicted in Figs. 5.1 and 5.2. Simulations were performed for the cases “rotating cone–stationary disk,” “rotating disk–stationary cone,” “co-rotating or contra-rotating disk and cone,” and “non-rotating conical diffuser.” Effects of the boundary conditions and various Prandtl/Schmidt numbers on the pressure, velocity, and temperature pattern, as well as on the Nusselt/Sherwood numbers, were studied.