End-Stop Nonlinearities in Vibration Energy Harvesters

Abstract

The chapter discusses mathematical modeling and numerical analysis of nonlinearities due to mechanical end-stops in vibration energy harvesters by eigenvalue approach and time domain simulations. We consider end-stops that limit the maximum displacement amplitude of the proof mass motion within finite package’s size. Proof mass motion is strongly nonlinear on impact at the end-stops. The system behavior is studied through its state equations. The phase space trajectories are investigated with varying system parameters and coefficients of restitution. The modeling of the restoring force for the coefficient of restitution equals zero simplifies the phase space trajectories at large acceleration amplitudes which otherwise is complicated. The average output power increases with mechanical excitations and then saturates at acceleration amplitude which leads to impacts. Thus, the average output power is weakly dependent on excitation levels. The power lost on impact for inelastic collision can be collected via integrated electronic circuits. Another smart solution is introducing active transducers replacing inactive end-stops in the harvester. The chapter presents a device concept of transducing end-stops scavenging additional power from the impacts. The transducing end-stops not only benefit total output power but also enhance response bandwidth.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

Vibration energy harvesters are gaining increase in popularity as a possible alternative to battery-based power sources. Vibration energy harvesters are typically resonant devices that produce appreciable output power when operating at resonance, but they often fail to deliver reliable power when they are made to vibrate at off-resonance frequencies. The energy sources of these devices are ambient vibrations, which are easily available and offer a wide variety of spectra, from narrowband to wideband. A wide range of vibration energy harvesters designed for various operating conditions has been proposed and demonstrated to date [1–8]. In particular, it is desirable to develop microscale energy harvesters that can perform efficiently when using excitation signals that are not only narrowbanded but are of variable frequency, either over time or from case to case in applications, or when using excitation signals that are relatively broadbanded [9, 10].

In that respect, nonlinear devices have emerged as a potential solution that can adapt to the various vibration spectra to increase both the bandwidth response and the output power. The nonlinearities may appear as part of the harvester design, such as the use of nonlinear springs that add nonlinearities to the device response at sufficiently large acceleration amplitudes and thus broaden the harvester’s bandwidth [10, 11]. Another solution to widen the response of the harvester uses the impact of the proof mass with end-stops that add additional nonlinearities to the harvester responses [9, 12, 13]. Even if the proof mass vibrates linearly between the end-stops, the behavior changes abruptly when the mass hits the end-stops. The frequency response obtained in this manner depends on the nonlinear springs in the suspension or on the contact linearity between the proof mass and the end-stops. It should be possible to produce a wider response than that obtained from a linear resonant device through appropriate design of the device nonlinearities.

The motion of the proof mass is generally nonlinear on impact with the end-stop, depending on the system and end-stop parameters [14]. The end-stops in the vibration energy harvester not only add nonlinearities and enhance the bandwidth but also saturate the harvester’s output power. Thus, the end-stops set an upper bound on the output power. This negative end-stop trait can be overcome by the introduction of sufficiently compliant end-stops to the device and collection of the lost energy at the end-stops on impact via integrated electronic circuits such as synchronous electric charge extraction (SECE) or synchronized switch harvesting on inductor (SSHI) circuits [15]. The energy that is otherwise lost in the end-stops can be used efficiently by introducing a transduction mechanism at the end-stops [13].

In this chapter, an overview of the use of end-stops in energy harvesters will be presented. The mathematical modeling of end-stop behavior in a harvester will be discussed in detail on the basis of phase space trajectories and eigenvalue problem. The effects of nonlinearities in the motion of the proof mass on variation of the coefficient of restitution and the device parameters will be demonstrated. The average output power from the harvester with end-stop nonlinearities for different coefficients of restitution will be shown in power graphs. Examples of devices with end-stop nonlinearities will be presented and discussed with respect to their experimental results, and conclusions will then be drawn.

General Aspects of Vibration Energy Harvesters

The schematic diagram in Fig. 7.1 shows a typical model of a vibration energy harvester. While this model, which was built up by William and Yates [16, 17] is mainly applicable to electromagnetic transducers, it can be applied to both piezoelectric and electrostatic transducers in appropriate ways. The model includes a proof mass m suspended from a mechanical spring with a stiffness k. The mechanical loss is represented by $c_{m}$, while the electrical loss $c_{e}$ comes from the coupling between the mechanical and electrical domains in the system for energy conversion. The power is obtained from the motion of the proof mass relative to the device package when the harvester is subjected to vibration. Because of the finite size of the device package, the proof mass displacement is always constrained by a maximum amplitude $|x(t)| \le X_{max}$. Under sinusoidal excitation with an angular frequency $\omega$ in the steady state [16, 17], the proof mass displacement amplitude and the power obtained are given by

$$\begin{aligned} \left| X \right| =\frac{A}{\sqrt{\left( {\omega _0^2 -\omega ^{2}} \right) ^{2}+\left( {c_m +c_e } \right) ^{2}\omega ^{2}/m^{2}}} \end{aligned}$$

(7.1)

$$\begin{aligned} P=\frac{1}{2}\frac{C_e\omega ^{2}A^{2}}{\left( {\omega _0^2 -\omega ^{2}} \right) ^{2}+\left( {c_m +c_e } \right) ^{2}\omega ^{2}/m^{2}} \end{aligned}$$

(7.2)

where A is the acceleration amplitude and $\omega _0 =2\pi f_0 =\sqrt{k/m}$. The optimum power is achieved when $c_{m}=c_{e}$. Additionally, the generated power is limited by $P_{lim } =\left( {2/\pi } \right) m\omega X_{max } A$ when $|X|=X_{max }$ [18, 19]. In addition, at resonance, for $|X|=X_{max }$, the power obtained is $P_{lim } =\left( {1/2} \right) m\omega X_{max } A$, which is approximately 78.1 % of $P_{lim }$.

Fig. 7.1

Typical diagram of a vibration energy harvester model

Depending on their transduction mechanisms, vibration energy harvesters can be classified into electrostatic energy harvesters [1–3], piezoelectric energy harvesters [4–6] and electromagnetic energy harvesters [7, 8]. In an electrostatic energy harvester, the displacement of the movable proof mass electrode varies the capacitance between the movable proof mass electrode and the fixed electrode when an appropriate bias is placed on either the movable proof mass electrode or the fixed electrode. Piezoelectric conversion is a function of the material properties; strain in the material produces an electric field in that material, and vice versa. The principle of operation of an electromagnetic energy harvester is based on Faraday’s law of induction. A variable electric field is generated in an electromagnetic energy harvester, creating an output voltage V, when the magnetic flux $\varPhi$ passes through an electrical circuit. The harvested power can either be used directly for a specific application or can be managed efficiently using power management circuits such as SSHI or buck–boost converter circuits [15, 20].

The spectra of the vibration signals vary from narrowband to wideband [21–25]. The role of the energy harvester is to respond effectively to the wideband spectra but not to the single peaks. However, for applications where the response from a single frequency peak is the case of interest, the harvester should work efficiently for that frequency peak.

The harvesters are excited by ambient vibrations, which introduce the relative motion of the proof mass with respect to the device frame. The vibration amplitudes can be unpredictable in many cases. The harvester designs must be able to adapt to the vibration conditions to maximize the output power, while the harvester performance is required to be both robust and effective. In the following analysis, a sinusoidal vibration with angular frequency $\omega =2\pi f$ and amplitude A is used to characterize the nonlinear behavior of the end-stops of vibration energy harvesters.

7.2 Modeling of the End-Stops

In conventional vibration energy harvesters, the end-stops are unavoidable in the real prototypes. The displacement is limited by the space constraints of the device package. The main function of the end-stops is to confine the proof mass motion under sufficiently large vibration conditions. In addition, they protect the beam structures and prevent degradation of the material properties. The end-stops set an upper bound on the output power at high acceleration amplitudes, i.e. they limit the harvested power, which would otherwise be infinitely high without the end-stops.

The end-stops introduce strong nonlinearities into the harvester response when the proof mass hits the end-stops under extreme accelerations. The positive and negative characteristics of the end-stops have been discussed in a number of papers. For example, the nonlinear behavior of proof mass motion in energy harvesters that include end-stops has been studied via both simulations and experiments [12, 15]. Mathematical modeling of the end-stops in an energy harvester will be discussed in detail in this section, followed by examples of working devices harvesting power from the active end-stops. Theoretical and experimental studies have been carried out to characterize the end-stops in the device design. In [4], a mechanical end-stop is applied only on one side of the cantilever beam of a piezoelectric energy harvester. The frequency response of this harvester is demonstrated by varying the end-stop parameters. In [12], the end-stops applied in an electromagnetic power generator increase the bandwidth of the frequency up-sweep while maintaining the same bandwidth for the down-sweep.

7.2.1 Mathematical Analysis

It is useful to have some tools that can provide an insight into the performance of an energy harvester with and without the end-stop nonlinearities using given parameters for the desired prototypes. A mathematical tool for nonlinearities related to the end-stops in vibration energy harvesters using an eigenvalue approach and time domain simulations is presented in this section. For this analysis, two end-stops that limit the motion of the proof mass are considered, where the motion is treated as a linear evolution between the impacts with velocity discontinuities at the end-stops.

An equivalent circuit for an energy harvester model with end-stop effects, irrespective of the transduction mechanism, is shown in Fig. 7.2, where m is the proof mass, $b_{m}$ is the mechanical damping, k is the electromechanical coupling factor, K is the effective spring stiffness, C is the transducer capacitance, $\Gamma =\sqrt{KC}$, and R is the load resistance. The excitation force is represented by $F_{ext}= ma$. The transducer model is similar to that of a velocity-damped resonant generator (VDRG). The end-stop effects are included as the impact force $F_{s}$ on the mechanical domain circuit. The impact force $F_{s}$ is activated when the proof mass displacement amplitude reaches its maximum.

At equilibrium, the total force on the proof mass and the voltage across the electrical load in the transducer are assumed to be zero. We observe deviations of the state variables from their equilibrium values when the harvester is excited, and these deviations depend on the strength of the excitation signal. The linear equations of proof mass motion under sinusoidal excitation can be formulated as Eqs. (7.3)–(7.7).

$$\begin{aligned} \frac{dx}{dt}=v \end{aligned}$$

(7.3)

$$\begin{aligned} \frac{dv}{dt}=-\omega _0^2 x-\frac{\omega _0^2 k}{\Gamma }q-\frac{\omega _0 }{Q}v+a \end{aligned}$$

(7.4)

$$\begin{aligned} \frac{dq}{dt}=-\frac{\omega _0 }{r}\Gamma kx-\frac{\omega _0 }{r}q \end{aligned}$$

(7.5)

$$\begin{aligned} \frac{da}{dt}=-\omega b \end{aligned}$$

(7.6)

$$\begin{aligned} \frac{db}{dt}=\omega a \end{aligned}$$

(7.7)

Fig. 7.2

Two-port linear transducer with end-stop effects

where x is the position of the proof mass, $\nu$ is the velocity, q is the transducer charge, $\omega$ is the angular driving frequency, t is the time, Q is the open circuit quality factor of the device, k is the electromechanical coupling factor, $\omega _0$ is the open circuit angular resonance frequency, $r=\omega _0 CR$, and acceleration $a=A\cos \omega t$, where A is the acceleration amplitude $A=\sqrt{a^{2}+b^{2}}$. To make the system autonomous, an auxiliary quantity $b=A\sin \omega t$ is introduced into the state equations.

Equations (7.3)–(7.7) are translated into dimensionless forms with reference to the dimensionless time (phase angle) $\theta =\omega _0 t$, frequency $\varsigma =\omega /{\omega _0 }$, and amplitude $\hat{{A}}=A/X_{max } \omega _0^2$. The dimensionless state variables then become

$$\begin{aligned} \hat{{x}}\left( \theta \right) ={x\left( t \right) }/{X_{max } } \end{aligned}$$

(7.8)

$$\begin{aligned} \hat{{v}}\left( \theta \right) ={v\left( t \right) }/{X_{max } }\omega _0 \end{aligned}$$

(7.9)

$$\begin{aligned} \hat{{q}}\left( \theta \right) ={q\left( t \right) }/{X_{max } }\Gamma \end{aligned}$$

(7.10)

$$\begin{aligned} \hat{{a}}\left( \theta \right) ={a\left( t \right) }/{X_{max } }\omega _0^2 \end{aligned}$$

(7.11)

$$\begin{aligned} \hat{{b}}\left( \theta \right) ={b\left( t \right) }/{X_{max } }\omega _0^2 \end{aligned}$$

(7.12)

where ${\pm }X_{max}$ denotes the end-stop positions, i.e., $\left| {x\left( t \right) } \right| \le X_{max }$. Typically, the motion of the proof mass before impact is linear, and thus the state vector is $\hat{{u}}=\left[ {{\begin{array}{lllll} {\hat{{x}}}&{} {\hat{{v}}}&{} {\hat{{q}}}&{} {\hat{{a}}}&{} {\hat{{b}}} \\ \end{array} }} \right] ^{T}$ and Eqs. (7.3)–(7.7) then read:

$$\begin{aligned} \frac{d\hat{{u}}}{dt}=-\hat{{L}}\hat{{u}} \end{aligned}$$

(7.13)

where

$$\begin{aligned} \hat{{L}}=\left[ {{\begin{array}{lllll} 0&{} {-1}&{} 0&{} 0&{} 0 \\ 1&{} {\frac{1}{Q}}&{} k&{} {-1}&{} 0 \\ {\frac{k}{r}}&{} 0&{} {\frac{1}{r}}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} \varsigma \\ 0&{} 0&{} 0&{} {-\varsigma }&{} 0 \\ \end{array} }} \right] \end{aligned}$$

(7.14)

and the linear evolution of the system from, for example $\theta =\theta _1$ to $\theta =\theta _2$, is given by

$$\begin{aligned} \hat{{u}}\left( {\theta _2 } \right) =\hat{{U}}\left( {\theta _2 -\theta _1 } \right) \hat{{u}}\left( {\theta _1 } \right) \end{aligned}$$

(7.15)

where

$$\begin{aligned} \hat{{U}}\left( \theta \right) =\exp \left( {-\theta \hat{{L}}} \right) \end{aligned}$$

(7.16)

If an impact occurs at the dimensionless time $\theta _1$, then the change in velocity at the time of impact is modeled as $\hat{{v}}\left( {\theta _1^+ } \right) =-{e}\hat{{v}}\left( {\theta _1^- } \right)$, where e is the coefficient of restitution and the superscript ± denotes a infinitesimally small time after/before $\theta _1$. Thus, the change in the state vector at the time of impact is given by

$$\begin{aligned} \hat{{u}}\left( {\theta _1^+ } \right) = S\hat{{u}}\left( {\theta _1^- } \right) \end{aligned}$$

(7.17)

where

$$\begin{aligned} S=\left[ {{\begin{array}{lllll} 1&{} 0&{} 0&{} 0&{} 0 \\ 0&{} {-e}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0 \\ \end{array} }} \right] \end{aligned}$$

(7.18)

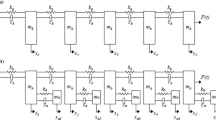
Figure 7.3 shows the end-stops model, where the end-stops are placed at the positions of ±X$_{max}$. Thus, the impacts occur at the normalized positions $\hat{{x}}=-1$ and $\hat{{x}}=+1$. If the sequence of impacts per cycle of motion is known, then all possible solutions can be found from the solution to the eigenvalue problem.

Fig. 7.3

Modeling of the impact at the end-stops

Let $\theta =0$ be the time of impact at $\hat{{x}}=-1$ and assume that, at some intermediate time $\theta _1$, another impact occurs at $\hat{{x}}=+1$, and then the next impact occurs at $\hat{{x}}=-1$ at time $\theta _2 ={2\pi }/\varsigma$, thus completing one whole cycle of the proof mass motion.

If the state vector is initially $\hat{{u}}\left( {0^{+}} \right) =u_0$, then the sequence of linear evolutions and impacts that occur up to the point in time just after the second impact at $\hat{{x}}=-1$ at time $\theta =\theta _2^+$ is given by

$$\begin{aligned} \hat{{u}}\left( {\theta _1^- } \right) =\hat{{U}}\left( {\theta _1 } \right) u_0 \end{aligned}$$

(7.19)

$$\begin{aligned} \hat{{u}}\left( {\theta _1^+ } \right) =S\hat{{u}}(\theta _1^- )=S\hat{{U}}\left( {\theta _1 } \right) u_0 \end{aligned}$$

(7.20)

$$\begin{aligned} \hat{{u}}\left( {\theta _2^- } \right) =\hat{{U}}\left( {\theta _2 -\theta _1 } \right) \hat{{u}}(\theta _1^+ )=\hat{{u}}\left( {\theta _2^- } \right) =\hat{{U}}\left( {\theta _2 -\theta _1 } \right) S\hat{{U}}\left( {\theta _1 } \right) u_0 \end{aligned}$$

(7.21)

$$\begin{aligned} \hat{{u}}\left( {\theta _2^+ } \right) =S\hat{{u}}\left( {\theta _2 } \right) =S\hat{{U}}\left( {\theta _2 -\theta _1 } \right) S\hat{{U}}(\theta _1^+ )u_0 \end{aligned}$$

(7.22)

If the period of motion is equal to the period of the vibration, then $\hat{{u}}\left( {\theta _2^+ } \right) =u_0$ in (7.22). Therefore, an admissible $u_0$ must be an eigenvector of the matrix $S\hat{{U}}\left( {\theta _2 -\theta _1 } \right) S\hat{{U}}(\theta _1$) with an eigenvalue of 1. Thus, solution of the eigenvalue problem provides possible solutions for the motion of the proof mass for one whole period of the driving force. The final result must be checked against unphysical solutions where the proof mass motion extends beyond the limits of the end-stops. The state vectors give the package acceleration amplitude.

Similar analyses can be conducted for other types of motion, e.g., with more than one impact per hit. However, the analysis quickly becomes complex when there are several impacts per period of motion, because that leads to several unknown impact times and a new eigenvalue problem must be formulated for each case. This technique is similar to the technique used in [14].

7.2.2 Analysis of the Numerical Results

System parameters are required for solution of the eigenvalue problem. In this chapter, the eigenvalue problem is demonstrated using system parameters that are identical to those given in [15], with $\varsigma =1$, $r=1, Q=350$, and $k^{2}=0.6\,\%$. The effects of changing the system parameters are also compared using the system parameters given in [13], with $\varsigma =1$, $r=1$, $Q=203.5$, and $k^{2}=2.52\,\%$. The simplest case that can be used to check the nonlinear behavior at the end-stops is to assume that the coefficient of restitution $e=1$, i.e., the end-stops are rigid and elastic collisions occur; no energy is gained or lost at the end-stops. If the end-stops are compliant by nature, then the coefficient of restitution is less than 1.

Fig. 7.4

Acceleration amplitude versus time between impacts for $e=1$

Fig. 7.5

Acceleration amplitude versus time between impacts for $e=0$

Fig. 7.6

Acceleration amplitude versus time between impacts for $e=0.3$

Fig. 7.7

A bare impact at the end-stops when $\hat{{A}}=0.00658$ and $e=1$

Figures 7.4, 7.5 and 7.6 show the physical and unphysical sets of solutions for one period of motion from the eigenvalue problem using Eqs. (7.19)–(7.22). Three different coefficients of restitution, i.e., $e=1$, $e=0$ and $e=0.3$, are used for illustration purposes here. Figure 7.4 shows that there is a single solution in which the first impact occurs at the midpoint of the cycle for a normalized amplitude of 1. As the amplitude increases, this solution splits into two solutions with opposite asymmetry in their times between impacts. The motion of the proof mass changes dramatically for compliant end-stops. Figure 7.5 shows that the proof mass motion is unphysical for the wider set of acceleration amplitudes when compared with the set of physical solutions. The motion of the proof mass becomes more complicated for $e=0.3$, as shown in Fig. 7.6. Not even single acceleration amplitude is detected for the physical motion from the eigenvalue problem. The eigenvalue approach used here cannot detect the motion of the proof mass other than as described in Eqs. (7.19)–(7.22). Figure 7.7 shows the acceleration amplitude where proof mass barely hits the end-stops.

The acceleration amplitude under the condition where the proof mass will barely hit the end-stops is given by

$$\begin{aligned} \hat{{A}}=\frac{\left( {r+k^{2}Q} \right) ^{2}+1}{\sqrt{\left( {Q^{2}+r^{2}Q^{2}} \right) \left( {r+k^{2}Q^{2}} \right) +Q^{2}+r^{2}Q^{2}}} \end{aligned}$$

(7.23)

To study the motion of the proof mass in detail, the acceleration amplitudes from each set of physical and unphysical solutions are selected for the given coefficient of restitution. Figures 7.8 and 7.9 show the motion of the proof mass for acceleration amplitudes $\hat{{A}}=1.0023$ and $\hat{{A}}=1.2271_{ }$ from the set of physical solutions and unphysical solutions for $e=1$, respectively.

The motion of the proof mass shown in Fig. 7.9 is complex. The proof mass tends to go beyond the displacement limit that has been set by the end-stops, while in Fig. 7.8, the period of the proof mass motion is equal to the period of the driving force with one impact at each end-stop per cycle of the driving force. The jump in velocity at the point of impact can be seen clearly in these figures.

Fig. 7.8

Proof mass motion for $e=1$ and $\hat{{A}}=1.0023$

Fig. 7.9

Proof mass motion for $e=1$ and $\hat{{A}}=1.2271$

Figure 7.10 shows the evolution of the proof mass motion for the acceleration amplitudes from the set of physical solutions for $e=1$. Figure 7.10 shows the different patterns of the proof mass motion for specific acceleration amplitudes. For $\hat{{A}}=1.0945$, the period of the proof mass motion is longer than the period of the driving force. The eigenvalue problem requires further improvement to detect the different motion patterns as separate entities for the given set of parameters. Figure 7.11 shows the complexity of the proof mass motion pattern for $e=0$. The acceleration amplitude $\hat{{A}}=1.0207\hbox {e}+003$ in Fig. 7.11 corresponds to the set of unphysical solutions that was detected by the solution to the eigenvalue problem.

Fig. 7.10

Proof mass motion for $e=1$ and acceleration amplitudes $\hat{{A}}=1.1778, 1.0329, 1.0945$, from left to right

Fig. 7.11

Proof mass motion for $e=0$ and $\hat{{A}}=1.0207\hbox {e}+003$

The coefficient of restitution $e=0$ is closer to the conditions of real-world collisions. The proof mass will lose all energy at the end-stops on each impact. As shown in Fig. 7.11, the proof mass tends to go beyond the displacement limit when the acceleration amplitudes are sufficiently high. The restoring force from the end-stop then comes into play and limits the displacement of the proof mass to prevent it from passing beyond the end-stop. The proof mass will leave the end-stop when the restoring force from the end-stop reverses its direction. The restoring force phenomenon is not modeled in the eigenvalue analysis.

The eigenvalue problem is a simple analysis that does not account for the initial transitions that occur in the system, which are otherwise always present during the experimental testing of the harvester. To characterize the system exclusively, it is important to simulate the system’s behavior over a time period that is long enough for these initial transitions to die out.

Fig. 7.12

Phase space trajectory for $e=1$ and $\hat{{A}}=0.01$

Fig. 7.13

Phase space trajectory for $e=1$ and $\hat{{A}}=0.1$

Fig. 7.14

Phase space trajectory for $e=1$ and $\hat{{A}}=0.25$

Fig. 7.15

Phase space trajectory for $e=1$ and $\hat{{A}}=1.002$

Fig. 7.16

Phase space trajectories for $e=1$ and $\hat{{A}}=0.25$ for the system parameters given in [13]

Fig. 7.17

Phase space trajectory for $e=0$ and $\hat{{A}}=0.05$

Fig. 7.18

Phase space trajectory for $e=0$ and $\hat{{A}}=1$

Fig. 7.19

Phase space trajectory for $e=0$ and $\hat{{A}}=1.1$ without a restoring force

To check whether simulation of the system for a large driving force cycle makes any difference to the proof mass motion patterns for given acceleration amplitudes, the phase space trajectories were studied. The phase space trajectories provide obvious visualizations of the proof mass motion with changing acceleration amplitudes for a given coefficient of restitution. Figures 7.12, 7.13, 7.14 and 7.15 show the phase space trajectories projected into the $x-v$ plane for $e=1$. Figure 7.12 shows the time evolution of the acceleration amplitude that is necessary to achieve the required impacts. The phase space trajectory shows the cyclic motion of the proof mass, but with the motion period being considerably longer than the period of the driving force. For slightly larger amplitudes, the phase space trajectory becomes very complex and chaotic, with no repeating patterns, as shown in Fig. 7.13. This may stem from the fact that eigenvalue analysis is unable to capture complex motion patterns.

For further increases in the acceleration amplitude, the motion pattern becomes simpler, as shown in Figs. 7.14 and 7.15. Figure 7.14 shows that the motion period of the proof mass is double the period of the driving force. Upon a further increase, the acceleration amplitude then lies in the region where the period of the proof mass motion is exactly equal to the period of the driving force with one impact at each end-stop per cycle, as shown in Fig. 7.15.

The motion of the proof mass depends significantly on the system parameters. The proof mass motion therefore varies with different sets of parameters for the same coefficient of restitution. Figure 7.16 shows the proof mass motion pattern based on the system parameters given in [13] for $e=1$. Comparison of Fig. 7.14 with Fig. 7.16, where both are based on the same acceleration amplitude and coefficient of restitution, shows that the motion periods for the different sets of system parameters are dissimilar. The motion pattern in Fig. 7.16 is much simpler than that shown in Fig. 7.14. The appearance of the phase space trajectories thus varies with the different coefficients of restitution for the given system parameters, and vice versa.

It is interesting to observe the evolution of the phase space trajectories for $e=0$ over time. Figures 7.17 and 7.18 show the trajectories for the acceleration amplitudes where the motion period is equal to that of the driving force. For an acceleration amplitude of more than 1, the proof mass motion becomes complicated, because it tends to go beyond the displacement limit that was set by the end-stops, as shown in Fig. 7.19. Thus, modeling of the restoring force for the acceleration amplitude for which the proof mass tends to cross the displacement limit simplifies the proof mass motion, as shown in Fig. 7.20.

With the restoring force at the end-stops, the equation system from Eqs. (7.3)–(7.7) is reformulated in the form of

$$\begin{aligned} \frac{d\hat{{u}}}{dt}=-\hat{{L}}_1 \hat{{u}} \end{aligned}$$

(7.24)

where

$$\begin{aligned} \hat{{L}}_1 =\left[ {{\begin{array}{lllll} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0 \\ {\frac{k}{r}}&{} 0&{} {\frac{1}{r}}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} \varsigma \\ 0&{} 0&{} 0&{} {-\varsigma }&{} 0 \\ \end{array} }} \right] \end{aligned}$$

(7.25)

Fig. 7.20

Phase space trajectory for $e=0$ and $\hat{{A}}=1.1$ with restoring force

For coefficients of restitution $0<e<1$, the analysis requires further investigation. For example, an impact with $e=0.3$ is not perfectly inelastic, and thus the proof mass will have a tendency to bounce back and forth toward the end-stops several times before attaining continuous motion. The bouncing motion of the proof mass must be taken into account to study the complete motion pattern of the proof mass. The $0<e<1$ range has not been analyzed in detail in this chapter.

The average output power is calculated using Eq. (7.26) for a linear model with no end-stop impact. The output power with the end-stop effects is given in Eq. (7.28) by averaging the instantaneous power over the motion period.

$$\begin{aligned} \hat{{P}}_{linear} =\frac{P_{linear}}{m {X_{max}^2} {\omega _0^3}}=\frac{1}{2}r\hat{A}^{2}\left| {\hat{{h}}\left( \varsigma \right) } \right| ^{2} \end{aligned}$$

(7.26)

Fig. 7.21

Average output power versus acceleration amplitude

where

$$\begin{aligned} \hat{{h}}\left( \varsigma \right) =\frac{i\varsigma k}{\left\{ {\left( {1-k^{2}} \right) -\left( {1+\frac{r}{Q}} \right) \varsigma ^{2}+i\varsigma \left[ {\frac{1}{Q}+r\left( {1-\varsigma ^{2}} \right) } \right] } \right\} } \end{aligned}$$

(7.27)

$$\begin{aligned} \hat{{P}}=\frac{1}{r}\left( {k\hat{{x}}+\hat{{q}}} \right) \end{aligned}$$

(7.28)

Figure 7.21 shows the average output power for the system with $e=1$ and $e=0$ that was simulated for large numbers of vibration cycles. The discontinuities shown in Fig. 7.21 for $e=1$ correspond to the acceleration amplitudes that produce complex phase space trajectories with motion periods that differ from the period of the driving force, as shown above.

Fig. 7.22

Average output power versus acceleration amplitude with a restoring force

The inset image for $e=0$ in Fig. 7.21 shows the complex pattern for an acceleration amplitude of more than 1, which corresponds to the phase space trajectories where the proof mass passes beyond the displacement limit, and thereby illustrates the need for the restoring force to be included in the model.

Figure 7.22 shows the average output power from the end-stop model when taking the restoring forces from the end-stops into account. The unevenness shown in Fig. 7.21 at acceleration amplitudes of more than 1 and for $e=0$ is evened out in Fig. 7.22.

The results in Fig. 7.21 show that the power with $e=0$ and $e=1$ follows almost identical curves. However, this may or may not be the case for practical harvester prototypes, where the impacts are imperfectly elastic ($e=0$). Additionally, many other factors affect the average output power, including the squeeze film damping coefficient, the slide film damping coefficient, overcutting in the fabrication process, fringing fields, parasitic capacitance, and the end-stop configurations. One interesting phenomenon that is shown in Fig. 7.21 is that the average output power is weakly dependent on the acceleration amplitude.

7.2.3 Transducing End-Stops

The negative effects of power saturation for $e=1$ and of the power loss for $0<e<1$ are obvious for the end-stops in vibration energy harvesters when the proof mass displacement reaches a maximum amplitude, as shown in Fig. 7.21. This effect has been demonstrated experimentally in many harvester prototypes [9, 11, 12, 26, 27]. The concept of replacement of passive end-stops with active end-stops to act as secondary transducers is illustrated in Fig. 7.23 [13, 28]. When the excitation levels are strong enough, the transducing end-stop is actuated by the force of the impact between the proof mass and the end-stop. The power from the end-stop transducer is added to that from the main transducer, and thus continuously increases the total power of the system when the acceleration level increases. As a result, the efficiency or effectiveness of the harvester is improved by this combination of the main transducer with the end-stop transducers.

Fig. 7.23

Active end-stops acting as transducers included within the device package [13, 28]

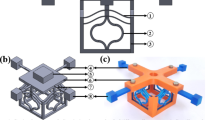
The end-stop mechanism can be one of three types: electrostatic, electromagnetic, or piezoelectric, as stated earlier. The important function of the transducing end-stop is to efficiently convert the kinetic energy from the impact force into electrical power while maintaining the net stiffness to confine the primary transducer’s motion. Figure 7.24 shows an example of a device that implements transducing end-stops based on electrostatic mechanisms. An overlap-varying comb-drive capacitor structure includes main transducers 1 and 2, which vary in anti-phase with each other. The end-stop transducer is a gap-closing capacitor structure. The masses of both the main and secondary transducers are suspended using linear folded springs. In the design, the maximum displacement amplitude of the main proof mass is $X_{max}=10\,\upmu$m. The end-stop transducer begins actuation when the relative displacement of the main proof mass passes beyond 6 $\upmu$m.

Fig. 7.24

a A schematic of the device prototype design using the active end-stop transducers, and b a close-up view of the fabricated device

Table 7.1 Design parameters for the device prototype

Fig. 7.25

Output voltage waveforms of the transducers for $A=1.2$ g

Figure 7.24a shows the main characteristics of the in-plane harvester design. Figure 7.24b shows part of the microelectromechanical system (MEMS) device, which was fabricated using the silicon-on-insulator multi-user MEMS processing (SOI-MUMPS) method with a device layer thickness of 25 $\upmu$m [29]. The total active area of the prototype is 4 $\times$ 5 mm$^{2}$. The design parameters of the device are listed in Table 7.1. In the experiments, all electrostatic transducers in the device prototype are biased using an external bias voltage $V_{b}=12$ V in continuous mode. The output powers from the end-stop and main transducers are obtained by connecting the fixed electrodes of the transducers to an external load with component value $R_{L}=18.5$ M$\Omega$, which is the optimum load for the main transducers.

At low acceleration levels, the proof mass motion of the main transducers is less than the maximum displacement amplitude. Therefore, there is no internal impact between the main transducers and the end-stop transducer. Thus, the transducing end-stops are deactivated and produce almost no output power. The harvester outputs are linear and mainly come from the main transducers, 1 and 2, in opposite phase. Figure 7.25 shows the output voltage waveforms of the main transducers and the end-stop transducer for an acceleration $A=1.2$ g. At this sufficiently large excitation level, the impact force between the masses is strong enough to drive the end-stop transduction significantly. The output voltage of the end-stop transducer then becomes comparable to that of the main transducers. This indicates that the energy conversion process is more effective with the addition of the end-stop transducer. The waveform of the end-stop transducer is characterized almost in transient time, which is restricted by the time interval between the impacts, as shown in Fig. 7.25. The gap-closing transduction in the end-stop transducer produces a motion period that is double that of the overlap-varying transduction in the main transducers.

Figure 7.26 shows the frequency responses of all measured output voltages for $A=1.2$ g. In the linear regime, the main transducers give a resonant frequency of $f_{0}=665$ Hz and a 3-dB bandwidth of 6.9 Hz. The dynamic interaction due to the impact between the proof masses adds nonlinearities to the frequency responses of both the main transducers and the end-stop transducer. The frequency responses form a hysteresis pattern with a jump-down frequency $f_{down}=653.1$ Hz and a jump-up frequency $f_{up}=730.4$ Hz. The frequency band between the jump frequencies of the up-sweep and down-sweep is 77.3 Hz, which is approximately 11 times higher than the 3 dB bandwidth in the linear regime. Thus, the positive nonlinearities broaden the harvester bandwidth based on the end-stop transducer impact mechanism. The intermediate frequency range shows a high-amplitude revolution in their responses.

Fig. 7.26

Measured output voltages of the transducers versus frequency up-sweep (solid line) and down-sweep (dashed line) for $A=1.2$ g

Additionally, the output voltage of the transducing end-stop is significant in the impact frequency range. During an impact, the main proof mass hits the end-stop and is then moved for an extra distance before it returns to the equilibrium position. The hysteresis observed in the low-frequency range is affected by the softening-spring nonlinearity [10, 30–32] because of the electrostatic pull of the end-stop transducer on the proof mass for small gap sizes. Therefore, the end-stop proof mass is driven toward a larger displacement amplitude, which leads to greater variation in the gap-closing capacitance in the end-stop transduction process. As shown in Fig. 7.26, the minimum gap for the end-stop transducer is achieved for $A=1.2$ g. The outputs of both the main transducers and the end-stop transducer reach their maximum levels.

Fig. 7.27

Measured output power of the prototype with the transducing end-stops compared with that of the reference prototype with rigid end-stops at their resonant frequencies

The benefits of the transducing end-stop can be seen by comparison with the reference harvester prototype under increasing acceleration amplitudes, as shown in Fig. 7.28. The reference transducers are designed to be identical to the main transducers in the same active area. Both prototypes have a maximum displacement amplitude $X_{max}=10\,\upmu$m. In the linear regime, the output power of the reference prototype is slightly higher than that of the impact prototype. This is because the reference harvester has a larger proof mass and higher transduction designed using the same constraints. The proof mass motion of the reference device reaches its maximum displacement amplitude at an acceleration $A=0.18$ g. A saturated output power of 35.0 nW is obtained for the reference device. With the additional power coming from the end-stop transducers, the total power of the impact prototype is higher than that of the reference harvester under the same conditions. The total power achieved is 81.5 nW at $A=0.91$ g, which is 2.3 times higher than that of the reference prototype.

Figure 7.27 shows one drawback where a large acceleration gap from $A=0.10$ g to $A =0.91$ g must be covered to enable the end-stop transducer to be effective. This is because the designed mechanical stiffness of the end-stop transducer is rather too stiff. Therefore, strong acceleration forces are required to enhance the end-stop transduction of the gap-closing capacitance, which varies as $\sim 1/{\left( {g^{2}-x_s^2 } \right) }$. This problem can be overcome by designing the end-stop transducer to have a compliant stiffness, as shown in Fig. 7.28. With a compliant end-stop, the total output power increases almost linearly when the benefits of the end-stop transducer become recognizable at $A=0.72$ g. The total power is higher than the saturated power of the impact device with the stiffer end-stop transducer for $A>1.42$ g. The high-amplitude orbit of the end-stop proof mass is achieved quickly when the net stiffness of the end-stop transducer is reduced. The end-stop transduction is considerable even at small acceleration amplitudes, and becomes complicated at high acceleration levels. These complications can be explained with reference to the phase space trajectories from the mathematical analysis of the end-stop effects that was illustrated earlier. In the later prototype, the transducing end-stops are used on both the right and left sides of the main transducers [13].

Fig. 7.28

Total output powers for two different end-stop designs

Alternatively, the mechanical stiffness of the end-stop transducer can be further reduced by increasing the bias voltages applied to the electrostatic end-stop transducer. The electrostatic force from the gap-closing transducer cancels the spring force to produce a low net stiffness while maintaining sufficient strength to secure any unstable pull-in effects. Therefore, the end-stop transducer becomes more compliant. The transducing end-stops will need further improvements to improve the total system output power with given displacement constraints.

7.3 Conclusions

The numerical analysis that was carried out above is a useful tool for study of the nonlinearities of end-stop effects in vibration energy harvesters. Through simple modeling of the end-stops, it was found that this simple motion is atypical and that solutions with complicated trajectories exist in phase space. The periods of motion for these solutions can be very different from the period of the driving force, if indeed they are periodic at all. The main effect of the end-stops on the output power is to produce saturation behavior during continuous mode operation. The phase space trajectories show that the motion of the proof mass in the energy harvester can be complex, depending on the acceleration amplitude, but that the output power is weakly dependent on the acceleration amplitude in the impact regime. Therefore, the effects of the impacts on device performance during continuous operation are minor. The consideration of the restoring force at the impacts is demonstrated using the phase space trajectories and an output power graph.

The inelastic collisions with $e=0$ will cause some energy to be lost in the end-stops on impact. This energy loss can be collected smartly using power conditioning circuits such as SECE or SSHI circuits. Alternatively, the lost energy on impact can be collected by introducing the transducing end-stops which not only increases the total output power of the harvester but also enhances its bandwidth. The compliant transducing end-stops harvest more power than rigid transducing end-stops, as demonstrated here using harvester prototypes. The harvester output can be further improved by efficient design of the stiffness of the end-stops.

The mathematical analysis described in this chapter can provide an insight into the device behavior for given system parameters. The tool can be used effectively and efficiently for energy harvester design. For example, when designing an energy harvester that uses the end-stops as switches for power conversion circuitry, the simulation approach illustrated in this chapter can be used to predict the switching on every cycle of the driving force, thus optimizing the power that is harvested.