Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The supply chain planning of food products is ruled by the dynamic nature of its products. Throughout the planning horizon, the characteristics of these products go through significant changes. The root cause for these changes may be related to, for example, the physical nature of the products or the value that the customer lends to them. Without acknowledging the perishable nature of food products, one may incur in avoidable spoilage costs (for example, in the case of meat products) or, on the other hand, sell the product before it is close enough to its best state (for example, in the case of cheese products). In this paper, we focus on perishable food products that start worsening their properties after being produced.

Fleischmann et al. [7] define planning as the activity that supports decision-making by identifying the potential alternatives and making the best decisions according to the objective of the planners. Let us look into the specific challenges of engaging in a production planning activity in the context of food products.

In order to identify the alternatives it is important to frame the decisions that the decision maker wants to make. It is common to organize the supply chain planning according to two dimensions: the supply chain process (procurement, production, distribution and sales) and the hierarchical level (strategic, tactical and operational). The scope of this paper is in the production supply chain process and we deal with problems arising at the tactical/operational decision level. Therefore, we will address food production planning problems that have to decide about the size of the lots to be produced and about the schedule of these production lots. In this problem, we usually determine the size of lots to be produced while trading off the changeover and stock holding costs. In food production, expiry dates may enforce constraints related to the upper bounds on lot-sizes and consequently the need of scheduling more often a given family of products (increasing the difficulty of sequencing). Expiry dates relate to the concept of perishability that is defined by Amorim et al. [4] as: “A good, which can be a raw material, an intermediate product or a final one, is called ‘perishable’ if during the considered planning period at least one of the following conditions takes place: (1) its physical status worsens noticeably (e.g. by spoilage, decay or depletion), and/or (2) its value decreases in the perception of a(n internal or external) customer, and/or (3) there is a danger of a future reduced functionality in some authority’s opinion.”. In this paper, we will consider goods that suffer a physical deterioration, for which customers’ attribute a decreasing value and for which authorities usually limit the commercialization period.

The second part of Fleischmann et al. [7] definition of planning relates to the objectives of the planners. The literature in production planning tackles most of the problems with traditional single objective models. The goal is usually related either to an operational measure, such as makespan, or to some monetary measure, such as cost or profit. In this paper, we show the interest of extending these objectives by including factors related to the food industry, such as spoilage costs. Moreover, the use of a multi-objective approach is described in order to account for the customer willingness for fresher products and to induce a risk conscious strategy. Acknowledging freshness in production planning besides avoiding products’ spoilage, may yield a substantial intangible gain derived from delivering fresher products to customers. Such considerations are closely related to the consumer purchasing behavior of perishable goods that should be the concern of any planner in a (food) company with a market orientation.

The key contribution of this paper is to provide a systematic approach to a problem that has been tackled sparsely in the literature. We believe that this road-map on mixed-integer models for production planning of perishable food products may be useful to any researcher or practitioner willing to start solving a problem in this field. For an extensive review in production planning problems dealing with perishability the readers are referred to Pahl and Voß [9] and for a more comprehensive review on supply chain planning problems dealing with perishability the readers are referred to Amorim et al. [4].

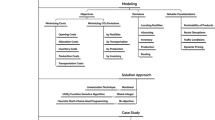
In the remainder of the paper, we present how a traditional base model dealing with the production planning of food products has to be changed in order to accommodate the characteristics of the products it has to deal with. Therefore, we start by presenting a deterministic base model in Sect. 2. In Sect. 3, we understand how the constraints have to be extended to incorporate key aspects, such as the fact that products have a limited shelf-life or that customers pick up the fresher available products. Section 4 analyses the possible changes in the objective function: discarding costs of perished goods and valuing in a different objective function the freshness. Section 5 tackles the possibility of having more information on key parameters – dependency between price and age and between demand and age. The “ingredients” presented throughout these section can be mixed together in various ways to form the “recipe” suitable for the production environment. In order to help understanding the implications of these “ingredients” in the solution structure, all models are solved for an illustrative example in Sect. 6. Section 7 discusses the extension of the deterministic base model to a stochastic setting in which demand or other parameters may be uncertain leading the notion of a risk-conscious planning. This model road-map is summarized in Fig. 1. Finally, in Sect. 8 the main conclusions are presented.

Fig. 1
figure 1

Road-map of the different “ingredients” presented in this paper

Full size image

2 Base Model

We start by presenting a base model for production planning in food industries. This model focuses on the packaging stage and has no considerations about the perishable nature of the products.

One important concept in the fast moving consumer food goods is the recipe. Usually, products belong to a certain recipe that requires a major setup and the products within the recipes just need a minor setup. This is known as production wheel policy by practitioners. We use an adaptation of the block planning formulation [8] that was designed for similar production environments to that of the food industry. To make it clearer, a block corresponds to a recipe and within and between recipes the sequence of products is set a priori. Therefore, the only decision to be made for each block/product, besides the sizing of the lots, is whether to produce it or not. This modeling approach increases the application potential of decision support systems in production planning, because decision makers are comfortable with the definition of the recipes and, simultaneously, the scheduling complexity is fairly reduced increasing the computational tractability of the related problems. In Fig. 2 a production schedule with two blocks, A and B, is depicted. Notice that before producing products of a given recipe a major setup is necessary. Afterwards, all products within the same recipe are produced after doing a minor setup. Block A has usually a lighter color or a less intense flavor than block B. Examples of this recipe structure can be found in the yoghurt, milk, juice and chocolate industries.

Fig. 2
figure 2

Adapted block planning concept [5]

Full size image

Let us now move to a formal description of the problem. Consider a set of products k = 1, …, K that are produced based on a certain recipe/block j = 1, …, N. There is only one recipe to produce each product and, therefore, a product is assigned to one block only. Hence, for each block j there is a set \(\mathcal{K}_{\mathcal{J}}\) of products k related to it. Blocks are to be scheduled on l = 1, …, L parallel production lines over a finite planning horizon consisting of periods t = 1, …, T with a given length. This length is related to the company’s practice of measuring external elements, such as demand or perishability (thus, periods correspond to days, weeks or months in most of the tactical/operational cases). According to the block structure, all scheduling decisions are already made for both recipes and products. Hence, the production sequence is determined beforehand, minimizing the setup times and costs according to the planner expertise [8]. This is particularly useful in practice, since companies have difficulties in measuring setups costs and setups times accurately. This limitation may reduce the applicability of traditional production planning objective functions.

Consider the following indices, parameters, and decision variables that are used hereafter.

Indices

 

\(l \in \mathcal{L}\)

parallel production lines

\(j \in \mathcal{N}\)

blocks

\(k \in \mathcal{K}_{\mathcal{J}}\)

products

\(t \in \mathcal{T}\)

periods

\(a \in \mathcal{A} =\{ a \in \mathbb{Z}_{0}^{+},t \in \mathcal{T}\vert a \leq t - 1\}\)

age (in periods)

Parameters

 

C lt

capacity (time) of production line l available in period t

e lk

capacity consumption (time) needed to produce one unit of product k on line l

c lk

production costs of product k (per unit) on line l

u k

shelf-life of product k just after production (time)

p k

price of product k

h k

inventory carrying cost of product k

m lj

minimum lot size (units) of block j on line l

\(\bar{s}_{lj}(\bar{\tau }_{lj})\)

setup cost (time) of a changeover to block j on line l

\(\underline{s}_{lk}(\underline{\tau }_{lk})\)

setup cost (time) of a changeover to product k on line l

d kt

demand for product k in period t (units)

Decision Variables

 

\(\rho _{ kt}^{a} \geq 0\)

initial inventory of product k with age a available at period t

\(\psi _{kt}^{a} \geq 0\)

fraction of the maximum demand for product k delivered with age a at period t

\(q_{lkt} \geq 0\)

quantity of product k produced in period t on line l

p lkt  ∈ { 0, 1}

equals 1, if line l is set up for product k in period t (0 otherwise)

y ljt  ∈ { 0, 1}

equals 1, if line l is set up for block j in period t (0 otherwise)

From the decision variables it is noticeable that we use an adaptation of the simple plant location (SPL) reformulation to model inventory and demand fulfillment decision variables. In the traditional SPL reformulation [6], it is known for which period the production of a given period refers to. In a food production planning context we are more interested in tracing the actual age of the product. Therefore, in this case, we know for each period the age of the inventory of a given product. This will be rather helpful in limiting the usage of stock based on the shelf-life of the products. Moreover, it can also be used to keep track of the freshness of the products delivered to the clients. These potentialities will be further explored in the next sections. Figure 3 shows how traditional decision variables for production quantities (q lkt ) are transformed through the adapted SPL reformulation. Basically, the products produced in a given period correspond to the inventory with age 0 (\(\rho _{kt}^{0}\)). This inventory has its age updated throughout the planning horizon and it has a straight correspondence to the age of the products when fulfilling demand (\(\psi _{kt}^{a}\)).

Fig. 3
figure 3

Schematic representation of the adaptation of the simple plant location reformulation with an emphasis on the inventory age

Full size image

The deployment of these two adapted concepts (block planning and simple plant location) results in a base model flexible enough to cope with the basic exigencies of production planning in food industries.

The base production planning model of food products (B-PP-FP) reads:

B-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}p_{k}\,d_{kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} - d_{ kt}\psi _{kt}^{a})\quad & &{}\end{array}$$
(1)

subject to:

$$\displaystyle{ \sum _{a}\psi _{kt}^{a} \leq 1\quad \forall k \in \mathcal{K},t \in \mathcal{T} }$$
(2)
$$\displaystyle{ \rho _{kt}^{a} =\rho _{ k,t-1}^{a-1} - d_{ k,t-1}\psi _{k,t-1}^{a-1}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}\setminus \{0\} }$$
(3)
$$\displaystyle{ \sum _{l}q_{lkt} =\rho _{ kt}^{0}\quad \forall k \in \mathcal{K},t \in \mathcal{T} }$$
(4)
$$\displaystyle{ p_{lkt} \leq y_{ljt}\quad \forall l \in \mathcal{L},j \in \mathcal{N},k \in \mathcal{K}_{\mathcal{J}},t \in \mathcal{T} }$$
(5)
$$\displaystyle{ q_{lkt} \leq \frac{C_{lt}} {e_{lk}} p_{lkt}\quad \forall l \in \mathcal{L},k \in \mathcal{K},t \in \mathcal{T} }$$
(6)
$$\displaystyle{ \sum _{j}\bar{\tau }_{lj}\,y_{ljt} +\sum _{k}(\underline{\tau }_{lk}\,p_{lkt} + e_{lk}\,q_{lkt}) \leq C_{lt}\quad \forall l \in \mathcal{L},t \in \mathcal{T} }$$
(7)
$$\displaystyle{ \sum _{k\in \mathcal{K}_{\mathcal{J}}}q_{lkt} \geq m_{lj}y_{ljt}\quad \forall l \in \mathcal{L},j \in \mathcal{N},t \in \mathcal{T} }$$
(8)
$$\displaystyle{ \psi _{kt}^{a},\,\rho _{ kt}^{a},\,q_{ lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\} }$$
(9)

The objective function (1) maximizes the profit of the producer over the planning horizon. Therefore, revenue that comes from sold products is subtracted by setup costs of recipes, setup costs of products, variable production costs and inventory costs. Note that the setup structure considers major and minor setup for the first product to be produced in a given block. For example, in the yoghurt production when changing from one kind of yoghurt to another a major setup might correspond to cleansing the lines and linking the new yoghurt tank, while the minor setup may correspond to setting up the machine to fill the yoghurt in a different type of package. These two operations can seldom be done in parallel.

Constraints (2) forbid the sum of all sold products of different ages to exceed the demand. Constraints (3) establish the inventory balance constraints, ageing the stock throughout the horizon. They state that the inventory of a given age is equal to the inventory in previous period with a younger age subtracted by the amount of products that was sold with the same younger age. Constraints (4) link the production variables to the inventory ones, setting all production in a given period in all lines to the initial stock with age 0. Constraints (5) and (6) ensure that a product can only be produced if both the correspondent block and product are set up, respectively. Limited capacity in the lines is to be reduced by setup times between blocks, setup times between products and also by the time consumed producing products (7). Constraints (8) introduce minimum lot-sizes for each block.

Final constraints (9) define the domain of the decision variables.

3 Extending the Constraints of the Base Model

Two main realistic factors may impact the production plans of perishable food products: the fact that inventory that is beyond the expiry date can no longer be sold (product-related), and the fact that customers in face of inventories with different shelf-lives, choose products with the farthest expiry date (customer-related). These issues are addressed in turn by limiting the feasibility domain as follows.

3.1 Inventory Expiry Constraints

In order to make sure that no expired products are used to satisfy demand it suffices to redefine the demand fulfillment related constraints dealing with these variables.

The production planning model of food products with inventory expiry constraints (IE-PP-FP) reads:

IE-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}p_{k}\,d_{kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} - d_{ kt}\psi _{kt}^{a})& & {}\\ \end{array}$$

subject to:

$$\displaystyle{ \sum _{a\leq u_{k}-1}\psi _{kt}^{a} \leq 1\quad \forall k \in \mathcal{K},t \in \mathcal{T} }$$
(10)
$$\displaystyle{ \rho _{kt}^{a} =\rho _{ k,t-1}^{a-1} - d_{ k,t-1}\psi _{k,t-1}^{a-1}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}\setminus \{0\}: a \leq u_{ k} }$$
(11)
$$\displaystyle\begin{array}{rcl} & \mbox{ (4), (5), (6), (7), and (8)} & {}\\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\}& {}\\ \end{array}$$

In constraint (10) we now limit the age of the products used to fulfill demand to be strictly below the product’s shelf-life (u k ). Constraint (11) updated the age of the products in stock until products reach their respective shelf-life. In fact, the market conditions can be even more adverse. Retailers usually do not accept products that have already passed one third of their total shelf-life. The remaining constraints are exactly the same as in the base model of Sect. 2.

3.2 Consumer Behaviour Constraints

In a context where the production process is tightened to the downstream supply chain processes satisfying final customers demand, it may be important to better incorporate the instinctive behaviour of consumers. Regarding food products, usually a last-expired-first-out (LEFO) policy is put in practice by customers. This behaviour may guide production plans towards a more just-in-time philosophy in which products’ freshness is a priority.

It is necessary to add a new decision variable \(\theta _{kt}^{a}\) in order to model this behaviour that equals 1, if inventory of product k with age a is used to satisfy demand in period t (0 otherwise).

The production planning model of food products incorporating consumer behaviour (CB-PP-FP) reads:

CB-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}p_{k}\,d_{kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} - d_{ kt}\psi _{kt}^{a})& & {}\\ \end{array}$$

subject to:

$$\displaystyle{ \psi _{kt}^{a} \leq \theta _{ kt}^{a}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}: a \leq u_{ k} - 1 }$$
(12)
$$\displaystyle{ \rho _{kt}^{a-1} - d_{ kt}\psi _{kt}^{a-1} \leq M(1 -\theta _{ kt}^{a})\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}\setminus \{0\}: a \leq u_{ k} - 1 }$$
(13)
$$\displaystyle\begin{array}{rcl} & \mbox{ (10), (11), (4)(5), (6), (7), and (8)}& \\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,\theta _{kt}^{a},\,p_{lkt},\,y_{ljt} \in \{ 0,1\} & {}\end{array}$$
(14)

In the previous models, it is assumed that the seller is able to assign optimal inventory quantities of different ages to customers in order to maximize profit. With constraints (12) and (13) this advantage no longer holds as the more instinctive consumer purchasing behaviour of perishable products that will drive customers to pick up products with the highest degree of freshness is mimicked. Thus, constraints (12) turn the value of \(\theta _{kt}^{a}\) to 1, whenever inventory of a given product k in period t with age a is used to satisfy demand. The value of this variable \(\theta _{kt}^{a}\) is used in constraints (13) to ensure that a fresher inventory can only be used after depleting the older inventory. In these constraints every time inventory of age a from a product k in period t is used (\(\theta _{kt}^{a}\)), then either all fresher inventory was used to satisfy demand (\(\rho _{kt}^{a-1} - d_{kt}\psi _{kt}^{a-1} = 0\)) or there was no such younger inventory (\(\rho _{kt}^{a-1} = 0\)). Note that parameter M denotes a big number.

4 Extending the Objective Function of the Base Model

The most common approach to grasp the perishability phenomena is to penalize the spoiled products with a discard cost in the objective function. This penalty cost makes sense if we acknowledge that products have a limited shelf-life and probably an associated discarding cost. Another approach derives from the awareness of the customers’ willingness to pay for fresher products while, simultaneously, the level of information regarding the detailed values of this willingness to pay is low. In this case, a new objective function is added to the one maximizing profit, aiming at maximizing the freshness of the products delivered.

4.1 Discarding Costs in the Objective Function

By incorporating discarding costs we extend the traditional production planning objective function by incorporating perishability related costs. We define the cost of spoiled products (\(\bar{p}_{k}\)) as an opportunity cost. This opportunity cost corresponds to the revenue yielded by the best alternative that could have been produced and sold instead of producing product k that got spoiled. However, it may also be regarded, in a more tangible manner, as a disposal cost for each unit of perished inventory that has to be properly discarded.

The production planning model of food products including discarding costs (DC-PP-FP) reads:

DC-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}p_{k}\,d_{kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} - d_{ kt}\psi _{kt}^{a})& & \\ -\sum _{k,t,a\geq u_{k}}\bar{p}_{k}\rho _{kt}^{a}\qquad & &{}\end{array}$$
(15)

subject to:

$$\displaystyle\begin{array}{rcl} & \mbox{ (2), (3), (4), (5), (6), (7), and (8)}& {}\\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\} & {}\\ \end{array}$$

The only difference to the model presented in Sect. 2 is reflected by the cost of spoilage tracked by the last term of (15). This cost is incurred whenever we hold stock that is beyond the product’s shelf-life (\(\rho _{kt}^{a} > 0: a \geq u_{k}\)).

4.2 Measuring Freshness as an Objective Function

In this model, the economic tangible profit is separated from the customer intangible value of having fresher products available in two distinct objective functions. The main motivation for such splitting comes from the fact that finding the willingness to pay for different customers is rather difficulty and lengthy to grasp in practice. The first objective continues to be the maximization of profit and the second one maximizes the average freshness of delivered products [2]. These two objectives are certainly conflicting since achieving a higher freshness of products delivered has to be done at the expense of more production lots that lead to higher setup costs. Therefore, we acknowledge the complete different nature of the two complementary objectives and the difficulty to attribute different monetary values to different degrees of freshness. As a result, the decision maker/planner will be offered a trade-off between freshness of delivered products and total profit. This trade-off can be represented by a set of solutions which do not dominate one another regarding both objectives (non-dominated or Pareto optimal front). We need to define the following additional parameter [d kt ] that is the number of non-zero occurrences in the demand matrix. This parameter is useful to have a more straightforward interpretation of the objective function value.

The model that accounts for a measure of freshness (MF-PP-FP) reads:

MF-PP-FP

$$\displaystyle{ \max \sum _{k,t,a}p_{k}\,d_{kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) }$$
(16)
$$\displaystyle{ \max \frac{1} {[d_{kt}]}\sum _{k,t,a}\frac{u_{k} - a} {u_{k}} \psi _{kt}^{a} }$$
(17)

subject to:

$$\displaystyle\begin{array}{rcl} & \mbox{ (2), (3), (4), (5), (6), (7), and (8)}& {}\\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\} & {}\\ \end{array}$$

The first objective function (16) maximizes profit in a similarly way of the base model. In the second objective (17) the mean freshness of products to be delivered is maximized. The number of periods before spoilage is estimated by u k − a and it is then normalized by the estimated shelf-life of the corresponding product. The cardinality of the non-zero demand occurrences is used to normalize this objective function between 0 and 1. This cardinality, for a given input set data, is constant and easily computed. Therefore, a value of 1 means that all products are delivered to customers in their fresher state.

This approach for modelling the production planning for food products has an interesting aspect to consider regarding inventory costs. When maximizing freshness in the second objective we are already trying to minimize stocks since we try to produce as late as possible in order to deliver products that were just produced. Therefore, if we had also included inventory costs in the first objective we would be somehow duplicating the inventory carrying cost effect and objective functions (16) and (17) would be too correlated (which must be avoided in multi-objective optimization).

5 Extending the Parameters of the Base Model

Another form of differentiating the base model of food production planning is by changing or detailing the input parameters, namely: price and demand. The key reasoning is that with more accurate information and more transparency across the supply chain partners, it would be possible to discriminate either price or demand in function of the actual age of the products.

5.1 Value of Freshness Parameter

In this model it is assumed that either the retailer or the final customer will be willing to pay a different price for products with different standards of freshness. Therefore, the price parameter is extended to \(\hat{p}_{k}^{a}\), price of product k paid when the product has an age a.

The production planning model of food products with different freshness values (VF-PP-FP) reads:

VF-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}\hat{p}_{k}^{a}\,d_{ kt}\,\psi _{kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} - d_{ kt}\psi _{kt}^{a})\qquad & &{}\end{array}$$
(18)

subject to:

$$\displaystyle\begin{array}{rcl} & \mbox{ (2), (3), (4), (5), (6), (7), and (8)}& {}\\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\} & {}\\ \end{array}$$

The only difference to the model presented in Sect. 2 is reflected in the dependency of the revenue to the age of the delivered products. Comparing with objective function (1), objective function (18) has a revenue term that is function of the age of the products sold. Remark that this is a straightforward extension from the base model (Sect. 2), because we have already incorporated a detailed demand fulfillment decision variable (\(\psi _{kt}^{a}\)) tracking the age of the products.

5.2 Demand Parameter

In this model we assume that according to the information about the customer purchasing behaviour, it is possible to determine a parameter \(\hat{d}_{kt}^{a}\) for the demand for product k with age a in period t. Furthermore, we assume that the demand decreases with the ageing of the products (Fig. 4). For understanding how this parameter may be generated using empirical data about products and customers’ willingness to pay the readers are referred to Amorim et al. [3], Tsiros and Heilman [13].

Fig. 4
figure 4

Schematic example of the age dependent demand

Full size image

The production planning model of food products with an extended demand parameter (DP-PP-FP) reads:

DP-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{k,t,a}p_{k}\,\hat{d}_{kt}^{0}\,\psi _{ kt}^{a} -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt} -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) -\sum _{k,t,a}h_{k}\,(\rho _{kt}^{a} -\hat{ d}_{ kt}^{0}\psi _{ kt}^{a})\qquad & &{}\end{array}$$
(19)

subject to:

$$\displaystyle{ \hat{d}_{kt}^{0}\psi _{ kt}^{a} \leq \hat{ d}_{ kt}^{a}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A} }$$
(20)
$$\displaystyle\begin{array}{rcl} & \rho _{kt}^{a} =\rho _{ k,t-1}^{a-1} -\hat{ d}_{k,t-1}^{0}\psi _{k,t-1}^{a-1}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}\setminus \{0\}& \\ & \mbox{ (2), (4), (5), (6), (7), and (8)} & \\ & \psi _{kt}^{a},\,\rho _{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\} &{}\end{array}$$
(21)

The formulation incorporating different demand levels according to the age of the product is very similar to the base model presented in Sect. 2, but in this model the demand parameter is replaced by an extended form that differentiates between products with different ages. Moreover, constraints (20) do not allow the quantity of sold products of a given age to be above the demand curve derived for the respective product (cf. Fig. 4).

6 Illustrative Example

The aim of this illustrative example is to understand the changes in the structure of the production plans when using the different models presented through Sects. 2, 3, 4, and 5.

The setting for the illustrative example consists in a production line (L = 1) that has to produce 2 blocks (N = 2), each with two products (K = 4). For all products/blocks e lk  = 1, m lj  = 3 and \(\underline{s}_{lj} =\underline{\tau } _{lj} = 1\). For Block 1 the setup cost (\(\bar{s}_{lj}\)) and the setup time (\(\bar{\tau }_{lj}\)) is 5 and 1, respectively. For Block 2 \(\bar{s}_{lj} = 5\) and \(\bar{\tau }_{lj} = 2\). The considered planning horizon has 4 periods (T = 4) and the capacity C lt equals 35 for all periods and lines. The remaining parameters are given in Table 1.

Table 1 Remaining parameters for the illustrative example
Full size table

We further consider, for the model of Sect. 4.1, that discarding costs \(\bar{p}_{k}\) equal to p k . In order to obtain one solution for the multi-objective model presented in Sect. 4.2, a weight of 200 was given to the freshness objective in order to have high freshness standards. In general, this is a parameter obtain in pre-computational experiments and it is dependent on the instances. With this weighted linear scalarizing factor, the problem objectives are aggregated in a single one. However, notice that in order to take full advantage of the multi-objective model and obtain the Pareto front a different method, such as the epsilon-constraint approach should be used instead. In the case in which a decreasing value is considered for the price paid for the product throughout its shelf-life (Sect. 5.1), we consider that for products with an age higher than 0, \(\hat{p}_{k}^{a} = 1\). Finally, for the last model (Sect. 5.2), all products suffer from a 50 % rate of decrease in the demand for each period of ageing (\(\hat{d}_{kt}^{a+1} = 0.5\hat{d}_{kt}^{a}\)).

6.1 Results and Discussion

Table 2 shows the results for the key decision variables under analysis \(q_{lkt},\,\rho _{kt}^{a},\,\psi _{kt}^{a}\) (production, inventory, demand fulfillment) for all models from Sects. 2, 3, 4, and 5. All instances were solved to optimality in less than two seconds by the solver IBM ILOG CPLEX 12.4 and the models were coded in the IBM ILOG OPL IDE. We purposely omitted the objective function values as they are not relevant for our discussion.

Table 2 Results for the decision variables \(q_{lkt},\,\rho _{kt}^{a},\,\psi _{kt}^{a}\) for all models (Sects. 2, 3, 4, and 5). Values that are the same across all models are in light grey and results that differ between the models (except the base one – B-PP-FP) are in bold. Notice that the relation between the time and age index is respected in this table (\(a \in \mathcal{A} =\{ a \in \mathbb{Z}_{0}^{+}\vert a \leq t - 1\}\))
Full size table

Overall, results seem to indicate that even for an illustrative example, by incrementally introducing different features and methods for better tackling the food production planning, different solutions are obtained for almost every model tested. The only production plan leading to spoiled products is the base model (B-PP-FP) when products 1 and 2 reach an age of 1 in period 4 (\(\rho _{14}^{1} =\rho _{ 24}^{1} = 5\)). All the other models are able to avoid the expiration of these products due to different reasons. For example, while the model considering inventory expiry (IE-PP-FP) avoids spoilage by the fact that we limit the demand fulfilment to products with a significant remaining shelf-life, the model introducing discarding costs (DC-PP-FP) is able to achieve the same solution by penalizing the occurrence of expired inventory.

One interesting analysis lies on the different solutions found with the inventory expiry model (IE-PP-FP) and the consumer behaviour one (CB-PP-FP). The only difference between these models in the inclusions of constraints (12) and (13) in the CB-PP-FP model, which mimic the fact that customers pick up the fresher available products. For product 4 in period 2 when 20 units are produced in both models (q 142 = 20), model IE-PP-FP is able to allocate in order to satisfy demand part of the production of period 2 and part of the production of period 1 with age 1 (\(\psi _{42}^{0} = 73\,\%\) and \(\psi _{42}^{1} = 27\,\%\)). On the contrary, the CB-PP-FP model is forced to satisfy all demand in period 2 with the production executed in the same day (\(\psi _{42}^{0} = 100\,\%\) and \(\psi _{42}^{1} = 0\,\%\)). These differences ultimately lead to the fact that customers in period 3 are penalized in the CB-PP-FP model as they will be satisfied with less fresh products (\(\psi _{43}^{2} = 40\,\%\)). This fact could potentially lead to lost sales and it reflects the importance of proper inventory control when dealing with perishable products.

From the seven models, it is clear that the last three are able to better incorporate the consumer eagerness for fresher products. In particular, the model measuring freshness (MF-PP-FP) and the model having an extended demand parameter (DP-PP-FP) have an equivalent behaviour. Both models incorporate explicitly the importance of satisfying customers with a high degree of freshness. The difference between them relies on the amount and quality of information the decision maker has when setting up the model (less information for the MF-PP-FP and more for the DP-PP-FP).

7 Risk-Conscious Planning

In the previous models (Sects. 2, 3, 4, and 5) a major assumption is the deterministic parameter of demand. As seen in the illustrative example (Sect. 6), in this setting spoiled products will only appear in case no perishability considerations are taken into account. This can be done by constraining the domain of the variables used to track both demand fulfillment and inventory levels. However, in this type of industries, producers and retailers struggle with significant amounts of spoiled products. These quantities are tightly correlated to the uncertainty in the forecast of demand. Explicitly acknowledging the existence of such uncertainty and adopting a risk conscious planning promise robust and sustainable gains. With this approach the distribution of the gains is sharper and further away from the loss side. This comes at the expense of a decrease in the expected profit.

In this section we start by extending the Base model (Sect. 2) in order to cope with an uncertain demand parameter and we then give an example of a risk-averse formulation that tackles explicitly the conditional value-at-risk. The section ends with an extension of the illustrative example of Sect. 6.

7.1 Risk-Neutral Model

The uncertainty of the demand parameter \(\tilde{d_{kt}^{v}}\) may be modeled though a set of scenarios \(\mathcal{V}\) that have a probability of occurrence ϕ v . In order to incorporate this stochastic parameter into the formulation, it is necessary to determine the moment in time in which demand is unveiled with certainty. In the most common setting, the planner has to decide about the sizing and scheduling of lots in the first-stage and then inventory allocation decisions are done with full knowledge of the demand parameter (second-stage).

To model the production planning of perishable foods good in an uncertain setting it is necessary to define the following second-stage decision variables:

Second-Stage Decision Variables

\(\tilde{\rho }_{kt}^{av} \geq 0\)

initial inventory of product k with age a available at period t in scenario v

\(\tilde{\psi }_{kt}^{av} \geq 0\)

fraction of the maximum demand for product k delivered with age a at period t in scenario v

The risk-neutral production planning model of food products (RN-PP-FP) reads:

RN-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{v}\phi _{v}[\sum _{k,t,a}p_{k}\,\tilde{d_{kt}^{v}}\,\tilde{\psi }_{ kt}^{av} -\sum _{ k,t,a}h_{k}\,(\tilde{\rho }_{kt}^{av} -\tilde{ d_{ kt}^{v}}\,\tilde{\psi }_{ kt}^{av})] -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt}& & \\ -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt})& &{}\end{array}$$
(22)

subject to:

$$\displaystyle{ \sum _{a}\tilde{\psi }_{kt}^{av} \leq 1\quad \forall k \in \mathcal{K},t \in \mathcal{T},v \in \mathcal{V} }$$
(23)
$$\displaystyle{ \tilde{\rho }_{kt}^{av} =\tilde{\rho }_{ k,t-1}^{a-1,v} -\tilde{ d}_{ k,t-1}\tilde{\psi }_{k,t-1}^{a-1,v}\quad \forall k \in \mathcal{K},t \in \mathcal{T},a \in \mathcal{A}\setminus \{0\},v \in \mathcal{V} }$$
(24)
$$\displaystyle{ \sum _{l}q_{lkt} =\tilde{\rho }_{ kt}^{0v}\quad \forall k \in \mathcal{K},t \in \mathcal{T},v \in \mathcal{V} }$$
(25)
$$\displaystyle\begin{array}{rcl} & \mbox{ (5), (6), (7), and (8)} & \\ & \tilde{\psi }_{kt}^{av},\,\tilde{\rho }_{kt}^{a},\,q_{lkt} \geq 0;\,p_{lkt},\,y_{ljt} \in \{ 0,1\}&{}\end{array}$$
(26)

The objective function (22) maximizes the expected profit of the producer over the planning horizon. In this two-stage stochastic formulation, both revenue and holding costs are now dependent on the scenario realization. The second-stage constraints related to inventory management and demand fulfillment (23), (24), and (25) were changed to incorporate the new stochastic setting.

7.2 Risk-Averse Model

In face of uncertainty the planner may take several attitudes in terms of risk. For a risk-conscious attitude it is necessary to introduce a risk measure into the formulation. Recent studies showed that for production planning of perishable food goods the conditional value-at-risk [10, 11], which is very used in portfolio optimization, is a good option as it reduces drastically the amount of expired products at the expense of a small loss on the expected profit [1]. To introduce this risk measure in the formulation we need to further define two decision variables and two parameters α and \(\lambda\). α controls the confidence interval of the conditional value-at-risk and \(\lambda\) controls the risk-aversion emphasis of the generated plan.

Conditional Value-at-Risk Decision Variables

η

value-at-risk

δ v

auxiliary variable for calculating the conditional value-at-risk

In Fig. 5 a graphical interpretation of this measure is given. Consider X to be a random profit distribution, from the figure it is easy to interpret that the conditional value-at-risk (cVaR) is then defined as \(\mathbb{E}[X\vert X \leq V aR(X)]\).

Fig. 5
figure 5

Graphical interpretation of the conditional value-at-risk measure (Adapted from Sarykalin et al. [12])

Full size image

The risk-conscious production planning model of food products (RC-PP-FP) reads:

RC-PP-FP

$$\displaystyle\begin{array}{rcl} \max \sum _{v}\phi _{v}[\sum _{k,t,a}p_{k}\,\tilde{d_{kt}^{v}}\,\tilde{\psi }_{ kt}^{av} -\sum _{ k,t,a}h_{k}\,(\tilde{\rho }_{kt}^{av} -\tilde{ d_{ kt}^{v}}\,\tilde{\psi }_{ kt}^{av})] -\sum _{ l,j,t}\bar{s}_{lj}\,y_{ljt}& & \\ -\sum _{l,k,t}(\underline{s}_{lk}\,p_{lkt} + c_{lk}\,q_{lkt}) +\lambda (\eta - \frac{1} {1-\alpha }\sum _{v}\phi _{v}\,\delta _{v})& &{}\end{array}$$
(27)

subject to:

$$\displaystyle\begin{array}{rcl} & \mbox{ (23), (24), (25), (5), (6), (7), and (8)} & \\ & \delta _{v} \geq \eta -(\sum _{k,t,a}p_{k}\,\tilde{d_{kt}^{v}}\,\tilde{\psi }_{kt}^{av} -\sum _{k,t,a}h_{k}\,(\tilde{\rho }_{kt}^{av} -\tilde{ d_{kt}^{v}}\,\tilde{\psi }_{kt}^{av}))\quad v \in \mathcal{V}& {}\end{array}$$
(28)
$$\displaystyle{ \tilde{\psi }_{kt}^{av},\,\tilde{\rho }_{ kt}^{a},\,q_{ lkt},\,\delta _{v} \geq 0;\,\eta \in \mathbb{R};\,p_{lkt},\,y_{ljt} \in \{ 0,1\} }$$
(29)

The objective function (27) maximizes the expected profit and, simultaneously, it maximizes the conditional value-at-risk with a confidence of α. The second-stage constraints (23), (24), and (25) are the same of the risk-neutral model. A new constraint (28) has to be added to attribute the variable δ v a value of zero, if scenario v yields a profit higher than η. Otherwise, variable δ v is given the difference between the value-at-risk η and the corresponding second-stage profit \(\sum _{k,t,a}p_{k}\,\tilde{d_{kt}^{v}}\,\tilde{\psi }_{kt}^{av} -\sum _{k,t,a}h_{k}\,(\tilde{\rho }_{kt}^{av} -\tilde{ d_{kt}^{v}}\,\tilde{\psi }_{kt}^{av})\).

7.3 Extended Illustrative Example

To understand the importance of a risk-conscious production planning of perishable food products let us use the illustrative example presented in Sect. 6. We have extended the data set by distinguishing three possible demand scenarios, all with the same probability of occurrence (0.33). A medium scenario in which the demand is equal to the one presented in Table 1, a low one in which demand is 50 % of its expected value and, finally, a high one in which demand is 50 % higher than in the medium scenario. Therefore, we use a simplified scenario-tree with only three scenarios. For assessing the impact of uncertainty and understanding the implications of a risk-conscious planning we obtained optimal solution values for three models: (1) the Base model presented in Sect. 2, (2) the Risk-neutral model RN-PP-FP presented in Sect. 7.1, and (3) a Risk-averse model based on RC-PP-FP presented in Sect. 7.2 (setting \(\lambda = 4\) and α = 0. 95). Results for the last two models are presented in Table 3. The Base model (B-PP-FP) has a solution with a profit of 157.0.

Table 3 Profit values for the Risk-neutral model, and a Risk-averse model
Full size table

Results indicate that with the stochastic demand parameter the expected profit drops considerably. Notice that demand parameter used in the Base model is the expected value of the uncertain demand parameter (\(\tilde{d_{kt}^{v}}\)). In the Risk-neutral approach there is one scenario that would result in a profit of 0. This “bad” scenario is mitigated by in the Risk-conscious model that has its worst scenario with a profit of 37.8. This more balanced overall solution with less dispersion of the profit distribution comes at the expense of a slightly lower expected value of profit.

8 Conclusions

In this paper, we have reviewed several ways of integrating different challenges related to exogenous factors (such as customer behaviour and the perishable nature of the products) arising in the production planning of food products. The formulations have the same base model as starting point and we have organised them based on the extensions of the model components required: constraints, objective function and parameters. In particular, we have analysed how to limit the inventory age based on an adapted simple plant location reformulation, how to incorporate the consumer behaviour within the inventory policy, how to include discarding costs in the objective function, how to model customer willingness for fresh products in a multi-objective framework and how to value freshness either in the price or demand parameters. To analyse the implications of each of these “ingredients”, an illustrative example is presented and solved, exposing the different solution structures achieved. The differences across the solutions show the importance of choosing an approach suitable to the particular business setting, in order to accommodate the multiple challenges present in these industries. Moreover, acknowledging the perishable nature of the products and evaluating the amount and quality of information at hands may be crucial in lowering disposal costs and achieving higher service levels. There are other ingredients not so related to the perishable nature of food products that are also important in food production planning. For example, Wang et al. [14] deals with the incorporation of batch traceability that is increasingly important with the recent cases of products recall.

In the last Section, we analyzed a recent trend in supply chain planning – risk-conscious planning. The mitigation of uncertainties in this industries is crucial since their effects are leveraged by the perishable nature of the products. The importance of a risk-averse approach is especially noticeable in terms of avoiding disastrous uncertain outcomes.

Future work should explore these extensions from a computational point of view. Therefore, devising which solution methods are more appropriate for each setting is still a gap to be addressed.