Matrix-Free Iterative Processes for Implementation of Implicit Runge–Kutta Methods

Abstract

In this work we present so-called generalized Picard iterations (GPI) – a family of iterative processes which allows to solve mildly stiff ODE systems using implicit Runge–Kutta (IRK) methods without storing and inverting Jacobi matrices. The key idea is to solve nonlinear equations arising from the base IRK method by special iterative process based on the idea of artificial time integration. By construction these processes converge for all asymptotically stable linear ODE systems and all A-stable base IRK methods at arbitrary large time steps. The convergence rate is limited by the value of “stiffness ratio”, but not by the value of Lipschitz constant of Jacobian. The computational scheme is well suited for parallelization on systems with shared memory. The presented numerical results exhibit that the proposed GPI methods in case of mildly stiff problems can be more advantageous than traditional explicit RK methods.

1 Generalized Picard Iterations

Consider an initial value problem for the system of ordinary differential equations

$$\begin{aligned} y'(t)=f(t,y(t)),\quad y(t_0)=y_0, \end{aligned}$$

(1)

where , and some base s-stage implicit Runge–Kutta (RK) method for this problem:

$$\begin{aligned} y_1=y_0+\tau \sum _{i=0}^s b_i f(t_0+c_i\tau , Y_i). \end{aligned}$$

Here $y_1\approx y(t_0+\tau )$, and are unknown stage values which satisfy the following system of nonlinear equations: $Y_i=y_0+\tau \sum _{j=0}^s a_{ij} f(t_0+c_j\tau , Y_j),\quad i=1,\ldots ,s.$ We use standard notation for RK method coefficients $\bigl (a_{ij}\bigr )_{i,j=1}^s=A$, $(b_1,\ldots ,b_s)^T=b$, $(c_1,\ldots , c_s)^T=c$. In practice it is handy to perform a standard change of variables to minimize roundoff issues: $Z_i=Y_i-y_0$:

$$\begin{aligned} r_i(Z)=-Z_i+\tau \sum _{j=1}^s a_{ij} f(t_0+c_j\tau , y_0+Z_j)=0,\quad i=1,\ldots , s, \end{aligned}$$

(2)

or simply

$$\begin{aligned} r(Z)=(r_1(Z),\ldots , r_s(Z))=0,\quad Z=(Z_1,\ldots , Z_s)^T. \end{aligned}$$

(3)

Our goal is to construct a method for matrix-free solution of (3), i.e. without storing and inverting Jacobian matrix of f, which is usually done when Newton’s or similar methods are used. In [1, 2] we proposed a family of such methods, which is called generalized Picard iterations. Let’s give a brief description of the approach.

The idea is to use artificial time integration of an ‘embedding’ differential equation $Z'=r(Z)$ by some auxiliary explicit one-step method of RK type with constant artificial time step $\omega$. This results in the process which we shall call the generalized Picard iteration (GPI). Its general form is simply

$$\begin{aligned} Z^{[m+1]}={\varPhi }(Z^{[m]}),\quad m=1,2,\ldots \end{aligned}$$

(4)

where ${\varPhi }$ is the time-stepping mapping of the auxiliary method. The key task now is to define this mapping, i.e. to determine the coefficients of the auxiliary method. We perform this by optimizing the convergence behavior of (4) on linear problems. To make this precise we shall give the following definition.

Definition 1

Consider the linear model ODE $y'(t)=\lambda y(t)$, , and corresponding GPI process (4) for the solution of induced RK equation of the form (3). A region , such that (4) converges for all $\lambda \tau \in D$ is called the linear convergence region of (4).

By substituting $f(t,y)=\lambda y$ in (2) we have

(5)

where $g_0=\lambda \tau A (y_0 \mathbf {1}_s)$, . In this case we have

$$\begin{aligned} {\varPhi }(Z)=R(\omega (\lambda \tau A-I))Z + Q(\omega ,\lambda \tau A-I)g_0, \end{aligned}$$

(6)

where R is the stability polynomial of the auxiliary method, $Q(\omega ,z)=(R(\omega z)-1)/z$. According to the convergence criterion of linear fixed-point iterations, the linear convergence region of GPI (4) in this case will be

$$\begin{aligned} D=\bigcap _{i=1}^s \mu _i^{-1}(\omega ^{-1} S + 1), \end{aligned}$$

(7)

where $\{\mu _i\}=\Sigma (A)$, $\Sigma (\cdot )$ is spectrum of a matrix, and S is the stability region of the auxiliary method: . Furthermore, the convergence factor of GPI process for (6) is determined by the spectral radius of $R(\omega (\lambda \tau A-I))$, which is equal to $K(\lambda \tau )$, where

$$\begin{aligned} K(z) = \max _i |R(\omega (z \mu _i-1))|. \end{aligned}$$

(8)

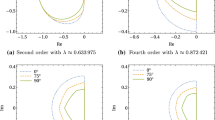
The examples of convergence regions for GPI based on (2) with 7th order RadauIIA base method [3, Sect. IV.5] and explicit Euler method being the auxiliary method are shown in the first row of Fig. 1. We see that generally as $\omega \rightarrow 0$ the area of D increases, but the overall convergence factor grows significantly.

Fig. 1.

Convergence regions of ordinary (upper) and ‘preconditioned’ (lower) GPI methods for base RadauIIA 4-stage method and auxiliary explicit Euler method. Black points are $\mu _i^{-1}$. Contour lines correspond to the constant values of convergence factor K(z) (8), (10).

In order to improve the situation instead of (2) we consider the ‘preconditioned’ RK system

$$\begin{aligned} r_i(Z)=-\sum _{j=1}^s \tilde{a}_{ij} Z_j+\tau f(t_0+c_i\tau , y_0+Z_i)=0,\quad i=1,\ldots ,s, \end{aligned}$$

(9)

where $(\tilde{a}_{ij})=\tilde{A} = A^{-1}$. If A is not singular this system is equivalent to (2), but the corresponding GPI process (4) behaves much better for $\lambda \tau \ll 0$ (in stiff case). Indeed, in scalar linear case instead of (5) now we have

$$\begin{aligned} r(Z)=(\lambda \tau I -\tilde{A} )Z + \lambda \tau \mathbf {1}_s y_0, \end{aligned}$$

and the convergence region and convergence factor become respectively

$$\begin{aligned} D=\bigcap _{i=1}^s(\mu _i^{-1}+\omega ^{-1} S)\quad \text {and}\quad K(z) = \max _i |R(\omega (z - \mu ^{-1}))|, \end{aligned}$$

(10)

see the second row in Fig. 1. We see that the preconditioned equation (9) is better to use in stiff case, but for $\lambda \tau \approx 0$ the ordinary RK equation (2) should be used.

The simple analysis of the preconditioned GPI process allows to prove the next important property.

Proposition 1

Let the base IRK method be A-stable and there exists $r_0>0$ such that the open disk of radius $r_0$ and center in $(-r_0,0)$ is entirely covered by the stability region of the auxiliary RK method. Then for any linear ODE system $y'=Jy$ with and any time step $\tau >0$ there exists $\omega _0>0$ such that the preconditioned GPI iterations (4), (9) converge for all $\omega \in (0,\omega _0)$.

As we see, in order to achieve faster convergence of GPI we need |R(z)| to take minimal possible values over the whole stability region S. In light of this we use the following scheme of auxiliary method construction:

• 1. Select the desired shape of stability region ${\varOmega }\approx S$ taking the condition ${\Sigma }{\left( \frac{\partial f}{\partial y}(t_0,y_0)\right) }\subset D$ as a reference point, see (7) and (10).

• 2. Choose $\sigma$ – the desired number of stages for the auxiliary method, and construct a stability polynomial R of degree $\sigma$ basing on the condition¹ $\iint _{\varOmega }|R(z)|^2 dz \rightarrow \min$. In our experiments we use minimization over an angular sector in the left halfplane:

  $$ \int _0^1\int _{\pi -\theta }^{\pi +\theta }|R(\rho {\mathrm e}^{{\mathrm i} \varphi })|^2d\varphi d\rho \rightarrow \min . $$

  We solve this problem numerically with higher-precision arithmetic using Mathematica system. For example, if the spectrum of Jacobian is close to the real axis we take $\theta =\pi /180$ and for $\sigma =7$ get a stability polynomial which stability region is shown in Fig. 2.

• 3. Build an explicit RK scheme which implements the constructed stability polynomial. This step can be performed in variety of ways. We use Lebedev’s approach briefly described in [3], see also [1]: the factorized stability polynomial $R(z)=R_1(z)R_2(z)\ldots R_M(z)$ yields the representation of ${\varPhi }$ as a composition of one and two-stage methods: ${\varPhi }={\varPhi }_1\circ {\varPhi }_2\circ \ldots \circ {\varPhi }_M,$ where

  $$\begin{aligned} R_k(z)={\left\{ \begin{array}{ll} 1+\delta z \quad \mathrm{for} \ { odd } \ \sigma \ \mathrm{and} \ k=1,\\ (1+\delta _k z)(1+\delta _k' z),\quad \text{ in } \text{ quadratic } \text{ case; } \end{array}\right. } \end{aligned}$$
  

  Here $\alpha _k=(\delta + \delta ')/2$, $\gamma _k=1-\delta \delta '/\alpha _k^2$, $k=1,\ldots ,M$, and $\delta$ are the coefficients which uniquely determine the auxiliary method mapping ${\varPhi }$.

Fig. 2.

Stability region of 7-stage auxiliary method optimized with $\theta =\pi /180$

In practice we perform iterations of GPI process (4) until the estimated error $\Vert Z^{[m]}-Z^*\Vert$, where $r(Z^*)=0$, is less than $0.05\times Atol$. Here Atol is, as usual, the required tolerance for the local error $y_1-y(t_0+\tau )$. The error estimation technique is based on the estimation of the convergence factor $\varTheta$ as described in [3, Section IV.8].

It is important to mention that the resulting method $y_1^{[m]}=y_0+\tau \sum _{i=1}^s f(t_0+c_i \tau , y_0+Z_i^{[m]})$ is equivalent to some explicit RK method of order one at least. Though instead of this form we use

$$\begin{aligned} y_1^{[m]}=y_0+\sum _{i=1}^s d_i Z_i^{[m]}, \end{aligned}$$

where $(d_1,\ldots ,d_s)^T=b^T A^{-1}$, which gives method of only order zero, but performs better on stiff problems (see [1] for details).

2 Numerical Experiments

Our experimental code based on GPI is written in C++ and has a parallelization option, which is implemented using OpenMP. If this option is enabled the independent components $r_i$ of the residual function r (3) are evaluated in parallel. The step size and error control is implemented in a standard way by using two methods of different order. In our case these are 4-stage RadauIIA and Gaussian methods of order 7 and 8 respectively. Since both of them are collocation methods, we effectively exploit the continuous polynomial approximation which they provide: this polynomial is used for predicting the initial approximation $Z^{[0]}$ for the error controller method and for the main method on new steps.

The Jacobian spectral radius estimate should be provided by the user in order to properly select the value of auxiliary time step $\omega$. In our tests we compute this estimate on each step using Gershgorin theorem. This estimate is also used for switching between ‘stiff’ and ‘non-stiff’ GPI methods. In stiff case we use the ‘preconditioned’ residual function (9) with 7-stage auxiliary method from Fig. 2. In non-stiff case we use ordinary residual (2) with explicit Euler auxiliary method which linear convergence regions have been shown in the first row of Fig. 1.

Further details of the implementation the interested reader can find in [1].

Since GPI methods are actually explicit, in its current state our code can not compete with implicit methods in cases when Newton’s method is applicable. That’s why we compare the performance of our code with highly-regarded DOP853 code, which implements explicit Dormand-Prince RK methods with variable order and is applicable in case of mildly stiff problems. We used C language version of this code². Each diagram shows results of the solvers with required absolute tolerance settings $Atol=10^{-i}$, $i=2,3,\ldots ,10$. The actual absolute error at the endpoint and elapsed CPU time measured in seconds are depicted in logarithmic scales.

The experiment was performed on a machine with 4-core Intel Core 2 Quad Q6600 2.4 GHz processor and Linux operating system.

2.1 HIRES Problem

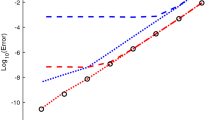
The first test problem is the well-known HIRES problem which describes a chemical reaction of photomorphogenesis [3, Section IV.10]. This is a system of 8 nonlinear ODEs. The endpoint of integration is 421.8122, the reference solution was downloaded from E. Hairer’s webpage³. The results of the experiment are shown in Fig. 3. We see that for moderate tolerances the serial GPI code outperforms DOP853, which is quite surprising. The parallel version works much slower, which is expected, since the dimension of the system is too small and thus the parallelization overhead is higher than the speed-up.

One may also note the unnatural behavior of GPI codes for $Atol=0.01$, which means that the error controlling mechanism needs to be tweaked.

Fig. 3.

HIRES problem test results.

2.2 BRUSS2D Problem

The second is another classic test problem BRUSS-2D which is a method-of-lines discretisation of two-dimensional parabolic reaction-diffusion PDE [3, Section IV.10]. We solved this problem on two spatial grids: ${64\times 64}$ (Fig. 4) and ${128\times 128}$ (Fig. 5). The value of the diffusion coefficient $\alpha$ is 1 in both cases.

Fig. 4.

BRUSS-2D problem with $N=64$, $\alpha =1$. The dimension of ODE is 8192.

Fig. 5.

BRUSS-2D problem with $N=128$, $\alpha =1$. The dimension of ODE is 32768.

For both of these tests the parallel version of GPI (running on 4 processors) was approximately 2.5 times faster than the serial.