Keywords

1 Introduction

Nowadays, new technologies have triggered the needs of new energy sources, smaller and more efficient. The research on energy harvesting system has increased substantially. Several different devices have been developed. In all these devices, a new way to harvest energy is the use of piezoelectric material as a transducer to harvest energy from ambient mechanical vibrations. Many researchers have recently explored this sort of energy harvesting based on piezoelectric material. As some examples, we mention that the piezoceramics can be used as piezomagnetoelasctic structure and harvest energy from an ambient vibration [1, 2]. A vast and important study of piezoelectric energy harvesting system can be found in [3–5]. These authors explored the reuse of the wasted energy that is very important nowadays to some applications, including renewable energy.

Linear and nonlinear piezoelectric coupling have been considered. The nonlinear coupling incorporates the more realistic effects of the piezo elements, because of the constitutive laws of piezoelectric materials specifically the nonlinear relationship between the strain and the electric field in the piezoceramic material [6–9]. A good approximation to a relation of the nonlinear piezoelectric coupling was firstly developed by Triplett and Quinn [10] that shows good results comparing to the experimental results. Hence, the authors conclude that the role of nonlinearities in the piezoelectric materials has a great impact over the responses of the system. Thus, for better design of an energy harvester, the nonlinear effects of electromechanical coupling must be taken into account [11].

In order to check this, we propose a new approximation of experimental curve of the piezoelectric material response to modelling this behaviour. Using the theoretical model of piezoelectric energy harvesting in [12–14], a comparison was performed among a reference function (RF) proposed by Triplett and Quinn [10] for piezoelectric coupling and the proposed model (PM) by us present in this work.

This chapter is organized into five sections. Section 1 is essentially an introduction to energy harvesting vibrating systems. Section 2 presents the proposed mathematical nonlinear piezoelectric coupling, showing how it can be relevant in the mathematical modelling of the real problem, taking into account the nonlinear coupling proposed by Triplett and Quinn [10]. Section 3 presents the mathematical modelling of the energy harvesting system considering a proposal nonlinear piezoelectric coupling. Section 4 exhibits the results of numerical simulations, those were carried out, comparing the average power using the reference function to the proposed model. Section 5 presents the main conclusion of the work.

2 The Proposed Nonlinear Coupling Term

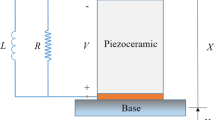
The piezoelectric element behaviour was checked experimentally by Crawley and Anderson [7] as we can observe in Fig. 1. Figure 1b shows the function to dimensionless piezoelectric coupling coefficient suggested by [10], where the dimensional piezoelectric coefficient d(x) were approximated to: \(d(x)=d_{linear}(1+d_{nonlinear}|x|)\), having defined as the dimensionless counter-party as: \(\hat{d}(x)=\theta (1+\varTheta |x|)\), where the piezoelectric coefficient is constituted by a linear part represented by \(\theta \) and a nonlinear part represented by \(\varTheta \). In Fig. 1a, the nonlinear model curve is the approximation stipulated by Triplett and Quinn [10].

Fig. 1
figure 1

a The experimental curve obtained by Crawley and Anderson [7]. b Reference approximation of piezoelectric nonlinearity defined by Triplett and Quinn [10]

Full size image

As can be seen in Fig. 1a, neither linear model and nonlinear approximation nor the model of Fig. 1b are good approximations of experimental model. We can also observe that the experimental model try to reach a saturation point, behaviour that is not observed in the models. The goal of this research is to determine a model which has a better mathematical representation of the experimental model. For this, we are going to consider an approximation normalized function \(y=d^*[pmV^{-1}]/408\) and \(x=Microstrain/500\) determined by using the least square method [15, 16]. The method could show us the approximation normalized functions as

$$\begin{aligned} y=\frac{0.0610646e^{5.6668x}}{1.01+0.06046e^{5.6668x}}+e^{-2.8x}(0.3654cos2x+1.2sin2x) \end{aligned}$$
(1)

In Fig. 2 we can observe a comparison considering the dimensional model proposed in (1).

Fig. 2
figure 2

Proposed model to approximation of piezoelectric nonlinearity

Full size image

3 Mathematical Modelling

In this section will be shown the energy harvesting mathematical model using a nonlinear piezoelectric coupling and the governing equations of movement of the system.

The energy harvesting model in Fig. 3 was proposed in [12–14], that are studied using the proposed nonlinear piezoelectric coupling of Triplett and Quinn [10]. This time, the new nonlinear piezoelectric coupling was used to compare its efficient with the other coupling in [10].

The coupled equations of motion were defined in the dimensionless form in [12–14] as:

$$\begin{aligned}&x^{\prime \prime }+\varepsilon \alpha x^\prime +\beta x+\varepsilon \beta _1 x^3+ \varepsilon \psi v=\varepsilon \delta _1 \phi ^{\prime \prime }cos\phi - \varepsilon \delta _2\phi ^{\prime 2}sin\phi \nonumber \\&\phi ^{\prime \prime }=\varepsilon \mu _1 - \mu _2 \phi ^\prime + \varepsilon \gamma x^{\prime \prime }cos\phi \nonumber \\&\rho v^{\prime } -\Psi x + v = 0 \end{aligned}$$
(2)

The parameter \(\Psi \) in (2) represents the piezoelectric coupling function. The dimensionless electrical power harvested from the system has the form \(P=\rho v^{\prime 2}\). The averaged power harvested is given by

$$\begin{aligned} P_{average}=\frac{1}{T}\int ^T_0 P(\tau )d\tau \end{aligned}$$
(3)
Fig. 3
figure 3

Mathematical model of the energy harvester proposed in [12–14]

Full size image

4 Numerical Simulations and Results

In Figs. 4 and 5, we can observe the behaviour of the system (2) for the following parameters [10, 14]: \(\alpha =0.01\), \(\beta =1.00\), \(\beta _1=0.25\), \(\rho =1.00\), \(\varepsilon =0.10\), \(\delta _1=0.40\), \(\delta _2=0.40\), \(\gamma =0.60\), \(\mu _2=1.50\), \(\theta =1.00\), \(\varTheta =1.00\), \(x_1(0)=0\), \(x_2(0)=0\), \(x_3(0)=0\), \(x_4(0)=0\), \(x_5(0)=0\). The \(\mu _1\) parameter had to be adjusted in order to reach the resonant frequency of the model for each of the tested functions.

Figure 4a, b are depicting the resonance curve of the system using the reference function RF, proposed model PM, and as can be seen the jumping occurs for the value of the parameter \(\mu _1=1.55\) and \(\mu _1=1.52,\) respectively.

Figure 5 shows the dynamic response of the system comparing the proposed model PM to the reference function RF proposed in [10]. Figure 5a, b show the phase plane and the time history of the displacement of the two functions, respectively. We observe that the PM starts with a higher amplitude and at steady state keeps a little higher amplitude of displacement than in the RF. To see what happens with the power harvested Fig. 5c, d show the time history of the power harvested and the average power, respectively. We can see the power harvested has higher peaks in the PM than in RF, but it doesn’t occur to the average power. We see that at steady state the average power of the PM is a little lower than the RF. It was expected by the fact shown in Fig. 2 that the PM approximates is closer to the experimental result than the RF. Hence, the energy harvesting would be a little lower in PM than in RF.

Fig. 4
figure 4

a Sommerfeld effect of the system (2). a Reference function. b Proposed model

Full size image
Fig. 5
figure 5

Dynamic response using the proposed model (blue line) and the reference function (black line). a Phase plane. b Time history of the displacement. c Time history of the harvested power. d Time history of the average power

Full size image

5 Conclusions

By using the least square method proposed in [15, 16], it was possible to obtain the nonlinear model, Fig. 2, which resulted in an approximation function that considers the operation mode \(d_{31}\), where mechanical strain is applied in the axial direction, but the voltage is obtained from the perpendicular direction. With the application of the proposed model, it was possible to observe the change of the Sommerfield effect (\(\mu _1=1.55\) (RF) for \(\mu _1=1.52\) (PM)). This is an important point because it indicates a reduction in the quantity of energy necessary to the system to achieve the resonant frequency corresponding to of maximum displacement that can harvest more energy.

We also observed in Fig. 5c, d that the curve represented by (1) has a little lower energy harvester forecast as regard to the reference function, indicating that we would be overestimating the power generation in numerical simulations, while the reference function continue to be a good approximation. This is because the overestimated power harvested is just a little part of it, considering the piezoelectric material harvests low amount of energy.

It can be concluded that the obtained results shown the efficiency of the proposed model in improving the prediction of the piezoelectric energy harvested in steady state, thereby correcting the values obtained previously by the reference function, due to a correct matching with the profile of the behaviour of the experimental curve in Fig. 1a.