Keywords

Introduction

From the point of view of generalized crystallography, Alan L. Mackay in 1962 published a short paper entitled “A Dense Noncrystallographic Packing of Equal Spheres” [1], which had made tremendous impact on particle, cluster, intermetallics, and quasicrystal researches in the past 40 years. With the advent of nanoscience and nanotechnology, the importance of this paper will become even more profound in the coming years.

The main part of Mackay’s paper is the icosahedral shell structure (iss) consisting of a set of concentric icosahedra of increasing sizes. Icosahedron is a regular polyhedron with the \( 2\overline{35} \) rotational symmetry, whose fivefold rotation is incompatible with the periodic translation of a crystal lattice and, therefore, noncrystallographic. Figure 1a–c shows, respectively, the sphere model of the first three icosahedral shells. From the packing of spheres in a triangle of these shells (one A sphere at the center), it is clear that they are the (111) planes of the face centered cubic (fcc) closely packed sequence ABCA…. The spheres along the fivefold axes are shown in solid circles, except for Fig. 1a in which only three spheres are drawn in solid circles. The A′ spheres in Fig. 1 are the equivalent ones of the A sphere and both of them are written A in the present paper; so are the B′ and C′ spheres. In addition to the 12 spheres (solid circles) at the vertices in the second shell (Fig. 1b), there is enough room at the midpoint of the 30 edges to accommodate further 30 spheres (open circles), adding to a total of 42 spheres. The third shell again has 12 spheres at the vertices, 60 spheres on the edges, and 20 more spheres at the centers of the 20 triangular faces, adding to 92 spheres (Fig. 1c). Using the cage notation @ introduced in the C60 literature, the first three icosahedral shells can be written as 1A@12B@42C@92A. Mackay showed that the number of spheres on the nth icosahedral shell is 10n 2 + 2(n ≥ 1) and the total number of spheres within the nth shell N = {10(n + 1)3 − 15(n + 1)2 + 11(n + 1) − 3}/3 for (n ≥ 1) is, in fact, the magic numbers of 13, 55, 147, 309, 561, 923, 1415, 2057, 2869, etc. In this context, it should be pointed out that earlier Pauling [2] has considered the icosahedral coordination with a coordination number CN12 in metal crystals and Frank [3] in liquid metals. Both of them emphasized the higher packing density and also the higher stability of the icosahedral coordination in comparison with the fcc and hcp (hexagonal close-packed) structures, also with CN12.

Fig. 1
figure 1

Mackay icosahedral shell (a–c) and faulted (d, e) structures (the origin is an A sphere). Solid circles are the spheres at the icosahedral vertices, except for the core icosahedron in (a) in which only three spheres are drawn in solid circles. The A′ spheres are equivalent ones of the A sphere and both of them are written A in the present paper; so are the B′ and C′ spheres. (a) First shell, 12 B spheres, the core icosahedron; (b) second shell, 42C spheres, the Mackay icosahedron (MI); (c) third shell, 92 A spheres; (d) a fault occurs in the interior of the triangular faces in the second shell, an A sphere atop three B spheres in (a); (e) B sphere in the third shell atop three C spheres in (b).

Full size image

The second and minor part of this paper, and nevertheless of equal importance, is the concept of the hierarchic icosahedral structure reported in the last paragraph. According to Mackay [1], Bernal had communicated to him in 1960 the hierarchic icosahedral structure: “The unit of packing is the arrangement of 13 spheres as an icosahedron making a quasi-sphere unit, 13 of which packed together to make a quasi-sphere of next order.” In other words, this is an icosahedron of icosahedra and this can extend hierarchically in space. Mackay made it clear that “However, there is a clear relationship between the early stages of such a hierarchic and the packing described above” and explained further that the hierarchic structure could be obtained from the iss by the introduction of a stacking fault in the fcc packing sequence of the latter, as shown in Fig. 1d, e. In other words, hierarchy could be an alternative of growth process to periodic translation. This brief hierarchic concept has inspired many research workers to probe it in greater depth as well as in broader scope.

The icosahedral multishell and hierarchic structures have been studied separately in the fields of particle science, cluster science, intermetallic compounds, and quasicrystals with different emphases and different terminology, although the underlying geometry should be the same. The present paper is trying to fill this gap by giving a unified geometrical presentation, especially the hierarchic icosahedral structures, and will begin with a brief description of some regular and semiregular polyhedra of icosahedral symmetry, followed by Mackay’s icosahedral shell structures, and Bernal–Mackay’s hierarchic icosahedral structures. For a recent review on the structure of atomic clusters, see the contribution of Dr. Echt in this volume.

Icosahedron and Related Polyhedra

Both of icosahedron (ICO) (Fig. 2a), and pentagonal dodecahedron (PD) (Fig. 2b), is platonic regular polyhedra consisting of regular faces and regular vertices. Their characteristics can best be represented by the Schläfli symbols of their vertices, 35 and 53, respectively. The superscript shows the number of faces, triangle (3) or pentagon (5), surrounding a vertex. The symbols 35 and 53 imply an exchange of face and vertex between an ICO and a PD. In other words, they are dual to each other. Such a dual relationship is important in constructing the iss. If atoms are added to cap the pentagons of a PD to form pentagonal pyramids (one of which is outlined in dotted lines in Fig. 2b), their apices may form an ICO and vice versa.

Fig. 2
figure 2

Polyhedra of icosahedral symmetry: (a) icosahedron (ICO), 35; (b) pentagonal dodecahedron (PD), 53; (c) icosi-dodecahedron (ID), 3.5.3.5. or (3.5)2; (d) rhombic triacontahedron (RT); (e) truncated icosahedron (TI), 5.62; (f) rhombic icosidodecahedron (RID), 3.4.5.4.

Full size image

Figure 2c is a polyhedron consisting of 20 triangles and 12 pentagons, i.e., a composite of ICO and PD. Hence, it is called icosi-dodecahedron (ID). Their faces are regular, but the 30 3.5.3.5 or (3.5)2 vertices are not. This is one of the Archimedian semiregular polyhedra with regular faces described by Kepler through the truncation of a regular polyhedron. Truncating the vertices of either an ICO or a PD at the midpoint of edges, an ID will result. Through dual operation, the 20 triangles and 12 pentagons of an ID are transformed into 20 regular threefold and 12 regular fivefold vertices, and a rhombic triacontahedron (RT) consisting of 30 rhombi will result (Fig. 2d). This can also be seen in Fig. 1d, where a pair of A spheres and the two C spheres on their two sides form a rhombus. In contrast to the semiregular polyhedra with regular polygons such as ID, RT belongs to the family of semiregular polyhedra with regular vertices formed by either three or five rhombi. This can also be obtained by capping the pentagons of a PD (Fig. 2b), so that the neighboring triangles sharing an edge are coplanar forming a rhombus. Needless to say, truncating and capping are dual operations.

If an ICO is truncated at one-third of the edges (see the dotted lines in Fig. 2a), 12 regular pentagons will appear normal to the fivefold axes, while the 20 triangles become smaller hexagons (Fig. 2e). This truncated icosahedron (TI) has 60 5.62 vertices and can accommodate 60 atoms, such as the Buckminsterfullerene C60 molecule. If an ID is further truncated at the midpoint of edges, the 30 (3.5)2 vertices become 30 rectangles or, after some readjustment, 30 squares. In the mean time, the 20 triangles and 12 pentagons are reduced to smaller ones. Such a 62-face polyhedron is called rhombic icosi-dodecahedron (RID) (see Fig. 2f and the 60 B spheres in Fig. 1e). Obviously, both TI and RID are semiregular polyhedra, consisting of 12 isolated regular pentagons with 60 equivalent vertices, but the polygons between the pentagons and thus the vertex types are different, one being 5.62 and the other 3.4.5.4.

All the polyhedra in Fig. 2 have icosahedral symmetry, because neither truncating the vertices of an icosahedron nor capping the faces of a pentagonal dodecahedron will change the inner symmetry of them, although their outer forms are different. Moreover, the number of faces (F), edges (E), and vertices (V) obeys the Euler rule of convex polyhedron, namely, F + V = E + 2.

Icosahedral Shell Structures

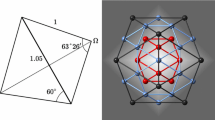
An icosahedron consists of 20 equilateral triangles and, therefore, can be visualized as 20 slightly distorted tetrahedra sharing a common vertex at its center. The edge of an icosahedron is about 1.05 times longer than its radius (the distance between its center and a vertex) and, hence, the vertex-center-vertex angle is 63.43°, rather than 60° of an equilateral triangle in a regular tetrahedron. In Fig. 1a–c, the spheres in the successive three shells are in B, C, and A positions, respectively. Mackay iss beautifully explained the icosahedral growth morphology [4–6] of the nanometer-sized icosa-twins (or, more generally, the multiple twin particles) of fcc metals as well as Si, diamond, TiC, etc. (for a recent review, see [7]). Recently, Volkov et al. [6] have observed by high-resolution electron microscopy a Pd particle consisting of five icosahedral shells with N = 561 atoms, exactly as Mackay predicted. In cubic crystals, successive twinning on {111} planes around a common [110] axis will yield fivefold twins. The dihedral angle between two {111} planes is about 71.5°, so that there is a gap of about 2.5° after five successive twinning operations around one <110 > axis. This will produce a noticeable strain in the icosahedral particle during growth and eventually it will change into a cuboctahedral particle. In other words, these cubic icosatwins are metastable and can only exist in nanometer scale. On the other hand, icosa-twins of rhombohedral crystals with = 63.43° would fill the three-dimensional space without leaving any gap and, therefore, could grow infinitely, or at least to a size of micron scale. Indeed, this was confirmed recently in the 30 m icosa-twin aggregates of the rhombohedral B6O with = 63.1° [8, 9], very close to the theoretical value of 63.43°. However, this came almost 40 years after Mackay’s prediction [1].

Cluster scientists became interested in Mackay’s icosahedral shells because they found icosahedral clusters of rare gases, especially the n = 2 and N = 55 cluster, showed minima of Lennard-Jones and Morse potentials [10, 11]. Moreover, this theoretical simulation was also supported by gas electron diffraction experiments made on argon clusters [12]. Hoare and Pal [10] called the N = 55 cluster “Mackay icosahedron” or simply MI. Hoare [11] concluded that the Mackay iss “far from being merely a crystallographic curiosity, have now been shown beyond doubt to be the dominant motif in the growth process of rare-gas microclusters in the important size range of N = 50 to N = 1000.” Several icosahedral shells with the number of atoms agreeing with Mackay’s 13, 55, and 147 have been identified in the mass spectroscopy of xenon and these numbers are called magic numbers in the cluster literature [13]. Such a study was later also extended to metal clusters, such as Na, Mg, Ca, and Sr clusters (for a recent review, see [14]). In Mg clusters, mass peaks occurred between the third shell of 147 atoms and the ninth shell of 2869 atoms have been observed [14, 15]. However, this does not guarantee an icosahedral structure because the cuboctahedral shells also have these magic numbers. Therefore, Martin et al. [14, 16], following Northby’s subshell growth concept [17], looked at the moderate mass peaks of the subshells between the fifth shell of 561 atoms and the sixth shell of 923 atoms in Ca clusters. They found that the number of atoms in the subshells agrees with the successive covering of the triangular faces of an icosahedron.

Smalley was interested in the studying of heavy metal (Mo) and semiconductor (Si, GaAs) clusters and had constructed a powerful laser-vaporization time-of-flight mass spectrometer. Kroto, Curl, Smalley, and their coworkers [18] used the strong laser beam to bombard a graphite target and surprisingly obtained a strong mass peak corresponding to 60 carbon atoms. They ingeniously suggested a spherical cage model of 60 carbon atoms located on the 60 vertices of a TI (see Fig. 2e) consisting of 12 pentagons and 20 hexagons, the molecular cluster of Buckminsterfullerene C60. Later, Martin et al. [14, 19] succeeded in producing even larger molecular clusters of (C60) N with N = 13, 55, and 147. Once more, they encountered the problem of differentiating between the icosahedral and the cuboctahedral shell packing and again used the mass peaks of subshells to prove the face capping of the icosahedral subshells.

Continuing his study of generalized crystallography, Mackay [20] independently developed a two-dimensional hierarchic pattern of pentagons similar to the celebrated Penrose pattern at about the same time as Penrose did [21] (see [22]). Mackay [23] called it “quasilattice” and produced its optical transform displaying clearly fivefold rotational symmetry. Following Ammann’s suggestion, Mackay constructed the three-dimensional (3-D) quasilattice built of rhombohedra of = 63.43° and 117.57°, respectively. Hargittai [22] considered this “predicting quasicrystal,” which was discovered independently by Shechtman et al. [24] without knowing Mackay’s work. Elser and Henley [25] as well as Guyot and Audier [26] suggested the MI in the cubic -(Al-Mn-Si) [27] with a composition of (Al,Si)42 Mn12 (Mn atoms occupy the vertices of the outer icosahedron, solid circles in Fig. 1b), while the center of the core icosahedron is vacant, as the structural motif of the Al-Mn-Si icosahedral quasicrystal. Since then MI was universally accepted as the fundamental structural motif for the family of Al-TM (transitional metal) icosahedral quasicrystals, which were called later the Mackay-type of quasicrystals [28].

Figure 3 is taken from Sung et al. [29] and modified to include the hierarchic icosahedral shells. Figure 3a shows one of the triangular faces of the first two icosahedral shells (MI) formed by adding spheres (solid circles) along the extended fivefold axes so that the successive shells are icosahedra of increasing sizes.

Fig. 3
figure 3

Schematic diagram of successive triangles of the icosahedral shells. (a) The first two shells of the MI cluster with an ABC sequence (see Fig. 1a, b); (b) stacking fault occurs after the ABC layers resulting in an ABCB sequence in the interior of the triangular faces (see Fig. 1e). An outer ICO centered at a C sphere along the fivefold axis \( {\overline{5}}_b \) shares a vertex B with the core ICO, thus producing an I13(V) cluster; (c) stacking fault occurs in the second shell resulting in an ABA sequence in the interior of triangles (see Fig. 1d). An outer ICO centered at a B sphere forms and penetrates into the core ICO, thus producing an I13(P) cluster. Spheres at the icosahedral vertices are drawn in solid circles (Taken from Sung et al. [29] and modified).

Full size image

The origin is an A sphere at the center and the first shell is the core ICO composed of B spheres. In the second icosahedral shell, however, the C spheres are not of the same distance from the origin, the spheres (solid circles) on the fivefold axes being slightly further away from the center than those at the midpoints of the edges (open circles). Thus, the second icosahedral shell can be divided into two subshells. One is the second ICO composed of 12 C spheres at the vertices (solid circles) and the other is an ID consisting of 20 triangles (open circles) and 12 pentagons [five spheres surrounding a fivefold axis (see Fig. 1b), although only two spheres are shown in Fig. 3a]. The pentagons in the first and second shells have the same orientation (along the \( {\overline{5}}_a \) axis, the triangle of the B spheres in the first shell and that of the C spheres in the second shell are parallel). This can be seen more clearly in Fig. 1a, b in which the B and C pentagons are parallel oriented. Two neighboring pentagons of the same orientation form a pentagonal prism (PP) with a relative large volume. Surrounding this MI/ID there is another ID about times larger, consisting of 156 atoms in the cubic -(Al-Mn-Si) [30, 31]. Yang [30] called it “double-Mackay icosahedron” or simply DMI. In the pseudo-body-centered cubic structure of -(Al-Mn-Si), a DMI is located at the origin and a MI at the body center so that they share a triangular face along the <111> directions [30, 31]. One set of the three orthogonal twofold axes of both the MI and DMI clusters is parallel to the cubic axes of -(Al-Mn-Si).

In fact, this DMI is nothing but the hierarchic icosahedral structure, suggested by Bernal to Mackay in a private communication reported in [1], an icosahedron of icosahedra. Mackay [1] mentioned the possibility of the occurrence of stacking faults in the fcc packing ABCA … of the triangular planes, for instance, the packing sequence of ABCB consisting of a fault plane of B spheres or a twin/hexagonal packing sequence of BCB. This is shown in Fig. 1a → Fig. 1b → Fig. 1e.

Hierarchic Icosahedral Structures

In Fig. 3b, the ID and ICO subshells of the second icosahedral shell in Fig. 3a become the second and third shells, respectively. In the Mackay iss, the next layer will be an A layer (see Fig. 1c). However, if a stacking fault is introduced in the ABC sequence so that the interior of a triangle in the fourth shell is made of B spheres (open circles), then a hexagonal BCB sequence instead of the fcc BCA sequence will be created. This is shown clearly in Fig. 1e in contrast to Fig. 1c. Twenty such B triangles (open circles in Fig. 3b) form 12 vertex-sharing pentagons around the fivefold axes, as well as 30 squares across the edges (Fig. 1e). This is the RID shown in Fig. 2f. The pentagon in the fourth shell is quite open and a sphere can be put above its center, namely, in the A position along an extended fivefold axis (solid circle), as in the Mackay iss. Thus, these 12 A spheres form the third ICO of the fifth shell. It is of interest to note that the five C spheres (open circles) surrounding the \( {\overline{5}}_b \) axis in the second shell and the five B spheres in the fourth shell have opposite orientations. This can also be seen in the orientation of the five C spheres (solid circles) in Fig. 1b and that of the five B spheres surrounding an A sphere in Fig. 1e. These two pentagons form a pentagonal antiprism (PAP) between them and this PAP, together with spheres on the \( {\overline{5}}_b \) axis in the first, third, and fifth shells, namely, B, C, and A spheres, form an ICO. This ICO is centered at the C sphere (solid circle) of the third shell and shares a B sphere in the first shell with the core ICO. In other words, they are a pair of ICOs sharing a common vertex along the \( {\overline{5}}_b \) axis. Thus, there are 12 outer icosahedra connected to the core ICO by sharing vertices, or a larger icosahedron consisting of 13 smaller ICOs. The hierarchic icosahedral shell sequence of 13 vertex-sharing ICOs in Fig. 3b, called I13(V), is:

$$ \begin{array}{c}\begin{array}{lll}I13\left(\mathrm{V}\right):\hfill & 1A@ICO12B@ ID30C@ICO12C@ RID60B@ICO12A\hfill & \mathrm{Total}\kern0.24em 127\kern0.24em \mathrm{spheres}\hfill \end{array}\\ {}MI55\end{array} $$

Obviously, a stacking fault occurs after the MI55. If the stacking fault of the twin/hexagonal sequence occurs in the second layer, as suggested by Northby [17], then an ABA sequence will occur, i.e., Fig. 1a → Fig. 1d. In Fig. 1d, an A sphere (open circle) is atop the center of three B spheres of the first shell in Fig. 1a, forming a tetrahedron. This is also shown in Fig. 3c in which there is an A sphere along the threefold axis capping the triangular face of three B spheres. This sphere A, together with other four equivalent ones, form a pentagon around the \( {\overline{5}}_c \) axis and 12 such pentagons form a PD of the second shell (see Fig. 1d). Moreover, this pentagon has an opposite orientation with respect to that in the core ICO, thus forming a PAP. Adding a C sphere along the \( {\overline{5}}_c \) axis atop of this pentagon forms a small ICO centered at the B sphere of the core ICO and, at the same time, a large ICO of the third shell. The ICOs centered at the origin and at the vertex B ICO are fused together forming an interpenetrated pair. The icosahedral shell sequence in Fig. 3c, called I13(P), is:

$$ \begin{array}{r}\hfill \begin{array}{rr}\hfill I13\left(\mathrm{P}\right):& \hfill 1A@ICO12B@PD20A@ICO12C\end{array}\\ {}\hfill \mathrm{Total}\kern0.24em 45\kern0.24em \mathrm{spheres}\end{array} $$

It is clear from Fig. 3 that a stacking fault in Mackay iss is necessary, either in the second or the third shell, to form hierarchic icosahedral structures. Such a fault is also called “twinning” [32, 33], “face capping” [17], or anti-Mackay packing [34] in cluster science. Hoare [32] obtained the multiple-twinning structure by a simulation based on Lennard-Jones potential and considered this “an indication of the nature of the free-energy barrier to crystallography.” Northby [17] gave this, besides a theoretical calculation, also a naive explanation. A sphere on the edge of an ICO, as in Fig. 1b, makes contact with only two spheres underneath it, whereas in the interior of a triangular face, as in Fig. 1d, it falls in the cavity of three spheres forming a tetrahedron, which is more stable. After completing an icosahedral shell, face capping of triangular faces will be preferred when atoms are added to form new subshells in the next shell. Based on these two kinds of stacking faults, two kinds of hierarchic icosahedral structures, vertex sharing and interpenetrating, respectively, of the core ICO and the 12 outer ICOs result. These two, as well as the 13 isolated ICOs, will be discussed below.

I13(I) Cluster

This term is coined to represent the icosahedrally connected 13 “isolated” ICOs. Earlier, Kreiner and Franzen [35] have used I13 to denote icosahedrally connected 13 ICOs. Here one letter in parentheses is added to indicate the type of linkage between the core ICO and the 12 outer ICOs. “Icosahedrally” means the centeres of these ICOs themselves form a hierarchic large ICO. “Isolated” or (I) means the core ICO forms bonds with the outer ICOs, but without any sharing of spheres between them. Figure 4a shows the connection of the core ICO and an outer ICO, all centeres being vacant. The order of the icosahedral shells is marked and the number N of spheres within the nth shell is given in parentheses. The first shell is the core ICO, and the second shell is a large ICO, consisting of one sphere from each of the 12 outer ICOs. The third shell consists of 12 pentagons forming a TI with 60 spheres (see Fig. 2e). This icosahedral cluster has 84 spheres, such as the B84 cluster in the structure of -B [36] and YB55 [37]. The pentagon in the third shell and the apex sphere in the second shell form an inverted pentagonal pyramid. The centeres and the outer pentagons of the outer ICOs in the next two shells are far away from each other and do not form any meaningful icosahedrally connected shell. The first three icosahedral shells for the B84 cluster with a vacant center (□) are:

Fig. 4
figure 4

The core and outer ICOs of three types of hierarchic icosahedral clusters. (a) I13(I), 13 isolated ICOs; (b) I13(V), 13 vertex-sharing ICOs; (c) I13(P), the similarly oriented core and outer ICOs form an intermediate ICO (dotted lines) between them, thus producing a chain of three mutually interpenetrated ICOs along a fivefold axis. The number in parentheses is the total number of spheres N within the nth shell.

Full size image
$$ \begin{array}{lll}{\mathrm{B}}_{84}:\hfill & @ICO12@ ICFO12@TI60\hfill & \mathrm{Total}\kern0.24em 84\kern0.24em atoms\hfill \end{array} $$

The hierarchical I13(I) cluster of -B can be written as B12(B12)12 and a schematic drawing of it has been given in Fig. 4b in [9].

I13(V) Cluster

In this hierarchic cluster, the 12 ICOs are linked to the core ICO through vertex sharing, as shown schematically in Fig. 4b. It has the same shell sequence as in Fig. 3b, but it shows more clearly the vertex sharing of two ICOs along a fivefold axis. In this case the core and outer ICOs are differently oriented, otherwise they will form a chain of three interpenetrated ICOs, as in Fig. 4c. Consequently, a PP exists between them. As shown in Fig. 3c, the spheres of the upper pentagon are C spheres. The first icosahedral shell is the core ICO and the second shell is an ID of 30 C spheres formed by sharing a vertex between two neighboring, lower pentagons of the outer ICOs (see the open circles in Fig. 1b). Obviously, all these 13 ICOs are linked by vertex sharing between the neighboring ICOs. The third shell is the second, large ICO composed of the central C spheres of the 12 outer ICOs. This is, in fact, the MI cluster of 55 atoms. The fourth shell consists of the 12 upper pentagons of the outer ICOs. Since these pentagons are further away from the center, compared with the lower pentagons, they are separated from each other and interlaced with squares and triangles forming a RID of 60 spheres (see Fig. 2f). A stacking fault occurs in this shell so that a RID composed of B spheres is formed and the packing sequence of the four shells becomes ABCB. Finally, the fifth shell is the third, even larger ICO of 12 A spheres.

Cenzual et al. [38] have considered the vertex sharing of neighboring ICOs in the I13(V) cluster in the structure of the cubic Sc57 Rh13 \( \left( Pm\overline{3},\kern0.24em a=1.4405\kern0.24em \mathrm{nm}\right) \) and the orthorhombic Hf54 Os17 (Immm, a = 1.3856, b = 1.4104, c = 1.450 nm). They used the general formula I114 C13 to represent this family of phases (I denotes the atoms in the icosahedral shell and C those at the center). It gives also 127 atoms in this I13(V) cluster. A schematic drawing of the 13 vertex-sharing ICOs in these compounds has been given in Fig. 1 in [38].

Yang [30] showed that in -(Al-Mn-Si) 30 more atoms are added above the squares of the RID, forming a second, larger ID in the sixth shell, so that the total number of atoms within the sixth shell is 156 (center vacant). This is his DMI. Tamura [39] has extended the icosahedral shell in -(Al-Mn-Si) from DMI (he called it large MI or LMI) to the seventh and eighth shells and calculated the deviation of the experimental atom positions in various shells from the theoretical positions in a hierarchic icosahedral model. The deviations in the center-vertex positions in the first three shells, i.e., the MI, are 0.0015 − 0.0087 nm, but increase to 0.021–0.0334 nm in the fourth and fifth shells of the DMI. Kreiner and Franzen [35] have also considered the giant (MI55)13 cluster, i.e., an icosahedron of MI. The hierarchic icosahedral shells in Sc57 Rh13 and -(AlMnSi) are:

$$ \begin{array}{c}MI55\\ {}\begin{array}{lll}{\mathrm{Sc}}_{57}R{\mathrm{h}}_{13}:\hfill & 1@ICO12@ ID30@ICO12@ RID60@ICO12\hfill & \mathrm{Total}\kern0.24em 127\kern0.24em \mathrm{atoms}\hfill \\ {}\left(\mathrm{AlMnSi}\right):\hfill & O@ICO12@ ID30@ICO12@ RID60@ICO12@ ID30\hfill & \mathrm{Total}\kern0.24em 156\kern0.24em \mathrm{atoms}\hfill \end{array}\\ {}\begin{array}{ll}MI54\hfill & DM156\hfill \end{array}\end{array} $$

I13(P) Cluster

In the hierarchic icosahedral cluster I13(P) shown in Fig. 4c, the core and outer ICOs not only share a vertex but also have the same orientation so that the two neighboring pentagons of the first and second shells are differently oriented. Thus, a PAP or a new ICO (drawn in dotted lines) centered at the common vertex B is formed between these two ICOs. The core, intermediate, and outer ICOs interpenetrate into the neighboring one, forming a chain of three ICOs or of three centered PAPs capped at both ends. The first two shells are the same as shown in Fig. 3c. The PAP layer block here is more compact than the PP layer block in Fig. 4b; thus, the second shell in I13(P) must be smaller than the ID in I13(V), but also consisting of 12 pentagons. The only possible pentagonal shell is the PD of 12 edge-sharing pentagons. The third shell is the second ICO, whereas the fourth shell is again composed of pentagons. Comparing with the pentagon shell of RID of 60 B spheres in I13(V), the pentagon shell in I13(P) should be somewhat smaller. The only possible case is the TI with 12 pentagons and 20 hexagons. Finally, there are 12 A spheres capping the pentagons forming the third ICO of the fifth shell. The hierarchic icosahedral shell structures of I13(P) together with those of the cubic Al5 Mg2Cu6 [40] (also the isostructural Mg2Z11 [41]) and (Al,Zn)49 Mg32 [42–46] (also the structural Al5 Li3 Cu [47, 48]) are:

$$ \begin{array}{c}\begin{array}{lll}{\mathrm{Al}}_5\mathrm{Mg}2{\mathrm{Cu}}_6:\hfill & 1@ICO12@PD20@ICO12\hfill & \mathrm{Total}\kern0.24em 45\kern0.24em \mathrm{atoms}\hfill \\ {}\mathrm{I}13\left(\mathrm{P}\right):\hfill & 1@ICO12@PD20@ICO12@TI60@ICO12\hfill & \mathrm{Total}\kern0.24em 117\kern0.24em \mathrm{spheres}\hfill \\ {}{\left(\mathrm{Al,Zn}\right)}_{49}{\mathrm{Mg}}_{32}:\hfill & O@UCI12@PD20@ICO12@TI60@ICO12@PD20\hfill & \mathrm{Total}\kern0.24em 136\kern0.24em \mathrm{atoms}\hfill \end{array}\\ {}\begin{array}{lll}RT44\hfill & 104\hfill & LRT136\hfill \end{array}\end{array} $$

In 1949, Samson first determined the crystal structure of the cubic Al5 Mg2 Cu6 (Pm3, a = 0.8311 nm, atoms) [40] and its isostructural Mg2Z11 [41]. Figure 5 shows the [001] projected view of the structure of Al5 Mg2Cu6: 6 Cu at (e), 12 Cu at (k), 1 Al at (b), 6 Al at (g), 8 Al at (i), and 6 Mg at (f). After the discovery of the Al-ZnMg quasicrystal, Pauling recalled [44] how he found the icosahedral shell structure of the cubic (Al,Zn)49 Mg32. “In 1950, I recognized that the 39-atom cubic structure of Al5Mg2Cu6 and Mg2Z11 (Samson19,20) could be obtained from a central icosahedron surrounded by a shell of 32 atoms.” From Fig. 5, it can be seen that around the central Al(b) atom there are 12 Cu(k) atoms of the core ICO (the three orthogonal golden rectangles are shaded). Adding 12 Mg(f) and 8 Al(i) atoms to cap the triangular faces of the core ICO will result in a PD [for the sake of clarity, only one of the 8 Al(i) atoms is shown at the bottom-left corner and 8 Mg(f) atoms are shown on the {100} planes in Fig. 5]. Thus, only tetrahedral interstices result by adding the second shell of a PD. A third shell of 12 Al(g) atoms (only 8 are shown in Fig. 5) are added above the pentagons of the PD. They lie on the extended lines (fivefold axes) connecting the central Al(b) atom to the 12 Cu(k) atoms of the core ICO, thus forming the outer ICO [see Fig. 4c]. This will produce a pentagonal bipyramid with an apex at Al(b) and another one at Al(g). Each pentagonal bipyramid can be visualized as 5 deformed tetrahedra sharing a common edge, namely, the fivefold rotational axis. Thus the 45-atom shell structure is a tetrahedrally close-packed (tcp) structure. According to Frank [3] and Boerdijk [49], tcp clusters are stable and occur frequently in metallic compounds, such as the Frank–Kasper phases [50], the tcp phases of the Shoemakers [51, 52], and the giant cubic phases of Samson [53, 54].

Fig. 5
figure 5

Samson’s schematic diagram of the cubic structure of Al5Mg2Cu6 [40] and its 45-atom, three-shell icosahedral cluster analyzed by Pauling [44, 45]; 1Al(b)@ICO12[12Cu(k)]@PD20[12 Mg(f),8Al(i)]@ICO12[12Al(g)], with the 12Al(g) and 12 Mg(f) atoms on {100} planes (Taken from Samson [40]).

Full size image

The outer shell of the 45-atom cluster is, in fact, a RT of 30 rhombi (Fig. 2d) or a capped PD of 60 triangles (Fig. 2b). Continuing the tetrahedral packing to obtain the structural model of (Al,Zn)49 Mg32, Pauling [45] added 60 more atoms atop the 60 triangles and finally obtained the fourth shell of a TI. Adding 12 more atoms above the pentagons to form the fifth shell and completes the I13(P) cluster. This 105-atom soccer ball-shaped icosahedral cluster as well as the 127-atom structural model of (Al,Zn)49 Mg32 obtained first by the stochastic method [45] are included in Pauling’s famous book “The Nature of the Chemical Bond and Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry” [55]. Following Pauling’s suggestion, Bergman et al. solved the complicate crystal structure of (Al,Zn)49 Mg32 first by X-ray powder method in 1952 [42] and later by single crystal diffraction in 1957 [43]. It turned out that the center of the core is 80 % occupied. Recently, Sun et al. [46] found the center is empty in an accurate redetermination of this structure. Therefore, this four-shell icosahedral cluster in fact has only 104 atoms. Cenzual et al. [38] denoted it by I104C13, where C13 means the 13 atoms at the centers of 13 ICOs and also gave a schematic drawing of the I13(P) cluster in their Fig. 2, in which the 12 outer ICOs are themselves edge-sharing between neighboring ones. Immediately after the first discovery of the Al-Mn icosahedral quasicrystal [24], Mackay [56] suggested that an alloy of the composition of (Al,Zn)49 Mg32 might be a suitable candidate for finding new quasicrystals. Indeed, such a quasicrystal was found independently at about the same time by Ramanchandrarao and Sastry [57], based on the icosahedral shell structure of the cubic (Al,Zn)49 Mg32. Since then the 104-atom hierarchic shell is often called the Bergman cluster and the icosahedral quasicrystals of this family the Bergman type quasicrystals [58, 59]. Considering the pioneer work of Samson on Al5Mg2Cu6 [40] and Pauling’s [45] stochastic model of (Al,Zn)49 Mg32, perhaps this family of quasicrystals might better be called Samson–Pauling–Bergman or SPB type of quasicrystals.

Instead of icosahedron, Samson [53, 54] likes to use truncated tetrahedron (TT) with four triangular faces opposite to four hexagonal faces to describe complicated metallic structures. As the icosahedron, this polyhedron can also be used to describe the structures of MgCu2, MgZn2, and MgNi2. Capping the four hexagonal faces of a TT with four more atoms yields a CN16 Kasper polyhedron with only tetrahedral interstices. Twenty such TTs can condense into a TI if each TT is sharing a hexagon with each of its three TT neighbors. The remaining hexagons of these TTs will form an outer shell of 20 hexagons with 12 pentagonal cavities or 12 inverted pentagonal pyramids. The remaining 20 triangles, one from each TT, form the core ICO with an empty center. Samson [53, 54] used the 104-atom TI unit to discuss not only the structure of (Al,Zn)49 Mg32 but also the giant cubic NaCd2 (a = 3.056 nm) and -Mg2Al3 (a = 2.8239 nm). Tillard–Charbonnel, Belin, and their co-workers [60–62] later used the 104-atom shell unit, called Samson polyhedron by them, to describe the structures of a number of ternary Ga compounds found by them. For instance, in the body-centered cubic Li13Cu6Ga21 [60], structurally similar to Al5Li3 Cu and (Al,Zn)49 Mg32, the Samson polyhedron at the center is connected to the other eight Samson polyhedra by sharing a hexagon with each of them along the <111> directions. Such a chain of hexagonsharing Samson polyhedra can produce a hexagonal structure, such as the Li68 Zn16 Ga133, with a = 1.3657 nm and c = 23435 nm [61]. In the cubic Na35Cd24Ga56 of a = 2.1286 nm, however, two Samson polyhedra are connected by sharing a pentagonal face [62]. Thus, it is suggested to call this 104-atom cluster the Samson–Pauling– Bergman cluster or SPB cluster.

Since the first discovery of the icosahedral quasicrystal in rapidly solidified Al-Mn alloys, both the MI54 of the cubic -(Al-Mn-Si) structure [25, 26] and the 104-atom Samson–Pauling–Bergman TI of the cubic (Al,Zn)49 Mg32/Al5Li3 Cu structure [58, 59] have been considered to be the main building blocks of icosahedral quasicrystals [28]. Moreover, Elser and Henley [25, 58] have further shown that substituting rational ratios of two successive Fibonacci numbers for the irrational golden number of a quasicrystal will yield an approximate crystalline structure, called approximant. A similar idea has also been put forward by Mackay [56] using 5/3, 8/5, and 21/13 of the ratios of Fibonacci numbers to substitute for the irrational in the aperiodic structure of quasicrystals to obtain the Hume–Rothery compounds. This is the fundamental crystallographic connection between a quasicrystal and its crystalline approximant.

Using X-ray and neutron diffraction made on a single grain of Al-Mn-Pd icosahedral quasicrystal, Janot and his co-workers [63, 64] obtained an incomplete MI with only 9 atoms in the core icosahedron in the form of a body-centered cube. They called this 51-atom cluster “pseudo-MI” or simply PMI because it is almost, but not exactly, icosahedral. Recently, this has found support in the structures of many crystalline approximants of icosahedral quasicrystals, in which a 9-atom body-centered cubic or a 15-atom centered rhombic dodecahedron core has been found [65–67]. Recently, Tsai et al. [68, 69] found binary Cd5.7Yb and Cd5.7Ca icosahedral quasicrystals close to the composition of the body-centered cubic Cd6Yb [70] and Cd6Ca [71], respectively. The 66-atom cluster in the structure of these cubic phases is a tetrahedral core surrounded successively by PD, ICO, and ID. This is another cluster of predominately, but not exactly, icosahedral symmetry. There will be more such new findings in the coming years which will enrich the structures of icosahedral quasicrystal and its approximants, but the icosahedral shell and hierarchic icosahedral structures first suggested by Mackay 40 years ago will remain the guiding concepts in the future.