Abstract
We provide a hierarchy of tree languages recognised by nondeterministic parity tree automata with priorities in \(\{0,1,2\}\), whose length exceeds the first fixed point of the \(\varepsilon \) operation (that itself enumerates the fixed points of \(x\mapsto \omega ^x\)). We conjecture that, up to Wadge equivalence, it exhibits all regular tree languages of index \([0,2]\).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This paper contributes to the close investigation of regular tree languages of index \([0,2]\). Our tool to measure and compare those languages is given by descriptive set theory through the notion of topological complexity. It is well known that deterministic parity tree automata recognize only languages in the \(\mathbf {\Pi }^{1}_{1}\) class (coanalytic sets), whereas nondeterministic automata recognize languages that are neither analytic, nor coanalytic. The expressive power of nondeterministic automata is nonetheless bounded by the second level of the projective hierarchy, and, by Rabin’s complementation result [7], all nondeterministic languages are in fact in the \(\mathbf {\Delta }^{1}_{2}\) class. A more discriminating topological complexity measure than the Baire and the projective hierarchy is therefore needed: the Wadge hierarchy, which relies on the notion of reductions by continuous functions (Wadge-reducibility). Complexity classes, called Wadge degrees, consist of sets Wadge-reducible to each other, and constitute a hierarchy whose levels, called ranks, can be enumerated with ordinals. We describe a series of operations on automata that preserve the index and lift the Wadge degrees of the recognized languagesFootnote 1. These operations help us generate a hierarchy of regular tree languages of higher and higher topological complexity, one level higher than the first fixed point of the ordinal functionFootnote 2 \(x\mapsto \varepsilon _{x}\) which itself enumerates the fixed points of the exponentiation \(x\mapsto \omega ^{x}\).
2 Preliminaries
2.1 The Wadge Hierarchy and the Wadge Game
The Wadge theory is in essence the theory of pointclasses Footnote 3 (see [1]). For \(\varGamma \) a pointclass, we denote by \(\check{\varGamma }\) its dual class containing all the subsets whose complements are in \(\varGamma \), and by \(\Delta (\varGamma )\) the ambiguous class \(\varGamma \cap \check{\varGamma }\). If \(\varGamma = \check{\varGamma }\), we say that \(\varGamma \) is self-dual.
Given any topological space \(X\), the Wadge preorder \(\le _{W}\) on \(\fancyscript{P}(X)\) is defined for \(A,B \subseteq X\) by \(A \le _{W}B\) if and only if there exists \(f\!\!: X \longrightarrow X\) continuous such that \(f^{-1}(B) = A\). It is merely by definition a preorder which induces an equivalence relation \(\equiv _{W}\) whose equivalence classes – denoted by \([A]_{W}\) – are called the Wadge degrees. A set \(A \subseteq X\) is self-dual if \([A]_{W}=[A^\complement ]_{W}\), and non-self-dual otherwise. We use the same terminology for the Wadge degrees. We have a direct correspondence between \((\fancyscript{P}(X), \le _{W})\) restricted to \(\varGamma \) and the pointclasses included in \(\varGamma \) with inclusion: the pointclasses are exactly the initial segments of the Wadge preorder. In particular, the Wadge hierarchy tremendously refines the Borel and the projective hierarchies.
The space \(T_{\varSigma }\) equipped with the standard Cantor topology is a Polish space, and is in fact homeomorphic to the Cantor space [2]. Let \(L,M \subseteq T_{\varSigma }\), the Wadge game \(W(L, M)\) is a two-player infinite game that provides a very useful characterization for the Wadge preorder. In this game, each player builds a tree, say \(t_{\mathrm {I}}\) and \(t_{\mathrm {II}}\). At every round, player I plays first, and both players add a finite number of children to the terminal nodes of their tree. Player II is allowed to skip her turn, but has to produce a tree in \(T_{\varSigma }\) throughout a game. Player II wins the game if and only if \(t_{I} \in L \Leftrightarrow t_{II} \in M\).
Lemma 1
([9]). Let \(L, M \subseteq T_{\varSigma }\). Then \(L \le _{W} M\) if and only if player \(\mathrm {II}\) has a winning strategy in the game \(W(L, M)\).
We write \(A<_{W}B\) when \(\mathrm {II}\) has a winning strategy in \(W(A,B)\) and \(\mathrm {I}\) has a winning strategy in \(W(B,A)\) Footnote 4. Given a pointclass \(\varGamma \) of \(T_{\varSigma }\) with suitable closure properties, the assumption of the determinacy of \(\varGamma \) is sufficient to prove that \(\varGamma \) is semi-linearly ordered by \(\le _{W}\), denoted \({{\mathrm{SLO}}}(\varGamma )\), i.e., that for all \(L, M \in \varGamma \),
and that \(\le _{W}\) is well founded when restricted to sets in \(\varGamma \) [1, 8]. Under these conditions, the Wadge degrees of sets in \(\varGamma \) with the induced order is thus a hierarchy called the Wadge hierarchy. Therefore, there exists a unique ordinal, called the height of the \(\varGamma \)-Wadge hierarchy, and a mapping \(d_W^{\varGamma }\) from the \(\varGamma \)-Wadge hierarchy onto its height, called the Wadge rank, such that, for every \(L,M\) non-self-dual in \(\varGamma \), \(d_W^{\varGamma }(L) < d_W^{\varGamma }(M)\) if and only if \(L <_W M\) and \(d_W^{\varGamma } (L) = d_W^{\varGamma } (M)\) if and only if \(L \equiv _W M\) or \(L\equiv _W M^{\complement }\). The wellfoundedness of the \(\varGamma \)-Wadge hierarchy ensures that the Wadge rank can be defined by induction as follows:
-
\(d_W^{\varGamma }(\emptyset )=d_W^{\varGamma }(\emptyset ^{\complement })=1.\)
-
\(d_W^{\varGamma }(L)=\sup \left\{ d_W^{\varGamma }(M)+1: M \text { is non-self-dual}, M <_{W}L\right\} \) for \(L>_{W}\emptyset \).
Note that given two pointclasses \(\varGamma \) and \(\varGamma '\), for every \(L \in \varGamma \cap \varGamma '\), we have \(d_W^{\varGamma }(L)=d_W^{\varGamma '}(L)\). Under sufficient determinacy assumptions, we can therefore safely speak of the Wadge rank of a tree language, denoted by \(d_W\), as its Wadge rank with respect to any topological class including it. However the main result of this article does not provide any Wadge rank for the canonical languages that are constructed, because we do not make use of any determinacy principle.
2.2 The Conciliatory Hierarchy
A conciliatory binary tree over a finite set \(\varSigma \) is a partial function \(t: \{0,1\}^{*} \rightarrow {\varSigma }\) with a prefix-closed domain. Such trees can have both infinite and finite branches. A tree is called full if \({{\mathrm{dom}}}(t)= \{0,1\}^{*}\). Let \(\mathcal {T}^{\le \omega }_{\varSigma }\) and \(T_{\varSigma }\) denote, respectively, the set of all conciliatory binary trees and the set of full binary trees over \({\varSigma }\). Given \(x \in {{\mathrm{dom}}}(t)\), we denote by \(t_{x}\) the subtree of \(t\) rooted at \(x\). Let \(\{0,1\}^{n}\) denote the set of words over \(\{0,1\}\) of length \(n\), and let \(t\) be a conciliatory tree over \(\varSigma \). We denote by \(t[n]\) the finite initial binary tree of height \(n+1\) given by the restriction of \(t\) to \(\bigcup _{0\le i \le n}\{0,1\}^{i}\).
For conciliatory languages \(L,M\) we define the conciliatory version of the Wadge game: \(C(L,M)\) [4, 5]. The rules are similar, except for the fact that both players are now allowed to skip and to produce trees with finite branches – or even finite trees. For conciliatory languages \(L,M\) we use the notation \(L \le _cM\) if and only if \(\mathrm {II}\) has a winning strategy in the game \(C(L,M)\). If \(L \le _cM\) and \(M \le _cL\), we will write \(L \equiv _c M\). The conciliatory hierarchy is thus the partial order induced by \(\le _c\) on the equivalence classes given by \(\equiv _{c}\). We write \(A<_{c}B\) when \(\mathrm {II}\) has a winning strategy in \(C(A,B)\) and \(\mathrm {I}\) has a winning strategy in \(C(B,A)\).
From a conciliatory language \(L\) over \(\varSigma \), one defines the corresponding language \(L^{b}\) of full trees over \(\varSigma \cup \{b\}\) by
where \(b\) is an extra symbol that stands for “blank”, and \(t_{[~/ b]}\), the undressing of \(t\), is informally the conciliatory tree over \(\varSigma \) obtained once all the occurrences of \(b\) have been removed in a top-down manner. More precisely, if there is a node \(v\) such that \(t(v)=b\), we ignore this node and replace it with \(v0\). If, for each integer \(n\), \(t(v0^{n}) = b\), then \(v \notin {{\mathrm{dom}}}(t_{[~/ b]})\). This process is illustrated by Fig. 1.
If \(\varGamma \) is a pointclass of full trees, we say that a conciliatory language \(L\) is in \(\varGamma \) if and only if \(L^{b}\) is in \(\varGamma \).
Lemma 2
Let \(L\) and \(M\) be conciliatory languages. Then
The mapping \(L \mapsto L^{b}\) gives thus a natural embedding of the preorder \(\le _c\) restricted to conciliatory sets in \(\varGamma \) into the \({\varGamma }\)-Wadge hierarchy. Hence, for \(\varGamma \) with suitable closure and determinacy properties, the conciliatory degrees of sets in \(\varGamma \) with the induced order constitute a hierarchy called the conciliatory hierarchy. We define, by induction, the corresponding conciliatory rank of a language:
-
\(d^{\varGamma }_{c}(\emptyset )=d^{\varGamma }_{c}(\emptyset ^{\complement })=1.\)
-
\(d^{\varGamma }_{c}(L)=\sup \{d^{\varGamma }_{c}(M)+1: M <_{c}L\}\) for \(L>_{c}\emptyset \).
Similarly to the Wadge case, given two pointclasses \(\varGamma \) and \(\varGamma '\), for every conciliatory \(L \in \varGamma \cap \varGamma '\), we have \(d_c^{\varGamma }(L)=d_c^{\varGamma '}(L)\). Under sufficient determinacy assumptions, we can therefore speak safely of the conciliatory rank of a conciliatory tree language, denoted by \(d_c\), as its conciliatory rank with respect to any topological class including it. Observe that the conciliatory hierarchy does not contain self-dual languages: a strategy for \(\mathrm {I}\) in \(C(L,L^{\complement })\) is to skip in the first round, and then copy moves of \(\mathrm {II}\).
2.3 Automata and Conciliatory Trees
A nondeterministic parity tree automaton \(\mathcal {A}=\langle \varSigma , Q, I, \delta , {{\mathrm{r}}}\rangle \) consists of a finite input alphabet \(\varSigma \), a finite set \(Q\) of states, a set of initial states \(I\subseteq Q\), a transition relation \(\delta \subseteq Q \times \varSigma \times Q \times Q\) and a priority function \({{\mathrm{r}}}: Q \rightarrow \omega \). A run of automaton \(\mathcal {A}\) on a binary conciliatory input tree \(t \in \mathcal {T}^{\le \omega }_{\varSigma }\) is a conciliatory tree \(\rho _{t} \in \mathcal {T}^{\le \omega }_{Q}\) with \({{\mathrm{dom}}}(\rho _{t})=\{\varepsilon \}\cup \{va:v\in {{\mathrm{dom}}}(t) \wedge a\in \{0,1\}\}\) such that the root of this tree is labeled with a state \(q\in I\), and for each \(v\in {{\mathrm{dom}}}(t)\), transition \(\left( \rho _{t}(v),t(v),\rho _{t}(v_1),\rho _{t}(v_1)\right) \in \delta \). The run \(\rho _{t}\) is accepting if parity condition is satisfied on each infinite branch of \(\rho _{t}\), i.e., if the highest rank of a state occurring infinitely often on the branch is even, and if the rank of each leaf node in \(\rho _{t}\) is even. We say that a parity tree automaton \(A\) accepts a conciliatory tree \(t\) if it has an accepting run on \(t\). The language recognized by \(A\), denoted \(L(A)\) is the set of trees accepted by \(A\). We let \(L^\omega (A)\) denote the set of full trees recognized by \(A\), i.e., \(L^\omega (A)=L(A) \cap T_{\varSigma }\). Notice that as the set of states is finite, the priority function is bounded. Moreover, shifting all ranks by an even number does not change the language recognized by a parity tree automaton. It is thus sufficient to consider parity tree automata whose priorities are restricted to intervals \([\iota ,\kappa ]\), for \(\iota \in \{0,1\}\). We say that an automaton is of index \([\iota ,\kappa ]\) if its priorities are restricted to intervals \([\iota ,\kappa ]\). A language is of index \([\iota ,\kappa ]\) if there is an automaton of index \([\iota ,\kappa ]\) that recognises it. This gives rise to the Mostowski-Rabin hierarchy [3]. Let \(W_{[0,2]}\) be the game tree language of index \([0,2]\). One can prove that \(L \le _{W}W_{[0,2]}\) holds for any regular tree language \(L\) of index \([0,2]\), but fails for \(L=W_{[0,2]}^\complement \).
Corollary 1
The mapping \(L \mapsto L^{b}\) embeds the conciliatory hierarchy for \(\mathbf{\Delta }^1_2\)-sets restricted to languages of index \([0,2]\) into the \(\mathbf{\Delta }^1_2\)-Wadge hierarchy restricted to languages of index \([0,2]\).
We use the following conventions in the diagrams. Nodes represent states of the automaton. Node labels correspond to state ranks. A red edge shows the state that is assigned to the left successor node of a transition, and a green edge goes to the right successor node. In order to lighten the notation, transitions that are not depicted on a diagram lead to some all-accepting state. Given automata \(\mathcal {A}\) and \(\mathcal {B}\), we write \(\mathcal {A} \le _c\mathcal {B}\) for \(L(\mathcal {A}) \le _cL(\mathcal {B})\), and same with \(<_{c},\le _{W},<_{W}\).
3 Operations on Languages and Their Automatic Counterparts
We present operations on conciliatory tree languages, which we then use to construct more and more complex languages. W.l.o.g. we assume the alphabet to be \(\varSigma = \{a,c\}\).
3.1 The Sum
For \(L, M\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), we define \(L \oplus M\) (the sum of \(L\) and \(M\)) as the language formed of all those trees \(t \in \mathcal {T}^{\le \omega }_{\varSigma }\) such that one of the following conditions holds:
-
\(t(10^{n})=a\) for each integer \(n\) and \(t_{0} \in M\);
-
the node \(10^{n}\) is the first on the path \(10^{*}\) labeled with \(c\) and either \(t(10^{n}0) = a\) and \(t_{10^{n}00}\in L\), or \(t(10^{n}0) = c\) and \(t_{10^{n}00}\in L^{\complement }\).
This operation behaves well regarding the conciliatory hierarchy.
Facts 1
([4, 5]). Given \(L\), \(M\), and \(M'\) any conciliatory tree languages over \(\varSigma \),
-
1.
\( (L \oplus M)^{\complement } \equiv _c L \oplus M^{\complement }\).
-
2.
The operation \(\oplus \) preserves the conciliatory ordering: if \(M' \le _cM\), then
$$L\oplus M' \le _cL\oplus M. $$ -
3.
Assuming enough determinacy:
$$\begin{aligned} d_c(L\oplus M)= d_c(L) + d_c(M). \end{aligned}$$
Let \(\mathcal {A}\) and \(\mathcal {B}\) be two automata that recognize, respectively, the conciliatory languages \(M\) and \(L\). Then the automaton  depicted in Fig. 2 recognizes the sum of \(L\) and \(M\). In this picture, \(\mathcal {C}\) is any automaton of index \([0,2]\) that recognizes a language equivalent to \(L^{\complement }\), and the parity \(i\) and \(j\) are defined as follows:
depicted in Fig. 2 recognizes the sum of \(L\) and \(M\). In this picture, \(\mathcal {C}\) is any automaton of index \([0,2]\) that recognizes a language equivalent to \(L^{\complement }\), and the parity \(i\) and \(j\) are defined as follows:
-
\(i =0\) if and only if the empty tree is accepted by \(\mathcal {A}\);
-
\(j=1\) if and only if \(L(\mathcal {A})\) is equivalent to
 , where
, where  denotes any automaton that rejects all trees.Footnote 5
denotes any automaton that rejects all trees.Footnote 5
Notice that if \(\mathcal {A}\) and \(\mathcal {B}\) are parity tree automata of index \([0,2]\) such that \(L(\mathcal {B})^{\complement }\) can be recognized by an automaton of index \([0,2]\), then  is a parity tree automata of index \([0,2]\).
is a parity tree automata of index \([0,2]\).
Lemma 3
Let \(L\), \(L'\), \(M\) and \(M'\) be conciliatory languages such that \(L<_{c}L'\) and \(M \le _cM'\). Then the following hold.
-
1.
\(M \oplus L <_{c}M' \oplus L'\);
-
2.
\(M <_{c}M \oplus L\).
3.2 Multiplication by a Countable Ordinal
In order to define the multiplication of a language by a countable ordinal, we first introduce the operation \(\sup _{n<\omega }\). Let \((L_{n})_{n\in \omega }\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) be a countable family of conciliatory languages. Define \(\sup _{n<\omega } L_{n}\) as the conciliatory tree language containing all of those trees \(t \in \mathcal {T}^{\le \omega }_{\varSigma }\) such that one of the following conditions holds:
-
\(t(1^{n})=a\) for all integer \(n\);
-
the node \(1^{n}\) is the first on the path \(1^{*}\) labeled with \(c\) and \(t_{1^{n}0}\in L_{n}\).
The multiplication by a countable ordinal is now defined as an iterated sum. Let \(L \subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), \(L \odot 1 = L\), \(L \odot (\alpha + 1) = (L \odot \alpha ) \oplus L\), and \(L \odot \lambda = \sup _{\alpha <\lambda } L \odot \alpha \), for \(\lambda \) limit.
Let \(\mathcal {A}\) be an automaton that recognizes the conciliatory languages \(L\). Then the automaton  depicted in Fig. 3(a) recognizes a language equivalent to \(L \odot \omega \). In this picture, \(\mathcal {C}\) is any automaton that recognizes a language equivalent to \(L^{\complement }\). The automaton
depicted in Fig. 3(a) recognizes a language equivalent to \(L \odot \omega \). In this picture, \(\mathcal {C}\) is any automaton that recognizes a language equivalent to \(L^{\complement }\). The automaton  that recognizes the complement of
that recognizes the complement of  , and thus a language equivalent to the complement of \(L \odot \omega \), is depicted in Fig. 3b. Notice that if \(\mathcal {A}\) is of index \([0,2]\), and if there exists an automaton that recognizes \(L(\mathcal {A})^{\complement }\) of index \([0,2]\), then both
, and thus a language equivalent to the complement of \(L \odot \omega \), is depicted in Fig. 3b. Notice that if \(\mathcal {A}\) is of index \([0,2]\), and if there exists an automaton that recognizes \(L(\mathcal {A})^{\complement }\) of index \([0,2]\), then both  and
and  are parity tree automata of index \([0,2]\). Hence, for every ordinal \(0 < \alpha <\omega ^{\omega }\) and for every automaton \(\mathcal {A}\), there exists an automaton
are parity tree automata of index \([0,2]\). Hence, for every ordinal \(0 < \alpha <\omega ^{\omega }\) and for every automaton \(\mathcal {A}\), there exists an automaton  that recognizes \(L(\mathcal {A}) \odot \alpha \). Moreover, if \(\mathcal {A}\) is of index \([0,2]\), and if there exists an automaton that recognizes \(L(\mathcal {A})^{\complement }\) of index \([0,2]\), then
that recognizes \(L(\mathcal {A}) \odot \alpha \). Moreover, if \(\mathcal {A}\) is of index \([0,2]\), and if there exists an automaton that recognizes \(L(\mathcal {A})^{\complement }\) of index \([0,2]\), then  is a parity tree automaton of index \([0,2]\).
is a parity tree automaton of index \([0,2]\).
As a corollary of Lemma 3 and Facts 1, the multiplication by a countable ordinal behaves well regarding the conciliatory hierarchy.
Corollary 2
Let \(L\) and \(M\) be conciliatory languages such that \(L <_{c}M\). Then for every countable ordinals \(0<\alpha <\beta <\omega ^{\omega }\):
-
1.
\(L \odot \alpha <_{c}L \odot \beta \);
-
2.
\(L \odot \alpha <_{c}M \odot \alpha \).
3.3 The Pseudo-Exponentiation
Let \(P\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) be a conciliatory tree language. For \(t \in \mathcal {T}^{\le \omega }_{\varSigma }\), let:
This process is illustrated in Fig. 4. The nodes in blue are called the main run. The blue arrows denote the dependency of a node of the main run on a subtree of auxiliary moves. If the auxiliary subtree of a main run node is not in \(P\), then we say that the node is killed.
Let \(L \subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), we define the action of \(P\) on \(L\), in symbols \((P,L)\), by
Let \(P_{\mathbf {\Pi }^{0}_{1}}\) be the complete closed set of all full trees over \(\varSigma \) with all nodes on the leftmost branch \(0^{*}\) labelled by \(a\). For \(L \subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), we denote by \((\mathbf {\Pi }^{0}_{1},L)\) the action of \(P_{\mathbf {\Pi }^{0}_{1}}\) on \(L\). This operation \((\mathbf {\Pi }^{0}_{1}, \cdot )\) behaves well regarding the conciliatory hierarchy.
Facts 2
([4, 5]). Let \(L\) and \(M\) be conciliatory tree languages over \(\varSigma \). Then the following hold.
-
1.
\((\mathbf {\Pi }^{0}_{1},L)^{\complement } \equiv _{c} (\mathbf {\Pi }^{0}_{1},L^{\complement })\).
-
2.
If \(L \le _cM\), then \((\mathbf {\Pi }^{0}_{1},L) \le _c(\mathbf {\Pi }^{0}_{1},M)\).
-
3.
If \(L <_{c}M\), then \((\mathbf {\Pi }^{0}_{1},L) <_{c}(\mathbf {\Pi }^{0}_{1},M)\).
-
4.
Assuming enough determinacy, \(d_c((\mathbf {\Pi }^{0}_{1},L))= \omega _{1}^{d_{c}(L) + \varepsilon }\), for Footnote 6 \(\varepsilon \in \{-1,0,1\}.\)
Without assuming any determinacy hypothesis, we can nonetheless prove the following Proposition that links \((\mathbf {\Pi }^{0}_{1}, \cdot )\) to \(\oplus \).
Proposition 1
Let \(L\), \(L'\) and \(M\) be conciliatory languages such that \(L <_{c}(\mathbf {\Pi }^{0}_{1},M)\) and \(L' <_{c}(\mathbf {\Pi }^{0}_{1},M)\). Then
-
1.
\(L \oplus L' <_{c}(\mathbf {\Pi }^{0}_{1},M)\);
-
2.
\(L \odot \alpha <_{c}(\mathbf {\Pi }^{0}_{1},M)\), for any \(\alpha <\omega ^{\omega }\).
Given any automaton \(\mathcal {A}\) recognizing \(L\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), the conciliatory language \((\mathbf {\Pi }^{0}_{1},L)\) is recognized by the automaton  defined from \(\mathcal {A}\) by replacing each state of \(\mathcal {A}\) by a “gadget”, as depicted in Fig. 5. By replacing a state by the gadget we mean that all transitions ending in this state should now end in the initial state of the gadget, and that all the transitions leaving this state should now start from the final state of the gadget. This sort of gadget first appeared in [5]. Notice that if \(L\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) is of index \([0,2]\), then \((\mathbf {\Pi }^{0}_{1},L)\) is also of index \([0,2]\). Observe also that the game language \(W_{[0,2]}\) is a fixed point for pseudo-exponentiation, i.e.,
defined from \(\mathcal {A}\) by replacing each state of \(\mathcal {A}\) by a “gadget”, as depicted in Fig. 5. By replacing a state by the gadget we mean that all transitions ending in this state should now end in the initial state of the gadget, and that all the transitions leaving this state should now start from the final state of the gadget. This sort of gadget first appeared in [5]. Notice that if \(L\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) is of index \([0,2]\), then \((\mathbf {\Pi }^{0}_{1},L)\) is also of index \([0,2]\). Observe also that the game language \(W_{[0,2]}\) is a fixed point for pseudo-exponentiation, i.e.,
4 Difference of Co-analytic Sets
The operations defined in Sect. 3 are Borel in the sense that when we apply them to Borel languages, the resulting language is still Borel. In order to describe the most of the Wadge hierarchy of languages recognized by parity tree automata of index \([0,2]\) we need to climb higher.
4.1 The Operation \((D_{2}(\mathbf {\Pi }^{1}_{1}), \cdot )\)
We define a conciliatory language of index \([0,2]\) that is \(D_{2}(\mathbf {\Pi }^{1}_{1})\)-complete (Fig. 6a) and such that its complement (Fig. 6b) is also of index \([0,2]\), via the automata that recognize each of them. We denote by \(A_{D_{2}(\mathbf {\Pi }^{1}_{1})}\) and \(A_{\check{D_{2}}(\mathbf {\Pi }^{1}_{1})}\) the conciliatory languages recognized respectively by \(\mathcal {A}_{D_{2}(\mathbf {\Pi }^{1}_{1})}\) and \(\mathcal {A}_{\check{D_{2}}(\mathbf {\Pi }^{1}_{1})}\).
For \(M \subseteq \mathcal {T}^{\le \omega }_{\varSigma }\), we denote by \((D_{2}(\mathbf {\Pi }^{1}_{1}), M)\) the action of \(L(\mathcal {A}_{D_{2}(\mathbf {\Pi }^{1}_{1})})\) on \(M\). Observe that this operation is highly non-Borel, since if we apply it to a \(\mathbf {\varSigma }^{0}_{1}\)-complete conciliatory language, the resulting language will be complete for the pointclass of all the countable unions of \(D_{2}(\mathbf {\Pi }^{1}_{1})\) languages. The operation \((D_{2}(\mathbf {\Pi }^{1}_{1}), \cdot )\) behaves well with respect to \(\le _c\).
Theorem 1
Let \(M,M' \subseteq \mathcal {T}^{\le \omega }_{\varSigma }\). If \(M \le _cM'\), then
-
1.
\( (D_{2}(\mathbf {\Pi }^{1}_{1}), M)^{\complement } \equiv _{c} (D_{2}(\mathbf {\Pi }^{1}_{1}), M^{\complement })\);
-
2.
\( (D_{2}(\mathbf {\Pi }^{1}_{1}), M) \le _c(D_{2}(\mathbf {\Pi }^{1}_{1}), M') \).
A winning strategy for \(\mathrm {I}\) in \(C(M ,M')\) can also be “remote controlled” to a winning strategy for \(\mathrm {I}\) in \( C((D_{2}(\mathbf {\Pi }^{1}_{1}), M),(D_{2}(\mathbf {\Pi }^{1}_{1}), M'))\), so that the following holds.
Corollary 3
Let \(M\) and \(M'\) be conciliatory languages such that \(M <_{c}M'\). Then
The operation \((D_{2}(\mathbf {\Pi }^{1}_{1}), \cdot )\) is much stronger than \((\mathbf {\Pi }^{0}_{1},\cdot )\), and is in fact a fixed point of it.
Proposition 2
Let \(M\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\). Then
Let \(\mathcal {A}\) be an automaton that recognizes \(M\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\). Then the conciliatory tree language \((D_{2}(\mathbf {\Pi }^{1}_{1}),M)\) is recognized by the automaton  defined from \(\mathcal {A}\) by replacing each state of \(\mathcal {A}\) by a “gadget”, as depicted in Fig. 7. As in the pseudo-exponentiation case, by replacing a state by the gadget we mean that all transitions ending in this state should now end in the initial state of the gadget, and that all the transitions starting from this state should now start from the final state of the gadget. Notice that if \(M\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) is of index \([0,2]\), then \((D_{2}(\mathbf {\Pi }^{1}_{1}),M)\) is also of index \([0,2]\), and that \(W_{[0,2]}\) is a fixed point of this operation. In particular the game language \(W_{[0,2]}\) is above all the differences of coanalytic sets, which is a strengthening of a result obtained by Finkel and Simonnet [6].
defined from \(\mathcal {A}\) by replacing each state of \(\mathcal {A}\) by a “gadget”, as depicted in Fig. 7. As in the pseudo-exponentiation case, by replacing a state by the gadget we mean that all transitions ending in this state should now end in the initial state of the gadget, and that all the transitions starting from this state should now start from the final state of the gadget. Notice that if \(M\subseteq \mathcal {T}^{\le \omega }_{\varSigma }\) is of index \([0,2]\), then \((D_{2}(\mathbf {\Pi }^{1}_{1}),M)\) is also of index \([0,2]\), and that \(W_{[0,2]}\) is a fixed point of this operation. In particular the game language \(W_{[0,2]}\) is above all the differences of coanalytic sets, which is a strengthening of a result obtained by Finkel and Simonnet [6].
5 A Fragment of the Wadge Hierarchy
Let \(\varphi _{2}(0)\) denote the first fixed pointFootnote 7 of the ordinal epsilon function, namely the one that enumerates the fixed points of the exponentiation of base \(\omega \):

Finally: \(\varphi _{2}(0)=\sup _{n<\omega } \overbrace{\varepsilon _{\ddots _{\varepsilon _0}}}^{n} ~. \)
We recall that every ordinal \(\alpha >0\) admits a unique Cantor normal form of base \(\omega ^{\omega }\) (CNF) which is an expression of the form \(\alpha ={\left( \omega ^{\omega }\right) }^{\alpha _k}\cdot \nu _k +\cdots + {\left( \omega ^{\omega }\right) }^{\alpha _0}\cdot \nu _0\) where \(k<\omega \), \(0<\nu _i<\omega ^\omega \) for any \(i\le k\), and \(\alpha _0<\cdots <\alpha _k<\alpha \).
For every ordinal \(0<\alpha <\varphi _{2}(0)\), we inductively define a pair of automata  whose languages are incomparable through the conciliatory ordering. If the CNF of \(\alpha \) is \(\alpha ={\left( \omega ^{\omega }\right) }^{\alpha _k}\cdot \nu _k +\cdots + {\left( \omega ^{\omega }\right) }^{\alpha _0}\cdot \nu _0\) we set
whose languages are incomparable through the conciliatory ordering. If the CNF of \(\alpha \) is \(\alpha ={\left( \omega ^{\omega }\right) }^{\alpha _k}\cdot \nu _k +\cdots + {\left( \omega ^{\omega }\right) }^{\alpha _0}\cdot \nu _0\) we set

where  and
and  are respectively
are respectively
-
 and
and  if \(\alpha _i=0\);
if \(\alpha _i=0\); -
 and
and  if \({\alpha _i}<{\left( \omega ^{\omega }\right) }^{\alpha _i}\);
if \({\alpha _i}<{\left( \omega ^{\omega }\right) }^{\alpha _i}\); -
 and
and  if \({\alpha _i}={\left( \omega ^{\omega }\right) }^{\alpha _i}\) holdsFootnote 8 and \(\alpha _i=\varepsilon _\beta \) for some \(\beta <\alpha _i\).
if \({\alpha _i}={\left( \omega ^{\omega }\right) }^{\alpha _i}\) holdsFootnote 8 and \(\alpha _i=\varepsilon _\beta \) for some \(\beta <\alpha _i\).
Lemma 4
For \(0<\alpha <\beta <\varphi _{2}(0)\), we have
-
1.
 and
and  .
. -
2.
 ;
;  ;
;  and
and  .
.
Applying the embedding \(L \mapsto L^{b}\), we have thus generated a family  of parity tree automata of index \([0,2]\) that respects the strict Wadge ordering: \(\alpha <\beta \) if and only if
of parity tree automata of index \([0,2]\) that respects the strict Wadge ordering: \(\alpha <\beta \) if and only if  . Hence the main result follows.
. Hence the main result follows.
Theorem 2
There exists a family  of parity tree automata of index \([0,2]\) such that
of parity tree automata of index \([0,2]\) such that
-
1.
they recognize languages of full trees over the alphabet \(\{a,b,c\}\);
-
2.
\(\alpha <\beta \) holds if and only if
 holds as well.
holds as well.
Let  be an automaton of index \([0,2]\) over the alphabet \(\{a,b,c\}\) that recognizes a language equivalent to \(W_{[0,2]}\). We formulate the following conjecture.
be an automaton of index \([0,2]\) over the alphabet \(\{a,b,c\}\) that recognizes a language equivalent to \(W_{[0,2]}\). We formulate the following conjecture.
Conjecture
Let \(L\) be a regular non-self-dual full language of index \([0,2]\). Then either \(L \equiv _{W}W_{[0,2]}\), or there exists  such that
such that  or
or  .
.
6 Conclusion
In this paper, we have produced a very long chain of parity tree automata of index \([0,2]\) but of different Wadge degrees. Its length is \(\varphi _{2}(0)+1\), where \(\varphi _{2}(0)\) is the first fixed point of the ordinal function that itself enumerates all fixed points of the ordinal exponentiation \(x\mapsto \omega ^{x}\). We conjecture that every regular non-self-dual language of index \([0,2]\) is, up to Wadge equivalence, recognized by an automaton in  . Since degrees of self-dual languages of index \([0,2]\) are always immediately above and below two non-self-dual degrees of languages of index \([0,2]\), this conjecture would imply that the height of the Wadge hierarchy of regular languages of index \([0,2]\) is exactly \(\varphi _{2}(0)+1\).
. Since degrees of self-dual languages of index \([0,2]\) are always immediately above and below two non-self-dual degrees of languages of index \([0,2]\), this conjecture would imply that the height of the Wadge hierarchy of regular languages of index \([0,2]\) is exactly \(\varphi _{2}(0)+1\).
The whole construction is effective, meaning that the mapping  ) is recursive. It also means that, for any \(0< \alpha <\beta < \varphi _{2}(0)\,+\,1\), the relation
) is recursive. It also means that, for any \(0< \alpha <\beta < \varphi _{2}(0)\,+\,1\), the relation  which stipulates that there exist two strategies – one that is winning for player \(\mathrm {II}\) in the game
which stipulates that there exist two strategies – one that is winning for player \(\mathrm {II}\) in the game  and another one that is winning for \(\mathrm {I}\) in the game
and another one that is winning for \(\mathrm {I}\) in the game  – can be established by recursively providing such strategies. However, we did not consider any decidability issue. It thus remains open whether one can decide, given any automaton \(\mathcal {B}\) and any ordinal \(0< \alpha < \varphi _{2}(0)+1\), whether
– can be established by recursively providing such strategies. However, we did not consider any decidability issue. It thus remains open whether one can decide, given any automaton \(\mathcal {B}\) and any ordinal \(0< \alpha < \varphi _{2}(0)+1\), whether  holds or not.
holds or not.
Notes
- 1.
We emphasize that this is done without any determinacy principle. In particular, we do not require \(\mathbf {\Delta }^{1}_{2}\)-determinacy.
- 2.
Not to be mistaken with an \(\varepsilon \)-move.
- 3.
A pointclass is a collections of subsets of a topological space that is closed under continuous preimages.
- 4.
This is in general stronger than the usual \(A<_{W}B\) if and only if \(A\le _{W}B\) and \(B\not \le _{W}A\), but the two definitions coincide when the classes considered are determined.
- 5.
A player in charge of
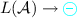 in a conciliatory game is like a player in charge of \(L(\mathcal {A})\), but with the extra possibility at any moment of the play to reach a definitively rejecting position.
in a conciliatory game is like a player in charge of \(L(\mathcal {A})\), but with the extra possibility at any moment of the play to reach a definitively rejecting position. - 6.
\( \varepsilon = {\left\{ \begin{array}{ll} -1 &{}\text { if } d_{c}(L)<\omega ; \\ 0 &{}\text { if } d_{c}(L) = \beta + n \text { and } {{\mathrm{cof}}}(\beta ) = \omega _{1}; \\ 1 &{}\text { if } d_{c}(L) = \beta + n \text { and } {{\mathrm{cof}}}(\beta ) = \omega . \end{array}\right. } \).
- 7.
Another way to characterise \(\varphi _{2}(0)\) is to remember that an ordinal is the set of its predecessors and notice that a nonzero ordinal is of the form respectively \(\omega ^\alpha \) iff it is closed under addition and \(\varepsilon _\alpha \) iff it is closed under \(x\longmapsto \omega ^x\). Then \(\varphi _{2}(0)\) is the first non null ordinal closed under \(x\longmapsto \varepsilon _x\) as well as \(x\longmapsto \omega ^x\) and \(x,y\longmapsto x+y\).
- 8.
Notice that we have \({\alpha _i}={\left( \omega ^{\omega }\right) }^{\alpha _i}\iff {\alpha _i}={\omega ^{\alpha _i}}\).
References
Andretta, A., Louveau, A.: Wadge degrees and pointclasses. In: Kechris, A.S., Löwe, B., Steel, J.R. (eds.) Wadge Degrees and Projective Ordinals: The Cabal Seminar, vol. II, pp. 3–23. Cambridge University Press, Cambridge (2012)
Arnold, A., Duparc, J., Murlak, F., Niwiński, D.: On the topological complexity of tree languages. Logic Automata: Hist. Perspect. 2, 9–29 (2007)
Arnold, A., Niwiński, D.: Rudiments of \(\mu \)-Calculus. Studies in Logic and the Foundations of Mathematics. Elseiver, Amsterdam (2001)
Duparc, J.: Wadge hierarchy and Veblen hierarchy, part I: Borel sets of finite rank. J. Symbolic Logic 66(1), 56–86 (2001)
Duparc, J., Murlak, F.: On the topological complexity of weakly recognizable tree languages. In: Csuhaj-Varjú, E., Ésik, Z. (eds.) FCT 2007. LNCS, vol. 4639, pp. 261–273. Springer, Heidelberg (2007)
Finkel, O., Simonnet, P.: On recognizable tree languages beyond the Borel hierarchy. Fundam. Informaticae 95(2–3), 287–303 (2009)
Rabin, M.O.: Decidability of second-order theories and automata on infinite trees. Trans. AMS 141, 1–23 (1969)
Van Wesep, R.: Wadge degrees and descriptive set theory. In: Kechris, A.S., Moschovakis, Y.N. (eds.) Cabal Seminar 76–77, pp. 151–170. Springer, Heidelberg (1978)
Wadge, W.W.: Reducibility and determinateness on the Baire space. Ph.D. thesis, University of California, Berkeley (1984)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Duparc, J., Fournier, K. (2015). A Tentative Approach for the Wadge-Wagner Hierarchy of Regular Tree Languages of Index [0, 2]. In: Shallit, J., Okhotin, A. (eds) Descriptional Complexity of Formal Systems. DCFS 2015. Lecture Notes in Computer Science(), vol 9118. Springer, Cham. https://doi.org/10.1007/978-3-319-19225-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-19225-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19224-6
Online ISBN: 978-3-319-19225-3
eBook Packages: Computer ScienceComputer Science (R0)






 , where
, where  denotes any automaton that rejects all trees.
denotes any automaton that rejects all trees.
 that recognizes
that recognizes 




 and
and  if
if  and
and  if
if  and
and  if
if  and
and  .
. ;
;  ;
;  and
and  .
. holds as well.
holds as well.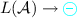 in a conciliatory game is like a player in charge of
in a conciliatory game is like a player in charge of