Metaheuristics for the Two-Dimensional Container Pre-Marshalling Problem

Abstract

We introduce a new problem arising in small and medium-sized container terminals: the Two-Dimensional Pre-Marshalling Problem (2D-PMP). It is an extension of the well-studied Pre-Marshalling Problem (PMP) that is crucial in container storage. The 2D-PMP is particularly challenging due to its complex side constraints that are challenging to express and difficult to consider with standard techniques for the PMP. We present three different heuristic approaches for the 2D-PMP. First, we adapt an existing construction heuristic that was designed for the classical PMP. We then apply this heuristic within two metaheuristics: a Pilot method and a Max-Min Ant System that incorporates a special pheromone model. In our empirical evaluation we observe that the Max-Min Ant System outperforms the other approaches by yielding better solutions in almost all cases.

1 Introduction

Containers are an essential component of today’s shipping industry. They are standardized to facilitate shipment and storage. Container shipment typically proceeds in chains of different transport modes, such as trains, ships or trucks. Container terminals are crucial to the overall shipment process since they act as hubs between the different transport modes. They deal with container exchange between vessels, and container storage until the appropriate vessels arrive.

Container storage planning is a key factor in container terminal organization and affects all other operations of the terminal. It is concerned with storing containers in such a way that they can be quickly retrieved when they are due for further shipment. Containers are stored in so-called container bays which are rows of adjacent container stacks. When a container is due for shipment it is typically removed from its bay by a gantry crane that can access the topmost containers of each stack. Due containers may sometimes be blocked by other containers that are stacked upon them. In this case, the blocking containers have to be relocated to access the due containers, which increases the loading time. This can cause severe delays for vessel loading and vessel departures, resulting in displeased terminal clients and ultimately additional costs. Therefore, container terminals rearrange (pre-marshal) container bays to assure that each container is reachable when it is due. The Pre-Marshalling Problem (PMP) is concerned with finding a sequence of container relocations of minimal length, such that in the resulting bay no container is blocked when removed according to its due-time.

In this paper we introduce a new variant of the PMP, the Two-Dimensional Pre-Marshalling Problem (2D-PMP), which occurs in smaller and medium-sized container terminals. Those terminals do not use gantry cranes to load vessels but so-called reach stackers. Reach stackers are powerful forklifts that can carry fully loaded containers, however, most conventional reach stackers can only access the leftmost and rightmost stacks of a container bay. This means that due containers can be blocked by containers stacked next to them, in addition to containers stacked upon them. Thus, a new 2-dimensional restriction on how containers may be stacked such that they can be removed according to their due-times without having to relocate blocking containers needs to be considered. Our use-case is based on the Ennshafen container terminal¹ in Enns, Austria. Another example of a smaller to medium-sized container terminal is the Frihamnen container terminal in Stockholm, Sweden. Space is an issue for them since they are located in the city center, so agile vehicles like the reach stacker are required to perform most of the work.

This work is based on a master thesis [1] which can be referred to for detailed algorithm explanations, further implementation details and more elaborate results.

Related Work

The classical PMP is known to be NP-hard [2] and is well-studied [3]. The 2D-PMP is a novel problem for which, to the best of our knowledge, no solution approach has yet been published. In the following, we therefore give a chronological overview of the most prominent methods for the PMP.

Lee and Hsu [4] present a MIP model in form of a multi-commodity flow formulation in which nodes represent slots in the container bay, and arcs connect slots. Thus, container moves are represented with flows, and constraints assure that the moves are valid. The number of moves is restricted by an upper bound, and the objective is to find a flow that yields a desirable bay in a minimal number of moves. This formulation grows substantially in the number of moves and therefore has difficulties to scale.

Caserta and Voß [5] propose a corridor-method based approach for solving the PMP. Given an initial solution (constructed by a method similar to the GRASP heuristic), the approach builds a corridor around the incumbent solution and performs low-level decisions using a combination of greedy heuristics and a roulette-wheel approach. In their experiments, the authors obtained new upper bounds for existing benchmarks with their approach.

Lee and Chao [6] introduce a neighbourhood search method that improves an initial feasible solution by applying different local search heuristics and an integer program that possibly reduces the length of the move sequence in the incumbent solution, yielding the same final bay configuration.

Exposito et al. [7] propose a “lowest priority first” construction heuristic, see Sect. 3, as well as an instance generator for the PMP. The heuristic aims at placing containers at positions that seem most suitable, starting with the container that will be removed last.

Bortfeldt and Forster [8] present a tree-search heuristic for the PMP, where the tree depth is restricted by an upper bound. The tree search incorporates a classification and ordering of the possible moves at each configuration, which drives the search towards promising directions. This method is competitive with the approaches from [5, 6].

Prandtstetter [9] proposes a dynamic programming approach for the PMP where states represent the container bay and are extended by container moves. This method is quite successful since symmetric and dominated states (with a weaker lower bound) are easily detected and discarded.

Rendl and Prandtstetter [10] introduce a constraint programming model for the PMP where decision variables represent the container bay state and moves are set exclusively by the search strategy, which applies the heuristic from [8].

Tierney et al. [11] present a novel solution technique for solving pre-marshalling problems to optimality using the A* and IDA* algorithms. Both algorithms perform a path-based search guided by a cost estimation heuristic. Additionally, the search is directed by combining branching rules, symmetry breaking and strong lower bounds. Branching rules are used to prevent move reversal, unrelated and transitive moves, and empty stack symmetry.

2 The Two-Dimensional Pre-Marshalling Problem

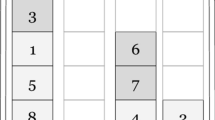
Pre-marshalling problems arise in container terminals where containers are stored in stacks that are arranged in container bays. A container bay consists of a number of adjacent stacks that may not exceed a maximum height; see Fig. 1 for a sample bay with four stacks. Each container is assigned a priority value that indicates when the container is due to be removed from the bay. The smaller the priority value, the sooner the container will be removed from the container bay.

The priority of a container is often not known at its arrival in the bay, therefore containers are frequently stacked more or less arbitrarily. As a consequence, due containers would often be blocked by other containers that are due at a later time. In the container bay in the left of Fig. 1, for example, the shaded containers are blocked since containers with higher priority values are placed upon them.

Fig. 1.

A container bay with four stacks where the numbers represent the priority values of the containers. Shaded containers are blocked for the gantry crane. The left figure shows the bay before pre-marshalling, the right thereafter.

The classical Pre-marshalling Problem (PMP) is concerned with relocating containers in a bay most economically in such a way that thereafter all containers can be immediately retrieved from the bay in the order given by the priority values. More specifically, the PMP seeks a minimal sequence of container moves that yields a container bay without blocked containers.

In large container terminals all container movements are performed exclusively by gantry cranes that can access the topmost container of each stack. In small and medium-sized terminals gantry cranes are only used to move containers within a bay, while reach stackers remove containers to load vessels.

Reach stackers are forklifts that can carry one container at a time, but their access is restricted to the top containers of the leftmost and rightmost stacks of a bay. This is a significant restriction, since containers can be blocked vertically (by containers in the same stack) but also horizontally (by containers in neighbouring stacks). The classical PMP only considers vertical blocking, and therefore does not sufficiently improve the container bay configuration in the scenario with reach stackers. For instance, Fig. 2(left) illustrates that the pre-marshalled configuration from Fig. 1(right) still has a blocked container when considering reach stackers for removal.

Therefore, we introduce the Two-Dimensional Pre-Marshalling Problem (2D-PMP) that considers blocking from two dimensions, i.e., vertically and horizontally.

Fig. 2.

Left: The classically pre-marshalled container bay from Fig. 1, now serviced by reach stackers. The shaded container is blocked horizontally. Right: A configuration where all containers can directly be removed by reach stackers.

2.1 Formal Definition of the 2D-PMP

The 2D-PMP considers a container bay with S stacks holding a set of containers ${\mathcal {C}}$. Stacks may not exceed a maximum height H. We denote the set of all stacks as ${\mathcal {S}}$ and the set of all tiers as ${\mathcal {T}}$. Each container $c \in {\mathcal {C}}$ is referred to by its priority value, i.e., $c\in \mathbb {N}$, which we assume without loss of generality to be unique; i.e., a complete ordering is specified for the containers.

We are given an initial bay configuration ${\mathcal {B}}$, where ${\mathcal {B}} _{s,t}$ is the container in the t-th tier in the s-th stack, with $(s,t) \in {\mathcal {S}} \times {\mathcal {T}}$ and write, ${\mathcal {B}} _{s,t} = 0$ if slot ${\mathcal {B}} _{s,t}$ is empty. The bay can be altered by performing moves: the topmost container from a (non-empty) stack can be moved to the top of another stack whose height is less than H. We denote such a container move from the top of stack i to the top of stack j by $m={\left( i,j\right) }$, where $i,j\in \{1,\ldots ,S\}$.

A container c that is located at ${\mathcal {B}} _{s,t}$ is called vertically blocked, if there exists another container $c'$ at ${\mathcal {B}} _{s,t'}$ with $t' > t$ (container $c'$ is placed above c) and $c' > c$. A stack s is called v-perfect, if no container in stack s is vertically blocked. A container c that is located at ${\mathcal {B}} _{s,t}$ is called horizontally blocked, if there exist two containers $c'$ and $c''$ where $c'$ is located at ${\mathcal {B}} _{s',t'}$ and $c''$ at ${\mathcal {B}} _{s'',t''}$ with $s' < s$ (stack $s'$ is left of stack s) and $s'' > s$ (stack $s''$ is right of stack s) and $c < c'$ and $c < c''$ (container c has the smallest priority value of the three containers). A stack s in which no container is horizontally blocked, is called h-perfect. The aim of the 2D-PMP is to obtain with minimum effort a bay configuration in which all stacks are v-perfect as well has h-perfect.

A solution is thus a sequence of container moves $\sigma = \{m_1, m_2, \dots , m_k\}$ that makes the initial bay configuration v- and h-perfect, and the 2D-PMP seeks an optimal solution having minimum length k.

3 Lowest Priority First Heuristic (LPFH)

The Lowest Priority First Heuristic (LPFH) has been proposed in [7] The general idea is to distinguish between well-located containers that may remain at their current position and non-located containers that are moved to obtain an unblocked configuration.

After classifying each container as well-located or non-located, the LPFH iteratively performs the following three steps until all containers are well-located:

• 1. select the non-located container c with highest priority value,

• 2. select a destination stack s for c so that c becomes well-located,

• 3. and compute feasible moves to relocate c to s and perform them.

3.1 The 2D Lowest Priority First Heuristic (2D-LPFH)

We extend the LPFH for the 2D-PMP into a new heuristic, 2D-LPFH, by applying two main changes. First, we adapt the notion of well-located and non-located containers, and second, we adapt the destination stack selection. The complete 2D-LPFH algorithm for the 2D-PMP is outlined in Algorithm 1. In the following, we highlight the differences to the classical LPFH.

Container Location. A container is called well-located in the 2D-PMP, if it is neither vertically nor horizontally blocked, and if it is located in one of the stacks foreseen for its priority (see below). A container is called non-located in the 2D-PMP, if at least one of the well-located criteria is violated.

Destination Stack Selection. The destination stack selection consists of three main steps: First, adequate stacks are identified that are as second step ordered according to the number of moves that are necessary to move the selected container to the respective stack. Third, the destination stack is randomly selected upon the best $\lambda _2$ adequate stacks, where $\lambda _2$ is an appropriately chosen strategy parameter. In the 2D-LPFH, containers with higher priority value are usually best placed in a central stack, while containers with low priority values are usually best placed in one of the outermost stacks. This way it is less likely that they are horizontally blocking or blocked by other containers. We incorporate this intuition in the stack selection, where we denote the set of adequate stacks ${\mathcal {A}} _{c}$ for container c: First, we calculate the average number of containers per stack as $cps=|\mathcal {C}|/S$. Second, we determine the first preferred stack as $s_1=\lfloor c/(2\cdot cps)\rfloor$. Third, we add the “mirror” stack $s_2=S-s_1$ as the second preferred stack $(if s_2\not =s_1)$, i.e., if the first preferred stack $s_1$ is closer to the left edge of the bay, then the second preferred stack $s_2$ will be closer to the right edge of the bay and have an equal number of stacks between itself and the right edge as the first preferred stack $s_1$ and the left edge. In case our configuration has an odd number of stacks, the middle stack does not have a second preferred stack. Fourth, in case $s_1$ and $s_2$ are not the outermost stacks, we allow some flexibility by adding the neighbouring stacks that are closer to the outer border to the set of adequate stack as $s_{1'}=s_1-1$ and $s_{2'}=s_2+1$. Finally, our set of adequate stacks is $\mathcal {R}_{c}=\{s_{1'},s_1,s_2,s_{2'}\}$. This calculation assumes unique priority values. When moving the selected container to the destination stack we have to enable the move by removing all containers placed on top of the selected container and all containers placed on top of the designated slot in the destination stack. These containers are called interfering containers and they are moved to temporary stacks; any stack with free slots except the source and destination stacks.

In case the source and destination stack are the only stacks with free slots and there is at least one interfering container, the algorithm is blocked and can not continue. In such cases it is recommended to restart the algorithm because it might perform a different sequence of moves due to it’s stochastic nature.

Compound Moves. In each iteration, the 2D-LPFH returns a compound move ${\mathcal {K}} = \{m_1,\dots ,m_k\}, k \ge 1$, i.e., a sequence of moves, corresponding to all the individual moves necessary to relocate a non-located container to a better location. This especially needs to be taken into account when applying the heuristic within a metaheuristic. Applying only a subsequence $\hat{{\mathcal {K}}} \in {\mathcal {K}}$ would in general result in a completely different and usually unintended and worse behaviour. For instance, $\hat{{\mathcal {K}}}$ might easily lead to a state having a higher objective value than when applying the complete ${\mathcal {K}}$. Therefore, when using the 2D-LPFH within a metaheuristic, we always consider only complete compound moves ${\mathcal {K}}$. However, this does not affect the behaviour of our metaheuristic algorithms as each regular or compound move can be viewed as a changeset applied to our current bay; the exact actions or their count are irrelevant to the metaheuristic.

4 Pilot Method

The Pilot method [12] is a meta-heuristic that applies a simpler construction heuristic H as a lookahead subheuristic to guide a master construction process towards a more promising solution. Starting from an initially “empty” solution $\theta$, the subheuristic H constructs n so-called pilot solutions $\theta _i,\ \forall i=1,\ldots ,n$, which are partial solutions built from up to k greedy construction steps. Each pilot solution $\theta _i$ is evaluated by a quality estimation function f that is able to evaluate partial solutions. The idea is that these quality estimates provide a better guidance for the master construction process than a simple greedy criterion. A most promising partial solution $\theta _i$ with the best quality estimation is then chosen and its first construction step adopted by the master procedure, i.e., $\theta$ is extended by the corresponding step. Then, the same construction process with the help of the subheuristic is repeated from the next step onward until a complete solution is obtained.

We use the Pilot method to solve the 2D-PMP by applying different construction methods operating on partial solutions. Recall that a solution to the 2D-PMP is a sequence of (compound) moves, therefore, a pilot solution $\theta _i$ is a sequence of (compound) moves $\theta _i = \{m_1, \dots , m_j\}$ with $j \ge 1 \le k$.

Evaluation Function. Given a bay configuration ${\mathcal {B}} _{\theta _i}$ that has been obtained by applying the pilot solution $\theta _i$ on the initial configuration ${\mathcal {B}}$, the evaluation function $f({\mathcal {B}} _{\theta _i})$ returns an estimate of the number of (compound) moves that are necessary to get an unblocked bay configuration. We define f as

$$\begin{aligned} f({\mathcal {B}} _{\theta _i}) = b_v({\mathcal {B}} _{\theta _i}) + \frac{1}{2} b_h({\mathcal {B}} _{\theta _i}) + b_t({\mathcal {B}} _{\theta _i}) \end{aligned}$$

(1)

where $b_v({\mathcal {B}} _{\theta _i})$ and $b_h({\mathcal {B}} _{\theta _i})$ represent the number of containers in ${\mathcal {B}} _{\theta _i}$ that are blocked vertically and horizontally, respectively, and $b_t({\mathcal {B}} _{\theta _i})$ is the cardinality of the set of containers placed upon all vertically blocked containers (excluding blocked containers).

Subheuristic. The subheuristic H is a heuristic that extends a current partial master solution $\theta$, by a (compound) move $m \in {\mathcal {M}} _{{\mathcal {B}} _{\theta }}$ where ${\mathcal {M}} _{{\mathcal {B}} _{\theta }}$ is the set of all legal (compound) moves for the current container bay ${\mathcal {B}} _{\theta }$. Therefore, applying k construction steps corresponds to appending k legal (compound) moves to $\theta$. We apply 2D-LPFH as a subheuristic.

5 An Ant Colony Optimization Approach

We developed a $\mathcal {MAX}$-$\mathcal {MIN}$ Ant System (MMAS) [13] to tackle the 2D-PMP. MMAS is a well known variant of Ant Colony Optimization (ACO) that strongly favours so-far best solutions. It is characterized by four features: First, only the best ant may update pheromone trails. Second, pheromone values have strict upper and lower bounds $\tau _{\min }$ and $\tau _{\max }$, respectively. Third, all pheromone values are initiated with $\tau _{\max }$ and the evaporation rate $\rho$ is kept low. Fourth, the algorithm performs restarts after finding no improvement for a certain number of iterations, to tackle stagnations.

For solving the 2D-PMP with MMAS, we consider the problem a path-construction problem, where nodes represent container bay states, and edges represent container movements. Thus, we search for a (shortest) path from the initial node to a node that is a valid final state.

We outline the main steps of the MMAS in Algorithm 2. In each iteration the algorithm constructs n ant solutions (line 3) that are subsequently improved using a simple local search procedure that is discussed in more detail in Sect. 5.3. The best constructed solution $\sigma$ is selected in line 11 and the global best solution $\sigma ^*$ possibly updated in line 13. In case the number of consecutive iterations without improvement exceeds the threshold $i_{\max }$ (line 17), the pheromone values are reinitialized (line 18). Finally the pheromone values are updated in lines 22 to 26. The decision whether to use the iteration best or global best solution is based on the probability $p_{\sigma *}$. These steps are repeated until either a maximum number of iterations or a time limit has been reached.

In the following sections we give a more detailed description of the different components of our approach. Section 5.1 outlines the pheromone model, Sect. 5.2 discusses the ant construction algorithm and Sect. 5.3 the local search procedure.

5.1 Pheromone Model

We studied different pheromone models in the design of the MMAS. First, we considered a state-based pheromone model where each container bay state ${\mathcal {B}}$ is associated with a pheromone value $\tau _{\mathcal {B}}$. However, since a state can be reached by different (compound) moves that are not taken into account by the pheromone model, this model gives little guidance to the agents/ants. We assume that this is the reason why the state-based model performed poorly in our initial experiments.

We thus extended that model to the move-based pheromone model. In it, we associate a pheromone value $\tau _{({\mathcal {B}},m)}$ to each state-move pair $({\mathcal {B}},m)$. This way the pheromone values direct the ants in a more traditional way into following promising (compound) moves, given the current container bay state. A crucial aspect hereby was to dynamically create pheromone values on the fly and efficiently maintain them in a hash table, as obviously we cannot store them all in a simple statically allocated matrix due to the state-space’s exponential size.

5.2 Ant Construction Algorithm

The ant construction algorithm is given in Algorithm 3. It takes three arguments: an initial state, an evaluation function and a heuristic function. In each iteration, it first determines all possible (compound) moves for the current state ${\mathcal {B}}$ (line 4) by querying the given heuristic algorithm h (e.g. 2D-LPFH). The heuristic algorithm returns a set of all possible (compound) moves ${\mathcal {M}}$ it can execute for the given state ${\mathcal {B}}$; i.e. the heuristic algorithm explores the whole search space for one step (one (compound) move) from the current state and returns all possibilities, allowing the ant construction heuristic to choose the next (compound) move. Then, for each possible (compound) move m, the probability $p_{{\mathcal {B}},m}$ of the ant applying (compound) move m to ${\mathcal {B}}$ is computed (line 9) by

$$\begin{aligned} p_{{\mathcal {B}},m} = \frac{[\tau _{{\mathcal {B}},m}]^\alpha [\eta _{{\mathcal {B}},m}]^\beta }{\sum _{l\in {\mathcal {M}} _{\mathcal {B}}} [\tau _{{\mathcal {B}},l}]^\alpha [\eta _{{\mathcal {B}},l}]^\beta }, \text {if } m \in {\mathcal {M}} _{\mathcal {B}}, \end{aligned}$$

(2)

where $\tau _{{\mathcal {B}},m}$ refers to the pheromone value of (compound) move m from state ${\mathcal {B}}$, $\alpha$ refers to the priority given to pheromone values, $\eta _{{\mathcal {B}},m}$ refers to the heuristic value of (compound) move m for state ${\mathcal {B}}$, and $\beta$ refers to the priority given to heuristic values. The heuristic value $\eta _{{\mathcal {B}},m}$ is acquired by evaluating the state ${\mathcal {B}} _{m}$ that is reached by applying (compound) move m to the current state ${\mathcal {B}}$. We then select one of the (compound) moves according to their probability and a random factor (line 11-19). This procedure is repeated until a complete solution has been constructed or a maximum number of moves has been reached (line 3).

In addition, we check if the final state can be directly reached by a (compound) move and in this case immediately select it without calculating probabilities (line 5). All ant solutions can be constructed in parallel, since the only shared resource are the read-only pheromone values.

5.3 Improvement Heuristic

We use an improvement heuristic that, given a solution $\sigma$, tries to find “shortcuts” in the solution. More specifically, the algorithm tries to detect non-consecutive states ${\mathcal {B}} _1$ and ${\mathcal {B}} _2$ that are connected with moves $\{m_1,\ldots ,m_k\} \in \sigma , k \ge 2$, which can be connected by a single move $m'$. In this case, the sequence $\{m_1,\ldots ,m_k\}, k \ge 2$ can be replaced by $m'$ in the solution and thus shortens the solution $\sigma$. Figure 3 illustrates such a shortcut between states ${\mathcal {B}} _2$ and ${\mathcal {B}} _5$, eliminating moves $m_2$, $m_3$ and $m_4$ and thus shortening the solution by two moves.

Fig. 3.

Finding a shortcut move $m'$ from ${\mathcal {B}} _2$ to ${\mathcal {B}} _5$ saving two moves.

The heuristic works as follows. For each move $m \in \sigma$ yielding bay state ${\mathcal {B}} _m$, two sets are computed: the set of states that are reachable (within one move) from ${\mathcal {B}} _m$, ${\mathcal {M}} _{\mathcal {B}}$, and the set of states that are visited in the solution after the successor of ${\mathcal {B}} _m$, denoted by ${\mathcal {M}} _\sigma$. If ${\mathcal {M}} _{\mathcal {B}} \cap {\mathcal {M}} _\sigma \ne \emptyset$, then a shortcut has been found, since the state(s) in ${\mathcal {M}} _{\mathcal {B}} \cap {\mathcal {M}} _\sigma$ can be reached by one move from ${\mathcal {B}} _m$. Therefore, we chose the state ${\mathcal {B}} '\in {\mathcal {M}} _{\mathcal {B}} \cap {\mathcal {M}} _\sigma$ with the largest number of moves from ${\mathcal {B}} _m$ and replace the moves between ${\mathcal {B}} _m$ and ${\mathcal {B}} '$ with move $m'$.

6 Experimental Evaluation

We perform experiments with the LPFH, the Pilot method and the MMAS. The experiments are all executed on the same machine in a sequential manner and each experiment was run on the same set of instances.

Problem Instances. We obtained problem instances from the PMP instance generator provided in [7]. Our instances have $s=\{4,6,8,10,12,14\}$ stacks with height $H=4$ and occupancy rates $q=\{50\,\%,75\,\%\}$ (i.e., fill level of the container bay). This yields 11 instance categories, because we leave out instances with $s=4$ and $q=75\,\%$ because they are too difficult to solve. Containers have unique priorities and are randomly positioned within the given bay. The instances are available online².

Algorithm Parameter Settings. The 2D-LPFH uses $\lambda _{2,3}=2$ (see [7]), after having applied parameter tuning tests with values $\lambda _2,\lambda _3 \in \{1,2,3,5,10\}$: restricting the search space ($\lambda _{2,3} = 1$) does not allow the algorithm enough flexibility to find good solutions, but loosening the search space too much ($\lambda _{2,3} \in \{5,10\}$) does not yield good results within a short time. The semi-greedy approach ($\lambda _{2,3}=2$) performs best. However, if given more time (5 min), the $\lambda _{2,3} \in \{5,10\}$ results improved significantly, but still remained inferior to the semi-greedy approach. The Pilot method experiments were run with 2D-LPFH as the subheuristic and $k \in \{2,3,4,5,6,7\}$ construction steps for each heuristic. Test have shown that $k \in \{5,6,7\}$ always performs significantly better than $k \in \{2,3,4\}$ with only slight differences among $k \in \{5,6,7\}$. After careful review of all results, $k = 7$ is chosen as the representing result since it yielded slightly better results than $k = 5$, but did not affect run time significantly. Finally, the MMAS uses 2D-LPFH to calculate the heuristic values during construction and the following parameters: $n=8$, $\alpha =1$, $\beta =2$, $\rho =0.02$, $i_{\max }=75$ and $p_{\sigma *}=0.1$. All experiments use the same evaluation function stated in Eq. (1), and after each algorithm has finished, the improvement heuristic (see Sect. 5.3) is applied. All of the mentioned parameter values were determined in preliminary tests or are based on recommended values from [7] and [14]. For more details on the parameter selection, see [1].

Experimental Setup. The experiments are carried out on a machine with four Intel Xeon E5645 processors, each with six cores at 2.40 GHz, along with 200 GB of RAM. The underlying system is Ubuntu 13.04. with Java 1.7. Our implementation of MMAS runs the ant construction algorithms in parallel.

All experiments have a time limit of 5 min (wall clock time, the machine not otherwise utilized) or 500 moves. The ant construction algorithm has a different move limit of 250 moves since we do not want bad solutions appearing in the pheromone trails. As you will notice in the results section, 500 moves is a very generous move limit since we expect solutions with less than 100 moves for the biggest instances. All our experiments are of stochastic nature so we repeat them until the final solution is not improved a consecutive number of runs. The 2D-LPFH, Pilot method and MMAS had a no-improvement iteration number of 25, 25 and 5, respectively.

We perform experiments with the 2D-LPFH, Pilot method and MMAS. Due to space limitations we only present each approach with its best setup:

• 1. 2D-LPFH: a single-run of the 2D-LPFH with $\lambda _{2,3}=2$

• 2. Pilot: the Pilot method with 2D-LPFH as construction-heuristic and $k=7$ lookahead moves

• 3. 2D-LPFH 5-min: the 2D-LPFH run sequentially for the same time as the MMAS, returning the best found result; same configuration as the 2D-LPFH

• 4. MMAS: the Max-Min Ant System with $n=8, \alpha =1, \beta =2$ and the 2D-LPFH as the heuristic function.

Table 1. Objective values over 50 instances for each category, where “s” denotes the number of stacks and q the occupancy rate; all stacks have maximum height 4. “avg” denotes the average objective value and “std” the standard deviation over all solved instances in the category. “sol” is the number of instances solved per category.

6.1 Results

Table 1 shows the detailed results for all four approaches: the average objective value (number of moves) for each instance category, the standard deviation, and the number of solved instances. We first see that the MMAS mostly provides the best results, closely followed by the 2D-LPFH with a 5-minute runtime. The third best results come from the Pilot method, followed by the single-run 2D-LPFH. This is clearly illustrated in Fig. 4, where the average objective is shown for each solving approach for both occupancy rates, clearly demonstrating that the MMAS provides the best results.

Furthermore, we observe in Table 1 that all approaches managed to solve all $q=50\,\%$ instances. For the $q=75\,\%$ categories, we notice that the MMAS and extended run time 2D-LPFH solved almost the same number of instances with the extended run time 2D-LPFH in a slight lead. They are followed by the Pilot method and 2D-LPFH.

Fig. 4.

Average number of moves per category for best algorithm configurations split by occupancy rate. Values for $q=0.50$ are shown on the left and $q=0.75$ on the right.

Note that the Pilot method, as well as the single-run 2D-LPFH only take several milliseconds, while the MMAS and 2D-LPFH take 5 min to run, so we do expect the latter approaches to provide better results. Using only the average number of moves and number of solved instances, the MMAS and extended run time 2D-LPFH are the overall best performing test cases. We confirmed this conclusion using the Wilcoxon Paired Rank Sum test.

Due to space constraints only the most interesting results are included in this section. For further experimental results and analysis please refer to [1].

7 Conclusions

In this work, we presented a novel challenging problem: the two-dimensional pre-marshalling problem (2D-PMP). This problem is an extension of the well studied NP-hard pre-marshalling problem (PMP). The 2D-PMP occurs in small to medium-sized container terminals and is characterized by complex side constraints imposed by the reach stackers used for moving containers to ships. These side constraints make it difficult to apply existing approaches for the PMP to the 2D-PMP.

We first extended an existing PMP construction heuristic, the LPFH, to consider the additional constraints and came up with 2D-LPFH. For obtaining better solutions, we further integrated it in two metaheuristics: a Pilot method and a novel Max-Min Ant System (MMAS) approach. The MMAS approach yielded in our tests mostly the best solutions. Also, we observed that by using 2D-LPFH as a heuristic, the MMAS and Pilot method are able to solve instances that the 2D-LPFH is not capable of solving itself.

Applying a MMAS approach to this kind of problem is rather unconventional. In fact, for the classical PMP, no ACO-based approaches have been published so far. However, for the 2D-PMP that incorporates complex side constraints that are cumbersome to express, MMAS could be shown to be an amenable solving approach, since the specialized pheromone model can guide the ants effectively. This demonstrates how problems that are difficult to model can be solved effectively by a learning-based algorithm such as Ant Colony Optimisation.

For future work it appears interesting to study further variants and refinements of 2D-LPFH,’ alternative metaheuristics, as well as A$^*$ or IDA$^*$ search and constraint programming techniques for solving small 2D-PMP instances exactly. Possibly look into adapting work from [11].