Grain Growth and Microstructure Development

Abstract

The properties of a ceramics are determined by its chemical composition intrinsically and microstructure extrinsically. For ceramics with a given composition, microstructure means the overall feature, which reflects its grain size and morphology, grain size distribution, porosity, pore size and distribution, type and quality of grain boundaries, as well as the nature and distribution of second-phases, and so on. For most applications, especially optical transparency, microstructural control means to achieve full densification, narrow distribution of grain size, least contamination, and so on.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

The properties of a ceramics are determined by its chemical composition intrinsically and microstructure extrinsically. For ceramics with a given composition, microstructure means the overall feature, which reflects its grain size and morphology, grain size distribution, porosity, pore size and distribution, type and quality of grain boundaries, as well as the nature and distribution of second-phases, and so on. For most applications, especially optical transparency, microstructural control means to achieve full densification, narrow distribution of grain size, least contamination, and so on [1, 2]. The microstructure of a ceramics is directly related the quality of the green compact, which is dependent on the properties of the precursor powder, as well as the consolidation method used to form the green body. Therefore, the control of microstructure of ceramics is a systematic engineering. When all other conditions have been fixed, controlling microstructure during the sintering process becomes especially important. Densification is almost inevitably accompanied by the growth of both grains and pores, which is known as microstructure coarsening. Densification process has been discussed previously; this chapter focuses on coarsening process and the interrelationship between densification and coarsening, in terms of microstructural control.

Although various factors have their influence on microstructure of a ceramics, the effect of grain growth is the most pronounced. There are two types of grain growth: normal and abnormal grain growth (AGG). Normal grain growth (NGG) means that the increase in grain size follows a trend of expected magnification, while the grain shapes have no significant change. In contrast, AGG is characterized by the presence of a limited number of extremely large grains, which are formed at the expense of the smaller ones surrounding them. AGG is usually thought to have a destructive effect on microstructure of ceramics, unless it is a specific requirement. Theoretical and experimental results indicate that the key to control the microstructure or avoid the AGG is to decrease the grain growth rate, but increase the densification rate. Strategies to achieve this include homogeneous packing of fine particles with a narrow size distribution, doping with secondary phase particles, use of liquid-phase sintering, application of external pressure and employment of new sintering techniques, e.g., spark plasma sintering or SPS.

8.2 General Concepts

8.2.1 Features of Grain Growth

Grain growth is to mean the dynamic increase in average grain size of a given ceramic system, which usually takes place at high temperatures during calcining and sintering processes. It is understood that an increase in grain size should be at the expense of smaller grains that surround relatively large growing ones. In other words, the consequence of grain growth is the decrease in the total number of grains. Statistical data indicated that only one eighth of the grains could survive when the average grain size of the system doubles every time. Therefore, grain growth is also called coarsening.

8.2.2 Microscopic Features of Grain Growth

Ceramics consist of crystalline grains and noncrystalline or disordered grain boundaries, which are defined as the regions between adjacent grains. Figure 8.1 shows schematically a section across two adjacent grains [3]. In most ceramics, the thickness of the grain boundary is 0.5–1 nm. Grain growth takes place through the diffusion of atoms or ions over less than an interatomic distance from one side of the boundary to the other side. As a result, one grain grows at the expense of other smaller ones. Generally, the atoms migrate from the convex surface to the concave surface, because the chemical potential of the atoms at the convex surface is higher than that of the atoms at the concave surface, as discussed in previous chapters. Due to the flux, the boundary moves toward its center of curvature, as shown in Fig. 8.2 [4].

Fig. 8.1

Classic picture of a grain boundary and its migration. The boundary migrates from left to right as the atoms diffuse from the convex side of the boundary to the concave side. Reproduced with permission from [3]. Copyright © 2007, Springer

Fig. 8.2

Movement of the grain boundaries toward their center of curvature. Reproduced with permission from [4]. Copyright © 2003, CRC Press

8.2.3 Driving Force of Grain Growth

Because the atoms or ions in disordered grain boundaries have higher energy than those in the bulk of crystalline grains. A specific energy, known as grain-boundary energy, γ _gb, is usually used to characterize the grain boundaries. The decrease in the energy through the reduction of the total area of the grain boundaries is the driving force of grain growth. Therefore, grain growth is also accompanied by the reduction in volume fraction of grain boundaries.

8.2.4 Abnormal Grain Growth

As mentioned above, there are two types of grain growth experienced by ceramics: (i) normal grain growth and (ii) abnormal grain growth. AGG is also known as several other names, including exaggerated grain growth, discontinuous grain growth, or secondary crystallization. NGG is more like a simple magnification in average grain size, without significant change in grain size distribution, so that it is generally known as scaling or self-similarity property. However, when AGG occurs, the ceramics would have a distinctive variation in microstructure, with the presence of extremely large grains that are embedded in a matrix of smaller ones. Therefore, a bimodal distribution is usually observed. The microstructures of the ceramics are generally characterized by nearly equiaxial grains. In some cases, grains with an elongated or plate-like morphology are observed, which usually is called anisotropic grain growth. Anisotropic grain growth in most cases is only observed in ceramics with special crystal structures. Representative SEM images and photograph of NGG and AGG of BaTiO₃ ceramics, which could be controlled through the variation of oxygen partial pressure during sintering, are shown in Fig. 8.3 [5].

Fig. 8.3

SEM images and photograph of the BaTiO₃ ceramics: a normal grain growth, b, c abnormal grain growth, and d abnormal anisotropic grain growth. Reproduced with permission from [5]. Copyright © 2006, Elsevier

8.2.5 Grain Growth Control

At least two reasons can be used to support the control of grain growth during sintering of ceramics. On the one hand, as the grain size is increased, the diffusion distance of matter transport is increased. Therefore, grain growth has a negative effect on densification. On the other hand, many properties of ceramics are directly determined by their grain size, especially mechanical strengths [1]. For instance, fracture strength of ceramics generally increases with decreasing grain size, G, following the relation of K _1c ∞ 1/G ^1/2 [6–8]. In this respect, control of grain growth while not sacrificing optical performance is still a challenge in the fabrication of transparent ceramics. Similarly, magnetic and electrical properties of ceramics are determined and also have close relation with their grain sizes.

As discussed previously, densification of ceramics is attributed to the flux of matter from the grain boundaries or source to the pores or sinks. When the sintering is governed by diffusion mechanisms, the rate of densification is dependent on grain size G, through the following equation:

$$\frac{1}{\rho }\frac{{{\text{d}}\rho }}{{{\text{d}}t}} = \frac{K}{{G^{m} }},$$

(8.1)

where K is a temperature-dependent constant, while the exponent has different values for different densification mechanisms, e.g., with m = 3 for lattice diffusion and m = 4 for grain-boundary diffusion.

Therefore, to have a high densification rate, there should be a short diffusion distance between the source of matter and the sink, i.e., the grain size must remain as small as possible. This is the reason why nanosized powders have high sinterability. Equation (8.1) also indicates that as the grain growth rate is increased, the densification rate would be decreased. As a result, prolonged sintering time is required to achieve the desired density, which in turn could trigger the occurrence of AGG. Once AGG takes place, the pores would be trapped inside the grains and thus cannot be removed. Therefore, grain growth control is an effective technique to achieve high densification rate. Generally, AGG should be avoided, but it is also useful in certain occasion, i.e., growth of single crystals from ceramic matrix, as discussed later.

8.3 Ostwald Ripening and LSW Theory

Ostwald ripening is defined as the coarsening of particles in a solid or liquid. Almost all grain growth and pore growth during sintering of ceramics can be described by the using Ostwald ripening. Figure 8.4 shows a system with spherical particles with different radii dispersed in a medium, in which the particles have certain level of solubility [4].

Fig. 8.4

Coarsening of particles in a medium by matter transport from the smaller particles to the larger ones. The rate of coarsening is controlled by two mechanisms: a reaction at the interface between the particles and the medium and b diffusion through the medium. Reproduced with permission from [4]. Copyright © 2003, CRC Press

As stated before, chemical potential of the atoms under the surface of a sphere with a radius a is given by:

$$\mu = \mu_{0} + \frac{{2\gamma\Omega }}{a},$$

(8.2)

where μ ₀ is the chemical potential of the atoms under a flat surface, γ is the specific energy of the interface between the sphere and the medium and Ω is the atomic volume. The atoms under the surface of the sphere have higher chemical potential and thus higher solubility in the surrounding medium than the atoms under a flat surface. If solutions are assumed to be ideal, chemical potential and concentration can be related by the following expression:

$$kT\ln \left( {\frac{C}{{C_{0} }}} \right) = \mu - \mu_{0} = \frac{{2\gamma\Omega }}{a},$$

(8.3)

where C is concentration of the solute surrounding a particle with radius of a, C ₀ is the concentration over a flat surface, k is the Boltzmann constant, and T is the absolute temperature. If ΔC = C − C ₀ is small, ln(C/C ₀) ≈ ΔC/C ₀, so that Eq. (8.3) becomes

$$\frac{{\Delta C}}{{C_{0} }} = \frac{{2\gamma\Omega }}{kTa}.$$

(8.4)

The smaller the particles, the higher the solute concentration around the particles will be. As a result, there is always a net flux of matter from the smaller particles to the larger ones, i.e., the smaller particles are continuously dissolved, while the particles keep growing, which is driven by the reduction in the interfacial area between the particles and the medium. This process is known as Ostwald ripening.

8.3.1 LSW Theory

The theory of Ostwald ripening is also known as the LSW theory [9–12]. The LSW theory is used to describe the coarsening process of idealized systems with three conditions. Firstly, a particle grows at a rate that is the same as the atomic flux at its surface. Secondly, the particles have a continuous size distribution. Lastly, the total volume or mass of the particles follows mass conservation.

Besides the above three basic conditions, there are also other assumptions: (i) the precipitate and the medium are isotropic fluids, (ii) the precipitates are spherical particles, (iii) the number of precipitates is sufficiently large to ensure continuous distribution of radius of the precipitates, (iv) radius of the precipitate is the only factor to determine the solute concentration at the surface of the precipitate, (v) nucleation and precipitate coalescence are neglected, and (vi) the total volume of the system is infinite.

The rate of coarsening is controlled by two mechanisms, i.e., interface reaction mechanism and diffusion-controlled mechanism, as shown in Fig. 8.4. For interface reaction mechanism, coarsening rate is controlled either by the solubility of the particles into the medium or the deposition of the solute onto the particle surfaces. For diffusion-controlled mechanism, the diffusion of atoms through the medium to combine with larger particles is the controlling step.

8.3.2 Interface Reaction Mechanism

In this case, it is assumed that the rate of transfer of atoms is proportional to the difference between the solute concentration around a precipitate with radius, a, which is given by Eq. (8.4) and the average concentration of the solute, C*, which is defined as the concentration that is in equilibrium with a precipitate with radius, a*, which is kept unchanged. Also, the change in C* with increasing a* is neglected. Therefore, the rate of change in the radius of the precipitate is given by [4]:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = - \alpha_{\text{T}}\Omega \left( {C_{\text{a}} - C^{*} } \right),$$

(8.5)

where α _T is a transfer constant, while the negative sign in the equation is used, because C _a − C* is positive for smaller precipitates, whereas the radius, a, decreases with time. If the total volume of the precipitates is constant, there is

$$4\pi \sum\limits_{i} {a_{i}^{2} } \frac{{{\text{d}}a_{i} }}{{{\text{d}}t}} = 0.$$

(8.6)

The summation means that all the precipitates in the system are included. Equation (8.5) can be rewritten as follows:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = \alpha_{\text{T}}\Omega \left[ {\left( {C^{*} - C_{0} } \right) - \left( {C_{\text{a}} - C_{0} } \right)} \right],$$

(8.7)

By putting Eq. (8.7) into Eq. (8.6), there is

$$\sum\limits_{i} {a_{i}^{2} } \left( {C^{*} - C_{0} } \right) = \sum\limits_{i} {a_{i}^{2} } \left( {C_{{{\text{a}}_{i} }} - C_{0} } \right).$$

(8.8)

By putting $C_{{{\text{a}}_{i} }} - C_{0} =\Delta C$ and ΔC from Eq. (8.4) into Eq. (8.8), there is

$$C^{*} - C_{0} = \frac{{2\gamma\Omega C_{0} }}{kT}\frac{{\sum {a_{i} } }}{{\sum {a_{i}^{2} } }}.$$

(8.9)

By putting Eq. (8.9) into Eq. (8.7), there is

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = \frac{{2\alpha_{\text{T}} \gamma \Omega^{2} C_{0} }}{kT}\left( {\frac{{\sum {a_{i} } }}{{\sum {a_{i}^{2} } }} - \frac{1}{a}} \right).$$

(8.10)

Let $a^{*} = \sum {a_{i}^{2} } /\sum {a_{i} }$, Eq. (8.10) becomes:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = \frac{{2\alpha_{\text{T}} \gamma\Omega ^{2} C_{0} }}{kT}\left( {\frac{1}{{a^{*} }} - \frac{1}{a}} \right).$$

(8.11)

Equation (8.11) indicates that the rate of change in the radius of the precipitate is proportional to the difference between the critical precipitate curvature and the actual precipitate curvature.

The evolution of the system of precipitates can be described by using a distribution function f(a, t), with which f(a, t) da represents the fractional number of precipitates in the radium range of (a, a + da). The distribution function must satisfy the continuity equation:

$$\frac{{{\text{d}}f}}{{{\text{d}}t}} + \frac{\partial }{\partial a}\left[ {f\left( {\frac{{{\text{d}}a}}{{{\text{d}}t}}} \right)} \right] = 0.$$

(8.12)

From the solution of the coupled differential Eqs. (8.11) and (8.12), it is found that the rate of the coarsening reaches a steady state, so that the precipitate size distribution remains stationary against time, after a prolonged duration of coarsening process. When a reduced size, s = a/a*, is used to represent the radius of the precipitate, the distribution function will have the following forms [4]:

$$f(s,t)\left\{ {\begin{array}{*{20}l} { \approx s\left( {\frac{2}{2 - s}} \right)^{5} \exp \left( { - \frac{3s}{2 - s}} \right),} \hfill & {\text{for}\quad 0 < s < 2,} \hfill \\ { = 0,} \hfill & {\text{for}\quad s > 2.} \hfill \\ \end{array} } \right.$$

(8.13)

This asymptotic distribution is independent on the initial distribution of the system before the coarsening starts. In this case, the average radius, $\bar{a},$ which is the arithmetic mean radius, is given by $\bar{a} = (8/9)a^{*} ,$ while the maximum particle radius is 2a*. The critical radius in this steady-state coarsening regime increases parabolically through the following equation:

$$\left( {a^{*} } \right)^{2} \, - \, \left( {a_{0}^{*} } \right)^{2} = \left( {\frac{{\alpha_{\text{T}} C_{0} \gamma\Omega ^{2} }}{kT}} \right)t.$$

(8.14)

8.3.3 Diffusion-Controlled Mechanism

Similar procedure can be used to derive the coarsening rate governed by the diffusion mechanism. The rate of change in the particle radius, which is related to the diffusive flux at the precipitate surface, is given by [4, 13]:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = - D\Omega \frac{{{\text{d}}C}}{{{\text{d}}a}},$$

(8.15)

where D is the diffusion coefficient of the solute atoms in the medium.

For a dilute dispersion of particles, Eq. (8.15) can be rewritten as follows:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = D\Omega \left( {\frac{{C^{*} - C_{\text{a}} }}{a}} \right) = \frac{{2D\gamma\Omega ^{2} C_{0} }}{kTa}\left( {\frac{1}{{a^{*} }} - \frac{1}{a}} \right).$$

(8.16)

From the solution of the coupled differential Eqs. (8.12) and (8.16), the distribution function for steady-state coarsening has the following forms [4, 13]:

$$f(s,t)\left\{ {\begin{array}{*{20}l} { \approx s^{2} \left( {\frac{3}{3 + s}} \right)^{7/3} \left( {\frac{3/2}{3/2 - s}} \right)^{11/3} \exp \left( {\frac{ - s}{3/2 - s}} \right),} \hfill & {{\text{for}}\quad 0 < s < 3/2,} \hfill \\ { = 0,} \hfill & {{\text{for}}\quad s > 3/2.} \hfill \\ \end{array} } \right.$$

(8.17)

The distribution function is also independent of the initial size distribution, but the average radius $\bar{a}$ should be equal to a*, while the maximum particle radius is equal to 3a*/2. For the mechanism of diffusion control, the critical or average radius in the steady-state coarsening regime increases with time following a cubic law, which is given by:

$$\left( {a^{*} } \right)^{3} - \left( {a_{0}^{*} } \right)^{3} = \left( {\frac{{8DC_{0} \gamma\Omega ^{2} }}{9kT}} \right)t.$$

(8.18)

8.3.4 Deviation and Modification of LSW Theory

Deviations have been found in the predictions of the LSW theory. For instance, a practical system could have broader and more symmetrical steady-state distribution in diffusion-controlled coarsening. Also, the rate constant predicted by the LSW theory is often different from the experimental observations. In addition, volume fraction of the precipitates sometimes should be included, which is assumed to have no effect in the LSW theory [14–16]. It is found that as the volume fraction increases, the rate constant is increased while the size distribution function is broadened with increasing volume fraction of the precipitates [17]. Further modifications have made the LSW theory to be more agreement with experimental results [15, 18].

8.3.5 Time-Dependent Ostwald Ripening

Before the scaling regime mentioned above is reached, the distribution function varies with time. The precipitates could have a modified Gaussian distribution of sizes, which is given by [19]:

$$Y(a) = a^{2} \exp \left[ { - \frac{{(a - a_{\text{m}} )^{2} }}{{2a_{\text{w}}^{2} }}} \right],$$

(8.19)

where the parameters a _m and a _w are the position of the maximum and width of the distribution, respectively.

By using the distributions with varying a _m and a _w, the variation in the properties of the distribution with time can be analyzed. For the distributions with a broad width, the standard deviation of the distribution decreases to the characteristic steady-state value, whereas for the distributions with a narrow width, the standard deviation increases to the steady-state value. We may interpret this behavior during the transient regime to mean that the scaling regime acts as a strong attractor for the evolution of the precipitate size distribution.

8.4 Topological and Interfacial Tensions

In most theories, grains and grain boundaries are treated as isolated items. However, a real dense polycrystalline solid consists of a space-filling array of grains, where have certain topological requirements of space filling and local requirements for equilibrium of the interfacial tensions. Figure 8.5 shows a two-dimensional section through a dense polycrystalline solid [3]. The structure consists of vertices joined by edges, also called sides, which surround faces.

Fig. 8.5

Sketch of a section through a dense polycrystalline solid. The sign of the curvature changes as the number of sides increases from less than six to more than six. The arrows indicate the direction in which the boundaries migrate. Reproduced with permission from [3]. Copyright © 2007, Springer

It is assumed that the face at infinity is not counted, the numbers of faces F, edges E, and vertices V follow the Euler’s equation:

$$F - E + V = 1.$$

(8.20)

For stable topological structures, i.e., those in which the topological features are not changed by small deformations, the number of edges that intersect at a vertex is 3. For isotropic grain-boundary energies, i.e., grain boundaries have the same value of γ _gb, if the grain-boundary tensions are balanced, the edges meet at an angle of 120°. In this case, if N is the number of sides, a hexagon with N = 6 has plane sides, while a polygon with N > 6 will have concave sides, whereas those with N < 6 have convex sides. Since the grain boundary migrates toward its center of curvature, grains with N > 6 tend to grow, while those with N < 6 tend to shrink.

In three dimension, the faces surround cells, if the cell at infinity is not counted, there is

$$F - E + V - C = 1,$$

(8.21)

where C is the number of cells. If the interfacial energies are assumed to be isotropic, the surfaces meet in groups of three at angles of 120° for interfacial tension to be balanced, along lines which themselves meet in groups of four mutually at an angle of 109.5°. This is the angle subtended by straight lines joining the corners of a regular tetrahedron. No regular polyhedron with plane sides has exactly this angle between its edges. The nearest approach to space filling by a regular plane-sided polyhedron is obtained with tetrakaidecahedra arranged on a body-centered cubic lattice, but even with this structure, the angles are not exactly those required and the boundaries must become curved to satisfy local equilibrium at the vertices. In general, real grains are arranged randomly and also have different sizes.

8.5 Normal Grain Growth in Dense Solids

8.5.1 The Burke and Turnbull Model

NGG in dense polycrystalline solids has been extensively studied in the open literature [20, 21]. The driving force for grain growth process in earlier models is considered to be the pressure gradient across the grain boundary that facilitates the transport of mass, whereas chemical potential gradient is used as the driving force in the later ones [22]. In the Burke and Turnbull model, an isolated part of the grain boundary is considered, with the assumption that the grain growth equation derived from the analysis describes the average behavior of the system. It is also assumed that the grain-boundary energy γ _gb is isotropic and independent on the crystallographic direction, with a constant grain-boundary width γ _gb.

If the instantaneous rate of grain growth is used to represent the average rate of grain-boundary migration v _b, also known as grain-boundary velocity, there is

$$v_{\text{b}} \approx \frac{{{\text{d}}G}}{{{\text{d}}t}},$$

(8.22)

where G is the average grain size. The average rate of grain-boundary migration v _b can be represented by the product of the driving force for the grain-boundary migration F _b and the grain-boundary mobility M _b, so that there is

$$v_{\text{b}} = M_{\text{b}} F_{\text{b}} ,$$

(8.23)

where M _b includes all effects related to the mechanism of migration. The pressure difference across the grain boundary is given by the equation of Young and Laplace:

$$\Delta p = \gamma_{\text{gb}} \left( {\frac{1}{{r_{1} }} + \frac{1}{{r_{2} }}} \right),$$

(8.24)

where γ _gb is the specific grain-boundary energy, i.e., energy per unit area and r ₁ and r ₂ are the principal radii of curvature of the boundaries. If the radius of the boundary is assumed to be proportional to the average grain size G, there is

$$\frac{1}{{r_{1} }} + \frac{1}{{r_{2} }} = \frac{\alpha }{G},$$

(8.25)

where α is a geometrical constant that is determined by the shape of the boundary. If the driving force for the atomic diffusion across the grain boundary is equal to the gradient in the chemical potential, there is

$$F_{\text{b}} = \frac{{{\text{d}}\mu }}{{{\text{d}}x}} = \frac{\text{d}}{{{\text{d}}x}}({\Omega \Delta }p) = \frac{1}{{\delta_{\text{gb}} }}\frac{{\Omega \gamma_{\text{gb}} \alpha }}{G},$$

(8.26)

where Ω is the atomic volume and dx = δ _gb is the width of the grain boundary. From Eq. (4.92), the atomic flux across the boundary is given by

$$J = \frac{{D_{\text{a}} }}{{\Omega kT}}\frac{{{\text{d}}\mu }}{{{\text{d}}x}} = \frac{{D_{\text{a}} }}{{\Omega kT}}\frac{{\Omega \gamma_{\text{gb}} \alpha }}{{\delta_{\text{gb}} G}},$$

(8.27)

where D _a is the atomic diffusion coefficient across the grain boundary. Therefore, the grain-boundary velocity becomes

$$v_{\text{b}} \approx \frac{{{\text{d}}G}}{{{\text{d}}t}} =\Omega J = \frac{{D_{\text{a}} }}{kT}\frac{\Omega }{{\delta_{\text{gb}} }}\frac{{\alpha \gamma_{\text{gb}} }}{G}.$$

(8.28)

Pressure difference across the grain boundary, αγ _gb/G, can also be used as the driving force, so that v _b is expressed as follows:

$$v_{\text{b}} \approx \frac{{{\text{d}}G}}{{{\text{d}}t}} = M_{\text{b}} \left( {\frac{{\alpha \gamma_{\text{gb}} }}{G}} \right).$$

(8.29)

By comparing Eqs. (8.28) and (8.29), M _b can be defined by the following expression:

$$M_{\text{b}} = \frac{{D_{\text{a}} }}{kT}\left( {\frac{\Omega }{{\delta_{\text{gb}} }}} \right).$$

(8.30)

Integrating Eq. (8.29) yields:

$$G^{2} - G_{0}^{2} = Kt,$$

(8.31)

where G ₀ is the initial grain size, i.e., G = G ₀, at t = 0, while K is a temperature-dependent growth factor, which is given by

$$K = 2\alpha \gamma_{\text{gb}} M_{\text{b}} .$$

(8.32)

Equation (8.31) is the parabolic grain growth law, with the same form as the LSW equation for interface reaction-controlled Ostwald ripening given in Eq. (8.14). The growth factor K as a function of temperature T can be described by using the Arrhenius equation, i.e., K = K ₀ exp(−Q/RT), where K ₀ is a constant, R is the gas constant and Q is the activation energy of the grain growth.

The boundary mobility M _b is determined by the diffusion coefficient D _a for the atomic migrates across the grain boundary of the pure material, which is called intrinsic boundary mobility. In ionic solids, because both cations and anions could diffuse, D _a is the diffusion coefficient of the species that are rate-limiting or lowest. In real ceramics, various drag forces, such as segregated solutes, inclusions, pores, and second-phase films, can be applied to the grain boundary. As a result, experimental boundary mobility is lower than the M _b given by Eq. (8.30) in most cases.

8.5.2 Mean-Field Theory

In mean-field theory, the change in size of an isolated grain is considered, which is embedded in an environment that represents the average effect of all the other grains [23]. In this theory, the rate of grain growth is related to the radius a through the following equation:

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = \alpha_{1} \gamma_{\text{gb}} M_{\text{b}} \left( {\frac{1}{{a^{*} }} - \frac{1}{a}} \right),$$

(8.33)

where α ₁ is a geometrical factor that is equal to 1/2 for two dimension and 1 for three dimension, a is the radius of circle or sphere that has the same area or volume as the grain, and a* is a critical grain size, i.e., if a > a*, the grain grows, while if a < a*, the grain shrinks.

Equation (8.33) is similar to the LSW equation of Eq. (8.11), where the rate of change in the radius of the grain in Ostwald ripening is controlled by the interface reaction, so that the critical radius for the rate of change is given by [23]:

$$\frac{{{\text{d}}\left( {a^{*} } \right)}}{{{\text{d}}t}} = \frac{1}{2}\alpha_{1} \gamma_{\text{gb}} M_{\text{b}} .$$

(8.34)

If it is assumed that the terms on the right-hand side of Eq. (8.34) are not varied with time, integration of the equation gives rise to parabolic grain growth kinetics, which is analogous to the Eq. (8.31). In addition, the size distribution during the steady-state grain growth can be expressed by the following equation [23]:

$$f(s,t) = (2e)^{\beta } \frac{\beta s}{{(2 - s)^{2 + \beta } }}\exp \left( {\frac{ - 2\beta }{2 - s}} \right),$$

(8.35)

where s is called reduced size, that is equal to a/a*; e is the base of the natural logarithm, i.e., e = 2.718, while β = 2 for two dimension and 3 for three dimension. The distribution predicted by using this equation has a sharp peak [24].

The mean-field approach has been further developed [25, 26]. If the grain size distribution is assumed to be lognormal and time-independent when plotted as a function of the reduced size $s = a/\bar{a} ,$ where $\bar{a}$ is the average grain size, similar parabolic growth kinetics could be obtained [25]. Alternatively, a random walk process is used to model the motion of grain boundary, by attributing the drift to larger average sizes to the fluctuation of the grain size. In this case, the grain growth kinetics is also parabolic, while a time invariant grain size distribution function can be obtained as follows [26]:

$$f(s,t) = As\,\exp \left( { - \frac{{s^{2} }}{2}} \right),$$

(8.36)

where A is a constant, with certain distribution functions [24, 27].

Therefore, all the theories indicate that the NGG in polycrystalline solids can be treated as the Ostwald ripening governed by the interface reaction mechanism. However, in practice, the grain growth data cannot be always described by the parabolic law, so that a general grain growth equation is used:

$$G^{m} - G_{0}^{m} = Kt,$$

(8.37)

where the exponent m is usually in the range of 2–4, which is dependent on temperature to a certain degree. Although m = 3 has been observed in most ceramics, it could be attributed to different mechanisms.

8.5.3 Topological Analysis

Topological requirements of space filling, which are neglected by the theories of grain growth, have an argument that the volume of a shrinking grain must be shared with all the grains in the structure [28]. Therefore, the changes in topological parameters, such as the numbers of faces, edges and vertices, must also be shared with the other grains. Two constants of grain growth, i.e., sweep constant θ and structure gradient σ, have been introduced. The sweep constant is defined as the number of grains that are lost when the grain boundaries throughout the structure sweep through an equivalent unit volume of the solid. There is some doubt about whether the sweep constant is indeed constant [29]. The structure gradient is defined as follows:

$$\sigma = \frac{{M_{\text{V}} S_{\text{V}} }}{{N_{\text{V}} }},$$

(8.38)

where M _V, S _V, and N _V are the curvature, surface area, and number of grains, respectively, per unit volume of the solid. Available experimental data have confirmed that σ is indeed constant.

In the kinetics of grain growth, the mean boundary is equal to the product of the mobility of the grain boundary and the force applied to it, which is given by

$$v_{\text{b}} = M_{\text{b}} \gamma_{\text{gb}} M_{\text{V}} .$$

(8.39)

With a unit volume of the solid, the volume sweeps out per unit time is v _b S _V, while the number of grains that are lost per unit time is θv _b S _V, according to the definition of the sweep constant. The total volume transferred from the grains that are going to disappear to the grains that are remained per unit time is θv _b S _V G, where V _G is the average volume of the grains. The rate of increase in the average volume per grain can be derived by:

$$\frac{{{\text{d}}V_{\text{G}} }}{{{\text{d}}t}} = \frac{{\theta v_{\text{b}} S_{\text{V}} V_{\text{G}} }}{{N_{\text{V}} }},$$

(8.40)

where N _V, the number of grains per unit volume, is equal to 1/V _G. When S _V and v _b are substituted with those derived from Eqs. (8.38) and (8.39), Eq. (8.40) becomes

$$\frac{{{\text{d}}V_{\text{G}} }}{{{\text{d}}t}} = \frac{{M_{\text{b}} \gamma_{\text{gb}} \theta \sigma }}{{N_{\text{V}} }}.$$

(8.41)

If it is assumed that the terms on the right-hand side of Eq. (8.41) are constant, integrating Eq. (8.41) yields:

$$V_{\text{G}} - V_{{\text{G}_{o} }} = \left( {\frac{{M_{\text{b}} \gamma_{\text{gb}} \theta \sigma }}{{N_{\text{V}} }}} \right)t,$$

(8.42)

where $V_{{\text{G}_{0} }}$ and $N_{{\text{V}_{0} }}$ are the average grain volume and the average number of grains at t = 0. Experimental data indicate that V _G indeed has a linear dependence on time.

8.5.4 Simulation of Normal Grain Growth

Computer simulations have been used to explore the complexities of grain growth [21]. Two-dimensional models are usually used to simulate grain growth, either for direct simulation where a boundary network is constructed [30–32] or for statistical approach in which ensemble probabilities for a collection of grains are determined from a series of interrelated equations to find the behaviors of typical grain types [21, 22]. The probabilistic models can include both the topological requirements of space filling and the detailed local effects of grain-boundary curvature in the simulations. The microstructure is mapped out onto a discrete lattice, in which each lattice site is assigned a number between 1 and Q, corresponding to the orientation of the grain in it [27]. Generally, a sufficiently large value of Q (>30) is selected to limit the impingement of grains of the same orientation. The grain-boundary segment is defined in between two sites with different orientations.

For two dimension, the average area per grain $\bar{A}$ is related to the average grain size G. After an initial simulation of a shrinking circular grain embedded in an infinite matrix, i.e., Q = 2, which is similar to the mean-field approach, it is found that the growth of the grain size with time can be described by the following equation:

$$\bar{A} - \bar{A}_{0} = Kt,$$

(8.43)

where $\bar{A}_{0}$ is the initial area of the grain and K is a constant. Therefore, the grain growth kinetics of the isolated grains is parabolic, which is in agreement with the prediction by the mean-field theories and the Burke–Turnbull theory.

For an interconnected network of polycrystalline grains, the kinetics is on longer parabolic. Grain growth exponent obtained in the simulations is m = 2.44, which is different from that value predicted by the mean-field theories, i.e., m = 2 [27]. In the mean-field theories, the driving force for grain growth is the reduction of the curvature or area of the boundary, whereas in the lattice models used in the simulations, the curvature is discretely allocated as kinks on the boundary, which can be eliminated by two mechanisms. First mechanism is the meeting and annihilation of two kinks with same orientation but opposite signs, which means that the grain growth is driven only by curvature. It is similar to the simulation of a circular grain embedded in an infinite matrix. The second mechanism is related to the adsorption of a kink at a vertex where more than two grains meet, which requires the presence of vertices. Vertices can reduce the curvature without causing grain growth by absorbing the kinks. Therefore, the growth is slower as compared to that of the circular grain in the infinite matrix, so that the value of m is relatively high.

8.6 Abnormal Grain Growth

As stated previously, the presence of extremely large grains is detrimental to full densification and thus some properties of ceramics. Therefore, in order to control AGG, it is necessary to understand its mechanism.

8.6.1 Origins of Abnormal Grain Growth

The occurrence of AGG is often attributed to nonuniform the distribution of particle size in the starting powders. Equation (8.35) indicates that a steady-state normal grain size distribution has a maximum or cut-off grain size, which means that AGG would take place if there are grains that are larger than twice the average size in two dimension. However, theoretical models can hardly predict AGG. For example, it is found in a Monte Carlo simulation that although there are large grains at certain stages, they would not grow abnormally, if the system is isotropic with uniform grain-boundary energy and mobility, as shown in a systematic study [33–35]. This is because the normal grains will grow at higher rates, so that the large or abnormal grains are eventually included in the normal size distribution.

When there is a large grain with a radius a is embedded in a matrix of fine normal grains, similar to Eq. (8.11), its growth rate can be expressed as [36]

$$\frac{{{\text{d}}a}}{{{\text{d}}t}} = 2\gamma_{\text{gb}} M_{\text{b}} \left( {\frac{1}{{a^{*} }} - \frac{1}{a}} \right),$$

(8.44)

where a* is the critical radius at which a grain neither grows nor shrinks. Therefore, the relative growth rate of the large grain is given by

$$\frac{\text{d}}{{{\text{d}}t}}\left( {\frac{a}{{a^{*} }}} \right) = \frac{1}{{\left( {a^{*} } \right)^{2} }}\left( {a^{*} \frac{{{\text{d}}a}}{{{\text{d}}t}} - a\frac{{{\text{d}}a^{*} }}{{{\text{d}}t}}} \right).$$

(8.45)

Because the number of the fine normal grains is much larger than that of the abnormal grain, the time dependence of a* can be described in a similar way to that given by Eq. (8.14):

$$\frac{{{\text{d}}a^{*} }}{{{\text{d}}t}} = \frac{{\gamma_{\text{gb}} M_{\text{b}} }}{{2a^{*} }}.$$

(8.46)

Putting Eqs. (8.44) and (8.46) into Eq. (8.45) yields

$$\frac{\text{d}}{{{\text{d}}t}}\left( {\frac{a}{{a^{*} }}} \right) = - \frac{{\gamma_{\text{gb}} M_{\text{b}} }}{{2aa^{*} }}\left( {\frac{a}{{a^{*} }} - 2} \right)^{2} .$$

(8.47)

Equation (8.47) indicates that the relative growth rate of the large grain is always negative, except for the case of a = a*, for which it is zero. Therefore, those abnormal grains, i.e., with grain sizes of a > 2a*, will not grow to a size that is significantly outside the normal grain size range, due to the upper limit of 2a*. Moreover, due to their irregularities in shape and fluctuations in size, they cannot remain unchanged in size at exactly 2a*, after they are included in the normal grain size distribution. Instead, they tend to shrink. As a result, size difference is not a sufficient condition to initiate AGG in isotropic systems.

Both computer simulations and theoretical analysis have demonstrated that AGG most likely occurs in anisotropic systems, i.e., the grain-boundary energy and mobility are variable [37–40]. Once the boundaries have a higher mobility and/or a lower energy than the surrounding matrix grains, AGG is triggered. It has been observed that the abnormal grain embedded in a fine-grained matrix could be 6 times larger than the average size, which has a mobility 7.5 times that of the fine grains [37]. According to prediction, the abnormal grain grows faster than the average-sized grains in the surrounding matrix.

The properties of grain boundaries can be varied in several ways in practical ceramics. One of the characteristics is the structure and mis-orientation of the grain boundary. Special or low-angle grain boundaries, which are formed when two grains have only a slight mis-orientation relative to one another, possess a lower energy than general boundaries that have high mis-orientation angles. Transfer of matter from the surrounding grains to the low-energy boundaries promotes AGG. Alternatively, low-energy grain boundaries are generally believed to have low mobility, so growth is slow normal to and rapid parallel to the low-energy boundaries, often resulting in faceting and anisotropic abnormal growth.

During the sintering process of ceramics, there could be happenings, such as the release of solutes, formation of secondary phases, and the presence of pores from moving grain boundaries, which bring out a sudden increase in the boundary mobility, thus leading to AGG. The formation of liquid phases has also been acknowledged to be a cause of AGG, because the boundary mobility can be significantly increased due to the presence of the liquid films at the grain boundaries. This is the reason why AGG is easily observed in liquid-phase sintering [41]. Inhomogeneities in physical properties and chemical compositions, e.g., inhomogeneous packing and nonuniform distribution of dopants and secondary phases, result in inhomogeneous microstructures, which is another major cause of AGG, because the local microstructural heterogeneity creates differences in the boundary mobility and energy.

8.6.2 Applications of Abnormal Grain Growth

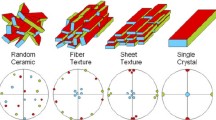
As mentioned above, it is desirable to prevent AGG. However, if AGG can be well controlled, it is also useful for several ceramic materials. For example, in situ growth of anisotropic abnormal grains in a fine-grained matrix, with controlled size distributions, has been used to increase the fracture toughness of SiC, Si₃N₄, Al₂O₃, and mullite ceramics [42–48]. Preferential alignment of growing anisotropic grains has been employed to fabricate ceramic materials with textured microstructure, which is also called template grain growth (TGG) [49–56].

Another application of AGG is to obtain single crystals through ceramic processing. Previously, various single crystals, such as ferrites and ferroelectrics, have been obtained by using this technique [57–60]. More importantly, this method has also been used to convert ceramics to solid-state laser single crystals [61–63]. Desirably, monodispersed starting powders should be used, so as to form a fine-grained matrix with a narrow size distribution. At the same time, a large seed crystal with high quality is embedded into the fine-grained matrix. The system is then annealed at high temperatures, so that the seed crystal will grow into the powder matrix through the migration of its boundary. Under proper conditions, the entire sample could be grown into a single grain, i.e., single crystal.

The derivation of single crystals from polycrystalline ceramics by sintering is known as solid-state crystal growth (SSCG) [64]. A schematic diagram of the single-crystal sintering method is shown in Fig. 8.6. First, a polycrystalline Nd:YAG ceramic material with a relative density of over 95 % was prepared. Then, one face was polished and contacted with a seed crystal, which could be single-crystal YAG with any crystal orientation of $\langle 111\rangle ,$ $\langle 100 \rangle$ and $\langle 110\rangle$. When the seeded ceramics was heated at a high temperature (below the melting point) of over 1700 °C, single crystallization occurred in the solid state due to continuous grain growth. When the surface energy of the fine grains of polycrystalline ceramic (E _p) is much greater than that of the seed crystal (E _s) (i.e., E _p ≫ E _s), the fine grains tend to change to a thermodynamically stable condition at higher temperature. As a result, fine grains are absorbed into the seed crystal, and grain growth occurs continuously. Finally, the polycrystalline materials change to single-crystal materials in a solid-state condition.

Fig. 8.6

Illustration of the production of single-crystal ceramic material by the sintering (nonmelting) conversion method. Reproduced with permission from [61]. Copyright © 2007, Elsevier

A trace amount of solid SiO₂, which in most cases is in the form of colloidal silica, was added to prepare Nd:YAG sintered bodies. Then, they were heat treated at 1780 °C for various soaking times: 0, 2, and 5 h. Reflected microscopic images are shown in Fig. 8.7. Upon reaching the sintering temperature, the microstructure was still characterized by grains with a uniform size distribution. However, as the sintering time was increased to 2 h, a few of abnormal grains with diameters of up to 1 mm were observed. As the sintering was further increased to 5 h, the abnormal grain sizes were largely increased. In this case, the silica acted as both a seed crystal and an accelerator of the grain growth. In solid-state crystal growth, the formation and growth of abnormal grains provides the driving force for continuous crystallization.

Fig. 8.7

Variation in microstructure of Nd:YAG ceramics doped with a small amount of SiO₂ sintered at 1780 °C for 0, 2, and 5 h. Reproduced with permission from [61]. Copyright © 2007, Elsevier

The relationship between the heat treatment temperature and rate of crystal growth has been studied. Crystallization started at about 1700 °C, and the crystal growth rate increased with an increase in heat treatment temperature. In this experiment, a maximum growth rate of 1.7 mm h⁻¹ was reached. Using the CZ method, the rate of crystal growth is generally about 0.2 mm h⁻¹. Therefore, greater or equivalent growth rate can be realized using the SSCG method.

The appearance of heavily doped Nd:YAG single crystals, with doping concentrations of 2.4, 3.6, and 4.8 %, prepared by the SSCG method is shown in Fig. 8.8a. A typical reflected (polarized) microscopic image of a near growth interface of a 2.4 % Nd:YAG sample is shown in Fig. 8.8b. It was confirmed that grain growth occurred from a seed crystal toward polycrystalline directions. It should be noted that heavily doped Nd:YAG single crystal can be produced by the SSCG method. Using the CZ (melt-growth) method, the segregation coefficient of Nd ions in the YAG host crystal is very small, and it is difficult to dope more than 1 at % Nd ions homogeneously into the YAG host crystal. In the case of the SSCG method, since there is no solid–liquid interface, the concept of segregation is not relevant for this solid process. In this process, polycrystalline grains are gradually absorbed into the seed single crystal.

Fig. 8.8

a Photographs of the 2.4, 3.6, and 4.8 at % Nd:YAG ceramics after heat treatment for single crystallization. b Microstructure of the 2.4 at.% Nd:YAG ceramic sample at the interface between the single crystal and polycrystal. Reproduced with permission from [61]. Copyright © 2007, Elsevier

Therefore, if the composition of each polycrystalline Nd:YAG grain is very homogeneous in the ceramic, then the homogeneity of the grown single-crystal ceramics will also be very high. Transmission electron microscopy (TEM) image and energy dispersive spectroscopy (EDS) analysis have been used to study the growth interface between single crystal and polycrystalline part. There was no boundary phase or secondary phase near the growth interface, and the growth interface was very similar to the grain boundary of the host polycrystalline ceramics. The EDS analysis results, however, showed a trace amount of Si (SiO₂) at the growth interface and at the grain boundaries, but not in the crystal grains. Studies on the crystal growth mechanisms are still under investigation, but it is certain that the Si component is closely involved in the growth mechanism.

Figure 8.9 shows XRD patterns of normal polycrystalline Nd:YAG ceramic, and the SSCG-grown single-crystal ceramics with $\langle 111\rangle$ and $\langle 110\rangle$ crystal orientations. In the case of normal sintered Nd:YAG ceramic without the seed crystal, random crystal orientations were observed. But in the case of the SSCG-grown single-crystal ceramics, the crystal orientations were the same as the seed crystal. Therefore, it was confirmed that single crystallization by sintering is technologically possible.

Fig. 8.9

XRD patterns of the polycrystalline (a), $\langle 111\rangle$ (b) and $\langle 110\rangle$  (c) seeded Nd:YAG samples. The characteristic peaks of the $\langle 111\rangle$ and $\langle 110\rangle$ seeded crystals are confirmed. Reproduced with permission from [61]. Copyright © 2007, Elsevier

SSCG-grown Cr⁴⁺:YAG single-crystal ceramic could be well bonded with a $\langle 100\rangle$-oriented seed crystal. Using this technology, it is possible to dope various types of laser active ions. This material was grown at 1700 °C, and the crystal growth rate was 4 mm h⁻¹. The crystal growth rate can be controlled mainly using (i) the seed crystal orientation, (ii) the grain size of the polycrystalline ceramic, and (iii) the heat treatment temperature. The maximum growth rate achieved was 5 mm h⁻¹.

Laser performance of the SSCG-grown Nd:YAG single-crystal ceramic and that of pore-free normal Nd:YAG polycrystalline ceramic, with Nd concentration of 2.4 at.%, have been compared. A Ti:sapphire laser was used as an excitation source. A 99.9 % reflection mirror and an output mirror with 5 % transmission were used. The laser gain media samples were AR coated, but the laser oscillation test was performed without optimizing the laser resonator. Both samples reached a slope efficiency of almost 60 %, but the single-crystal ceramic showed about 6 % higher efficiency than the polycrystalline ceramic. This improvement was probably because scattering due to grain boundaries does not occur in the single-crystal ceramic material. Since the single-crystal ceramic materials produced by the SSCG method have no grain boundaries, it is considered that this kind of material is the best quality for laser materials.

Various garnet crystals of Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ were grown from Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ polycrystalline precursors, by using controlled AGG at temperatures between 1750 and 1850 °C [65]. The composition of the expected Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ single crystal was Nd_0.01:(Y_0.85La_0.05Lu_0.05Gd_0.05)_2.99:(Sc_0.3Al_0.7)₅O₁₂. The Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ precursor materials were prepared using stoichiometric amounts of the following analytical grade reagents: yttrium oxide (Y₂O₃), scandium oxide (Sc₂O₃), lanthanum oxide (La₂O₃), lutetium oxide (Lu₂O₃), gadolinium oxide (Gd₂O₃), neodymium oxide (Nd₂O₃), aluminum nitrate hydrate (Al(NO₃)₃·9H₂O), nitric acid (HNO₃), and ammonia (NH₃·4H₂O).

Y₂O₃, Sc₂O₃, La₂O₃, Lu₂O₃, Gd₂O₃, and Nd₂O₃ were dissolved in nitric acid. Aluminum nitrate was dissolved in distilled water. The two solutions were then mixed together. An appropriate amount of the mixture was stirred for 3 h at the same temperature. In the following step, ammonia (NH₃·4H₂O) was added drop-wise to the above-described solutions as a precipitator with continuous stirring. The sediment was washed several times using deionized water and then filtered. The sediment was then dried in an oven for 24 h at 100 °C.

The sediment was ground in an agate mortar, sieved, placed in alumina crucibles, and burned for 2 h at 850 °C in air (heating rate of 1 °C min⁻¹). The powder was compacted into pellets with diameter of 20 mm at 20–30 MPa and was then cold-isostatically pressed at 200 MPa. The localized codoping of the disks was achieved by applying colloidal SiO₂ with 15 wt% in H₂O to one point of each disk. The codoped disks were allowed to dry for at least 5 min prior to sintering. After sintering at 1750–1850 °C for 20 h under a H₂ atmosphere without pressure in a tungsten wire furnace, the specimens were cut and double-polished to 1 mm in thickness for spectral analysis.

The samples obtained were transparent. Figure 8.10 shows a photograph of a Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ single crystal produced using the solid-state single-crystal conversion (SCC) process [65]. The size of the single crystal of Nd-doped (Y,Gd,La,Lu)₃(Sc,Al)₅O₁₂ was approximately 4 mm and thickness was 0.8 mm. The relative density was 99.8 %. Figure 8.11 shows an SEM image of interface between the grown single-crystal and the polycrystalline ceramics [65]. The grains of the polycrystalline ceramics were equiaxed, with an average grain size of ~30 μm. Many residual pores with small sizes at the grain boundaries and within the grain interiors could be observed. Single crystals with a maximum size of 4 mm and promising optical performances could be obtained by using this method.

Fig. 8.10

Photograph of the mixed-metal garnet single crystal by using solid-state ceramic conversion process (polished sample with thickness = 0.8 mm). Reproduced with permission from [65]. Copyright © 2014, Elsevier

Fig. 8.11

SEM image of interface between the polycrystalline and the as-prepared single-crystal part. Reproduced with permission from [65]. Copyright © 2014, Elsevier

Yttrium aluminum garnet (YAG) ceramics with stoichiometric Y₂O₃:Al₂O₃ = 3:5 ratio, as well as with excessive either Y₂O₃ or Al₂O₃ of up to 5 mol%, were compared, in order to study the composition effect of YAG on crystal growth behavior during the SSCG process [62]. This work was carried out, because previous results doped yttrium aluminum garnet Y₃Al₅O₁₂ (YAG) ceramics were contradictory, in terms of crystal growth rate with respect to compositions of the YAG studies.

All the ceramics were prepared through solid-state reaction of nanopowders of Y₂O₃ and Al₂O₃, which were synthesized by using chemical precipitation from yttrium nitrate and ammonium–aluminum sulfate with ammonium bicarbonate solution as precipitant. All mixed powders were compacted at uniaxial pressure 20 MPa first and further consolidated by using CIP at 200 MPa into pellets with diameter of 10 mm and thickness of 2 mm. The samples were then sintered in vacuum at 1730–1750 °C for 5–10 h. Besides the stoichiometric 3:5 composition, excessive Y₂O₃, or Al₂O₃ were from 0.2 to 5 mol%. 0.8 mol% of Nd₂O₃ was included in some samples.

(111) YAG-polished crystal seed plates with 200-nm SiO _x layers deposited on them by magnetron sputtering were pressed onto polished ceramic disks [66]. Thermal annealing was conducted at 1800–1850 °C or 1890 °C for 10–12 in, in N₂ + 5 % O₂, at heating/cooling rates of 150 °C h⁻¹. Slices of 1 mm thick, perpendicular to the seed–ceramics contacting surfaces, were cut from the samples after thermal annealing, with both sides to be polished.

Figure 8.12 shows photographs of representative samples. Stoichiometric ceramics samples were transparent, samples with 1 % excess Y₂O₃ or Al₂O₃ were translucent, and those with 3 % and more excess oxides were opaque. Grain size in all samples was about 20 μm. Porosity increased slightly with increasing contents of the excessive oxides.

Fig. 8.12

a Photographs of representative YAG:Nd and YAG ceramics. Every sample differs from its neighbors by 1 mol% excessive Y₂O₃ (1Y, 2Y) or Al₂O₃ (1A, 2A), while “0” means stoichiometric Y/Al ratio of 3:5. b Porosity (vol.%) as a function of Y/Al ratio for pure and Nd-doped YAG ceramics with different levels of excessive oxides. Reproduced with permission from [62]. Copyright © 2013, Elsevier

Figure 8.13 shows SEM image of the grown crystal after thermal etching. Grain boundaries were clearly observed in etched ceramic part, while newly grown single-crystal part has no grain boundaries. Experimental results indicated that the growth rates of the samples with excessive Al₂O₃ were higher that of the stoichiometric sample. The sample with 5 % excessive Al₂O₃ at 1890 °C exhibited the highest growth rate of 0.15 mm h⁻¹, which was about higher than that of stoichiometric sample by nearly 20 times.

Fig. 8.13

SEM image of the grown crystal after thermal etching to show the grain boundaries in the ceramics, without boundary being observed in the grown crystal. Reproduced with permission from [62]. Copyright © 2013, Elsevier

Nonuniform growth was observed in central part of the sample with 1.5 mol% excessive Y₂O₃, as shown in Fig. 8.14. The central part had a higher growth rate than the rest area by about three times, which was different from normal growth behavior, i.e., such growths are from outer parts toward central part. The anomaly was attributed to possible nonuniform contact at the seed crystal–ceramics interface. In addition, there is no difference in SSCG rate between undoped and 0.8 mol% Nd-doped samples.

Fig. 8.14

Nonuniform growth of the crystal layer in the center part of the YAG ceramics with 1.5 mol% excessive Y₂O₃. Diagram of the layered structure is shown at the top panel 1 seed YAG crystal, 2 ceramics, 3 SiO _x layer, and 4 grown crystal layer. Reproduced with permission from [62]. Copyright © 2013, Elsevier

The effect of contact between the seed crystal and the ceramics on the SSCG growth efficiency has been examined. One example is shown in Fig. 8.15, where the two edges of same seed had different contacting qualities, i.e., one was better than the other. Poor contact led to slow growth rate and the formation of pores, as shown Fig. 8.15a. In contrast, high-quality contact resulted in high growth rate and reduced number of pores, as demonstrated in Fig. 8.15b.

Fig. 8.15

Lateral growth of the crystals in the ceramics with 4.7 mol% excessive Y₂O₃: a low rate of lateral growth and b high rate of lateral growth. (1 seed YAG crystal, 2 ceramic, and 3 SiO _x layer). Reproduced with permission from [62]. Copyright © 2013, Elsevier

EDS measurement results indicated that, in direction perpendicular to the seed-ceramic interface, some local regions possessed enrichment in Y or Al after annealing at temperatures of >1800 °C. The number and dimension of such regions increased with increasing content of excessive Y₂O₃ and Al₂O₃ in the initial compositions. Meanwhile, the Y–Al ratio was very close to the stoichiometric ratio of 3:5 in other areas. These either Y or Al enriched regions could participate the formation of liquid phase with SiO _x , which promoted crystal conversion and pore elimination. This interesting issue deserves further investigation.

Abnormal grain growth (AGG) can also be used to directly convert polycrystalline Al₂O₃ (PCA) ceramics into single crystals, without using seeds. For example, more than 30–40 % of polycrystalline, MgO-doped Al₂O₃ tubes were converted into single crystals of sapphire by AGG in the solid state at a high temperature of 1880 °C [67]. Most crystals were 4–10 cm in length in the tubes with wall thicknesses of 1/2 and 3/4 mm and outer diameters of 5 and 7 mm, respectively, with their c-axes being oriented ~90° and 45° to the tube axis. The AGG was initiated, due to the low values of MgO concentration of about 50 ppm in the bulk. The unconverted parts had grains with millimeter sizes. The difference in grain structures between the converted and the unconverted tubes was attributed to nonuniform concentration of MgO in the extruded tubes.

The growth front of the migrating crystal boundary possessed nonuniform shapes, while the interface between the single crystal and the polycrystalline matrix contained “curved” boundary segments, characterizing typical AGG in a single-phase material. The average velocity of most migrating crystal boundaries was as high as 1.5 cm h⁻¹. The average grain-boundary mobility at 1880 °C was estimated to be 2 × 10⁻¹⁰ m³ (N s)⁻¹, which was the highest value for Al₂O₃ and was higher than the calculated intrinsic mobility by a factor of 2.5. Such a conversion could on take place, when a codopant of CaO, La₂O₃, or ZrO₂ was used at concentrations of several hundred ppm.

A commercial alumina powder, mixed with 620 ppm of MgO using magnesium nitrate as a precursor and appropriate amounts of organic binder and lubricant, was used to extrude tubes. The alumina powder had a specific surface area of 8.8 m² g⁻¹ and median particle size of 0.31 μm. Tubes of 100 cm in length were extruded, which were dried for 16 h at 100 °C and prefired at 1050 °C in air to remove organic binders. Finally, the tubes were sintered at 1880 °C in H₂ for different time durations. The average concentrations of MgO (C _MgO) and impurities were measured in sintered PCA tubes by using wet chemical analysis.

Figure 8.16 shows C _MgO and grain size the samples as a function of sintering time duration [67]. After sintering 3 h, the C _MgO in the PCA decreased from the initial value of 660 ppm to about 380 ppm. The MgO content continued to decrease to 40–55 ppm after sintering form 9 h, which showed no further significant decrease thereafter when tubes were converted to single crystals. The solid-state crystal conversion (SSCC) event was started at about 9 h, which was found to be related with very low C _MgO of 50 ppm. Due to their very low levels, the concentrations of impurities had no obvious effects on the SSCC event.

Fig. 8.16

Average MgO concentration and grain size in PCA tubes with 5 mm OD as a function of sintering time at 1880 °C. Reproduced with permission from [67]. Copyright © 2002, John Wiley & Sons

The average grain size of the polycrystalline matrix increased rapidly from 0.3 μm in the green tube to about 30 μm in the sample sintered at 1880 °C for 3 h. After that, the grains slowly increased from 30 to 60 μm, as the sintering time was increased from 3 to 18 h. The sizes of the largest grains in the polycrystalline regions were about twice the average grain size, indicating that the event was still NGG. The average size of the “surface” grains on the outer diameter (OD) surface of the sample sintered for 9 h was 65 μm, which was larger than the interior grain size of 50 μm by about 30 %. In this sample, the largest surface grains were 200–250 μm, 3–4 times larger than the average grain size. It means that the largest surface grains started to grow abnormally, while those in the sample interior and on the inner diameter (I)D surface of the sintered tube still experienced NGG.

Figure 8.17a shows a detailed image of the single crystal/PCA interface [67]. The interfacial boundary between the single crystal and the polycrystalline matrix with an average grain size of ~30 μm consisted of many “curved” boundary segments, indicative of typical AGG. There were two distinctive types of surface features in newly grown single crystals. The surface sapphire crystal undulations appeared to be preexisting on the PCA material before conversion, which was even more visible in Fig. 8.17b. Also, single or groups of isolated PCA grains were observed the grown crystal. These isolated grains were Al₂O₃ grains that were mis-oriented with the grown crystal. This is a low-cost process of SSCC that could be used to convert complex shapes of polycrystalline ceramics into single crystals through AGG, which is believed to be applicable to other materials and thus deserves further investigation.

Fig. 8.17

a Typical interface between a growing single crystal and the PCA matrix on the OD surface. b Optical micrograph of the interface showing the “ghost” structure in the single-crystal region. Reproduced with permission from [67]. Copyright © 2002, John Wiley & Sons

Another example is on the conversion of polycrystalline MgO-doped Al₂O₃ tubes to single-crystal sapphire with the codoping of SiO₂ [68]. The intentional codoping with SiO₂ before sintering was used to trigger the occurrence of AGG, leading to full conversion of tube surfaces to single crystal without adversely affecting the densification. The degree of surface conversion was strongly dependent on experimental parameters, such as sintering temperature and codoping level. Surface-converted tubes had excellent physical properties, including good thermal cycling resistance and optical properties.

Figure 8.18a shows microstructure of an MgO-doped PCA tube without codoping with SiO₂, which was sintered at an optically calibrated temperature of 1886 °C for 4 h [68]. The grains were equiaxed with an average grain size of ~30 μm, while small-sized residual pores both at the grain boundaries and in grain interiors could be observed. The tube exhibited good translucency. Microstructure of an MgO–SiO₂-codoped Al₂O₃ tube sintered at 1886 °C for 4 h is shown in Fig. 8.18b. It was found that the localized codoping of one end of prefired MgO-doped Al₂O₃ tubes with a very small amount of colloidal SiO₂ before sintering led to the full conversion of the tube surface to single-crystal sapphire. The remaining core was still dense PCA. Nearly 1/4 of the length of the tube (~4 mm) were fully converted to single crystal across the entire thickness of the tube wall. The remaining length of the tube at the other end was converted in the surface regions of ~200 μm in thickness, a central of PCA core region of 300 μm in thickness was enveloped by the single-crystal layers. Figure 8.19 shows high magnification graphs of the MgO–SiO₂-codoped Al₂O₃ tube of Fig. 8.18b, near to (a) and away from the codoped end (b), respectively.

Fig. 8.18

Optical micrographs of the microstructure: a an MgO-doped PCA tube (not codoped) sintered at 1886 °C for 4 h and b an MgO–SiO₂-codoped Al₂O₃ tube (10 μL SiO₂) sintered at 1886 °C for 4 h, in which codoping of one end of the tube with colloidal SiO₂ before sintering resulted in full densification followed by the full conversion of the surface to single crystal. Reproduced with permission from [68]. Copyright © 2004, John Wiley & Sons

Fig. 8.19

Optical micrographs that show magnified views of the MgO–SiO₂-codoped Al₂O₃ tube in Fig. 3, a near to and b away from the codoped end. Reproduced with permission from [68]. Copyright © 2004, John Wiley & Sons

Mechanism of the conversion to single crystals from an MgO-doped PCA precursor has been studied [69]. The single crystals were grown through controlled AGG at temperatures between 1670 and 1945 °C. It was observed that CaO impurities segregated at the boundary between the single crystal and the polycrystalline matrix, at which a thin layer of wetting intergranular film was formed. The presence of this film facilitated to produce highly mobile grain boundaries that were required to trigger the single-crystal conversion. The measured grain-boundary mobilities agreed well with the values calculated from the data for a grain boundary containing a film with properties of bulk glass. It was found that the highest grain-boundary mobility was an extrinsic effect, rather than intrinsic behavior of the materials.

The samples were prefired Al₂O₃ tubes doped with 500 ppm MgO, with an inner diameter (ID) of 1.25 mm, an outer diameter (OD) of 3.30 mm, and a length of 30 mm. Sintering was conducted in a refractory metal furnace, in which the samples were placed vertically on the end of a 0.1-mm-diameter molybdenum wire. Sintering conditions were N₂–5 %H₂ at 1945 °C, N₂–7 %H₂ at 1840 °C, N₂–10 %H₂ at 1800 °C, and pure H₂ at 1670 °C for 0–2 h.

Single crystals with sizes of up to 30 mm could be grown reproducibly. The size of the single crystals was only limited by the size of the hot zone of the furnace. Figure 8.20 shows an image of the interface between a grown single crystal and the polycrystalline matrix [69]. Such boundaries were found to be curved at all scales and rough on the atomic scale. AGG took place after a certain while at the sintering temperatures. An intergranular film with a thickness of 10–20 nm was observed at the grain boundaries in quenched samples. Figure 8.21 shows a diffuse dark-field image of the boundary, indicating that the film was amorphous. The thickness of film varied only very slightly from individual boundary to the other. Chemical analysis of EDS suggested that calcium is the only detectable segregant at the grain boundary. The normal grains in front of the growing single crystal did not contain such a film. Therefore, the mechanism of the SSCC in polycrystalline alumina is due to the rapid diffusion through an intergranular film that behaves in a manner similar to bulk glass, rather than intrinsic grain growth.

Fig. 8.20

Polished and etched interface between a growing single crystal and the polycrystalline region. Reproduced with permission from [69]. Copyright © 2007, John Wiley & Sons

Fig. 8.21

Diffuse dark-field image of an intergranular film on the boundary of a growing single crystal that was quenched during growth. Reproduced with permission from [69]. Copyright © 2007, John Wiley & Sons

The principle and the current status of solid-state conversion of single crystals from polycrystalline precursors have been well summarized recently [70]. As discussed before, NGG has a linear dependence on boundary migration with respect to the driving force. Figure 8.22 shows schematically the free energy state of an atom across a boundary. When there is an energy barrier Δg*, i.e., activation energy for diffusion, and an energy difference of the atom, Δg, i.e., the driving force, between the two states on grain I and grain II, a net atomic flux between them results in the migration of the boundary. For a system in which the energy difference between the two adjacent grains comes from a nonzero curvature of the boundary, i.e., curvature-driven boundary migration is present, the driving force is expressed as the capillary energy, so that the mobility varies as an exponential function of the activation energy. In this diffusion-controlled boundary migration, it is assumed that the energy state of the atom is only position-dependent, g _I on grain I and g _II on grain II.

Fig. 8.22

Schematic demonstrating the energy state of atoms, g _I and g _II, on the surfaces of two adjacent grains, grain I and grain II, with an atomically disordered boundary. The energy states of an atom before and after jumping across the boundary are the same as those on grain I and grain II, g _I and g _II. Δg* is the activation energy for atom diffusion across the boundary and Δg is the driving force for atom diffusion. Reproduced with permission from [70]. Copyright © 2015, John Wiley & Sons

It is acknowledged that boundary migration involves at least two steps: (i) jump of atoms from one grain to its adjacent one—diffusion across the boundary and then (ii) attachment onto the adjacent grain—interface reaction. In this case, the migration is governed by the slower step, either diffusion or interface reaction [71, 72]. In all the conventional mechanisms, the migration has been assumed to be controlled only by the diffusion. However, if the free energy state for the attachment of the atom is increased to a level that is higher than the original state, the atom will detach and jump back to the original grain, with the free energy diagram shown in Fig. 8.23a. The migration of the boundary is thus governed by a stable attachment, which means that the interface reaction is similar to the case of the two-dimensional nucleation on a single crystal. If the energy increase for the attachment of an atom on a flat surface is lower than the driving force, as shown in Fig. 8.23b, the attached atom will be stable and will not return to the original grain. In this case, the diffusion of atoms governs the overall kinetics.

Fig. 8.23

Schematic of the energy state of an atom before and after jumping across a boundary with an atomically ordered structure, for the cases of the energy increase of the attached atom a larger and b smaller than the driving force for atom diffusion, Δg. Reproduced with permission from [70]. Copyright © 2015, John Wiley & Sons

According to the mean-field concept for boundary migration, every individual grain has its own driving force, depending on its size relative to the average size, so that the driving force for growth of grains in a polycrystalline system has a distribution, with the largest grain having the maximum value, Δg _max [71, 72]. Grain growth behavior is then governed by the value of Δg _max relative to Δg _c. The principle of microstructural evolution is deduced for solid/liquid two-phase systems with the coupling effect of Δg _max and Δg _c. Totally, there are four types of grain growth behavior: (i) normal grain growth (NGG) if Δg _c = 0, (ii) pseudo-normal grain growth (PNGG) if 0 < Δg _c ≪ Δg _max, (iii) abnormal grain growth (AGG) if 0 < Δg _c ~ Δg _max, and (iv) stagnant grain growth (SGG) if Δg _max ≪ Δg _c.

In order for solid-state conversion of single crystals, grain growth in the matrix should be suppressed. Preferably, the condition of Δg _max < Δg _c should be maintained during the conversion, while the driving force for the growth of the seed crystal, Δg _seed, should be larger than Δg _c. Therefore, it is necessary to adjust Δg _max and Δg _c. The maximum driving force is determined by the average grain size and the grain size distribution. As a result, the properties of the initial powder determine the magnitude of Δg _max at the beginning of the sintering. The critical driving force Δg _c is dependent on temperature, doping, and atmosphere, e.g., oxygen partial pressure. In solid-state conversion experiments, the seed crystal can be placed either on top of the sintered polycrystalline ceramics or embedded within the powder compact, as schematically shown in Fig. 8.24 [70]. The seed crystal can also be created through nucleation from the polycrystalline matrix by using temperature gradient or dopant.

Fig. 8.24

Schematics illustrating the solid-state conversion of single crystals by a diffusion bonding and b embedding of a seed crystal. Reproduced with permission from [70]. Copyright © 2015, John Wiley & Sons

8.7 Grain-Boundary Mobility

For single-phase solids, the grain-boundary mobility M _b is called intrinsic boundary mobility, which is defined by Eq. (8.30), so that the grain growth is controlled by the diffusion of the atoms in the grains across the grain boundary. In this case, the effects of various other factors, such as dopants, impurities, secondary phases and pore, which are almost always present in ceramics, on the rate of atom diffusion across the grain boundary, are neglected. In practice, boundary mobilities obtained from experimental grain growth data are usually significantly lower than the intrinsic mobility predicted by the theories.

8.7.1 Effect of Fine Second-Phase Particles

It is assumed that a polycrystalline solid contains randomly dispersed fine second-phase particles, also known as fine inclusions or precipitates, which are insoluble and immobile in the system. When a grain boundary encounters a fine particle during its movement driven due to its curvature, it will be pinned by the particle, while the rest portion of the grain boundary continues to move. The grain boundary will break away only as the rest portion has moved for a sufficiently far distance. Therefore, if the grain boundary encounters a sufficient number of particles, it could be entirely pinned, i.e., the motion of the grain boundary is completely inhibited. This scenario can be described by using two models.

If the pinning particles are assumed to be monosized, spherical, insoluble, immobile and randomly distributed in the polycrystalline solid, for a grain boundary with principal radii of curvature, a ₁ and a ₂, the driving force per unit area for the motion of the grain boundary is given by [73]:

$$F_{\text{b}} = \gamma_{\text{gb}} \left( {\frac{1}{{a_{1} }} + \frac{1}{{a_{2} }}} \right).$$

(8.48)

If both a ₁ and a ₂ are proportional to the grain size G, there is

$$F_{\text{b}} = \frac{{\alpha \gamma_{\text{gb}} }}{G},$$

(8.49)

where α is a geometrical shape factor, e.g., α = 2 for a spherical grain. When the grain boundary intersects a particle, it is dragged by the particle, as shown in Fig. 8.25a, b. Due to the dragging effect of the particle, the grain boundary needs additional work to migrate, as compared to a particle-free boundary, i.e., there is a retarding force applied to the grain boundary. If r is the radius of the inclusion, as shown in Fig. 8.26c, the retarding force of the particle applied to the boundary is given by

Fig. 8.25

Interaction of a grain boundary with an immobile particle. a Approach of the boundary toward the particle. b Interaction between the grain boundary and the particle leading to a retarding force on the boundary. c Detailed geometry of the particle–grain boundary interaction. Reproduced with permission from [4]. Copyright © 2003, CRC Press

Fig. 8.26

Sketch of the solute drag effect produced by the segregation of dopants to the grain boundaries. a Symmetrical distribution of the dopant in the region of a stationary grain boundary. b For a moving boundary, the dopant distribution becomes asymmetrical if the diffusion coefficient of the dopant atoms across the boundary is different from that of the host atoms. The asymmetrical distribution produces a drag on the boundary. c Breakaway of the boundary from the dopant leaving a solute cloud behind. Reproduced with permission from [4]. Copyright © 2003, CRC Press

$$F_{\text{r}} = \gamma_{\text{gb}} \cos \theta (2\pi r\sin \theta ).$$

(8.50)

Therefore, the retarding force is the product of the perimeter of contact and the grain-boundary tension, which is in an opposite direction to that of the grain-boundary migration. At θ = 45°, sinθcosθ = 1/2, so that the retarding force is maximized, which is given by

$$F_{\text{r}}^{\hbox{max} } = \pi r\gamma_{\text{gb}} .$$

(8.51)

If there are N _A inclusion particles per unit area in the grain boundary, the maximum retarding force per unit area of the boundary is given by

$$F_{\text{d}}^{\hbox{max} } = N_{\text{A}} \pi r\gamma_{\text{gb}} .$$

(8.52)

Although it is difficult to determine N _A, it is related to N _V, the number of inclusions per unit volume, which is given by

$$N_{\text{A}} = 2rN_{\text{V}} .$$

(8.53)

If the volume fraction of the inclusions in the solid is f, there is

$$N_{\text{V}} = \frac{f}{{(4/3)\pi r^{3} }}.$$

(8.54)

When N _A in Eq. (8.52) is substituted with N _V determined by Eqs. (8.53) and (8.54), the retarding force becomes:

$$F_{\text{d}}^{\hbox{max} } = \frac{{3f\gamma_{\text{gb}} }}{2r}.$$

(8.55)

The net driving force per unit area of the grain boundary is thus given by

$$F_{\text{net}} = F_{\text{b}} - F_{\text{d}}^{\hbox{max} } = \gamma_{\text{gb}} \left( {\frac{\alpha }{G} - \frac{3f}{2r}} \right).$$

(8.56)

When F _net = 0, the grain boundary stops migrating, which occurs if the following equation is valid:

$$G = G_{L} = \frac{2\alpha }{3}\frac{r}{f},$$

(8.57)

where G _L is called the limiting grain size. Equation (8.57) is also known as the Zener relationship [73], which means that the limiting grain size is proportional to the size of the inclusion particle and inversely proportional to the volume fraction of inclusion particle. Although there have been various modifications to the Zener model, the dependence of G _L on f is the same [74–77].

Monte Carlo computer simulation has been modified to analyze NGG of single-phase solids that are dispersed with fine secondary phase particles that are assumed to be monosized, spherical, insoluble, immobile, and randomly distributed [34, 78–80]. It is found that the grain growth is finally limited at a specific size. During the growing of the grains, the microstructures have the characteristics of NGG, with the same grain size distribution and growth exponent as those of the systems without the secondary phase inclusions. Comparatively, the simulated microstructures for NGG with the presence of inclusions possess grains with irregular shapes.

It is also revealed that both the time used to reach the limiting grain size and the value of the limiting grain size decrease with increasing volume fraction of the secondary phase particles, f. Furthermore, when the total number of inclusions is constant, the fraction of inclusions $\phi_{\text{p}}$ that are located at the grain boundaries decreases with time. This occurrence becomes more and more pronounced, with decreasing volume fraction of the secondary phase particles, f. The limiting grain size G _L is given by

$$G_{\text{L}} = K_{\text{S}} \frac{r}{{\left( {\varphi_{\text{p}} f} \right)^{1/3} }},$$

(8.58)

where K _S is a constant and r is radius of the inclusions. Comparatively, the Zener model overestimates the driving force for grain growth, because the effect of the inclusions on the curvature of the boundary is neglected, while only the work to drag the inclusion is considered. Disagreement is occasionally observed between the simulation results and experimental data, demonstrating the complicated situations of real materials [81–88].

8.7.2 Effect of Dopants–Solute Drag

Dopant is also called solute, which is dissolved as solid solution in polycrystalline solids. If there is an interaction potential for the solute to be attracted to or repelled from the grain boundary, the solute atoms or ions will have a nonuniform distribution at the grain boundaries. The interaction could be due to lattice strain energy caused by size mismatch between the solute and host ions and/or electrostatic potential energy for aliovalent solutes.

When the grain boundary is at a stationary state, the concentration profiles of the solute ions at both sides of the boundary are symmetrical, as shown in Fig. 8.26a. Because the forces of interaction at the two sides are balanced, the net force of interaction is zero. Once the boundary starts to migrate, the profiles of the dopant concentration at both sides will become asymmetrical, because the diffusion rate of the solute ions across the boundary is different from that of the host diffusion, as shown in Fig. 8.26b. This asymmetry of dopant concentration profile produces a retarding force or drag applied to the grain boundary, so as to decrease the driving force for migration of the boundary. When the driving force for the migration of the grain boundary is sufficiently high, the boundary will break away from the solute, which also known as solute cloud, as shown in Fig. 8.26c. In this case, mobility of the grain boundary is close to its intrinsic value. Various models have been developed to describe grain-boundary migration with solute drag [89–93].

The chemical potential of the solute atoms in the near grain-boundary region is given by

$$\mu = kT\ln C(x) + U(x) + U_{0} ,$$

(8.59)

where C(x) and U(x) are concentration and energy functions of x, while U ₀ is a constant, such that U(∞) = 0. At steady-state conditions, the composition profile of the solute can be described by the following equation:

$$\frac{{{\text{d}}C}}{{{\text{d}}t}} = - v_{\text{b}} \frac{{{\text{d}}C}}{{{\text{d}}x}}.$$

(8.60)

According to diffusion equation, the flux of the solute atoms is given by

$$J = - \frac{{D_{\text{b}} C}}{\Omega kT}\frac{{{\text{d}}\mu }}{{{\text{d}}x}},$$

(8.61)

where D _b is the diffusion coefficient for the solute atoms across the grain boundary. According to Eq. (8.59), Eq. (8.61) can be rewritten as follows:

$$J = - \frac{{D_{\text{b}} }}{\Omega }\frac{{{\text{d}}C}}{{{\text{d}}x}} + \frac{{D_{\text{b}} C}}{{\Omega kT}}\frac{{{\text{d}}U}}{{{\text{d}}x}}.$$

(8.62)

The concentration profile of the solute can now be calculated from the continuity, which is given by

$$\frac{{{\text{d}}J}}{{{\text{d}}x}} + \frac{1}{\Omega }\frac{{{\text{d}}C}}{{{\text{d}}t}} = 0,$$

(8.63)

where the boundary conditions are dC/dx = 0, dU/dx = 0, and C(x) = C _∞ at x = ∞. The concentration C _∞ can be taken as that in the interior of the grain. Therefore, C(x) must satisfy the equation:

$$D_{\text{b}} \frac{{{\text{d}}C}}{{{\text{d}}x}} + \frac{{D_{\text{b}} C}}{kT}\frac{{{\text{d}}U}}{{{\text{d}}x}} + v_{\text{b}} (C - C_{\infty } ) = 0.$$

(8.64)

The solute atom applies a force −(dU/dx) to the grain boundary, so that the net force applied by all the solute atoms is given by

$$F_{\text{s}} = - N_{\text{V}} \int\limits_{ - \infty }^{\infty } {[C(x) - C_{\infty } ]} \frac{{{\text{d}}U}}{{{\text{d}}x}}{\text{d}}x,$$

(8.65)

where N _V is the number of host atoms per unit volume. In the analysis, the C(x) derived from Eq. (8.64) is used to calculate F _s with Eq. (8.65). It is found that there is an approximate solution that is valid for both low and high boundary velocities, which is given by:

$$F_{\text{s}} = \frac{{\alpha C_{\infty } v_{\text{b}} }}{{1 + \beta^{2} v_{\text{b}}^{2} }},$$

(8.66)

where the parameters α and β are given by the following expressions:

$$\alpha = 4N_{\text{V}} kT\int\limits_{ - \infty }^{\infty } {\frac{{\sinh^{2} [U(x)/2kT]}}{{D_{\text{b}} (x)}}} {\text{d}}x,$$

(8.67)

$$\frac{\alpha }{{\beta^{2} }} = \frac{{N_{V} }}{kT}\int\limits_{ - \infty }^{\infty } {\left( {\frac{{{\text{d}}U}}{{{\text{d}}x}}} \right)} D_{{\text{b}}} (x){\text{d}}x.$$

(8.68)

In this case, α is the solute drag per unit velocity and per unit dopant concentration in the low boundary velocity limit, while 1/β is the drift velocity of impurity atom moving across the grain boundary. According to Eq. (8.67), solutes with either attractive or repulsive interaction energy, with the same magnitude, will apply a similar drag force to the grain boundary.

The total drag force on the boundary is the sum of the intrinsic drag F _b and the drag due to the dopant atoms F _s, which is given by

$$F = F_{\text{b}} + F_{\text{s}} = \frac{{v_{\text{b}} }}{{M_{\text{b}} }} + \frac{{\alpha C_{\infty } v_{\text{b}} }}{{1 + \beta^{2} v_{\text{b}}^{2} }},$$

(8.69)

where M _b is the intrinsic boundary mobility defined by Eq. (8.30). With the low boundary velocity limit, because the term β ² v ²_b in Eq. (8.69) can be neglected, there is

$$v_{\text{b}} = \frac{F}{{1/M_{\text{b}} + \alpha C_{\infty } }}.$$

(8.70)

At the beginning, the mobility due to solute drag is constant. However, as the velocity increases, the grain boundary continually separates from the solute. When the velocity becomes sufficiently high, the boundary will migrate at its intrinsic velocity. Therefore, a transition is observed from the solute drag-limited velocity to the intrinsic velocity, over a range of driving forces [94–96].

According to Eq. (8.70), the boundary mobility M′_b is equal to v _b/F, which can be expressed in terms of the intrinsic component M _b and the solute drag component M _s:

$$M^{\prime}_{\text{b}} = \left( {\frac{1}{{M_{\text{b}} }} + \frac{1}{{M_{\text{s}} }}} \right)^{ - 1} ,$$

(8.71)

where M _s = 1/αC _∞. If the solute segregates at the grain boundary and the center of the boundary contributes most significantly to the drag effect, α can be expressed by the following equation:

$$\alpha = \frac{{4N_{\text{V}} kT\delta_{\text{gb}} Q}}{{D_{\text{b}} }},$$

(8.72)

where Q is a partition coefficient (>1) for the dopant to distribute between the boundary region and the interior of the grain, such that the solute concentration in the boundary region is QC _∞. Therefore, mobility due to the solute drag is given by

$$M_{\text{s}} = \frac{{D_{\text{b}} }}{{4N_{\text{V}} kT\delta_{\text{gb}} QC_{\infty } }}.$$

(8.73)

This equation indicates that the presence of dopants is the most effective way to reduce the boundary mobility if the diffusion coefficient of the rate-limiting species D _b is low and the segregated solute concentration QC _∞ is high.

8.8 Grain Growth and Pore Evolution

Densification is accompanied by grain growth, while migration of the boundaries during the grain growth leads to coalescence of the pores, so that the average size of the pores also increases, as shown in Fig. 8.27 [3]. Both the grain growth and pore coalescence contribute to the coarsening at the later stages of sintering of ceramics.

Fig. 8.27

Schematic illustration of grain growth accompanied by pore coalescence. Reproduced with permission from [3]. Copyright © 2007, Springer

8.8.1 Thermodynamics of Pore–Boundary Interactions

Whether a pore shrinks or not is determined by the free energy change that accompanies the change in pore size. If the pore shrinks, there will be a decrease in the free energy due to the decrease in the pore surface area, while there is also an increase due to the increase in the grain-boundary area. If the pore shrinks, the former (decrease) must be larger than the latter (increase). The equilibrium shape of the pore is determined by the dihedral angle ψ, which is defined by

$$\cos \frac{\psi }{2} = \frac{{\gamma_{\text{gb}} }}{{2\gamma_{\text{SV}} }},$$

(8.74)

where γ _SV and γ _gb are the interfacial tensions at the pore surface and in the grain-boundary interface, respectively.

In two dimensions, a pore can have a dihedral angle ψ = 120°, which is surrounded by N other grains. The number N is called the pore coordination number (CN). Similar to the case of a grain surrounded by other grains, if N = 6, the pore has straight sides; otherwise, it has convex sides for N < 6 and concave sides for N > 6, as shown in Fig. 8.28. The surface of the pore will move toward its center of curvature, so the pore with N < 6 will shrink, whereas the one with N > 6 will expand. The pore is metastable for N = 6, so that the number is called critical pore CN, or N _c. Accordingly, if the pores have convex sides, i.e., N < 6, the decrease in the pore surface energy is larger than the increase in the grain-boundary energy. In contrast, if the pores have concave sides (N > 6), the decrease in pore surface energy is smaller than the increase in grain-boundary energy. For the metastable pores (N = 6), the increase in grain-boundary energy is balanced by the decrease in pore surface energy.

Fig. 8.28

Pore stability in two dimensions for a dihedral angle of 120° : a shrinking pore, b metastable pore and c growing pore. Reproduced with permission from [4]. Copyright © 2003, CRC Press

The geometrical considerations can be extended to three dimensions, in which the pore is a polyhedron [97]. Taking r _s as the radius of curvature of the circumscribed sphere around a polyhedral pore surrounded by grains, the ratio of the radius of curvature of the pore, r to r _s, depends both on the dihedral angle and the pore CN. When the surfaces of the pore become flat (r = ∞), the pore is metastable. As a result, the pore neither grows nor shrinks. In this case, the ratio r _s/r is zero, with which N _c is defined. For example, when a pore has a dihedral angle of 120°, N _c = 12. Therefore, a pore with N < 12 will shrink, while the one with N > 12 will expand. However, theoretical analysis indicated that, in practice, the pore with N > N _c will grow to a limited size and then stop, instead of grow continuously [98, 99].

Therefore, when powder is poorly compacted, the compact will contain pores that are larger than the grain size. In this case, it is very difficult to densify the compact, especially when the pores have low dihedral angles, due to the large CN. In order to avoid this problem, it is necessary to prepare compacts with high green density and uniform pore size distribution, by using advanced techniques, such as cold isostatic pressing and colloidal methods for compaction.

8.8.2 Kinetics of Pore-Boundary Interactions

With the definition of the pore mobility, it is possible to analyze the influence of the interactions between the pores and the grain boundaries on the kinetics of grain growth. There are two cases that can be considered: (i) the pore becomes separated from the boundary and (ii) the pore remains attached to the boundary.

When v _p < v _b, pore separation will be observed, and this condition can also be written as follows:

$$F_{\text{p}} M_{\text{p}} < FM_{\text{b}} ,$$

(8.75)

where F is the effective driving force on the boundary. If F _d is the drag force exerted by a pore, then the balance of the forces requires that F _d is equal and opposite to F _p. Considering unit area of the boundary in which there are N _A pores, Eq. (8.75) can be written as follows:

$$F_{\text{p}} M_{\text{p}} < \left( {F_{\text{b}} - N_{\text{A}} F_{\text{p}}} \right)M_{b} ,$$

(8.76)

where F _b is the driving force on the pore-free boundary due to its curvature. Rearranging Eq. (8.76), the condition for pore separation can be expressed as follows:

$$F_{\text{b}} > N_{\text{A}} F_{\text{p}} + \frac{{F_{\text{p}} M_{\text{p}} }}{{M_{\text{b}} }}.$$

(8.77)

The condition for pore attachment to the boundary is v _p = v _b, which can also be written as follows:

$$F_{\text{p}} M_{\text{p}} = \left( {F_{\text{b}} - N_{\text{A}} F_{\text{p}} } \right)M_{\text{b}} .$$

(8.78)

Putting v _p = F _p M _p = v _b Eq. (8.78) and rearranging, there is

$$v_{\text{b}} = F_{\text{b}} \frac{{M_{\text{p}} M_{\text{b}} }}{{N_{\text{A}} M_{\text{b}} + M_{\text{p}} }}.$$

(8.79)

Two limiting conditions can be defined. When N _A M _b ≫ M _p, there is

$$v_{\text{b}} = \frac{{F_{\text{b}} M_{\text{p}} }}{{N_{\text{A}} }}.$$

(8.80)

The effective driving force on the boundary is F = F _b − N _A F _p, and from Eq. (8.78), there is F = v _p/M _b. From v _p = v _b = F _b M _p/N _A, there is F = F _b M _p/N _A M _b ≪ F _b. The driving force on the boundary is almost balanced by the drag of the pores, while the boundary migration is limited by the pore mobility. This condition is referred to as pore control. The other limiting condition is N _A M _b ≪ M _p, in which case:

$$v_{\text{b}} = F_{\text{b}} M_{\text{b}} .$$

(8.81)

The drag exerted by the pores is N _A F _p = N _A(F _b M _b/M _p) ≪ F _b. The presence of the pores has almost no effect on the boundary velocity, which is a condition known as boundary control.

8.8.3 Grain Growth Kinetics

With the simplified model for nearly spherical isolated pores on the grain boundary, the equations for the grain growth kinetics can be derived, if it is assumed that the grain growth is controlled by the pore mobility, i.e., pore control. If pore migration occurs through surface diffusion, there is

$$v_{\text{b}} \approx \frac{{{\text{d}}G}}{{{\text{d}}t}} = \frac{{F_{\text{b}} }}{{N_{\text{A}} }}\frac{{D_{\text{s}} \delta_{\text{s}}\Omega }}{{\pi kTr^{4} }}.$$

(8.82)

Taking F _b ≈ 1/G, N _A ≈ 1/X ² ≈ 1/G ², where X is the interpore distance, and assuming that the coarsening is due to the grain growth and pore coalescence, so that r ≈ G. Rearranging Eq. (8.82) gives

$$\frac{{{\text{d}}G}}{{{\text{d}}t}} = \frac{{K_{1} }}{{G^{3} }},$$

(8.83)

where K ₁ is a constant at a given temperature. Integration of Eq. (8.83) yields

$$G^{4} = G_{0}^{4} + K_{2} t,$$

(8.84)

where G ₀ is the grain size at t = 0 and K ₂ is a constant. Similarly, grain growth equations can be derived by the same procedure for the other mechanisms.

Using the general form of the grain growth equation, G ^m = G ^m₀  + Kt, the exponent m for the various mechanisms can be obtained. Except for the mechanism involving solution of second-phase particles (m = 1), the m values lie in the range 2–4. In many ceramics, m = 3 has been reported. Therefore, this value can correspond to at least five mechanisms. In other words, the m values determined from grain growth data cannot be reliably used to imply physical significance.

8.9 Simultaneous Densification and Grain Growth

In solid-state sintering, the processes of densification and grain growth (coarsening) are usually discussed separately. However, at the final stage of sintering, the two processes take place simultaneously with their rates have mutual influence. To fully understand and control the sintering process, it is necessary to consider both densification and coarsening and their interaction. Because each process by itself is already, it is unrealistic to have a theoretical model that is able to predict the coupling of densification and coarsening. Therefore, in practice, simpler approaches are generally employed to have a qualitative understanding of the interaction. As a reference, two models are discussed in this part: (i) Brook model and (ii) Yan, Cannon and Chowdhry model.

Various theoretical models to describe simultaneous densification and grain growth, as well as the transition to AGG, have been well established [100, 101]. It is assumed that an idealized final-stage microstructure consists of a nearly spherical pore on at isolated grain boundary, the considerations in this case include the transition from pore drag-controlled boundary migration to intrinsic or solute drag boundary migration, with the pores either attached or separated from the boundary, which are as functions of grain size G and pore size 2r. As mentioned earlier, there are two limiting cases: pore control and boundary control. The conditions that separate these two cases are represented by a curve, called the equal mobility curve, and defined by the condition that the pore mobility is equal to the boundary mobility, which is,

$$N_{\text{A}} M_{\text{b}} = M_{\text{p}} .$$

(8.85)

If the pore migration occurs through surface diffusion, the appropriate relations for M _b and M _p can be derived. If N _A ≈ 1/X ², where X is the interpore distance, and X ≈ G, Eq. (8.82) gives

$$G_{\text{em}} = \left( {\frac{{D_{\text{a}} \pi }}{{D_{\text{s}} \delta_{\text{s}} \delta_{\text{gb}} }}} \right)^{1/2} r^{2} ,$$

(8.86)

where G _em is the grain size at the condition of the equal mobility. Using logarithmic axes plot G versus 2r, the equal mobility condition is represented by a straight line with a slope of 2.

In determining the conditions for separation of the boundary from the pore, the maximum force exerted by the grain boundary on a pore to drag it along is given by Eq. (8.51), which is

$$F_{\text{p}}^{\hbox{max} } = \pi r\gamma_{\text{gb}} .$$

(8.87)

The maximum velocity for the pore is therefore given by:

$$v_{\text{p}}^{\hbox{max} } = M_{\text{p}} F_{\text{p}}^{\hbox{max} } .$$

(8.88)

If the velocity of the boundary with the attached pore exceeds $v_{\text{p}}^{\hbox{max} } ,$ separation will occur. The limiting condition for separation can therefore be written as follows:

$$v_{\text{b}} = v_{\text{p}}^{\hbox{max} } .$$

(8.89)

Substituting for v _b in Eq. (8.79), there is

$$\frac{{M_{\text{b}} M_{\text{p}} }}{{N_{\text{A}} M_{\text{b}} + M_{\text{p}} }}F_{\text{b}} = M_{\text{p}} F_{\text{b}}^{\hbox{max} } .$$

(8.90)

When N _A ≈ 1/X ², there is

$$G_{\text{sep}} = \left( {\frac{\pi r}{{X^{2} }} + \frac{{D_{\text{s}} \delta_{\text{s}} \delta_{\text{gb}} }}{{D_{aa} r^{3} }}} \right)^{ - 1} ,$$

(8.91)

where G _sep is the grain size when the boundary separates from the pore. If X ≈ G, Eq. (8.91) can be written as

$$\left( {\frac{{D_{\text{s}} \delta_{\text{s}} \delta_{\text{gb}} }}{{D_{aa} r^{3} }}} \right)G_{\text{sep}}^{2} - G_{\text{sep}} + \pi r = 0.$$

(8.92)

The solution to this quadratic equation determines the separation curve.

It is to be expected that factors such as grain size distribution, the number of pores at the grain boundaries, and the dihedral angle all have effect on the simple relationships between the grain-boundary curvature and pore size for the separation condition [98, 99]. In a refined model, it is demonstrated that when pore separation occurs, the assumption of X ≈ G is not valid [102–105]. The effect of dihedral angle has also been considered [106–108]. As shown in Fig. 8.29, the effective area of the boundary intersected by a pore with a constant volume increases as the dihedral angle decreases, resulting in greater pore drag and less boundary separating from the pore [106].

Fig. 8.29

Schematic of the distortion that accompanies the motion of pores attached to grain boundaries and the atomic flux from the leading surface to the trailing surface. Reproduced with permission from [106]. Copyright © 1983, John Wiley & Sons. Adopted from permission from [3]. Copyright © 2007, Springer

The effects of a grain size distribution and solute drag have also been incorporated into the basic model [109, 110]. The critical density at which pore separation occurs is significantly lower for the powder compacts with a wide distribution of particle size than for the powder with a narrow size distribution. Separation of only a fraction of the pores from the boundary is sufficient to cause AGG, which is different from the assumption in the simple analysis that all pores should separate from the boundaries.

Another theoretical analysis of simultaneous densification and grain growth is the Yan, Cannon and Chowdhry model [110]. In this model, the final-stage microstructure is assumed to consist of tetrakaidecahedral grains with spherical pores at the grain corners, the dependences of the achievable final density and the extent of coarsening on the ratio of the coarsening rate to the densification rate can be determined. The instantaneous rate of change in the pore radius r is given by:

$$\frac{{{\text{d}}r}}{{{\text{d}}t}} = \left( {\frac{{{\text{d}}r}}{{{\text{d}}t}}} \right)_{P} + \left( {\frac{{{\text{d}}r}}{{{\text{d}}t}}} \right)_{G} ,$$

(8.93)

where the first term on the right-hand side is the rate of change in the pore size at constant porosity, due to the coarsening process, which is a positive value, while the second term is the rate of change at constant grain size, due to the densification process, which is a negative value. For a coarsening process involving grain growth and pore coalescence, there is

$$\frac{{{\text{d}}r}}{{{\text{d}}t}} = \frac{r}{G}\left( {\frac{{{\text{d}}G}}{{{\text{d}}t}}} \right)_{P} + \left( {\frac{{{\text{d}}r}}{{{\text{d}}t}}} \right)_{G} .$$

(8.94)

Since dG/dr = (dG/dt)/(dr/dt), there is

$$\frac{{{\text{d}}G}}{{{\text{d}}r}} = \frac{{{\text{d}}G/{\text{d}}t}}{{(r/G)({\text{d}}G/{\text{d}}t) + ({\text{d}}r/{\text{d}}t)_{G} }}.$$

(8.95)

This equation can be written as follows:

$$\frac{{{\text{d}}\ln G}}{{{\text{d}}\ln r}} = \frac{\Gamma }{{\Gamma - 1}},$$

(8.96)

where Γ is the ratio of the coarsening rate to the densification rate, which is given by:

$$\Gamma = - \frac{{(r/G)({\text{d}}G/{\text{d}}t)}}{{({\text{d}}r/{\text{d}}t)_{G} }}.$$

(8.97)

In this case, Γ is calculated by assuming specific models for densification and grain growth, where only one densification mechanism and one coarsening mechanism are dominant.

The Yan, Cannon and Chowdhry model has been modified by including the conditions to separate the boundary from the pore [111, 112]. The calculated results for Al₂O₃, where the densification is controlled by lattice diffusion, while the grain growth or coarsening is controlled by surface diffusion-controlled pore drag, are shown in Fig. 8.30 [112]. Due to the combined features of grain size versus density trajectory and the conditions for separation, the treatment is effective to discuss the influence of dopants, temperature, and other variables on microstructural evolution. It is observed that the separation region is shifted to larger grain sizes, when MgO is used as a dopant. This is because the presence of MgO decreases the grain-boundary mobility of Al₂O₃. As a result, the grain size versus density trajectory bypasses the separation region. Flattening of the trajectory means that densification rate is increased, while the grain growth rate is suppressed. In addition, the trajectory can also be flattened by controlling the heating steps during the sintering, e.g., two-step sintering, as discussed later.

Fig. 8.30

Grain size–density map for Al₂O₃, illustrating the effect of raising the surface diffusion coefficient by a factor of 4, reducing the lattice diffusion coefficient by a factor of 2, and reducing the grain-boundary mobility by a factor of 34. This has the effect of flattening the grain size–density trajectory and raising the separation region to larger grain sizes, thereby making it possible to sinter to full density. Reproduced with permission from [112]. Copyright © 1990, John Wiley & Sons

8.10 Strategies to Control Microstructure of Ceramics

Most applications of ceramics require products with high-density and controlled (small) grain size [110, 113–117]. The discussion of the previous section indicates that when suitable processing procedures are employed, such an end point is achievable through fabrication routes that have the effect of increasing the ratio of the densification rate to the grain growth (coarsening) rate or avoiding the separation region (abnormal grain growth). The principles governing these fabrication routes are discussed as follows.

8.10.1 Sintering at External Pressures

When compared to sintering, hot pressing produces an increase in the driving force for densification. For an equivalent microstructure, the dependence of the densification rate on the driving force can be written as follows:

$$\dot{\rho }_{\text{hp}} \sim (\Sigma + p_{\text{a}} ),\quad \dot{\rho }_{\text{s}} \sim \Sigma ,$$

(8.98)

where the subscripts in $\dot{\rho }_{\text{hp}}$ and $\dot{\rho }_{\text{s}}$ stand for hot pressing and normal sintering, respectively, Σ is the sintering stress and p _a is the applied pressure. Since the grain-boundary mobility is not changed, there is

$$\dot{G}_{\text{hp}} \approx \dot{G}_{\text{s}} .$$

(8.99)

When p _a ≫ Σ, there is $\left( {\dot{\rho }/\dot{G}} \right)_{\text{hp}} \gg \left( {\dot{\rho }/\dot{G}} \right)_{\text{s}} .$ Therefore, by using hot pressing, it is possible to produce ceramics with high density coupled with small grain size, due to the ability to increase the value of $\dot{\rho }/\dot{G}.$ This is the simple reason why HP, HIP, and SPS could be used to produce ceramics with high densification and small grain sizes.

8.10.2 Use of Dopants and Inclusions

The effects of dopants on microstructure of ceramics are important but complex. If the dopants segregate at the grain boundary, they will reduce the boundary mobility by the so-called solute drag effect. In this case, there is $\dot{G}_{\text{doped}} < \dot{G}_{\text{undoped}} .$ Dopants can also influence the densification process, although this effect is usually relatively weaker compared to the effect on grain growth rate. The effectiveness of dopants is reflected by the ability to reduce the value of $\dot{G}$ or that to increase the value of $\dot{\rho }/\dot{G}.$

The role of inclusions sometimes is similar to that of dopants. If the drag on the grain boundary is sufficiently strong, the boundary could be pinned. Similarly, their effect on densification is not very significant. The effectiveness of inclusions is almost the same as that of dopants, in terms of $\dot{G}$ or $\dot{\rho }/\dot{G}.$

It has been that similar dopants could have different and even opposite effects on grain growth. One example has been shown for AlON transparent ceramics doped with Y₂O₃ and La₂O₃ [118]. In this study, γ-AlON powder was mixed with different concentrations of Y₂O₃ (99.99 % purity) and La₂O₃ (99.99 % purity) by using high-energy ball milling. The mixtures were then dried and passed through a 200-mesh sieve. Cylindrical pellets with a diameter of 20 mm and a thick of 4 mm were pressed at a uniaxial pressure of 5 MPa and then isostatically pressed at a pressure of 200 MPa. The pellets with a relative density of about 50 % were pressureless sintered at 1820–1950 °C for different durations in nitrogen.

Figure 8.31 shows optical transmittance and grain size of the AlON transparent ceramics, as a function of concentration of Y₂O₃ and La₂O₃ [118]. The grain size increased gradually with increasing concentration of Y₂O₃ from 0.06 to 0.19 wt%, which means that the presence of Y³⁺ enhanced the mobility of grain boundary. This was probably attributed to the formation of Y₂O₃–Al₂O₃ liquid phase at the grain boundaries, which significantly enhanced the mass transfer of the samples during the sintering process, because of the increase in the liquid diffusion coefficient. In contrast, the grain size decreased with increasing content of La₂O₃, as shown in Fig. 8.31b, i.e., La³⁺ acted as a grain-boundary inhibitor. Although two possible reasons, i.e., pore drag and particle pinning mechanisms, could be employed to explain the observation, given the fact that the doping level was relatively low, the particle pinning was not likely to be the key mechanism. Therefore, dragging effect of the solute ions La³⁺ along the pore-free sections of the boundaries was the grain growth inhibition mechanism.

Fig. 8.31

Reproduced with permission from [118]. Copyright © 2015, Elsevier

The different effects of the two dopants could be combined to form a codopant for AlON. On the one hand, a small amount of La³⁺ could largely decelerate the mass transfer and hence suppressed the grain growth. At the same time, a low grain-boundary mobility would be more effective for the pores to escape along the grain boundaries instead of from interior of the grains. On the other hand, a large quantity of Y³⁺ accelerated the mass transfer during the sintering process, which thus facilitated the migration atoms toward pores and enhanced the elimination of pores. An optimized codoping was 0.12 wt% Y₂O₃ plus 0.09 wt% La₂O₃.

8.10.3 Use of Fine Particles with Uniform Packing

Uniformly compacted fine powders have small pores with low CN (i.e., N < N _c). The densification rate for such a system is higher than for a similar system with heterogeneous packing. Furthermore, if the particle size distribution is narrow, the driving force for grain growth due to the curvature of the boundary is small. The effectiveness of this route can therefore be interpreted in terms of an increase in the value of $\dot{\rho }/\dot{G} .$

8.10.4 Control of Firing Schedule

When a powder system has a higher activation energy for densification than that for grain growth, it is possible to heat it up quickly to a sufficiently high temperature to achieve a high densification without significant grain growth, i.e., $\dot{\rho }/\dot{G} .$ With this principle, new sintering strategies to control grain size and microstructure have emerged, including two-step [116, 117] and multiple-step sintering [119, 120]. Especially, two-step sintering has been widely used to process transparent ceramics [121–127].

Figure 8.32 shows representatively schematic diagrams of normal single-step and two-step sintering [128]. The heating and cooling rates were 100 °C h⁻¹, which can be varied according to the properties of materials or specific requirements. Usually, the first-step temperature (T ₁) is higher than the second-step temperature (T ₂). There are various combinations of the two temperatures, thus providing high flexibility and feasibility.

Fig. 8.32

Heating programs of a single and b two-step sintering methods. Reproduced with permission from [128]. Copyright © 2012, Elsevier

A successful instance has been demonstrated for Y₂O₃ ceramics [116]. The green body was first heated to a higher temperature to achieve an intermediate density and then cooled down a lower temperature, at which the sample was held until it was fully densified. For pure nanosized Y₂O₃, the sample was first heated to 1310 °C and then cooled to 1150 °C, full density was achieved after holding for 20 h, during which there was no grain growth. For different compositions, the scheme should be different.

The key to the two-step sintering is to get a sufficiently high starting density during the first step. It has been shown that, when the density of a ceramic compact is above 70 %, all pores become subcritical and unstable against shrinkage. These pores can be readily filled, so long as it is allowed by the grain-boundary diffusion, even though the particle network is frozen. Generally, densities of >75 % are sufficient to maintain the second-step sintering. The absence of grain growth in second-step sintering can be attributed to kinetics. Grain growth is significantly dynamic, so that the microstructure of the sintered body constantly refreshes. As mentioned earlier, one eighth of all grains would survive when the size of the grains doubles every time. Such an evolution could be an origin of enhanced kinetics. This is the reason why the final-stage sintering always is accompanied by a rapid grain growth. In the two-step sintering, the microstructure form in the first-step sintering at the higher temperature is “frozen” and in the second-step sintering at a lower temperature. In this case, the kinetics is slowed down, but it is still sufficient for densification.

A two-step sintering method, in which the sample was first heat to 1800 °C without dwelling and cooled 1600 °C by holding for 8 h, was used to fabricate transparent YAG ceramics in vacuum (10⁻³ Pa) [125]. The YAG powder was synthesized, from Y(NO₃)₃·6H₂O (>99.9 % purity) and Al(NO₃)₃·9H₂O (>99.9 % purity), by using a coprecipitation method with ammonium hydrogen carbonate as the precipitant. The as-synthesized YAG powders were ball milled with 0.5 wt% sintering aid tetraethoxysilane (TEOS) for 12 h. The milled powders were dry-pressed at 10 MPa into Φ20 mm pellets and then cold-isostatically pressed at 200 MPa. The pressed samples were presintered at 1000 °C for 10 h in air. Finally, the powder compacts were sintered in a molybdenum wire-heated vacuum furnace by using a two-step sintering schedule at a vacuum of 10⁻³ Pa.

During the two-step sintering, the samples were first heated to 1800 °C without soaking, but immediately cooled down and held at 1600 °C for 8 h, i.e., 1800 °C for 0 h + 1600 °C for 8 h. The sintered samples were annealed at 1450 °C for 6 h in air. Two single-step sintering schemes, 1800 and 1600 °C, were included for comparison. For the 1800 °C scheme, the samples were rapidly heated to the sintering temperature and immediately cooled down to room temperature. For the 1600 °C scheme, the samples were sintering at the temperature for 8 h.

Figure 8.33 shows microstructures of samples sintered with different schemes [125]. As shown in Fig. 8.33a, the two-step sintered sample exhibited a dense and pore-free microstructure, consisting of uniform grains of about 4 μm without AGG. However, the single-step sintered samples at 1800 °C for 0 h and 1600 °C for 8 h, as shown in Fig. 8.33b, c, respectively, possessed obvious pores. After reaching 1800 °C, a sufficiently high density was achieved so sustain the two-step sintering, as shown in Fig. 8.33d. The second-step sintering at 1600 °C for 8 h was sufficient to promote the grain-boundary diffusion through the continuous framework formed during the first-step sintering, while effectively suppressing the grain-boundary migration.

Fig. 8.33

SEM images of the ceramics sintered with different schemes: a two-step sintering (1800 °C for 0 h + 1600 °C for 8 h), b single-step sintering at 1800 °C for 0 h, c single-step sintering at 1600 °C for 8 h and d single-step sintering at 1800 °C for 0 h. The images of a–c were from fractured surfaces, while that of d was from polished surface. Reproduced with permission from [125]. Copyright © 2012, Elsevier

8.10.5 Use of Liquid-Phase Sintering

A second-phase that forms a liquid at the firing temperature can provide a fast diffusion path for densification but grain growth by the Ostwald ripening process may also be enhanced. In this case, high density is normally accompanied by appreciable grain growth. This commonly used fabrication approach is the subject of the next chapter.

8.11 Concluding Remarks

Grain and microstructural development during solid-state sintering of polycrystalline ceramics are governed by basic principles. With simple models, equations for kinetics of NGG could be derived, which, however, are usually for the analysis of an isolated grain boundary or a single grain, without considering the topological requirements of space filling. Computer simulations are playing an increasing role in this aspect. The reduction of uniform grain-boundary energy cannot be used to explain AGG. Two possible reasons have been acknowledged: (i) there is a local driving force that is higher than that due to the geometry or (ii) the boundary mobility of a growing grain is higher than that of ordinary boundaries. AGG should be avoided in general ceramic processing, but it can be utilized specifically to realize solid-state crystal conversion from polycrystalline ceramics. Various strategies could be explored to obtain transparent ceramics with high density, together with controlled grain size and desired microstructure.