Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Consider the following deterministic process on a graph \(G=(V,E)\). Initially, every vertex in \(V\) can be either active or passive. A passive vertex can become active depending on the state of its neighbors. Once active, a vertex cannot change its state. Such a process is called bootstrap percolation. In Sect. 2, we will describe some families of graphs and transition rules that have been already studied and what is known about the resulting processes.

The set of active vertices grows monotonically. Therefore, for a finite graph, a fixed point has to be reached after a finite number of steps. If the fixed point is such that all vertices have become active, then we say that the initial set of active vertices percolates on \(G\).

The basic question is to determine the ratio of initial active vertices one needs to choose randomly in order to percolate the whole graph with high probability. More precisely, suppose that the elements of the initial set of active vertices \(A \subseteq V\) are chosen independently with probability \(p\). The problem consists in finding values of \(p\) for which percolation of \(A\) is likely to occur. The least \(p\) for which percolation will happen with probability greater than or equal to \(1/2\) will be called the critical probability.

In the (simple) majority bootstrap percolation [1], each passive vertex \(v\) becomes active if at least \(\lceil \frac{deg(v)}{2} \rceil \) of its neighbors are active, where \(deg(v)\) denotes the degree of node \(v\) in \(G\). In the present paper we study the strict majority bootstrap percolation process. In this case, each passive node \(v\) becomes active if it has strictly more active than passive neighbors. More precisely, it will change if at least \(\lceil \frac{deg(v)+1}{2} \rceil \) of its neighbors are active. Note that if \(deg(v)\) is odd, the rules for the strict and simple majority bootstrap percolation process coincide. Our decision to use strict majority, as opposed to the simple version, is related to our augmentation of a graph with a universal vertex, i.e. one that is connected to every other vertex in the graph. Intuitively, the simple majority percolation process in the augmented graph is somehow equivalent to the strong majority process in the original one.

A natural question to ask about the strict majority bootstrap percolation process is what graphs result in the critical probability being small. This problem, which motivates the present work, has not been addressed yet. Nevertheless, it is possible to conclude, from a paper of Balogh and Pittel [2], that the critical probability of the strict majority bootstrap percolation for random 7-regular graphs is 0.269.

Here we test empirically two different families of graphs. The first class is the set of augmented 2D-tori. The other family is the set of augmented random \(k\)-regular graphs. The results of the numerical experiments, in Sect. 3, show that for the augmented 2D-torus, the estimated critical probability (call it \(p_c\)) is about 0.185. For the augmented random \(d\)-regular graph, we obtain unexpectedly high values for \(p_c\). For “small” values of \(d\), that is \(d\le 16\), we obtain \(p_c>0.33\). This is surprising (especially when \(d=4\)) because the relatively high girth of the graphs and a simple characterization of the vertices that will remain passive suggests that the value for \(p_c\) should be small.

2 Related and Previous Work

A common activation rule in literature is as follows: A passive vertex changes to the active state if at least \(k\) of its neighbors are already active. The resulting process is known as \(k\) -neighbor bootstrap percolation, and was proposed by Chalupa et al. [3]. Since its introduction this percolation process has mainly been studied in the \(d\)-dimensional grid \([n]^d=\{1,\ldots ,n\}^d\) [4–7]. The precise definition of critical probability that has been used is the following:

$$\begin{aligned} p_c([n]^d,k)= \inf \{p \in [0,1]\!: \mathbb {P}_{}\left( A\, \text {percolates on}\, [n]^{d}\right) \ge 1/2\}. \end{aligned}$$
(1)

The result of [9] is the culmination of many efforts aiming to obtain a sharp threshold for \(p_c([n]^d,k)\). The result states that for every \(d \ge k \ge 2\):

$$ p_c([n]^d,k)= \left( \frac{\lambda (d,k)+o(1)}{\log _{(k-1)}n}\right) ^{d-k+1}\!\!, $$

where \(\lambda (d,k) < \infty \) for every \(d \ge k \ge 2\). Bootstrap percolation has also been studied on other graphs such as high dimensional tori [1, 10–13], infinite trees [14–16] and random regular graphs [2, 17].

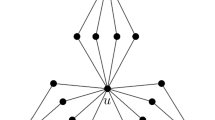
In [18] the authors gave explicit constructions of two (families of) graphs for which the critical probability is also small (but higher than 0.269). The idea behind these constructions is the following. Consider a regular graph of even degree \(G\). Let \(G*u\) denote the graph \(G\) augmented with a single universal vertex \(u\). The strict majority bootstrap percolation dynamics on \(G*u\) has two phases. In the first phase, assuming that vertex \(u\) is not initially active, the dynamics restricted to \(G\) corresponds to the strict majority bootstrap percolation. If more than half of the vertices of \(G\) become active, then the universal vertex \(u\) also becomes active, and the second phase begins. In this new phase, the dynamics restricted to \(G\) follows the simple majority bootstrap percolation (and full activation becomes much more likely to occur). This justifies our interest in the strict majority activation rule.

The two augmented graphs studied in [18] were the wheel \({\textsc {W}}_n = u * R_n\) and the toroidal grid plus a universal vertex \({\textsc {TW}}_n = u*R_n^2\) (where \(R_n\) is the ring on \(n\) vertices and \(R_n^2\) is the toroidal grid on \(n^2\) vertices). For a family of graphs \(\mathcal {G}=(G_{n})_n\), the following parameter was defined (\(A\) again denotes the initial set of active nodes, however now the dynamics is driven by the strict majority bootstrap percolation process):

$$\begin{aligned} p^+_c({\mathcal {G}})=\inf \left\{ p\in [0,1]\!\!: \liminf _{n\rightarrow \infty } \mathbb {P}_{}\left( A\,\text {percolates on}\, G_n\right) = 1 \right\} \!. \end{aligned}$$
(2)

Note that in the last definition the limit of the probability has to be equal to \(1\). This seems to be in conflict with the definition in Eq. 1, in which we demand the probability of percolation to be greater than \(1/2\). There is no contradiction, though. Considering \(\liminf _{n\rightarrow \infty } \mathbb {P}_{}\left( A\, \text { percolates on}\, G_n\right) \) as function of \(p\), it is easy to prove that its value will transition from \(0\) to \(1\) at \(p^+_c({\mathcal {G}})\), i.e. it is a step function. Thus, the definition in Eq. 2 could be rewritten demanding the limit to be greater than \(1/2\).

Now consider the families \(\mathcal {W}=({\textsc {W}}_n)_n\) and \({\mathcal {TW}}=({\textsc {TW}}_n)_{n}\). It was proved in [18] that \(p^+_c({\mathcal {W}})= 0.4030...\), where \(0.4030...\) is the unique root in the interval \([0,1]\) of the equation \(x+x^2-x^3 = \frac{1}{2}\). For the toroidal case it was shown that \(0.35\le p^+_c({\mathcal {TW}})\le 0.372\).

Computing the critical probability of the (one-dimensional) wheel is a trivial task. Nevertheless, if we increase the radius of the vertices from \(1\) to any other constant, then the situation becomes much more complicated. More precisely, let \(R_n(r)\) be the ring where every vertex is connected to its \(r\) closest vertices to the left and to its \(r\) closest vertices to the right. Obviously, \(R_n=R_n(1)\).

Kiwi et al. [19] studied the strict majority bootstrap percolation process in a generalization of the wheel that is called \(r\)-wheel \({\textsc {W}}_n(r) = u * R_n(r)\). A peculiarity of the model in this paper is that the initial state of the universal vertex is always set to 0. This is somewhat arbitrary, but simplifies the analysis and allows to find an upper bound for \(p^+_c({\mathcal {W}}(r))\) when the universal vertex can be initialized randomly. The main result in [19] is that for the class of r-wheels \({\mathcal {W}}(r)\),

$$\lim _{r\rightarrow \infty } p^+_c({\mathcal {W}}(r)) = 1/4.$$

This is the smallest critical probability that has been proved for any class of graphs. We would like to point out that the deterministic counterpart of both the simple majority and the strict majority bootstrap percolation processes have been intensively studied. In fact, bounds have been derived for the minimum number of vertices one needs to activate in order to end up activating the whole graph. These sets of vertices are called irreversible dynamic monopolies or irreversible dynamos [20–29].

3 Experiments and Results

The purpose of our experiments is to estimate \(p^+_c({\mathcal {G}})\) for a given \({\mathcal {G}}\). Informally, we choose an \(n\) which is “large enough”, create \(G\in \mathcal {G}\) of size \(n\). We then activate vertices with probability \(p\) (forcing the universal vertex to \(0\), following [19]) and simulate the strict majority bootstrap percolation process on it until it reaches a fixed point. We then analyze the fixed point and determine whether the initial set percolates on \(G\). We can repeat the experiment several times and compute the fraction of replicas that resulted in percolation on \(G\) (call it \(f\)). Since \(f\) is an estimation of the probability of the initial set percolating on \(G\), we can try different values of \(p\) until \(f\approx 1/2\). We will refer to this particular value of \(p\) as \(p_c\). This will be our estimation of \(p^+_c({\mathcal {G}})\). The goal of our simulation is finding a family of grpahs for which \(p^+_c({\mathcal {G}})<1/4\).

For our simulations we used an in-house program written in C. The total amount of CPU time needed to generate the results we are presenting was approximately 10 days.

3.1 Augmented Toroidal Grid

By analogy with the generalization of the wheel in [19], we define an augmented torus. Let \(R_n^2\) be as before and let \(R_n^2(r)\) be the graph so every node \(v\) is connected to all vertices whose Moore distance from \(v\) is less than or equal to \(r\). Now \({\textsc {TW}}_n(r) = u * R_n^2(r)\). We finally define the class of \(r\)-tori \({\mathcal {TW}}(r)= ({\textsc {TW}}_n(r))_n\). Intuitively, they are tori of \(n\times n\) size, with vertices connected to all other vertices at distances no greater than \(r\). Besides, there is the universal vertex connected to all other nodes in the grid.

For the experiments, we run our simulator for \(r=1,2,3\). For each value of \(r\) we tried different values of \(p\) and measured \(f\). As it is well known, some percolation problems are hard to study using simulations, because the asymptotic behavior of the system as (say) \(n\) grows is not apparent until \(n\) is so large that simulation is not feasible. As a simple (heuristical) test, we run our simulations for \(n=2000\) and \(n=4000\). By comparing the estimations of \(p_c\) we obtained from both variants we can have a rough idea of the reliability of our results.

Due to running time constraints we had to adjust the number of replicas we used to compute \(f\). For \(r=1, n=2000\) we run 100 replicas per value of \(p\) (that is, a single data point in Fig. 1). For \(r=1, n=4000\) we used 20 replicas per point. For \(r=2, n=2000\) we computed \(50\) replicas per point and for \(r=2, n=4000\) we did 20 replicas per point. Similarly, for \(r=3\) and \(n=2000,400\) we had 100 and 25 replicas per point respectively.

Figures 1, 2 and 3 describe the \(r=1,2\) and \(3\) cases respectively.

Fig. 1.
figure 1

\(f\) vs. \(p\) for \({\textsc {TW}}_n(1)\). \(n=2000,4000\)

Full size image
Fig. 2.
figure 2

\(f\) vs. \(p\) for \({\textsc {TW}}_n(2)\). \(n=2000,4000\)

Full size image
Fig. 3.
figure 3

\(f\) vs. \(p\) for \({\textsc {TW}}_n(3)\). \(n=2000,4000\)

Full size image

3.2 Random Regular Graphs

Since they have been also heavily studied, we run experiments using random regular graphs. There is another powerful motivation though. Consider a 4-regular graph. It is easy to prove that if there is a cycle where all vertices belonging to it are passive, they will all remain passive under the dynamics imposed by the by the strict majority activation rule. Moreover, this condition characterizes precisely the set of vertices that never become active. Since random regular graphs have a “large” girth, in a probabilistic sense, the intuition is that with high probability, those cycles will have at least one active node unless, of course, \(p\) is very small. This intuition led us to hope for a very small \(p_c\).

Given \(n\) and \(k\), generating \(k\)-regular graphs with \(n\) vertices (with uniform probability) is a very challenging computational task. The intuitive and simple algorithms are slow while faster methods are very cumbersome to implement. For an introduction to the problem algorithms see [30]. To reduce development time we used some existing code written by Golan Pundak, uploaded to MATLAB central. This function generates a \(k\) regular random graph with \(n\) vertices using the pairing model, also described in [30]. The graphs generated by this code were fed into our simulator.

The running times for generating each graph were long. The extreme case was \(k=50, n=100000\): it takes 2 days of CPU time to create a single graph. Therefore we adopted the following strategy: for \(n=100000\), for \(k=4,8,16,50\), we generated a single graph. That is, we generated four graphs in total. For each one of these graphs we estimated the value of \(p_c\) and the results are displayed in Fig. 4. As a matter of fact we obtained the analogous results for \(n=2000\) and \(n=10000\). The values we computed for \(p_c\) changed very little with \(n\). The differences where in the third or fourth significative digits. Therefore the resulting plots would have been almost the same as Fig. 4 and hence we omitted them.

Fig. 4.
figure 4

\(p_c\) vs \(d\) for d-regular random graphs with \(n=100000\).

Full size image

3.3 Analysis of the Simulations

Our experiments for \({\mathcal {TW}}(r)\) show a \(p_c\approx 0.2963\) for \(r=1\), and \(p_c\approx 0.187\) for \(r=2\). Since the estimations were very similar regardless of the values of \(n\), our heuristic suggests \(n\) was large enough for the simulations to capture the asymptotic behavior. Therefore \(p_c\) should be a reasonable approximation to \(p_c^+\). When \(r=3\) there is a bigger discrepancy between the \(n=2000\) and \(n=4000\) runs than before. For the former, \(p_c\approx 0.19\). For the latter, \(p_c\approx 0.20\). We suspect \(p_c < 0.185\) if \(n\) is large enough. This is based on some preliminary simulation results, but considering it would require weeks of CPU time (with the current software) to explore the \(r=3, n=8000\) case we do not expect the approach based on direct simulations to scale up much more.

Nonetheless, obtaining estimations below \(0.19\) is encouraging as they suggest \(\mathcal {G}=({\textsc {TW}}_n(2))_n\) is a good candidate for having the new lowest known \(p_c^+(\mathcal {G})\). Further, the successive values for \(p_c\) we obtained when increasing \(r\) were \(0.2963\), \(0.187\) and \(0.185\). Although the last one is still dubious, this points to a decreasing monotonicity of \(p_c^+({\mathcal {TW}}(r))\) w.r.t. \(r\). Based on these simulations and previous results in [19], we expect it to be the case.

For the random \(d\)-regular graphs (see Fig. 4), we note three features in the results. The first one is that the estimations for \(p_c\) are larger than what we obtained for the augmented tori or has been proved for wheels. This is surprising since our heuristic argument suggested the opposite had to happen. Another feature is the similarity of \(p_c\) values for different \(d\)’s. Besides, there is the lack of monotonicity in \(p_c\) w.r.t. \(d\). We are unable at this time to explain these phenomena. Finally, we see how our addition of the universal vertex can dramatically affect the value of the critical probability. For our model, when \(d=4\), we obtain \(p_c\approx 0.37\). This contrasts with the case without the universal vertex, were \(p_{c}^{+}(\mathcal {G})=0.667\), as proved by Ballogh and Pittel in [2].

4 Conclusion and Open Problems

We performed numerical experiments simulating the strict majority bootstrap percolation process on two families of graphs. The objective is to advance toward the resolution of this problem: Is there a class \(\mathcal {G}=(G_n)_n\) of graphs such that the critical probability \(p_{c}^{+}(\mathcal {G})\) is \(0\), and if not, what is the smallest achievable critical probability?

Our experiments strongly suggest that determining \(p_{c}^{+}({\textsc {TW}}_n(2))_n\) will yield a lower value than the lowest known today \(p_{c}^{+}(\mathcal {TW}(r))=1/4\). Further, the question of whether or not \(p_{c}^{+}({\textsc {TW}}_n(r))_n\) is monotonically decreasing w.r.t. \(r\) is open, although we conjecture it is the case. From the above, it would be interesting to calculate the limit (as \(r\rightarrow \infty \)) of \(p_{c}^{+}({\textsc {TW}}_n(r))_n\), or at least to determine if it is zero or not. The same questions can be generalized to higher dimensional augmented tori.

Finally, in spite of the \(k\)-random regular graphs failing dramatically at yielding a small value for \(p_c\), it would be interesting to know why the intuition was invalid, why the value of \(p_c\) almost did not change for different values of \(k\) and determine whether \(p_c^+(\mathcal {G})\) is not monotonic.