Cycle Equivalence of Finite Dynamical Systems Containing Symmetries

Abstract

Two dynamical systems are cycle equivalent if they are topologically conjugate when restricted to their periodic points. In this paper, we extend our earlier results on cycle equivalence of asynchronous finite dynamical systems (FDSs) where the dependency graph may have a nontrivial automorphism group. We give conditions for when two update sequences $\pi ,\pi '$ give cycle equivalent maps $F_\pi , F_{\pi '}$, and we give improved upper bounds for the number of distinct cycle equivalence classes that can be generated by varying the update sequence. This paper contains a brief review of necessary background results and illustrating examples, and concludes with open questions and a conjecture.

1 Introduction

When studying finite dynamical systems (FDSs) of the form

$$\begin{aligned} F = (F_1, F_2, \ldots , F_n) :K^n \longrightarrow K^n \;, \end{aligned}$$

(1.1)

it is typically unrealistic to determine the entire phase space explicitly. Even a moderately small value for $n$ and binary state space $K=\{0,1\}$ leads to a number of states that, at best, is challenging to handle computationally. Based on this, reasoning about the dynamics of (1.1) in terms of the map structure itself can often give more insight as outlined in the following.

To the map in (1.1) one may associate its dependency graph. Assuming states are given as $x = (x_1, \ldots , x_n)$, the dependency graph has vertex set $\{1,2, \ldots , n\}$, and there is a directed edge from vertex $j$ to vertex $i$ if $F_i :K^n \longrightarrow K^n$ depends non-trivially on $x_j$. Here, non-trivially means that there is some $x\in K^n$ such that $F(x) \ne F(x')$ where $x$ and $x'$ only differ in the $j^{\text {th}}$ coordinate. In general, this graph is directed and it may contain loops.

The map $F$ in (1.1) may also have a specific structure or may have been constructed in a specific manner. One example of this is where $F$ has resulted through composition of maps that may only modify one of the states $x_v$. Specifically, we may have maps of the form $F_v :K^n \longrightarrow K^n$ where

$$\begin{aligned} F_v(x_1, \ldots , x_n) = (x_1, \ldots , x_{v-1}, f_v(x_1, \ldots , x_n), x_{v+1}, \ldots , x_n)\; \end{aligned}$$

(1.2)

and where $F$ is given as

$$\begin{aligned} F = F_n \circ F_{n-1} \circ \cdots \circ F_{1} \;. \end{aligned}$$

In this case the map $F$ has been constructed by sequentially (or asynchronously) applying the maps $F_i$ in the sequence $(1,2,\ldots , n)$. In general one may consider other composition sequences such as a permutation $\pi$ of the vertex set. We would like to know how the sequence $\pi$ influences the dynamics of $F$, and we would also like to compare the dynamics resulting from two different update sequences. We will write $F_\pi$ instead of $F$ whenever we have a map assembled through composition of maps of the form $F_i$ in (1.2) using the sequence $\pi =\pi _1\pi _2\cdots \pi _n$.

As we illustrate in the background section, many aspects of the dynamics can be analyzed directly in terms of the dependency graph or the update sequence. These are examples of structure-to-function results. Rather than using brute-force, exhaustive computations, we derive insight about the dynamics using the structural properties of the map $F$ in (1.1).

In this paper, we demonstrate how the dependency graph allows us to reason about the long-term dynamics of the class of maps of the form $F_\pi$ as defined above. These are sometimes called asynchronous automata networks [6], sequential dynamical systems [11], or asynchronous cellular automata.

Throughout, $X$ is an undirected, loop-free graph with vertex set $V={\mathrm {v}}[X]$ (usually $\{1,\ldots ,n\}$) and edge set $E={\mathrm {e}}[X]$. For a vertex $v$ of degree $d(v)$, we let $n[v]$ denote its $1$-neighborhood, which has size $d(v)+1$. The set of permutations of $V$ is denoted $S_X$. An element of $S_X$ represents a total ordering of the vertices, which we write as $\pi =\pi _1\pi _2\cdots \pi _n$.

Each vertex $v$ takes on a vertex state $x_v\in K$ where $K$ is some finite set. The global state is denoted by $x=(x_v)\in K^V$, and the $v$ -local state is $x[v]=(x_v)\in K^{n[v]}$. We will omit the qualifiers vertex, global and $v$-local when specifying states if no ambiguity can arise.

Additionally, each vertex $v$ is assigned a vertex function $f_v:K^{n[v]} \longrightarrow K$ and an $X$-local function $F_v:K^V\longrightarrow K^V$ given by

$$\begin{aligned} F_v(x_1, \ldots , x_n) = (x_1, \ldots , x_{v-1}, f_v(x[v]),x_{v+1} \ldots , x_n) \;. \end{aligned}$$

(1.3)

Here, the vertex function $f_v$ updates the state $x_v$ from time $t$ to time $t+1$ locally. The reason for introducing $X$-local functions is that they can be composed.

A vertex function $f_v$ is symmetric if any permutation of the input vector does not change the function. Common examples of symmetric functions include logical AND, OR, XOR, and their negations. A slightly weaker condition is being outer symmetric, which means that $f_v$ is symmetric in the arguments corresponding to the states of the $d(v)$ neighbors of $v$ in $X$. A sequence $(g_i)_{i=1}^n$ of symmetric functions, where $g_k :K^i \longrightarrow K$, induces a sequence of vertex functions $(f_v)_v$ on $X$ by setting $f_v=g_{d(v)+1}$. Outer symmetric functions also can induce vertex functions, though slighly more care is needed in the notation.

Let $(F_v)_{v\in V}$ be a sequence of $X$-local functions and $\pi \in S_X$. The asynchronous finite dynamical system map $F_\pi :K^n \longrightarrow K^n$ is given by

$$\begin{aligned} F_\pi = F_{\pi (n)} \circ F_{\pi (n-1)} \circ \cdots \circ F_{\pi (1)} \;. \end{aligned}$$

In other words, the map $F_\pi$ is constructed by applying the vertex functions $f_v$ in the sequence given by $\pi$. The map $F_\pi$ is sometimes called a sequential dynamical system or an asynchronous automata network. If the vertex functions are induced we also say that the map $F_\pi$ is induced.

A sequence of local functions $(F_v)_{v\in V}$ defines a (directed) dependency graph. However, for the questions we want to address, it is advantageous to use the undirected, simple, loop-free graph $X$. From the dependency graph, one may always construct the graph $X$ by omitting loops and converting every directed edge into an undirected edge while eliminating multiple edges.

Fig. 1.

The graph ${\mathrm {Wheel}}_4$ from Example 1.

Example 1

Let $X' = {\mathrm {Circ}}_4$, the circle graph on $4$ vertices, and let $X = {\mathrm {Wheel}}_4 = X' \oplus 0$ be the graph obtained form $X'$ as the vertex join of $X'$ and $0$, as shown in Fig. 1. In this case $n[1] = (0,1,2,4)$ whereas $n[0] = (0,1,2,3,4)$. We assign each vertex a state in $K = {\mathbb {F}}_2 = \{0,1\}$ and let the vertex functions be induced by the logical NOR functions

$$ {\mathrm {nor}}_m :K^m\longrightarrow K\,,\qquad \qquad {\mathrm {nor}}_m(x_1,\dots ,x_m)=\prod _{i=1}^m(1+x_i)\,. $$

In other words, ${\mathrm {nor}}_m$ returns $1$ if and only if all its arguments are $0$. As an example, the $X$-local function $F_1 :K^5 \longrightarrow K^5$ is here defined by

$$\begin{aligned} F_1(x_0, x_1, x_2, x_3, x_4) = (x_0, {\mathrm {nor}}_4(x[1]), x_2, x_3, x_4)\;. \end{aligned}$$

If we use the permutation $\pi = (0,1,2,3,4)$ we get the composed map

$$\begin{aligned} F_\pi = F_4 \circ F_3 \circ F_2 \circ F_1 \circ F_0 \;, \end{aligned}$$

which in particular means that $F_\pi (0,0,0,0,0) = (1,0,0,0,0)$. If we instead use the sequence $\pi ' = (1,0,2,3,4)$, we get $F_{\pi '}(0,0,0,0,0) = (0,1,0,1,0)$, illustrating the fact that the choice of sequence affects the dynamics. For comparison, note that using a parallel update scheme the state $(0,0,0,0,0)$ maps to the state $(1,1,1,1,1)$.

2 Equivalence of Maps of the Form $F_\pi$

In this section we review the notions of functional equivalence, dynamical equivalence and cycle equivalence along with condensed versions of the key results. These are all needed for our consideration of how symmetries of $X$ govern results on cycle equivalence.

2.1 Functional Equivalence

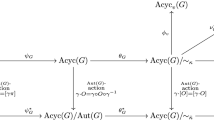
Functional equivalence is simply equality of functions. Every permutation $\pi =\pi _1\pi _2\cdots \pi _n$ of the vertices of $X$ canonically determines a partial order on $X$, or equivalently, an acyclic orientation $O_\pi$ of $X$ (under a slight absuse of notation, we will use both of these terms interchangeably). Specifically, orient edge $\{i,j\}$ as $(i,j)$ if $i$ appears before $j$ in $\pi$. This defines a mapping

$$ S_X\longrightarrow {\mathrm {Acyc}}(X)\,,\qquad \pi \longmapsto O_\pi \,\,. $$

where ${\mathrm {Acyc}}(X)$ is the set of acyclic orientations of $X$. The fibers of this map define an equivalence relation $\sim _\alpha$ on $S_X$, and it is easily seen that $\pi \sim _\alpha \pi '$ if and only if both are linear extensions of the same $O\in {\mathrm {Acyc}}(X)$. Since any two linear extensions of the same finite poset differ by a sequence of transposing adjacent incomparable elements, the following result is immediate.

Proposition 1

Let $(F_v)_{v\in V}$ be a sequence of $X$-local functions and $\pi ,\pi '\in S_X$. If $O_\pi =O_{\pi '}$ then $F_\pi = F_{\pi '}$.

Thus, $\alpha (X):=|{\mathrm {Acyc}}(X)|$ is an upper bound for the number of distinct maps $F_\pi$, where $\pi \in S_X$. For certain classes functions, such as when each vertex function is a ${\mathrm {nor}}$-function, this bound is known to be sharp [1].

It is well-known that the quantity $\alpha (X)$ satisfies the deletion-contraction recurrence

$$ \alpha (X)=\alpha (X\!\setminus \!e)+\alpha (X/e)\,, $$

for any edge $e$ of $X$. Here, $X\!\setminus \!e$ is the graph $X$ with the edge $e$ deleted, $X/e$ is the graph $X$ with $e$ contracted. As such, $\alpha (X)=T_X(2,0)$, where $T_X$ is the Tutte polynomial of $X$ (see [14]).

Example 2

We continue Example 1 using the graph $X = {\mathrm {Wheel}}_4$. The two update sequences $\pi = (0,2,4,1,3)$ and $\pi ' = (0,4,2,3,1)$ give identical maps $F_\pi$ and $F_{\pi '}$ since $O_\pi =O_{\pi '}$. Both acyclic orientations orient the edges of $X$ as $(0,1)$, $(0,2)$, $(0,3)$, $(0,4)$, $(4,1)$, $(2,1)$, $(2,3)$, and $(4,3)$.

Using the deletion/contraction recursion above, one obtains $\alpha (X) = 78$. In other words, for this graph and a fixed sequence $(F_v)_v$ of $X$-local functions, there are at most 78 distinct composed maps of the form $F_\pi$. If all vertex functions are ${\mathrm {nor}}$-functions, this bound is sharp, and the 78 corresponding compositions are indeed distinct.

2.2 Dynamical Equivalence

Two finite dynamical systems $\phi ,\psi :K^n\longrightarrow K^n$ are dynamically equivalent (or topologically conjugate in the discrete topology) if there is a bijection $h :K^n\longrightarrow K^n$ such that

$$\begin{aligned} \psi \circ h = h \circ \phi \,. \end{aligned}$$

(2.1)

This is equivalent to saying that the phase spaces $\varGamma (\phi )$ and $\varGamma (\psi )$ are isomorphic as directed graphs.

The automorphism group of $X$, denoted by ${\mathrm {Aut}}(X)$, acts on ${\mathrm {Acyc}}(X)$ by

$$\begin{aligned} O \mathop {\longmapsto }\limits ^{\gamma } \gamma O\;, \qquad (\gamma O)(\{v,w\}) = \gamma \bigl ( O \bigr ( \{\gamma ^{-1}(v), \gamma ^{-1}(w)\}\bigr ) \bigr )\,, \end{aligned}$$

(2.2)

where $\gamma (v,w)=(\gamma (v),\gamma (w))$. Let $\bar{\alpha }(X)$ denote the number of orbits under this action. In [11], the bijection

$$\begin{aligned} {\mathrm {Fix}}(\gamma )\longrightarrow {\mathrm {Acyc}}(\langle \gamma \rangle \setminus X)\; \end{aligned}$$

(2.3)

is established. Here $\langle \gamma \rangle \setminus X$ is the orbit graph of $X$ and the cyclic group $\langle \gamma \rangle$. This is the multi-graph whose vertices (resp. edges) are the orbits of the action of $\langle \gamma \rangle$ on $V$ (resp. $E$). An edge (orbit) connects the vertex orbits corresponding to any of its edges. Note that the orbit graph may have loops and parallel edges. The orbit graph $\langle (13)(24)\rangle \setminus {\mathrm {Wheel}}_4$ is illustrated in Fig. 2.

Fig. 2.

The orbit graph $\langle (13)(24)\rangle \setminus {\mathrm {Wheel}}_4$.

Combining (2.3) with Burnside’s Lemma, one obtains

$$\begin{aligned} \bar{\alpha }(X)=\frac{1}{|{\mathrm {Aut}}(X)|}\sum _{\gamma \in {\mathrm {Aut}}(X)}| {\mathrm {Fix}}(\gamma )| =\frac{1}{|{\mathrm {Aut}}(X)|}\sum _{\gamma \in {\mathrm {Aut}}(X)} \alpha (\langle \gamma \rangle \setminus X)\;. \end{aligned}$$

(2.4)

The computation of $\bar{\alpha }(X)$ is simplified by the fact that the orbit graph often contains loops and therefore has no acyclic orientations.

Any $\sigma \in S_X$ defines a canonical mapping ${\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ by permuting the coordinates:

$$ \sigma :(x_1,\dots ,x_n)\longmapsto (x_{\sigma ^{-1}(1)},\dots , x_{\sigma ^{-1}(n)})\,. $$

A sequence of vertex functions $(f_v)_{v\in V}$ is ${\mathrm {Aut}}(X)$ -invariant if either of the following two equivalent conditions hold:

• $f_v = f_{\gamma (v)}$ for all $\gamma \in {\mathrm {Aut}}(X)$;

• $\gamma \circ F_v\circ \gamma ^{-1}=F_{\gamma (v)}$ for every $v$ and all $\gamma \in {\mathrm {Aut}}(X)$.

Note that vertex functions induced by a set of symmetric or outer-symmetric functions $(g_i)_{i=1}^n$ are always ${\mathrm {Aut}}(X)$-invariant.

Theorem 1

For any sequence $(f_v)_{v\in V}$ of ${\mathrm {Aut}}(X)$-invariant vertex functions, the maps $F_\pi$ and $F_{\gamma \pi }$ are dynamically equivalent, and $\bar{\alpha }(X)$ is an upper bound for the number of such maps, up to dynamical equivalence.

We conjecture that this upper bound is sharp, but so far, this has only been shown for a few graph classes.

Example 3

We continue our running example with $X = {\mathrm {Wheel}}_4$, whose automorphism group is ${\mathrm {Aut}}(X)\cong D_4$, the symmetry group of the square:

$$\begin{aligned} {\mathrm {Aut}}(X) = \{{\text {id}},\;(1234),\;(13)(24),\;(1432),\; (14)(23),\;(12)(34),\;(13),\;(24)\}\,. \end{aligned}$$

(2.5)

Taking $\gamma = (1234)$ and $\pi = (0,1,2,3,4)$ we have $\gamma \pi = (0,2,3,4,1)$. With ${\mathrm {nor}}$-functions at each vertex, the conditions in Theorem 1 are satisfied and we conclude that two update sequences $\pi$ and $\pi '=\gamma \pi$ yield dynamically equivalent maps $F_\pi$ and $F_{\pi '}$.

To determine the upper bound $\bar{\alpha }(X)$, we compute the orbits graphs $\langle \gamma \rangle \setminus X$ for $\gamma \in {\mathrm {Aut}}(X)$. Note that $\langle {\text {id}} \rangle \setminus X$ is always isomorphic to $X$ while the orbit graphs corresponding to $\gamma \in \{(1234), (1432), (13)(23),(12)(34) \}$ have loops and therefore no acyclic orientations. The orbit graphs resulting from $\gamma \in \{(13),(24) \}$ are isomorphic to the square with a diagonal which has 18 acyclic orientations. This leaves $\gamma = (13)(24)$, whose orbit graph $\langle \gamma \rangle \setminus X$ is shown in Fig. 2 which has $6$ acyclic orientations. Using (2.4), we obtain

$$\begin{aligned} \bar{\alpha }(X) = \tfrac{1}{8} (78 + 0 + 6 + 0 + 0 + 0 + 18 + 18) = 15\;, \end{aligned}$$

which implies that there are at most $15$ dynamically distinct maps $F_\pi$ over $X$ arising from a fixed sequence of ${\mathrm {Aut}}(X)$-invariant functions.

2.3 Cycle Equivalence

Cycle equivalence is a coarsening of dynamical equivalence. In this case, we only compare the periodic points of the maps. For a discrete dynamical system $F :K^n\longrightarrow K^n$, let ${\mathrm {Per}}(F)$ denote its periodic points and let ${\mathrm {Fix}}(F)$ denote its fixed points. Two dynamical systems $\phi :K_1^n \longrightarrow K_1^n$ and $\psi :K_2^n \longrightarrow K_2^n$ are cycle equivalent if there is a bijection $h :{\mathrm {Per}}(\phi ) \longrightarrow {\mathrm {Per}}(\psi )$ such that the equation

$$\begin{aligned} \psi \circ h = h \circ \phi \end{aligned}$$

holds when restricted to ${\mathrm {Per}}(\phi )$. When $K$ is finite, it follows that $\phi$ and $\psi$ are cycle equivalent if their multi-sets of periodic orbits sizes are the same. It is clear that functional and dynamical equivalence both imply cycle equivalence.

Given an update sequence $\pi =\pi _1\pi _2\cdots \pi _n\in S_X$, define

$$ {\mathrm {shift}}(\pi )=\pi _2\pi _3\cdots \pi _n\pi _1\,,\qquad \text {and}\qquad {\mathrm {reverse}}(\pi )=\pi _n\pi _{n-1}\cdots \pi _1\,. $$

The following theorem shows how shifts and reversals of the update sequence give rise to cycle equivalent composed maps. One of these requires the functions to be update sequence independent, which means that ${\mathrm {Per}}(F_\pi )$, set-wise, is independent of $\pi \in S_X$. This perhaps peculiar requirement holds for 104 of the 256 elementary cellular automata rules [7]. It is needed because it ensures that $F_\pi$ and $F_{{\mathrm {reverse}}(\pi )}$ are inverses when restricted to their periodic points.

Theorem 2

([9]). For any set $(f_v)_{v\in V}$ of vertex functions, the maps $F_\pi$ and $F_{{\mathrm {shift}}(\pi )}$ are cycle equivalent. Moreover, if $|K| = 2$ and $(f_i)_{i\in V}$ is update sequence independent, then $F_\pi$ and $F_{{\mathrm {reverse}}(\pi )}$ are cycle equivalent.

It is easy to extend this result from update sequences that are permutations to general words over $V$.

On the level of acyclic orientations, transforming $\pi$ into ${\mathrm {shift}}(\pi )$ corresponds to converting $\pi _1$ from a source in $O_\pi$ to a sink in $O_{{\mathrm {shift}}(\pi )}$. Such an operation is called a flip, and it generates an equivalence relation on ${\mathrm {Acyc}}(X)$ called toric equivalence and denoted by $\sim _{\kappa }$. The equivalence classes are called toric posets. The name is motivated from a bijection between the toric posets over $X$ and the chambers of the toric graphic (hyperplane) arrangement ${\mathcal {A}}_{{{\mathrm{tor}}}}(X)$ in the torus ${\mathbb {R}}^V/{\mathbb {Z}}^V$, analogous to the bijection between ordinary posets over $X$ and the chambers of the graphic arrangement ${\mathcal {A}}(X)$ in ${\mathbb {R}}^V$ (see [4]). Similarly, transforming $\pi$ into ${\mathrm {reverse}}(\pi )$ corresponds to reversing each edge orientation in $O_\pi$ to obtain $O_{{\mathrm {reverse}}(\pi )}$ – we call this a reversal, and denote the equivalence relation generated by flips and reversals by $\sim _{\delta }$. We let $\kappa (X)$ and (resp. $\delta (X)$) denote the number of $\sim _{\kappa }$-equivalence (resp. $\sim _{\delta }$-equivalence) classes.

Let $P=v_1v_2,\dots ,v_k$ be a path in $X$ and define the function $\nu _P:{\mathrm {Acyc}}(X)\longrightarrow {\mathbb {Z}}$, where $\nu _P(O_X)$ is the number of edges oriented as $(v_i,v_{i+1})$ (the “forward edges”), minus the number of edges oriented as $(v_{i+1},v_i)$ (“backward edges”). If $P$ is a cycle then $\nu _P$ is preserved under flips, so $\nu _P$ extends to a map $\bar{\nu }_P:{\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }\longrightarrow {\mathbb {Z}}$ on toric posets over $X$. Two acyclic orientations are torically equivalent if and only if $\nu _C(\omega )=\nu _C(\omega ')$ for all cycles $C$ in $X$. Moreover, $\omega \sim _{\delta }\omega ''$ if and only if $\nu _C(\omega )=\pm \nu _C(\omega '')$. The $\delta$-equivalence classes can be enumerated from the toric equivalence classes, which satisfy a deletion-contraction recurrence for any cycle edge $e$ of $X$:

$$\begin{aligned} \begin{array}{l} \kappa (X)=\kappa (X\!\setminus \!e)+\kappa (X/e) = T_X(1,0)\;, \\ \delta (X)=\lceil \kappa (X)/2\rceil \,, \end{array} \end{aligned}$$

(2.6)

We can now summarize our results on cycle equivalence for maps of the form $F_\pi$.

Theorem 3

([7, 9, 10]). Let $K$ be a finite set, let $(f_i)_{v\in V}$ be a fixed sequence of vertex functions over $X$. If $O_\pi \sim _{\kappa }O_{\pi '}$ then $F_\pi$ and $F_{\pi '}$ are cycle equivalent. If $|K| = 2$ and $(f_v)_{v\in V}$ is update sequence independent, then $F_\pi$ and $F_{\pi '}$ are cycle equivalent if $O_\pi \sim _{\delta }O_{\pi '}$.

Theorem 3 provides an easy way to test if $F_\pi$ and $F_{\pi '}$ are cycle equivalent: first choose a cycle basis for $X$ and then evaluate $\nu$ for $O_\pi$ and $O_{\pi '}$. If these are identical then the two maps are cycle equivalent. If $\nu (O_\pi )=\pm \nu (O_{\pi '})$, then the maps are also cycle equivalent, provided the functions are update sequence independent. Of course, since this is a sufficient condition, the two maps may still be cycle equivalent if this condition fails to hold.

Example 4

Returning to our running example with $X = {\mathrm {Wheel}}_4$, we first see that $\kappa (X) = 14$. To see this, one can either use the deletion/contraction recursion relation (2.6) or resort to Proposition 3 (placed in the next section for the purpose of exposition) using the vertex $v = 0$. As a consequence, there are at most 14 distinct long-term behaviors for any finite dynamical system of the form $F_\pi$ over $X$ assuming fixed functions $(F_v)_{v\in V}$.

As a consequence of Proposition 3, we note that representative update sequences for these 14 classes can be obtained as follows: first direct each edge $\{0,i\}$ as $(0,i)$ where $1 \le i \le 4$ and then orient the remaining edges so that the graph is acyclic. There are 14 such acyclic orientations. The representative update sequences result by choosing precisely one linear extension for each of these 14 acyclic orientations.

3 Main Results

The results presented above for cycle equivalence do not consider the effects of symmetries in the graph $X$. Here we will complete the analysis through an extension of Theorem 1 from Sect. 2.2. As before, when considering graph symmetries, we need to assume that the vertex functions are ${\mathrm {Aut}}(X)$-invariant.

For $\gamma \in {\mathrm {Aut}}(X)$, linear extensions $\pi$ of $O$ and $\pi '$ of $\gamma O$ give dynamically equivalent maps $F_\pi$ and $F_{\pi '}$. In the following, we will show that ${\mathrm {Aut}}(X)$ acts on ${\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }$ via $\gamma [O] = [\gamma O]$. From this it follows that ($i$) linear extensions of $\kappa$-classes on the same ${\mathrm {Aut}}(X)$-orbit give cycle-equivalent maps, and ($ii$) the number of cycle equivalence classes is bounded above by the number $\bar{\kappa }(X)$ of orbits of the action of ${\mathrm {Aut}}(X)$ on ${\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }$. The same statement holds for $\delta$-classes and the corresponding number $\bar{\delta }(X)$.

To start, we first observe that if $v$ is a source (resp. sink) in the acyclic orientation $O$ then $\gamma (v)$ is a source (resp. sink) in $\gamma O$. Assume that $v$ is a source in $O$ and let $c=c_v$ be the length one flip-sequence mapping $O^1$ to $O^2$. We have a commutative diagram

(3.1)

which can be verified by examining what happens to each edge $\{u,w\}$.

Lemma 1

For $\sim \,\in \{{}\!\!\sim _{\kappa }, {}\!\!\sim _{\delta }\}$, the group ${\mathrm {Aut}}(X)$ acts on ${\mathrm {Acyc}}(X)/\!\!\sim$ by $\gamma [O]=[\gamma O]$.

Proof

By vertically concatenating diagrams of the form (3.1), we see that the mapping

$$ {\mathrm {Aut}}(X)\times {\mathrm {Acyc}}(X)/\!\!\sim \;\longrightarrow {\mathrm {Acyc}}(X)/\!\!\sim \,, \qquad (\gamma ,[O])\longmapsto [\gamma O] $$

is well-defined. It is a group action because the group ${\mathrm {Aut}}(X)$ acts on ${\mathrm {Acyc}}(X)$ by $\gamma O = \gamma \circ O \circ \gamma ^{-1}$; see for example [11].

Corollary 1

Let $\gamma \in {\mathrm {Aut}}(X)$. For any permutation $\pi$ with $O_\pi \in [O]$ and $\pi '$ for which $O_{\pi '}\in \gamma [O]$, the two maps $F_\pi$ and $F_{\pi '}$ are cycle equivalent.

Since ${\mathrm {Aut}}(X)$ acts on ${\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }$ and ${\mathrm {Acyc}}(X)/\!\!\sim _{\delta }$, we may use Burnside’s Lemma to determine $\bar{\kappa }(X)$ and $\bar{\delta }(X)$.

Proposition 2

Let $X$ be a finite, undirected graph. Then

$$\begin{aligned} \bar{\kappa }(X) = \frac{1}{|{\mathrm {Aut}}(X)|}\sum _{\gamma \in {\mathrm {Aut}}(X)} |{\mathrm {Fix}}(\gamma )| \;, \end{aligned}$$

(3.2)

where ${\mathrm {Fix}}(\gamma ) = \{[O] \mid \gamma [O] = [O]\}$.

In this form it is, however, not easy to determine $|{\mathrm {Fix}}(\gamma )|$. It would be desirable to develop a result analogous to the orbit graph correspondence that what we have when ${\mathrm {Aut}}(X)$ acts on ${\mathrm {Acyc}}(X)$ as in (2.4). The following results provide parts of this [3, 8].

Proposition 3

For any fixed vertex $v$ of $X$, the set ${\mathrm {Acyc}}_v(X)\subset {\mathrm {Acyc}}(X)$ consisting of all acyclic orientations where $v$ is the unique source, is a complete set of toric equivalence class representatives.

For determining ${\mathrm {Fix}}(\gamma )$, this proposition has an immediate consequence if $\gamma$ fixes a vertex.

Corollary 2

Let $\phi _v :{\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }\longrightarrow {\mathrm {Acyc}}_v(X)$ be the map that assigns to $[O]$ its unique element in ${\mathrm {Acyc}}_v(X)$. If $\gamma \in {\mathrm {Aut}}(X)$ fixes the vertex $v\in V$ then $[O] \in {\mathrm {Fix}}(\gamma )$ if and only if $\gamma \phi _v([O]) = \phi _v([O])$.

Proof

For any $v\in V$ the automorphic image of an element of ${\mathrm {Acyc}}_v(X)$ is also an element of ${\mathrm {Acyc}}_v(X)$. If $\gamma$ fixes $v$ then it follows that $\gamma$ fixes $[O]$ if and only if $\gamma$ fixes $\phi _v([O])$.

It follows that in this case one can derive a result analogous to the orbit graph enumeration in  (2.4), however, in this case one must take care to only consider those acyclic orientations where $v$ is the unique source.

The fact that the $\nu$-function is a complete invariant for toric equivalence offers an alternative approach:

Proposition 4

Let $X$ be a graph, let $v\in {\mathrm {v}}[X]$ and let $\mathcal {C}$ be a cycle basis for $X$. Then

$$\begin{aligned} \bar{\kappa }(X) = \frac{1}{|{\mathrm {Acyc}}(X)|} \sum _{\gamma \in {\mathrm {Aut}}(X)} N(\gamma ) \end{aligned}$$

where $N(\gamma ) = |\{O\in {\mathrm {Acyc}}_v(X) \mid \nu _{\mathcal {C}}(O) = \nu _{\mathcal {C}}(\gamma O)\}|$.

Proof

This follows from the fact that $\nu$ evaluated on any cycle-basis is a complete invariant for toric equivalence [12].

The following examples illustrates how Proposition 4 can be used to determine $\bar{\kappa }(X)$ as well as $\bar{\delta }(X)$. We also include the other graph measures mentioned above.

Example 5

As a specific example, take $X$ to be the double square graph as illustrated in Fig. 3. Here

$$\begin{aligned} {\mathrm {Aut}}(X) = \{{\text {id}}, \tau = (1,6)(2,5)(3,4), \sigma = (1,3)(4,6), \sigma \tau = (1,4)(2,5)(3,6) \}, \end{aligned}$$

(3.3)

Fig. 3.

The graph of Example 5 with orientations for the fundamental cycles of the cycle basis.

Fig. 4.

The transversal ${\mathrm {Acyc}}_2(X)$ for $\kappa$-equivalence of the graph in Example 5.

leading to $\alpha (X) = 98$, $\bar{\alpha }(X) = 28$, $\kappa (X) = 9$ and $\delta (X) = 5$. Nine torically non-equivalent elements in ${\mathrm {Acyc}}_2(X)$ are shown in Fig. 4. The letters in parentheses on the left show five $\delta$-class representatives. The $\nu$-values are indicated inside each fundamental cycle of the chosen cycle basis.

Let $(\nu _1, \nu _2)$ denote the value of $\nu$ on $O$. Then $\nu (\tau O ) = (-\nu _1, -\nu _2)$, $\nu (\sigma O ) = (\nu _2, \nu _1)$, and $\nu (\tau \sigma O ) = (-\nu _2, -\nu _1)$. From this we conclude that $N({\text {id}}) = 9$, $N(\tau ) = 1$, $N(\sigma ) = 3$ and $N(\tau \sigma ) = 3$. As a result we have $\bar{\kappa }(X) = (9+1+3+3)/4 = 4$.

In the same manner we obtain $\bar{\delta }(X) = 4$. Specifically, we have $|{\mathrm {Fix}}({\text {id}})| = 5$, $|{\mathrm {Fix}}(\tau )| = 5$, and $|{\mathrm {Fix}}(\sigma )| = 3$, $|{\mathrm {Fix}}(\tau \sigma )| = 3$, leading to $\bar{\delta }(X) = (5+5+3+3)/4 =~4$.

Corollary 3

Let $X$ be the graph in Example 5. Then there are at most four cycle classes for maps of the form ${\mathrm {Nor}}_\pi$ (each vertex function is a ${\mathrm {nor}}$-function) where $\pi \in S_X$.

This follows directly since ${\mathrm {nor}}$-functions are symmetric and Boolean. There are $6! = 720$ possible permutation update sequences for this graph. However, for this class of functions, there are at most four distinct long-term behaviors. In our opinion, this is a remarkable result.

Example 6

For the running example with $X = {\mathrm {Wheel}}_4$ we can use Corollary 2 to take advantage of the fact that this graph is the vertex join of $0$ and ${\mathrm {Circ}}_4$ and that $0$ has maximal degree. To determine ${\mathrm {Fix}}(\gamma )$ in ${\mathrm {Acyc}}(X)/\!\!\sim _{\kappa }$, we can now simply reason about the transversal ${\mathrm {Acyc}}_0(X)$ and use the orbit graph construction. For example, there are 2 elements of ${\mathrm {Acyc}}_0(X)$ fixed under the automorphism $\gamma = (13)(24)$. Accounting for each $\gamma \in {\mathrm {Aut}}(X)$ using the order in which they appear in (2.5) gives

$$\begin{aligned} \bar{\kappa }(X) = \frac{1}{8}(14 + 0 + 2 + 0 + 0 + 0 + 4 + 4) = 3 \; \end{aligned}$$

which equals $\bar{\kappa }({\mathrm {Circ}}_4)$.

The fact that $\bar{\kappa }({\mathrm {Circ}}_4 \oplus 0) = \bar{\alpha }({\mathrm {Circ}}_4)$ clearly generalizes. We state this without proof:

Proposition 5

If $X = X' \oplus v$ where $X'$ has no vertex of maximal degree, then $\bar{\kappa }(X) = \bar{\alpha }(X')$.

We include one more example illustrating the various graph measure for the three-dimensional cube.

Example 7

Let $X = Q_2^3$, the $3$-dimensional binary hypercube, i.e., the cube. Straightforward (but somewhat tedious) calculations show that

$$\begin{aligned} \alpha (Q_2^3) = 1862,\quad \kappa (Q_2^3) = 133, \quad \bar{\alpha }(Q_2^3) = 54, \text { and } \bar{\kappa }(Q_2^3) = \bar{\delta }(Q_2^3) = 8. \end{aligned}$$

Again, in the context of dynamical systems of the form $F_\pi$ induced by a sequence of ${\mathrm {Aut}}(X)$-invariant Boolean functions, this means that there are at most $8$ distinct periodic orbit configurations for induced, symmetric permutation SDS over $Q_2^3$. This should be compared to the total number of permutation over $S_X$ which is $8! = 40320$.

4 Summary

In this paper, we extended results on cycle equivalence for finite dynamical systems of the form $F_\pi$. The results provide a sufficient condition for determining when $F_\pi$ and $F_{\pi '}$ are cycle equivalent when taking into account the symmetries of the graph. The restriction that the vertex functions be ${\mathrm {Aut}}(X)$-invariant functions is not as artificial as it may seem – it includes all symmetric and outer-symmetric functions, which are very common in practice. We also derived a bound for the number cycle-equivalence classes for such maps $F_\pi$. As for the measures $\alpha (X)$, $\bar{\alpha }(X)$, $\kappa (X)$ and $\delta (X)$, the conditions and enumerations do not depend on the particular choice of functions – they are graph measures. This means that we can reason about dynamics of maps $F_\pi$ using only the graph structure. It is another example of mapping structure to dynamics rather than performing brute-force phase space computations.

The structures we have covered above are relevant to other areas beyond asynchronous finite dynamical systems. One example is in the study of Coxeter groups and their Coxeter elements [2]. Let $(W,S=\{s_1,\ldots ,s_n\})$ be a Coxeter system with (unlabeled) Coxeter graph $X$. It is well-known that there is a bijection between ${\mathrm {Acyc}}(X)$ and the set of Coxeter elements $C(W) = \{c_{\pi (n)} \cdots c_{\pi (1)} \mid \pi \in S_X\}$. Moreover, $O\sim _{\kappa }O'$ if and only if the corresponding Coxeter elements are conjugate [5, 8]. It follows that $\alpha (X) = T_X(2,0)$ and $\kappa (X)=T_X(1,0)$ enumerate the number of Coxeter elements and their conjugacy classes. Moreover, it can be shown that $\bar{\kappa }(X)$ is an upper bound for the number of spectral class of Coxeter elements, see for example [13]. We are not aware of any significance for $\bar{\delta }(X)$ in the context of Coxeter groups.

We close with two questions and a conjecture that we invite the reader to explore further:

Question 1

Is it possible to compute $\bar{\delta }(X)$ from $\bar{\kappa }(X)$ in a manner similar to that of $\delta (X) = \lceil \kappa (X)/2 \rceil$? For which graphs are $\bar{\delta }(X)$ and $\bar{\kappa }(X)$ the same?

Question 2

Is there a simpler way to determine $\bar{\kappa }$ than the one in Proposition 4? Is there a result involving $\nu _{\mathcal {C}}( {\mathrm {Acyc}}_v(X) )$ analogous to (2.4) with orbit graphs?

Conjecture 1

The bounds $\bar{\kappa }(X)$ and $\bar{\delta }(X)$ are sharp. In other words, for any graph $X$, there is a function sequence $(F_v)_{v\in V}$ such the that the number of cycle classes of the maps $F_\pi$ equals $\bar{\kappa }(X)$ (resp. $\bar{\delta }(X)$).