Gradient Projection for Regularized Cryo-Electron Tomographic Reconstruction

Abstract

Cryo-ET has recently emerged as a leading technique to investigate the three-dimensional (3D) structure of biological specimens at close-to-native state. The technique consists of acquiring many two-dimensional (2D) projections of the structure under scrutiny at various tilt angles under cryogenic conditions. The 3D structure is recovered through a number of steps including projection alignment and reconstruction. However, the resolution currently achieved by cryo-ET is well below the instrumental resolution mainly due to the contrast transfer function of the microscope, the limited tilt range and the high noise power. These limitations make the 3D reconstruction procedure very challenging. Here, we propose a new regularized reconstruction technique based on projected gradient algorithm. Using the gold-standard method for resolution assessment, the Fourier Shell Correlation, we show that the proposed technique outperforms the commonly used reconstruction methods in ET, including the filtered back projection and the algebraic reconstruction techniques.

1 Introduction

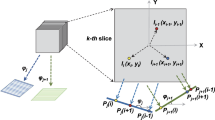
Over the last decade, cryo-Electron Tomography (cryo-ET) has drawn the attention of researchers. It is considered the most powerful imaging technique to address fundamental questions on biological structures at both cellular and molecular levels [1]. It also bridges the gap between low-resolution imaging techniques (e.g. light microscopy) and high-resolution techniques (e.g. single particle electron microscopy). Cryo-ET merges the principles of transmission electron microscopy (TEM) and the principle of tomographic imaging by acquiring several two- dimensional projection images of biological structures at limited tilt range and close-to-native condition. These two-dimensional projection images are then reconstructed to a three-dimensional image (called tomogram), after passing through a pipeline of alignment and restoration procedure as shown in Fig. 1. For a more in-depth description of the cryo-ET and the associated image processing pipeline see [2].

Fig. 1

Cryo-ET image processing pipeline

The resolution of the reconstructed tomogram, however, is affected by the low signal to noise ratio (SNR) of the projection images (typically 0.1–0.01) and the limited angular coverage (typically $\pm 60$–$70^{\circ }$) resulting in wedge-shaped missing information in Fourier space, the so-called “missing wedge”, making the reconstruction process very challenging and demanding [3]. Therefore, developing a reconstruction technique that incorporates the sparsely sampled data, the noise level, and that preserves the structural edges while pushing the limits of resolution further, is highly desirable.

One technique, that was recently investigated in the context of cryo-ET [4], is the direct Fourier reconstruction using a non-uniform fast Fourier transform, but it is still hampered by the high computational cost. Therefore, the current standard method in cryo-ET is the weighted (filtered) back projection (WBP) based on Radon transform [5], which backprojects the high-pass filtered projection data into the tomogram. One of the main drawbacks of WBP, however, are the typical streak artifacts due to the missing wedge of data, as well as the corresponding degraded resolution.

Recently, due to the increasing availability of high performance computing, variants of the algebraic reconstruction technique (ART) have been employed and extended in the context of cryo-ET [6–8], which formulate the reconstruction problem as a large system of linear equations to be solved iteratively. In this manner, the missing wedge effect can be minimized, but the reconstruction performance is still degraded due to the noisy input data.

The projected gradient-based algorithm [9] has recently been used in several applications such as compressed sensing [10], X-ray computed tomography [11] and in sparse signal recovery [12] to solve the $L_{2}-L_{1}$ optimization problem (LASSO). In this paper, the reconstruction problem is formulated as an unconstrained, regularized optimization problem, using the projected gradient-based algorithm to solve the problem on a feasible bounded set. In the following we denote this approach as Gradient-based Projection Tomographic Reconstruction, in short GPTR.

2 Problem Formulation

2.1 Notation and Concept

The three-dimensional reconstructed tomogram is represented as a discretized, linearized vector $x\in \mathbb {R}^n$, with $n\in \mathbb {N}$. The forward problem can be formulated using the discrete version of the Radon Transform [5] for each measurement $j\in \{1,\ldots ,m\}$:

$$\begin{aligned} b_{j}=\sum _{i=1}^{n}a_{ij}x_{i}\qquad \text {or in short}\qquad b=Ax, \end{aligned}$$

(1)

where $b\in \mathbb {R}^{m}$ represents the measured projection data, $(a_{ji})=A\in \mathbb {R}^{m\times n}$ represents the weighting matrix, where $a_{ji}$ is the weight with which each voxel in the image vector $x\in \mathbb {R}^{n}$ contributes to the jth projection measurement.

For computational simplicity, we treat the three-dimensional tomogram as a stack of two-dimensional slices, which are reconstructed individually and then stacked together again to a three-dimensional tomogram.

2.2 Formulation as an Optimization Problem

The tomographic reconstruction problem of solving $b=Ax$ for the unknown x in cryo-ET is underdetermined due to the limited tilt angles, as well as ill-posed, for example due to the measurement noise. Hence a direct solution is not feasible. Instead, a least squares approach is adopted to find an approximate solution

$$\begin{aligned} x_{\textit{LS}}= \mathop {\mathrm {arg\,min}}_x \Vert b-Ax \Vert _{2}^{2}, \end{aligned}$$

(2)

where $\Vert \cdot \Vert _2$ denotes the Euclidean norm. This least squares problem can be solved iteratively following a weighted gradient descent approach,

$$\begin{aligned} x^{k+1}=x^k+s_{k}g_{k}, \qquad k=0,1,\ldots , \end{aligned}$$

(3)

with a starting value $x^0$, step size $s_k$ and a weighted gradient $g_k=\textit{QA}^TD(b-Ax^k)$. Standard techniques such as SIRT or SART can be expressed in this form by choosing $s_k$ and $g_k$ appropriately (for example we can get SIRT by setting Q and D to the identity matrix in $g_k$, and $s_k\in [0,2]$). This is also true for the recently developed techniques I-SIRT, M-SART or W-SIRT [6–8]. To accelerate convergence, a standard numerical method like the LSQR variant of the conjugate gradient algorithm [13] can be used instead.

However, due to the strong measurement noise, a least squares approach will lead to noise amplification in later iterates $x^k$. To combat this, a regularization term $\phi (x)$ is added to stabilize the solution,

$$\begin{aligned} x_{\textit{opt}}=\mathop {\mathrm {arg\,min}}_{x\in \varOmega } \Vert b-Ax \Vert _{2}^{2} +\beta \phi (x) \end{aligned}$$

(4)

with a Lagrangian multiplier $\beta >0$ describing the strength of the regularizer, and further restricting the solution to a feasibility region $\varOmega =\big \{x=(x_i)\in \mathbb {R}^n:\ x_i\in [l,u]\big \}$, where $l,u\in \mathbb {R}$ denote lower and upper bounds of the signal.

A popular choice for the regularization term is the isotropic total variation, $\phi (x)=\Vert Dx\Vert _1$, where D is an operator computing the gradient magnitude using finite differences and circular boundary conditions, and $\Vert \cdot \Vert _1$ denotes the $\ell _1$-norm. However, isotropic TV is non-smooth and thus poses problems for the optimization procedure.

3 Methodology

3.1 Problem Statement

We investigate the regularized optimization problem as in Eq. (4), that is optimizing the objective function

$$\begin{aligned} f(x) = \Vert b-Ax\Vert _2^2 + \beta \phi (x). \end{aligned}$$

(5)

To overcome the non-smoothness of isotropic total variation, we use the smooth Huber function $\phi _\text {huber}$ [14], replacing the $\ell _1$-norm of total variation. $\phi _\text {huber}$ is illustrated in Fig. 1 and is expressed by

$$\begin{aligned} \phi _{\textit{huber}}(z)={\left\{ \begin{array}{ll} 0.5\left| z \right| ^{2} &{} \left| z \right| \le \tau \\ \tau \left| z \right| -0.5\tau ^{2} &{} \text {else,} \end{array}\right. } \end{aligned}$$

(6)

where the threshold parameter $\tau$ is estimated by the median absolute deviation, $\tau =\textit{median}(\left| z-\textit{median}(z) \right| )$. Using $\phi (x) := \phi _\text {huber}(Dx)$ the objective function f(x) is now smooth and convex, so the projected gradient method can be applied to find a feasible solution $x\in \varOmega$.

3.2 Projected Gradient Algorithm

The projected gradient method [9] is an extended version of gradient descent, where the solution is iteratively projected onto the convex feasible set $\varOmega$, as illustrated in Fig. 1. Starting with an initial value $x_0$, it is expressed by:

$$\begin{aligned} x^{k+1}=P_\varOmega (x^{k}+s_{k}g_{k}),\qquad k=0,1,\ldots ,n_\text {iter} \end{aligned}$$

(7)

where $g_{k}=\nabla f(x)$ is the gradient of the objective function in (5), and $s_{k}$ is the step size. The step size $s_k$ is computed using an inexact line search, limiting the gradient step by the Armijo conditions [15], ensuring the curvature and a sufficient decrease of the objective function as follows:

$$\begin{aligned} f(x(s_k))-f(x)\le \frac{\alpha }{s_{k}}\left\| x(s_k)-x \right\| ^{2}, \end{aligned}$$

(8)

where $\alpha$ is a scalar constant.

The algorithm Gradient Projection for Tomographic Reconstruction (GPTR) is illustrated in Fig. 1 and can be described as follows:

• 1. Input: The algorithm is fed with the aligned projections b associated with the tilt angle, and the forward projector matrix A [16].

• 2. Set the initial conditions: The initial reconstructed tomogram is set to $x^0\in \varOmega =\big \{x=(x_i)\in \mathbb {R}^n:\ x_i\in [l,u]\big \}$ with lower and upper bounds $l,u\in \mathbb {R}$, a tolerance and the maximum number of iterations $n_\text {iter}$.

• 3. Iterate for $k=0,1,\ldots ,n_\text {iter}$

  • a. Compute the objective function f(x): The data fidelity term $\Vert b-Ax^k\Vert ^2_2$ and the regularization term $\phi (x^k)=\phi _\text {huber}(Dx^k)$ are computed.

  • b. Compute the gradient $g_{k}$: The gradient $g_k=\nabla f(x^k)$ is computed.

  • c. Compute the gradient step $s_{k}$: Initialize $s_{k}=1$. Check the Armijo condition in Eq. (8) and iteratively reduce $s_k$ by $90\,\%$ until the condition is met (or a maximum number of iterations are performed).

  • d. Update the solution estimate $x^{k+1}$: Compute $x^{k+1}$ by computing the gradient descent update step $x^k+s_kg_k$ and projecting it onto $\varOmega$ as in Eq. (7).

• 4. Output: $x^{k+1}$ is the output once the iteration has converged (i.e. the tolerance was reached) or the maximum number of iterations has been reached.

Convergence of the GPTR algorithm with a regularized objective function has not been investigated yet. However, a detailed analysis for a similar problem can be found in [17].

4 Experiments and Results

The proposed reconstruction method has been examined on real data, a tomographic tilt series of a vitrified freeze-substituted section of HeLa cells [18], which were collected from $-58$ to $58^{\circ }$ at $2^{\circ }$ intervals and imaged at a pixel size of 1.568 nm using Tecani T10 TEM, equipped with 1k $\times$ 1k CCD camera. To keep the computational complexity manageable, the projection data was down-sampled by a factor of eight. The solution of the proposed technique GPTR was compared with those of the most commonly used techniques in the field of cryo-ET, namely WBP, LSQR, and SART. The parameters were set to $\beta =0.1$, a tolerance of $10^{-2}$, $n_{\textit{iter}}=50$ and $[u,l]=[0.01,1000]$.

4.1 Fourier Shell Correlation

The Fourier Shell Correlation (FSC), the typical quantitative analysis of the resolution within the cryo-EM and cryo-ET community [19], was applied to the different reconstruction methods to assess the resolution. The tomograms were reconstructed from even and odd projections separately and the Fourier transform of each tomogram was calculated ($F_n$ and $G_n$ for even and odd tomograms respectively). Then the Fourier plane was binned into K shells from 0 to the Nyquist frequency as shown in Fig. 2b. The FSC is calculated as follows:

$$\begin{aligned} \textit{FSC}(K)=\frac{\sum _{n\in K}F_{n}G_{n}^{*}}{\sqrt{\sum _{n\in K}\left| F_{n} \right| ^{2}\sum _{n\in K}\left| G_{n} \right| ^{2}}}, \end{aligned}$$

(9)

where K is the Fourier shell and $*$ is the conjugate Fourier transform.

The results are shown in Fig. 2a. The 0.5-FSC-criterion is usually used as an indicator of the achieved resolution. It is quite clear that the FSC of the GPTR method crosses the 0.5-FSC-line at high spatial frequencies, outperforming the FSCs of the traditional methods. Moreover, the high frequency components (noise) are attenuated in GPTR (indicating robustness to noise), while the noise was aligned with the data in the SART technique. Also, we observed that the GPTR reached the tolerance in 6–8 iterations, while the LSQR did not converge in 10 iterations.

Fig. 2

FSC curves for different reconstruction techniques (WBP, LSQR, SART and GPTR) with their cutoff frequency 0.164, 0.216, 0.28 and Inf respectively. a FSC curves. b Fourier shells

4.2 Line Profile

Fig. 3

Reconstructed tomograms and their line profiles (LP). a WBP. b LSQR. c SART. d GPTR. e The intensity LP. f The un-normalized intensity LP

Another experiment was performed using $n_{\textit{iter}}=7$, leaving the other parameters unchanged. Then an intensity line profile (LP), the dashed line in Fig. 3b, was drawn for the different reconstructed tomograms from Fig. 3a–d to investigate the edge preservation, the noise effects and the non-negativity of the intensity values. The LP was drawn for both the normalised sections in Fig. 3e and the un-normalised ones in Fig. 3f. It is clear from Fig. 3f that the LP behaviour of GPTR is similar to theSART, which follows the underlying object smoothly, while the GPTR preserves the edges better. Additionally, GPTR by construction produces positive intensities, while WBP and LSQR are affected clearly by the noise and the negative values.

5 Conclusion

In this paper, the gradient projection for tomographic reconstruction (GPTR) was proposed to solve the regularized optimization problem for the Electron tomographic reconstruction. A proof of principle was demonstrated on real ET data using the gold standard for resolution measurement, FSC. A gain of several nanometers in resolution (0.5-FSC criterion) was achieved without affecting the sharpness of the structure (line-profile criterion). Extending the work for large data sets and/or in the field of cryo-ET is currently under development.