Geometric Singular Perturbation Analysis of Bursting Oscillations in Pituitary Cells

Abstract

Dynamical systems theory provides a number of powerful tools for analyzing biological models, providing much more information than can be obtained from numerical simulation alone. In this chapter, we demonstrate how geometric singular perturbation analysis can be used to understand the dynamics of bursting in endocrine pituitary cells. This analysis technique, often called “fast/slow analysis,” takes advantage of the different time scales of the system of ordinary differential equations and formally separates it into fast and slow subsystems. A standard fast/slow analysis, with a single slow variable, is used to understand bursting in pituitary gonadotrophs. The bursting produced by pituitary lactotrophs, somatotrophs, and corticotrophs is more exotic, and requires a fast/slow analysis with two slow variables. It makes use of concepts such as canards, folded singularities, and mixed-mode oscillations. Although applied here to pituitary cells, the approach can and has been used to study mixed-mode oscillations in other systems, including neurons, intracellular calcium dynamics, and chemical systems. The electrical bursting pattern produced in pituitary cells differs fundamentally from bursting oscillations in neurons, and an understanding of the dynamics requires very different tools from those employed previously in the investigation of neuronal bursting. The chapter thus serves both as a case study for the application of recently-developed tools in geometric singular perturbation theory to an application in biology and a tutorial on how to use the tools.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Techniques from dynamical systems theory have long been utilized to understand models of excitable systems, such as neurons, cardiac and other muscle cells, and many endocrine cells. The seminal model for action potential generation was published by Hodgkin and Huxley in 1952 and provided an understanding of the biophysical basis of electrical excitability (Hodgkin and Huxley (1952)). A mathematical understanding of the dynamic mechanism underlying excitability was provided nearly a decade later by the work of Richard FitzHugh (FitzHugh (1961)). He developed a planar model that exhibited excitability, and that could be understood in terms of phase plane analysis. A subsequent planar model, published in 1981 by Morris and Lecar, introduced biophysical aspects into the planar framework by incorporating ionic currents into the model, making the Morris-Lecar model a very useful hybrid of the four-dimensional biophysical Hodgkin-Huxley model and the two-dimensional mathematical FitzHugh model (Morris and Lecar (1981)). These planar models serve a very useful purpose: they allow one to use powerful mathematical tools to understand the dynamics underlying a biological phenomenon.

In this chapter, we use a similar approach to understand the dynamics underlying a type of electrical pattern often seen in endocrine cells of the pituitary. This pattern is more complex than the activity patterns studied by FitzHugh, and to understand it we employ dynamical systems techniques that did not exist when FitzHugh did his groundbreaking work. Indeed, the mathematical tools that we employ, geometric singular perturbation analysis with a focus on folded singularities, are still being developed (Brons et al. (2006); Desroches et al. (2008a); Fenichel (1979); Guckenheimer and Haiduc (2005); Szmolyan and Wechselberger (2001, 2004); Wechselberger (2005, 2012)). The techniques are appealing from a purely mathematical viewpoint (see Desroches et al. (2012) for review), but have also been used in applications. In particular, they have been employed successfully in the field of neuroscience (Erchova and McGonigle (2008); Rubin and Wechselberger (2007, 2008); Wechselberger and Weckesser (2009)), intracellular calcium dynamics (Harvey et al. (2010, 2011)), and chemical systems (Guckenheimer and Scheper (2011)). As we demonstrate in this chapter, these tools are also very useful in the analysis of the electrical activity of endocrine pituitary cells. We emphasize, however, that the analysis techniques can and have been used in many other settings, so this chapter can be considered a case study for biological application, as well as a tutorial on how to perform a geometric singular perturbation analysis of a system with multiple time scales.

The anterior region of the pituitary gland contains five types of endocrine cells that secrete a variety of hormones, such as prolactin, growth hormone, and luteinizing hormone, into the blood. These pituitary hormones are transported by the vasculature to other regions of the body where they act on other endocrine glands, which in turn secrete their hormones into the blood, and on other tissue including the brain. The pituitary gland thus acts as a master gland. Yet the pituitary does not act independently, but instead is controlled by neurohormones released from neurons of the hypothalamus, which is located nearby.

Many endocrine cells, including anterior pituitary cells, release hormones through a stimulus-secretion coupling mechanism. When the cell receives a stimulatory message, there is an increase in the concentration of intracellular Ca²⁺ that triggers the hormone secretion. More often than not, the response to the input is a rhythmic output due to oscillations in the Ca²⁺ concentration. Here we are interested in the dynamics of these Ca²⁺ oscillations. There are actually two possibilities, and both can be found in pituitary cells. First, Ca²⁺ oscillations can be due to the cell’s electrical activity. In this case, oscillations in electrical activity bring Ca²⁺ into the cell through ion channels in the plasma membrane. This is called a plasma membrane oscillator, because the channels responsible for electrical activity and letting in Ca²⁺ are on the cell membrane. Another mechanism for intracellular Ca²⁺ oscillations is the periodic release of Ca²⁺ from intracellular stores, through channels on the membrane of these stores. The main Ca²⁺-storing organelle is the endoplasmic reticulum (ER), so this mechanism is called an ER oscillator. In both cases we get rhythmic Ca²⁺ increases. Although the two mechanisms can interact, we will not look deeply into their interactions here and instead focus on each separately. This chapter describes work performed to understand the dynamics underlying these two types of rhythmic Ca²⁺ increase that underlie hormone secretion from the endocrine cells of the anterior pituitary.

Like neurons and other excitable cells, pituitary cells can generate brief electrical impulses (also called action potentials or spikes). Different ion concentrations across the plasma membrane and ion channels specific for certain types of ions create a difference in the electrical potential across the membrane (the membrane potential, V ). Electrical activity in the form of impulses is caused by the regenerative opening of membrane ion channels, which allows ions through the membrane according to their concentration gradient. The opening of channels is controlled by V, which accounts for positive and negative feedback mechanisms. Usually channels open when V increases (depolarizes), so channels permeable to Na⁺ or Ca²⁺ which flows into the cell and thus creates inward currents that further depolarize the membrane, will provide the positive feedback that underlies the rapid rise of V at the beginning of a spike. Channels permeable to K⁺, which is more concentrated inside the cells, produce an outward current that acts as negative feedback to decrease V and to terminate a spike. There are many types of ion channels expressed in pituitary cells, and the combination of ionic currents mediated by these channels determines the pattern of spontaneous electrical activity exhibited by the cells (see Stojilković et al. (2010) for review). In a physiological setting, this spontaneous activity is subject to continuous adjustment by hypothalamic neuropeptides, by hormones from other glands such as the testes or ovaries, and by other pituitary hormones (Freeman (2006); Stojilković et al. (2010)).

One typical pattern of electrical activity in pituitary cells is bursting. This consists of episodes of spiking followed by quiescent phases, repeated periodically. Such bursting oscillations have been observed in the spontaneous activity of prolactin-secreting lactotrophs, growth hormone-secreting somatotrophs, and ACTH-secreting corticotrophs (Van Goor et al. (2001a,b); Kuryshev et al. (1996); Tsaneva-Atanasova et al. (2007)), as well as GH4C1 lacto-somatotroph tumor cells (Tabak et al. (2011)). The bursting pattern has a short period and the spikes tend to be very small compared with those of tonically spiking cells (Fig. 1A). In fact, the spikes don’t look much like impulses at all, but instead appear more like small oscillations. This type of bursting is often referred to as pseudo-plateau bursting (Stern et al. (2008)). A very different form of bursting is common in gonadotrophs that have been stimulated by gonadotropin releasing hormone (GnRH), their primary activator (Li et al. (1995, 1994); Tse and Hille (1992)), as well as other stimulating factors (Stojilković et al. (2010)). These bursts have much longer period than the spontaneous pseudo-plateau bursts (Fig. 1B). Since the biophysical basis for this bursting pattern is periodic release of Ca²⁺ from an internal store, we refer to it as store-generated bursting. Both forms of bursting elevate the Ca²⁺ concentration in the cytosol of the cell and evoke a higher level of hormone secretion than do tonic spiking patterns (Van Goor et al. (2001b)). This is the main reason that endocrinologists are interested in electrical bursting in pituitary cells, which in turn motivates mathematicians to develop and analyze models of the cells’ electrical activity.

Fig. 1

Recordings of electrical bursting using the perforated patch method with amphotericin B. (A) Bursting in an unstimulated cell from the GH4C1 lacto-somatotroph cell line. (B) Bursting in a pituitary gonadotroph stimulated with GnRH (1 nM). Note the different time scale

Bursting patterns also occur in neurons (Crunelli et al. (1987); Del Negro et al. (1998); Lyons et al. (2010); Nunemaker et al. (2001)) and in pancreatic β-cells, another type of endocrine cell that secretes the hormone insulin (Dean and Mathews (1970); Bertram et al. (2010)). The ubiquity of the oscillatory pattern and its complexity has attracted a great deal of attention from mathematicians, who have used various techniques to study the mechanism(s) underlying the bursting pattern. The earliest models of bursting neurons were developed in the 1970s, and bursting models have been published regularly ever since. Over the past decade several books have described some of these models and the techniques used to analyze them (Coombes and Bressloff (2005); Izhikevich (2007); Keener and Sneyd (2008)). The primary analysis technique takes advantage of the difference in time scales between variables that change quickly and those that change slowly. This “fast/slow analysis” or “geometric singular perturbation analysis” was pioneered by John Rinzel in the 1980s (Rinzel (1987)) and has been extended in subsequent years (Coombes and Bressloff (2005)). While modeling and analysis of bursting in neurons and pancreatic β-cells has a long history and is now well developed, the construction and analysis of models of bursting in pituitary cells is at a relatively early stage. The burst patterns in pituitary cells are very different from those in cells studied previously, and the fast/slow analysis technique used in neurons is of limited use for studying pseudo-plateau bursting in pituitary cells (Toporikova et al. (2008); Teka et al. (2011a)). Instead, a new fast/slow analysis technique has been developed for pseudo-plateau bursting that relies on concepts such as folded singularities, canards, and the theory of mixed-mode oscillations (Teka et al. (2011a); Vo et al. (2010)). In the first part of this chapter we describe this technique and how it relates to the original fast/slow analysis technique used to analyze other cell types.

One fundamental difference between the spontaneous bursting observed in many lactotrophs and somatotrophs and that seen in stimulated gonadotrophs is that in the former the periodic elevations of intracellular Ca²⁺ are in phase with the electrical activity, while in the latter they are 180^o out of phase. This is because the former is driven by electrical activity, which brings Ca²⁺ into the cell through plasma membrane ion channels, while the latter is driven by the ER oscillator, which periodically releases a flood of Ca²⁺ into the cytosol. This Ca²⁺ binds to Ca²⁺-activated K⁺ channels and activates them, resulting in a lowering (hyperpolarization) of the membrane potential and terminating the spiking activity. Thus, each time that the Ca²⁺ concentration is high it turns off the electrical activity. In the second part of this chapter we describe a model for this store-operated bursting and demonstrate how it can be understood in terms of coupled electrical and Ca²⁺ oscillators, again making use of fast/slow analysis.

2 The Lactotroph/Somatotroph Model

We use a model for the pituitary lactotroph developed in Tabak et al. (2007) and recently used in Teka et al. (2011b), Teka et al. (2011a, 2012), and Tomaiuolo et al. (2012). This model can also be thought of as a model for the pituitary somatotroph, since lactotrophs and somatotrophs exhibit similar behaviors and the level of detail in the model is insufficient to distinguish the two. This consists of ordinary differential equations for the membrane potential or voltage (V ), an activation variable describing the fraction of activated K⁺ channels (n), and the intracellular free Ca²⁺ concentration (c):

$$\displaystyle\begin{array}{rcl} C_{m}\frac{dV } {dt} & =& -[I_{Ca}(V ) + I_{K}(V,n) + I_{SK}(V,c) + I_{BK}(V )]{}\end{array}$$

(1.1)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt} & =& \frac{n_{\infty }(V ) - n} {\tau _{n}} {}\end{array}$$

(1.2)

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt}& =& -f_{c}(\alpha I_{Ca} + k_{c}c).{}\end{array}$$

(1.3)

The parameter C _m in Eq. 1.1 is the membrane capacitance, and the right-hand side is the sum of ionic currents. I _Ca  is an inward current carried by Ca²⁺ flowing through Ca²⁺ channels and is responsible for the upstroke of an action potential. It is assumed to activate instantaneously, so no activation variable is needed. The current is

$$\displaystyle{ I_{Ca}(V ) = g_{Ca}m_{\infty }(V )(V - V _{Ca}) }$$

(1.4)

where g _Ca is the maximum conductance (a parameter) and the instantaneous activation of the current is described by

$$\displaystyle{ m_{\infty }(V ) = \left (1 +\exp \left (\frac{v_{m} - V } {s_{m}} \right )\right )^{-1}. }$$

(1.5)

The parameters v _m and s _m set the half-maximum location and the slope, respectively, of the Boltzman curve. Since this is an increasing function of V, I _Ca  becomes activated as V increases from its low resting value toward v _m . The driving force for the current is (V − V _Ca ), where V _Ca is the Nernst potential for Ca²⁺.

I _K is an outward delayed-rectifying K⁺ current with activation that is slower than that for I _Ca . This current, largely responsible for the downstroke of a spike, is

$$\displaystyle{ I_{K}(V,n) = g_{K}n(V - V _{K}) }$$

(1.6)

where g _K is the maximum conductance, V _K is the K⁺ Nernst potential, and the activation of the current is described by Eq. 1.2. The steady state activation function for n is

$$\displaystyle{ n_{\infty }(V ) = \left (1 +\exp \left (\frac{v_{n} - V } {s_{n}} \right )\right )^{-1} }$$

(1.7)

and the rate of change of n is determined by the time constant τ _n .

Some K⁺ channels are activated by intracellular Ca²⁺, rather than by voltage. One type of Ca²⁺-activated K⁺ channel is the SK channel (small conductance K(Ca) channel). Because channel activation is due to the accumulation of Ca²⁺ in the cell (i.e., an increase in c), and this occurs more slowly than changes in V, the current through SK channels contributes little to the spike dynamics. Instead, it contributes to the patterning of spikes. The current through this channel is modeled here by

$$\displaystyle{ I_{SK}(V,c) = g_{SK}s_{\infty }(c)(V - V _{K}) }$$

(1.8)

where g _SK is the maximum conductance and the c-dependent activation function is

$$\displaystyle{ s_{\infty }(c) = \frac{c^{2}} {c^{2} + K_{d}^{2}} }$$

(1.9)

where K _d is the Ca²⁺ level of half activation.

The final current in the model reflects K⁺ flow through other Ca²⁺-activated K⁺ channels called BK channels (large conductance K(Ca) channels). These channels are located near Ca²⁺ channels and are gated by V and by the high-concentration Ca²⁺ nanodomains that form at the mouth of the open channel. As has been pointed out previously (Sherman et al. (1990)), the Ca²⁺ seen by the BK channel reflects the state of the Ca²⁺ channel, which is determined by the membrane potential. Thus, activation of the BK current can be modeled as a V -dependent process:

$$\displaystyle{ I_{BK}(V ) = g_{BK}b_{\infty }(V )(V - V _{K}) }$$

(1.10)

where

$$\displaystyle{ b_{\infty }(V ) = \left (1 +\exp \left (\frac{v_{b} - V } {s_{b}} \right )\right )^{-1}\;\;. }$$

(1.11)

Because this current activates rapidly with changes in voltage (due to the rapid formation of Ca²⁺ nanodomains), it limits the upstroke and contributes to the downstroke of an action potential.

The differential equation for the free intracellular Ca²⁺ concentration (Eq. 1.3) describes the influx of Ca²⁺ into the cell through Ca²⁺ channels (α I _Ca ) and the efflux through Ca²⁺ pumps k _c c. The parameter α converts current to molar flux and the parameter k _c is the pump rate. Finally, parameter f _c is the fraction of Ca²⁺ in the cell that is free, i.e., not bound to Ca²⁺ buffers. Default values of all parameters are listed in Table 1.

Table 1 Default parameter values for the lactotroph model

3 The Standard Fast/Slow Analysis

The three model variables change on different time scales. The time constant for the membrane potential is the product of the capacitance and the input resistance: $\tau _{V } = C_{m}/g_{total}$, where $g_{total} = g_{Ca} + g_{K} + g_{SK} + g_{BK}$ is the total membrane conductance. This varies with time as V changes, and during the burst shown in Fig. 2, g _total ranges from about 0.5 nS during the silent phase of the burst to about 3 nS during the active phase of the burst, so 3. 3 < τ _V < 20 mS. The variable n has a time constant of τ _n = 43 ms. The time constant for c is $\frac{1} {f_{c}k_{c}} = 625$ ms. Hence, $\tau _{V } <\tau _{n} <\tau _{c}$ and V is the fastest variable, while c is the slowest.

Fig. 2

Bursting produced by the lactotroph model. (A) Voltage V exhibits small spikes emerging from a plateau. (B) The variable n is sufficiently fast to reliably follow V. (C) The variable c changes on a much slower time scale, exhibiting a saw-tooth time course

The time courses of the three variables shown in Fig. 2 confirm the differences in time scales. The spikes that occur during each burst in V are reliably reflected in n, but are dampened in c. Indeed, c is an accumulating variable, similar to what one observes in the recovery variable during a relaxation oscillation. This observation motivates the idea of analyzing the burst trajectory just as one would analyze a relaxation oscillation with a fast variable V and a slow recovery variable c. That is, the trajectory is examined in the c-V plane and the c and V nullclines are utilized. However, since the system is 3-dimensional, one replaces the nullcline of the fast variable (V ) with the fast subsystem (V and n) bifurcation diagram, where the slow variable c is treated as the bifurcation parameter. This is the fundamental idea of the standard fast/slow analysis, which is illustrated in Fig. 3A. The fast-subsystem bifurcation diagram, often called the z-curve, consists of a bottom branch of stable steady states (solid curve), a middle branch of unstable saddle points (dotted curve), and a top branch of stable and unstable steady states. The three branches are joined by lower and upper saddle-node bifurcations (LSN and USN, respectively), and the stability of the top branch changes at a subcritical Hopf bifurcation (subHB). The Hopf bifurcation gives rise to a branch of unstable periodic solutions that terminates at a homoclinic bifurcation (HM). Thus, we see that the fast subsystem has an interval of c values where it is bistable between lower (hyperpolarized) and upper (depolarized) steady states. This interval extends from LSN to subHB. The c nullcline intersects the z-curve between subHB and USN. This intersection is an unstable equilibrium of the full system of equations.

Fig. 3

2-fast/1-slow analysis of pseudo-plateau bursting. The 3-branched z-curve consists of stable (solid) and unstable (dotted) equilibria and a branch of unstable periodic solutions (dashed). Bifurcations include a lower saddle-node (LSN), upper saddle-node (USN), subcritical Hopf (subHB), and homoclinic (HM) bifurcations. (A) With default parameter values, the burst trajectory (thick black curve) only partially follows the z-curve. (B) When the slow variable is made slower by reducing f _c from 0.01 to 0.001 the full-system trajectory follows the z-curve much more closely

The next step in the fast/slow analysis is to superimpose the burst trajectory and analyze the dynamics using a phase plane approach. Since the c variable is much slower than V, the trajectory largely follows the z-curve, as it would follow the nullcline of the fast variable during a relaxation oscillation. Below the c-nullcline the flow is to the left, and above the nullcline it is to the right. Hence, during the silent phase of the burst the trajectory moves leftward along the bottom branch of the z-curve. When LSN is reached there is a fast jump up to the top branch of the z-curve. The trajectory follows this rightward until subHB is reached, at which point it jumps down to the bottom branch of the z-curve, restarting the cycle.

As is clear from Fig. 3A, the trajectory does not follow the z-curve very closely. One explanation for this is that the equilibria on the top branch are weakly attracting foci, and the “slow variable” c changes too quickly for the trajectory to ever get close to the branch of foci. Thus, weakly damped oscillations are produced during the active phase, and these damped oscillations are the spikes of the burst. This interpretation is supported in Fig. 3B, where the slow variable is made 10-times slower by decreasing f _c from 0.01 to 0.001. Now the trajectory moves much more closely along both branches of the z-curve. During the active phase there are a few initial oscillations which quickly dampen. Once the trajectory passes through subHB there is a slow passage effect (Baer et al. (1989); Baer and Gaekel (2008)) and a few growing oscillations before the trajectory jumps down to the lower branch.

This analysis, which we will call a 2-fast/1-slow analysis, provides some useful information about the bursting. For example, this approach was used to understand the mechanism for active phase termination during a burst, by constructing the 2-dimensional stable manifold of the fast subsystem saddle point (Nowacki et al. (2010)). This approach was also used to understand the complex burst resetting that occurs in response to upward voltage perturbations (Stern et al. (2008)). We have shown how the z-curve for this pseudo-plateau bursting relates to that for the plateau bursting often observed in neurons (Teka et al. (2011a)). This is illustrated in Fig. 4, using the Chay-Keizer model for bursting in pancreatic β-cells (Chay and Keizer (1983)). (The equations for this model are given in the Appendix.) The standard z-curve for plateau bursting is shown in panel A. It is characterized by a branch of stable periodic solutions that are the spikes of the burst. In this figure they emanate from a supercritical Hopf bifurcation (supHB). With this stable periodic branch, the spikes tend to be much larger than those produced during pseudo-plateau bursting and they do not dampen as the active phase progresses. If the activation curve for the hyperpolarizing K⁺ current is moved rightward by increasing v _n , the cell becomes more excitable. As a result, the Hopf bifurcation moves rightward and becomes subcritical (Fig. 4B). Most importantly, the region of bistability between a stable spiking solution and a stable hyperpolarized steady state has largely been replaced by bistability between two stable steady states of the fast subsystem: one hyperpolarized and one depolarized. When the activation curve is shifted further to the right (Fig. 4C), the stable periodic branch has been entirely replaced by a stable stationary branch and the z-curve is that for pseudo-plateau bursting. Other maneuvers that make the cell more excitable, such as moving the activation curve for the depolarizing I _Ca current leftward, increasing the conductance g _Ca for this current or decreasing the conductance g _K for the hyperpolarizing I _K current, have the same effect on the z-curve (Teka et al. (2011b)). In addition to changing the fast-subsystem bifurcation diagram, the speed of the slow variable must also be modified to convert between plateau and pseudo-plateau bursting (it must be faster for pseudo-plateau bursting, which is achieved by increasing the value of f _c ). In a separate study, Osinga and colleagues demonstrated that the fast-subsystem bifurcation structure of both plateau and pseudo-plateau bursting could be obtained by unfolding a codimension-4 bifurcation (Osinga et al. (2012)). This explains why the pseudo-plateau bifurcation structure was not seen in an earlier classification of bursting that was based on the unfolding of a codimension-3 bifurcation (Bertram et al. (1995)).

Fig. 4

The Chay-Keizer model is used to illustrate the transition between plateau and pseudo-plateau bursting. (A) The z-curve for plateau bursting, using default parameter values given in Appendix, is characterized by a branch of stable periodic spiking solutions arising from a supercritical Hopf bifurcation (supHB). (B) Increasing the value of v _n from − 16 mV to − 14 mV moves the Hopf bifurcation rightward and converts it to a subHB, with an associated saddle-node of periodics (SNP) bifurcation. (C) Increasing v _n further to − 12 mV creates the z-curve that characterizes pseudo-plateau bursting. From Teka et al. (2011b)

Although the 2-fast/1-slow analysis provides useful information about the pseudo-plateau bursting, it has some major shortcomings. Most obviously, the burst trajectory does not follow the z-curve very closely unless the slow variable is slowed down to the point where spikes no longer occur during the active phase (Fig. 3). Also, the explanation for the origin of the spikes is not totally convincing, since it is based on a local analysis of the steady states of the top branch, while the bursting trajectory is not near these steady states. It also provides no information about how many spikes to expect during a burst. Finally, as illustrated in Fig. 5, it fails to explain the transition that occurs from pseudo-plateau bursting to continuous spiking when the c-nullcline is lowered. In this figure, reducing the k _c parameter lowers the nullclline without affecting the z-curve. In both panels B and D the nullcline intersects the z-curve to form an unstable full-system equilibrium (labeled as “A”) as well as the unstable periodic branch, forming an unstable full-system periodic solution. Yet, in one case the system bursts (panel A), while in the other it spikes continuously (panel C). This is a clear indication that predictions made regarding pseudo-plateau bursting with this type of analysis may not be reliable.

Fig. 5

A 2-fast/1-slow analysis fails to explain the transition from pseudo-plateau bursting to spiking in the lactotroph model when the c-nullcline is lowered. (A) Bursting produced using default parameter values. (B) The standard fast/slow analysis of the bursting pattern. (C) The bursting is converted to continuous spiking when k _c is reduced from 0.16 ms⁻¹ to 0.1 ms⁻¹. (D) It is not apparent from the fast/slow analysis why the transition took place. From Teka et al. (2012)

4 The 1-Fast/2-Slow Analysis

In the analysis above, the variable with the intermediate time scale (n) was associated with the fast subsystem, and the bursting dynamics analyzed by comparing the full-system trajectory to what one would expect if the single slow variable (c) were very slow. That is, by going to the singular limit f _c → 0 and constructing a fast-subsystem bifurcation diagram with c as the bifurcation parameter. Alternatively, one could associate n with the slow subsystem and then study the dynamics by comparing the bursting to what one would expect if the single fast variable were very fast. That is, by going to the singular limit C _m → 0. We take this 1-fast/2-slow analysis approach here, where the variable V forms the fast subsystem and n and c form the slow subsystem. This is formalized using non-dimensional equations in Teka et al. (2011a) and Vo et al. (2010), where more details and derivations can also be found. A recent review of mixed-mode oscillations (Desroches et al. (2012)) gives more detail on the key dynamical structures described below.

4.1 Reduced, Desingularized, and Layer Systems

In the following, we assume that C _m is small, so that the V variable is in a pseudo-equilibrium state. Define the function f as the right-hand side of Eq. 1.1:

$$\displaystyle{ f(V,n,c) \equiv -(I_{Ca} + I_{K} + I_{SK} + I_{BK}). }$$

(1.12)

and then

$$\displaystyle{ \tilde{f}(V,n,c) \equiv f(V,n,c)/g_{max} }$$

(1.13)

where g _max is a representative conductance value, for example, the maximum conductance during an action potential. Then the dynamics of the fast subsystem are, in the singular limit, given by the layer problem:

$$\displaystyle\begin{array}{rcl} \frac{dV } {dt_{f}}& =& \tilde{f}(V,n,c){}\end{array}$$

(1.14)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt_{f}}& =& 0{}\end{array}$$

(1.15)

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt_{f}}& =& 0\;\;.{}\end{array}$$

(1.16)

where $t_{f} = (g_{max}/C_{m})t$ is a dimensionless fast time variable. The equilibrium set of this subsystem is called the critical manifold, which is a surface in $\mathbb{R}^{3}$:

$$\displaystyle{ S \equiv \{ (V,n,c) \in \mathbb{R}^{3}: f(V,n,c) = 0\}. }$$

(1.17)

Since f is linear in n, it is convenient to solve for n in terms of V and c:

$$\displaystyle{ n = n(V,c) = - \frac{1} {g_{K}}\left [h(V ) + g_{SK}s_{\infty }(c)\right ] }$$

(1.18)

where

$$\displaystyle{ h(V ) = g_{Ca}m_{\infty }(V )\left (\frac{V - V _{Ca}} {V - V _{K}} \right ) + g_{BK}b_{\infty }(V ). }$$

(1.19)

The critical manifold is a folded surface consisting of three sheets connected by two fold curves (Fig. 6). The one-dimensional fast subsystem is bistable; for a range of values of n and c there is a stable hyperpolarized steady state and a stable depolarized steady state, separated by an unstable steady state. The stable steady states form the attracting lower and upper sheets of the critical manifold (denoted as S _a ⁺ and S _a ⁻ and where $\frac{\partial f} {\partial V } < 0$), while the separating unstable steady states form the repelling middle sheet (denoted as S _r and where $\frac{\partial f} {\partial V } > 0$). The sheets are connected by fold curves denoted by L ⁺ and L ⁻ that consist of points on the surface where

$$\displaystyle{ \frac{\partial f} {\partial V } = 0. }$$

(1.20)

That is,

$$\displaystyle{ L^{\pm }\equiv \{ (V,n,c) \in \mathbb{R}^{3}: f(V,n,c) = 0\;\mathrm{and}\; \frac{\partial f} {\partial V }(V,n,c) = 0\}. }$$

(1.21)

The projection of the top fold curve onto the lower sheet is denoted P(L ⁺), while the projection of the lower fold curve onto the top sheet is denoted P(L ⁻). Both projections are shown in Fig. 6.

Fig. 6

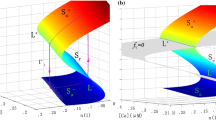
The critical manifold is the set of points in $\mathbb{R}^{3}$ for which the fast variable V is at equilibrium (Eq. 1.17). The two fold curves are denoted by L ⁺ and L ⁻. The projections along the fast fibers of the fold curves are denoted by P(L ⁺) and P(L ⁻). Also shown is the folded node singularity (FN) and the strong canard (SC) that enters the folded node. From Teka et al. (2011a)

The critical manifold is not only the equilibrium set of the fast subsystem, but is also the phase space of the slow subsystem. This slow subsystem, also called the reduced system, is described by

$$\displaystyle\begin{array}{rcl} f(V,n,c)& =& 0{}\end{array}$$

(1.22)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt} & =& \frac{n_{\infty }(V ) - n} {\tau _{n}} {}\end{array}$$

(1.23)

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt}& =& -f_{c}(\alpha I_{Ca} + k_{c}c).{}\end{array}$$

(1.24)

This differential-algebraic system describes the flow when the trajectory is on the critical manifold, which is given as a graph in Eq. 1.18. We can thus present the system in a single coordinate chart (V, c) including the neighborhood of the two folds. A condition is then needed to constrain the trajectories to the critical manifold. It is the total time derivative of f = 0 that provides this condition. That is,

$$\displaystyle{ \frac{d} {dt}\ f(V,n,c) = \frac{d} {dt}0 }$$

(1.25)

or

$$\displaystyle{ -\frac{\partial f} {\partial V } \frac{dV } {dt} = \frac{\partial f} {\partial c} \frac{dc} {dt} + \frac{\partial f} {\partial n} \frac{dn} {dt}. }$$

(1.26)

Using Eqs 1.23, 1.24,

$$\displaystyle{ -\frac{\partial f} {\partial V } \frac{dV } {dt} = -f_{c}(\alpha I_{Ca} + k_{c}\,c)\frac{\partial f} {\partial c} + \left (\frac{n_{\infty }(V ) - n(V,c)} {\tau _{n}} \right )\frac{\partial f} {\partial n}. }$$

(1.27)

The reduced system then consists of the differential equations Eqs. 1.24 and 1.27 where n(V, c) is given by Eq. 1.18.

The reduced system is singular at the fold curves (where $\frac{\partial f} {\partial V } = 0$), so the speed of a trajectory approaches $\infty$ as it approaches a fold curve. (This can be seen by solving Eq. 1.27 for $\frac{dV } {dt}$ and noting that the denominator approaches 0, but the numerator does not, as a fold curve is approached.) The singularity can be removed by introducing a rescaled time $d\tau = -( \frac{\partial f} {\partial V })^{-1}dt$. This produces a system that behaves like the reduced system, except at the fold curves, which are transformed into nullclines of the c variable. With this rescaled time, the following desingularized system is formed:

$$\displaystyle\begin{array}{rcl} \frac{dV } {d\tau } & =& F(V,c){}\end{array}$$

(1.28)

$$\displaystyle\begin{array}{rcl} \frac{dc} {d\tau } & =& f_{c}(\alpha I_{Ca} + k_{c}\,c) \frac{\partial f} {\partial V }\;\;,{}\end{array}$$

(1.29)

where F(V, c) is defined as

$$\displaystyle{ F(V,c) \equiv -f_{c}(\alpha I_{Ca} + k_{c}\,c)\frac{\partial f} {\partial c} + \left (\frac{n_{\infty }(V ) - n(V,c)} {\tau _{n}} \right )\frac{\partial f} {\partial n}. }$$

(1.30)

Like the reduced system, Eqs. 1.28–1.30 along with Eq. 1.18 describe the flow on the top and bottom sheets of the critical manifold. They also describe the flow on the middle sheet, but in this case the flow is backwards in time due to the time rescaling. The jump from one attracting sheet to another is described by the layer problem, which was discussed above.

A singular periodic orbit can be constructed by gluing together trajectories from the desingularized system and the layer system such that the resulting orbit returns to its starting point. An example is shown in Fig. 6. Beginning from a point on the singular periodic orbit that lies on S _a ⁺, the desingularized system is solved to yield a trajectory that moves along S _a ⁺ until it reaches L ⁺ (black curve with single arrow). From here, it moves to the bottom sheet following a fast fiber (black curve with double arrows). From a point on P(L ⁺) the desingularized equations are again solved to yield a trajectory that moves along S _a ⁻ until L ⁻ is reached. The trajectory then moves along a fast fiber to a point on P(L ⁻) on the top sheet. From here the desingularized equations are again solved and the trajectory continues until the starting point is reached.

4.2 Folded Singularities and the Origin of Pseudo-Plateau Bursting

There are two very different types of equilibria of the desingularized system: ordinary and folded singularities. An ordinary singularity of the desingularized system satisfies

$$\displaystyle{ f(V,n,c) = 0 }$$

(1.31)

$$\displaystyle{ n = n_{\infty }(V ) }$$

(1.32)

$$\displaystyle{ c = c_{\infty }(V ) = -f(\alpha I_{Ca} + k_{c}c)\;\; }$$

(1.33)

and is an equilibrium of the full system Eqs. 1.1–1.3. A folded singularity lies on a fold curve and satisfies

$$\displaystyle{ f(V,n,c) = 0 }$$

(1.34)

$$\displaystyle{ F(V,c) = 0 }$$

(1.35)

$$\displaystyle{ \frac{\partial f} {\partial V } = 0. }$$

(1.36)

As previously noted, in the reduced system (Eqs. 1.24, 1.27, and 1.18), trajectories pass through a fold curve with infinite velocity. Folded singularities are an exception: at these points both numerator and denominator approach 0, and hence a trajectory passes through a folded singularity with finite speed. In the full system near the singular limit, the trajectory can pass through the fold curve and move along the middle sheet of the slow manifold for some time before jumping off.

A linear stability analysis of a folded singularity indicates whether it is a folded node (two real eigenvalues of the same sign), folded saddle (real eigenvalues of opposite sign), or folded focus (complex conjugate pair of eigenvalues). In the full system, singular canards exist in the neighborhood of a folded node and a folded saddle (Benoit (1983); Szmolyan and Wechselberger (2001)). These trajectories enter the folded singularity, in our case along S _a ⁺, and move through it in finite time, emerging on the repelling sheet S _r and traveling along this sheet for some time. For the parameter values used in Fig. 6 there is a folded node (FN) on L ⁺. In such a case, there is a whole sector of singular canards, bounded by L ⁺ and the strong singular canard (denoted by SC in Fig. 6) associated with the trajectory that is tangent to the eigendirection of the strong eigenvalue of the FN. This sector is called the singular funnel. A singular periodic orbit that enters the singular funnel will exhibit canard-induced mixed-mode oscillations (MMOs) away from the singular limit (i.e., when C _m > 0) (Brons et al. (2006)).

According to Fenichel theory (Fenichel (1979)), for C _m > 0 the critical manifold perturbs smoothly to a slow manifold consisting of invariant attracting and repelling manifolds. We denote the attracting manifolds as $S_{a,C_{m}}^{+}$ and $S_{a,C_{m}}^{-}$, and the repelling manifold as $S_{r,C_{m}}$. Since the critical manifold loses hyperbolicity at L ⁺ and L ⁻, Fenichel theory does not apply there. Indeed, the critical manifold near a folded node perturbs to twisted sheets (Guckenheimer and Haiduc (2005); Wechselberger (2005)). This is illustrated in Fig. 7, where $S_{a,C_{m}}^{+}$ (blue) and $S_{r,C_{m}}$ (red) come together near the FN. The numerical technique used to compute the twisted sheets utilizes continuation of trajectories that satisfy boundary value problems, and was developed in Desroches et al. (2008a) and Desroches et al. (2008b).

Fig. 7

The twisted slow manifold near a folded node, calculated using C _m = 2 pF with default parameter values. The primary strong canard (SC, green) flows from $S_{a,C_{m}}^{+}$ to $S_{r,C_{m}}$ with a half rotation. The secondary canard $\xi _{1}$ flows from $S_{a,C_{m}}^{+}$ to $S_{r,C_{m}}$ with a single rotation. The other secondary canards ($\xi _{2}$, $\xi _{3}$) have two and three rotations, respectively. The full system has an unstable equilibrium near $S_{r,C_{m}}$ (cyan circle). The pseudo-plateau bursting trajectory (PPB) is superimposed and has two rotations. From Teka et al. (2011a)

The singular strong canard perturbs to a primary strong canard that moves from $S_{a,C_{m}}^{+}$ to $S_{r,C_{m}}$ with only one twist, or one half rotation. In addition, there is a family of secondary canards that move through the funnel and exhibit rotations as they flow from $S_{a,C_{m}}^{+}$ to $S_{r,C_{m}}$. The maximum number of rotations produced, S _max , is determined by the eigenvalue ratio of the linearization at the folded node. If $\lambda _{s}$ and $\lambda _{w}$ are the strong and weak eigenvalues of the linearization at the FN, then define

$$\displaystyle{ \mu = \frac{\lambda _{w}} {\lambda _{s}}. }$$

(1.37)

The maximum number of oscillations is then (Rubin and Wechselberger (2008); Wechselberger (2005))

$$\displaystyle{ S_{max} = \left [\frac{\mu +1} {2\mu } \right ] }$$

(1.38)

which is the greatest integer less than or equal to $\frac{\mu +1} {2\mu }$. For C _m > 0, but small, there are S _max − 1 secondary canards that divide the funnel into S _max sectors (Brons et al. (2006)). The first sector is bounded by SC and the first secondary canard $\xi _{1}$ and trajectories entering this sector have one rotation. The second sector is bounded by $\xi _{1}$ and $\xi _{2}$ and trajectories entering here have two rotations, etc. Trajectories entering the last sector, bounded by the last secondary canard and the fold curve L ⁺, have the maximal S _max number of rotations (Rubin and Wechselberger (2008); Vo et al. (2010); Wechselberger (2005)). Many of these small oscillations are so small that they would be practically invisible, particularly in an experimental voltage trace where they would be obscured by noisy fluctuations.

Figure 7 shows a portion of the pseudo-plateau burst trajectory (PPB, black curve) superimposed onto the twisted slow manifold. Since it enters the funnel between the first and second secondary canards it exhibits two rotations as it moves through the region near the FN. These rotations are the small spikes that occur during the active phase of the burst. The full burst trajectory, then, consists of slow flow along the lower and upper sheets of the slow manifold, followed by fast jumps from one attracting sheet to another. The jump from $S_{a,C_{m}}^{+}$ down to $S_{a,C_{m}}^{-}$ is preceded by a few small oscillations, which are the spikes of the burst. As C _m is made smaller, the burst trajectory looks more and more like the singular periodic orbit, and indeed the small oscillations disappear in the singular limit (Vo et al. (2010)).

4.3 Phase-Plane Analysis of the Desingularized System

Because the desingularized system is two-dimensional, one can apply phase-plane analysis techniques to it (Rubin and Wechselberger (2007); Teka et al. (2011a)). This is illustrated in Fig. 8, where the nullclines and equilibria are shown. The V -nullcline satisfies F(V, c) = 0 and is the single z-shaped curve in the figure. The c-nullcline satisfies

$$\displaystyle{ f_{c}(\alpha I_{Ca} + k_{c}\,c) \frac{\partial f} {\partial V } = 0 }$$

(1.39)

and thus

$$\displaystyle{ \alpha I_{Ca} + k_{c}\,c = 0 }$$

(1.40)

or

$$\displaystyle{ \frac{\partial f} {\partial V } = 0. }$$

(1.41)

The first set of solutions forms the c-nullcline of the full system and is labelled CN1 in Fig. 8. The second set of solutions forms the two fold curves L ⁺ and L ⁻. Intersections of the V -nullcline with CN1 produce ordinary singularities and are equilibria of the full system (Eqs. 1.1–1.3). There is one such equilibrium in Fig. 8A, labelled as point A, which is an unstable saddle point of the desingularized system. Intersections of the V -nullcline with one of the fold curves produce folded singularities. In Fig. 8A there is a folded focus singularity on L ⁻ and a folded node singularity on L ⁺. The folded node is stable, and will generate canards. The folded focus is also stable, but it produces no canards.

Fig. 8

Nullclines of the desingularized system. (A) An ordinary singularity (point A) occurs where the V -nullcline and the CN1 branch of the c-nullcline intersect. This equilibrium is a saddle point of the desingularized system and a saddle-focus of the full system. Two folded equilibria occur where the V -nullcline intersects the fold curves. One folded singularity is a stable folded node (FN), while the other is a stable folded focus (FF). (B) When g _BK  is increased from 0.4 nS to 2.176 nS the saddle point and folded node coalesce at a transcritical bifurcation (TR). This is also known as a folded saddle-node of type II. (C) When g _BK = 4 nS the ordinary singularity, which now occurs on the top sheet of the critical manifold, is stable. The folded node has become a folded saddle and is unstable

One advantage of having a planar system is that it facilitates understanding of the effects of parameter changes. For example, increasing the parameter g _BK  changes the shape of the V -nullcline and brings L ⁺ and L ⁻ closer together, but has no effect on CN1. As this parameter is increased the FN and the equilibrium point A move closer together, and eventually coalesce (Fig. 8B). When the parameter is increased further the stability is transferred from the folded node to the full-system equilibrium (Fig. 8C). Thus, the desingularized system undergoes a transcritical bifurcation as g _BK  is increased. On the other side of the bifurcation, the folded node has become a folded saddle and no longer attracts trajectories off of its one-dimensional stable manifold. The intersection point A is now stable, and is a stable equilibrium of the full system of equations. Thus, beyond the transcritical bifurcation the full system is at rest at a high-voltage (depolarized) steady state. This transcritical bifurcation of the desingularized system is also called a type II folded saddle-node bifurcation (Krupa and Wechselberger (2010); Milik and Szmolyan (2001); Szmolyan and Wechselberger (2001)). In contrast, a type I folded saddle-node bifurcation is the coalescence of a folded saddle and a folded node singularity, and does not involve full-system equilibria (Szmolyan and Wechselberger (2001)).

The transcritical bifurcation of the desingularized system is a signature of a singular Hopf bifurcation of the full system (Desroches et al. (2012); Guckenheimer (2008)). The ordinary saddle point of the desingularized system in Fig. 8A is a saddle focus of the full system, and trajectories can approach the saddle focus along its one-dimensional stable manifold and leave along the two-dimensional unstable manifold with growing oscillations. In fact, with an appropriate global return mechanism, this can be a mechanism for MMOs that is different from that due to the folded node (which co-exists with the saddle focus). In this case, the small oscillations are characterized by a monotonic increasing amplitude, which may or may not be the case for canard-induced MMOs. Interestingly, these two mechanisms for MMOs are not mutually exclusive; in Fig. 21 of Desroches et al. (2012) an example is shown of an MMO whose first few small oscillations are due to a twisted slow manifold induced by a folded node and whose remaining small oscillations are due to growing oscillations away from a saddle focus.

4.4 Bursting Boundaries

One useful application of the 1-fast/2-slow analysis is the determination of the region of parameter space for which bursting occurs. A change in a parameter can convert bursting to spiking, as in Fig. 5, or can convert bursting to a stable steady state, as would occur in Fig. 8. Since the pseudo-plateau bursting is closely associated with the existence of a folded node singularity, one necessary condition for this type of bursting is the existence of a folded node. We have seen that a folded node can be created/destroyed via a type II folded saddle-node bifurcation. That is, when the weak eigenvalue crosses through the origin, and thus μ = 0. A folded node can also change to a folded focus, which has no canard solutions. This occurs after the eigenvalues coalesce, i.e., when μ = 1. Since a folded node singularity exists only when 0 < μ < 1, canard-induced mixed-mode oscillations only occur for parameter values for which 0 < μ < 1 at the folded singularity. This is predictive for pseudo-plateau bursting, at least in the case where C _m  is small. For larger values of C _m  the singular theory may not hold up, so bursting may occur for parameter values at which the singular theory predicts a continuous spiking solution.

Another condition for canard-induced MMOs is that there is a global return mechanism that periodically injects the trajectory into the funnel. When this occurs, the trajectory moves through the twisted slow manifold and produces small oscillations that are the spikes of pseudo-plateau bursting. If instead the trajectory is injected outside of the funnel, on the other side of the strong canard, continuous spiking will occur. To quantify this, a distance measure δ is used. This is defined using the singular periodic orbit, and is best viewed in the c-V plane (Fig. 9). When the orbit jumps from the bottom sheet of the critical manifold at L ⁻ it moves along a fast fiber to a point on P(L ⁻) on the top sheet. The horizontal distance from this point to the strong canard is defined as δ. If the point is on the strong canard, then δ = 0, while if it is in the funnel then δ > 0 by convention. Thus, a necessary condition for the existence of canard-induced MMOs, and pseudo-plateau bursting, is δ > 0.

Fig. 9

Projection of the singular periodic orbit and key structures onto the c-V plane. The upper fold curve (L ⁺) and strong canard (SC) delimit the singular funnel. The singular periodic orbit jumps from L ⁻ onto a point on P(L ⁻). The distance in the c direction from this point to the strong canard is defined as δ, and by convention δ > 0 when the point is in the funnel. From Teka et al. (2011a)

With these constraints on δ and μ one can construct a 2-parameter bifurcation diagram characterizing the behavior of the full system. One such diagram is illustrated in Fig. 10, where the maximum conductances of the delayed rectifier (g _K ) and the large-conductance K(Ca) (g _BK ) currents are varied. In the diagram, the upper curve (magenta) consists of type II folded saddle-node bifurcations that give rise to a folded node, and thus is characterized by μ = 0. Above this curve the full system equilibrium is stable and the system goes to a depolarized steady state. Below this curve μ > 0. The lower curve (green) consists of points in which δ = 0. Above this curve δ > 0, while below it δ < 0. Both conditions for MMOs are satisfied between the two curves, so this is the parameter region where mixed-mode oscillations occur.

Fig. 10

The singular analysis predicts whether the full system should be continuously spiking, bursting, or in a depolarized steady state. The folded node becomes a folded saddle above the μ = 0 curve and the ordinary singularity of the desingularized system becomes stable. Between the μ = 0 and δ = 0 curves the two conditions are met for mixed-mode oscillations, and pseudo-plateau bursting is predicted to occur. Below the δ = 0 curve the singular periodic orbit does not enter the singular funnel, resulting in relaxation oscillations. Away from the singular limit (for C _m > 0) these become a periodic spike train

4.5 Spike-Adding Transitions

In the region of parameter space where MMOs occur, one can characterize the number of small oscillations (spikes) that occur in different subregions. Such an analysis was performed in Vo et al. (2012), using a variant of the lactotroph model (described in the Appendix) that we have been using thus far. It was motivated by the observation that, in a 4-variable lactotroph model containing an A-type K⁺ current, pseudo-plateau bursting can occur even if one fixes the c variable at its average value (Toporikova et al. (2008)). Thus, to simplify the analysis, c is clamped and the model reduced to 3 dimensions. This 3-dimensional model is what we consider now, where the major difference with the 3-dimensional lactotroph model discussed previously is that the SK and BK currents are replaced by leakage and A-type K⁺ currents, and the calcium variable c is replaced by an inactivation variable e for the A-type channels. The bursting boundaries were determined with this model in the plane of the two parameters g _K  and g _A . In this case, the left bursting boundary occurs when μ = 0 and the folded node becomes a folded saddle at a type II folded saddle-node bifurcation. Unlike in Fig. 10, however, the right boundary for mixed-mode oscillations occurs when μ = 1 and the folded node becomes a folded focus (Fig. 11). A third boundary occurs where δ = 0, and the fourth boundary occurs where a stable equilibrium of the full system is born at a saddle-node on invariant circle (SNIC) bifurcation. Both conditions for MMOs are satisfied within the trapezoidal region bounded by these line segments (Fig. 11).

Fig. 11

Bursting boundaries and the maximum number of spikes per burst in a variant of the lactotroph model (described in Appendix). The left and right boundaries occur when the folded node becomes a folded saddle (μ = 0) or a folded focus (μ = 1). The lower boundary occurs when the periodic orbit jumps to the strong canard that delimits the singular funnel (δ = 0). The upper boundary occurs when a stable equilibrium of the full system is born at an SNIC bifurcation. The maximum number of spikes (S _max ) is determined by μ. From Vo et al. (2012)

The maximum number of small oscillations that occur in the mixed-mode oscillations (S _max ) depends on μ, the eigenvalue ratio, according to Eq. 1.38. In this model, the eigenvalues depend only on g _K , and only slightly on g _A . Thus, the subregions of constant S _max  are separated by almost-vertical line segments (g _K  values where the value of the greatest integer function changes). Near the right boundary μ ≈ 1, so by Eq. 1.38 there is at most one small oscillation per burst. (There will be an additional oscillation, due to the trajectory jumping from the lower sheet to the upper sheet of the slow manifold; after the jump, the voltage is initially large and then slowly declines, producing the first spike of the burst.) For g _K ≈ 5 nS, S _max increases to 2, and then to 3 for g _K ≈ 4. 4 nS. The maximum number of oscillations continues to increase as the left boundary is approached, where μ = 0 and $S_{max} \rightarrow \infty$.

While the eigenvalue ratio tells half of the story, the other half is determined by where the periodic orbit lands when it jumps to the top sheet of the slow manifold (i.e., it depends on the value of δ). If the orbit jumps to a point close to the primary strong canard, then δ is near 0. In this sector, bounded on one side by the primary strong canard and on the other by the first secondary canard, one small oscillation will be produced, regardless of the eigenvalue ratio μ. This is the case near the bottom of the MMO region in the parameter plane. The distance measure δ becomes larger for larger values of g _A , and thus the number of small oscillations produced during a burst increases as the trajectory jumps into sectors that are further from the primary strong canard. In summary, the parameter g _K  controls the eigenvalue ratio μ and thus the maximum number of spikes per burst. It also determines the number of secondary canards, which delimit sectors of the funnel. The parameter g _A  controls the distance measure δ and thus which sector the orbit jumps into when it jumps to the top sheet of the slow manifold. In the two-parameter diagram of Fig. 11, the number of spikes per burst will increase as one moves to the left or upward in the MMO region.

If δ is held constant by fixing g _A , and μ is varied by varying g _K , what will the bifurcation structure of the spike adding transitions look like? How are the MMO solution branches connected to one another? That is, how does a bursting branch with n spikes connect to a bursting branch with n + 1 spikes? These questions were addressed in Vo et al. (2012), first by performing a bifurcation analysis with the continuation program AUTO (Doedel (1981); Doedel et al. (2007)), and then by using return maps of both the singular and non-singular systems to better understand the spike adding behavior. Figure 12 shows the L ₂ norm of the solution over a range of values of g _K  for g _A = 4 nS. For g _K  below about 3.7 nS there is a stable depolarized steady state (E _D ). This becomes unstable at a subcritical Hopf bifurcation. The family of periodic solutions born at this bifurcation consists of continuous spiking, labeled here as s = 0 (no small oscillations). The first family of bursting solutions (s = 1 branch) connects to the spiking branch at a period doubling bifurcation (at g _K ≈ 3. 592 nS, shown in the left inset) and later at a second period doubling bifurcation (at g _K ≈ 6. 127 nS). This bursting pattern has one spike induced by a folded node, in addition to the initial spike due to the jump up to and initial motion down the top sheet. The next bursting branch, with s = 2, is connected to neither the spiking branch nor the s = 1 branch. Instead, it is an isola formed by a pair of saddle-node of periodics bifurcations (right inset of Fig. 12). This family of solutions extends over a smaller range of g _K  values than the s = 1 family, and the stable portion of the branch in particular is only about a quarter as long as that of the s = 1 branch. Other bursting families are isolas similar to the s = 2 family, and the range of each successive family is shorter than its predecessor. There is an accumulation point as g _K  is decreased (toward the point where μ = 0) as the stable range of the bursting families approaches 0 and $s \rightarrow \infty$.

Fig. 12

Spike adding transitions over a range of values of g _K  and with g _A = 4 nS and C _m = 2 pF. Only the s = 1 bursting family is connected to the spiking branch (s = 0). All other families of bursting solutions (e.g., the s = 2 family) form isolas. The lactotroph model variant is used. From Vo et al. (2012)

4.6 Prediction Testing on Real Cells

Figures 10 and 11 provide predictions about how the number of spikes per burst vary with parameter values and the boundaries between continuous spiking, bursting, and stationary behavior. These predictions have proven to be quite good (Teka et al. (2011a); Vo et al. (2010)) even in cases where the singular parameter C _m  is large, within the right range for pituitary cells ( ≈ 5 pF). Importantly, these predictions also apply to real pituitary cells. For example, if a pituitary cell is spiking continuously, then it should be possible to convert it to a bursting cell by increasing the conductance of the BK-type or A-type K⁺ currents, or by decreasing the conductance of the delayed-rectifier K⁺ current. Also, if the cell is bursting, then the number of spikes in a burst should increase if g _BK  or g _A  is increased, or if g _K  is decreased. These predictions were tested using the dynamic clamp technique, which records the voltage from a real cell using an electrode, then uses a mathematical model to compute a current, which is injected into the cell in real time. Thus, the dynamic clamp allows one to add a voltage-dependent current to a real cell, using the cell’s membrane potential to calculate that current (Milescu et al. (2008); Sharp et al. (1993)).

Figure 13 shows the result of adding a BK current to a GH4C1 cell (a lacto-somatotroph cell line). With no added BK conductance the cell spikes continuously (Fig. 13A). However, once BK current is added with a sufficiently large conductance the cell exhibits a pseudo-plateau bursting pattern intermixed with spiking (Fig. 13B). Adding more conductance increases the burstiness of the cell, that is, the fraction of events that are bursts. Also, as predicted by the analysis, adding more g _BK  increases the number of spikes in a burst (Fig. 13C). The change in burstiness with added BK conductance is quantified in panel D, where the burstiness is calculated over the entire time course for each value of the added g _BK . Panel E shows the quantification of the mean even duration, including both spikes and bursts. Both the burstiness and the event duration increase with an increase in the added g _BK , as predicted by the analysis. The transition between spiking and bursting with addition or subtraction of a BK current using the dynamic clamp was shown repeatedly in GH4C1 cells and primary pituitary gonadotrophs (Tabak et al. (2011); Tomaiuolo et al. (2012)).

Fig. 13

Patch clamp recording from a GH4C1 lacto-somatotroph cell using dynamic clamp to add a model BK-type current (Eq. 1.10). (A) With no added current the cell spikes continuously. (B) When 0.5 nS of BK conductance is added the cell exhibits bursts intermingled with spikes. (C) With a larger added BK conductance, 1 nS, the burstiness is increased, as is the number of spikes per burst. (D) Quantification of the burstiness over the entire time course for the three values of the added g _BK . The burstiness increases with g _BK . (E) Quantification of the mean event duration for the three values of the added g _BK . The event duration increases with g _BK

It is also possible to use the dynamic clamp to add a negative conductance to the cell, thereby subtracting an ionic current. One can, for example, develop a model for the I _K current that reflects the characteristics of this current in the real cell. Then the dynamic clamp technique can be used to subtract off some of this current from the cell, by adding a negative g _K  conductance. This can be superior to using pharmacological agents to remove a current, since such agents are often non-specific. Also, the dynamic clamp approach allows the investigator to subtract off only a fraction of the current, in a controlled manner. We use this approach to subtract off g _K  conductance, and thus reduce the effective g _K  value in the cell (the native g _K  minus that subtracted off with dynamic clamp). The prediction is that a spiking cell should become a burster when a sufficient amount of g _K  is subtracted, and as more is subtracted the number of spikes in a burst should increase (Fig. 12). The results of applying the dynamic clamp to a GH4C1 cell are shown in Fig. 14. The top panel shows that the cell is mostly spiking, with a low degree of burstiness and no more than 2 spikes per burst, prior to subtraction of g _K . When some delayed rectifier conductance is subtracted ( − 1 nS) the burstiness of the cell increases (Fig. 14B). Subtracting off even more conductance ( − 2 nS) further increases the burstiness and increases the number of spikes per burst (Fig. 14C). These effects are quantified in panels D and E, where burstiness and mean even duration are computed over the entire time course durations. As predicted by the singular analysis, reducing g _K  in the cell increases the likelyhood that it wil burst, and increases the number of spikes within a burst.

Fig. 14

Patch clamp recording from a GH4C1 lacto-somatotroph cell using dynamic clamp to subtract a delayed rectifier K⁺ current (Eq. 1.6). (A) With no added current the cell has very low burstiness, with at most two spikes per burst. (B) When 1 nS of delayed rectifier K conductance is subtracted the burstiness of the cell increases. (C) When more delayed rectifier conductance is subtracted, 2 nS, the burstiness increases further and the number of spikes per burst increases. (D) Quantification of the burstiness over the entire time course for the three values of the subtracted g _K . The burstiness increases when more g _K  is subtracted. (E) Quantification of the mean event duration for the three values of the subtracted g _K . The event duration increases when more g _K  is subtracted

5 Relationship Between the Fast/Slow Analysis Structures

We began with a description of the standard fast/slow analysis technique applied to bursting oscillations in which the full 3-dimensional system is decomposed into a 2-dimensional fast subsystem and a 1-dimensional slow subsystem. We then described an alternate decomposition, with a 1-dimensional fast subsystem and a 2-dimensional slow subsystem. Each approach made use of key structures that organized the behavior of the system. In the case of the 2-fast/1-slow analysis (Fig. 3), the z-curve (equilibria of the fast subsystem) and the subcritical Hopf bifurcation point on the upper portion of the z-curve are two key structures. In addition, the nullcline of the slow variable (the c-nullcline) is important since it determines the direction of the slow flow. In the case of the 1-fast/2-slow analysis, the critical manifold, the folded node singularity, and the nullclines of the desingularized system are key organizational structures (Figs. 6, 8). In Teka et al. (2012) the lactotroph model (with SK and BK currents, and calcium variable c) was used to investigate the relationship between these sets of structures. In this section we discuss the key findings of this investigation.

5.1 The f _c → 0 Limit

The nullclines of the desingularized system shown in Fig. 8A are redrawn in Fig. 15A. These were computed using f _c = 0. 01, which is the typical value for this parameter (the ratio of free to bound Ca²⁺ in the cell). Superimposed is the z-curve obtained from the 2-fast/1-slow decomposition, computed using C _m = 10 pF. This z-curve is the stationary branch of the 2-variable fast subsystem, where c is treated as a parameter, so it tacitly assumes that f _c = 0. It is clear that the V -nullcline and z-curve are very similar, and the CN1 nullcline of the desingularized system is the c-nullcline of the 2-fast/1-slow system. The point A is the single intersection of all three curves, and is both an equilibrium of the desingularized system and an equilibrium of the full system. The subcritical Hopf bifurcation of the 2-fast/1-slow system lies on the top branch of the z-curve, but below L ⁺, which means that it is located on the middle sheet of the critical manifold (Fig. 15B). In addition, the two saddle-node bifurcations of the z-curve are on the middle sheet of the critical manifold. The folded node of the desingularized system is located close to the subcritical Hopf bifurcation point, but on the upper fold of the critical manifold.

Fig. 15

(A) The nullclines of the desingularized system with the z-curve (black) superimposed. (B) The critical manifold of the reduced system with the z-curve superimposed. In both cases, g _K = 4 nS, g _BK = 0. 4 nS, C _m = 10 pF (for the z-curve), and f _c = 0. 01 (for the desingularized system). Redrawn from Teka et al. (2012)

We now take the limit f _c → 0, so that the variable c becomes infinitesimally slow. Taking this limit has no effect on the z-curve, which already assumes that f _c = 0. It also has no effect on L ⁺, L ⁻, or CN1, since f _c divides out of the equations for these curves. However, it does influence the V -nullcline of the desingularized system,

$$\displaystyle{ -f_{c}(\alpha I_{Ca} + k_{c}\,c)\frac{\partial f} {\partial c} + \left (\frac{n_{\infty }(V ) - n} {\tau _{n}} \right )\frac{\partial f} {\partial n} = 0. }$$

(1.42)

When f _c → 0 the first term disappears, and for the second term to equal 0 either $n = n_{\infty }(V )$ or $\frac{\partial f} {\partial n} = g_{k}(V - V _{K}) = 0$. Since V > V _K , and g _K ≠ 0, we must have $n = n_{\infty }(V )$, so that $\frac{dn} {dt} = 0$. Thus, the V -nullcline of the desingularized system satisfies $\frac{dV } {dt} = 0$ and $\frac{dn} {dt} = 0$, which are the same equations defining the z-curve.

Although the V -nullcline and the z-curve superimpose in the f _c → 0 limit, the folded node and the Hopf bifurcation do not (Fig. 16). Instead, in this limit, the Hopf bifurcation remains on the middle sheet of the critical manifold.

Fig. 16

The V -nullcline (green) converges to the z-curve (black) in the f _c → 0 limit. The folded node and subcritical Hopf bifurcation remain separated. The z-curve was computed using C _m = 10 pF. From (Teka et al. (2012))

5.2 The C _m → 0 Limit

While the limit f _c → 0 makes c infinitesimally slow, the limit C _m → 0 makes V infinitely fast. We now take this limit, returning f _c to its default value of 0.01. The desingularized system is formed from the limit C _m → 0, so taking this limit only affects the z-curve of the 2-fast/1-slow decomposition. This curve of fast-subsystem equilibria is defined by f(V, n, c) = 0 and $n = n_{\infty }(V )$, and C _m appears in neither equation. Thus, the locations of the equilibria that comprise the z-curve are unaffected by C _m . However, the stability of these points does change with C _m , since C _m is in the ordinary differential equation for V (Eq. 1.1). In fact, as C _m → 0 the Hopf bifurcation migrates toward the fold curve L ⁺ (Fig. 17).

Fig. 17

In the C _m → 0 limit the Hopf bifurcation on the z-curve migrates to the fold curve L ⁺. In this figure C _m = 0. 1 pF, so it is very close to L ⁺, but has not yet reached it (inset). The V -nullcline of the desingularized system is computed with the default f _c = 0. 01. From Teka et al. (2012)

To understand this convergence to L ⁺, note that the Jacobian matrix of the 2-dimensional fast subsystem (Eqs. 1.1, 1.2) is

$$\displaystyle{ \mathbf{J} = \left (\begin{array}{*{10}c} \frac{1} {C_{m}} \frac{\partial f} {\partial V } & \frac{1} {C_{m}} \frac{\partial f} {\partial n} \\ \frac{\partial g} {\partial V } & \frac{\partial g} {\partial n} \end{array} \right ) }$$

(1.43)

where $g(V ) \equiv \frac{n_{\infty }(V )-n} {\tau _{n}}$. The trace of J is

$$\displaystyle{ \mathrm{trace}(\mathbf{J}) = \frac{1} {C_{m}} \frac{\partial f} {\partial V } + \frac{\partial g} {\partial n} }$$

(1.44)

and at a Hopf bifurcation trace(J) = 0. Thus, at the Hopf,

$$\displaystyle{ \frac{\partial f} {\partial V } + C_{m} \frac{\partial g} {\partial n} = 0\;\;. }$$

(1.45)

In the C _m → 0 limit the second term disappears, requiring that $\frac{\partial f} {\partial V } = 0$. This is the equation for the fold curve.

5.3 The Double Limit

In the C _m → 0 limit the Hopf bifurcation point migrated to the upper fold curve, but remained distinct from the folded node singularity since the V -nullcline of the desingularized system does not overlay the z-curve. The two coalesce when, in addition to taking C _m → 0, one takes the f _c → 0 limit. In this double limit the V -nullcline converges to the z-curve and the Hopf bifurcation is on the fold curve L ⁺, and thus the folded node singularity of the desingularized system and the Hopf bifurcation of the 2-dimensional fast subsystem of the 2-fast/1-slow decomposition are the same point.

It is interesting to see how the bursting orbit changes as the double limit is approached from the f _c  direction and from the C _m  direction. Fig. 18A shows the bursting orbit computed with f _c = 0. 01 and C _m = 10 (within the range of values for a pituitary lactotroph or somatotroph), superimposed with the V -nullcline of the desingularized system and the z-curve. In this case, the system is far from any singular limit, so the orbit is only somewhat close to the z-curve and the spikes are large. When f _c  is reduced by a factor of 10 the bursting orbit (which is actually more like a relaxation oscillation) is clearly organized by the z-curve (Fig. 18B). During the silent phase it moves along the bottom branch, while during the active phase it moves along the top branch. It passes through the subcritical Hopf bifurcation, and follows the unstable branch for some time before moving away with oscillations of increasing size. Thus, it exhibits the slow passage effect that is well documented for an orbit of a fast/slow system as it moves through a subcritical Hopf bifurcation (Baer et al. (1989); Baer and Gaekel (2008)). If f _c  is returned to its original value and C _m  is reduced by a factor of 100, then the system is organized by the structures of the desingularized system. Fig. 18C shows that in this case the burst trajectory passes very close to the folded node singularity as it moves along the V -nullcline. The spikes are small, and first decrease and then increase in amplitude as the orbit moves along the twisted slow manifold, which is typical for passage near a folded node singularity (Desroches et al. (2012)). If C _m  is kept at this small value and f _c  is now reduced by a factor of 10, then the bursting orbit again moves through the folded node along the V -nullcline, but this time with more spikes and a much more extreme decrease in amplitude near the folded node. Also, since this is near the double limit, the trajectory passes near the z-curve, and the folded node and Hopf bifurcation are close together.

Fig. 18

Bursting orbits together with the z-curve and V -nullcline of the desingularized system for different approaches to the double limit. (A) With physiological values of f _c  and C _m  the orbit (cyan) follows neither the z-curve nor the V -nullclline and the spikes are relatively large. (B) As the double limit is approached in the f _c  direction the bursting orbit follows the z-curve. (C) As the double limit is approached in the C _m  direction the orbit follows the V -nullcline and passes through the folded node. (D) Near the double limit the orbit passes through the folded node, but also moves close to the z-curve and the Hopf bifurcation. From Teka et al. (2012)

6 Store-Generated Bursting in Stimulated Gonadotrophs

The pseudo-plateau bursting that we have discussed so far is common in the spontaneous activity of pituitary somatotrophs and lactotrophs, and is sometimes observed in the spontaneous activity of gonadotrophs (Stojilković et al. (2010)). More often, though, gonadotrophs exhibit a tonic spiking pattern that yields little hormone release (Van Goor et al. (2001b)). However, when stimulated by the physiological stimulator gonadotropin-releasing hormone (GnRH) the gonadotrophs typically produce a bursting pattern with period of roughly 4–15 sec that results in a much higher level of luteinizing hormone release (Stojilković et al. (2010)). This was first observed using Ca²⁺ imaging, where a train of Ca²⁺ spikes was observed in the presence of GnRH (Shangold et al. (1988)). In a series of papers published in the 1990s, it was shown that this bursting pattern is due to the interaction of a Ca²⁺ oscillator stimulated by GnRH and an electrical oscillator that produces tonic spiking when the Ca²⁺ oscillator is turned off (Kukuljan et al. (1994), Stojilković et al. (1992, 1993), Stojilković and Tomić (1996); Tse and Hille (1992), Tse et al. (1994, 1997)). A key element of this research was the development of a mathematical model that helped with the interpretation of the data and guided experiments (Li et al. (1994, 1995), Rinzel et al. (1996)). In this section we discuss a simplified version of this model that retains the key biophysical and dynamic elements (Sherman et al. (2002)).

6.1 Closed-Cell Dynamics

We begin with the Ca²⁺ oscillator. Here, oscillations in the free cytosolic Ca²⁺ concentration (c) are due to the cycling of Ca²⁺ into and out of the endoplasmic reticulum (ER). Denote the ER Ca²⁺ concentration as c _ER . In the closed-cell model we analyze first, the total number of Ca²⁺ ions in the cell is conserved; ions simply move back and forth between the cytosolic compartment and the ER compartment. Denote the total free Ca²⁺ concentration in the cell as c _tot . Then

$$\displaystyle{ c_{tot} = c +\sigma c_{ER} }$$

(1.46)

where $\sigma$ is the ratio of the “effective ER volume” $\bar{V }_{ER} = \frac{V _{ER}} {f_{ER}}$ (V _ER is the ER volume and f _ER is the fraction of unbound Ca²⁺ in the ER), to the “effective cytosol volume” $\bar{V }_{c} = \frac{V _{c}} {f_{c}}$. That is,

$$\displaystyle{ \sigma = \frac{V _{ER}f_{c}} {V _{c}f_{ER}}\;\;. }$$

(1.47)

Rewriting,

$$\displaystyle{ c_{ER} = (c_{tot} - c)/\sigma \;\; }$$

(1.48)

where c _tot is constant. The differential equation for the cytosolic Ca²⁺ concentration is

$$\displaystyle{ \frac{dc} {dt} = (J_{ER-out} - J_{ER-in})/\bar{V }_{c} }$$

(1.49)

where J _ER−in  and J _ER−out  are the calcium fluxes into and out of the ER, respectively (Fig. 19A).

Fig. 19

Diagram of the Ca²⁺ fluxes in (A) the closed-cell model, (B) the open-cell model with constant influx, and (C) the open-cell model with influx through voltage-gated Ca²⁺ channels

The flux of Ca²⁺ into the ER is through pumps powered by the hydrolysis of adenosine triphosphate (ATP). These are called SERCA (Sarcoplasmic-Endoplasmic Reticulum Calcium ATPase) pumps. The pump rate is an increasing function of the cytosolic Ca²⁺ concentration, and in some models includes a dependence on the ER Ca²⁺ concentration (Sneyd et al. (2003)). We use a simple second-order Hill function of c to describe the flux through SERCA pumps,

$$\displaystyle{ J_{ER-in} = \frac{V _{1}c^{2}} {K_{1}^{2} + c^{2}} }$$

(1.50)

where K ₁ is the Ca²⁺ concentration for the half-maximal pump rate and V ₁ is the maximum pump rate.

The flux of Ca²⁺ out of the ER has two components. First, there is leakage that is assumed to be proportional to the difference in the ER and cytosolic Ca²⁺ concentrations,

$$\displaystyle{ J_{leak} = L(c_{ER} - c)\;\;. }$$

(1.51)

The Ca²⁺ concentration in the ER is greater than that in the cytosol, so the leakage is from the ER into the cytosol. The second component is only active when GnRH binds to receptors in the cell’s plasma membrane, generating the intracellular signaling molecule inositol 1,4,5-trisphosphate (IP₃). This molecule binds to IP₃ receptors in the ER membrane and can activate them. Once activated, the IP₃ receptors behave like Ca²⁺ channels, allowing Ca²⁺ to flow out of the ER and into the cytosol down the Ca²⁺ gradient. Cytosolic Ca²⁺ ions can also bind to regulatory sites on the receptor, increasing its open probability. Thus, the IP₃ receptors are gated by both IP₃ and cytosolic Ca²⁺. There is a third binding site on each receptor subunit, for Ca²⁺-induced inactivation of the receptor. This negative feedback operates on a slower time scale, so that in the presence of IP₃, Ca²⁺ provides both fast positive feedback and slower negative feedback onto the IP₃ receptor. Thus, the IP₃ receptor has dynamics that are very similar to those of the voltage-gated Na⁺ channel that is ubiquitous in neurons, as was demonstrated by Li and Rinzel (1994). In the expression that we use for the probability that the IP₃ receptor/channel is open the kinetics of IP₃ binding and Ca²⁺ binding to the activation site are instantaneous, while the Ca²⁺ binding to the inactivation site occurs with a time constant τ _h . The IP₃ open probability is then multiplied by the Ca²⁺ gradient, which provides the driving force for Ca²⁺ flux:

$$\displaystyle{ J_{IP3} = P\left ( \frac{c^{3}} {(c + k_{a})^{3}}\right )\left ( \frac{IP_{3}^{3}} {(IP_{3} + k_{i})^{3}}\right )h^{3}\left (c_{ ER} - c\right ) }$$

(1.52)

where P is a parameter representing the flux through an open channel, k _a , k _i are parameters, IP ₃ is the intracellular IP₃ concentration, and h is an inactivation variable satisfying the differential equation

$$\displaystyle{ \frac{dh} {dt} = (h_{\infty }- h)/\tau _{h} }$$

(1.53)

where

$$\displaystyle{ h_{\infty }(c) = \frac{K_{d}} {K_{d} + c} }$$

(1.54)

and

$$\displaystyle{ \tau _{h}(c) = \frac{A} {K_{d} + c}\;\;. }$$

(1.55)

Here K _d is the dissociation constant for Ca²⁺ binding to the inactivation site (i.e., the unbinding rate k ⁻ divided by the binding rate k ⁺). Parameter A is the inverse of k ⁺ and is convenient for setting the speed of the negative feedback. The exponent of 3 in Eq. 1.52 reflects the fact that the IP₃ receptor is a homotrimer, with three identical subunits. Finally,

$$\displaystyle{ J_{ER-out} = J_{leak} + J_{IP3}. }$$

(1.56)

Parameter values are given in Table 2.

Table 2 Parameter values for the gonadotroph model. In the open-cell models c _tot is not a parameter, and in the bursting model J _in is not a parameter

Summarizing, the closed-cell model consists of the two differential equations

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt} = (J_{ER-out} - J_{ER-in})/\bar{V }_{c}& &{}\end{array}$$

(1.57)

$$\displaystyle{ \frac{dh} {dt} = (h_{\infty }- h)/\tau _{h} }$$

(1.58)

where J _ER−out is given by Eq. 1.56, J _ER−in is given by Eq. 1.50, $h_{\infty }$ is given by Eq. 1.54, and τ _h is given by Eq. 1.55.

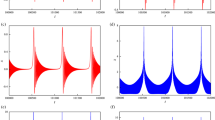
Figure 20 shows the dynamics of the closed-cell model in response to a pulse of IP₃. Initially the system is at rest with c near 0 and h near 1 (the IP₃ receptors are not inactivated). When IP₃ is introduced the system produces periodic c spikes (Fig. 20A, black curve). The upstroke of each spike is due to Ca²⁺ activation of the IP₃ receptors and the subsequent release of Ca²⁺ from the ER into the cytosol. The downstroke of each spike is due to Ca²⁺ inactivation of the IP₃ receptors reflected in a decline in h (Fig. 20A, red curve). Each spike causes release of Ca²⁺ from the ER (Fig. 20B, black curve) and the ER is subsequently replenished by flux through SERCA pumps (Fig. 20B, red curve) that occurs between spikes. Thus, the total flux from the ER to the cytosol (J _tot ) is positive during the Ca²⁺ spike and negative during the refilling stage between spikes (Fig. 20C, black curve). If the total flux is averaged over time, then one observes a rise in the time average ( < J _tot > ) during a spike and a slower decline during the refilling stage (Fig. 20C, red curve). When < J _tot > reaches 0 the system has been completely reset and another spike is produced.

Fig. 20

Dynamics of the closed-cell gonadotroph model in response to a square pulse of IP₃ (0.8 μM). (A) When IP₃ is present the system produces a continuous train of Ca²⁺ spikes that are due to fast activation and slow inactivation of IP₃ receptors. (B) In the time frame during and after the first spike, there is an initial release of Ca²⁺ from the ER and a subsequent phase of refilling. (C) The initial net movement of Ca²⁺ from the ER to the cytosol is compensated by a slower replenishment of Ca²⁺ into the ER. Note the difference in time scales between the upper and lower panels

The level of GnRH acting on the gonadotrophs is transduced into an IP₃ level via the Gα _q signaling pathway, and this determines the Ca²⁺ dynamics of the cell (Stojilković et al. (1993)). This is demonstrated with the closed-cell bifurcation diagram in Fig. 21. At low IP₃ concentrations the system is at rest, represented by the lower stable stationary branch of the bifurcation diagram. The stationary solution loses stability at an SNIC (Saddle-Node on Invariant Circle) bifurcation and a stable periodic solution is born. The periodic oscillations resemble “spikes” produced in neural system, and are often referred to as calcium spikes. As IP₃ is increased further the periodic spiking solution loses stability at a saddle-node of periodics bifurcation, and the system is attracted to a stationary solution born at a subcritical Hopf bifurcation. Thus, oscillations occur only for an intermediate range of IP₃ values. This is shown in Fig. 22 in terms of the c time courses. As IP₃ is increased in steps the system moves from a stationary, to an oscillatory, and back to a stationary state, but now with an elevated level of c. Note also that the oscillation frequency is greater at IP ₃ = 1. 2 μM than at IP ₃ = 0. 72 μM, as one would expect since the spiking solution is born near IP ₃ = 0. 7 μM at an infinite-period SNiC bifurcation. The dynamics of a closed cell system was shown with a more detailed model in Li and Rinzel (1994) and Li et al. (1994).

Fig. 21

Bifurcation diagram of the closed-cell gonadotroph model with IP₃ concentration as bifurcation parameter. The stationary solution loses stability, and an infinite-period spiking solution is born, at an SNIC bifurcation for IP ₃ = 0. 7 μM. The stationary solution regains its stability at a subcritical Hopf bifurcation (IP ₃ = 1. 2 μM), and for a small interval is bistable with the spiking solution, which ultimately disappears at a saddle-node of periodics bifurcation

Fig. 22

The closed-cell gonadotroph model exhibits frequency modulation in response to step increases in the IP₃ concentration. When the concentration is too low or too high the system has a globally stable rest state

6.2 Open-Cell Dynamics

In the actual gonadotroph, Ca²⁺ enters and leaves the cell through the plasma membrane. We incorporate these fluxes next (Fig. 19B). For now we treat the Ca²⁺ influx as a parameter, J _in ,

$$\displaystyle{ J_{mem-in} = J_{in}. }$$

(1.59)

The removal of Ca²⁺ from the cell is through plasma membrane pumps, which is modeled as a second-order Hill function, as it was with flux through SERCA pumps:

$$\displaystyle{ J_{mem-out} = \frac{V _{2}c^{2}} {K_{2}^{2} + c^{2}} }$$

(1.60)

where V ₂ is the maximum pump rate and K ₂ is the Ca²⁺ level for half maximal pumping. Adding these additional Ca²⁺ fluxes to the c equation we obtain

$$\displaystyle{ \frac{dc} {dt} = \left [J_{ER-out} - J_{ER-in} +\eta (J_{mem-in} - J_{mem-out})\right ]/\bar{V }_{c} }$$

(1.61)

where η is the ratio of the plasma membrane to ER surface area. There is also a new differential equation, for the total Ca²⁺ concentration in the cell:

$$\displaystyle{ \frac{dc_{tot}} {dt} =\eta (J_{mem-in} - J_{mem-out})/\bar{V }_{c}. }$$

(1.62)

The open cell model with constant Ca²⁺ influx then consists of the three differential equations

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt} = \left [J_{ER-out} - J_{ER-in} +\eta (J_{mem-in} - J_{mem-out})\right ]/\bar{V }_{c}& &{}\end{array}$$

(1.63)

$$\displaystyle{ \frac{dh} {dt} = (h_{\infty }- h)/\tau _{h} }$$

(1.64)

$$\displaystyle{ \frac{dc_{tot}} {dt} =\eta (J_{mem-in} - J_{mem-out})/\bar{V }_{c} }$$

(1.65)

where all functions other than those above are identical to those used in the closed-cell model. Parameter values are given in Table 2.

The response of the open-cell model to a pulse of IP₃ is shown in Fig. 23A. As with the closed-cell model, a train of Ca²⁺ spikes is produced (black curve) due to the cycling of Ca²⁺ between the cytosol and the ER. However, when the influx of Ca²⁺ into the cell is turned off, both the amplitude and the frequency of the spike train decline over time as the total Ca²⁺ concentration in the cell declines (red curve). Eventually there is not enough Ca²⁺ in the cell to sustain the oscillations and the system comes to rest at a low level of c. This simulation replicates experimental findings done in a Ca²⁺-deficient medium (Li et al. (1994)).

Fig. 23

The open-cell gonadotroph model with Ca²⁺ influx to the cell treated as a parameter, J _in . (A) When J _in = 1200 aMol s⁻¹ and the application of IP₃ (0.7 μM) is simulated the system produces a train of Ca²⁺ pulses. These decline and become slower when Ca²⁺ influx is terminated, due to a slow decline in the total Ca²⁺ concentration in the cell. (B) In the plane of the fast variables, the decline of the slow variable c _tot moves the system from stable periodic motion (green asterisk) through a range of cycles of diminishing amplitude and period to a stable rest state (red circle)

The influence of the Ca²⁺ influx parameter can be described in terms of a 2-fast/1-slow analysis. Here, c and h form the fast subsystem and c _tot is the single slow variable. When there is sufficient Ca²⁺ flux into the cell c _tot is elevated, and when IP₃ is present the fast system exhibits stable periodic motion. Thus, there is a stable limit cycle in the h-c plane, the thick curve labeled with a green asterisk in Fig. 23B. When Ca²⁺ influx is terminated c _tot slowly declines, with subsequent modification of the fast-subsystem limit cycle. The limit cycle shifts slowly rightward and the amplitude in the c variable becomes smaller. When c _tot reaches ≈ 2 μM the rest state of the fast subsystem becomes stable (Fig. 23B, red circle). Thus, the dynamics of this open-cell model are essentially the same as those of the closed-cell model, where the parameter c _tot is replaced by a slowly changing variable.

This is illustrated in another way in Fig. 24. In this bifurcation diagram, IP₃ is held constant at 0.7 μM and c _tot is treated as a bifurcation parameter. Periodic spiking occurs for a large range of c _tot values, and is replaced by stable stationary solutions at low and high c _tot values. The spiking branch is born at an SNIC bifurcation, so for parameter values near here the spiking will be slow. For larger c _tot values the amplitude and frequency of the oscillation increase, and eventually the periodic solution terminates at a saddle-node of periodics bifurcation. There is a fairly large interval in which the spiking and stationary solutions are both stable.

Fig. 24

Bifurcation diagram for the open-cell gonadotroph model with IP ₃ = 0. 7 μM and c _tot treated as the bifurcation parameter. The periodic spiking branch is born at an SNIC bifurcation (c _tot = 2. 1 μM) and disappears at a saddle-node of periodics bifurcation (c _tot = 6 μM). The stationary branch regains stability at a subcritical Hopf bifurcation (c _tot = 4. 6 μM) and there is a substantial interval of bistability between periodic and stationary solutions

An alternate mechanism for IP₃-induced Ca²⁺ oscillations involves the feedback of Ca²⁺ onto IP₃ production or degradation. In this case, the IP₃ concentration itself oscillates, evoking periodic release of Ca²⁺ from the ER. While this is not the mechanism for agonist-mediated Ca²⁺ oscillations in gonadotrophs (Stojilković et al. (1993)), it can be the mechanism in other cell types (Sneyd et al. (2006)). In this report, Sneyd and colleagues describe an experimental method based on exogenous pulses of IP₃ for determining which type of the two feedback mechanisms for agonist-induced Ca²⁺ oscillations, called class 1 and class 2, is responsible for the observed Ca²⁺ oscillations in two cell types, pancreatic acinar cells and airway smooth muscles. Both mechanisms, Ca²⁺-induced Ca²⁺ release and Ca²⁺-dependent changes in IP₃ concentration, likely are present in a typical cell, so the real question is which, if either, mechanism dominates the Ca²⁺ dynamics.

In recent work (Harvey et al. (2010, 2011)), the authors used geometric singular perturbation theory (GSPT) to study the underlying dynamic nature in many models of Ca²⁺ dynamics. Identifying the different time scales in a given Ca²⁺ model provides a first simple diagnostic tool to predict class 1 or class 2 dominated Ca²⁺ dynamics. Furthermore, GSPT is able to explain observed anomalous delays in the Ca²⁺ dynamics (Harvey et al. (2010)) that are usually not predicted by the IP₃ pulse protocol experiment (Sneyd et al. (2006)). Canard theory in arbitrary dimensions (Wechselberger (2012)) is the key to explain this ‘anomalous’ phenomenon.

6.3 Store-Generated Bursting

We now add the final component to the model by replacing the constant Ca²⁺ influx parameter J _in  with a term reflecting Ca²⁺ influx through Ca²⁺ ion channels (Fig. 19C). The channels are gated by the membrane potential V, which is itself determined by ionic current through a number of ion channels. In our minimal model only three ion channel types are included. Ionic current through L-type Ca²⁺ channels, I _Ca , is responsible for the upstroke of an electrical action potential and also brings Ca²⁺ into the cell. It is modeled as in the lactotroph model,

$$\displaystyle{ I_{Ca}(V ) = g_{Ca}m_{\infty }(V )(V - V _{Ca}). }$$

(1.66)

The downstroke of an action potential is due to the slower-activating delayed-rectifying K⁺ current,

$$\displaystyle{ I_{K}(V,n) = g_{K}n(V - V _{K}). }$$

(1.67)

Finally, there is an SK-type K⁺ current that is gated by cytosolic Ca²⁺,

$$\displaystyle{ I_{SK}(V,c) = g_{SK}s_{\infty }(c)(V - V _{K}). }$$

(1.68)

The differential equations for the cell’s electrical activity are:

$$\displaystyle\begin{array}{rcl} C_{m}\frac{dV } {dt} & =& -\left [I_{Ca}(V ) + I_{K}(V,n) + I_{SK}(V,c)\right ]{}\end{array}$$

(1.69)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt} & =& \frac{n_{\infty }(V ) - n} {\tau _{n}(V )}.{}\end{array}$$

(1.70)

Steady state and time constant functions are:

$$\displaystyle\begin{array}{rcl} m_{\infty }(V )& =& \frac{1} {2}\left (1 +\tanh \left (\frac{V - V _{3}} {s_{1}} \right )\right ){}\end{array}$$

(1.71)

$$\displaystyle\begin{array}{rcl} n_{\infty }(V )& =& \frac{1} {2}\left (1 +\tanh \left (\frac{V - V _{4}} {s_{2}} \right )\right ){}\end{array}$$

(1.72)

$$\displaystyle\begin{array}{rcl} \tau _{n}(V )& =& \left (\phi \cosh \left (\frac{V - V _{4}} {2s_{2}} \right )\right )^{-1}{}\end{array}$$

(1.73)

$$\displaystyle\begin{array}{rcl} s_{\infty }(c)& =& \frac{c^{4}} {(K_{SK}^{4} + c^{4})}.{}\end{array}$$

(1.74)

The ordinary differential equations for the cell’s electrical activity are coupled to those for Ca²⁺ handling, which again are

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt}& =& \left [J_{ER-out} - J_{ER-in} +\eta (J_{mem-in} - J_{mem-out})\right ]/\bar{V }_{c}{}\end{array}$$

(1.75)

$$\displaystyle\begin{array}{rcl} \frac{dh} {dt} & =& (h_{\infty }- h)/\tau _{h}{}\end{array}$$

(1.76)

$$\displaystyle\begin{array}{rcl} \frac{dc_{tot}} {dt} =\eta (J_{mem-in} - J_{mem-out})/\bar{V }_{c}& &{}\end{array}$$

(1.77)

All functions are identical to those defined previously, except that the Ca²⁺ influx to the cell is no longer constant, but is:

$$\displaystyle{ J_{mem-in} = -\alpha I_{Ca}(V ) }$$

(1.78)

where α converts current into Ca²⁺ ion flux. It is this term that provides the coupling from the electrical activity to the Ca²⁺ dynamics. Equation 1.68 provides the feedback from the Ca²⁺ dynamics to the electrical activity. Parameter values are given in Table 2.

The time course of the full gonadotroph model is shown in Fig. 25. In the absence of the agonist GnRH the model cell produces a tonic spiking pattern since the Ca²⁺ level in the cytosol is low, so there is very little activation of the hyperpolarizing SK current. When IP₃ is added to the model cell, simulating the effects of the physiological activator GnRH, the Ca²⁺ oscillator is activated. This is reflected in the large Ca²⁺ spikes in Fig. 25B. Each spike activates Ca²⁺-activated SK channels, hyperpolarizing the cell for the duration of the Ca²⁺ spike. The resulting electrical bursting is then due to periodic interruptions in the tonic spiking pattern caused by the Ca²⁺ oscillator. Unlike the pseudo-plateau bursting in which c is highest during the active phase of the burst, in this store-generated bursting the peaks in the cytosolic Ca²⁺ concentration occur during the silent phase of the burst.

Fig. 25

The open-cell gonadotroph model with Ca²⁺ influx through voltage-dependent Ca²⁺ channels. (A) The tonic spiking pattern is converted to bursting when IP₃ (0.7 μM) is added to the model cell. (B) The cytosolic Ca²⁺ level is low until the Ca²⁺ oscillator is activated by IP₃, producing spikes of Ca²⁺ efflux from the ER into the cytosol

7 Conclusion

In this chapter we have provided examples of how mathematical modeling can be and has been used to better understand electrical and calcium dynamics in bursting pituitary cells. The difference in the bursting mechanisms of the different cell types parallels differences in secretion patterns. Lactotrophs and somatotrophs can secrete their hormones spontaneously, due to their bursting pattern that facilitates Ca²⁺ entry. Gonadotrophs, on the other hand, usually exhibit spikes that are too brief to allow much Ca²⁺ entry. Significant luteinizing hormone release only occurs when the cells are stimulated by GnRH to produce large rhythmic Ca²⁺ releases from the ER that drive secretion. Bursting oscillations also occur in some of the hypothalamic neurons that modulate the activity of pituitary cells. For example, bursting occurs in oxytocin neurons of the paraventrical nucleus during lactation, and a potential mechanism for these oscillations has been demonstrated through mathematical modeling (Rossoni et al. (2008)). Bursting also occurs in vasopressin neurons that are responsible for osmoregulation, and this too has been modeled (Clayton et al. (2010)). Bursting in hypothalamic GnRH neurons has been the focus of several modeling studies (Duan et al. (2011); Fletcher and Li (2009); LeBeau et al. (2000); Lee et al. (2010)). Yet, there is much work ahead in this field, both in understanding the intrinsic dynamics of individual cell types, and in understanding their interactions. It is likely that mathematical modeling and analysis will play a key role.

8 Appendix

Computer codes for all models discussed in this chapter are available as freeware from http://www.math.fsu.edu/~bertram/software/pituitary.

1.1 8.1 The Chay-Keizer Model

The Chay-Keizer model for bursting in the pancreatic β-cell (Chay and Keizer (1983)) was one of the first bursting models analyzed using a fast/slow analysis technique (Rinzel and Lee (1985)). A modified form of the model was used in Teka et al. (2011b) to analyze the transition between plateau and pseudo-plateau bursting, and was used for this purpose in Fig. 4. The modified Chay-Keizer model is similar in many ways to the lactotroph model used in most of this article. The differential equations are:

$$\displaystyle\begin{array}{rcl} C_{m}\frac{dV } {dt} & =& -[I_{Ca}(V ) + I_{K}(V,n) + I_{SK}(V,c) + I_{K(ATP)}(V )]{}\end{array}$$

(1.79)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt} & =& \frac{n_{\infty }(V ) - n} {\tau _{n}} {}\end{array}$$

(1.80)

$$\displaystyle\begin{array}{rcl} \frac{dc} {dt}& =& -f_{c}(\alpha I_{Ca}(V ) + k_{c}c).{}\end{array}$$

(1.81)

where in place of the V -dependent BK K⁺ current there is a K⁺ current whose conductance is regulated by intracellular levels of ATP. If, as assumed here, the ATP concentration is constant, then g _K(ATP) is a constant-conductance K⁺ current given by

$$\displaystyle{ I_{K(ATP)}(V ) = g_{K(ATP)}(V - V _{K})\;\;. }$$

(1.82)

The form of the steady state activation curves $m_{\infty }(V )$ and $n_{\infty }(V )$ are the same as for the lactotroph model (Eqs. 1.5, 1.7). The steady state activation function for the SK current is a third-order Hill function, rather than second-order:

$$\displaystyle{ s_{\infty }(c) = \frac{c^{3}} {c^{3} + K_{d}^{3}}. }$$

(1.83)

Parameter values for this model are given in Table 3.

Table 3 Parameter values for the simplified Chay-Keizer model

1.2 8.2 The Lactotroph Model with an A-Type K⁺ Current

An alternate lactotroph model was developed by Toporikova et al. (2008) and analyzed in Vo et al. (2010) and Vo et al. (2012). In this model, the equation for intracellular Ca²⁺ concentration is removed, as are the SK and BK currents. Instead, an A-type K⁺ current is included that activates instantaneously and inactivates on a slower time scale. The differential equations are:

$$\displaystyle\begin{array}{rcl} C_{m}\frac{dV } {dt} & =& -[I_{Ca}(V ) + I_{K}(V,n) + I_{A}(V,e) + I_{L}(V )]{}\end{array}$$

(1.84)

$$\displaystyle\begin{array}{rcl} \frac{dn} {dt} & =& \frac{n_{\infty }(V ) - n} {\tau _{n}} {}\end{array}$$

(1.85)

$$\displaystyle\begin{array}{rcl} \frac{de} {dt}& =& \frac{e_{\infty }(V ) - e} {\tau _{e}} \;\;.{}\end{array}$$

(1.86)

where the I _Ca and I _K currents are as before, I _L is a constant-conductance leakage current, and I _A is the A-type K⁺ current:

$$\displaystyle\begin{array}{rcl} I_{L}(V )& =& g_{L}(V - V _{K}){}\end{array}$$

(1.87)

$$\displaystyle\begin{array}{rcl} I_{A}(V,e)& =& g_{A}a_{\infty }e(V - V _{K})\;\;.{}\end{array}$$

(1.88)

The activation function for I _A  is

$$\displaystyle{ a_{\infty }(V ) = \left (1 +\exp (\frac{v_{a} - V } {s_{a}} )\right )^{-1} }$$

(1.89)

and the inactivation function is

$$\displaystyle{ e_{\infty }(V ) = \left (1 +\exp (\frac{V - v_{e}} {s_{e}} )\right )^{-1}\;\;. }$$

(1.90)

Parameter values are given in Table 4.

Table 4 Parameter values for the lactotroph model with A-type K⁺ current