Keywords

Research, Theory and the “Detachment Principle”

This paper is an introduction, or better an invitation, to the Anthropological Theory of the Didactic (ATD), a research framework where I have been working for more than twenty years now, growing in it as a researcher and having the chance of participating in its development. At the beginning we were a small team of French and Spanish people collaborating with Yves Chevallard in Marseilles, a group that has now become a community of about one hundred researchers mainly from Europe, Canada and Latin American countries.Footnote 1

In spite of the word “theory”, the ATD is, as the Hans Freudenthal Award recognises it, “a major cumulative programme of research” in mathematics education. As in many other cases, theory is used here as a synecdoche to refer to a whole research activity naming only one of its elements: the organisation of concepts, assumptions, relationships and other notional tools used to problematise reality in order to get more insight and modify it in a given wished direction. Many centuries of diffusion strategies seem to have overvalued theories as the main entrance to knowledge organisations. However, and even if we are used to it, the theory is not always the best way to access a research approach. Another entry is chosen here: the one of the research problems raised and of the main methodological “gestures” used to approach them, including the kind of empirical evidence considered. To be more concrete, we will restrict the entry and focus on a single case study, the problem of school algebra, which has been at the core of the ATD development since its very beginning and can provide a rich illustration of the different treatments this research framework proposes.

Even if the ATD is much more than a theory, it is also true that the role played by its theoretical constructions is essential in a very specific sense, which can be subsumed in a basic principle that permeates all its methods of study. I will call it the “detachment principle”, after the work of the sociologist Norbert Elias (1987). Because researchers in didactics deal with a reality that takes place in social institutions, and because they often participate at these institutions (as researchers, teachers, students, or in several positions at the same time), we need to protect ourselves—to emancipate—from the institutional viewpoints on this reality and, more particularly, from the common-sense models used to understand it. This effort of detachment is a basic gesture in sociological and anthropological research (see, for instance, Bourdieu et al. 1968; Berger and Luckmann 1966; Elias 1978; among many others). It is also coherent with the double assumption made by the ATD that persons are the subject of the set of institutions they enter during their lives and that what they think or do (their knowledge and know-how) derives in a personalised way from institutional knowledge and know-how.

The word “institution” is taken here in a non-bureaucratic sense, as it is used by the anthropologist Mary Douglas in her work How institutions think (Douglas 1986). As Y. Chevallard presents it (Chevallard 2005, our translation):

An institution lives through its actors, that is, the persons that are subjected to it—its subjects—and serve it, consciously or unconsciously. […] Freedom of people results from the power conferred by their institutional subjections, together with the capacity of choosing to play such or such subjection against a given institutional yoke.

In this context, human practices and human knowledge are entities arising in institutional settings. A person acquires knowledge and practice by entering the institutions where this knowledge and practice exist. At the same time, it is through the changes introduced by their subjects that institutions evolve. This dialectic between the personal and the institutional perspective is at the core of the ATD. It is important to say that the personal subjection to institutions must be understood as a productive subjection instead of as a loss of freedom. We do not act nor know as individuals, but as part of some collective constructions we participate in, assuming their rules and contributing to making them evolve. The idea of being empowered (both cognitively and practically) through the subjection to institutions can be illustrated by the metaphor of the bicycle: when the wheels are free, the bicycle does not move; movement is possible through the subjection of the wheels. The principle of “detachment” has to be understood in this context, since researchers’ institutional subjections affect the way of conceiving and understanding reality: one has to get off the bicycle to understand the mechanism of the subjection of the chain.

When trying to adopt an external perspective of the reality we want to study, we often need to question the institutional dominant viewpoints, which initially appear as “transparent” or natural to the subjects of the institution. It is here where theoretical constructions acquire their functionality, by providing alternative conceptions about this reality. Furthermore, except if we adopt a hyper-empiricist perspective, which we will not, the way of delimiting and even defining this reality also depends on the perspective adopted. As will be shown later, the detachment required by the ATD methodology also implies an important enlargement of the empirical unit of analysis considered.

But let me first introduce one of the main theoretical notions of ATD which is also part of the effort of detachment we are considering here. In didactics research, almost all problems deal with teaching and learning processes where “something” is learnt or taught. This something is usually a particular “piece of knowledge” that can be of a different size: the whole of “mathematics”, the practice of “mathematical modelling”, a whole domain as when we talk about “algebra” or “geometry”, a sector of this domain like “first degree equations” or “similar triangles”, or even a smaller piece like “the concept of variable” or “transposing and cancelling”. The ATD proposes that we talk about praxeologies to refer to any kind of knowledge and, more generally, to any human practice, including mathematical and teaching and learning activities (Chevallard 1999, 2006; see also Barbé et al. 2005). The term “praxeology”, made of the Greek words praxis and logos, enables us to consider two terms that are often opposed within the same entity: the “practical block” or know-how and the “theoretical block” or knowledge (in its narrow sense) made of the discursive elements (logos) used to describe and justify the practice. A praxeology is made of four components: types of tasks, techniques, technologies and theories (sometimes called the “four Ts”). The praxis or “practical block” contains a set of types of tasks to be carried out and a set of techniques to do so, technique being considered here in a very general sense of ways of doing. The logos, or theoretical block, is made of a double-levelled discourse. A technology or “discourse on the technique” to explain what is done, to let others interpret it and to provide a first justification or control of it. The general models, notions and basic assumptions that validate the technological discourse and organise the praxeological elements as a whole, form what we call the theory. Types of tasks, techniques, technologies, and theoretical discourses can be elaborated, made explicit and well-grounded, but they can also be just incipient, as growing entities or, on the contrary, long-established, routine-based and naturalised.

Scientific praxeologies try to make their technologies and theories explicit, so as to control the assumptions made, to formulate the problems and phenomena approached and, as Allan Schoenfeld outlines it in his Reflections of an Accidental Theorist, “to elaborate clearly for yourself ‘what counts’ and how things supposedly fit together” […] as well as to “hold yourself accountable to data” (Schoenfeld 2011, p. 220). The synecdoche I mentioned before about referring to a whole research praxeology by naming only its theoretical component is a classic one when dealing with scholar knowledge. In contrast, praxeologies culturally considered of a lower level are usually designated through an opposite synecdoche, naming only the practical component as if there were no theoretical block associated to it, that is, as if there was nothing to say about the practice or, at least, as if there was not a strong enough institutional theoretical construction around it. The use of the term “praxeology” enables us to escape from these institutional evaluations and consider the different mathematical, teaching and learning praxeologies through the same prism. It is meaningful, for instance, that we can easily talk about educational theories, but tend to refer to teaching practices much more than to teaching theories.

What Is “School Algebra”? Didactic Transposition Processes

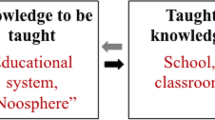
The first “detachment gesture” proposed by the anthropological approach has to be found in the initial formulation of the didactic transposition process (Chevallard 1985). It consists in questioning the nature and origin of the mathematical knowledge that is taught at school, looking at the work done by different institutions during different periods of time to select, reorganise, adapt and develop the mathematical praxeologies from their first appearances in the scholar institution (the main site responsible for the production of knowledge) to their designation as “knowledge to be taught” and their implementation at school as taught knowledge. A lot of decisions are made during this transposition process that should be taken into consideration to better understand what conditions (in terms of praxeologies) are made available to teachers and students and what constraints hinder or even impede the development of many others.

The notion of didactic transposition appeared as a powerful theoretical tool to break with the dominant viewpoints with regard to the “disciplinary knowledge” didactics research has to deal with. Before focusing on how children learn and how we can teach them—the viewpoint of the teachers’ institution—the attention is first put on what is learnt and taught, its nature (what it is made of), origin (where it comes from) and function (what it is for). In spite of the dominant viewpoint on mathematics brought about by the scholar and the school institution, leading to the impression that there is only one school algebra and that the problem is how to teach or learn it (as if these decisions were always beyond the epistemological dimension of teaching and learning processes), the ATD starts questioning “what is being taught” and showing its undefined nature. What is this thing called school algebra? What kind of praxeologies is it made of? What could it be made of under other institutional constraints? How does it vary from one school institution to another, both in time (from one historical period to another) and in the institutional space (from one country or educational system to another)? Where does it come from? What legitimates its teaching?

To answer those questions, the kind of empirical evidence necessary may not be reduced to the teaching and learning processes as they are currently taking place in the classroom. It becomes necessary to look into the different institutions (present and also past ones) that influence transposition processes, amongst them the institution responsible for producing mathematical praxeologies, that we will call “scholar mathematics”, and the one responsible for selecting it and introducing it at school, called the “noosphere”, that is, the sphere of people who think and make decisions about educational processes, such as curriculum developers, policy makers, associations of teachers, educational researchers, etc.

Research about the teaching of elementary algebra in France (Chevallard 1984, 1989a, b, c, 1990; Assude 1993; Grugeon 1995; Coulange 2001a, b; Artigue et al. 2001) and their contrast with the Spanish case (Gascón 1993, 1999, 2011; Bolea 2003; García et al. 2006; Ruiz-Munzón 2010) have all shown a similar evolution of the didactic transposition processes that has led to a dispersion of the content traditionally assigned to “elementary algebra” in secondary school curricula, splitting up the classic triad of arithmetic-algebra-geometry that used to structure school mathematics curricula before the New Mathematics reform. With slight variations depending on the historical periods and regions, we can observe that the existence of algebra as a school mathematical domain (or “block of content”) is, at the most, fluctuating. For instance, it disappeared from the French and Spanish official curricula, and has only recently been reintroduced in some Spanish regions. It is not the case of Catalonia, where the present curriculum (2007) proposes five blocks of content: Numeration and calculation; Relations and change; Space and shape; Measure; Statistics and randomness. These blocks appear to be very similar to the overarching ideas proposed by the OECD/PISA commission: Quantity; Space and shape; Change and relationship; Uncertainty (OECD 2009). In this new organisation of mathematics proposed by the PISA evaluators, the correspondence with what is called the “traditional topics classification” confines algebra to the “Change and relationship” strand (OECD 2009, p. 28), as if there were no need for algebraic techniques in the other domains. It could be interesting to study how transpositive processes are currently influenced by this type of international evaluation, a phenomenon that is certainly affecting the different societies that take part in these processes in a similar way, although the effects appearing in each educational system may be fairly different.

Apart from the loss of visibility of the mathematical organisation of school algebra as a mathematical domain, which may vary significantly from one country to another, what is much more common and has been commented in numerous research projects is the establishment of a formal approach to the algebraic tool and the difficulty to move it into a functional approximation, in which algebra would appear as a way of modelling other kinds of systems or mathematical realities (Chevallard 1989a). In the traditional teaching preceding Modern Mathematics, the introduction of algebra and the use of letters to name both known and unknown quantities allowed students to systematically solve the corpus of problems of elementary and mercantile arithmetic that represented most of the mathematical work done at primary school. At that time, arithmetic calculations and the structured corpus of arithmetic problems acted as the reference and starting point of the new algebraic construction, which in turn marked the entrance to a higher level of education. For algebra to appear as a generalised arithmetic in this sense, the interplay between parameters and unknowns is essential to cope with the richness of the discursive models that support arithmetical techniques (Chevallard 1989a, b, c; Bosch 1994).

Nowadays, however, the reference to traditional arithmetic and its important corpus of problems that used to give the teaching of algebra its rationale has disappeared. The opposition—which was also a connection—between arithmetic and algebraic problem-solving techniques, which for a long time marked the entrance to algebraic work, no longer makes sense. In contemporary secondary schools, elementary algebra is largely identified with solving equations, mainly of first and second degrees, with some subsequent applications to a set of word problems coming out of nowhere. This limited domain is often preceded by a short introduction to the language of algebra used to introduce the specific terminology required (algebraic expression; evaluation; terms, members and coefficients; similar terms; equations, equalities and identities; etc.), a formal frame where students learn how to develop, factorise and simplify expressions as a goal in itself. Without the possibility to refer to the arithmetic world, algebraic expressions and equalities between expressions cannot be presented by what they designate, but only by their formal structure and their mathematical objects. This formal learning is unable to recreate the large variety of manipulations that are needed to use algebra in a functional way, and which will be required when students arrive at higher secondary education and suddenly find “completely algebraised” mathematics.

The analysis of the didactic transposition processes and the way they may hinder teaching and learning processes should not be taken as simple criticism of the praxeological entities that comprise school algebra. Knowing how algebra is understood in mathematics classrooms, at school and even in our societies, as well as the kind of praxeological elements that are not (but could be) conceived as part of it, is, however, an essential questioning to investigate the conditions of possibility for educational changes not being reduced to mere local innovations. It is important to understand the transpositive constraints that have shaped school algebra, especially when some of the detected traits (that have only been briefly described here) seem robust and stable enough to remain in most current educational systems.

The Didactic Ecology of School Algebra

The analysis of didactic transposition processes points out the existence of different constraints influencing the teaching of algebra at secondary school. Its study concerns the ecology of the praxeologies (Chevallard 2002), that is, the set of conditions necessary for a specific praxeological organisation to exist in a given institutional setting and the constraints hindering its possible evolution. For instance, the possibility (or impossibility) of referring to long-established arithmetic techniques when introducing algebra is a condition that shapes the kind of praxeologies that can be taught and, at the same time, restricts their development to other forms of activity. These conditions and constraints can be of a very specific nature, related to the way different domains, sectors, themes and questions are organised in a given mathematical curriculum. They can also be more generic, not directly related to mathematics and affecting the teaching and learning of any discipline at school, or at any educational institution, or even affecting the dissemination of any kind of knowledge in the society at large. Chevallard (2002, 2007) introduced a hierarchy of “levels of didactic codetermination” to clarify the scope of the considered constraints and also to uphold the view that the study of phenomena arising at very general levels of determination should be taken into account by research in didactics, since they can strongly affect the conditions of possibility and the evolution of teaching and learning processes. The scale consists in the following sequence (Fig. 1).

Fig. 1
figure 1

Scale of levels of didactic codetermination

Full size image

The case of school algebra leads us to identify important constraints in almost all levels of codetermination, especially phenomena arising at the level of our Western civilisation. It thus provides a good illustration of how the most generic levels can influence mathematical praxeologies at the lowest levels of specification.

The Western Relationship to Orality and Literacy

According to the work of the classical and humanistic scholars, Eric Havelock (1963) and Walter Ong (1982), in traditional Western cultures, oral formulations are regarded as the direct expression of thought, and writings are viewed as the mere written transposition of oral discourse. The French philosopher Jacques Derrida (1967) describes this metaphysical position as logocentrism. It is assumed that thought is something residing in our head that first comes out through the discourse before being transcribed to writings. Thus, (verbal) reasoning is often opposed to (written) calculations, as illustrated by the current recommendation “First say it with words, then write it down”. This assumption permeates our teaching practices and can explicitly be found in several teaching documents about the danger of introducing writing manipulation too early, before the meaning is constructed. See, for instance, the following suggestion about the construction of number sense in early arithmetic by Julia Anghileri (2006, p. 45) quoting the British Department of Education and Employment:

Current recommendations propose that “oral and mental competence” is established “before written calculation methods are introduced” […]. This does not mean that there will be no written recording but that children will learn to record their thinking with progressive formalization, learning first to use words to record results they can already talk about.

A comment that is preceded by a synthetic indication about how “Progression in learning may be summarized” (Ibid., p. 44):

DOING … TALKING ABOUT … WRITING ABOUT … SYMBOLIZING

It is important to underline that in the algebraic manipulations, this relationship between oral and written work is reversed: algebraic objects are written by nature, they are not the written transcription of oral objects. Thus orality becomes a secondary accompaniment of written algebraic formulations, which are furthermore not always easy to “oralise” (ecs squared minus three equals…). Contrary to our mental habits, written algebraic symbolism is not a derivation of oral language: it is the source, the manifestation and the touchstone of algebraic thinking.

The school ecology of algebra has always been hindered by what we can call a cultural incomprehension of its written nature. In fact, the relationship to symbolism is still an important barrier to the acceptance of scientific work in the realm of highly valued cultural practices. A small sample of this situation can be the number of books in different languages pretending to popularise scientific fields using no or very little symbolism: ‘Spaceflight without formulae’, ‘Special relativity without formulae’, ‘Quantum mechanics without formulae’, ‘Statistics without formulae’, and even the Russian ‘Mathematics without formulae’ in two volumes! (Pujnachov and Popov 2008). In the introduction to the book, we can read the following statement that the authors attribute to the famous mathematician Sofia Kolvalésvkaya that reintroduces the common idea that formulae are something secondary in the production of knowledge (our translation):

In mathematical works, the most important is the content, ideas, concepts, and only afterwards, to express all this, mathematicians have their language: formulae.

The lack of meaning assigned to written formulae by our Western culture has its effects in the school introduction of algebra. As we have shown in our research on the ostensive or semiotic tools used in mathematics (Bosch and Chevallard 1999), the “rupture” between arithmetic and algebra is also a cultural break from an essentially discursive world, based on oral techniques scanned by simple operations—the “reasoning” realm—to a mostly written world, where techniques are difficult to “oralise” and where a specific descriptive discourse (a technology of the written calculations) has to be explicitly constructed. Algebra thus appears as a kit of tools that enables one to do things more quickly to the detriment of the meaning or reasoning, as written mechanics against verbal thought. A quotation of an old French textbook of elementary algebra would give an idea of this dominant viewpoint that has still not completely disappeared (Blanc and Soler 1933, p. 12, our translation):

If the algebraic solution is quicker than the arithmetic solution, we do not have to forget than it is the latter which mainly contributes to develop reasoning. Thus with problems the solution of which includes reasoning, it is necessary to find both solutions: the arithmetic and the algebraic one.

The Cultural Pejoration of Algebra

The first investigations on school algebra carried out within the framework of the ATD (Chevallard 1985, 1994) immediately highlighted a fact of society closely related to the primarily written nature of algebra and that can be designed as the cultural pejoration of algebra. As we showed (Chevallard and Bosch 2012), research carried out at the beginning of the 1980s using a semantic differentiator technique displayed what seems to be an almost invariable trait in secondary school students: while to them geometry would be pretty, warm, deep and feminine, algebra turned out to be ugly, cold, superficial and masculine. Again, we can find several pieces of evidence that our society maintains such a relationship with algebra. A quite surprising one comes from a voluntarily provocative comment from the great mathematician Sir Michael Atiyah, clearly expressing this cultural pejoration of algebra (Atiyah 2001, p. 659):

Algebra is the offer made by the devil to the mathematician. The devil says: ‘I will give you this powerful machine, it will answer any question you like. All you need to do is give me your soul: give up geometry and you will have this marvellous machine. […] the danger to our soul is there, because when you pass over into algebraic calculation, essentially you stop thinking; you stop thinking geometrically, you stop thinking about the meaning. I am a bit hard on the algebraists here, but fundamentally the purpose of algebra always was to produce a formula that one could put into a machine, turn a handle and get the answer. You took something that had a meaning; you converted it into a formula; and you got out the answer.

It is not strange that, in this state of mind, the mathematical domain par excellence to introduce students to “proof”, “demonstration” or “deductive reasoning” is usually geometry, and rarely algebra. It will be difficult to accept algebra as a domain of proof when algebraic work seems to consist mainly in calculations, supposedly implying little “reasoning”.

Let me finish this illustration of constraints coming from the generic levels of the scale of didactic codetermination with a final example of a fact that can be located at the society level, even if in this case the society is one that I, as a citizen, am not so familiar with. Some years ago, to introduce the proposal of “algebrafying” into an elementary mathematics experience, James Kaput depicted the result of an evolution of the American didactic transposition process that led to what the author names “Algebra the Institution” (Kaput 1998, p. 25):

‘Algebra the Institution’ is a peculiarly American enterprise embodying the standard courses, textbooks, tests, remediation industry, and their associated economic arrangements, as well as the supporting intellectual and social infrastructure of course and workplace prerequisites, cultural expectations relating success in algebra to intellectual ability and academic promise, special interests, relations between levels of schooling, and so on. Exhortation for and legislation of Algebra For All tacitly assume the viability and legitimacy of this Institution. But this algebra is the disease for which it purports to be the cure! It alienates even nominally successful students from genuine mathematical experience, prevents real reform, and acts as an engine of inequity for egregiously many students, especially those who are the least advantaged of our society.

Again algebra is detached from cultural and useful practices. And the process of didactic transposition seems to have imposed specific restrictions that seem as serious as unforeseen.

The scale of levels of didactic codetermination is a productive methodological tool for the detachment principle I mentioned at the beginning of this paper: to be aware of the factors that influence what can or could be done at school related to the teaching and learning of algebra, and avoid taking for granted the current assumptions, evaluations and judgements about the nature of algebra and its functions in knowledge practices. However, as we said before, the best way to free research from all these implicit institutional assumptions that always impregnate teaching and learning processes, is to build an alternative reference model from which to look at the phenomena from another point of view and, of course, with other assumptions that research theory should try to make as explicit as possible. This is especially important when dealing with the specific levels of codetermination, when we are considering what school algebra is made of.

What Could Algebra Be? a Reference Epistemological Model

When analysing any teaching or learning process of mathematical content, questions arise related to the interpretation of the mathematics involved in it. The different institutions interfering in the didactic processes propose more or less explicit answers to said questions. If researchers assume those answers uncritically, they run the risk of not dealing with the empirical facts observed in a sufficiently unbiased way. Therefore the ATD proposes to elaborate what are called reference epistemological models for the different mathematical sectors or domains involved in teaching and learning processes (Bosch and Gascón 2005). This explanation of the specific epistemological viewpoint adopted—which is always an a priori assumption constantly evolving and continuously questioned—determines, amongst other things, the amplitude of the mathematical field where research problems are set out; the didactic phenomena which will be “visible” to researchers; and the attempted explanations and actions that are considered “acceptable” in a given field of research.

In the ATD, those reference epistemological models are formulated in terms of local and regional praxeologies and of sequences of linked praxeologies. With respect to school algebra, our proposal is to interpret it as a process of algebraisation of already existing mathematical praxeologies, considering it as a tool to carry out a modelling activity that ends up affecting all sectors of mathematics. Therefore, algebra does not appear as one more piece of content of compulsory mathematics, at the same level as the other mathematical praxeologies learnt as school (like arithmetic, statistics or geometry) but as a general modelling tool of any school mathematical praxeology, that is, as a tool to model previously mathematised systems (Bolea et al. 2001a, b, 2004; Ruiz-Munzón 2010; Ruiz-Munzón et al. 2007, 2011). In this interpretation, algebra appears as a practical and theoretical tool, enhancing our power to solve problems, but also of questioning, explaining and rearranging already existing bodies of knowledge.

This vision of algebra can provide an answer to the problem of the status and rationale of school algebra in current secondary education. On the one hand, algebra appears as a privileged tool to approach theoretical questions arising in different domains of school mathematics (especially arithmetic and geometry) that cannot be solved within these domains. A well-known example is the work with patterns or sequences where a building principle is given and one needs to make a prediction and then find the rule or general law that characterises it. This feature highlights another differential feature of algebra that is usually referred to as universal arithmetic: the possibility of using it to study relationships independently of the nature of the related objects, leading to generalised solutions of a whole type of problems, instead of a single answer to isolated problems, as is the case in arithmetic. Another essential aspect of the rationale of algebra is the need to organise mathematical tasks in types of problems and to introduce the idea of generalisation in the resolution process, a process making full use of letters as parameters.

In this perspective, the introduction of the algebraic tool at school needs to previously have a system to model, that is, a well-known praxeology that could act as a milieu (in the sense given to this term in the Theory of Didactic Situations) and that is rich enough to generate, through its modelling, the different entities (algebraic expressions, equations, inequalities, formulae, etc.) essential to the subsequent functioning of the algebraic tool. In the model proposed, this initial system is the set of calculation programmes (CP). A CP is a sequence of arithmetic operations applied to an initial set of numbers or quantities that can be effectuated “step by step”—mostly orally and writing the partial results—and provides a final number of quantity as a result. The corpus of problems of classic elementary arithmetic (and also some geometrical ones) can all be solved through the verbal description of a CP and its execution: what was called a “rule” in the old arithmetic books. The starting point of the reference epistemological model for elementary algebra is therefore a compound of elementary arithmetical praxeologies with techniques based on the verbal description of CP and their step by step effectuation.

Working with CP soon presents some technical limitations and also raises theoretical questions about, on the one hand, the reasons for obtaining a given result, justifying and interpreting it and, on the other hand, the possible connections between different kinds of problems and techniques. All these questions lead to an enlargement of the initial system through successive modelling processes giving rise to different stages of the “algebraisation” process that we will briefly summarise hereafter. A more detailed description can be found in Ruiz-Munzón (2010), Ruiz-Munzón et al. (2012).

The first stage of the algebraisation process starts when it is necessary to consider a CP not only as a process but as a whole, representing it in a sufficiently material way—for instance written or graphically—to manipulate it. This does not necessarily mean the use of letters to indicate the different numbers or quantities intervening in a CP (the variables or arguments of a CP). However, it requires making the global structure of the CP explicit and taking into account the hierarchy of arithmetic operations (the “bracket rules”). This new practice generates the need of new techniques to create and simplify algebraic expressions and a new theoretical environment to justify these techniques. It is here where the notions of algebraic expression—as the symbolic model of a CP—and of equivalence between two CP can be defined. Following the classic terminology about equations, we can say that this stage requires the operation of simplifying and transposing equivalent terms but not the operation of cancelling.

The passage to the second stage of algebraisation occurs when the identity between CP needs to be manipulated. In this stage, algebraic techniques include considering equations (of different degrees) as new mathematical objects, as well as the technical transformations needed to solve them. This case includes the resolution of equations with one unknown and one parameter, that is, the case where problems are modelled with CP with two arguments and the solutions are given as a relationship between the arguments involved. In the specific case where one of the numeric arguments takes a concrete value, the problem is reduced to solving a one-variable equation. Nowadays, school algebra mainly remains in this last case (without necessarily having passed through the first one): solving one-variable equations of first and second degree and the word problems that can be modelled with these equations, without achieving the second stage of the algebraisation process.

The third stage of the algebraisation process appears when the number of arguments of the CP is not limited and the distinction between unknowns and parameters is eliminated. The new praxeology obtained contains the work of production, transformation and interpretation of formulae. It is not often present in contemporary secondary schools even if it appears under a weak form in other disciplines (like physics or chemistry). At least in Spain, the use of algebraic techniques to deal with formulae is hardly disseminated outside the study of the general linear and quadratic cases. However, they play an essential role in the transition from elementary algebra to functions and differential calculus, a transition that is nowadays quite weakened in school mathematics. Furthermore, secondary school mathematics does not usually include the systematic manipulation of the global structure of the problems approached, which can be reflected in the fact that letters used in algebraic expressions only play the role of unknowns (in equations) or variables (in functions), while parameters are rarely present. However, it can be argued (Chevallard and Bosch 2012) in which sense the omission of parameters—that is, the use of letters to designate known as well as unknown quantities—can limit the development of efficient modelling algebraic tools and constitutes a clear denaturalisation of the algebraic activity carried out at school.

The effort to explicitly state an epistemological reference model for elementary algebra has different purposes. It can first be used as a descriptive tool to analyse what kind of algebra is taught and learnt in the different educational systems, what elements are left out of the teaching process and what other elements could be integrated under specific conditions (to be established). It is also a productive tool when trying to connect investigations about school algebra carried out from different theoretical perspectives as it helps specify the reference epistemological model of algebra more or less explicitly assumed by each research, and compare the results provided by each one. An example would be looking at the similarities and differences between the structural approach of the research strand on Early algebra (Carraher et al. 2000, 2006; Malara 2003; Subramaniam and Banerjee 2004; Warren 2004) or the “algebrafying” paradigm promoted by Kaput (2000) and the first stage of the algebraisation process with its possible implementation in the classroom. Another interesting exploitation consists in considering what aspects of elementary algebra are not taught at school and inquire about the possible reasons of their absence, as well as the nature and origin of these reasons. This kind of study, which in the ATD is called the “possibilistic problem” (Chevallard and Bosch 2012), would help us progress in our knowledge of the conditions needed to modify a given institutional ecology in a given way. As we will see in the next section, the epistemological reference model also provides a way to experiment new teaching processes that are supposed to bring a new insight on this institutional ecology from the response obtained to the changes operated in it. A clinical analysis of the teaching interventions can really reinforce the approach of the possibilistic problem, as it usually highlights restrictions that are normally hidden or silent. Finally, we will just mention a last important use of reference epistemological models in the research cooperative work with teachers or directly in teachers’ training programmes (Sierra et al. 2011).

How to Teach Algebra at School? Study and Research Paths

Given the results obtained by the ecological analysis of school systems related to the teaching and learning of algebra, it could seem that the only possible way to integrate algebra as a modelling tool in compulsory education is to operate effective changes in both the pedagogical and epistemological models prevailing in these institutions. However, the final aim of the ecological analysis cannot be reduced to the description of how things are and why they seem to be as they are, but to enquire into the possible ways of making them evolve. Of course not much can be changed without understanding the constraints or barriers of any kind (material as well as ideological or conceptual) that hinder the set of praxeologies that can be brought into play in the classroom, at school as well as outside school. The phenomenon of logocentrism and the written symbolism pejoration, the cultural supremacy of discourse and of geometrical work in front of algebraic calculations, or the disappearing of formulae from school mathematical work are part of these constraints and are affecting any local proposal of modification. As a consequence, it could seem that any attempt to renew the teaching of school algebra requires significant changes going far away from the classroom.

The way chosen by the anthropological approach to face this situation is to carry out clinical analyses of teaching and learning processes (Chevallard 2010), proposing strong local modifications, studying the conditions of possibility of such modifications and exploring the answers or reactions to them. To progress in this way, and in the frame of investigations focused on the new problematic opened by the paradigm of questioning the world recently introduced by Yves Chevallard, most of our investigations since 2005 have been centred on the implementation of new teaching proposals based on research and study paths (RSP), working in close collaboration with secondary school teachers from the metropolitan area of Barcelona. In the case of school algebra, these RSP have been designed so that the initial questions that are at the starting point of the process would promote the transition through the different stages of the process of algebraisation.

The first type of RSP are built around the well-known “Think-of-a-number” games, which are used as a milieu to informally introduce the students to simple arithmetical calculation programmes. Carrying out these games can soon highlight the limitations of arithmetical techniques (based on step-by-step calculations) and raises new theoretical questions about how to justify the magic of the games, for instance that the result of a given CP is always 75 or that, independently of the initial number taken, the final result of two different CP is always the same, etc. The work carried out during this study generates the need to progress through the first and second stages of the algebraisation process.

In close relation to this RSP, and once students can work at the first level of algebraisation with the writing and simplification of algebraic expressions (without solving equations yet), a second kind of didactic process is introduced, more tightly led by the teacher, with the aim of introducing negative numbers in the context of the algebraic work (Cid and Bolea 2010; Cid and Ruiz Munzón 2011). In this proposal, instead of putting the conceptual construction of negative numbers as vector quantities before their formal manipulation, the chosen option is to propose situations where negative numbers appear as natural needs of the algebraic work (for instance to simplify expressions obtained by a modelling process, such as (3x + 2) − (x + 8) or (a − 3)(b − 4)) and afterwards deduce the kind of theoretical construction that can give coherence to the manipulations carried out.

The second type of RSP has been carried out with school students in the transition from lower to upper secondary level. They are based on initial questions of different natures, related to economics and financial issues (“Selling T-shirts”, “Saving plans”) so that their study and resolution need the transition from the second to the third stage of the algebraisation process and the connection with functional modelling, which is usually absent from Spanish secondary school curricula (Ruiz-Munzón 2010; Ruiz-Munzón et al. 2012).

These investigations have shown different gaps to make the ecology of algebraic teaching practices evolve. We can mention, for instance, the possibility to introduce algebraic techniques of the different stages of the algebraisation process, motivated by the study of questions related to the technical and theoretical limitations of the previous stage. These questions can also be taken from situations where algebra appears as a tool to progress in the modelling of both mathematical and extra-mathematical issues. Furthermore, we have confirmed the possibility for the students to work, from the first stages of algebraisation, with expressions involving several variables, exchanging the role of letters as unknowns and as parameters. However, a lot of constraints have appeared, some of which can be located at the levels of didactic codetermination linked to the curricular organisation of contents (sublevels of the discipline) and to the discipline and pedagogy levels, especially related to the change of the didactic and pedagogical contract that hinder the passage from the paradigm of “visiting the works” to the one of “questioning the world” (Bosch 2010).

We are currently studying the new needs in mathematical and didactic infrastructures required by the implementation of SRP at secondary and tertiary level, and beginning to analyse the possible use of SRP, together with the reference epistemological and pedagogical models that support them, in pre- and in-service teachers’ training programmes. This work is part of the latest developments of the ATD which focus its research efforts on the study and development of a new school ecology based on the “questioning the world” paradigm. This opens new and complex problems the scope of which seem to go beyond the research work done in classroom laboratories and even beyond the collaborative research work with pre- and in-service teachers. However, the small progress already made in these contexts seems to open a fruitful line of research. It also shows that the “detachment gestures” I mentioned at the beginning of this paper are completely useless if we are not able to get efficiently involved in the social problems that we should face as mathematics educators.