Use of the Differential Calculus for Finding Caustics by Reflection

Abstract

In Chapters 6 through 8 of the Analyse, l’Hôpital studies various kinds of envelopes: curves that are tangent to all the members of some family of lines or curves. In Chapter 6, l’Hôpital studies caustics by reflection, or catacaustics. This problem derives from optics and is essentially the study of envelopes made by light rays reflected in a mirror. L’Hôpital considers a variety of shapes of mirrors and of sources of light rays.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

FormalPara Definition I.

[104] If we imagine that an infinity of rays BA, BM, and BD (see Figs.  6.1, 6.2), which emanate from a radiant point¹ B, are reflected when they encounter a curved line AMD, so that the angles of reflection are equal to the angles of incidence, then the line HFN, which touches the reflected rays or their prolongations AH, MF, and DN, is called the Caustic by reflection.²

Fig. 6.1

Caustic by Reflection, Concave Case

Fig. 6.2

Caustic by Reflection, Convex Case

FormalPara Corollary I.

$\mathrm{(\S 110)}$ If we prolong HA to I (see Fig. 6.1) , so that AI = AB, and if we evolve ³ the caustic HFN beginning at the point I, we describe the curve ILK so that the tangent FL is continually (see §75) equal to the portion FH of the caustic plus the straight line HI. Moreover, if we imagine two incident and reflected rays Bm and mF, infinitely close to BM and MF, and if we prolong Fm to l and describe the little arcs MO and MR with centers F and B, then we form the little right triangles MOm and MRm, which are similar and equal. This is because the angles $\mathit{OmM} = \mathit{FmD} = \mathit{RmM}$ , and furthermore the hypotenuse Mm is common, and so the little sides Om and Rm are equal to each other. Now, because Om is the differential of LM, and Rm is the differential of BM, and because this always happens no matter where we take the point M, it follows that ML − IA or $\mathit{AH} + \mathit{HF} -\mathit{MF}$ , the sum (see §96) of all the differentials Om in the portion AM of the curve, is $= \mathit{BM} -\mathit{BA}$ , the sum (see §96) of the of all the differentials Rm in the same portion AM. Therefore, the portion HF of the caustic HFN is equal to $\mathit{BM} -\mathit{BA} + \mathit{MF} -\mathit{AH}$ .

There could be different cases, according to whether the incident ray BA is greater or less than BM, and whether the [105] reflected ray AH evolves or envelops⁴ the portion HF to arrive at MF. However, we will still prove, as we have just done, that the difference of the incident rays is equal to the difference of the reflective rays, by joining to one of them the portion of the caustic that it evolves before falling on the other. For example (see Fig.  6.2), $\mathit{BM} -\mathit{BA} = \mathit{MF} + \mathit{FH} -\mathit{AH}$; from which we conclude that $\mathit{FH} = \mathit{BM} -\mathit{BA} + \mathit{AH} -\mathit{MF}$.

If we describe the circular arc of AP with center B (see Figs.  6.1, 6.2), then it is clear that PM is the difference of the incident rays BM and BA. Moreover, if we suppose that the radiant point B becomes infinitely distant from the curve AMD, the incident rays BA and BM (see Fig.  6.3) become parallel and the arc AP becomes a straight line perpendicular to these rays.

Fig. 6.3

Caustic by Reflection, Infinitely Distant Radiant Point

FormalPara Corollary II.

$\mathrm{(\S 111)}$ If we imagine that the figure BAMD (see Fig. 6.1) is reflected in the same plane, so that the point B falls on the point I, and that therefore the tangent at A to the curve AMD in its first position, still touches it in this new position, and if we make the curve aMd roll on the curve AMD, that is to say on itself, so that the portions aM and AM are always equal, then I say that the point B describes by this motion a kind of roulette ILK whose evolute is the caustic HFN.

This is because it follows from the generation that:

• 1. The line LM drawn from the describing point L to the point of contact M is (see §43) perpendicular to the curve ILK.

• 2. La or IA = BA, and LM = BM.

• 3. The angles made by the straight lines ML and BM on the common tangent at M are equal, and consequently if we prolong LM to F, the ray MF is the reflected ray of the incident ray BM.

From this we see that the perpendicular LF touches the caustic HFN, and because this always happens whenever we take the point L, it follows that the curve ILK is formed by the evolution of the caustic HFN, plus the straight line HI.

It follows from this that the portion FH or $\mathit{FL} -\mathit{HI} = \mathit{BM} + \mathit{MF} -\mathit{BA} -\mathit{AH}$. [106] This is what we have just demonstrated in another way in the preceding Corollary.

FormalPara Corollary III.

$\mathrm{(\S 112)}$ If the tangent DN becomes infinitely close to the tangent FM, it is clear that the point of contact N, and the point of intersection V will coincide with the other point of contact F. Thus, to find the point F where the reflected ray MF touches the caustic HFN, we need only find the point of intersection of the infinitely close reflected rays MF and mF. Indeed, if we imagine an infinity of incidence rays infinitely close to one another, we will see a polygon with an infinity of sides, the assemblage of which makes up the caustic HFN born of the intersections of the reflected rays.

FormalPara Proposition I.

General Problem.

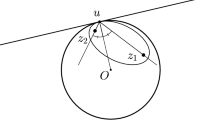
$\mathrm{(\S 113)}$ Given the nature of the curve AMD (see Fig. 6.4) , the radiant point B, and the incident ray BM, we wish to find the point F on the reflected ray MF, given in position, where it touches the caustic.

Fig. 6.4

Intersection of Reflected Ray with the Caustic

By the previous chapter, we find the length MC of the radius of the evolute at the point M. We take the infinitely small arc Mm, and draw the straight lines Bm, Cm, and Fm. We describe the little arcs MR and MO with centers B and F, and we drop the perpendiculars CE, Ce, CG, and Cg on the incident and reflected rays. We then denote the given quantities BM by y, and ME or MG by a.

Given this, we prove, as in the first Corollary (see §110), that the triangles MRm and MOm are similar and equal, and thus MR = MO. Now, because of the equality of the angles of incidence and reflection, we also have CE = CG and Ce = Cg, and consequently CE −Ce or $\mathit{EQ} = \mathit{CG} -\mathit{Cg}$ or SG. Therefore, because of the similar triangles BMR and BEQ, and FMO and FGS, we have [107] $\mathit{BM}+\mathit{BE}(2y-a): \mathit{BM}(y):: \mathit{MR}+\mathit{EQ}\,\mbox{ or }\mathit{MO}+\mathit{GS}: \mathit{MR}\,\mbox{ or }\mathit{MO}:: \mathit{MG}(a): \mathit{MF} = \frac{\mathit{ay}} {2y-a}$.

If the radiant point B falls on the other side of the point E with respect to the point M, or (what is the same thing) if the curve AMD is convex towards the radiant point B, then y changes from positive to negative, and consequently we have $\mathit{MF} = \frac{-\mathit{ay}} {-2y-a}$ or $\frac{\mathit{ay}} {2y+a}$.

If we suppose that y becomes infinite (see Fig.  6.3), that is to say that the point B is infinitely distant from the curve AMD, the incident rays are parallel to one another, and we have $\mathit{MF} = \frac{1} {2}a$, because a is null with respect to 2y.

FormalPara Corollary I.

$\mathrm{(\S 114)}$ Because we have found only one value for MF (see Figs. 6.1, 6.2) along the radius of the evolute, it follows that a curved line AMD may have but a single caustic HFN by reflection, because (see §80) it has but a single evolute.

FormalPara Corollary II.

$\mathrm{(\S 115)}$ When AMD is geometric (see Fig. 6.4) , it is clear (see §85) that its evolute is also geometric, that is to say that we find all of its points C geometrically. From this it follows that all points F of its caustic are also determined geometrically (see Figs. 6.1, 6.2) , that is to say that the caustic HFN is geometric. However, I say furthermore, that this caustic is always rectifiable, because it is clear (see §110) that we may find straight lines equal to any of its portions with the assistance of the curve AMD, which we assume to be geometric.

FormalPara Corollary III.

$\mathrm{(\S 116)}$ If the curve AMD (see Fig. 6.4) is convex towards the radiant point B, then the value of $\mathit{MF}\left ( \frac{\mathit{ay}} {2y+a}\right )$ is always positive, and consequently we must take the point F on [108] the same side as the point C with respect to the point M, as we have assumed in making the calculations. From this we see that infinitely close reflected rays are divergent.

However, if the curve AMD is concave towards the radiant point B, the value of $\mathit{MF}\left ( \frac{\mathit{ay}} {2y-a}\right )$ is positive when y is greater than $\frac{1} {2}a$, negative when it is less than, and infinite when it is equal. From this it follows that if we describe a circle that has half of the radius of the evolute MC as its diameter, then the infinitely close reflecting rays are convergent when the radiant point B falls outside of its circumference, they are divergent when falls inside, and finally they are parallel when it falls on the circumference.

FormalPara Corollary IV.

$\mathrm{(\S 117)}$ If the incident ray BM touches the curve AMD at the point M, we have ME(a) = 0, and consequently MF = 0. Because the reflected ray is therefore in the direction of the incident ray, and because the nature of the caustic consists of touching all reflected rays, it follows that it will also touch the incident ray BM at the point M. That is to say that the caustic and the given curve have the same tangent at the point M, which is common to them.

If the radius MC of the evolute is null, we also have ME(a) = 0, and consequently MF = 0. From this we see that the given curve and the caustic make an angle equal to the angle of incidence between them at their common point M.

If the radius CM of the evolute is infinite, then the little arc Mm becomes a straight line, and we have MF = ∓y, because when ME(a) is infinite, y is null with respect to a. Now, because this value is negative when the point B falls on the same side as the point C with respect to the line AMD, and positive when it falls on the opposite side, it follows that the infinitely close reflected rays are always divergent when the line AMD is straight.

FormalPara Corollary V.

[109] $\mathrm{(\S 118)}$ It is clear that given any two of the three points B, C, and F, we easily find the third.

• 1. Let the curve AMD (see Fig.  6.5) be a Parabola, which has the radiant point B as its focus. It is clear by the elements of the conic sections, that all reflected rays are parallel to the axis, and consequently MF is always infinite wherever we suppose the point M to be. Therefore, we have a = 2y. From this it follows that if we take ME to be twice MB, and if we draw the perpendicular EC, it cuts MC perpendicular to the curve AMD at a point C, which is on the evolute of this curve.

  Fig. 6.5

  

  Caustic of the Parabola by Reflection

• 2. Let the curve AMD (see Fig.  6.6) be an Ellipse, which has the radiant point B as one of its foci. Again, it is clear that all reflected rays MF meet in the same point F, which is the other focus. If we denote MF by z, we have (see §113) $z = \frac{\mathit{ay}} {2y-a}$, from which we find the quantity that we wish to find, $\mathit{ME}(a) = \frac{2\mathit{yz}} {y+z}$. However, if the curve AMD (see Fig.  6.7) is a Hyperbola, the focus F falls on the other side, and consequently MF(z) becomes negative. From this it follows that we therefore have $\mathit{ME}(a) = \frac{-2\mathit{yz}} {y-z}$ or $\frac{2\mathit{yz}} {z-y}$. This gives the following construction, which also serves for the Ellipse.

  Fig. 6.6

  

  Caustic of the Ellipse by Reflection

  Fig. 6.7

  

  Caustic of the Hyperbola by Reflection

Let ME (see Figs.  6.6, 6.7) be taken as the fourth proportional to the transverse semi-axis,⁵ the incident ray, and the reflected ray. Let EC be drawn perpendicular; it cuts the line MC, which is perpendicular to the conic section, at a point C that is on the evolute.

FormalPara Example I.

$\mathrm{(\S 119)}$ Let the curve AMD (see Fig.  6.8) be a Parabola, whose incident rays PM are perpendicular to its axis AP. We wish to find the points F on the reflected rays MF where they touch the caustic AFK.

Fig. 6.8

Caustic of the Parabola by Reflection, Incident Rays Perpendicular to the Axis

[110] It is clear that if we draw the radius MC of the evolute, and drop the perpendicular CG to the reflected ray MF, we must (see §113) take MF equal to half of MG. However, this construction can be shortened, considering that if we draw MN parallel to the axis AP, and draw the straight line ML to the focus L, then the angles LMP and FMN are equal, because by the property of the parabola LMQ = QMN, and by assumption PMQ = QMF. If we now add the same angle PMF to both sides, the angle LMF is equal to the angle PMN, that is to say a right angle. Now, we have just demonstrated (see §118, no. 1) that the perpendicular LH on ML meets the radius MC of the evolute at its midpoint H. Therefore, if we draw MF parallel and equal to LH, it is one of the reflected rays and it touches the caustic AFK at F. This is what we were required to find.

If we suppose that the reflected ray MF is parallel to the axis AP, it is clear that the point F of the caustic will be the furthest possible from the axis AP, because the tangent at this point is parallel to the axis. Thus, in order to determine this point on all caustics, such as AFK, formed by incident rays perpendicular to the axis of the given curve, we need to only consider that MP is equal to PQ. This gives dy = dx. Let ax = yy; we have $\mathit{dy} = \frac{a\,\mathit{dx}} {2\sqrt{ax}} = \mathit{dx}$, from which we conclude $\mathit{AP}(x) = \frac{1} {4}a$, that is to say if the point P falls on the focus L, the reflected ray MF is parallel to the axis. What is also clear is that because in this case MP coincides with LM, MF must also coincide with MN, and LH with LQ. From this we see that MF is therefore equal to ML, and consequently that if we draw FR perpendicular to the axis, we have AR or $\mathit{AL} + \mathit{MF} = \frac{3} {4}a$. We also see that the portion AF of the caustic is equal, in this case, to the parameter, because it is always (see §110) equal to PM +MF.

To determine the point K where the caustic AFK meets the axis AP, we must find the value MO, and [111] make it equal to MF, because it is clear that if the point F falls on K, the lines MF and MO become equal to each other. Therefore, denoting the unknown MO by t, the angle PMO cut equally in two by MQ, perpendicular to the curve, gives $\mathit{MP}(y): \mathit{MO}(t):: \mathit{PQ}\left (\frac{y\,\mathit{dy}} {\mathit{dx}} \right ): \mathit{OQ} = \frac{t\,\mathit{dy}} {\mathit{dx}}$, and consequently $\mathit{OP} = \frac{t\,\mathit{dy}+y\,\mathit{dy}} {\mathit{dx}} = \sqrt{\mathit{tt } - \mathit{yy}}$, because of the right triangle MPO. Dividing both sides by t + y, we find $\frac{\mathit{dy}} {\mathit{dx}} = \sqrt{\frac{t-y} {t+y}}$, from which we conclude $\mathit{MO}(t) = \frac{y\,\mathit{dx}^{2}+y\,\mathit{dy}^{2}} {\mathit{dx}^{2}-\mathit{dy}^{2}} = \mathit{MF}\left (\frac{1} {2}a\right ) = \frac{\mathit{dx}^{2}+\mathit{dy}^{2}} {-2\mathit{ddy}}$, because (see §77) $\mathit{ME}(a) = \frac{\mathit{dx}^{2}+\mathit{dy}^{2}} {-\mathit{ddy}}$. This gives $\mathit{dy}^{2} - 2y\,\mathit{ddy} = \mathit{dx}^{2}$, which is used to find the point P such that if we draw the incident ray PM and the reflected ray MF, this latter touches the caustic AFK at the point K where it meets the axis AP.

For the parabola $y = x^{\frac{1} {2} }$, we have $\mathit{dy} = \frac{1} {2}x^{-\frac{1} {2} }\,\mathit{dx}$ and $\mathit{ddy} = -\frac{1} {4}x^{-\frac{3} {2} }\,\mathit{dx}^{2}$, and substituting these values in the preceding equation, we find $\frac{1} {4}x^{-1}\,\mathit{dx}^{2} + \frac{1} {2}x^{-1}\,\mathit{dx}^{2} = \mathit{dx}^{2}$, from which we conclude $\mathit{AP}(x) = \frac{3} {4}$ of the parameter.

To find the nature of the caustic AFK in the manner of Descartes,⁶ we must find an equation that expresses the relationship of the abscissa AR(u) to the ordinate RF(z), which is done in the following way. Because $\mathit{MO}(t) = \frac{y\,\mathit{dx}^{2}+y\,\mathit{dy}^{2}} {\mathit{dx}^{2}-\mathit{dy}^{2}}$, we have $\mathit{PO}\left (\frac{t\,\mathit{dy}+y\,\mathit{dy}} {\mathit{dx}} \right ) = \frac{2y\,\mathit{dx}\,\mathit{dy}} {\mathit{dx}^{2}-\mathit{dy}^{2}}$, and because of the similar triangles MPO and MSF, we form the following proportions: $\mathit{MO}\left (\frac{y\,\mathit{dx}^{2}+y\,\mathit{dy}^{2}} {\mathit{dx}^{2}-\mathit{dy}^{2}} \right )$: $\mathit{MF}\left (\frac{\mathit{dx}^{2}+\mathit{dy}^{2}} {-2\mathit{ddy}} \right )$ or $-2y\,\mathit{ddy}: \mathit{dx}^{2}-\mathit{dy}^{2}:: \mathit{MP}(y): \mathit{MS}(y-z) = \frac{\mathit{dx}^{2}-\mathit{dy}^{2}} {-2\mathit{ddy}}:: \mathit{PO}\left ( \frac{2y\,\mathit{dx}\,\mathit{dy}} {\mathit{dx}^{2}-\mathit{dy}^{2}} \right ): \mathit{SF}\,\mbox{ or }\,\mathit{PR}(u-x) = \frac{\mathit{dx}\,\mathit{dy}} {-\mathit{ddy}}$. We therefore have the following two [112] equations $z = y + \frac{\mathit{dy}^{2}-\mathit{dx}^{2}} {-2\mathit{ddy}}$ and $u = x + \frac{\mathit{dx}\,\mathit{dy}} {-\mathit{ddy}}$, which can be used with the equation of the given curve to form a new equation where x and y are no longer present, and which consequently expresses the relationship of AR(u) to FR(z).

When the curve AMD is a parabola, as we have assumed in this example, we find $z = \frac{3} {2}x^{\frac{1} {2} } - 2x^{\frac{3} {2} }$, or (by squaring each side) $\frac{9} {4}x - 6\mathit{xx} + 4x^{3} = \mathit{zz}$ and u = 3x, from which we derive the equation we wish to find, $\mathit{azz} = \frac{4} {27}u^{3} -\frac{2} {3}\mathit{auu} + \frac{3} {4}\mathit{aau}$, which expresses the nature of the caustic AFK. We may remark that PR is always twice AP, because AR(u) = 3x. This again gives us a new method for determining the point F that we wish to find on the reflected ray MF.

FormalPara Example II.

$\mathrm{(\S 120)}$ Let the curve AMD (see Fig.  6.9) be a semi-circle that has the line AD as its diameter and its center at the point C. Let the incident rays PM be perpendicular to AD.

Fig. 6.9

Caustic of the Semi-circle by Reflection, Incident Rays Perpendicular to the Diameter

Because the evolute of the circle is a single point which is its center, it follows (see §113) that if we cut the radius CM equally in two at the point H, and we drop the perpendicular HF to the reflected ray MF, then it cuts this ray at a point F where it touches the caustic AFK. It is clear that the reflected ray MF is equal to half the incident ray PM. From this it follows that:

• 1. If the point P falls on C, then the point F falls on the midpoint of CB at K.

• 2. The portion AF is three times MF, and the caustic AFK is three times BK.

We also see that if we make the angle AMC half of a right angle, the reflected ray MF is parallel to AC, and consequently the point F is higher above the diameter AD than any other point of the caustic.

The circle with diameter MH passes through the point F, because the angle HFM is a right angle. If we describe the circle KHG with [113] center C and radius CK or CH, half of CM, then the arc HF is equal to the arc HK. This is because the angle CMF is equal to⁷ CMP or HCK, so the arcs $\frac{1} {2}\mathit{HF}$ and HK, which measure these angles in the circles MFH and KHG, are to each other as $\frac{1} {2}\mathit{MH}$ is to HC, the radii of these circles. From this we see that the Caustic AFK is a Roulette formed by the revolution of the mobile circle MFH around the immobile circle KHG, whose origin is at K, and whose vertex is at A.

FormalPara Example III.

$\mathrm{(\S 121)}$ Let the curve AMD (see Fig.  6.10) be a circle with the line AD as diameter and the point C as center. Let the radiant point, from which all the incident rays AM emanate, be A, one of the extremities of this diameter.

Fig. 6.10

Caustic of the Circle by Reflection, Radiant Point on the Circumference

If we drop the perpendicular CE from the center C to the incident ray AM, it is clear by the property of the circle, that the point E cuts the chord AM into two equal parts, and thus that $\mathit{ME}(a) = \frac{1} {2}y$. We therefore have $\mathit{MF}\left ( \frac{\mathit{ay}} {2y-a}\right ) = \frac{1} {3}y$, that is to say we must take the reflected ray MF equal to one-third of the incident ray AM. From this we see that $\mathit{DK} = \frac{1} {3}\mathit{AD}$, $\mathit{CK} = \frac{1} {3}\mathit{CD}$, and that (see §110) the caustic $\mathit{AFK} = \frac{4} {3}\mathit{AD}$, as well as that its portion $\mathit{AF} = \frac{4} {3}\mathit{AM}$. If we take AM = AC, the reflected ray MF is parallel to the diameter AD, and consequently the point F is the highest possible above this diameter.

If we take $\mathit{CH} = \frac{1} {3}\mathit{CM}$, and we draw HF perpendicular to MF, the point F is on the caustic, for if we draw HL perpendicular to AM, it is clear that $\mathit{ML} = \frac{2} {3}ME = \frac{1} {3}\mathit{AM}$, because $\mathit{MH} = \frac{2} {3}\mathit{CM}$. The circle with diameter MH therefore passes through the point F of the caustic, and if we describe another circle KHG with center C and with radius CK or CH, it will be equal to it, and the arc HK [114] will be equal to the arc HF, because in the isosceles triangle CMA, the external angle $\mathit{KCH} = 2CMA = \mathit{AMF}$. Consequently the arcs HK and HF, the measures in the equal circles, are also equal. From this it follows that the Caustic AFK is again a Roulette described by the revolution of the mobile circle MFH around the immobile circle KHG, whose origin is at K, and whose vertex is at A.

We might also prove this by the following other method. If we describe a roulette by the revolution of a circle equal to the circle AMD around that circle, starting at the point A, we demonstrated in the second corollary (see §111) that its evolute is the caustic AFK. Now (see §100), this evolute is a roulette of the same kind, that is to say that the diameters of the generating circles are equal, and we determine the point K by taking CK as the third proportional to CD +DA and to CD, that is to say equal to $\frac{1} {3}\mathit{CD}$. Therefore, etc.

FormalPara Example IV.

$\mathrm{(\S 122)}$ Let the curve AMD (see Fig.  6.11) be an ordinary half-roulette described by the revolution of the semi-circle NGM on the straight line BD, whose vertex is at A, and whose origin at D. Let the incident rays KM be parallel to the axis AB.

Fig. 6.11

Caustic of the Half-Cycloid by Reflection, Incident Rays Parallel to the Axis

Because (see §95) MG is equal to half the radius of the evolute, it follows (see §113) that if we draw GF perpendicular to the reflected ray MF, the point F will be on the caustic DFB. From this we see that MF must be taken equal to KM.

If we draw the radii HG and HM from the center H of the generating circle MGN to the point of contact G and to the describing point M, then it is clear that HG is perpendicular to BD, and that the angle $\mathit{GMH} = \mathit{MGH} = \mathit{GMK}$, from which we see that the reflected ray MF passes through the center H. Now, the circle with diameter GH also passes through the point F, because the angle GFH is a right angle. Therefore, the arcs GN and $\frac{1} {2}\mathit{GF}$, which measure the same angle GHN, are to each other as the MN is to GH, the diameters [115] of their circles, and consequently the arc $\mathit{GF} = \mathit{GN} = \mathit{GB}$. It is therefore clear that the Caustic DFB is a Roulette described by an entire revolution of the circle GFH on the straight line BD.

FormalPara Example V.

$\mathrm{(\S 123)}$ Let the curve AMD (see Fig.  6.12) again be an ordinary half-roulette, whose base BD is equal to the semi-circumference ANB of the generating circle. Additionally, let the incident rays PM now be parallel to the base BD.

Fig. 6.12

Caustic of the Half-Cycloid by Reflection, Incident Rays Parallel to the Base

If we draw GQ perpendicular to PM, the right triangles GQM and BPN are equal and similar, and therefore MQ = PN. From this we see (see §95, 113) that we must take MF equal to the corresponding ordinate PN in the generating semi-circle ANB.

In order that the point F is the furthest possible from the axis AB, it is necessary that the tangent MF at this point be parallel to this axis. The angle PMF is therefore a right angle, its half PMG or PNB is half a right angle, and consequently the point P falls on the center of the circle⁸ ANB.

It is worth remarking, that if the point P then continually approaches the extremity B, the point F also moves closer the axis AB up to a certain point K, after which it moves away to D, so that the caustic AFKFD has a cusp at K .

To determine this, I remark (see §110, 111) that the portion $\mathit{AF} = \mathit{PM} + \mathit{MF}$, the portion $\mathit{AFK} = \mathit{HL} + \mathit{LK}$, and the portion KF of the part KFD is $= \mathit{HL} + \mathit{LK} -\mathit{PM} -\mathit{MF}$, from which we see that HL +LK must be the greatest. That is why if we denote AH by x, HI by y, and the arc AI by u, we have $\mathit{HL} + \mathit{LK} = u + 2y$, whose differential gives $\mathit{du} + 2\,\mathit{dy} = 0$ and $\frac{a\,\mathit{dx}} {y} + 2\,\mathit{dy} = 0$ by substituting the value $\frac{a\,\mathit{dx}} {y}$ for du. From this we derive $a\,\mathit{dx} = -2y\,\mathit{dy} = 2x\,\mathit{dx} - 2a\,\mathit{dx}$ because of the circle, and consequently $\mathit{AH}(x) = \frac{3} {2}a$.

FormalPara Corollary.

[116] $\mathrm{(\S 124)}$ The space AFM or AFKFM enclosed by the portions of the curves AF or AFKF, AM, and by the reflected rays MF, is equal to half of the circular space APN. This is because its differential, which is the sector FMO, is equal to half of the rectangle PpSN, the differential of the space APN, because the right triangles MOm and MRm are equal and similar, so MO is equal to MR or NS or Pp, and furthermore MF = PN.

FormalPara Example VI.

$\mathrm{(\S 125)}$ Let the curve AMD (see Fig.  6.13) be the half-roulette formed by the revolution of the circle MGN around an equal circle AGK, whose origin is at A, and whose vertex is at D. Let the incident rays be AM, which all emanate from the point A. The line BH that joins the centers of these two generating circles continually passes through the point of contact G, and the arcs GM and GA, as well as their chords, are always equal. So the angle HGM = BGA and the angle GMA = GAM. Now, the angle $\mathit{HGM} + \mathit{BGA} = \mathit{GMA} + \mathit{GAM}$, because if we add the same angle AGM to both sides, we form two right angles. Thus, the angle HGM is always equal to the angle GMA, and consequently also to the angle of reflection GMF. From this it follows that MF is always passes through the center H of the mobile circle.

Fig. 6.13

Caustic of an Epicycloid by Reflection

If we now drop the perpendiculars CE and GO on the incident ray AM, it is clear that MO = OA, and that $\mathit{OE} = \frac{1} {3}\mathit{OM}$, because (see §100) since the point C is on the evolute $\mathit{GC} = \frac{1} {3}\mathit{GM}$. We therefore have $\mathit{ME} = \frac{2} {3}\mathit{AM}$, that is to say $a = \frac{2} {3}y$, and consequently $\mathit{MF}\left ( \frac{\mathit{ay}} {2y-a}\right ) = \frac{1} {2}y$. From this we see that if we draw GF perpendicular to MF, the point F is on the caustic AFK.

The circle with diameter GH passes through the point F, and the arcs GM and $\frac{1} {2}\mathit{GF}$, which measure the same angle GHM, being [117] to each other as MH is to GH, the diameters of their circles, the arc GF is equal to the arc GM, and consequently to the arc GA. From this it is clear that the Caustic AFK is a Roulette described by the revolution of the mobile circle HFG around the immobile circle AGK.

FormalPara Corollary.

( $\S \mathrm{126}$ ) If we describe a circle with center at the point B, and whose radius is a straight line equal to BH or AK, that has an infinity of straight lines parallel to BD that fall on its circumference, it is clear (see §120) that by reflection the rays form the same caustic AFK.

FormalPara Example VII.

$\mathrm{(\S 127)}$ Let the curve AMD (see Fig.  6.14) be a logarithmic spiral, with incident rays AM that all of emanate from the center A.

Fig. 6.14

Caustic of the Logarithmic Spiral by Reflection

If we draw the straight line CA from the extremity C of the radius of the evolute perpendicular to the incident ray AM, it meets it (see §91) at the center A. This is why AM(y) = a, and consequently $\mathit{MF}\left ( \frac{\mathit{ay}} {2y-a}\right ) = y$. The triangle AMF is therefore isosceles, and because the angles of incidence and reflection, AMT and FMS, are equal to each other, it follows that the angle AFM is equal to the angle AMT. From this it is clear that caustic AFT is a logarithmic spiral which differs from the given AMD only in its position.

FormalPara Proposition II.

Problem .  $\mathrm{(\S 128)}$ Given the caustic by reflection HF (see Fig. 6.15) with its radiant point B, we wish to find an infinity of curves, such as AM, of which it is the caustic by reflection.

Fig. 6.15

The Inverse Problem: Finding the Original Curve from its Caustic

Take the point A at will on any tangent HA to be one of the points on the curve AM that we wish to find. [118] We describe the circular arc AP with center B and interval BA, and with any other interval BM, we describe another circular arc. If we take $\mathit{AH} + \mathit{HE} = \mathit{BM} -\mathit{BA}$ or PM, we evolve the caustic HF beginning at the point E, and we describe by this motion the curved line EM that cuts the arc of the circle described from the radius BM at a point M that is (see §110) on the curve AM. This is because by the construction, $\mathit{PM} + \mathit{MF} = \mathit{AH} + \mathit{HF}$.

Alternately, if we attach a thread BMF by its extremities at B and to F, then we make this thread tight by means of a stylus placed at M, and we make it move so that we envelop the caustic HF with the part MF of this thread, it is clear that by this motion the stylus describes the curve MA that we wish to find.

FormalPara Alternate Solution.

$\mathrm{(\S 129)}$ If we draw at will a tangent FM, other than HA, we wish to find a point M on it, such that $\mathit{BM} + \mathit{MF} = \mathit{BA} + \mathit{AH} + \mathit{HF}$. This is done in the following manner.

Let FK be taken $= \mathit{BA} + \mathit{AH} + \mathit{HF}$, and if we divide BK in the middle at G, then let the perpendicular GM be drawn; it meets the tangent FM at the point M that we wish to find. This is because BM = MK.

If the point B is infinitely far from the curve AM (see Fig.  6.16), that is to say that the incident rays BA and BM are parallel to a straight line given in position, the first construction will still hold, by considering that the circular arcs described from the center B become straight lines perpendicular to the incident rays. However, this latter construction becomes useless, which is why we must substitute it with the following.

Fig. 6.16

The Inverse Problem: Radiant Point at Infinity

Let FK be taken $= \mathit{AH} + \mathit{HF}$. If we find the point M, so that MP is parallel to AB and perpendicular to AP, and is equal to MK, it is clear (see §110) that this point is on the curve AM that we wish to find, because $\mathit{PM} + \mathit{MF} = \mathit{AH} + \mathit{HF}$. Now, this is done as follows.

Let KG be drawn perpendicular to AP. If we take KO = KG, let KP be drawn parallel to OG and PM parallel to GK, I say that the point M is the one we wish to find. [119] This is because GKO and PMK are similar triangles, so that we have PM = MK, because GK = KO.

If the caustic HF is a single point, the curve AM becomes a conic section .

FormalPara Corollary I.

$\mathrm{(\S 130)}$ It is clear that the curve that passes through all the points K is formed by the evolution of the curve HF beginning at A, and that its nature changes as the point A changes its position on the tangent AH. Thus, because the curves AM are all born from these curves by the same construction, which is geometric, it follows (see §108) that they are of a different nature from each other, and that they are geometric only when the caustic HF is geometric and rectifiable.

FormalPara Corollary II.

$\mathrm{(\S 131)}$ Given a curved line DN (see Fig. 6.17) with a radiant point C, we wish to find an infinity of lines, such as AM, so that the reflected rays DA and NM meet at a given point B, after being reflected again upon meeting any such line AM.

Fig. 6.17

An Application of the Inverse Problem: Constructing a Focus

If we imagine that the curve HF is the caustic of the given curve DN, formed by the radiant point C, it is clear that this line HF must also be the caustic of the curve AM having the given point B as its radiant point, so that $\mathit{FK} = \mathit{BA} + \mathit{AH} + \mathit{HF}$, and $\mathit{NK} = \mathit{BA} + \mathit{AH} + \mathit{HF} + \mathit{FN} = \mathit{BA} + \mathit{AD} + \mathit{DC} -\mathit{CN}$, because (see §118) $\mathit{HD} + \mathit{DC} = \mathit{HF} + \mathit{FN} + \mathit{NC}$. This gives the following construction.

If we take the point A at will on any reflected ray to be one of the points on the curve AM that we wish to find and, on any other reflected ray NM that we wish, we take the part $\mathit{NK} = \mathit{BA} + \mathit{AD} + \mathit{DC} -\mathit{CN}$, then we find the point M that we wish as above in §129.