Keywords

4.1 Introduction

The main objective of the present work is to demonstrate the advantages of applying an appropriate hybrid modelling method in order to study the dynamics of a class of mechanical structures in an accurate and effective way. The method applied in the present work can be used to determine the dynamic behavior of vehicle superstructures. This is a necessary step in order to capture, explain and improve the dynamic behavior of many contemporary complex mechanical systems. At the same time, this leads to an accurate identification of points where the critical (largest) stresses appear in the structural part of interest. This is done by applying a numerical method for determining the equations of motion for the superstructure of the vehicle, while the dynamic characteristics of the remaining components are taken into account through the application of appropriate experimental measurements.

More specifically, the above procedure can be easily extended to systems with more than two structural components. In particular, the procedure followed in this work is applicable to all cases of vehicles carrying superstructures, where the supporting system (suspension and wheels) is not modeled, since its dynamic characteristics are not known. Essentially, it involves the following basic steps. First, the vehicle superstructure is divided in a number of substructures, which are discretized geometrically by application of the finite element method. The resulting model for each substructure is then updated through an experimental investigation of its dynamic response in a support-free state. In this way, all the elements of the matrix with the frequency response functions (FRFs) required for determining the response of the substructure are determined by imposing impulsive loading. Based on the measured FRFs, the natural frequencies and damping ratios of each substructure are then estimated. The natural frequencies provide a basis for checking the accuracy of similar results obtained by the corresponding finite element models, while the damping ratios are used for updating the corresponding damping matrices. Next, a series of experimental trials are performed in real operating conditions, aimed at recording the acceleration histories at the connection points of the superstructure with the chassis. These histories are subsequently used as a ground excitation for the finite element model resulting by performing a synthesis of all the components of the superstructure, as explained in the first part of this section. In this way, the stresses developed under the specific loading conditions are evaluated. From these numerical results, the critical points of the superstructure are finally selected, based on the level of the larger magnitude stresses observed.

The organization of this paper is as follows. In the following section, a brief but complete outline of the methodology applied is presented. Then, the effectiveness and accuracy of this methodology is first demonstrated in the third section, by presenting numerical and experimental results obtained for an experimental small scale vehicle model, involving suspensions with nonlinear characteristics. In the fourth section, results for a real military vehicle are presented. Here, the reliability of the methodology was tested by placing strain gauges at the critical points of the superstructure and performing a new set of measurements under similar dynamic load conditions, in order to experimentally verify the stress levels developed. The study concludes by presenting a summary of the results obtained.

4.2 Class of Mechanical Systems Examined: Equations of Motion

The equations of motion of mechanical systems with complex geometry are commonly set up by applying finite element techniques. Quite frequently, a systematic investigation of the dynamics of large scale mechanical structures leads to models involving an excessive number of degrees of freedom. Therefore, a computationally efficient solution requires application of methodologies reducing the numerical dimension of the original model [1–11]. Next, the basic philosophy of a time domain reduction method, which was part of the hybrid methodology applied, is presented briefly.

For simplicity, consider a mechanical system consisting of two subsystems, say A and B. Moreover, let the equations of motion for subsystem A be derived in the following classical form

$$ {\widehat{M}}_A{\underset{\bar{\mkern6mu}}{\ddot{x}}}_A+{\widehat{C}}_A{\underset{\bar{\mkern6mu}}{\dot{x}}}_A+{\widehat{K}}_A{\underset{\bar{\mkern6mu}}{x}}_A={\underset{\bar{\mkern6mu}}{\widehat{f}}}_A(t), $$
(4.1)

where \( {\widehat{M}}_A \), Ĉ A and \( {\widehat{K}}_A \) are the mass, damping and stiffness matrix of the subsystem, respectively, while the vector \( {\widehat{\underset{\bar{\mkern6mu}}{f}}}_A(t) \) represents the external forcing. For a typical model, the number of these equations may be quite large. However, for a given level of forcing frequencies it is possible to reduce significantly the number of the original degrees of freedom, without sacrificing the accuracy in the numerical results, by applying standard component mode synthesis methods [1, 5, 12]. This can be achieved through an approximate coordinate transformation with form

$$ {\underset{\bar{\mkern6mu}}{x}}_A={\Psi}_A{\underset{\bar{\mkern6mu}}{q}}_A. $$
(4.2)

The transformation matrix Ψ A includes an appropriately chosen set of the lowest frequency normal modes of component A, corresponding to support-free conditions [1]. The number of these modes depends on the accuracy required in the response frequency range examined. Consequently, matrix Ψ A is completed by a set of static correction modes of component A [4, 5, 13]. Employing this transformation, the original set of Eq. 4.1 can be replaced by a considerably smaller set of equations, expressed in terms of a new generalized coordinates \( {\underset{\bar{\mkern6mu}}{q}}_A \). More specifically, application of the Ritz transformation Eq. 4.2 into the original set of Eq. 4.1 yields the much smaller dimension set

$$ {M}_A{\underset{\bar{\mkern6mu}}{\ddot{q}}}_A+{C}_A{\underset{\bar{\mkern6mu}}{\dot{q}}}_A+{K}_A{\underset{\bar{\mkern6mu}}{q}}_A={\underset{\bar{\mkern6mu}}{f}}_A(t), $$
(4.3)

where

$$ {M}_A={\Psi}_A^T{\widehat{M}}_A{\Psi}_A,\ \,{C}_A={\Psi}_A^T{\widehat{C}}_A{\Psi}_A,\ \,{K}_A={\Psi}_A^T{\widehat{K}}_A{\Psi}_A\ \,\mathrm{and}\ \,{\underset{\bar{\mkern6mu}}{f}}_A={\Psi}_A^T{\underset{\bar{\mkern6mu}}{\widehat{f}}}_A. $$

Moreover, the set of unknowns can be split in the form

$$ {\underset{\bar{\mkern6mu}}{q}}_A=\Big(\begin{array}{cc}\hfill {\underset{\bar{\mkern6mu}}{p}}_A^T\hfill & \hfill {\underset{\bar{\mkern6mu}}{x}}_b^T\Big){}^T\hfill \end{array}, $$

where \( {\underset{\bar{\mkern6mu}}{p}}_A \) includes coordinates related to the response of internal degrees of freedom of component A, while \( {\underset{\bar{\mkern6mu}}{x}}_b \) includes the boundary points of component A with component B. Next, similar sets of equations of motion are obtained for component B. Namely, the equations of motion are first set up in the form

$$ {M}_B{\underset{\bar{\mkern6mu}}{\ddot{q}}}_B+{C}_B{\underset{\bar{\mkern6mu}}{\dot{q}}}_B+{K}_B{\underset{\bar{\mkern6mu}}{q}}_B={\underset{\bar{\mkern6mu}}{f}}_B(t), $$
(4.4)

with coordinates

$$ {\underset{\bar{\mkern6mu}}{q}}_B={\left(\begin{array}{cc}\hfill {\underset{\bar{\mkern6mu}}{p}}_B^T\hfill & \hfill {\underset{\bar{\mkern6mu}}{x}}_b^T\hfill \end{array}\right)}^T. $$

Then, a proper combination of Eqs. 4.3 and 4.4 leads to the equations of motion of the composite system in the classical form

$$ M\underset{\bar{\mkern6mu}}{\ddot{q}}+C\underset{\bar{\mkern6mu}}{\dot{q}}+K\underset{\bar{\mkern6mu}}{q}=\underset{\bar{\mkern6mu}}{f}(t), $$
(4.5)

with coordinates

$$ \underset{\bar{\mkern6mu}}{q}={\left(\begin{array}{ccc}\hfill {\underset{\bar{\mkern6mu}}{p}}_A^T\hfill & \hfill {\underset{\bar{\mkern6mu}}{p}}_B^T\hfill & \hfill {\underset{\bar{\mkern6mu}}{x}}_b^T\hfill \end{array}\right)}^T. $$

As usual, the stiffness matrix of the composite system can be obtained by considering the total potential energy of the system. Likewise, the mass matrix of the composite system is obtained by considering the corresponding kinetic energy, while the forcing vector is determined by considering the virtual work [1, 5].

4.3 Application to Laboratory Vehicle Model

In this section, the emphasis is placed on applying the methodology proposed to a laboratory vehicle model. First in Sect. 4.3.1 the study is purely numerical and the emphasis is placed in demonstrating and verifying the accuracy and validity of the methodology applied. Then, in Sect. 4.3.2, the method is applied and examined in the experimental device of the vehicle, using real measurements.

4.3.1 Numerical Application to a Small Scale Vehicle-Like Frame Structure

The accuracy and effectiveness of the methodology demonstrated by applying it to a complex mechanical system, shown in Fig. 4.1. Specifically, the example system is a laboratory structure, which was designed in order to simulate the frame structure of a vehicle in a small scale. Details of material and geometrical dimensions of the frame can be found in previous studies [14, 15]. In brief, the selected frame structure comprises a frame structure with predominantly linear response and high modal density plus four supporting systems with strongly nonlinear action. These supporting systems consist of a lower set of linear discrete spring-damper units, connected to a concentrated mass, simulating the wheel subsystems, as well as of an upper set of a nonlinear discrete spring-damper (bushings) units connected to the frame and simulating the action of the vehicle suspension. The measurement points, indicated by 1–4, correspond to connection points between the frame and its supporting structures, while the measurement points 5–7 shown were chosen on the frame.

Fig. 4.1
figure 1

(a) Experimental set up of the structure tested, (b) frame substructure nonlinear simulated supports and measurement locations

Full size image

Based on the geometric details and the material properties of the structure, a detailed finite element model of the vehicle frame was first created. This model was built using mainly quadrilateral shell and hexahedral solid elements. The final model of the frame consists of 45,564 DOF. The wheel subsystems were simulated with linear spring, damper and mass elements, while the suspension subsystems were simulated with nonlinear bushing elements. More specifically, the nonlinear restoring and damping forces in the suspensions were selected to have the following specific forms

$$ {f}_k={k}_sx+{\mu}_k{x}^3\kern0.5em \mathrm{and}\kern0.5em {f}_c={c}_s\dot{x}+{\mu}_c{\dot{x}}^3, $$
(4.6)

respectively, with \( x={x}_1-{x}_w \).

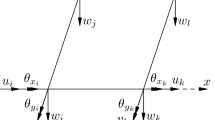
The basic idea of the applied methodology is to re-run the model by using the accelerations obtained at the boundary locations between the frame and the four supporting systems, as a base excitation to the frame, in order to calculate its dynamic response. More specifically, a nonlinear transient response analysis of the full vehicle model (frame and supports) was performed first, by applying four different transient displacement base excitation histories to the wheel subsystems in the vertical direction (Z). The model was then solved by using a numerical method belonging to the well-known class of Newmark’s methods (instead of performing experiments) and the acceleration histories at the selected locations 1–7 were calculated. The form of the applied excitation in the first wheel is presented in Fig. 4.2, while the “measured” histories of the acceleration at boundary location 1, in the three directions (X-longitudinal, Y-transverse, Z-vertical), are presented in Fig. 4.3.

Fig. 4.2
figure 2

Displacement history applied as base excitation in the vertical direction at first wheel

Full size image
Fig. 4.3
figure 3

Acceleration histories at boundary measurement location 1 in the: (a) X-longitudinal, (b) Y-transverse and (c) Z-vertical direction

Full size image

The “measured” acceleration histories at the boundary locations 1–4, in all three directions, were then used as base excitation to the frame of the vehicle. Next, the model for the frame was solved by performing a linear transient response analysis and the accelerations at the selected locations 1–7 were obtained. Results for the acceleration predictions obtained by this analysis are presented in Fig. 4.4 for the reference location 6 at the top of the vehicle frame, along the three directions. The predictions are compared with the simulated measurements of the full nonlinear model. In these figures, the results of the full nonlinear model are represented by the broken lines, while the results obtained for the linear substructure are represented by the black continuous lines. Again, direct comparison shows that the acceleration predictions are virtually the same as those obtained by the complete model.

Fig. 4.4
figure 4

Comparison of acceleration histories obtained at reference location 6 by the full nonlinear model (broken lines), the full linear model (continuous lines) and the reduced linear model (dotted lines) of the vehicle frame in the: (a) X-longitudinal, (b) Y-transverse and (c) Z-vertical direction

Full size image

Next, in order to check the accuracy of the coordinate reduction method presented in section 2, the same calculations were repeated with a model resulting by keeping only some of the lowest linear modes of the frame structure. It was found that by keeping modes with frequency up to about 500 Hz, leading to a new (reduced) model with only 50° of freedom, the results obtained were sufficiently accuracy. The corresponding results, shown in Fig. 4.4 by the dotted lines, are indistinguishable from those obtained by the full model.

4.3.2 Experimental Application to a Small Scale Vehicle-Like Frame Structure

Next the method applied and validated to the experimental device of the small scale vehicle which presented in Fig. 4.1a. More specifically, in the experimental process used the same setup with the numerical application (boundary and internal measurement locations), with one difference. We have in our disposal only one electromagnetic shaker and for this reason it is impossible to apply four different transient displacement base excitation histories to the wheel subsystems. Thus, the electromagnetic shaker placed in the location (E) which presented in Fig. 4.1b.

In this application, the acceleration time histories at the selected locations 1–7 were measured, by applying a force with the shaker in the vehicle frame. The measured acceleration histories at the boundary locations 1–4, in all three directions, were then used as base excitation to the FE model of the frame. This FE model was updated and validated, by applying a modal analysis procedure and Bayesian techniques in previous works [14, 16, 17]. Next, the model of the frame was solved by performing a linear transient response analysis and the accelerations at the selected locations 1–7 were obtained.

Results for the acceleration predictions obtained by this analysis are presented in Fig. 4.5 for the reference locations 5 and 6, in the vertical direction. More specifically in these figures presented results that corresponds to resonance region close to 3.4 Hz, which is dominated by local wheel body deflections. To achieve this, apply with the shaker a harmonic force with forcing frequency at 3.4 Hz. This case was selected because at this resonance region it is observed that is obtained a large uncertainty in the response spectra. The predictions are compared with the measurements of the full nonlinear model. In these figures, the experimental measurements of the full nonlinear model are represented by broken black line, while the results obtained for the linear substructure are represented by the red continuous lines. Direct comparison shows that the acceleration predictions are very close to the experimental measurements of the full nonlinear model.

Fig. 4.5
figure 5

Comparison of the experimental measurements of the full nonlinear model (broken black line) with the results obtained for the linear substructure (red continuous lines) of the vehicle frame at resonance frequency 3.4 Hz, in the: (a) location 5 and (b) location 6

Full size image

4.4 Experimental Application to a Real Vehicle

The vehicle superstructure examined is shown in Fig. 4.6. In this application, the superstructure consisted of two main substructures. The first part includes the main body of the platform, while the second part includes the spacer. Both of these parts are presented in Fig. 4.7a, b, respectively. The geometry of these structures was discretized mainly by rectangular and triangular shell finite elements. In addition, some other elements like solid (hexahedral), bar and rigid body elements were also used. The total number of degrees of freedom of the resulting model was about 520,000. Due to the large size of this model, the development and solution of the finite element model was completed by using appropriate commercial software [18, 19].

Fig. 4.6
figure 6

Vehicle superstructure and corresponding finite element model of its two substructures

Full size image
Fig. 4.7
figure 7

Schematic illustration of the measurement geometry: (a) main body and (b) spacer

Full size image

After development of the overall finite element model, including the coordinate reduction and synthesis part, an experimental modal analysis survey of the vehicle superstructure was performed to quantify its dynamic characteristics and verify the dynamic predictions of the model. The experimental modal analysis procedure was applied separately for the two parts. All the necessary elements of the FRF matrix required for determining the response of the two substructures were determined by imposing impulsive loading [15–17, 20–23]. A schematic illustration of the measurement geometry of the test structures is presented in Fig. 4.7a, b. Based on the measured FRFs, the natural frequencies and the damping ratios of the frame substructure were estimated by applying the “Rational Fraction Polynomial Method” (RFPM).

After testing the accuracy of the superstructure finite element model, the ultimate goal was the identification of those areas where the larger stresses appear for the given loading. To achieve this, triaxial accelerometers were placed initially at 18 selected positions. These positions with the measurement directions are presented in Fig. 4.8 and include the connection points of the superstructure with the chassis of the vehicle as well as some other characteristic positions of the superstructure.

Fig. 4.8
figure 8

Measurement locations of acceleration histories

Full size image

The measured acceleration histories corresponding to the biggest response amplitudes (worst case) were imported as a ground excitation in the finite element model of the superstructure. A reduction in the dimensions of the original system was also performed, so that the results are accurate in the frequency range 0–1,024 Hz. The total number of degrees of freedom of the reduced model was about 2,400, which is much smaller than the number of degrees of freedom of the original model. Then, the resulting model was solved numerically in order to calculate the maximum stresses developed. Figure 4.9, shows selected results, in which some indicative points of the superstructure with maximum stresses are presented.

Fig. 4.9
figure 9

Points of the superstructure where maximum stresses appear

Full size image

Finally, in order to test the reliability of the method applied, strain gauges were placed at 16 selected critical points of the superstructure and a new set of measurements was carried out under similar dynamic loading conditions, to experimentally verify the stress levels developed. Some of the experimental and numerical results are summarized in Table 4.1. In this table are presented the maximum values of the von Mises stress obtained for five selected tests (indicated by MT1–MT5) and for all the points where measurements were taken (denoted by S1–S16). More specifically, in the penultimate column are presented the maximum values of all tests, for each measurement location, while in the last columns are presented the corresponding maximum values obtained by the finite element model and their percentage difference. Finally, in an effort to further illustrate the accuracy of the results, in Fig. 4.10 is presented a comparison of experimentally measured (continuous lines) and numerically determined (broken lines) acceleration time histories at two indicative locations of the vehicle superstructure.

Table 4.1 Types of base changes
Full size table
Fig. 4.10
figure 10

Comparison of experimentally measured (continuous lines) and numerically determined (broken lines) accelerations at two locations

Full size image

4.5 Conclusions

In this work, presented a systematic methodology for determining the dynamic response and identifying the critical points of the superstructure of a large real vehicle, without knowing the dynamic characteristics of the vehicle supporting structure. The basic idea was to start the solution process by first discretizing geometrically the superstructure with the finite element method. The damping parameters of the resulting model were then updated through an experimental investigation of its dynamic response in a support-free state. Then, a series of experiments was performed in real operating conditions, aimed at recording the acceleration histories at the connection points of the superstructure with the vehicle chassis. Next, a component mode synthesis method was applied in order to eliminate a substantial number of degrees of freedom of the original model. The measured acceleration histories were subsequently used as a ground excitation for the reduced finite element model and the stresses developed under specific loading conditions were evaluated. From these numerical results, the critical points of the superstructure were selected, based on the level of the largest stresses. Finally, a new set of measurements was carried out in order to experimentally verify the stress levels developed. Before application to the real vehicle, the validity and reliability of the method was also verified numerically in two simpler example structures. In all cases, comparison of numerical and experimental results indicated that the methodology applied gives accurate results and provides a useful tool in predicting the critical stress levels developed in the vehicle superstructure under given loading conditions.