Keywords

14.1 Introduction

First appeared in the early 1950s, adaptive control has been a constant subject of research because of its important role in aeronautics and control of time parameter changing systems and processes [1]. A major fact involved on adaptive control is that the on-line system parameter identification, used for tuning proposes on the adaptive controllers, most of them have requirements and limitations such as the need of persistent excitation and slow convergence of the estimation. In other words, the adaptive control schemes have the natural handicap of the on-line identification methods proper characteristics and limitations [2–5].

On the other hand, active vibration control in structures involves a systematic set of issues such as specialized sensors, actuators, and, at the very first stages of its implementation, the need of an accurate understanding of the inherent dynamic characteristics of the structure by means of a mathematical model and, for these purposes, the modal model of the structure is very descriptive and useful when the final goal of the modeling process is to perform a response forecasting in the context of harmonic excitations [6, 12–16]. In [7] an on-line and time domain algebraic identification approach for the estimation of modal parameters on multiple degrees-of-freedom mechanical structures is proposed, this identification scheme implies the possibility of a fast and adaptive-like tuning of a specific controller.

In this paper, an algebraic on line time domain identification in conjunction with a Positive Position Feedback control scheme is evaluated on an experimental building-like structure for reducing the overall system response resulted from ground excitation. The resulting adaptive-like control scheme consists of identification of the characteristic polynomial of the overall structure, considering that one of the outputs is available for the implementation of the parameter estimation scheme. The identification of the ground excitation forces is then possible by using the identified parameters.

14.2 Three Story Building-Like Structure

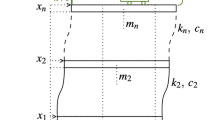
The experimental setup consists on a three story building like structure as shown in Fig. 14.1, which consists of three aluminum alloy plates coupled by two flexible aluminum columns. Here x i , i = 1, 2, 3, are the displacements of three masses representing the floors or Degrees-Of-Freedom (DOF) of the structure, respectively. The columns are modeled as flexural springs with equivalent stiffness k i and the structural damping ratios c i are considered as proportional or Rayleigh damping [8, 9]. The structure is mounted over a frictionless bearing rail such that the ground excitation motion on the x axis is performed by an electromagnetic shaker Labworks®, model ET-139, which moves the overall structure for both, experimental modal analysis purposes and ground excitation forces for the performance evaluation of vibration control schemes.

Fig. 14.1
figure 1

Three story building-like structure with PZT stack actuator. (a) Schematic diagram. (b) Experimental setup

Full size image

The simplified mathematical model of this flexible mechanical system of 3 DOF under harmonic excitation f is given by the ordinary differential equation

$$ M\ddot{x}+C\dot{x}+Kx=f(t)+{B}_f{u}_{pzt}(t),\kern1em {B}_f,x,f\in {R}^3,\kern0.5em {u}_{pzt}\in R $$
(14.1)

where \( x\ \in {R}^3 \) is the vector of generalized coordinates (displacements) of each floor respect to the main frame reference, u pzt is the voltage control input applied to the PZT stack actuator. Moreover, \( {f}_{pzt}(t)={B}_f{u}_{pzt}(t) \) represents the control force to be used for active vibration control of the overall building-like structure. In addition, B f is the input matrix, and M, C and K are symmetric inertia, damping and stiffness \( n\times n \) matrices, respectively, given by

$$ M=\left[\begin{array}{c@{\quad}c@{\quad}c} {m}_1 & 0 & 0 \\ 0 & {m}_2 & 0 \\ 0 & 0 & {m}_3 \end{array}\right],\kern1.5em C=\left[\begin{array}{c@{\quad}c@{\quad}c} {c}_1+{c}_2 & -{c}_2 & 0 \\ -{c}_2 & {c}_2+{c}_3 & -{c}_3 \\ 0 & -{c}_3 & {c}_3 \end{array}\right], \kern1.25em K=\left[\begin{array}{c@{\quad}c@{\quad}c} {k}_1+{k}_2 & -{k}_2 & 0 \\ -{k}_2 & {k}_2+{k}_3 & -{k}_3 \\ 0 & -{k}_3 & {k}_3 \end{array}\right] $$
(14.2)

It is easy to verify that system (14.1) is completely controllable and observable, as long as K is positive definite and \( C\equiv 0 \), and asymptotically stable when C is positive definite (see, e.g., Inman [10]). It is important to take into consideration that the harmonic excitation by the ground (base) motion \( z(t)= Zsin\left({\omega}_0t\right) \), provides the force f as defined in expression (14.1) (see [20]), hence f is given by:

$$ f(t)=- Me\ddot{z}(t) $$
(14.3)

Here \( e={\left[1,1,1\right]}^T\in {R}^3 \) is used to describe the displacements of each mass due to the ground acceleration \( \ddot{z}(t) \) thus, each component of the excitation input vector f i is given by:

$$ {f}_i=-{m}_i\ddot{z}(t)=-{m}_i\frac{d^2\left(Z \sin \left({\omega}_0t\right)\right)}{d{t}^2}={m}_i{\omega}_0^2Z \sin \left({\omega}_0t\right),\kern3em i=1,2,3 $$
(14.4)

where ω o and Z are the excitation frequency and amplitude of the ground motion, respectively. It is well-known that, the mathematical model (14.1) (considering at first that \( {u}_{pzt}(t)\equiv \) 0) can be transformed to modal (principal) coordinates q i , i = 1, 2, ⋯, n, as follows (see, e.g., [6])

$$ {\ddot{q}}_i+2{\zeta}_i{\omega}_i{\dot{q}}_i+{\omega}_i^2{q}_i={\Psi}^Tf $$
(14.5)

with

$$ x(t)=\Psi q(t) $$
(14.6)

where ω i and ξ i denote the natural frequencies and damping ratios associated to the i-th vibration mode, respectively, and Ψ is the so-called \( 3\times 3 \) modal matrix given by

$$ \Psi =\left[\begin{array}{c@{\quad}c@{\quad}c} {\psi}_{11} & {\psi}_{12} & {\psi}_{13} \\ {\psi}_{21} & {\psi}_{22} & {\psi}_{23} \\ {\psi}_{31} & {\psi}_{32} & {\psi}_{33} \end{array}\right] $$
(14.7)

Therefore, the modal analysis representation of the vibrating mechanical system (14.1) is expressed by

$$ {\ddot{q}}_i+2{\xi}_i{\omega}_i{\dot{q}}_i+{\omega}_i^2{q}_i={\psi}_{1i}{f}_1+{\psi}_{2i}{f}_2+{\psi}_{3i}{f}_3 $$
(14.8)

In notation of Mikusiński operational calculus [17, 18], this modal model is then described as

$$ \left({s}^2+2{\xi}_i{\omega}_is+{\omega}_i^2\right){q}_i(s)={\psi}_{1i}{f}_1(s)+{\psi}_{2i}{f}_2(s)+{\psi}_{3i}{f}_3(s)+{p}_{o,i}+{p}_{1,i}s $$
(14.9)
$$ {q}_i(s)=\frac{\psi_{1i}{f}_1(s)+{\psi}_{2i}{f}_2(s)+{\psi}_{3i}{f}_3(s)+{p}_{o,i}+{p}_{1,i}s}{\left({s}^2+2{\xi}_i{\omega}_is+{\omega}_i^2\right)} $$
(14.10)

where p o,i are constants depending on the system initial conditions at the time \( {t}_0\ \ge\ 0 \). From (14.4) and (14.7), one then obtains that

$$ {x}_i(s)={\displaystyle \sum_{j=1}^3}\frac{\psi_{ij}{\psi}_{ji}{f}_j(s) + {\psi}_{ij}\left({p}_{o,i}+{p}_{1,i}s\ \right)}{\left({s}^2+2{\xi}_j{\omega}_js+{\omega}_j^2\right)} $$
(14.11)

Therefore, the physical displacements x i are given by

$$ {p}_c(s){x}_i(s)={\displaystyle \sum_{k=1}^3}\left[\displaystyle \sum_{j=0}^4\left[\left({\beta}_{ji}{s}^j{f}_k(s)\right.\right]\right] +{r}_{0i}+{r}_{1i}s+{r}_{2i}{s}^2+{r}_{3i}{s}^3+{r}_{4i}{s}^4+{r}_{5i}{s}^5 $$
(14.12)

with

$$ {p}_c(s)={s}^6+{a}_5{s}^5+{a}_4{s}^4+{a}_3{s}^3+{a}_2{s}^2+{a}_1s+{a}_0 $$
(14.13)

where p c (s) is the characteristic polynomial of the mechanical system, r ij are constants which depend on the initial conditions of the system as well as the modal matrix components ψ ij and the constants β ji depend on the modal matrix components ψ ij and the roots of the p c (s). The roots of the characteristic polynomial (14.10) provide the damping factors and damped natural frequencies and, hence, the natural frequencies and damping ratios of the flexible structure.

14.3 On-Line Algebraic Identification of the Harmonic Excitation

Consider the mathematical model (14.8), where only measurements of some position variable x i is available to be used in the synthesis of the on-line algebraic identification scheme for the estimation of the coefficients a k as reported in [1]. We consider, at first, that \( {f}_k(t)\equiv 0 \) and the system has a change in its initial conditions, for identifying the characteristic polynomial of the system. Now, consider the mathematical model (14.9), where the coefficients a k have been estimated as described before, if the ground acceleration produces the forces f k and we consider them as harmonic and sinusoidal, we have, in terms of operational calculus

$$ {f}_k(s)={m}_k{\omega}_0^2Z\frac{\omega_0^2}{s^2+{\omega}_0^2} $$
(14.14)

Note that the frequency ω 0 and the amplitude Z are the same for each component of the input force vector, therefore substituting (14.11) in (14.9) one obtains:

$$ {p}_c(s){x}_i(s)=\frac{B_t(s)Z{\omega}_0^2}{s^2+{\omega}_0^2}+{r}_{0i}+{r}_{1i}s+{r}_{2i}{s}^2+{r}_{3i}{s}^3+{r}_{4i}{s}^4+{r}_{5i}{s}^5 $$
(14.15)

where \( {B}_t(s)={\beta}_4{s}^4+{\beta}_3{s}^3+{\beta}_2{s}^2+{\beta}_1s+{\beta}_1 \) is a polynomial which coefficients depend on the mass of each floor and the modal matrix components. By multiplying (14.15) by \( \left({s}^2+{\omega}_0^2\right) \) is obtained:

$$ \left({s}^2+{\omega}_0^2\right)\ {p}_c(s){x}_i(s)={B}_t(s)Z{\omega}_0^2+\left({s}^2+{\omega}_0^2\right)\ \left({r}_{0i}+{r}_{1i}s+{r}_{2i}{s}^2+{r}_{3i}{s}^3+{r}_{4i}{s}^4+{r}_{5i}{s}^5\right) $$
(14.16)
$$ \left({s}^8+{\widehat{a}}_5{s}^7+{\widehat{a}}_4{s}^6+{\widehat{a}}_3{s}^5+{\widehat{a}}_2{s}^4+{\widehat{a}}_1{s}^3+{\widehat{a}}_0{s}^2\right){x}_i(s)=-{\omega}_0^2{p}_c(s)+\Gamma (s) $$
(14.17)

with \( \Gamma (s)={\uplambda}_0+{\uplambda}_1{s}^2+{\uplambda}_2{s}^3+{\uplambda}_3{s}^4+{\uplambda}_4{s}^5+{\uplambda}_5{s}^6+{\uplambda}_6{s}^7 \). To eliminate the influence of the constants λ k , the Eq. (14.17) is derived eight times with respect to the complex variable s, the result is multiplied by \( {s}^{-8} \) and transformed back to the time domain resulting in

$$ N(t)={\omega}_0^2D(t) $$
(14.18)

where

$$ \begin{array}{l}N(t)={\displaystyle \sum_{k=0}^8}{\left(-1\right)}^{8-k}\frac{(8)!(8)!}{k!\left(8-k\right)!\left(8-k\right)!}{\displaystyle \underset{t_0}{\overset{(k)}{\int }}}{\left(\Delta t\right)}^{8-k}{x}_i(t)+{\widehat{a}}_5{\displaystyle \sum_{k=0}^7}{\left(-1\right)}^{8-k}\frac{(8)!(7)!}{k!\left(8-k\right)!\left(8-1-k\right)!}{\displaystyle \underset{t_0}{\overset{\left(k+1\right)}{\int }}}{\left(\Delta t\right)}^{8-k}{x}_i(t)+\\ {\widehat{a}}_4{\displaystyle \sum_{k=0}^6}{\left(-1\right)}^{8-k}\frac{(8)!(6)!}{k!\left(8-k\right)!\left(8-2-k\right)!}{\displaystyle \underset{t_0}{\overset{\left(k+2\right)}{\int }}}{\left(\Delta t\right)}^{8-k}{x}_i(t)+\dots +{\widehat{a}}_1{\displaystyle \sum_{k=0}^1}{\left(-1\right)}^{8-k}\frac{(8)!}{k!\left(8-k\right)!\left(1-k\right)!}{\displaystyle \underset{t_0}{\overset{(k)}{\int }}}{\left(\Delta t\right)}^{8-k}{x}_i(t)+{\widehat{a}}_0{\displaystyle \underset{t_0}{\overset{(8)}{\int }}}{\left(\Delta t\right)}^8{x}_i(t)\end{array} $$
(14.19)
$$ \begin{array}{l}D(t)={\displaystyle \sum_{k=0}^6}{\left(-1\right)}^{6-k}\frac{(8)!(6)!}{k!\left(8-k\right)!\left(8-2-k\right)!}{\displaystyle \underset{t_0}{\overset{(k)}{\int }}}{\left(\Delta t\right)}^{6-k}{x}_i(t)+{\widehat{a}}_5{\displaystyle \sum_{k=0}^5}{\left(-1\right)}^{6-k}\frac{(8)!(5)!}{k!\left(8-k\right)!\left(8-1-k\right)!}{\displaystyle \underset{t_0}{\overset{\left(k+1\right)}{\int }}}{\left(\Delta t\right)}^{6-k}{x}_i(t)\\ +{\widehat{a}}_4{\displaystyle \sum_{k=0}^6}{\left(-1\right)}^{8-k}\frac{(8)!(4)!}{k!\left(8-k\right)!\left(8-2-k\right)!}{\displaystyle \underset{t_0}{\overset{\left(k+2\right)}{\int }}}{\left(\Delta t\right)}^{6-k}{x}_i(t)+\dots +{\widehat{a}}_1{\displaystyle \sum_{k=0}^1}{\left(-1\right)}^{6-k}\frac{(8)!}{k!\left(8-k\right)!\left(8-k\right)!}{\displaystyle \underset{t_0}{\overset{(k)}{\int }}}{\left(\Delta t\right)}^{6-k}{x}_i(t)+{\widehat{a}}_0{\displaystyle \underset{t_0}{\overset{(8)}{\int }}}{\left(\Delta t\right)}^6{x}_i(t)\end{array} $$
(14.20)

where \( \Delta t=t-{t}_0 \) and \( {\displaystyle \underset{t_0}{\overset{(N)}{\int }}}\phi (t) \) are iterated integrals of the form \( {\displaystyle \underset{t_0}{\overset{t}{\int }}}{\displaystyle \underset{t_0}{\overset{\sigma_1}{\int }}}\dots {\displaystyle \underset{t_0}{\overset{\sigma_{N-1}}{\int }}}\phi \left({\sigma}_N\right)d{\sigma}_N\cdots d{\sigma}_1 \) with \( {\displaystyle \underset{t_0}{\overset{(1)}{\int }}}\phi (t)={\displaystyle \underset{t_0}{\overset{(t)}{\int }}}\phi \left(\sigma \right)d\sigma, \kern0.75em {\displaystyle \underset{t_0}{\overset{(0)}{\int }}}\phi (t)=\phi (t) \), and N a positive integer. Due to the fact that \( {\omega}_0^2>0 \) we have that

$$ \left|D(t)\right|{\omega}_0^2=\left|N(t)\right| $$
(14.21)

Thus, we can get an expression for estimating the excitation frequency ω 0. To avoid singularities and, at the same time getting smoother behavior for the estimation the Eq. (14.20) is integrated twice with respect to the time

$$ {\widehat{\omega}}_0=\sqrt{\frac{n_i}{d_i}},\kern3em t>{t}_0 $$
(14.22)

where

$$ {n}_i={\displaystyle \underset{t_0}{\overset{(2)}{\int }}}\left|{N}_1\right|,\kern1.5em {d}_i={\displaystyle \underset{t_0}{\overset{(2)}{\int }}}\left|{D}_1\right|, \kern1.75em t>{t}_0 $$
(14.23)

Note that, it is possible to identify the excitation frequency using any of the outputs x i obtaining a similar result. Moreover, the estimation of the excitation frequency \( {\widehat{\omega}}_0 \) is independent on the amplitude Z and the system initial conditions.

14.4 An Adaptive-Like Positive Position Feedback Control Scheme

The final goal of implementing a vibration control scheme is to minimize the undesired overall movement in presence of harmonic excitation of some degree of freedom of the structure or, in the best case, all of them. The positive position feedback control scheme is a well-known dynamic output feedback controller as a modal control method for vibration attenuation [9, 20]. This control scheme adds an additional degree-of-freedom to the original system considered as a virtual passive absorber, that is, a second order low pass filter. In order to make clear how the PPF controller works, one considers the simplified model of the three story building-like structure (14.1) perturbed by ground motion. Here the PZT stack actuator is placed between the base and the first level of the structure, so that, this actuates directly over the first floor dynamics, however, the output variable to be used for active vibration control is the displacement of the third floor as shown in Fig. 14.2.

Fig. 14.2
figure 2

Block diagram of an adaptive-like PPF vibration absorption scheme

Full size image

The position or displacement of the third floor is positively feed to the virtual passive absorber, and the position of the compensator in this case, the PZT actuator is positively feedback to the building-like structure. In our particular case the output variable to be used for identification of the system parameters and active vibration control purposes is the displacement of the third floor x 3, whereas the control effort is produced by the PZT stack actuator attached to the first lower lateral column, therefore, this particular vibration control problem corresponds to a non-collocated sensor and actuator case [9, 20]. Taking into consideration that the excitation frequency ω 0 is identified by using the algebraic identifier (14.24) and, afterwards, this estimation is used to tune a PPF controller to minimize/attenuate this undesired perturbation, then we get that

$$ \begin{array}{c}M\ddot{x}+C\dot{x}+Kx=f(t)+{B}_f{u}_{pzt}(t),\kern2.5em x,f\in {R}^3,{u}_{pzt}\in R\\ \ddot{\eta}+2{\xi}_f{\widehat{\omega}}_0\dot{\eta}+{\omega}_f^2=g{\widehat{\omega}}_0^2{B}_0^Tx,\kern5.25em \eta \in R\\ {u}_{pzt}=g{\omega}_0^2\eta\ \end{array} $$
(14.24)

Because \( {B}_0 = \left[1\ 0\ 0\right] \) the output variable for control is x 3, which couples the virtual passive absorber by the terms \( g{{\widehat{\omega}}^2}_0{B}_0^T \) and \( g{{\widehat{\omega}}^2}_0\eta \), where g is a design control gain. The virtual passive absorber has relative damping ξ f and natural frequency ω f . The overall closed-loop system is described, in compact form, as follows

$$ \left[\begin{array}{c@{\quad}c} M & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} \ddot{x} \\ \ddot{\eta} \end{array}\right]+\left[\begin{array}{c@{\quad}c} C & 0 \\ 0 & 2{\zeta}_f{\widehat{\omega}}_0 \end{array}\right]\left[\begin{array}{c} \dot{x} \\ \dot{\eta} \end{array}\right]+\left[\begin{array}{c@{\quad}c} K & -{B}_fg{{\widehat{\omega}}^2}_0 \\ -g{B}_0^T{{\widehat{\omega}}^2}_0 & {{\widehat{\omega}}^2}_0 \end{array}\right]\left[\begin{array}{c} x \\ \eta \end{array}\right]=\left[\begin{array}{c} f \\ 0 \end{array}\right] $$
(14.25)

Due to the fact that the mass matrix M is symmetric and positive definite, the overall mass matrix in (14.25) is also symmetric and positive definite, besides, the proportional damping matrix C is also symmetric and positive definite and, as a consequence, the overall damping matrix C in (14.25) has similar properties. Even though the stiffness matrix K is symmetric and positive definite in the above closed loop system, the sensor and actuator are not collocated (i.e., \( {B}_f\ne {B}_0 \)). Therefore, it is necessary to select an appropriate gain g value and a fast and stable estimation of the frequency \( {\widehat{\omega}}_0 \) to guarantee the closed-loop asymptotic stability, that is, it is necessary that the matrix

$$ {\widehat{K}}_{CL}=\left[\begin{array}{c@{\quad}c} K & -{B}_fg{{\widehat{\omega}}^2}_0 \\ -g{B}_0^T{{\widehat{\omega}}^2}_0 & {{\widehat{\omega}}^2}_0 \end{array}\right] $$
(14.26)

be positive definite [9]. Thus, in presence of (bounded) ground motion, the dynamic system response will asymptotically converge to a bounded steady-state response.

Now, for experimental validation, consider that the building like structure shown in Fig. 14.1 is excited by harmonic ground acceleration with frequency ω 0 resulting in undesired vibrations, specially in the third floor. The experimental results for validating the closed loop performance of the PPF controller and the algebraic identifiers for the on line estimation of the characteristic polynomial and the excitation frequency are shown in Fig. 14.2. The excitation was a ground sinusoidal acceleration of approximately \( {Z}_0 = 1.8\ g \) excitation with frequency \( {\omega}_0=9\ Hz \), whereas the design parameters for the PPF controller are \( {\xi}_f=0.25 \) and \( g=1.8 \) the natural frequency of the passive absorber is selected as \( {\omega}_f={\widehat{\omega}}_0 \), using the algebraic identifier (14.24).

Figure 14.3 shows the identification and vibration absorption sequence, first, the system’s characteristic polynomial coefficients are fast and effectively estimated in a period of \( {T}_0=0.2\ s \) as shown in Fig. 14.3a. After that, these coefficients are used in the identifier (14.24) for estimating the excitation frequency, although the excitation frequency is ready after a short period of time as small as 1.3 s, the controller is activated after 5 s to guarantee the convergence and stabilization of the estimation with the possibility for this delay to be reduced. Here we achieve a strong attenuation of 40 % with small control efforts considering that we use a piezostack actuator also shown in Fig. 14.3b. Note that, it is possible to use the presented adaptive-like PPF vibration absorption scheme in pre-compensated control approaches, where the control strategy is strongly related to cancel undesired harmonic excitations and the on line estimation of amplitude and phase of the perturbation is required (see [11]).

Fig. 14.3
figure 3

On-line algebraic identification of the characteristic polynomial coefficients of the three story building-like structure

Full size image

14.5 A Multi Positive Position Feedback Control Approach

If we consider that the building-like structure has dominant vibration modes, even though this flexible structure is a distributed parameters system, we can make a natural extension of the PPF control scheme. For experimental modal analysis purposes, we perform a sinusoidal sweep on the building-like structure in an interest bandwidth. The experimental FRF is shown in Fig. 14.4. Three dominant modes are shown by means of acceleration measurements on the third floor.

Fig. 14.4
figure 4

Experimental FRF computed from a sine sweep from 0.1 to 60 Hz

Full size image

The multi-PPF control scheme consists of the simultaneous attenuation of vibration modes [9], in our particular case, and as we can observe in Fig. 14.4, we are interested in attenuate three main or dominant vibration modes, corresponding to \( {\omega}_{n1}=8.89\ Hz,\ {\omega}_{n1}=28.19\ Hz \) and \( {\omega}_{n3}=38.34\ Hz \). Here, we estimate the three natural frequencies of the building-like structure as exposed in [1] and then, the Multi-PPF controller is tuned to perform the multi mode attenuation. In matrix form we have

$$ \left[\begin{array}{c@{\quad}c} M & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} \ddot{x} \\ \ddot{\eta} \end{array}\right]+\left[\begin{array}{c@{\quad}c} C & 0 \\ 0 & 2{Z}_f\widehat{W} \end{array}\right]\left[\begin{array}{c} \dot{x} \\ \dot{\eta} \end{array}\right]+\left[\begin{array}{c@{\quad}c} K & -{B}_fG{\widehat{W}}^2 \\ -G{B}^T{\widehat{W}}^2 & {\widehat{W}}^2 \end{array}\right]\left[\begin{array}{c} x \\ \eta \end{array}\right]=\left[\begin{array}{c} f \\ 0 \end{array}\right] $$
(14.27)

where \( {\mathrm{Z}}_f\in {R}^{3\times 3} \) is the design diagonal damping matrix. In this case, the three virtual absorbers are coupled to the primary system (14.1) by the positive injection term GŴ 2 B T x where G is the diagonal design gain matrix. Finally, Ŵ is a diagonal matrix containing the three estimated natural frequencies to tune the Multi-PPF control scheme. Once again, to guarantee closed-loop stability the matrix

$$ {K}_{MPPF}=\left[\begin{array}{c@{\quad}c} K & -{B}_fG{\widehat{W}}^2 \\ -G{B}^T{\widehat{W}}^2 & {\widehat{W}}^2 \end{array}\right] $$
(14.28)

must be positive definite, which is achieved by selecting the appropriate values of the gains in matrix G, and the correct and fast convergence of the estimations in the estimated frequency matrix \( \widehat{W} \).

Some experiments were performed on the experimental setup to validate the performance of the natural frequency identification considering that the system is firstly excited only by an initial conditions change. The fast and effective estimations are shown in Fig. 14.5. With these parameters we implement the Multi-PPF vibration absorption scheme and validate the closed-loop system performance by applying a sinusoidal sweep in order to make visually clear the attenuation of the undesired vibrations on the third floor, as shown in Fig. 14.6. Here, the MPPF control parameters were selected as \( {g}_1=1.8,\kern0.5em {g}_1=0.12,\kern0.5em {g}_3=0.5 \), \( {\xi}_{f1}=0.15,\kern0.5em {\xi}_{f2}=0.12,\kern0.5em {\xi}_{f3}=0.15 \) and the three natural frequencies equal to the on-line estimations as \( {\omega}_1={\widehat{\omega}}_{n1},{\omega}_2={\widehat{\omega}}_{n2} \) and \( {\omega}_3={\widehat{\omega}}_{n3} \). Note how the first lateral mode is attenuated about 50 % with respect to the open-loop response, employing small control efforts.

Fig. 14.5
figure 5

Free vibration response of the third floor x 3 and on-line algebraic estimation of natural frequencies

Full size image
Fig. 14.6
figure 6

Closed-loop system performance with adaptive like multi-PPF control scheme

Full size image

14.6 Conclusions

It is proposed an adaptive-like vibration absorption scheme by using a time domain algebraic identification approach for on-line estimation of the harmonic ground excitation and natural frequencies for a multiple degrees-of-freedom mechanical system. The values of the coefficients of the characteristic polynomial of the mechanical system are firstly estimated in real-time, and then it is possible to estimate the excitation frequency. In the design process, for both, identification and control implementations, it is considered that only measurements of some position output variable are available for the identification scheme. However, the identification and control can be implemented using acceleration measurements. In general, the simulation and experimental results show a satisfactory performance of the proposed identification approach with fast and effective estimations and good attenuation properties using the adaptive-like vibration controller on the first vibration mode.