Keywords

7.1 Introduction

The interest in human-structure interaction (HSI) has increased during the last two decades due to the number of reports of structures with vibration problems due to crowds. During the design process it is common to model the human loads as static force depending only on the mass of the occupants [1]. However, this does not correctly represent the interaction between humans and structure.

The effects of human loads in structures are difficult to predict because they depend on the type of activity people are performing. However, models for typical activities such as standing, sitting, and jumping have been proposed in the literature. Traditional models represent the human body as a system of lumped masses, dampers and springs when people do not jump [2–6]. Arguably, these models might not fully represent the human body because lumped masses, dampers and springs cannot add energy to the overall system. Furthermore, people could react differently at different levels of excitation and other environmental conditions.

Ortiz et al. [7] proposed a new type of model for human-structure interaction. The new model uses a close loop control from systems theory. This model is able to add energy to the system, and could be a more representative way to model the human in HSI problems. The controller parameters could change depending on the characteristics of the human body and how it reacts to the changing environments [8]. Although control theory concepts have been applied to structural engineering, closed loop control systems have not been widely studied for HSI problems [9–12].

This paper compares HSI models using a closed loop control system with the traditional models based on lumped masses, dampers and springs (MDS) systems. The control theory based models are a Proportional and Derivative controller (PD), and a Proportional, Integrative and Derivative controller (PID). These controllers use information about the present, past and future errors (in case of PID), or present and future errors (if PD is used), calculated as the difference between the real and desired value. MDS systems are modeled using the human body as a single and two degree of freedom systems [2]. All models have been developed for a single occupant in a standing position with straight knees. The structure is modeled as a single degree of freedom system.

The paper is organized as follows. Section 7.2 gives an overview of the models and the model updating process to estimate the model parameters. The description of the tests as well as the method to compare the performance of each model are discussed in Sect. 7.3. In Sect. 7.4, tests results are compared with experimental tests. Finally, some conclusions about the similarities and constraints of these models is discussed. All work was carried out in accordance with the Code of Ethics of the World Medical Association [13].

7.2 Background

7.2.1 HSI Modelling

The dynamic behavior of structures occupied by humans has been widely studied in recent years. A literature review published by Zivanovic et al. [9] indicates that there are two different types of models for the human body. The first, and more general, are called mass models. These models only use the mass of the human and do not model any HSI. The second type are based on mass-damper-stiffness (MDS) systems, which are likely used in problems related to human-structure interaction. Many authors have developed MDS models ranging from single degree of freedom to multiple degree of freedom models in order to represent the dynamics of the human body [2, 5, 14–17].

7.2.2 Mass-Spring-Damper (MDS) Models

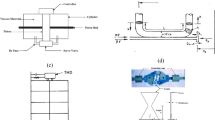
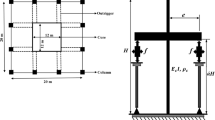
Many authors have proposed MDS models for modeling the human body. The mechanical representation of the models considered on this paper are given in Fig. 7.1.

Fig. 7.1
figure 1

Single and two degree of freedom models commonly used for modeling human dynamics

Full size image

The SDOF model was proposed by Matsumoto and Griffin [2], Falati [14], Brownjohn [16] in a deterministic fashion. The model parameters are described by single values of mass (m 1), stiffness (k 1) and damping constant (c 1). Equation (7.1) shows the response of the system for an excitation p(t).

$$\displaystyle{ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = p(t) }$$
(7.1)

The equation describing the dynamics of a 2DOF is the same (Eq. 7.1) but the terms are replaced by matrices of mass, damping and stiffness (Eq. 7.2), and a vector of forces for each degree of freedom:

$$\displaystyle{ M = \left [\begin{array}{*{10}c} m_{1} & 0 \\ 0 &m_{2} \end{array} \right ], C = \left [\begin{array}{*{10}c} c_{1} + c_{2} & -c_{2} \\ -c_{2} & c_{2} \end{array} \right ], K = \left [\begin{array}{*{10}c} k_{1} + k_{2} & -k_{2} \\ -k_{2} & k_{2} \end{array} \right ] }$$
(7.2)

7.2.3 Controller Models

The controller system for modeling the human structure interaction follows two concepts: (i) the human does not have constant parameters of stiffness and damping and, (ii) these values depend on the interaction with the structure. The term closed-loop control always implies the use of feedback control action in order to reduce the system error. Figure 7.2 shows the block diagram of a close loop control system where G(s) is the structural system and H(s) is the controller. The terms R(s) and C(s) represent the forces acting on the structure and outputs of the system. B(s) is the force used to control the structure.

Fig. 7.2
figure 2

Block diagram of a closed loop control system

Full size image

The transfer function TF(s) for a closed loop control system as shown in Fig. 7.2 is defined as (Eq. 7.3):

$$\displaystyle{ TF(s) = \frac{G(s)} {1 + G(s)H(s)} }$$
(7.3)

Where the terms G(s) and H(s) are the mathematical representations of the structure and the transfer function of the controller in the Laplace domain. For simplicity the structure G(s) is modeled as a single degree of freedom (SDOF) system, even though modeling errors are expected. The values of mass and stiffness of the SDOF are expected to be different than the actual mass and stiffness of the structure due to these modeling errors. For a single degree of freedom, the term G(s) is defined as (Eq. 7.4):

$$\displaystyle{ G(s) = \frac{ \frac{1} {m}} {s^{2} + \frac{c} {m}s + \frac{k} {m}} }$$
(7.4)

The transfer function of H(s) depends on the controller. In this paper, the common PID (Proportional, Integrative and Derivative) and PD (Proportional and Derivative) are used, then the transfer function for the PID is (Eq. 7.5):

$$\displaystyle{ H(s) = K_{p}(1 + T_{d}s + \frac{1} {T_{i}s}) }$$
(7.5)

Where K p , T d and T i are the proportional, derivative and integrative terms of the controller. For a PD controller the transfer function can be represented as (Eq. 7.6):

$$\displaystyle{ H(s) = K_{p}(1 + T_{d}s) }$$
(7.6)

7.2.4 Model Updating

The dynamic behavior of mechanical and controller systems presented in the previous section depends on parameters that can be updated. In this paper Bayesian inference is used to update the parameters of the models based on experimental data [18, 19]. Bayes inference is based on the use of conditional probability (Eq. 7.7):

$$\displaystyle{ P(\Theta \vert D) \propto P(D\vert \Theta )P(\Theta ) }$$
(7.7)

Where \(P(\Theta \vert D)\) is the posterior probability density functions (PDF) of the parameters \(\Theta \) given the observation D. \(P(\Theta )\) is the prior PDF of the parameters θ and it represents the knowledge that we have about the parameters before updating. \(P(D\vert \Theta )\) is the likelihood of the occurrence of the measurement D given the vector of parameters \(\Theta \).

The process is performed in two steps. First, the parameters of the structure (\(\Theta _{e} = k_{s},c_{s},m_{s}\)) are estimated using experimental data of the empty condition. Then, the parameters of the system created by the human and the structure are estimated using data from the occupied structure (\(\Theta _{o}\)). Table 7.1 shows the variables to update for each of the models presented in the previous section.

The information gained in the first model for the empty condition is then used as prior information for the human-structure interaction models. Therefore the parameters of the structure are updated using

$$\displaystyle{ P(\Theta _{e}\vert D_{e}) \propto P(D_{e}\vert \Theta _{e})P(\Theta _{e}) }$$
(7.8)

And the parameters of the structure and the HSI models are estimated using

$$\displaystyle{ P(\Theta _{o}\vert D_{e},D_{o}) \propto P(D_{o}\vert \Theta _{o})P(\Theta _{e}\vert D_{e})P(\Theta _{h}) }$$
(7.9)

Where \(\Theta _{h}\) are the prior of the variables used by HSI models showed by the Table 7.1. The previous equation indicates that our prior considers that the parameters of the structure are not dependent on the parameters of the HSI models. This is \(P(\Theta _{o}) = P(\Theta _{h})P(\Theta _{e}\vert D_{e})\).

Table 7.1 Variables used for each model
Full size table

The prior distributions for the structural parameters (k s , m s , and c s ) are defined based on the measurements of the structure. The prior PDF for the mass (m s ) is considered as a Normal distribution with mean 330 kg and a standard deviation of 30 kg. A non-informative distribution is used as prior for k s . The prior information for the damping coefficient (c s ) is estimated based on a free vibration test of the structure. A damping ratio of ζ = 0. 2 % is estimated. Therefore the prior PDF for c is P(c) = N(31, 3. 1). The prior PDFs assume that the parameters are not dependent. However, as shown in the results, Bayes inference allows us to find dependencies between parameters.

Experimental data is taken in two steps. First, data of the empty structure is obtained and the experimental transfer functions of the empty structure (D e ) are estimated. Then, the process is repeated for the structure with a person standing, which obtains the occupied experimental transfer function D o . Experimental transfer functions are estimated using impact hammer tests. An accelerometer is placed in the middle of the span close to the location where the person stands. More information about the experimental setup is discussed in the following section. The estimation of the transfer function is performed using (Eq. 7.10)

$$\displaystyle{ \widehat{TF} = \frac{P_{xy}(f)} {P_{xx}(f)} }$$
(7.10)

Where P xy is the cross power spectral density between the acceleration of the structure and the force of the hammer, and P xx is the auto power spectral density of the force of the hammer.

The likelihood is defined as a Gaussian distribution to maximize entropy. For example, for the empty structure, the likelihood is expressed by the equation

$$\displaystyle{ P(D_{e}\vert \Theta _{e}) =\prod \limits _{ i=1}^{n} \frac{1} {\sqrt{2\pi }\sigma _{TF_{e}}}e^{\left (-\frac{1} {2} \frac{TF_{e,i}-\widehat{TF}_{e,i}} {\sigma _{TF_{e}}} \right )} }$$
(7.11)

where n is the total number of points of the Transfer Function (TF e ). TF and \(\widehat{TF}\) represent the Transfer function using the Analytical and Experimental approach respectively.

7.3 Experimental Setup

The structure was specifically designed to represent flexible conditions similar to slabs with vibration problems and inspired on an existing structure built at Bucknell University [15]. Experimental tests for empty and occupied conditions were performed using impact hammer testing. The ratio between live and dead load was close to 0.2, similar to those used in service structures. The tests for occupied conditions consist of a single human standing with straight knees. Similar tests could be found in Matsumoto and Griffin [2], Salyards and Noss [15] and Brownjohn [20]. The person involved in the tests is a man, 29 years old, who has a mass of 72 kg. Five tests with the empty structure and five tests with the person over a slab were used to get experimental data.

7.3.1 Instrumentation and Tests

The structure was instrumented with one PCB 333B50 accelerometer with a sensitivity of 100 mV/g. Impacts were performed using a PCB 096D50 Hammer with a sensitivity 0.2305 mV/N. The Hammer has a measurement range of ± 22240N peak. The sensor was placed in the vertical direction in the middle of the span, below the person. The hit was induced in the middle of the span, in a distance of less than 10 cm from the border of the concrete slab and in the middle of the person’s legs. The acquisition system consists of a modular NI CompactDAQ with a NI9234 module. Data was acquired using a sampling frequency of 1,652 Hz, then resampled to 150 Hz. The records had a duration of 20 s, included 5 s before the hit.

7.3.2 Structural Parameters

The parameters of the empty structure \(\Theta _{e} = k_{s},m_{s},c_{s}\) are estimated before the parameters of the HSI models (\(\Theta _{o}\)). The likelihood was estimated using the n = 25 points closer to the peak on the transfer function. This corresponds to the values of the transfer function between 28 rad∕s and 38 rad∕s. Figure 7.3 shows the experimental transfer function for the empty condition.

Fig. 7.3
figure 3

Analytical (Gray-scale) and experimental (black) transfer functions after Gibbs sampling

Full size image

Figure 7.3 also compares the analytical and experimental transfer functions. The analytical Transfer Functions were obtained using Gibbs sampling [21] with 200,000 samples for the posterior PDF (\(P(\Theta _{e}\vert D_{e}\)). Figure 7.4 shows the marginal histograms for each variable. The figure shows a high correlation between the stiffness k s and mass m s . This correlation is expected because the location of the peak in the Transfer Function corresponds to the main natural frequency of the structure. This natural frequency is dependent on the mass and stiffness of the structure. The figure also shows that both mass m s and stiffness k s are independent of the damping constant c s .

Fig. 7.4
figure 4

Histograms of \(k_{s},\,m_{s},\,c_{s}\) for SDOF model of the structure

Full size image

7.4 Results

The posterior PDF of the parameters of all models were sampled using Gibbs sampling. The marginal distributions as well as the correlation between parameters can be observed from the samples. Figures 7.5 and 7.6 show the samples of \(P(\Theta _{o}\vert D_{e},D_{o})\) for the SDOF human model. Figure 7.6 shows no correlation between the variables of the human model and the variables for the structure. The values of the mass are close to the expected value (72 kg). This indicates that given the experimental data collected for this paper, the parameters of the human are independent to the dynamic characteristics of the structure. Further research should be performed to explore the validity of this conclusion based on more experimental data (e.g. structures with higher and lower damping, etc). The results for the 2DOF, PD and PID models show a similar behavior and are omitted from the paper.

Fig. 7.5
figure 5

Histograms of \(k_{h},\,m_{h},\,c_{h}\) for SDOF model of the human body

Full size image
Fig. 7.6
figure 6

Samples for structure parameters \(\Theta _{e} = k_{s},\,m_{s},\,c_{s}\) and human model \(\Theta _{o} = k_{h},\,m_{h},\,c_{h}\) (SDOF human model)

Full size image

The performance of the different models is evaluated by comparing the transfer functions of each model with the experimental transfer function (similar to Fig. 7.3). Figure 7.7 shows the results for all models. The models based on closed loop control theory show better agreement with the experimental data (black line) than the models based on MDS systems. The analytical transfer function is shown in gray-scale. Darker color indicate a higher probability than lighter color.

Fig. 7.7
figure 7

Transfer function comparison. (a) SDOF model. (b) 2DOF model. (c) PD model. (d) PID model

Full size image

7.5 Conclusions

This paper studies the performance of four different models for HSI. Two models are based on closed loop control theory and two models are based on traditional MDS models. Models are used to simulate a human with straight knees in a structure that can be modeled as a SDOF. Overall all models did a good job representing the transfer function between the force applied to the structure and the acceleration of the structure. However, the closed loop controller models did over performed the traditional MDS models. The performance of the models can be seeing in Fig. 7.7. The human model based on a SDOF system does not effectively represent the shape of the peak of the transfer function. This implies that this model is not being able to represent the damping of the overall HSI model. The line representing the model’s transfer function is also wider than other models, indicating higher uncertainty.

The 2DOF human model shows a better agreement than the SDOF, however, it has six variables. Models based on closed loop control theory present the best agreement with the experimental transfer function. These models also have the less number of variables. The PD model only has a total of two variables. Small differences were found between the PD and PID models. This suggests that the T i has little influence on the model and it could be omitted.