Model Reduction for Nonlinear Multibody Systems Based on Proper Orthogonal-and Smooth Orthogonal Decomposition

Abstract

Flexible multibody simulation, subject to holonomic constraints, results in nonlinear differential algebraic systems. As computation time is a major issue, we are interested in applying model order reduction techniques to such multibody systems. One possible method called Proper Orthogonal Decomposition is based on minimizing the displacements euclidian distance while the more recently presented method Smooth Orthogonal Decomposition considers not only displacements but also their time derivatives. After a short introduction to the theory, this contribution presents a comparison of both methods on an index-reduced system. The methods are tested against each other in order to identify advantages and disadvantages.

39.1 Introduction

Multibody system (MBS) simulations are commonly modeled by automated modeling strategies. Due to easier automatisms mainly redundant sets of coordinates are chosen. Unfortunately by using redundant degrees of freedom (DOFs) one ends up with a larger set of coordinates than typically needed. Even though several of these rather unnecessary DOFs are commonly restrained by constraint equations, all DOFs enter the solver algorithm and therefore must be handled. Although computation resources increase rapidly it is wishfull to simplify multibody systems to the essential DOFs—the minimum set of coordinates. When dealing with flexible multibody systems even further DOFs are added, representing a finite element (FE) body described via well known reduction processes like e.g. Computational Mode Synthesis [1, 2]. As the number of modes characterizing the flex-body must be chosen prior to the multibody simulation, one may end up with a too high number of flex-body coordinates. During the last decades several MBS coordinate reduction methods, based on constraint orthogonalization [3] and coordinate partitioning [4] have been proposed. Heirmann et al. [5] presented a hypothetical combination of coordinate transformation and coordinate partitioning. More recently Proper Orthogonal Decomposition (POD), also known as Karhune-Loève Decomposition [6] has been proposed as a reduction method to implicit differential-algebraic equation (DAE) systems of differential index (d-index) one [7]. Smooth Orthogonal Decomposition (SOD) was proposed in the field of randomly excited vibration systems to extract linear normal modes and natural frequencies by Chelidze [8]. Chelidze [9] recently applied SOD as a model order reduction tool to linear dynamical systems with local nonlinearities. This paper compares POD and SOD model reduction on a planar nonlinear flexible multibody system of differential index one. The first part introduces the d-index one multibody system as well as the reduced order model derived by flat Galerkin projection as proposed by Ebert [7]. The second part gives a short review about the POD and SOD Method and their relation to each other. In the third part a planar flexible slider crank example is investigated. Finally results are discussed and summarized.

39.2 Multibody System Modelling

39.2.1 Full Order Modelling

Assuming a flexible multibody system subject to holonomic constraints, the later modelling strategy produces a d-index three nonlinear DAE system of second order as shown in Eq. (39.1).

$$\displaystyle{ \begin{array}{c} \boldsymbol{M(\boldsymbol{q})} \cdot \boldsymbol{\ddot{ q}} +\boldsymbol{ Q}(\boldsymbol{q},\boldsymbol{\dot{q}},t) +\boldsymbol{ C_{q}}^{T}\cdot \boldsymbol{\lambda } = 0\\ \\ \boldsymbol{C(\boldsymbol{q})} =\boldsymbol{ 0}\end{array} }$$

(39.1)

The number of rigid DOFs may be defined for planar examples by $k = 3 \cdot b$ with b as the number of bodies included. Adding a flex-body, l further flexible DOFs appear. The total number of DOFs is given by $n = k + l$. Further let m be the number of constraints $\boldsymbol{C}\left (\boldsymbol{q}\right )$. In order to use ODE solver packages, both d-index and order reduction must be carried out. The derived d-index one system is presented in Eq. (39.2).

$$\displaystyle{ \mathop{\underbrace{\left [\begin{array}{cc} \boldsymbol{M}\left (\boldsymbol{q}\right ) &\boldsymbol{C_{q}}^{T}\left (\boldsymbol{q}\right ) \\ \boldsymbol{C_{q}}\left (\boldsymbol{q}\right )& 0 \end{array} \right ]}}\limits _{\boldsymbol{M}_{ext}\left (\boldsymbol{q}\right )}\cdot \left (\begin{array}{c} \boldsymbol{\ddot{q}}\\ \boldsymbol{\lambda } \end{array} \right ) = \left (\begin{array}{c} \boldsymbol{Q}\left (\boldsymbol{q},\boldsymbol{\dot{q}},t\right )\\ \boldsymbol{\gamma }\left (\boldsymbol{q},\boldsymbol{\dot{ q}} \right ) \end{array} \right ) }$$

(39.2)

Assuming $\boldsymbol{M}_{e}xt$ is nonsingular, Eq. (39.2) can be solved for $\boldsymbol{\ddot{q}}$ and $\boldsymbol{\lambda }$:

$$\displaystyle{ \left (\begin{array}{c} \boldsymbol{\ddot{q}}\\ \boldsymbol{\lambda } \end{array} \right ) =\boldsymbol{ M}_{e}xt\cdot \left (\begin{array}{c} \boldsymbol{Q}\left (\boldsymbol{q},\boldsymbol{\dot{q}},t\right )\\ \boldsymbol{\gamma }\left (\boldsymbol{q},\boldsymbol{\dot{ q}} \right ) \end{array} \right ) = \left (\begin{array}{c} \boldsymbol{A}\left (\boldsymbol{q},\boldsymbol{\dot{q}},t\right )\\ \boldsymbol{\Lambda }\left (\boldsymbol{q},\boldsymbol{\dot{ q}} \right ) \end{array} \right ) }$$

(39.3)

In order to avoid the drift problem, the Baumgarte stabilization [10] $\boldsymbol{\gamma }= -\boldsymbol{C_{qq}}\left (\boldsymbol{\dot{q},\dot{q}}\right ) -\alpha \boldsymbol{ C_{q}}\boldsymbol{\dot{q}} -\beta \boldsymbol{ C}\left (\boldsymbol{q}\right )$ is used. Hence, MBS simulation is carried out using the first order d-index one system Eq. (39.4).

$$\displaystyle{ \begin{array}{c} \boldsymbol{\dot{q}} =\boldsymbol{ v}\\ \\ \boldsymbol{\dot{v}} =\boldsymbol{ A}\left (\boldsymbol{q},\boldsymbol{v},t\right )\end{array} }$$

(39.4)

It must be stated that the validity of the above model is strongly depending on the chosen Baumgarte stabilization parameters α and β. Therefore we expect those to be chosen correctly for all upcoming considerations. For further insight into the topic of (flexible) multibody system dynamics the interested reader is referred to Shabana [11].

39.2.2 Reduced Order Modeling

Flat Galerkin projection, defined by Eq. (39.5), projects a high dimensional original system onto some smaller subspace $\mathcal{Y}$ spanned by $\boldsymbol{\Phi }$. The projection matrix $\boldsymbol{\Phi }$ may be derived from various methods, in our case POD and SOD. $\boldsymbol{\Phi }$ is split into a dominant part $\boldsymbol{\Phi }_{r}$ and a neglectable part $\boldsymbol{\Phi }_{n-r}$. Neglecting the second part of the subspace, the projection changes from a pure transformation into an approximation.

$$\displaystyle{ \boldsymbol{q} \approx \boldsymbol{\tilde{ q}} =\boldsymbol{ \Phi }_{r} \cdot \boldsymbol{ q}_{red}\quad \boldsymbol{\Phi }_{r}\epsilon \mathbb{R}^{nxr},\;\boldsymbol{q}\epsilon \mathbb{R}^{r},\;r \ll n }$$

(39.5)

Applying the flat Galerkin projection to the mechanical system defined in Eq. (39.4), it must be stated that according to the work of Ebert [7] the reduction process may transform the DOFs but must not change any constraint equations as this could lead to unphysical phenomena. Considering this restriction, the reduced model is defined in Eq. (39.6).

$$\displaystyle{ \begin{array}{c} \boldsymbol{\tilde{v}} =\boldsymbol{ U}_{red}^{T} \cdot \boldsymbol{\dot{ q}}_{red}\\ \\ \boldsymbol{\dot{\tilde{v}}} =\boldsymbol{ U}_{red}^{T} \cdot \boldsymbol{M}_{ext}\left (\boldsymbol{\tilde{q}}\right )^{-1} \cdot \left (\begin{array}{c} \boldsymbol{Q}\left (\boldsymbol{\tilde{q}},\boldsymbol{\tilde{v}},t\right )\\ \gamma \left (\boldsymbol{\tilde{q}},\boldsymbol{\tilde{ v}} \right ) \end{array} \right ) \end{array} }$$

(39.6)

With

$$\displaystyle{ \boldsymbol{U}_{red}:= \left [\begin{array}{cc} \boldsymbol{\Phi }_{r}& \boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{I}_{m} \end{array} \right ] }$$

(39.7)

with $\boldsymbol{I}_{n-r}$ being a unit matrix of dimension m. It must be stated that due to the nonlinear character, the projection must be carried out in each time-step t _i repetitive with re-evaluated system matrices/vectors $\boldsymbol{M}$,$\boldsymbol{Q}$, etc.

39.3 Reduction Methods

39.3.1 Proper Orthogonal Decomposition

During the last couple of years, the linear Galerkin projection method POD established as a commonly used model reduction technique [6]. It is based on the idea of finding a proper orthogonal subspace to the observation space given by observation data. The subspace to be found minimizes the euclidean distance in terms of the captured signal energy. Let $\boldsymbol{X}\epsilon \mathbb{R}^{nxh}$ be the time-series of a multibody simulation with $t = \left [t_{0},\ldots,t_{h}\right ]$. In the field of POD the observation data matrix $\boldsymbol{X}$ is called ${\it \text{snapshot-matrix}}$, meaning every column vector $\boldsymbol{q}_{i}$ represents a snapshot of the system at time t _i . The method of POD investigates this snapshot matrix $\boldsymbol{X}$ in order to define a low-dimensional subspace, spanned by r− basis vectors, so-called Proper Orthogonal Modes (POMs), with r < n. Therefore $\boldsymbol{X}$ is processed by the singular value decomposition (SVD) in Eq. (39.8)

$$\displaystyle{ \boldsymbol{X} =\boldsymbol{ \Phi } \cdot \boldsymbol{ \Sigma } \cdot \boldsymbol{ W}^{T} }$$

(39.8)

The n x n SVD-matrix $\boldsymbol{\Phi } = \left [\boldsymbol{\phi }_{1},\ldots,\boldsymbol{\phi }_{n}\right ]$ consists of already mentioned POMs $\boldsymbol{\phi }_{i}$, also called left singular vectors, defining the orthogonal subspace to $\boldsymbol{X}$. The column vectors $\boldsymbol{w}_{i}$ summarized in $\boldsymbol{W}$ are called right singular vectors. The dimension of the orthogonal subspace may be defined by the singular values, also called Proper Orthogonal Values (POVs), arranged in the diagonal matrix $\boldsymbol{\Sigma } = diag\left (\mbox{ $\sigma $}_{1},\ldots,\sigma _{n}\right )$ with $\sigma _{1} \leq \sigma _{2} \leq \ldots \leq \sigma _{n}$. The singular value σ _i indicates the amount of signal energy captured by the associated basis vector $\boldsymbol{\phi }_{i}$. As the singular values decrease rapidly, a drop-point, as indicated in Fig. 39.1 may be found which characterizes the number of basis vectors $\boldsymbol{\phi }_{i}$ needed to span an orthogonal subspace delivering sufficient result quality. Assuming a drop-point is detectable within r− singular values, the model reduction matrix $\boldsymbol{\Phi }_{r}\epsilon \mathbb{R}^{n\,x\,r} = \left [\boldsymbol{\phi }_{1},\ldots,\boldsymbol{\phi }_{r}\right ]$ with r < n can be defined. As a matter of fact, if there is no drop-point detectable, the system may not be reducable. Further, POMs $\boldsymbol{\phi }_{i}$ may also be derived from the eigenvalue problem given in Eq. (39.9)

$$\displaystyle{ \boldsymbol{X} \cdot \boldsymbol{ X}^{T} \cdot \boldsymbol{ v}_{ i} =\lambda _{i} \cdot \boldsymbol{ v}_{i} }$$

(39.9)

with

$$\displaystyle{ \boldsymbol{\phi }_{i} = \frac{1} {\sqrt{\lambda _{i}}} \cdot \boldsymbol{ X} \cdot \boldsymbol{ v}_{i} }$$

(39.10)

and POVs defined as $\sigma _{i} = \sqrt{\lambda _{i}}$.

Fig. 39.1

Singular values

Recalling the linear Galerkin projection, the system transformation is defined as

$$\displaystyle{ \boldsymbol{\tilde{q}} =\boldsymbol{ \Phi }_{red} \cdot \boldsymbol{ q}_{red} }$$

(39.11)

It is worth mentioning, that if all basis vectors $\boldsymbol{\phi }_{i}$ are used, the projection in Eq. (39.11) is only transforming the system but achieves no reduction at all.

39.3.2 Smooth Orthogonal Decomposition

Chelidze [8] introduced a Smooth Karhunen-Loève Decomposition called Smooth Orthogonal Decomposition (SOD). The method has been used as a model order reduction tool for linear systems with local nonlinearities in [9]. Similarities to POD are not only found in the name but also in the basic process of Smooth Orthogonal Modes (SOMs) and -Values (SOVs). Given a snapshot matrix $\boldsymbol{X}_{SOD}\epsilon \mathbb{R}^{hxn}$, which may be simply the transposed POD snapshot matrix, SOD further rests on the velocity snapshot matrix $\boldsymbol{\dot{X}}_{SOD}$. SOMs and SOVs are derived by solving the generalized eigenvalue problem in Eq. (39.12).

$$\displaystyle{ \boldsymbol{\Sigma }_{\boldsymbol{X}_{SOD}\boldsymbol{X}_{SOD}} \cdot \boldsymbol{ v}_{i} =\lambda _{i} \cdot \boldsymbol{ \Sigma }_{\boldsymbol{\dot{X}}_{SOD}\boldsymbol{\dot{X}}_{SOD}} \cdot \boldsymbol{ v}_{i} }$$

(39.12)

With the correlation matrices $\boldsymbol{\Sigma _{X_{SOD}X_{SOD}}} = \frac{1} {n} \cdot \boldsymbol{ X_{SOD}}^{T} \cdot \boldsymbol{ X}_{ SOD}$ and $\boldsymbol{\Sigma _{\dot{X}_{SOD}\dot{X}_{SOD}}} = \frac{1} {n} \cdot \boldsymbol{\dot{ X}_{SOD}}^{T} \cdot \boldsymbol{\dot{ X}_{ SOD}}$. The SOVs are hereby given as λ _i and SOMs are defined as $\boldsymbol{\phi }_{i} =\boldsymbol{ v}_{i}^{-T}$. Depending on the number of snapshots taken into account, the general eigenvalue problem solver may fail and therefore SOMs can be derived from the general singular value decompositions Eq. (39.13).

$$\displaystyle{ \begin{array}{c} \boldsymbol{X}_{SOD} =\boldsymbol{ W}_{1} \cdot \boldsymbol{ \Sigma }_{1} \cdot \boldsymbol{ \Phi }^{T} \\ \boldsymbol{\dot{X}}_{SOD} =\boldsymbol{ W}_{2} \cdot \boldsymbol{ \Sigma }_{2} \cdot \boldsymbol{ \Phi }^{T}\end{array} }$$

(39.13)

with SOMs again defined as $\boldsymbol{\phi }_{i}$. SOVs are derived by the term-by-term division of $diag\left (\boldsymbol{\Sigma }_{1}^{T} \cdot \boldsymbol{ \Sigma }_{1}\right )$ and $diag\left (\boldsymbol{\Sigma }_{2}^{T} \cdot \boldsymbol{ \Sigma }_{2}\right )$.

Proceeding as already explained for the POD method, the flat Galerkin reduction consists of r− SOMs indicated by a drop-point found in the SOVs as seen in Fig. 39.1. Due to the velocity snapshot matrix, SOD is not only accounting static but also dynamic characteristica. While POD minimizes the euclidean distance of the captured signal energy, in other words maximizes the energy in the projected signal, SOD further maximizes the variance (the smoothness) in the projection. In this manner SOD finds deterministic trends, which may be of interest for MBS reduction. Taking a look onto Eq. (39.12) and substituting the unity matrix $\boldsymbol{I}$ for $\boldsymbol{\Sigma _{\dot{X}_{SOD}\dot{X}_{SOD}}}$ the POD method is derived from the SOD method by the SVD of $\boldsymbol{X_{SOD}} =\boldsymbol{ W}_{1} \cdot \boldsymbol{ B}_{1} \cdot \boldsymbol{ \Phi }^{T}$. Regarding normal mode (NM) identification, Feeny [12] stated that while POD is able to identify NMs for undamped system it fails to identify a linearly damped dynamical system in general. SOD overcomes this drawback and is able to identify a linearly damped dynamical systems NMs as presented by Farooq and Feeny [13].

39.4 Numerical Example

39.4.1 Model Data

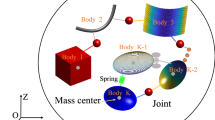
The model subject to both reduction methods is presented in Fig. 39.2a. In order to get a maximum set of redundant coordinates, all planar rigid DOFs $\left (x_{cart},y_{cart},\phi _{cart},x_{pendulum},y_{pendulum},\phi _{pendulum}\right )$ are used, acting in the respective center of mass. Further, two flex-DOFs, defined by free-free modes, describing the flexible pendulum are added. The MBS therefore consists of $n = 2 \cdot 3 + 2 = 8$ rigid-body and flex-body DOFs. Finally, the following constraints are introduced, representing the carts planar restrictions and a hinge joint between the cart and the pendulum:

$$\displaystyle{ C_{1}: x_{c} - y_{c} = 0 }$$

(39.14)

Fig. 39.2

Full and reduced model representation. (a) Redundant formulation. (b) Minimum set formulation

$$\displaystyle{ C_{2}: phi_{c} = 0 }$$

(39.15)

$$\displaystyle{ C_{3}: \left [\begin{array}{c} x_{c} - x_{p} \\ y_{c} - y_{p} \end{array} \right ]-\boldsymbol{B}_{p}\cdot \left (\boldsymbol{u}_{p} +\boldsymbol{ s}_{p} \cdot \boldsymbol{ q}_{f}\right ) = 0 }$$

(39.16)

With $\boldsymbol{B}_{p }$ describing the pendulum rotation matrix, $\boldsymbol{u}_{p} = \left [0,l_{p}/2\right ]^{T}$ representing the position vector from the pendulums center of mass to the hinge-joint and $\boldsymbol{s}_{p}\epsilon \mathbb{R}^{lx2}$ representing the first two free-free bending modes. Let the cart further be subject to linear springs and dampers acting in global x and y directions. Given cart mass m _c  = 1 kg, pendulum mass m _p  = 0. 004 kg, pendulum length l _p  = 0. 8 m, spring stiffness c _c  = 100 N/m and damping constant d _c  = 0. 1, the model is excited by a sinusoidal force with Amplitude A = 10 N and frequency f = 10 Hz, acting on the rigid cart and forcing it to move diagonal in plane. The simulation is carried out in SciLab v5.5.0—http://www.scilab.org—using the included ODEPACK BDF solver with flexible time stepping for t _end  = 1 s. The excitation force and body modes are fitted to excite the first flex body mode (f ₁ = 16 Hz) only. The second flex body mode is set to a high eigenfrequency f ₂ > 1 kHz. Considering the given constraint equations which introduce zero rows for restrained DOFs, the snapshot matrices $\boldsymbol{X}$, $\boldsymbol{\dot{X}}$ as well as the correlation matrices $\boldsymbol{\Sigma _{X_{SOD}X_{SOD}}}$ and $\boldsymbol{\Sigma _{\dot{X}_{SOD}\dot{X}_{SOD}}}$ are rank deficient.

39.4.2 Results

A full model simulation collects the snapshot matrices $\boldsymbol{X}$ and $\boldsymbol{\dot{X}}$ at a sample rate of 100 Hz. In a next step, the POD-SVD of $\boldsymbol{X}$ and the generalized SOD-SVD of $\boldsymbol{X}_{SOD}$ and $\boldsymbol{\dot{X}}_{SOD}$ are generated as shown in Fig. 39.3a. As mentioned in the beginning the model reduction techniques should be evaluated on their ability to reduce the redundant set of coordinates to the minimal set of coordinates. The minimal set of coordinates of the given example is defined by n _min  = 4 DOFs, for example $\boldsymbol{q}_{min} = \left [x_{min,c},x_{min,p},y_{min,p},q_{f,1}\right ]^{T}$ as indicated in Fig. 39.2b.

Fig. 39.3

POVs and SOVs plot. (a) All POVs and SOVs. (b) Independent SOVs

Looking at the POD findings in Fig. 39.3a, a noticeable drop-point is detected after $\sigma _{POD,6}$. The POD reduced model-dimension is expected as the snapshot matrix $\boldsymbol{X}$ is of rank = 6. The reduction matrix $\boldsymbol{\Phi }_{POD}$ may therefore consist of r _POD  = 6 POMs which project the n = 8 original DOFs onto r _POD  = 6 reduced DOFs $\boldsymbol{q}_{red}$. Due to numerical reasons SciLab assigns full rank to the POM matrix instead of the actual rank. Investigating the calculated SOVs in Fig. 39.3a the drop-point between first and second SOV marks an infinite singular value. Regarding Eq. (39.12) and recalling that the velocity correlation matrix $\boldsymbol{\Sigma }_{\boldsymbol{\dot{X}}_{SOD}\boldsymbol{\dot{X}}_{SOD}}$ is singular, the generalized eigenvalue problem yields one infinite eigenvalue for each row/column equal to zero. To get deeper insight into the SOVs, the rank of the SOM matrix is calculated showing rank deficiency. As expected the SOM-rank is calculated to a value of five as it has to be the same as the correlation velocity matrix rank. SOMs $\{\boldsymbol{\Phi }_{SOD,1},\boldsymbol{\Phi }_{SOD,7},\boldsymbol{\Phi }_{SOD,8}\}$ are chosen as linear dependent columns which imply that the corresponding SOVs may not be taken into account for SOD model reduction. Dependent SOVs are omitted and the remaining SOVs are plotted in Fig. 39.3b. Although the independent-SOV plot is showing minor drop-points a significant drop-point like POD is missing. As a result all independent SOMs are used to generate the SOD reduced model subspace. Due to the fact that the SOMs are not orthogonal, a Gram-Schmidt Orthogonalization is applied to the SOMs prior to simulation. Examining Fig. 39.4, POD and SOD model results are almost congruent to the full simulation results. Error plots in Fig. 39.5 are derived from the error measure

$$\displaystyle{ e_{i}\left [t\right ] = \frac{\Delta q_{i}\left [t\right ]} {\|max\ q_{red,i}\|} }$$

(39.17)

with $\Delta q_{i}\left [t\right ] = q_{full,i}\left [t\right ] -\tilde{ q}_{i}\left [t\right ]$. Investigating the error plots, the order five SOD model causes a slightly higher error than the order six POD model. Unfortunately, due to the dependent SOMs a further increase of the SOD subspace is not possible. Comparing simulation times, the POD reduced model saves about 12 % compared to the full model while SOD reduces the simulation time by almost 30 %.

Fig. 39.4

Simulation results—r _POD  = 6 and r _SOD  = 5. (a) Cart. (b) Pendulum

Fig. 39.5

Error plot—r _POD  = 6 and r _SOD  = 5. (a) Cart. (b) Pendulum

Looking at Table 39.1 the POMs may be split into a group of four pendulum bending-modes and into four rigid body modes. The bending POMs thereby also include the second bending mode, which is excited only by numerical diffusion during simulation ($max\left \vert q_{f,2}\right \vert \approx 1e^{-23}$) while SOD omits it. Comparing the modes, SOMs similar to POMs can be found, like e.g. $\{\boldsymbol{\Phi }_{POD,2} \leftrightarrow \boldsymbol{ \Phi }_{SOD,4},\boldsymbol{\Phi }_{POD,4} \leftrightarrow \boldsymbol{ \Phi }_{SOD,7}\}$.

Table 39.1 Proper-/smooth orthogonal modes

At the end we would like to report the practically important observation, that the POD approach is more robust in terms of “standard numerical tools” as SOD. To illustrate this statement we increase the sample rate from 100 to 300 Hz in order to use more snapshots for SOD. The third component in Table 39.1 shows what is called refined SOMs (rSOMs) which are SOMs generated from a larger number of snapshots. While the POD rank stays constant for this higher sample rate, the rSOM rank increases. This is related to numerical reasons, as numerical rank determination is in need of high singular value drop-offs which are not present. One rSOM changing from dependent to independent is identified as the first SOM related to the theoretically infinite first rSOV. Given a rSOM-matrix of rank six would indicate six linear independent modes which are not case within this example as the velocity correlation matrix is of rank five. Actually using this r _rSOD  = 6 subspace, the simulation results worsen as indicated in the error plot Fig. 39.6 which implies that SOD is numerically sensitive. It also confirms that the rank computation suffers from the lack of high drop-offs and fails to identify the actual rank.

Fig. 39.6

Error plot—r _rSOD  = 5 and r _rSOD  = 6. (a) Cart. (b) Pendulum

39.5 Conclusion

This paper tries to compare and evaluate POD and SOD model order reduction applied to a flexible redundant multibody systems. Based on the order reduced d-index one DAE system both reduction methods are summarized and applied to a flexible planar cart pendulum model. The POD reduction identifies two out of four redundant coordinates ending up with a total number of r _POD  = 6 DOFs. Further, the simulation time decreases by about 12 % compared to the full model. SOD reduces the model to r _SOD  = 5 DOFs and reduces the simulation time by about 30 %. POD shows a numerically robust behavior, indifferent to sample-rate variations which is further underlined by a clear singular value drop-point. SOD delivers a smaller reduced model (five SOMs instead of six POMs) and saves about 30 % of simulation time. As SOD is sensitive to sample-rate variations it shows less numerical robustness. Due to the lack of a clear SOV drop-point, numerical rank determination is negatively effected. Finally SOMs need to be orthogonalized prior to reduced simulation in order to achieve a more effective time integration. Both methods presented may suffer from issues when dealing with models starting from locations outside the global origin, meaning initial position values different from zero. As the used type of flat Galerkin projection is approximating the system, omitted DOFs may also lead to loosing their initial conditions. Future work will focus on this initial condition issues as well as on adapted POD and SOD methods in order to end up with models closer to the minimal set of coordinates. Further, in order to minimize not only DOFs but also constraint equations, the constraint restriction posted by Ebert will be softened to allow special types of constraints to be removed.