Non-linear Dynamics of Jointed Systems Under Dry Friction Forces

Abstract

Dry friction devices are usually adopted to reduce structure vibrations. Generally, an optimisation procedure is required to tune the system coefficients by performing the best effect. In this paper a continuous structure coupled with a lumped dissipative system is studied. This second system is alternatively loaded by a dry friction force, so that two states can be recognized: contact and not-contact. Aim of this work is the study of the system parameters influence on the structure response when the system passes through the different states before presented. In particular, during the contact state a stick-slip motion of the lumped system is considered. The analysis is focused on the transition between chaotic and non-chaotic behaviour and on the correspondent power flows between continuous and lumped system during the motion.

2.1 Introduction

Aim of this paper is to present some results concerning the nonlinear coupling of a continuous mechanical system and a lumped one. The nonlinearity is due to a friction force between the mass of the lumped system and a moving belt.

The motion of the system is composed of a sequence of stick and slip phases: during the stick phase the relative velocity of the mass in contact with the belt is null, on the contrary during the slip phase the relative velocity controls the friction force.

In the past many works investigated this phenomenon, because in the field of applied sciences the phenomenon of friction and in particular stick-slip systems are very interesting [1–3].

In this paper a parametric analysis varying the belt velocity is performed by considering some indicators (bifurcation diagrams and Lyapunov exponents, see [3–5]). The nature of the system response is investigated in order to understand if the system exhibits a chaotic motion.

The study is also focused on the power flows between the jointed systems.

2.2 Mechanical Model

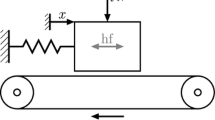
The system shown in Fig. 2.1 is made up of a continuous beam and an harmonic oscillator with two degrees of freedom driven by a belt, the belt has a constant speed v _dr . The two systems are linked to each other via a spring k ₁.

During its motion, the mass m can have two different behaviours: it can be attached to the belt (stick motion) and moves with it, or slide on the belt (slip motion). A non constant contact force is considered through a stiffness k ₃ between mass and belt along x(t).

In the following, the motion equations of the global system are derived.

Fig. 2.1

Mechanical system

2.2.1 Dimensional Motion Equations

The continuous system is modelled using the Euler-Bernoulli theory of beam, its motion equation is expressed by the following equation:

$$\displaystyle{ EI \frac{\partial ^{4}w(z,t)} {\partial z^{4}} +\rho A\frac{\partial ^{2}w(z,t)} {\partial t^{2}} = k_{1}\left [y(t) - w(z,t)\right ]\delta (z - z_{A}) }$$

(2.1)

The beam has length L, Young modulus E, moment of inertia of area I, mass density ρ and a cross section area A.

The Dirac delta δ(z − z _A ) allows to consider the influence of the harmonic oscillator in the link point z = z _A .

The harmonic oscillator is modelled with two degrees of freedom: x(t) and y(t).

Along the x(t) direction the motion can be influenced of the non continuous contact between mass and belt.

There is mass-belt contact if x(t) > 0. In this case a contact force, N(t), rises and it is equal to:

$$\displaystyle{ N(t) = k_{3}x(t) }$$

(2.2)

On the other hand, if there is no mass-belt contact, the normal force is N(t) = 0.

The equation of motion along x(t) is:

$$\displaystyle{ m\ddot{x}(t) + k_{2}x(t) + N(t) = 0 }$$

(2.3)

Along the y(t) direction the stick-slip condition must be taken into account.

There is stick motion on the mass m if all the external forces acting on it are bounded in absolute value by the static friction force $T_{s}(t) =\mu _{s}N(t)$, moreover the mass velocity $\dot{y}(t)$ must be equal to the belt speed v _dr .

In mathematical terms the stick condition is expressed by:

$$\displaystyle{ \left \vert k_{1}\left [y(t) - w(z_{A},t)\right ]\right \vert <\mu _{s}N(t)\ \mbox{ and}\ \dot{y}(t) = v_{dr} }$$

(2.4)

The stick motion equation is the following:

$$\displaystyle{ m\ddot{y}(t) = 0 }$$

(2.5)

The initial condition for Eq. (2.5) are:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \left.y(t)\right \vert _{t=0} = 0 \quad \\ \left.\dot{y}(t)\right \vert _{t=0} = v_{dr}\quad \end{array} \right. }$$

(2.6)

If the stick condition [Eq. (2.4)] is not verified, there is sliding between the mass and the belt and a dynamic friction force T _d (t) rises. The slip equation of motion is:

$$\displaystyle{ m\ddot{y}(t) + k_{1}\left [y(t) - w(z_{A},t)\right ] = T_{d}(t) }$$

(2.7)

where the non linear dynamical friction force T _d (t) is expressed by:

$$\displaystyle{ T_{d}(t) = - \frac{\mu _{s}N(t)} {1 +\gamma \left [\dot{y}(t) - v_{dr}\right ]}\mathrm{sgn}\left [\dot{y}(t) -\mbox{ $v$}_{dr}\right ] }$$

(2.8)

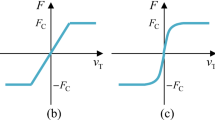
In Fig. 2.2 the dynamic friction force plot is shown, the γ parameter represents the slope of the curve and its dimension is the inverse of the velocity.

Fig. 2.2

Dynamical friction force

2.2.2 Dimensionless Motion Equations

In order to generalize the problem, the general motion equation are written in a dimensionless form.

According to the Buckingham π theorem, the dimensional variables are the following:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \alpha _{1} = EI\quad \\ \alpha _{2} = L \quad \\ \alpha _{3} =\rho A \quad \end{array} \right. }$$

(2.9)

The dimensionless constants (⋅ )^∗ are the following:

$$\displaystyle{ \begin{array}{llll} &t^{{\ast}} = t\alpha _{1}^{1/2}\alpha _{2}^{-2}\alpha _{3}^{-1/2}\quad & & y^{{\ast}}(t^{{\ast}}) = y(t)\alpha _{2}^{-1} \\ & k_{1}^{{\ast}} = k_{1}\alpha _{1}^{-1}\alpha _{2}^{3}\quad & & w^{{\ast}}(z^{{\ast}},t^{{\ast}}) = w(z,t)\alpha _{2}^{-1} \\ & k_{2}^{{\ast}} = k_{2}\alpha _{1}^{-1}\alpha _{2}^{3}\quad & & \delta ^{{\ast}}(z^{{\ast}}- z_{A}^{{\ast}}) =\delta (z - z_{A})\alpha _{2} \\ & k_{3}^{{\ast}} = k_{3}\alpha _{1}^{-1}\alpha _{2}^{3}\quad & & T_{d}^{{\ast}}(t^{{\ast}}) = T_{d}(t)\alpha _{1}^{-1}\alpha _{2}^{2} \\ & m^{{\ast}} = m\alpha _{2}^{-1}\alpha _{3}^{-1}\quad & & v_{dr}^{{\ast}} = v_{dr}\alpha _{1}^{-1/2}\alpha _{2}\alpha _{3}^{1/2} \\ & x^{{\ast}}(t^{{\ast}}) = x(t)\alpha _{2}^{-1}\quad & & \gamma ^{{\ast}} =\gamma \alpha _{ 1}^{1/2}\alpha _{2}^{-1}\alpha _{3}^{-1/2} \end{array} }$$

Substituting the dimensionless constants in Eq. (2.1), the beam dimensionless equations is obtained:

$$\displaystyle{ \frac{\partial ^{4}w^{{\ast}}(z^{{\ast}},t^{{\ast}})} {\partial z^{{\ast}4}} + \frac{\partial ^{2}w^{{\ast}}(z^{{\ast}},t^{{\ast}})} {\partial t^{{\ast}2}} = k_{2}^{{\ast}}\left [y^{{\ast}}(t^{{\ast}}) - w^{{\ast}}(z^{{\ast}},t^{{\ast}})\right ]\delta ^{{\ast}}(z^{{\ast}}- z_{ A}^{{\ast}}) }$$

(2.10)

The same procedure of the beam is applied to the harmonic oscillator.

Along $x^{{\ast}}(t^{{\ast}})$ the motion equation is:

$$\displaystyle{ m^{{\ast}}\ddot{x}^{{\ast}}(t^{{\ast}}) + k_{ 2}^{{\ast}}x^{{\ast}}(t^{{\ast}}) + N^{{\ast}}(t^{{\ast}}) = 0 }$$

(2.11)

where the mass-belt contact force is:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} N^{{\ast}}(t^{{\ast}}) = k_{ 3}^{{\ast}}x^{{\ast}}(t^{{\ast}})\ \quad &\mbox{ if}\ x^{{\ast}}(t^{{\ast}}) > 0 \\ N^{{\ast}}(t^{{\ast}}) = 0\ \quad &\mbox{ else} \end{array} \right. }$$

(2.12)

Along $y^{{\ast}}(t^{{\ast}})$, the motion equation of the harmonic oscillator is:

$$\displaystyle{ m^{{\ast}}\ddot{y}^{{\ast}}(t^{{\ast}}) = K(t^{{\ast}}) }$$

(2.13)

where K(t ^∗) is the force due to the following stick-slip condition:

$$\displaystyle{ \left \vert k_{1}^{{\ast}}\left [y^{{\ast}}(t^{{\ast}}) - w^{{\ast}}(z_{ A}^{{\ast}},t^{{\ast}})\right ]\right \vert <\mu _{ s}N^{{\ast}}(t^{{\ast}})\ \mbox{ and}\ \dot{y}^{{\ast}}(t^{{\ast}}) = v_{ dr}^{{\ast}} }$$

(2.14)

the force K(t ^∗) is expressed by:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} K(t^{{\ast}}) = 0\ \quad &\mbox{ (stick)} \\ K(t^{{\ast}}) = -k_{1}^{{\ast}}\left [y^{{\ast}}(t^{{\ast}}) - w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})\right ] + T_{d}^{{\ast}}(t^{{\ast}})\ \quad &\mbox{ (slip)} \end{array} \right. }$$

(2.15)

where the dimensionless dynamic friction force $T_{d}^{{\ast}}(t^{{\ast}})$ is:

$$\displaystyle{ T_{d}^{{\ast}}(t^{{\ast}}) = - \frac{\mu _{s}N^{{\ast}}(t^{{\ast}})} {1 +\gamma ^{{\ast}}\left [\dot{y}^{{\ast}}(t^{{\ast}}) - v_{dr}^{{\ast}}\right ]}\mathrm{sgn}\left [\dot{y}^{{\ast}}(t^{{\ast}}) -\mbox{ $v$}_{ dr}^{{\ast}}\right ] }$$

(2.16)

2.2.3 Solution Method

Applying the Bubnov-Galerkin method and using the eigenfunction of the simply supported beam, it is possible to write:

$$\displaystyle{ w^{{\ast}}(z^{{\ast}},t^{{\ast}}) =\sum _{ i=1}^{N}\phi _{ i}^{{\ast}}(z^{{\ast}})q_{ i}^{{\ast}}(t^{{\ast}}) }$$

(2.17)

where the eigenfunctions $\phi _{i}^{{\ast}}(z^{{\ast}})$ are expressed by:

$$\displaystyle{ \phi _{i}^{{\ast}}(z^{{\ast}}) =\sin (i\pi z^{{\ast}}) }$$

(2.18)

and the beam eigenvalues are:

$$\displaystyle{ \omega _{i}^{{\ast}} = i^{2}\pi ^{2} }$$

(2.19)

Projecting the motion equation on a different eigenfunction basis $\phi _{j}^{{\ast}}(z^{{\ast}})$, integrating on the domain and adopting the following orthonormalization conditions:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \sum _{i=1}^{N}\int _{0}^{1}\phi _{j}^{{\ast}}(z^{{\ast}})\phi _{i}^{{\ast}IV }(z^{{\ast}})dz^{{\ast}} =\omega _{ i}^{{\ast}2}\delta _{ij}\quad \\ \sum _{i=1}^{N}\int _{0}^{1}\phi _{j}^{{\ast}}(z^{{\ast}})\phi _{i}^{{\ast}}(z^{{\ast}})dz^{{\ast}} =\delta _{ij} \quad \end{array} \right. }$$

(2.20)

the following N ordinary differential equations are obtained:

$$\displaystyle{ \ddot{q}_{j}^{{\ast}}(t^{{\ast}}) + \left [\omega _{ j}^{{\ast}2} + k_{ 2}^{{\ast}}\phi _{ j}^{{\ast}2}(z_{ A}^{{\ast}})\right ]q_{ j}^{{\ast}}(t^{{\ast}}) = k_{ 2}^{{\ast}}y^{{\ast}}(t^{{\ast}})\phi _{ j}^{{\ast}}(z_{ A}^{{\ast}})\quad j = 1,2,\ldots,N }$$

(2.21)

With the modal basis expansion expressed in Eq. (2.17) the stick condition becomes:

$$\displaystyle{ \left \vert k_{1}^{{\ast}}\left [y^{{\ast}}(t^{{\ast}}) -\sum _{ i=1}^{N}\phi _{ i}^{{\ast}}(z_{ A}^{{\ast}})q_{ i}^{{\ast}}(t^{{\ast}})\right ]\right \vert <\mu _{ s}N^{{\ast}}(t^{{\ast}})\ \mbox{ and}\ \dot{y}^{{\ast}}(t^{{\ast}}) = v_{ dr}^{{\ast}} }$$

(2.22)

and the force K(t ^∗):

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} K(t^{{\ast}}) = 0\ \quad &\mbox{ (stick)} \\ K(t^{{\ast}}) = -k_{1}^{{\ast}}\left [y^{{\ast}}(t^{{\ast}}) -\sum _{i=1}^{N}\phi _{i}^{{\ast}}(z_{A}^{{\ast}})q_{i}^{{\ast}}(t^{{\ast}})\right ] + T_{d}^{{\ast}}(t^{{\ast}})\ \quad &\mbox{ (slip)}\end{array} \right. }$$

(2.23)

2.3 Results

In this section the most relevant results for the system studied are shown.

Different simulations were done in order to evaluate the sensitivity of the system solution to the variation of the belt velocity.

In Table 2.1 the dimensionless parameters used for the simulation are shown.

It is important to advance a consideration about the magnitude of the belt velocity. For small values of the velocity the system usually shows a continuous switching motion from stick to slip, while for big values of the velocity there will be an initial stick before a complete slip behavior for the whole simulation.

Therefore, the velocity range is selected in order to have the system in stick-slip motion (see Table 2.1).

Table 2.1 Model parameters

2.3.1 Bifurcation Diagrams

In order to calculate the bifurcation diagram for every Lagrangian coordinates, the procedure based on the Poincaré map is used. The Lagrangian coordinates are:

$$\displaystyle{ \left \{\begin{array}{@{}l@{\quad }l@{}} \mathcal{L}_{1} = x^{{\ast}}(t^{{\ast}}) \quad \\ \mathcal{L}_{2} = y^{{\ast}}(t^{{\ast}}) \quad \\ \mathcal{L}_{3} = w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})\quad \end{array} \right. }$$

(2.24)

By considering the bifurcation diagram for the $\mathcal{L}_{i}$ coordinate, the n-dimensional phase space of the studied system can be intersected with a (n − 1)-dimensional surface passing through $\dot{\mathcal{L}}_{i} = 0$. All the points $\mathcal{L}_{i}$ on the Poincaré section are plotted for each value of the belt speed [1, 3].

In Fig. 2.3a–c, the bifurcation diagrams of all the Lagrangian coordinates are shown for the belt velocity range $v = v_{dr}^{{\ast}} = 10^{-4} \div 3 \cdot 10^{-2}$.

The bifurcation diagram for $\mathcal{L}_{1}$ (Fig. 2.3a) shows a limit cycle for all the belt velocities, as expected. The mass motion along $x^{{\ast}}(t^{{\ast}})$ is not affected by the beam dynamics and the stick-slip motion, does not appear.

While for $\mathcal{L}_{3}$ (Fig. 2.3c) the system shows a regular behaviour (for each value of the velocity $v_{dr}^{{\ast}}$ there is a limit cycle that increases with the belt speed), for $\mathcal{L}_{2}$ (Fig. 2.3b) the system have an unpredictable motion, showing the period doubling phenomenon for a belt velocity range ($v_{dr}^{{\ast}}\in \left [2.5 \cdot 10^{-3};9 \cdot 10^{-3}\right ]$), for big values of $v_{dr}^{{\ast}}$ the coordinate $\mathcal{L}_{2}$ moves on a limit cycle. This kind of behaviour of the bifurcation diagram shows that the system response is sensitive to the variation of the belt velocity.

From the diagrams analysis, three different kind of motions can be detected for $\mathcal{L}_{2}$: a pure stick-slip motion ($v_{dr}^{{\ast}} < 2.5 \cdot 10^{-3}$), a bifurcating motion corresponding to the period doubling velocity range ($v_{dr}^{{\ast}}\in \left [2.5 \cdot 10^{-3};9 \cdot 10^{-3}\right ]$) and a pure slip motion ($v_{dr}^{{\ast}} > 9 \cdot 10^{-3}$).

Fig. 2.3

Bifurcation diagrams of $x^{{\ast}}(t^{{\ast}})$ (a), $y^{{\ast}}(t^{{\ast}})$ (b) and $w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})$ (c)

2.3.2 Time and Frequency Domain

For the belt speed $v_{dr}^{{\ast}} < 2.5 \cdot 10^{-3}$, the stick-slip behaviour is clearly shown in Figs. 2.4b and 2.5c. During the stick phase the mass velocity is constant and equal to the belt speed, while during the slip one there is a relative velocity between mass and belt.

Fig. 2.4

Phase spaces of $x^{{\ast}}(t^{{\ast}})$ (a), $y^{{\ast}}(t^{{\ast}})$ (b) and $w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})$ (c) at $v_{dr}^{{\ast}} = 0.0005$

Fig. 2.5

Time evolution and FFT of $y^{{\ast}}(t^{{\ast}})$ and $dy^{{\ast}}(t^{{\ast}})/dt^{{\ast}}$ at $v_{dr}^{{\ast}} = 0.0005$

In the time domain (see Fig. 2.5a, c) a stick-slip period T _s  = 0. 54 can be detected. The system response in the frequency domain is characterized by the stick slip frequency f _s and by its super-harmonics as shown in Figs. 2.5c and 2.6c, moreover some of them are very close the beam natural frequencies causing the excitation of some modes in the beam (see Fig. 2.6a, c).

Fig. 2.6

Time evolution and FFT of $w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})$ and $dw^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})/dt^{{\ast}}$ at $v_{dr}^{{\ast}} = 0.0005$

The power exchanged between mass and belt is regular for the whole simulation, and different than zero only when the mass slides on the belt (see Fig. 2.7a, as expected; on the other hand the beam exchange more power with the mass (see Fig. 2.7c), cause of the modes excitation, and the power evolution in very irregular due to all the sub and super harmonics of the stick-slip frequency (see Fig. 2.6d).

Fig. 2.7

Time evolution and FFT of the exchanged power between belt and mass $W_{f}^{{\ast}}(t^{{\ast}})$ and between mass and beam $W_{b}^{{\ast}}(t^{{\ast}})$ at $v_{dr}^{{\ast}} = 0.0005$

In the bifurcating belt speed ($v_{dr}^{{\ast}}\in \left [2.5 \cdot 10^{-3};0.9 \cdot 10^{-3}\right ]$) the stick-slip behaviour is visible just in the first few time steps (see Figs. 2.8 and 2.9c), but it is possible also in this case to detect a frequency f _s  = 0. 25 that is responsible the complex response of the system due to the presence of some super-harmonics of f _s (see Figs. 2.9c and 2.10c).

Fig. 2.8

Phase spaces of $x^{{\ast}}(t^{{\ast}})$ (a), $y^{{\ast}}(t^{{\ast}})$ (b) and $w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})$ (c) at $v_{dr}^{{\ast}} = 0.005$

Fig. 2.9

Time evolution and FFT of $y^{{\ast}}(t^{{\ast}})$ and $dy^{{\ast}}(t^{{\ast}})/dt^{{\ast}}$ at $v_{dr}^{{\ast}} = 0.005$

Fig. 2.10

Time evolution and FFT of $w^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})$ and $dw^{{\ast}}(z_{A}^{{\ast}},t^{{\ast}})/dt^{{\ast}}$ at $v_{dr}^{{\ast}} = 0.005$

As shown in the bifurcation diagram in Fig. 2.3c, the beam response is predictable and its phase space increases with the belt speed, that is the reason why the power exchanged with the belt has always the same shape (see Fig. 2.11c) but different scaling factor.

Fig. 2.11

Time evolution and FFT of the exchanged power between belt and mass $W_{f}^{{\ast}}(t^{{\ast}})$ and between mass and beam $W_{b}^{{\ast}}(t^{{\ast}})$ at $v_{dr}^{{\ast}} = 0.005$

The power received by the mass from the belt (see Fig. 2.11a) is less regular in this velocity range and it is influenced by the beam response (see Fig. 2.11b, d).

2.3.3 Maximum Lyapunov Exponent

In order to check if the system response is sensitive to a variation of the initial conditions, the characteristic Lyapunov exponent is considered.

The stability of a generic trajectory $\bar{\mathbf{x}}(t)$, obtained by a perturbation of the initial conditions, is checked by considering its distance from the reference trajectory $\mathbf{x}(t)$. The maximum Lyapunov exponent is defined by:

$$\displaystyle{ \varLambda _{max} =\lim _{t\rightarrow \infty }\lim _{\varDelta (0)\rightarrow 0}\frac{1} {t}\ln \left [ \frac{\varDelta (t)} {\varDelta (0)}\right ] }$$

(2.25)

where Δ(0) is the perturbation of the initial condition and Δ(t) is the trajectories distance for each time [4, 5].

A positive value of the maximum Lyapunov exponent represents a divergence in time of the two considered trajectories, underlining the system dependence of the initial conditions.

For a selected belt velocity ($v_{dr}^{{\ast}} = 0.0005$) the maximum Lyapunov exponent has the time evolution shown in Fig. 2.12.

Fig. 2.12

Time evolution of the maximum Lyapunov exponent at $v_{dr}^{{\ast}} = 0.0005$

For few time steps the exponent reaches negative values but the dynamics of the global system exhibits its chaotic characteristic with a positive value of the exponent for the last time step and also for the most of its evolution.

Figure 2.13 shows the variation of the last value of the exponent with the belt speed, it is positive for all the belt speed range. The plot shows the three different behaviours identified in the bifurcation diagram of $\mathcal{L}_{2}$ (Fig. 2.3b): a stick-slip ($v_{dr}^{{\ast}} < 2.5 \cdot 10^{-3}$), a bifurcating ($v_{dr}^{{\ast}}\in \left [2.5 \cdot 10^{-3};9 \cdot 10^{-3}\right ]$) and a pure slip range ($v_{dr}^{{\ast}} > 9 \cdot 10^{-3}$).

During the stick-slip range the exponents is positive but its trend is decreasing, in the bifurcating range the exponent slope is positive while in the pure slip range a new decreasing trend is shown, underlining that the system is going to reach a stable limit cycle.

Fig. 2.13

Maximum Lyapunov exponent versus belt velocity

2.4 Concluding Remarks

In this paper the behavior of a continuous dynamical system, joint by a lumped system excited by a belt is studied.

The continuous system is modeled as an Euler-Bernoulli beam, and the coupling one is described by a two degrees of freedom harmonic oscillator excited by a belt at a constant speed along one direction.

The analysis is focused on the influence of the belt speed on the global system behavior. This induces either stick-slip phenomena (low speed of the belt) or only slip (high speed of the belt).

The system sensitivity to the variation of the belt speed and to the system initial conditions are investigated, these phenomena are studied by the bifurcation diagrams and the maximum Lyapunov exponent. Further investigations are focused to understand the chaotic nature of the phenomenon.

A particular attention is posed on the study of system response and on the power balance of the excited system. The stick-slip phenomenon induces super harmonics which effect is the excitation of the natural frequencies of the continuous system.