Motion Planning of a Spherical Mobile Robot

Abstract

As a new member of mobile robot family, spherical mobile robot (shortly spherical robot) is well-known for its compact structure and agile motion, but its special motion principle and nonholonomic characteristic complicate its motion planning. This chapter first overviews the previous research work of the motion planning of spherical robot, and then introduces the structure and motion principle of spherical robot BHQ-1, and last presents one kinematic motion planning method and one dynamic motion planning method for BHQ-1 respectively. Compared with other motion planning methods of spherical robot, those two methods realize the motion planning of a spherical robot in 3D space and focus more on practical applications.

1 Introduction

Spherical mobile robot (shortly spherical robot) is a new type of mobile robot boomed in recent decades [1–8, 18], which usually has a ball-shaped outer shell to include all its mechanism, control system and batteries inside. Different from those traditional mobile robots, such as wheeled robot, legged robot and tracked robot, spherical robot has no apparent locomotion mechanism and its outer shell works as that. Although many different kinds of spherical robots have been developed, there are mainly two principles to realize its motion: center of gravity displacement and angular momentum conservation. Spherical robot is characterized as compact structure and agile motion, which make it very suitable to be applied in those unmanned environments. For example, like a tumbler a spherical robot can never overturn, even if suffered with collision or falling down it can resume stability quickly. The research on spherical robot mainly focuses on the mechanism design and motion control.

From the control point of view, spherical robot is a nonholonomic system that can control more configuration variables than the number of its degrees of freedom or control inputs but accompanied with much more complexity. Aarne Halme et al. established the kinematic motion model and dynamic motion equation of a spherical robot in one dimensional space by regarding it as a rolling disk, and analyzed its such motion capabilities as uphill motion and overrunning an obstacle as well as some basic motion features [1, 13]. Antonio Bicchi et al. deduced a planar quasi-static kinematic model of a spherical robot by linking a unicycle and a plate-ball system together through some constraints, and planned its motion through solving a set of nonlinear equations [2, 14, 15]. Bhattacharya and Agrawal deduced a first-order mathematical motion model of a spherical robot under the constraints of non-slip and angular momentum conservation, and presented three types of motion planners by considering feasibility, minimum energy and minimum time separately [3]. Mukherjee et al. presented two geometric motion planning strategies to realize the partial and complete reconfiguration of a spherical robot respectively, and the partial reconfiguration strategy uses spherical triangles to bring the sphere to a desired position and a specific orientation and the complete reconfiguration strategy generates a four-steps motion to move the sphere along a trajectory composed of straight lines and curves [4, 16]. Javadi et al. established a dynamic model of a spherical robot with Newton formulation and presented a trajectory planning method by directly calculating the best solution of each step-motor’s movement [5]. Cameron et al. discussed the kinematic and dynamic modeling of nonholonomic system and deduced a simplified Boltzmann-Hamel equation for both holonomic and nonholonomic systems [9]. Zhan et al. established a dynamic model of a spherical robot with the simplified Boltzmann-Hamel equation, based on which the motion of a spherical robot is divided into linear motion and circular motion so as to realize complex trajectory planning by dividing it into line segments and curve segments [10]. Chen et al. presented a time and energy optimal trajectory planning method based on quasi-velocity motion model and Hamiltonian function, and discussed the influence of three key factors on the shape and direction of the planned trajectory [11]. Jaimez et al. established the dynamic model of a spherical robot Omnibola with Newton-Euler equations and compared its actual motions with the simulated ones through experiments [18].

In the following of this chapter, a brief introduction of spherical robot BHQ-1 will be given first, and then one motion planning method based on kinematics and one motion planning method based on dynamics will be introduced separately.

2 Brief Introduction of Spherical Robot BHQ-1

BHQ-1 is the first kind of spherical robot designed by our lab and the first prototype was implemented in 2001 [8], which is designed for the exploration of unmanned environments. As shown in Fig. 1, BHQ-1 is mainly composed of two motors, one hollow axle, one mass, one camera, one controller and battery combination, and one ball-shaped shell. In Fig. 1 frame {X$_\mathrm{b}$Y$_\mathrm{b}$Z$_\mathrm{b}$} is a body frame attached to the hollow axle and its origin is coincident with the geometric center of the sphere. The hollow axle connects with the shell through two ball bearings at the two ends and serves as a chassis or frame to install other components, so the outer shell can rotate around the axis of the hollow axle freely and the camera installed on the hollow axle can keep a relatively steady posture no matter BHQ-1 is moving or static. Motor 1 is installed on the hollow axle but its output axle is fixed to the shell, so its rotation can result in the displacement of the mass along Y$_\mathrm{b}$ direction. Motor 2 is also installed on the hollow axle and its output axle is fixed to a link so as to drive the mass along X$_\mathrm{b}$ direction. Installed on the hollow axle the camera is used to take pictures of environments which can be transmitted to a remote control center through a wireless image transmission system. According to the received pictures an operator can not only observe the environment but also control the motion of the spherical robot through a joy stick.

Fig. 1

Structure of spherical robot BHQ-1 (1: motor 1, 2: motor 2, 3: mass, 4: shell, 5: camera, 6: bearing, 7: controller & battery, 8: hollow axle)

The motion principle of the spherical robot is that the rotations of motor 1 and motor 2 make the mass rotate about axes X$_\mathrm{b}$ and Y$_\mathrm{b}$ respectively and result in the displacement of the center of gravity of the whole system, which produces a displacement moment to counteract the friction moment and makes the robot move. As shown in Fig. 1, when motor 1 rotates and motor 2 keeps still, the mass, the hollow axle, the controller and battery combination, and motor 2 will rotate about the axis of the hollow axle. If the angle displacement $\uptheta \ge \theta _{0}$ ($\theta _{0}$ is the angle displacement of the mass to balance the moment caused by static friction), the robot will move forward or backward. Because the moment caused by dynamic friction is less than that caused by static friction, the mass will stay at a position where the angle displacement of the mass is less than $\theta _{0}$. So the system is balanced and the robot can go forward or backward continuously. If motor 1 and motor 2 both rotate the mass will rotate around both axes X$_\mathrm{b}$ and Y$_\mathrm{b}$, and the compound motion of the mass will produce a displacement gravity moment to cause the robot to turn to the side where the mass stays. For example, if the mass moves to the $+\mathrm{X}_\mathrm{b}$ direction the robot will turn to $+\mathrm{X}_\mathrm{b}$ direction and if the mass moves to the –Y$_\mathrm{b}$ direction the robot will turn to the –Y$_\mathrm{b}$ direction. So any required motion of spherical robot BHQ-1 can be easily achieved by the separate control or compound control of two motors.

3 Kinematics Based Motion Planning of BHQ-1

3.1 Nonholonomic Constraint Equations of BHQ-1

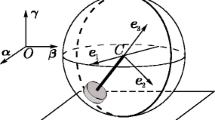
In order to describe the configuration of spherical robot BHQ-1, such following frames are established as shown in Fig. 2. Frame {OXYZ} is the reference frame, frame {O$_\mathrm{b}$X$^\prime$Y$^\prime$Z$^\prime$} is a body reference frame with its origin locating at the geometric center of the sphere and its orientation the same as that of reference frame {OXYZ}, frame {O$_\mathrm{b}$X$_\mathrm{b}$Y$_\mathrm{b}$Z$_\mathrm{b}$} is the body frame fixed to the hollow axle of BHQ-1 and its origin is the geometric center of the sphere. It’s obvious that BHQ-1 cannot move along Z axis, so it requires five variables to describe its configuration: $x,y,\psi ,\theta ,\varphi$, among which $x,y$ are the position coordinates of the geometric center of BHQ-1 expressed in the reference frame {OXYZ}, $\psi ,\theta ,\varphi$ are the ZXZ Euler angle to describe the orientation of BHQ-1.

Fig. 2

Frames describing the configuration of BHQ-1

When spherical robot BHQ-1 moves on the ground, it will come under a velocity constraint due to rolling without slipping: the velocity of the contact point of BHQ-1 and the ground must be the same. Then the following velocity constraint equations can be deduced.

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{x}+r(\dot{\varphi }\cos \psi \sin \theta -\dot{\theta }\sin \psi )=0} \\ {\dot{y}+r(\dot{\varphi }\sin \psi \sin \theta +\dot{\theta }\cos \psi )=0} \\ \end{array} }} \right. \end{aligned}$$

(1)

where, r is the radius of BHQ-1.

For nonholonomic systems quasi-coordinates are widely used due to its several advantages when compared with generalized coordinates. For example, the nonholonomic constraints could be expressed more easily with quasi-coordinates and the projections of kinetic energy can be expressed more simply with quasi-velocities. Normally, the left part of the nonholonomic constraint equations of some systems can be chosen as quasi-velocities and the choice of other quasi-velocities should facilitate the calculation [12].

Here, five quasi-velocities $\omega _1$, $\omega _2$, $\omega _3$, $\omega _4$, $\omega _5$ of spherical robot BHQ-1 are chosen as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\omega _1 =\dot{\varphi }\sin \psi \sin \theta +\dot{\theta }\cos \psi } \\ {\omega _2 =-\dot{\varphi }\cos \psi \sin \theta +\dot{\theta }\sin \psi } \\ {\omega _3 =\dot{\psi }+\dot{\varphi }\cos \theta } \\ {\omega _4 =\dot{x}-r\omega _2 } \\ {\omega _5 =\dot{y}+r\omega _1 } \\ \end{array} }} \right. {}{}{} \end{aligned}$$

(2)

where $\omega _{1},\omega _{2},\omega _{3}$ are the projections of the angle velocities of BHQ-1 on the three axes of frame ${\{\mathrm O}_b {\mathrm X}'{\mathrm Y}'{\mathrm Z}'\}, \omega _{4},\omega _{5}$ are defined according to the rolling without slipping constraint equations (1). It is easy to get $\omega _{4}=0,\omega _{5}=0$.

3.2 Optimized Motion Planning Based on Hamiltonian Function

Spherical robot includes all the energy sources inside its shell, so the available energy sources are limited to its size and structure. In order to make a spherical robot move further with the limited energy sources, time and energy based optimized motion planning is greatly preferred.

When spherical robot BHQ-1 moves on the ground, its hollow axle will always keep horizontal except it turns aside. Furthermore, for the ZXZ Euler angles the first two rotations angles $\psi$ and $\theta$ cannot result in the rotation of the hollow axle around Y$_\mathrm{b}$ axis, that means only $\varphi$ can do that, so we can suppose $\varphi =0$ in order to simplify the motion planning problem, and then the configuration of BHQ-1 is simplified as $P=[x,y,\psi ,\theta ]^{T}$. So Eq. (2) can be simplified as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\omega _1 =\dot{\theta }\cos \psi } \\ {\omega _2 =\dot{\theta }\sin \psi } \\ {\omega _3 =\dot{\psi }} \\ {\omega _4 =\dot{x}-r\omega _2 =0} \\ {\omega _5 =\dot{y}+r\omega _1 =0} \\ \end{array} }} \right. \end{aligned}$$

(3)

From Eq. (3) we can get the kinematics model of BHQ-1 as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{x}=r\omega _2 } \\ {\dot{y}=-r\omega _1 } \\ {\dot{\psi }=\omega _3 } \\ {\dot{\theta }=\omega _1 \sec \psi } \\ \end{array} }} \right. \end{aligned}$$

(4)

Rewrite Eq. (4) in the matrix form as

$$\begin{aligned} \left[ {{\begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ {\dot{\psi }} \\ {\dot{\theta }} \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} 0 &{} r &{} 0 \\ {-r} &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ {\sec \psi } &{} 0 &{} 0 \\ \end{array} }} \right] \cdot \left[ {{\begin{array}{lll} {\omega _1 } \\ {\omega _2 } \\ {\omega _3 } \\ \end{array} }} \right] =f(P,u),u=[{\begin{array}{lll} {\omega _1 }&{} {\omega _2 }&{} {\omega _3 } \\ \end{array} }]^{T} \end{aligned}$$

(5)

In order to plan an optimized trajectory from the initial configuration $P_{i}=[x_{i},y_{i},\psi _{i},\theta _{i}]^{T}$ to the goal configuration $P_{g}=[x_{g},y_{g},\psi _{g},\theta _{g}]^{T}$, following cost function is introduced.

$$\begin{aligned} J = \int _0^{t_g } {\left[ {k+\frac{1}{2}(1-k)(b_1 \omega _1^2 +b_2 \omega _2^2 +b_3 \omega _3^2 )} \right] } dt, \quad (b_1 \ge 0,b_2 \ge 0,b_3 \ge 0, 0\le k\le 1) \end{aligned}$$

(6)

where, k describes the tendency of the function to the least time or the least energy, if k is much smaller the function trends to approach the least energy more, if k is much bigger the function trends to approach the least time more; $b_{1},b_{2},b_{3}$ describes the weight values of three angle velocities $\omega _{1},\omega _{2},\omega _{3}$.

A Hamiltonian function is constructed as follows.

$$\begin{aligned} H&=L+\lambda ^{T}f(P,u) \nonumber \\&=\left[ \!{k+\frac{1}{2}(1-k)(b_1 \omega _{1}^{2} +b_{2} \omega _{2}^{2} +b_{3} \omega _{3}^{2})} \!\right] +\,\lambda _{1} r\omega _{2} -\lambda _{2} r\omega _{1} +\lambda _{3} \omega _{3} +\lambda _{4} \omega _{1} \sec \psi \end{aligned}$$

(7)

where, $\lambda =[\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}]^{T}$ is the Lagrange multiplier vector. In order to optimize the trajectory of BHQ-1, $\dot{\lambda }=-(\frac{\partial H}{\partial P})^{T}$ must be satisfied, namely

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{\lambda }_1 =-\frac{\partial H}{\partial x}=0} \\ {\dot{\lambda }_2 =-\frac{\partial H}{\partial y}=0} \\ {\dot{\lambda }_3 =-\frac{\partial H}{\partial \psi }=-\lambda _4 \omega _1 \sin \psi \sec ^{2}\psi } \\ {\dot{\lambda }_4 =-\frac{\partial H}{\partial \theta }=0} \\ \end{array} }} \right. \end{aligned}$$

(8)

From Eq. (8) we can find that $\lambda _{1},\lambda _{2},\lambda _{4}$ are all constants, but $\lambda _{3}$ is a variable on the entire trajectory. In order to optimize the quasi-velocities $\omega _{1}, \omega _{2}, \omega _{3}$, the entire trajectory should satisfy $\frac{\partial H}{\partial u}=0$, namely

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{\partial H}{\partial \omega _1 }=0\Rightarrow (1-k)b_1 \omega _1 -\lambda _2 r+\lambda _4 \sec \psi =0} \\ {\frac{\partial H}{\partial \omega _2 }=0\Rightarrow (1-k)b_2 \omega _2 +\lambda _1 r=0} \\ {\frac{\partial H}{\partial \omega _3 }=0\Rightarrow (1-k)b_3 \omega _3 +\lambda _3 =0} \\ \end{array} }} \right. \end{aligned}$$

(9)

From Eq. (9) the optimized quasi-velocities can be got as following.

$$\begin{aligned} \left\{ {{\begin{array}{l} {\omega _1 =\frac{\lambda _2 r-\lambda _4 \sec \psi }{b_1 (1-k)}} \\ {\omega _2 =-\frac{\lambda _1 r}{b_2 (1-k)}} \\ {\omega _3 =-\frac{\lambda _3 }{b_3 (1-k)}} \\ \end{array} }} \right. \end{aligned}$$

(10)

Because on the entire optimized trajectory Hamiltonian function must be 0 [9], namely

$$\begin{aligned} H=L+\lambda ^{T}f(x,u)&=k+\frac{1}{2}(1-k)(b_1 \omega _1^2 +b_2 \omega _2^2 +b_3 \omega _3^2 )+\lambda _1 r\omega _2 -\lambda _2 r\omega _1 \nonumber \\&\quad +\lambda _3 \omega _3 +\lambda _4 \omega _1 \sec \psi =0 \end{aligned}$$

(11)

Substitute the three optimized angle velocities in Eq. (10) for those in Eq. (11) we can get

$$\begin{aligned} \lambda _3 =\pm \sqrt{-b_3 \frac{2b_1 b_2 (k^{2}-k)+r^{2}(b_1 \lambda _1^2 +b_2 \lambda _2^2 )-2rb_2 \lambda _2 \lambda _4 \sec \psi +b_2 \lambda _4^2 \sec ^{2}\psi }{b_1 b_2 }} \end{aligned}$$

(12)

From the above equation we can find $\lambda _{3}=\lambda _{3}(\psi )$. The symbol of $\lambda _{3}$ can be got from experiments, and for spherical robot BHQ-1 we choose it as a negative one according to experience. Then the trajectory equation of spherical robot BHQ-1 can be deduced from Eq. (4) as follows.

$$\begin{aligned} \begin{array}{l} \left. {\begin{array}{l} \dot{x}=r\omega _2 \\ \dot{\psi }=\omega _3 \\ \end{array}} \right\} \Rightarrow \frac{dx}{d\psi }=\frac{r\omega _2 }{\omega _3 }=\frac{\lambda _1 r^{2}b_3 }{\lambda _3 b_2 }=h_1 (\psi ) \\ \left. {\begin{array}{l} \dot{y}=-r\omega _1 \\ \dot{\psi }=\omega _3 \\ \end{array}} \right\} \Rightarrow \frac{dy}{d\psi }=-\frac{r\omega _1 }{\omega _3 }=\frac{(\lambda _2 r-\lambda _4 \sec \psi )rb_3 }{\lambda _3 b_1 }=h_2 (\psi ) \\ \end{array} \end{aligned}$$

(13)

From Eq. (13) we can find that $\frac{dx}{d\psi },\frac{dy}{d\psi }$ are all functions of $\psi$, which means the calculation of x, y can be greatly simplified because it can be got by integrating the above equation from initial $\psi =0$ to final $\psi =\psi _g$, namely

$$\begin{aligned} \left\{ {\begin{array}{l} x=\int _0^{\psi _g } {h_1 } (\psi )d\psi \\ y=\int _0^{\psi _g } {h_2 } (\psi )d\psi \\ \end{array}} \right. \end{aligned}$$

(14)

It’s clear that Eq. (14) has no variables of time t, so there is no need to find the final time t $_{g}$ when computing x and y. However, $\psi$ cannot be a monotone function, so it should be divided into several segments and the piecewise points are those that make $\dot{\psi }=0$. Thus in each segment $\psi$ will increase or decrease monotonously. From Eq. (4) we can find that $\upomega _{3}=0$ must be satisfied in order to make $\dot{\psi }=0$, and then from Eqs. (8) and (10) we can get $\lambda _3 =\lambda _3 (\psi )=0$, so those piecewise points can be decided according to the equation. So the optimized trajectory of spherical robot BHQ-1 can be deduced.

In real applications a group of suitable or optimized coefficients $\lambda _1, \lambda _2, \lambda _4$ should be decided first for the given goal position and orientation $(x_g, y_g, \psi _g, \theta _g)$, and which are usually got according to experiences.

For spherical robot BHQ-1, suppose the initial configuration is $P_i =[0,0,\frac{\pi }{2},0]$ and the final configuration is $p_g =[1.25,1.25,\frac{\pi }{2},0]$, then the optimized motion can be planned as follows. First, choose a group of coefficients $\lambda _1, \lambda _2, \lambda _4$, here according experience we choose $\lambda _1 =0.5,\lambda _2 =0.5,\lambda _4 =0.3$. Then we choose $k=0.5$, $b_1 =b_2 =b_3 =1$. The optimized trajectory and the changes of two orientation variables of spherical robot BHQ-1 are shown in Fig. 3. From the simulations we can find that the planned trajectory and the curves of two orientations are all smooth.

Fig. 3

Trajectory planning simulations a Planned trajectory. b Change of $\psi$. c Change of $\theta$

3.3 The Influence of $\lambda _1, \lambda _2, \lambda _4$ on Planned Trajectory

In order to facilitate the choice of coefficients $\lambda _{1},\lambda _{2},\lambda _{4}$, of which the influence on the trajectory shape and the moving direction of robot BHQ-1 are discussed by a group of simulations. Here, suppose $\psi _{g}=\frac{2\pi }{5}$.

First, let $\lambda _{2}$ and $\lambda _{4}$ be constants and let $\lambda _{1}$ change from $-1.5$ to 1.5, different planned trajectories are shown in Fig. 4. From the simulation results we can find that the change of $\lambda _{1}$ can affect the trajectory shape greatly and the symbol of $\lambda _{1}$ can affect the moving direction of BHQ-1 along Y direction.

Fig. 4

Trajectory planning results when $\lambda _1$ changes

Then let $\lambda _{1}$ and $\lambda _{4}$ be constants and let $\lambda _{2}$ change from $-0.9$ to 0.9, those different planned trajectories are shown in Fig. 5. From the simulation results we can find that the change of $\lambda _{2}$ affects the trajectory shape little and the symbol of $\lambda _{2}$ cannot change the moving direction of spherical robot BHQ-1.

Fig. 5

Trajectory planning results when $\lambda _2$ changes

At last, let $\lambda _{1}$ and $\lambda _{2}$ be constants and let $\lambda _{4}$ change from $-0.3$ to 0.3, those different planned trajectories are shown in Fig. 6. From the simulation results we can find that the change of $\lambda _{4}$ can greatly affect the trajectory shape and the final position (x, y), and the symbol of $\lambda _{4}$ can change the moving direction of BHQ-1 along X direction.

Fig. 6

Trajectory planning results when $\lambda _4$ changes

The above simulations reveal the influence of $\lambda _{1}, \lambda _{2}, \lambda _{4}$ on the planned trajectory of spherical robot BHQ-1 respectively, which can help to decide a group of suitable $\lambda _{1}, \lambda _{2}, \lambda _{4}$ for a real application by experience.

One way to directly get a group of optimized $\lambda _{1}, \lambda _{2}, \lambda _{4}$ has been proposed in [17], which is called “shooting” method. Using the “shooting” method, we can plan an optimal trajectory of spherical robot BHQ-1 from start position (0, 0) to final position (1.5, 3), as shown in Fig. 7. Here, $k=0.5,b_1 =b_2 =b_3 =1,\lambda _1 =0.08,\lambda _2 =0.78,\lambda _4 =0.56$. Although the “shooting” method can get the optimized variables, it’s not always effective for some cases.

Fig. 7

Optimal trajectory from (0, 0) to (1.5, 3) by shooting method

3.4 Motion Planning Experiments

In order to validate the proposed trajectory planning method motion experiments of spherical robot BHQ-1 avoiding an obstacle were done. BHQ-1 is planned to move straight first, but there is an obstacle in its path, when it detects the obstacle it will avoid it. An infrared sensor was used by BHQ-1 to detect obstacles, and the motion commands were sent to BHQ-1 from a PC through a wireless system. The radius of the experimental spherical robot BHQ-1 is 200 mm, and its total mass is about 2.5 kg.

Figure 8 shows some pictures of one experiment during which spherical robot BHQ-1 avoided an obstacle successfully. To be honest, there were also several cases that BHQ-1 could not avoid the obstacle successfully due to some practical reasons, such as the motion errors, the delay on re-planning.

Fig. 8

Motion planning experiments of BHQ-1

4 Dynamics Based Motion Planning of BHQ-1

4.1 Dynamic Model of BHQ-1

Compared with kinematics based motion planning, dynamics based motion planning can achieve more steady motion and better performance when meeting unpredicted external disturbances. But not all the dynamic modeling methods can be used for nonholonomic systems except Gibbs-Appell equation, improved Lagrange equation, Kane equation and Boltzmann-Hamel equation, etc. However, it is always difficult to use those methods to establish a simplified dynamic model of a spherical robot that can be used in real applications due to the complex deduction procedures and time-consuming computations.

From D’Alembert-Lagrange principle: $\displaystyle \mathop {\sum }\nolimits _{k=1}^n {(\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_k }-\frac{\partial T}{\partial q_k }-Q_k )\delta q_k =0}$, Cameron et al. deduced a simplified Boltzmann-Hamel equation that can be applied to both holonomic system and nonholonomic system [9], shown in the following.

$$\begin{aligned} \frac{d}{dt}\frac{\partial \bar{{E}}}{\partial \omega _I }+\sum _{j=1}^n {\sum _{i=1}^n {\eta _{iI} \gamma _{ij} } } \frac{\partial \bar{{E}}}{\partial \omega _j }-\sum _{j=1}^n {\eta _{jI} \frac{\partial \bar{{E}}}{\partial q_j }} =M_I \end{aligned}$$

(15)

where, $\upomega$ is the vector of quasi-velocities, E is the kinetic energy, M is the generalized driving force, $\eta$ and $\gamma$ are coefficients, I denotes the independent quasi-coordinates, n is the number of the generalized coordinate $q_{j}$, t is the time.

Different from the traditional Boltzmann-Hamel equation, the new one is expressed explicitly in terms of generalized coordinate $q_{j}$ and coefficient $\gamma$ can be easily calculated. So the dynamic model has a more compact expression and can be used more easily.

A configuration vector $P=[x,y,\psi ,\theta ,\varphi ]^{T}$ is used to describe the position and orientation of spherical robot BHQ-1, and the definition of those variables are the same as that in Sect. 3.

Rewrite Eq. (2) in matrix form as

$$\begin{aligned} \left[ {{\begin{array}{l} {\omega _1 } \\ {\omega _2 } \\ {\omega _3 } \\ {\omega _4 } \\ {\omega _5 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 0&{} 0&{} 0&{} {\cos \psi }&{} {\sin \theta \sin \psi } \\ 0&{} 0&{} 0&{} {\sin \psi }&{} {-\sin \theta \cos \psi } \\ 0&{} 0&{} 1&{} 0&{} {\cos \theta } \\ 1&{} 0&{} 0&{} {-r\sin \psi }&{} {r\sin \theta \cos \psi } \\ 0&{} 1&{} 0&{} {r\cos \psi }&{} {r\sin \theta \sin \psi } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ {\dot{\psi }} \\ {\dot{\theta }} \\ {\dot{\varphi }} \\ \end{array} }} \right] =\alpha \left[ {{\begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ {\dot{\psi }} \\ {\dot{\theta }} \\ {\dot{\varphi }} \\ \end{array} }} \right] \end{aligned}$$

(16)

where $\alpha$ is a $5 \times 5$ transformation matrix. From Eq. (16) we can deduce

$$\begin{aligned} \left[ {{\begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ {\dot{\psi }} \\ {\dot{\theta }} \\ {\dot{\varphi }} \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 0&{} r&{} 0&{} 1&{} 0 \\ {-r}&{} 0&{} 0&{} 0&{} 1 \\ {-\sin \psi \cot \theta }&{} {\cos \psi \cot \theta }&{} 1&{} 0&{} 0 \\ {\cos \psi }&{} {\sin \psi }&{} 0&{} 0&{} 0 \\ {\sin \psi \csc \theta }&{} {-\cos \psi \csc \theta }&{} 0&{} 0&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\omega _1 } \\ {\omega _2 } \\ {\omega _3 } \\ {\omega _4 } \\ {\omega _5 } \\ \end{array} }} \right] =\beta \left[ {{\begin{array}{l} {\omega _1 } \\ {\omega _2 } \\ {\omega _3 } \\ {\omega _4 } \\ {\omega _5 } \\ \end{array} }} \right] \end{aligned}$$

(17)

where $\beta$ is also a $5 \times 5$ transformation matrix.

Coefficient $\gamma _{ij}$ in Eq. (15) can be calculated by $\alpha$ and $\beta$ according to the following equation.

$$\begin{aligned} \gamma _{ij} =\sum _{k=1}^5 {\sum _{s=1}^5 {\omega _s \beta _{ks} } } \left( \frac{\partial \alpha _{ij} }{\partial q_k }-\frac{\partial \alpha _{kj} }{\partial q_i }\right) \end{aligned}$$

(18)

Kinetic energy $\bar{E}$ of spherical robot BHQ-1 is

$$\begin{aligned} \bar{{E}}=\frac{1}{2}m(\dot{x}^{2}+\dot{y}^{2})+\frac{1}{2}\times \frac{2}{5}mr^{2}\cdot (\dot{\psi }^{2}+\dot{\theta }^{2}+\dot{\varphi }^{2}+2\dot{\psi }\dot{\varphi }\cos \theta ) \end{aligned}$$

(19)

where m is the total mass of BHQ-1. Equation (19) can be expressed by quasi-velocities as

$$\begin{aligned} \bar{{E}}=\frac{1}{2}m\left[ \frac{5}{7}r^{2}(\omega _1 ^{2}+\omega _2 ^{2})+\frac{2}{5}r^{2}\omega _3 ^{2}+2r\omega _2 \omega _4 -2r\omega _1 \omega _5 +\omega _4 ^{2} +\omega _5 ^{2}\right] \end{aligned}$$

(20)

From Eq. (20) we can get

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \bar{{E}}}{\partial \omega _1 }=\frac{7}{5}mr^{2}\omega _1 -mr\omega _5 \\ \frac{\partial \bar{{E}}}{\partial \omega _2 }=\frac{7}{5}mr^{2}\omega _2 +mr\omega _4 \\ \frac{\partial \bar{{E}}}{\partial \omega _3 }=\frac{2}{5}mr^{2}\omega _3 \\ \end{array}} \right. \end{aligned}$$

(21)

Because $\upomega _{4}=\upomega _{5}=0$, we can get the simplified form of Eq. (21) as

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \bar{{E}}}{\partial \omega _1 }=\frac{7}{5}mr^{2}\omega _1 \\ \frac{\partial \bar{{E}}}{\partial \omega _2 }=\frac{7}{5}mr^{2}\omega _2 \\ \frac{\partial \bar{{E}}}{\partial \omega _3 }=\frac{2}{5}mr^{2}\omega _3 \\ \end{array}} \right. \end{aligned}$$

(22)

From Eq. (19) we can get $\frac{\partial \bar{E}}{\partial x}=\frac{\partial \bar{E}}{\partial y} =\frac{\partial \bar{E}}{\partial \psi }=\frac{\partial \bar{E}}{\partial \varphi }=0$.

Substituting those calculated $\eta ,\gamma$ and Eq. (21) for those in Eq. (15) the dynamic model of spherical robot BHQ-1 can be deduced as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{7}{5}mr^{2}\dot{\omega }_1 =m_1^0 -rf_2^0 } \\ {\frac{7}{5}mr^{2}\dot{\omega }_2 =m_2^0 +rf_1^0 } \\ {\frac{2}{5}mr^{2}\dot{\omega }_3 =m_3^0 } \\ \end{array} }} \right. \end{aligned}$$

(23)

where, $m_{1}^{0}, m_{2}^{0}, m_{3}^{0}$ are the projections of the principal moment $m^{0}$ on the three axes of the body reference frame $\{O_b {X}'{Y}'{Z}'\}$, $f_{1}^{0}$, $f_{2}^{0}$ are the projections of the principal force $f^{0}$ on axes ${X}',{Y}'$ of frame $\{O_b {X}'{Y}'{Z}'\}$, $f^{0}$ and $m^{0}$ are the principal force and principal moment imposed on the geometric center of spherical robot BHQ-1 respectively.

4.2 Motion Planning Based on Dynamic Model of BHQ-1

4.2.1 Linear Trajectory Planning

In Fig. 9, frame $\{\mathrm{o}'\mathrm{ijk}\}$ is located on the geometric center of BHQ-1 and its orientation is the same as that of frame $\{oxyz\}$. When spherical robot BHQ-1 moves along a linear trajectory its hollow axle and those installed components will rotate around axis i to reach a high position supposed as the one shown in Fig. 9.

Fig. 9

Straight motion

Because there is no rotation about axes j and $k, \psi =0$ and $\varphi =0$ are obtained, substituting them for the variables in Eq. (16), we can get those quasi-velocities as

$$\begin{aligned} \omega _1 =\dot{\theta },\omega _2 =0,\omega _3 =0,\omega _4 =0,\omega _5 =0 \end{aligned}$$

(24)

In Fig. 9, the gravity direction is along the $-k$ direction (downward vertically), so the projection of gravity on plane $i{o}'j$ is zero, that it to say $f_{1}^{0}= 0$, $f_{2}^{0 }=0$, substituting them for the variables in the dynamic model (23), the following simplified dynamic model of BHQ-1 can be got.

$$\begin{aligned} \left\{ {{\begin{array}{l} {m_1^0 =\frac{7}{5}mr^{2}\ddot{\theta }} \\ {m_2^0 =0} \\ {m_3^0 =0} \\ \end{array} }} \right. \end{aligned}$$

(25)

So the gravity moment exists only around axis i and the mass sways only in the plane ${o}'kj$. From Eq. (25) and

$$\begin{aligned} m_1^0 =mg\vec {l}_j +\vec {f}r \end{aligned}$$

(26)

we can get the driving moment of motor 1 is

$$\begin{aligned} M_1 \left( t \right) =mg\vec {l}_{j}+mL^{2}\ddot{\beta }= -\frac{7}{5}mr\ddot{y}(t)- \vec {f}\cdot r+mL^{2}\ddot{\beta }(t) \end{aligned}$$

(27)

where, L is the distance between the center of the mass and the rotation axis of the hollow axle, ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{j}}}$ is the projection vector of L on axis j, $\beta$ is the angle that the mass deviates from axis k, f is the friction vector imposed on the spherical robot by the ground, g is the gravity acceleration. The driving moment of motor 2 is

$$\begin{aligned} M_2 \left( t \right) =0. \end{aligned}$$

(28)

If spherical robot BHQ-1 moves along a straight trajectory with a constant velocity it is obvious that $\ddot{y}=0$. So we get $\dot{\omega }_1 =0$ from Eq. (16), $\ddot{\theta }=0$ from Eq. (24) and $m_1^0=0$ from Eq. (25), substituting them for the variables in Eq. (26) we can get

$$\begin{aligned} \vec {l}_j =-\frac{\vec {f}\cdot r}{mg} \end{aligned}$$

(29)

$$\begin{aligned} \beta \left( t \right) =\arcsin \frac{\vec {l}_j }{L}=\arcsin \left( -\frac{\vec {f}\cdot r}{mgL}\right) \end{aligned}$$

(30)

Thus when spherical robot BHQ-1 moves along a straight trajectory with a constant velocity the driving moments of two motors are

$$\begin{aligned} \left\{ {{\begin{array}{l} {M_1 =mg\vec {l}_j =-\vec {f}r} \\ {M_2 =0} \\ \end{array} }} \right. \end{aligned}$$

(31)

The simulation results of BHQ-1 moving straight are shown in Fig. 10, where the dashed line is the planned trajectory in theory or the target trajectory and the solid line is the planned trajectory by adding 1 % noise disturbance. From the simulation we can conclude that BHQ-1 can realize motion along a linear trajectory with the deduced dynamic model.

Fig. 10

Simulation results of BHQ-1 moving straight

4.2.2 Circular Trajectory Planning

Assume spherical robot BHQ-1 moves along a circular trajectory from the initial configuration to the final configuration, as shown in Figs. 11 and 12. In Fig. 11, a frame {$o_i x_i y_i$} is established on the geometric center of BHQ-1 with its axis $x_i$ pointing to the center of the circular trajectory and its axis $y_i$ pointing to the tangential direction of the circular trajectory.

Fig. 11

Theoretic trajectory of circular motion of BHQ-1

Fig. 12

Two views of the mass during circular motion

With similar derivation to that of linear trajectory planning, we can deduce $f_{1}^{0}=0,f_{2}^{0}=0,m_{3}^{0}$. Let $p=\frac{7mr^{2}}{5}$ and substitute the above variables for those Eq. (23), we can get

$$\begin{aligned} \left\{ {{\begin{array}{l} {m_1^0 =p\dot{\omega }_1 } \\ {m_2^0 =p\dot{\omega }_2 } \\ {\dot{\omega }_3 =0} \\ \end{array} }} \right. \end{aligned}$$

(32)

Because $m_1^0$, $m_2^0$ are projections of the principal moment on axes i and j, it’s easy to get

$$\begin{aligned} \left\{ {{\begin{array}{l} {m_1^0 \left( t \right) =mg {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{y}}} + {{\mathop {j}\limits ^{\rightharpoonup }}_{\!\!{y}}} \cdot r} \\ {m_2^0 \left( t \right) =mg {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{x}}} + {{\mathop {f}\limits ^{\rightharpoonup }}_{\!\!{x}}} \cdot r} \\ \end{array} }} \right. \end{aligned}$$

(33)

where, ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{x}}}, {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{y}}}$ are the projections of length L on axes x and y respectively, ${{\mathop {f}\limits ^{\rightharpoonup }}_{\!\!{x}}}, {{\mathop {f}\limits ^{\rightharpoonup }}_{\!\!{y}}}$ are the projections of the friction force f on axes x and y respectively.

From Eqs. (16), (32) and (33), we can get

$$\begin{aligned} \left\{ {{\begin{array}{l} {{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{x}}}= \frac{1}{mg}\left( \frac{p}{r}\ddot{x}-{{\mathop {f}\limits ^{\rightharpoonup }}_{\!\!{x}}}\cdot r\right) } \\ {{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{x}}}= \frac{1}{mg}\left( -\frac{p}{r}\ddot{y}-{{\mathop {f}\limits ^{\rightharpoonup }}_{\!\!{x}}}\cdot r\right) } \\ \end{array} }} \right. \end{aligned}$$

(34)

Through coordinates transformation we can get

$$\begin{aligned} \left[ {{\begin{array}{l} {l_{x_i} } \\ {l_{yi} } \\ 0 \\ \end{array} }} \right] =R(z,-\alpha )\cdot \left[ {{\begin{array}{l} {l_x } \\ {l_y } \\ 0 \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} {\cos (-\alpha )}&{} {-\sin (-\alpha )}&{} 0 \\ {\sin (-\alpha )}&{} {\cos (-\alpha )}&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \cdot \left[ {{\begin{array}{l} {l_x } \\ {l_y } \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(35)

where, $\alpha$ is the angle that spherical robot BHQ-1 has moved along the circular trajectory from origin o (as shown in Fig. 11), $l_x,l_y$ are the norms of ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{x}}}, {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{y}}}$ respectively, ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{xi}}}, {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{yi}}}$ are the projections of length L on axes $x_{i}$ and $y_{i}$ respectively (shown in Fig. 11), $l_{xi}, l_{yi}$ are the norms of ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{xi}}}, {{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{yi}}}$ respectively.

From Eqs. (34) and (35) we can obtain

$$\begin{aligned} \left\{ {{\begin{array}{l} {l_{xi} =\frac{p}{mgr}(\ddot{x}\cos \alpha -\ddot{y}\sin \alpha )} \\ {l_{yi} =-\frac{p}{mgr}(\ddot{x}\sin \alpha +\ddot{y}\cos \alpha )+\frac{f\cdot r}{mg}} \\ \end{array} }} \right. \end{aligned}$$

(36)

Because $\alpha =\omega t$, the driving moment of motor 1 can be got as

$$\begin{aligned} M_1 =mg{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{j}}}+ m\ddot{\beta }_y L^{2}=-\frac{p}{r}(\ddot{x}\sin \alpha +\ddot{y}\cos \alpha )+m\ddot{\beta }_y L^{2} \end{aligned}$$

(37)

where, ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{j}}}$ is the projection vector of L on axis $j,\beta _{y}$ is the angle that the mass deviates from axis k measured on plane ${o}'kj$ (as shown in Fig. 12).

The driving moment of motor 2 is

$$\begin{aligned} M_2 = mg{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{i}}}+ m\ddot{\beta }_x L^{2}=\frac{p}{r}(\ddot{x}\cos \alpha -\ddot{y}\sin \alpha )+m\ddot{\beta }_x L^{2} \end{aligned}$$

(38)

where, ${{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{i}}}$ is the projection vector of L on axis i, $\beta _{x}$ is the angle that the mass deviates from axis k measured on planes ${o}'ki$ (as shown in Fig. 12).

If spherical robot BHQ-1 moves along a circular trajectory with a fixed velocity its acceleration $A=\frac{v^{2}}{R}$ should point to the center of the circular trajectory and the tangential velocity of circular trajectory $v=\omega R$ should be a constant. Where, R is the radius of the circular trajectory, is the angle velocity of BHQ-1. The projections of the acceleration A on axes x and y are

$$\begin{aligned} \left\{ {{\begin{array}{l} {A_x =-A\cos (\pi -\alpha )=-A\cos (\pi -\omega t)} \\ {A_y =-A\sin (\pi -\alpha )=-A\sin (\pi -\omega t)} \\ \end{array} }} \right. \end{aligned}$$

(39)

From, $\left\{ \begin{array}{l}\ddot{x}=A_{x}\\ \ddot{y}=A_{y}\end{array}\right.$, Eqs. (16), (32), (39) we can get

$$\begin{aligned} \left\{ {{\begin{array}{l} {m_1^0 (t)=\frac{pA}{r}\sin (\omega t)} \\ {m_2^0 (t)=\frac{pA}{r}\cos (\omega t)} \\ \end{array} }} \right. \end{aligned}$$

(40)

From Eqs. (2), (17), (36) and (40) and the values of p and A, we can get

$$\begin{aligned} \left\{ {{\begin{array}{l} {l_{xi} =\frac{7rv^{2}}{5gR}} \\ {l_{yi} =\frac{f\cdot r}{mg}} \\ \end{array} }} \right. \end{aligned}$$

(41)

From Eq. (41) we can get

$$\begin{aligned} \left\{ {{\begin{array}{l} {\beta _{x_1 } =\arcsin \left( \frac{{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{i}}}}{L}\right) =\arcsin \left( \frac{7rv^{2}}{5gRL}\right) } \\ {\beta _{y_1 } =\arcsin \left( \frac{{{\mathop {l}\limits ^{\rightharpoonup }}_{\!\!{j}}}}{L}\right) = \arcsin \left( \frac{fr}{mgL}\right) } \\ \end{array} }} \right. \end{aligned}$$

(42)

If spherical robot BHQ-1 moves along a circular trajectory with a fixed velocity the driving moments of two motors are

$$\begin{aligned} \left\{ {{\begin{array}{l} {M_1 =mg\cdot l_j =\textit{fr}} \\ {M_2 =mg\cdot l_i=\frac{7mrv^{2}}{5R}} \\ \end{array}}} \right. \end{aligned}$$

(43)

A simulation result of spherical robot BHQ-1 moving along a circular trajectory is shown in Fig. 13, where the dashed circle is the planned trajectory in theory or the target trajectory and the solid circle is the planned trajectory by adding 1 % noise disturbance. From the simulation we can conclude that BHQ-1 can realize circular motion with the deduced dynamic model.

Fig. 13

Simulation of circular motion of BHQ-1

Fig. 14

Motion simulation of a complex trajectory planning of BHQ-1

4.2.3 Complex Trajectory Planning

Theoretically any complex trajectory can be approximately divided into line segments and curve segments, so the deduced linear trajectory motion planning model and circular trajectory motion planning model can also be used to plan the motion of complex trajectories. In order to validate that, a motion planning simulation of spherical robot BHQ-1 moving along a complex trajectory was presented in Fig. 14. The given trajectory is composed of three straight line segments and two curves, which are described by functions as

$$\begin{aligned} y=\left\{ {{\begin{array}{ll} 0 &{} {0\le x<1} \\ {6-\sqrt{36-(x-1)^{2}}} &{} {1\le x<4} \\ {\frac{\sqrt{3}}{3}x+6-\frac{13}{3}\sqrt{3}} &{} {4\le x<7} \\ {6-3\sqrt{3}-\sqrt{4-(x-8)^{2}}} &{} {7\le x<9} \\ {-\frac{\sqrt{3}}{3}x+6+\sqrt{3}} &{} {9\le x\le 10} \\ \end{array} }} \right. \end{aligned}$$

(44)

In Fig. 14, the given trajectory is shown in dashed line and the planned trajectory is shown in solid line. 1 % disturbance noise was introduced to the dynamic trajectory planning method in order to test the robustness of the method. From the simulation we can find that the dynamic motion planning method can plan an accurate trajectory for spherical robot BHQ-1, and the small error comes from the noise added intentionally. If there is no disturbance noise the planned trajectory will superpose the target one.

5 Conclusion

Spherical mobile robot has compact structure and flexible motion, but because of its special nonholonomic characteristic, traditional motion planning methods proposed for wheeled mobile robots cannot be applied to it. This chapter introduces two motion planning methods for spherical robot BHQ-1, one is a kinematics based motion planning method and another is a dynamics based motion planning method. The kinematic motion planning method uses Hamiltonian function to realize the time and energy based optimal motion planning, and the characteristics of three coefficients $\lambda _{1},\lambda _{2},\lambda _{4}$ are revealed through simulations. The dynamic motion planning method uses a simplified Boltzmann-Hamel equation to get the dynamic model of spherical robot BHQ-1, and the moments of two motors to realize the linear motion and circular motion are deduced respectively. Simulations and experiments are provided in order to validate those motion planning methods. It should be noted that although the two methods are proposed for spherical robot BHQ-1, which can be also used by other spherical robots with similar structure or similar motion principle.

Thanks very much for the help and research work of my students JIA Chuan, LIU Zengbo, CHI Xing and SHANG Zhimeng.