Automatic Segmentation of the Spinal Cord Using Continuous Max Flow with Cross-sectional Similarity Prior and Tubularity Features

Abstract

Segmenting tubular structures from medical image data is a common problem; be it vessels, airways, or nervous tissue like the spinal cord. Many application-specific segmentation techniques have been proposed in the literature, but only few of them are fully automatic and even fewer approaches maintain a convex formulation. In this paper, we show how to integrate a cross-sectional similarity prior into the convex continuous max-flow framework that helps to guide segmentations in image regions suffering from noise or artefacts. Furthermore, we propose a scheme to explicitly include tubularity features in the segmentation process for increased robustness and measurement repeatability. We demonstrate the performance of our approach by automatically segmenting the cervical spinal cord in magnetic resonance images, by reconstructing its surface, and acquiring volume measurements.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The segmentation of oriented tubular structures in the body is a common task in medical applications. Examples include measuring functional vessel volumes in patients of cardiovascular diseases, or quantifying spinal cord atrophy (i.e., the loss of nervous tissue) in a variety of neurodegenerative diseases. Multiple sclerosis (MS) is a prominent example among the latter diseases. Clinical MS studies have shown relationships between the degree of cord atrophy and both the strength of disease [1] and disease duration [2]. Therefore, in recent years, assessing spinal cord atrophy has become a highly active topic of research, resulting in a number of methods that were specifically tailored towards the segmentation of the spinal cord (see e.g. the recently published segmentation approaches of Asman et al. [3], De Leener et al. [4] and the methods referenced therein, or the earlier review of Miller et al. [5]). Only few of these methods, however, make extensive use of the fact that the spinal cord is an inherently tubular structure.

In this paper, we present an automated method that aims at the more general goal of segmenting tubular structures in image volumes. Manual intervention on the target data is reduced to placing a landmark if the segmentation result is ambiguous. As a proof of concept, we successfully demonstrate the practicability of our method by segmenting the spinal cord in magnetic resonance (MR) images and acquiring volume measurements from surface reconstructions of the segmentation results.

We adjust Yuan et al.’s continuous max-flow framework [6] to include a cross-sectional similarity prior. This prior exploits the fact that an oriented elongated structure shows only little change in shape along its orientation. Thus, the prior may guide the segmentation in regions where image information is missing or ambiguous. A related approach of including a similarity prior is pursued by Qiu et al. [7]. Due to their different problem setting (they aim for axial symmetry), they formulate parts of the problem in a discrete setting, while our formulation is continuous. We also propose a way to include tubularity features in the segmentation process. Specifically for the segmentation of the spinal cord, we furthermore introduce the new csfness feature, which is designed to improve discrimination between the spinal cord and the cerebrospinal fluid (CSF) that immediately surrounds it.

2 Method

In the following subsections, we introduce our adaptation of the max-flow approach and define the flow capacity functions together with the features that we use in experiments. We present an algorithm to solve the adapted problem, and we conclude the section by proposing a scheme to reconstruct the surface from the segmentation result, which we use for quantitative measurements.

Notation. Let $I:\Omega \rightarrow \mathcal {I}$ denote the intensity non uniformity corrected image [8] with intensities in the normalized intensity space $\mathcal {I}=[0,1]$, where $x=(x_{1},x_{2},x_{3})^{\mathsf {T}}\in \Omega$ are the coordinates in the continuous image domain $\Omega \subset \mathbb {R}^{3}.$ Throughout the whole section, we furthermore assume that the tubular structure of interest is roughly oriented parallel to the $x_{3}$ axis. Figuring out the orientation should be straightforward for most clinical applications, as the subject’s orientation with respect to the image can be determined from the image’s meta data for most clinical imaging modalities.

Original max-flow formulation. A general formulation for the continuous max-flow problem with spatial flow $p(x)$, source flow $p_{s}(x)$, sink flow $p_{t}(x)$, and corresponding flow capacities $C(x),$ $C_{s}(x)$, $C_{t}(x)$ is stated by Yuan et al. [6] as

$$\begin{aligned} \max _{p_{s},p_{t},p}\int \limits _{\Omega }p_{s}{\mathrm{{d}}}{x}, \end{aligned}$$

(1)

subject to the flow capacity constraints

$$\begin{aligned} p_{s}(x)\le C_{s}(x),\quad p_{t}(x)\le C_{t}(x),\quad \left\| p(x)\right\| \le C(x) \end{aligned}$$

(2)

and the flow conservation constraint

$$\begin{aligned} {{\mathrm{div}}}\, p(x)-p_{s}(x)+p_{t}(x)=0. \end{aligned}$$

(3)

2.1 Cross-Sectional Similarity Prior

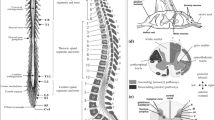
Following our goal to impose a cross-sectional similarity prior on the segmentation, we split the spatial flow $p(x)$ into an in-slice component $q:\Omega \rightarrow \mathbb {R}^{2}$ and a through-slice component $r:\Omega \rightarrow \mathbb {R}$ with respect to slices that lie perpendicular to the $x_{3}$ axis (see Fig. 1a). The resulting continuous max-flow problem can then be written as follows:

$$\begin{aligned} \max _{p_{s},p_{t},q,r}\int \limits _{\Omega }p_{s}{{\mathrm{{d}}}}{x}, \end{aligned}$$

(4)

subject to the new flow capacity constraints

$$\begin{aligned} p_{s}(x)\le C_{s}(x),\quad p_{t}(x)\le C_{t}(x),\quad \left\| q(x)\right\| \le \alpha (x),\quad |r(x)|\le \beta (x) \end{aligned}$$

(5)

and the new flow conservation constraint

$$\begin{aligned} {{\mathrm{{{\mathrm{div}}}_{{12}}}}}q(x)+r^{\prime }(x)-p_{s}(x)+p_{t}(x)=0, \end{aligned}$$

(6)

where ${{\mathrm{{{\mathrm{div}}}_{{12}}}}}q$ denotes the divergence of $q$ perpendicular to the $x_{3}$ axis and $r^{\prime }$ denotes the derivative of $r$ along the $x_{3}$ axis.

Fig. 1

Method overview. a Proposed flow configuration: the spatial flow is split into an in-slice component $q$, perpendicular to the axis along which the tubular structure is oriented, and a through-slice component $r$, parallel to the axis. b Sample sagittal slice of one of the images used for evaluation. c Segmentation result. d Surface reconstruction with cutting planes for volume measurement

The flow formulation now possesses the desired property of having the spatial flow capacity $C(x)$ of [6] represented by two separate terms, namely the in-slice flow capacity $\alpha (x)$ and the through-slice flow capacity $\beta (x)$. The latter capacity, $\beta (x)$, represents the cross-sectional similarity prior that allows for precise control over the through-slice flow behavior: For example, we may choose an edge-based cost function for $\alpha (x)$ that drives the segmentation towards edges in $I$, while setting $\beta (x)=\beta _{0}$ to enforce constant similarity throughout all slices. Or we may calculate $\beta (x)=\beta (x_{3})$ as a slice wise cost-function that, for each slice, adjusts the similarity prior to the in-slice noise level (reinforcing the similarity prior if the noise level is high and relaxing it if the noise level is low). Other combinations are possible, of course: note that both $\alpha$ and $\beta$ may be formulated pointwise.

Dual formulation. Introducing the Lagrange multiplier $u=u(x)$ and following the steps in [6], the max-flow problem can be reformulated as the equivalent primal-dual model

$$\begin{aligned} \max _{p_{s},p_{t},q,r}\min _{u}\int \limits _{\Omega }p_{s}{\mathrm{{d}}}{x}+\int \limits _{\Omega }u\cdot ({{\mathrm{{{\mathrm{div}}}_{{12}}}}}q+r^{\prime }-p_{s}+p_{t}){\mathrm{{d}}}{x} \end{aligned}$$

(7)

subject to the capacity constraints (5). The equivalent dual model representing a relaxed min-cut problem then becomes

$$\begin{aligned} \min _{u\in [0,1]}E(u)\mathbin {:=}\int \limits _{\Omega }\left\{ (1-u)C_{s}+uC_{t}+\alpha |{{\mathrm{\nabla _{{12}}}}}u|+\beta |u^{\prime }|\right\} {\mathrm{{d}}}{x}. \end{aligned}$$

(8)

Here, ${{\mathrm{\nabla _{{12}}}}}u$ denotes the in-slice gradient and $u^{\prime }$ denotes the through-slice derivative of $u$ with respect to the $x_{3}$ axis, similar to the definitions of ${{\mathrm{{{\mathrm{div}}}_{{12}}}}}q$ and $r^{\prime }$ above. It can be shown that each level set function $u^{\ell }(x),\,\ell \in (0,1]$ given by

$$\begin{aligned} u^{\ell }(x)\mathbin {:=}{\left\{ \begin{array}{ll} 1, &{} u^{*}(x)>\ell \\ 0, &{} u^{*}(x)\le \ell \end{array}\right. }\quad {\text {with}}\quad u^{*}\mathbin {:=}\mathop {\mathrm{{argmin}}}\limits _{u}E(u) \end{aligned}$$

(9)

is a global binary solution of the adapted problem stated in Eq. (4).

Fig. 2

Features used in segmentation. a Image intensities. b Vesselness response. c Csfness response

2.2 Tubularity Features

As our goal is to segment tubular structures in the image, it appears natural to include tubularity features in the flow capacity calculations. A well-known tubularity feature is Frangi’s measure of vesselness [9] (see Fig. 2b), $v^{*}(x)=\max _{\xi \in S_{v}}v(x;\xi )$, where, for each scale $\xi$ in the predefined set of scales $S_{v}$, the vesselness $v(x;\xi )$ of bright tubular structures on dark background is

$$\begin{aligned} v(x;\xi )={\left\{ \begin{array}{ll} 0,\qquad \lambda _{2}\ge 0\vee \lambda _{3}\ge 0\\ \left( 1-\exp (-2\frac{\lambda _{2}^{2}}{\lambda _{3}^{2}})\right) \exp (-2\frac{\lambda _{1}^{2}}{\lambda _{2}\lambda _{3}})\left( 1-\exp (-\frac{\sum _{i=1}^{3}\lambda _{i}^{2}}{2h^{2}})\right) \quad {\text {else}}, \end{array}\right. } \end{aligned}$$

(10)

with $\lambda _{i}=\lambda _{i}(x)$ denoting the ordered eigenvalues ($\left| \lambda _{1}\right| \le \left| \lambda _{2}\right| \le \left| \lambda _{3}\right|$) of the pointwise Hessian matrices that result from convolving the input image $I$ with Gaussian derivatives of standard deviation $\xi$. We define $h$ as half of the maximum Hessian norm at the current scale as suggested by Frangi [9].

In our experiments on segmenting the spinal cord, we decided to include another feature that specifically describes the background that immediately surrounds the target structure. The spinal cord is embedded in cerebrospinal fluid (CSF), which appears dark in the used MR sequences. As the CSF also appears largely elongated, but exhibits both tube-like and plate-like properties, we adapt Frangi’s vesselness feature to a csfness feature $w^{*}(x)$ (see Fig. 2c) that discriminates between blob-like structures and non-blobs. We do so by replacing the eigenvalue ratio terms of $v^{*}$ with an equivalent term composed of $\lambda _{1}$ and $\lambda _{3}$, as it is the latter ratio that discriminates both vessels and plates from blobs in Hessian eigenvalue analysis [9]. Consequently, we define $w^{*}(x)=\max _{\xi \in S_{w}}w(x;\xi )$ for dark non-blobs on bright background in the scales $S_{w}$ with

$$\begin{aligned} w(x;\xi )={\left\{ \begin{array}{ll} 0, &{} \lambda _{3}\le 0\\ \exp (-2\frac{\lambda _{1}^{2}}{\lambda _{3}^{2}})\left( 1-\exp (-\frac{\sum _{i=1}^{3}\lambda _{i}^{2}}{2h^{2}})\right) &{} {\text {else}}. \end{array}\right. } \end{aligned}$$

(11)

Combining the features. Let $\mathcal {V}=[0,1]\ni v^{*}$, $\mathcal {W}=[0,1]\ni w^{*}$ be the vesselness and csfness feature spaces, let $\mathcal {Y}=\mathcal {I}\times \mathcal {V\subset \mathbb {R}}^{2}$ and $\mathcal {Z}=\mathcal {I}\times \mathcal {V}\times \mathcal {W}\subset \mathbb {R}^{3}$ be two combined feature spaces, let $I_{2}:\Omega \rightarrow \mathcal {Y}$, $I_{3}:\Omega \rightarrow \mathcal {Z}$ be two new image functions that map to the combined feature spaces, and let $y\in \mathcal {Y}$, $z\in \mathcal {Z}$ be the coordinates in the combined feature spaces.

Furthermore, let $Y_{f}=\{y_{f}^{i}\}_{i=1}^{M},Y_{b}=\{y_{b}^{j}\}_{j=1}^{N}$ be two sets holding samples of $\mathcal {Y}$ with known foreground and background membership, respectively. Based on these training sets, we propose to calculate the capacities for the terminal flow constraints (5) using kernel density estimates:

$$\begin{aligned} C_{s}(y)&=C_{s}(I_{2}(x))=\frac{\frac{1}{M}\sum _{i=1}^{M}K_{\mathsf {\Sigma }_{f}}(y-y_{f}^{i})}{\frac{1}{M}\sum _{i=1}^{M}K_{\mathsf {\Sigma }_{f}}(y-y_{f}^{i})+\frac{1}{N}\sum _{j=1}^{N}K_{\mathsf {\Sigma }_{b}}(y-y_{b}^{j})},\end{aligned}$$

(12)

$$\begin{aligned} C_{t}(y)&=C_{t}(I_{2}(x))=1-C_{s}(y), \end{aligned}$$

(13)

where $K_{\mathsf {\Sigma }_{.}}$ is a Gaussian kernel with zero mean and diagonal covariance matrix $\mathsf {\Sigma }_{.}$, holding variances $\sigma _{d}^{2}$ for the feature dimensions $d$ as diagonal elements. Terminal capacities for the feature space $\mathcal {Z}$ may be calculated in a similar way. For the sake of simplicity, we choose the non-terminal capacities as constants in our experiments: $\alpha (x)=\alpha _{0}$, $\beta (x)=\beta _{0}$.

2.3 Algorithm

In accordance with the original max-flow approach, we propose to find a global solution to our adapted formulation by setting up the respective augmented Lagrangian equation as

$$\begin{aligned} L_{c}(p_{s},p_{t},q,r,u)&\mathbin {:=}\int \limits _{\Omega }p_{s}{\mathrm{{d}}}{x}+\int \limits _{\Omega }u\cdot ({{\mathrm{{{\mathrm{div}}}_{{12}}}}}q+r^{\prime }-p_{s}+p_{t}){\mathrm{{d}}}{x}\nonumber \\&\quad \; -\frac{c}{2}\left\| {{\mathrm{{{\mathrm{div}}}_{{12}}}}}q+r^{\prime }-p_{s}+p_{t}\right\| ^{2}, \end{aligned}$$

(14)

and iteratively optimizing it using Algorithm 1, based on the algorithm in [6].

2.4 Surface Reconstruction

As can be concluded from Eq. (9), reconstructing the surface of the segmented structure amounts to finding the isosurface of level $\ell \in (0,1]$ in the segmentation result $u^{*}$ (see Fig. 1c, d). We propose to extract the isoline as a polygon of $m$ vertices for each slice along the $x_{3}$ axis and successively connect the resulting dots in space. This provides us with the slicewise contours of the segmentation at no additional cost, which then facilitates estimating the centerline, namely as a curve fit through the centroids of the contours. A centerline estimate, in turn, may be useful to acquire quantitative measurements from the reconstruction (see Sects. 3, 4).

If there are multiple foreground regions in $u^{*}$, a point of reference may be used to choose the region closest to it. Likewise, heuristic criteria like sudden jumps of the centroid or a threshold on the contour line’s convexity may be used to determine a cutoff for the tubular structure of interest. In the spinal cord segmentation experiments below, we define a point of reference by an anatomical landmark, and we define two cutoff criteria as finding either a distance $>d$ between the centroids of two consecutive slices or finding a contour line with convexity $<t$. As a measure of convexity, we employ the ratio of the contour line’s area and the area of its convex hull.

3 Materials

Applicability of our approach is shown by segmenting the spinal cord in MR images of healthy volunteers (Figs. 1b, 2a) and MS patients.

To assess accuracy and reproducibility, 11 healthy volunteers (3 female, 8 male, mean age 32.7 year, range 26–44 year) were scanned on a $3\,\mathrm{{T}}$ whole-body MR scanner (Verio, Siemens Medical, Germany) with a T1-weighted MPRAGE sequence (TR/TI/TE/$\alpha ={2.0}\,{\mathrm{{s}}}$/${1.0}\,\mathrm{{s}}$/${3.4}\,\mathrm{{ms}}$/${8}^\circ$); 192 slices in sagittal orientation parallel to the interhemispheric fissure were acquired with an isotropic resolution of ${1}\,\mathrm{{mm}}^3$. Image volumes were corrected for gradient nonlinearity distortions using the scanner manufacturer’s correction routine.

To show applicability to clinical data, we used follow-up data of 32 MS patients (21 female, 11 male, mean age 47.1 year, range 22–60 year; 22 patients with relapsing-remitting MS, 10 patients with primary progressive MS, mean disease duration 13.8 year, range 3–31 year, median EDSS $3.0$, range $1.5$–$6.0$). The patients were scanned on a 1.5 T whole-body MR scanner (Avanto, Siemens Medical, Germany) with a T1-weighted MPRAGE sequence (TR/TI/TE/$\alpha ={2.08}\,\mathrm{{s}}$/${1.1}\,\mathrm{{s}}$/${3.93}\,\mathrm{{ms}}$/${15}^{\circ }$); 160 slices in sagittal orientation parallel to the interhemispheric fissure were acquired with an in-slice resolution of ${0.98}\,\mathrm{{mm}}\times 0.98\,\mathrm{{mm}}$ and a slice thickness of ${1}\,\mathrm{{mm}}$. Scans were acquired at two points in time approximately 5  years apart (mean ${5.04}\,\mathrm{{year}}$, range $4.55$–${5.41}\,\mathrm{{year}}$); demographic data above is given with respect to the earlier scan. Distortion correction was applied to the surface reconstructions using the method of Janke et al. [11].

For the calculation of the terminal flow constraints $C_{.}(y)$ and $C_{.}(z)$, sample sets were acquired on 150 separate scans of MS patients. The training patients were scanned with the same MPRAGE sequence as the 32 MS patients above. Foreground/background membership of the training samples was determined using a graph cuts-based [12] semi automated method described as presegmentation in [13]. To speed up calculations, features were discretized to $50$ bins in the $[0,1]$ interval in each feature dimension. Silverman’s rule of thumb with $\sigma _{d}=4^{\frac{1}{D+4}}\left( n(D+2)\right) ^{\frac{-1}{D+4}}\hat{\sigma }_{d}$ provided a $\sigma _{d}^{2}$ estimate, where $n$ is the number of samples, $\hat{\sigma }_{d}$ is the sample standard deviation in $d$, and $D$ is $2$ for $C_{.}(y)$ and $3$ for $C_{.}(z)$. To avoid zero bins, a small additive constant of $0.0001k$ was added to the resulting bin values, where $k$ is the maximum value of all bins.

For all experiments, the following parameters were applied: $\alpha _{0}=0.5$, $\beta _{0}=2.5$, $S_{v}=[{2}\,\mathrm{{mm}},{4}\,\mathrm{{mm}}]$ (16 values), $S_{w}=[{1}\,\mathrm{{mm}},{2}\,\mathrm{{mm}}]$ (8 values) for the flow capacities; $\ell =0.5$, $m=60$, $d={10}\,\mathrm{{mm}}$, $t=0.95$ for the surface reconstruction. Likewise for all reported volume measurements, the volume of a spinal cord surface segment of ${50}\,\mathrm{{mm}}$ centerline length, which was clipped by planes perpendicular to the centerline and which was located approximately ${25}\,\mathrm{{mm}}$ inferior of a manually marked landmark, was evaluated as described in [13].

4 Results

Scan–rescan evaluation. In two experiments on scan–rescan data, we evaluated the accuracy and reproducibility of our method. To show the benefits of splitting the spatial flow into an in-slice component and a through-slice component, we repeated all experiments using Yuan et al.’s original formulation [6] for segmentation, setting the spatial flow capacity $C(x)$ (see Eq. (2)) to a value of $C(x)=1.0$, as this parameter choice provided the highest number of successful surface reconstructions in the second experiment below. For the experiments, we scanned the 11 healthy volunteers (see Sect. 3) three times in a row (scans S1, S2, S3), without repositioning between S1 and S2 and with repositioning between S2 and S3, resulting in 33 scans altogether.

Accuracy: As we work with human in-vivo data, it was not possible to acquire quantitative ground truth measurements, for example, via histologic specimen. We therefore used manual segmentations of the image data as a gold standard for comparison in the first experiment. To make such manual measurements feasible, a semiautomated approach that allows for human feedback in the segmentation process seemed appropriate. We thus segmented all scan–rescan datasets with the method described as presegmentation in [13], placing foreground/background seeds manually and adjusting them in an iterative manner until we acquired a satisfying binary segmentation. We then compared the overlap of this gold standard segmentation with the binarized results of the automated segmentation for a ${50}\,\mathrm{{mm}}$ cord segment, located ${25}\,\mathrm{{mm}}$ inferior of the manually marked landmark. As a measure of overlap agreement, we calculated Dice coefficients for the region overlaps.

With our approach, we gained a mean Dice coefficient of $0.88$ using the proposed feature combination $\mathcal {Z}$ (i.e., intensity + vesselness + csfness) and $0.82$ using feature combination $\mathcal {Y}$ (i.e., intensity + vesselness). With Yuan et al.’s approach, we gained a mean Dice coefficient of $0.86$ using $\mathcal {Z}$ and $0.79$ using $\mathcal {Y}$. Therefore, our approach proves superior in the given problem setting. Furthermore, it can be seen that including the csfness feature into the segmentation process improves the segmentation accuracy.

Reproducibility: In the second experiment, we assessed the reproducibility of our method. The cervical spinal cord was segmented using feature combinations $\mathcal {Y}$ and $\mathcal {Z}$, its surface was reconstructed, and the volume of the ${50}\,\mathrm{{mm}}$ cord surface segment (see Sect. 3) was compared between scans and rescans. As a measure of reproducibility, we calculated the coefficients of variation (CV; i.e., the sample standard deviation over the mean) of the measured volumes for all possible S1–S2 comparisons (i.e., without repositioning) and S1–S3 comparisons (i.e., with repositioning). An overview of the mean CVs is given in Table 1.

For our proposed segmentation approach, the subsequent reconstruction of the complete surface segment succeeded for $30$ out of $33$ scans using $\mathcal {Y}$ and $32$ out of $33$ scans using $\mathcal {Z}$. All failures happened for the same subject, whose scans showed an extremely low signal-to-noise ratio upon visual inspection. For Yuan et al.’s segmentation approach, the surface reconstruction succeeded for $25$ out of $33$ scans using $\mathcal {Y}$ and $28$ out of $33$ scans using $\mathcal {Z}$.

Table 1 Coefficients of variation (%) for spinal cord segment volume measurements, using feature combinations $\mathcal {Y}$ and $\mathcal {Z}$ with Yuan et al.’s and our segmentation method

Fig. 3

Comparison of the segmentation approaches on noisy, low-contrast case. a Input image. b Segmentation result using the original max-flow formulation [6]. c Segmentation result using our max-flow formulation

As one could expect, CVs are lower for the S1–S2 comparison, due to the fact that the subjects were not repositioned. Furthermore, including the csfness feature makes the segmentation more robust (more successful surface reconstructions) while at the same time having beneficial effects on the reproducibility (substantially lower CVs for the more realistic S1–S3 comparisons). Similar statements on improved robustness and reproducibility can be made when comparing our adapted max-flow formulation with the original formulation: in both aspects, our method proves largely superior. And while for feature combination $\mathcal {Z}$ the S1–S3 CV of the original approach is better than ours, one has to keep in mind that ours is calculated on a higher number of successful reconstructions, including the more challenging ones on which the original approach failed.

An exemplary case where the surface reconstruction failed for the original max-flow formulation while succeeding for our adapted formulation is shown in Fig. 3. As can be seen, the segmentation stops early for the original formulation while it extends further down into the noisy image regions for ours. Relaxing $C(x)$ in this case would possibly enable the original formulation to also extend further down; however, this would come at the price of an overall higher susceptibility to noise. By contrast, controlling $\alpha (x)$ and $\beta (x)$ separately in our approach enables us to largely circumvent this tradeoff.

On the whole, the CVs we obtained by our method are higher than those of established methods that are actually used in MS research (most notably, Losseff et al. [1] and the methods compared in [13]). On the one hand, however, one should keep in mind the substantially higher amount of manual intervention in these approaches. On the other hand, we see our presented framework in its current state more as a proof of concept than as a tool that is ready for clinical use.

Evaluation on patient data. A comparison of the five-year follow-up MS patient data (see Sect. 3), using the proposed max-flow formulation for segmentation, showed a mean yearly atrophy of ${25.4}\,\mathrm{{mm}}^{3}$ in the ${50}\,\mathrm{{mm}}$ cord surface segment (maximum loss: ${194.3}\,\mathrm{{mm}}^{3}$, maximum gain: ${53.4}\,\mathrm{{mm}}^{3}$). The mean yearly percentage loss was ${0.9}\,{\%}$ (maximum loss: ${7.0}\,{\%}$, maximum gain: ${2.0}\,{\%}$). These measurements agree well with the observation of cord atrophy during MS progression reported in the literature [2]. Nevertheless, due to the high variability, our measurements should again be interpreted as a proof of concept for our segmentation method rather than as hard clinical data.

Computational performance. As we implemented the max-flow segmentation on the GPU based on code provided by the authors of [6, 10], results can be acquired extremely fast, namely in the order of seconds. Other parts of the implementation also show a high parallelization potential in that they are mainly pointwise (such as the feature calculation and the surface extraction). We therefore assume that the complete chain of steps from feature calculation to quantitative measurements could be optimized to run in less than a minute per subject.

5 Conclusion

We presented a new segmentation algorithm based on continuous max flow that was specifically tailored towards the segmentation of elongated structures: a cross-sectional similarity prior was introduced, which guides the segmentation in regions of missing or contradictory image information. We showed how tubularity features may be used in the flow capacity constraints to increase segmentation robustness and measurement repeatability. Finally, we successfully demonstrated the clinical applicability of our method by segmenting the spinal cord in both healthy volunteers and multiple sclerosis patients.