The Maximum Labeled Path Problem

Abstract

In this paper, we study the approximability of the Maximum Labeled Path problem: given a vertex-labeled directed acyclic graph $D,$ find a path in $D$ that collects a maximum number of distinct labels. Our main results are a $\sqrt{OPT}$-approximation algorithm for this problem and a self-reduction showing that any constant ratio approximation algorithm for this problem can be converted into a PTAS. This last result, combined with the APX-hardness of the problem, shows that the problem cannot be approximated within a constant ratio unless $P=NP$.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Optimization network design problems over labeled graphs have been widely studied in the literature [2–8, 10, 11]. Since these problems are usually $NP$-hard, they have been mainly investigated toward the goal of finding efficiently approximate solutions. Most of these studies consider edge-labels that represent kinds of connections and the optimization concerns the number of different kinds of connections used. Our motivation is different, we consider vertex-labels that represent membership to different components. Our goal is then to maximize the number of components visited by a path in a directed graph. More precisely, the problem is defined on a directed graph with labels on the vertices and the objective is to find a path visiting a maximum number of distinct labels. We call this problem Max-Labeled-Path. Actually, the vertex-labeled and edge-labeled versions of this problem are equivalent but the vertex-labeled version is closer to our initial motivation. To our knowledge, there is no prior work on this simple and natural problem. A related problem is the Min LP $s-t$ problem that asks to find a path between $s$ and $t$ minimizing the number of different labels in this path. In [7] Hassin et al. achieves a $\sqrt{n}$ ratio for this problem and they show that it is hard to approximate within $O(\log n)$. We used a similar approach for our hardness result and the comparison is interesting since the maximization requires a much more precise analysis.

1.1 Contributions

In this paper we report both positive and negative results about the Max-Labeled-Path. Namely, we prove that this problem does not admit a constant factor approximation algorithm unless $P=NP$ and we propose an algorithm that returns a solution of value at least $\sqrt{OPT}$ where ${OPT}$ is the value of an optimal solution. In Sect. 2, the hardness proof starts with a reduction from MAX 3SAT preserving the approximation and therefore proving that Max-Labeled-Path is APX-hard. In Sect. 3, a polynomial self-reduction shows that finding a solution on a more complex graph enables us to find a solution with a better ratio on the initial graph. This, combined with the APX-hardness of the problem, shows that the problem cannot be approximated within a constant ratio unless $P=NP$. In Sect. 4, we describe a $\sqrt{OPT}$-approximation algorithm for Max-Labeled-Path. This algorithm requires a specific preprocessing and an inductive analysis that uses the poset structure of the problem.

1.2 Preliminaries

A vertex-labeled Directed Acyclic Graph $D=(V,A)$ is a DAG whose vertices are labeled by a function $l : V \rightarrow \mathcal{L}$. For each vertex $u \in V$, we denote by $\lambda (u)$ and call the level of $u,$ the maximum number of vertices in a path having $u$ as end-vertex. The ith level set $L_i$ of $D$ consists of all vertices $u \in V$ such that $\lambda (u)=i.$ The vertices of $L_1,$ i.e. having no ingoing arcs, are called the sources of $D.$ The vertices having no outgoing arcs are called the sink. Let $k$ be the largest integer such that $L_k\ne \emptyset .$ $L_k$ is a subset of the sinks. Let $P$ be a (directed) path in $D.$ $P$ is maximal by inclusion if and only if it connects a source to a sink. The set of labels collected by $P$ is the set $\{l(u):u\in P\}$ of labels of vertices in $P.$ Given a vertex-labeled DAG $D,$ the problem Max-Labeled-Path consists in finding a path $P$ in $D$ maximizing the number of distinct labels collected by $P.$ Any solution can be extended into a maximal path without decreasing its value, therefore we only consider solutions that connects a source to a sink. In this paper, we consider only maximization problem. Let $D$ be an instance of a maximization problem, we denote by $OPT(D)$ its optimum. We say that an algorithm achieves a constant performance ratio $\alpha ,$ if for every instance $D,$ it returns a solution of value at least $\alpha \,OPT(D).$

2 Maximum Labeled Path Is APX-Hard

In this section, we describe a reduction from Max-3SAT establishing that Max-Labeled-Path is APX-hard even when restricted to instances satisfying the following conditions:

• (C1) All maximal (by inclusion) paths of $D$ contain the same number $k$ of vertices.

• (C2) $D$ contains a path that collects all the labels, $OPT(D)=|\mathcal{L}|.$

• (C3) $D$ contains a path that collects each label exactly once, $OPT(D)=k=|\mathcal{L}|.$

• (C4) $OPT(D)=k=|\mathcal{L}|$ is a power of two.

Note that (C4) is stronger than (C3) which is stronger than (C2). Applying our initial reduction to satisfiable instances of Max-3SAT, we produce instances Max-Labeled-Path satisfying conditions (C1) with $k\le 3|\mathcal{L}|$ and (C2) and proves Theorem 2. Then, we proceed in two steps: first we establish the APX-hardness for instances satisfying conditions (C1) and (C3) in Theorem 3 and then the APX-hardness for instances satisfying conditions (C1) and (C4) in Theorem 4. In the next section we use a self-reduction of Max-Labeled-Path to prove that Max-Labeled-Path does not belong to APX. This self-reduction is valid only for instances satisfying conditions (C1) and (C4).

Theorem 1

(Håstad [9]) Assuming $P \ne NP$, no polynomial-time algorithm can achieve a performance ratio exceeding $\frac{7}{8}$ for Max-3SAT even when restricted to satisfiable instances of the problem.

Theorem 2

Assuming $P \ne NP,$ no polynomial-time algorithm can achieve a performance ratio exceeding $\frac{7}{8}$ for Max-Labeled-Path even when restricted to instances satisfying conditions (C1) with $k\le 3|\mathcal{L}|$ and (C2).

Before proving Theorem 2, we establish the following lemma showing that (C1) is not a strong requirement in the sense that each instance of Max-Labeled-Path can be converted into an equivalent instance satisfying (C1). The proof of Lemma 1 is omitted due to space limitation.

Lemma 1

Given an instance $D$ of Max-Labeled-Path, it is possible to construct an instance $D'$ satisfying condition (C1) and such that there exists a mapping between the set of maximal paths in $D$ and the set of maximal paths in $D'$ preserving the number of labels collected.

Proof

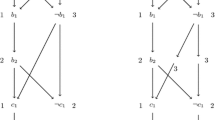
(of Theorem 2 ). Given an instance $F$ of Max-3SAT, we define an instance $D_F=(V,A)$ of Max-Labeled-Path as follows. Let $\{ w^1,w^2,...,w^q\}$ be the set of variables of $F.$ For all $j \in \{1,...,q\},$ we denote by $|w^j|$ the number of occurrences of the literal $w^j$ and by $|\lnot w^j|$ the number of occurrences of its negation. We create $|w^j|+|\lnot w^j|$ vertices and call them $w^j_1, w^j_2,...,w^j_{|w^j|}$ and $\lnot w^j_1, \lnot w^j_2,...,\lnot w^j_{|\lnot w^j|}$. We connect in a directed path $P(w^j)$ the vertices which represent the literal $w^j$, i.e. we create an arc $(w^j_i,w^j_{i+1})$ for all $i\in \{1,\ldots ,|w^j|-1\}$. In the same way, we connect in a directed path $P(\lnot w^j)$ the vertices representing $\lnot w^j$. For all $j \in \{1,...,q-1\}$, we connect by an arc the last vertices of $P(w^j)$ and $P(\lnot w^j)$ to the first vertices of $P(w^{j+1})$ and $P(\lnot w^{j+1}).$ Let us define the labeling function $l : V \rightarrow \mathcal{L}:=\{1,\ldots , m\}$ where $m$ is the cardinality of the set of clauses $\{C_1,C_2,\ldots ,C_{m}\}$ of $F.$ There is a one to one correspondence between the occurrences of the literals in the clauses and the vertices of $D_F.$ A vertex $u$ receives the label $j$ if $u$ corresponds to an occurrence of a literal in the clause $C_j$ (see Fig. 1).

Applying the reduction to a satisfiable instance $F$ of Max-3SAT, we obtain an instance $D_F$ of Max-Labeled-Path that contains a path collecting all the labels, i.e. that satisfies condition (C2). Moreover, since each clause contains at most three literals, the number $k$ of vertices in a maximal path of $D_F$ is at most thrice the number $m$ of labels, i.e. $k\le 3m.$ In the resulting graph $D_F,$ each maximal path $P$ is a path from a vertex in $\{w^1_1, \lnot w^1_1\}$ to a vertex in $\{w^q_{|w^q|}, \lnot w^q_{|\lnot w^q|}\}$ that contains for all $j\in \{1,\ldots ,q\}$ either $P(w_j)$ or $P(\lnot w_j)$ but not both. Therefore, it represents in an obvious way an assignment of the variables ($w_j = true \Leftrightarrow P(w_j)\subset P$). From the choice of the labeling of vertices in $D_F,$ it is easy to verify that an assignment of the variables satisfying $n$ clauses corresponds to a maximal path collecting $n$ labels. This transformation produces in polynomial time an instance $D_F$ satisfying the conditions (C2) with $k\le 3|\mathcal{L}|$. It remains to ensure (C1), this can be done by applying the transformation of Lemma 1. Together with Theorem 1, this concludes the proof of Theorem 2.   $\Box$

Fig. 1.

The digraph $D_F$ for the formula $F=(a \vee b \vee c) \wedge (\lnot a \vee b \vee \lnot c) \wedge (\lnot b \vee c)$ before the transformation of Lemma 1 (to the left) and after (to the right).

The next step consists in showing that the problem Max-Labeled-Path remains APX-hard even when restricted to instances such that all maximal paths have the same number of vertices and contain a path collecting each label exactly once.

Theorem 3

Assuming $P \ne NP,$ no polynomial time algorithm can achieve a performance ratio exceeding $\frac{23}{24}$ for Max-Labeled-Path even when restricted to instances satisfying (C1) and (C3).

Proof

Consider a DAG $D=(V,A)$ with a labeling function $l$ that satisfies the conditions (C1) with $k\le 3|\mathcal{L}|$ and (C2). Every maximal path in $D$ contains the same number $k$ of vertices. Let $m:=|\mathcal{L}|\le k$ be the number of labels of vertices in $D.$ We construct a DAG $D'$ by adding to $D,$ for each vertex $v\in V,$ a set $\{v^1,\ldots ,v^r\}$ of $r:=k-m$ copies of the vertex $v.$ There is an arc between two vertices in $D'$ if and only if there is an arc between their preimages in $D$ (the preimage of a vertex $v\in V$ is $v$ itself). Every maximal path in $D'$ corresponds to a maximal path in $D,$ in particular it contains exactly $k$ vertices. The set of labels of $D'$ is $\mathcal{L}':= \mathcal{L} \cup \{m+1,m+2,\ldots ,m+r=k\}.$ For each vertex $v$ of $D$ and each integer $j\in \{1,2,\ldots ,r\}$ the label of the vertex $v^j$ is $m+j.$ The labels in $D'$ of the vertices that belong to $D$ remain unchanged. We call the resulting instance $D'$ the extension of the instance $D.$

The following two lemmata (whose proofs are omitted due to space limitation) establish a close relationship between the optimum of the instances $D$ and $D'$.

Lemma 2

If there is a path in $D$ collecting $n$ labels then there is a path in $D'$ collecting $n+r$ labels. If there is a path in $D'$ collecting $n$ labels then there is a path in $D$ collecting at least $n-r$ labels.

Lemma 3

If there exists a polynomial time algorithm that achieves a performance ratio $1-\epsilon$ for Max-Labeled-Path restricted to instances satisfying conditions (C1) and (C3) then there exists a polynomial time algorithm that achieves a performance ratio $1-3\epsilon$ for Max-Labeled-Path restricted to instances satisfying conditions (C1) with $k\le 3|\mathcal{L}|$ and (C2).

To complete the proof of Theorem 3, suppose that there exists a polynomial time algorithm ALG$'$ achieving a ratio exceeding $\frac{23}{24}$ for the problem Max-Labeled-Path restricted to instances satisfying conditions (C1) and (C3). Then, by Lemma 3, we deduce that there exists a polynomial time algorithm ALG achieving a ratio exceeding $\frac{7}{8}$ for the problem Max-Labeled-Path restricted to the instances satisfying conditions (C1) with $k\le 3|\mathcal{L}|$ and (C2), this cannot occur by Theorem 2, unless $P=NP$.   $\Box$

The last result of this section shows that the problem remains APX-hard if we add the condition that the number of vertices in any maximal path is a power of two. The proof of Theorem 4 is similar to the one of Theorem 3 and has been omitted due to space limitation.

Theorem 4

Assuming $P \ne NP,$ no polynomial time algorithm can achieve a performance ratio exceeding $\frac{47}{48}$ for Max-Labeled-Path even when restricted to instances satisfying conditions (C1) and (C4).

3 Maximum Labeled Path Does Not Belong to APX

In this section, using a self-reduction of the problem Max-Labeled-Path, we will prove the following result:

Theorem 5

Assuming $P\ne NP,$ no polynomial time algorithm can achieve a constant performance ratio for Max-Labeled-Path even when restricted to instances satisfying conditions (C1) and (C4).

3.1 Self-reduction

In Sect. 3, we will consider only instances of Max-Labeled-Path satisfying conditions (C1) and (C4). Namely, a DAG $D=(V,A)$ whose vertices are labeled by a function $l : V \rightarrow \mathcal{L}=\{1,\ldots ,k\}$ such that there exists a path collecting each label exactly once and the number $k=|\mathcal L|$ of vertices in any maximal path is a power of two. We will prove that such instances of the problem Max-Labeled-Path cannot be approximated in polynomial time within a constant factor. For the sake of simplicity, we also assume that there is only one source $s$ and one sink $t$. Therefore, any maximal path is a path from $s$ to $t$ and all vertices of $D$ belong to a path from $s$ to $t.$ Recall that, for each vertex $u \in V$, $\lambda (u)$ is the number of vertices in a path from $s$ to $u$ (all such paths have the same length because $D$ satisfies (C4)). For all $u\in V,$ $\lambda (s)=1\le \lambda (u) \le k=\lambda (t).$

Pseudo Square and Pseudo Cubic Acyclic Digraph. The pseudo square digraph ${\bar{D}}$ of $D$ is obtained from $D$ by replacing each vertex $u \in V$ by a copy $D_u$ of the digraph $D$. We denote by $v_u$ the copy of the vertex $v\in V$ in the digraph $D_u.$ There is an arc $v_uw_u$ in ${\bar{D}}$ if and only if there is an arc $vw$ in $D.$ In addition to the arcs of the subgraphs $D_u,$ $u\in V$, we add to ${\bar{D}}$ an arc $t_us_v$ for each arc from $uv$ in $D.$ The pseudo cubic digraph $\tilde{D}$ of $D$ is obtained from ${\bar{D}}$ by replacing each vertex $v_u$ of ${\bar{D}}$ by a path $P(v_u)$ with $k$ vertices. Each arc entering a vertex $v_u$ in ${\bar{D}}$ is replaced by an arc of $\tilde{D}$ entering the first vertex of $P(v_u).$ Analogously, each arc leaving the vertex $v_u$ in ${\bar{D}}$ is replaced by an arc of $\tilde{D}$ leaving the last vertex of $P(v_u)$ (see Fig. 2). We define a new instance of Max-Labeled-Path on the digraph $\tilde{D}$ with the first vertex of $P(s_s)$ as a source and the last vertex of $P(t_t)$ as a sink and a labeling function $\tilde{l}$ defined as follows.

Fig. 2.

An example of pseudo square digraph ${\bar{D}}$ with $k=|\mathcal{L}|=4.$ An optimal path $P$ in $D$ and the corresponding optimal path ${\bar{P}}$ in $\bar{D}$ are drawn in bold. In the subgraph $D_a$, each vertex $v$ of ${\bar{D}}$ is labeled by the subset of labels received by the vertices of the path $P(v)$ of ${\tilde{D}}.$ In ${\tilde{D}},$ the vertex $f_d$ of ${\bar{D}}$ is replaced by the path $P(f_d)=(f_d^1,f_d^2,f_d^3,f_d^4).$

Labeling. Let $v_u$ be a vertex of $\tilde{D}$, the set of labels of the vertices of $P(v_u)$ will depend on the labels of $u$ and $v$ in $D$ and on the level of $u$ in $D$. Since either all vertices of $P(v_u)$ are visited by a path from the source to the sink or none of them are, our labeling function assigns a set of labels to the path $P(v_u)$ and does not precise the order in which the labels appear on $P(v_u).$ The set of labels $\tilde{\mathcal{L}}$ used to define the labeling of $\tilde{D}$ consists of $k$ disjoint subsets $\tilde{\mathcal{L}_1},\ldots , \tilde{\mathcal{L}_k}$ such that $|\tilde{\mathcal{L}_1}|=\ldots = |\tilde{\mathcal{L}_k}|=k^2$. For each label $c\in \mathcal{L}$ and each level $i\in \{1,\dots , k\},$ we construct a partition $\mathcal{S}_{i,c}:=\{S_{i,c}(c') : c'\in \mathcal{L}\}$ of $\tilde{\mathcal{L}}_c$ into $k$ subsets of size $k$ such that any two subsets arising from different partitions intersect in exactly one label, i.e. if $i_1\ne i_2$ for all $c',c''\in \mathcal{L},$ $|S_{i_1,c}(c') \cap S_{i_2,c}(c'')| = 1.$ Since $k^2$ is a power of two ($k^2=2^r$), such partitions can be easily constructed as classes of parallel lines of a finite affine plane (each class of parallel lines induces a partition in which the subsets are the lines). The construction of finite affine planes from finite fields is described for instance in [1]. This construction can be done in polynomial time in the size of $D$ by first identifying an irreducible polynomial of degree $r$ by brute force and then constructing the corresponding finite fields $GF(2^r)$. The labeling function $\tilde{l}$ assigns to the vertices of $P(v_u)$ the labels that belong to the subset $S_{\lambda (u),l(u)}(l(v))$ of the partition $\mathcal{S}_{\lambda (u),l(u)}.$

Claim

There is a path in $\tilde{D}$ that collects each label in $\tilde{\mathcal{L}}$ exactly once.

Proof

Let $P$ be the path of $D$ collecting all the labels in $\mathcal{L}.$ Consider the path ${\tilde{P}}$ passing via each subgraph $D_{u}$ for all $u\in P$ and such that the subpath ${\tilde{P}}_u$ of ${\tilde{P}}$ inside the subgraph $D_u$ consists of the vertices $v_u$ for all $v\in P$ (see Fig. 2). Since $P$ collects each label in $\mathcal{L}$ once, the subpath ${\tilde{P}}_u$ collects every subset of the partition $\mathcal{S}_{\lambda (u),l(u)}.$ This implies that ${\tilde{P}}_u$ collects each label of ${\tilde{\mathcal{L}}}_{l(u)}$ once. Applying this assertion to all vertices $u\in P$ and using again that $P$ collects each label in $\mathcal{L},$ we conclude that ${\tilde{P}}$ collects all the labels of ${\tilde{\mathcal{L}}} = \bigcup _{u\in P} {\tilde{\mathcal{L}}}_{l(u)}$ once.   $\Box$

The previous claim and the fact that $|\tilde{\mathcal{L}}|$ is a power of two ensure that $\tilde{D}$ is an instance of Max-Labeled-Path satisfying the conditions of (C1) and (C4). Clearly, the instance $\tilde{D}$ can be constructed in polynomial time from the instance $D.$

3.2 Proof of Theorem 5

Let $g$ denote the reciprocal function on the interval $[0,1]$ of the following continuous and strictly increasing function $h$:

$$ h(x) := \left\{ \begin{array}{ll} h_1(x):= x( x^2 -x+1 )&{} \text{ if } 0<x < \frac{1}{2}; \\ h_2(x):=x^2-\frac{1}{4}x+\frac{1}{4} &{} \text{ if } \frac{1}{2} \le x \le 1. \end{array} \right. $$

Lemma 4

For each $0<\beta <1$, the sequence $\beta _n$ defined by $\beta _0= \beta$ and $\beta _{n+1}= g(\beta _n)$ has a limit of $1.$

In the next section, we show the following two results:

Lemma 5

Given any path $Q$ in $\tilde{D}$ that collects at least $\beta k^3$ labels, a path $P$ in $D$ that collects at least $g(\beta )k$ labels can be computed in polynomial time.

Lemma 6

If there is a polynomial-time algorithm with a ratio $\beta$ for Max-Labeled-Path then there is a polynomial-time algorithm with a ratio $g(\beta )$ for Max-Labeled-Path.

Proof

Suppose there exists a polynomial time algorithm ALG$_\beta$ with a ratio at least $\beta$ for Max-Labeled-Path. Let $D$ be an instance of Max-Labeled-Path, we use the following algorithm:

This algorithm is clearly polynomial because all the steps are, thus we have a polynomial time algorithm with a ratio $g(\beta )$ for Max-Labeled-Path.   $\Box$

Suppose there exists an approximation algorithm with a constant factor $\beta$ for Max-Labeled-Path. By Lemma 4, there exists an integer $n$ such that $\beta _{n} > \frac{47}{48}$. Applying $n$ times Lemma 6, we derive a polynomial-time algorithm for the problem Max-Labeled-Path with a ratio exceeding $\frac{47}{48}.$ A similar argument shows that any constant factor approximation algorithm for Max-Labeled-Path can be converted into a PTAS for this problem. Such an algorithm does not exist unless $P=NP$ by Theorem 4. Assuming Lemma 5, this concludes the proof of Theorem 5.

3.3 Proof of Lemma 5

We explain how to construct in polynomial time a path $P$ in $D$ that collects a set $\mathcal{L}^P\subseteq \mathcal{L}$ containing at least $g(\beta ) k$ labels from a path $Q$ in $\tilde{D}$ that collects a set $\tilde{\mathcal{L}}^Q\subseteq \tilde{\mathcal{L}}$ containing at least $\beta k^3$ labels. We denote by $V^Q\subseteq V$ the set of vertices $u$ such that $Q$ passes via $D_u$ and by $\mathcal {L}^Q\subseteq \mathcal {L}$ the set of labels of the vertices in $V^Q$. For each vertex $u \in V^Q$, we define $W_u^Q\subseteq V$ the set of vertices $v$ such that $Q$ contains $P(v_u)$ as a subpath and by $\mathcal {L}_u^Q\subseteq \mathcal {L}$ the set of labels of the vertices in $W_u^Q$. Let $\alpha _u := |\mathcal {L}_u^Q|/k.$ We will prove that either $|\mathcal {L}^Q| \ge g(\beta ) k$ or there exists a vertex $u\in V^Q$ such that $|\mathcal {L}_{u}^Q| = \alpha _{u} k \ge g(\beta ) k$. In the first case, the vertices of $V^Q$ induce in $D$ a path that collects $g(\beta ) k$ labels. In the second case, the vertices of $Q$ that belong to the subgraph $D_{u}$ induce in $D$ a path that collects $g(\beta ) k$ labels. Therefore, if one of the two assertions hold, one can derive in polynomial time a path $P$ of $D$ collecting $g(\beta ) k$ labels and we are done.

Suppose by way of contradiction that none of the two assertions hold. Namely, $|\mathcal {L}^Q| < g(\beta )k$ and for all $u \in V^Q,$ $\alpha _u < g(\beta )$. Let $c$ be a label in $\mathcal {L}^Q.$ We denote by $V^Q_{c} \subseteq V^{Q}$ the set of vertices $u \in V^Q$ such that $l(u)=c$ and we define $\alpha _c := \max _{u \in V^Q_c} \alpha _u$ and $u_c := \mathrm{arg\,max }_{u \in V^Q_c} \alpha _u.$ By assumption, $\alpha _c<g(\beta ).$ In $D_{u_c}$, $Q$ collects $\sum \limits _{c' \in \mathcal {L}^Q_{u_c}} |S_{c,\lambda (u)}(c')| = \sum \limits _{c' \in \mathcal {L}^Q_{u_c}} k = \alpha _c k^2$ labels.

Let $u$ be a vertex of $V^Q_{c} - \{u_c\}.$ The number of labels collected by $Q$ in $D_u$ that are not collected by $Q$ in $D_{u_c}$ is the sum over all labels $c'\in \mathcal{L}_u^Q$ of

$$ \begin{array}{rcl} \left| S_{c,\lambda (u)}(c') - \bigcup \limits _{c'' \in \mathcal {L}^Q_{u_c}} S_{c,\lambda (u_c)}(c'') \right| &{}=&{} k-\left| \bigcup \limits _{c'' \in \mathcal {L}^Q_{u_c}} \left( S_{c,\lambda (u)}(c') \cap S_{c,\lambda (u_c)}(c'')\right) \right| \\ &{}=&{} k-\sum \limits _{c'' \in \mathcal {L}^Q_{u_c}} \left| S_{c,\lambda (u)}(c') \cap S_{c,\lambda (u_c)}(c'')\right| \\ &{}=&{} k-\sum \limits _{c'' \in \mathcal {L}^Q_{u_c}} 1 \\ &{}=&{} k-\alpha _c k \\ \end{array}$$

The first equation follows $\left| S_{c,\lambda (u)}(c')\right| =k$ and trivial set properties. For the second equation, recall that the family $\{S_{c,\lambda (u_c)}(c'') : c'' \in \mathcal {L}^Q_{u_c} \}$ is a partition of ${\tilde{\mathcal{L}}}_{c}.$ The choice of the partitions used to define the labeling function of ${\tilde{D}}$ ensures that $\left| S_{c,\lambda (u)}(c') \cap S_{c,\lambda (u_c)}(c'')\right| =1$ and yields the third equation. For the last equation, we use $|\mathcal {L}^Q_{u_c}|=\alpha _c k.$ We conclude that the number of labels collected by $Q$ in $D_u$ and not collected by $Q$ in $D_{u_c}$ is $|\mathcal {L}^Q_{u}| (k-\alpha _c k).$ Since $(k-\alpha _c k) \ge 0$ and $|\mathcal {L}^Q_{u}|=\alpha _u k\le \alpha _c k$, this number is at most $\alpha _c k (k-\alpha _c k).$

Using this bound for all vertices $u \in V^Q_c-\{u_c\}$ and the fact that $\alpha _c k^2$ labels are collected by $Q$ in $D_{u_c},$ we obtain that the following bound on the number of labels of $\tilde{\mathcal{L}}_c$ collected by $Q$:

$$ \begin{array}{rcl} \left| \tilde{\mathcal{L}}^Q\cap \tilde{\mathcal{L}}_c\right| &{} \le &{} \alpha _c k^2 + (|V^Q_c |-1) \alpha _c k (k-\alpha _c k)\\[3pt] &{} \le &{} k^2(\alpha _c +\alpha _c (|V^Q_c |-1) (1-\alpha _c) ) \end{array} $$

Summing over all labels $c\in \mathcal{L}^Q,$ we obtain that the total number of labels collected by $Q$ is upper bounded as follows:

$$ \begin{array}{rcl} \left| \tilde{\mathcal{L}}^Q\right| &{} \le &{} k^2 \sum \nolimits _{c \in \mathcal {L}^Q} \left( \alpha _c +\alpha _c (|V^Q_c |-1) (1-\alpha _c) \right) \\[3pt] &{} < &{} k^2 \sum \nolimits _{c \in \mathcal {L}^Q} \left( g(\beta ) +\alpha _c (|V^Q_c |-1) (1-\alpha _c) \right) \ \ \ \ \ \ \ (*) \end{array} $$

This last inequality is obtained using the initial assumption $\alpha _c < g(\beta )$.

We distinguish two cases depending on the value of $g(\beta ).$ First, suppose that $g(\beta ) \ge \frac{1}{2}.$ Note that the maximum $\frac{1}{4}$ of the function $x(1-x)$ on the interval $[0,1]$ is realized for $x= \frac{1}{2}$. Therefore for all $c \in \mathcal {L}^Q,$ $\alpha _c \left( 1-\alpha _c\right) \le \frac{1}{4}$ and we derive from $(*)$:

$$ \begin{array}{rcl} \left| \tilde{\mathcal{L}}^Q\right| &{} < &{} k^2\sum \nolimits _{c \in \mathcal {L}^Q} \left( g(\beta ) +\frac{1}{4} (|V^Q_c |-1) \right) \\[3pt] &{} < &{} k^2\left( \left( g(\beta )- \frac{1}{4}\right) \sum \nolimits _{c \in \mathcal {L}^Q} 1+ \frac{1}{4} \sum \nolimits _{c \in \mathcal {L}^Q} |V^Q_c |\right) \\[3pt] &{} < &{} k^2\left( \left( g(\beta )- \frac{1}{4}\right) g(\beta )k+ \frac{1}{4} k\right) \\[3pt] &{} < &{} k^3\left( g(\beta )^2-\frac{1}{4} g(\beta ) + \frac{1}{4}\right) \\[3pt] &{} < &{} k^3\left( h(g(\beta ))\right) \\[3pt] &{} < &{} k^3 \beta \end{array} $$

In the third inequality, the upper bound on the left operand follows from the initial assumption $g(\beta ) k > |\mathcal {L}^Q| = \sum _{c \in \mathcal {L}^Q} 1$ and $(g(\beta )-\frac{1}{4}) \ge 0.$ The upper bound on the right operand follows from the fact that any path in $D$ from $s$ to $t$ contains exactly $k$ vertices, therefore $\sum _{c \in \mathcal {L}^Q} |V^Q_c|=k.$ The last equation contradicts the choice of $Q$ and concludes the proof for the case $g(\beta )\ge \frac{1}{2}.$

Now, suppose that $g(\beta ) < \frac{1}{2}.$ Since the function $x(1-x)$ is a strictly increasing function on the interval $[0, \frac{1}{2}]$ and $|V^Q_c|-1\ge 0$ for all $c\in \mathcal{L}^Q$, we can replace $\alpha _c$ by $g(\beta )$ in the inequality $(*)$:

$$ \begin{array}{rcl} |\tilde{\mathcal{L}}^Q | &{} < &{} k^2\sum \nolimits _{c \in \mathcal {L}^Q} \left( g(\beta ) +g(\beta ) (|V^Q_c |-1) \left( 1-g(\beta )\right) \right) \\[3pt] &{} < &{} k^2 g(\beta )\left( \sum \nolimits _{c \in \mathcal {L}^Q} 1- \left( 1- g(\beta )\right) +|V^Q_c| \left( 1-g(\beta )\right) \right) \\[3pt] &{} < &{} k^2 g(\beta )\left( g(\beta ) \sum \nolimits _{c \in \mathcal {L}^Q} 1+\left( 1-g(\beta )\right) \sum \nolimits _{c \in \mathcal {L}^Q} |V^Q_c| \right) \\[3pt] &{} < &{} k^2 g(\beta )\left( g(\beta )^2 k +\left( 1-g(\beta )\right) k \right) \\[3pt] &{} < &{} k^3 g(\beta )\left( g(\beta )^2 - g(\beta ) +1 \right) \\[3pt] &{} < &{} k^3 h(g(\beta ))\\[3pt] &{} < &{} k^3 \beta \end{array} $$

Again we use $\sum _{c \in \mathcal {L}^Q} 1 < g(\beta ) k$ and $\sum _{c \in \mathcal {L}^Q} |V^Q_c|=k$ to derive the fourth inequality. In the two cases, we obtain a contradiction with the assumption that the path $Q$ collects at least $\beta k^3$ labels. This concludes the proof of Lemma 5.

4 $\sqrt{OPT}$-Approximation for Max-Labeled-Path

4.1 Algorithm

In this section, we describe a polynomial algorithm that computes for each instance $D$ of Max-Labeled-Path, a path of $D$ collecting $\sqrt{OPT(D)}$ labels. Again, for the sake of simplicity, we assume that there is only one source $s$ and one sink $t.$ Our algorithm can be easily adapted to handle the case with several sources and several sinks. First, we define a function $F : V \rightarrow \mathbb {N}$ such that $F(u)$ can be computed for all vertices $u\in V$ in time $O(|V|^3)$. Then, we prove that, for any vertex $u\in V,$ $F(u)$ is an upper bound on the number of labels collected by a path from $s$ to $u.$ Finally, we describe an algorithm that computes for any vertex $u\in V$ a path that collects at least $\lfloor \sqrt{ F(u)} \rfloor$ labels. Applying this algorithm to $t,$ we obtain a path from $s$ to $t$ that collects at least $\lfloor \sqrt{OPT} \rfloor$ labels.

For each pair of vertices $u,v \in V,$ let $D_{u,v}$ be the subgraph of $D$ consisting of all paths from $u$ to $v$. We denote by $\varGamma (u,v)$ the number of labels in $D_{u,v}$. Let $F : V \rightarrow \mathbb {N}$ be the function recursively defined as follows :

$$F(u) :=\left\{ \begin{array}{ll} 1, \text { if u=s ;} \\ \max \limits _{P \in \mathcal {P}^u} \min \limits _{ww'\in P} F(w) + \varGamma (w',u), \text { otherwise.} \end{array} \right. $$

where $\mathcal {P}^u$ denotes the set of the paths from $s$ to $u$. Let $P(u)$ be a path in $\mathcal {P}^u$ that realizes the maximum, i.e. such that $F(u) = \min \limits _{ww'\in P(u)} F(w) + \varGamma (w',u)$.

The following lemma shows that, for any vertex $u\in V,$ $F(u)$ is an upper bound on the number of labels that can be collected by a path from $s$ to $u$.

Lemma 7

If $P=(s=u_0,u_1,...,u_n=u)$ is a path between $s$ and $u$ that collects $\alpha$ labels then $F(u) \ge \alpha$.

Proof

By induction on $n$. For $n=0$, $F(u_0) =F(s) = 1$. For $n>0$, consider a path $P=(s=u_0,u_1,...,u_n=u)$ that collects $\alpha$ labels. For any $i=1,\ldots ,n,$ let $\alpha _i$ be the number of labels collected by the path $(u_0,u_1,...,u_i)$. The path $(u_i,...,u_n)$ collects at least $\alpha - \alpha _{i-1}$ labels and belongs to $D_{u_i,u}$, therefore $\varGamma (u_i,u) \ge \alpha - \alpha _{i-1}$. Since, by induction, $F(u_{i-1}) \ge \alpha _{i-1},$ $F(u_{i-1})+ \varGamma (u_i,u) \ge \alpha$ for any $i=1,\ldots ,n$ yielding $F(u) \ge \alpha$.   $\Box$

Corollary 1

If $OPT$ is the maximum number of labels that can be collected by a path from $s$ to $t$ then $F(t) \ge OPT$.

Suppose that $F(v)$ and $P(v)$ have been already computed for all $v\in V,$ this can be done in $O(|V|^3)$ using standard data structures. Let $u$ be a vertex in $V.$ The algorithm ComputePath returns a path between $s$ and $u$ that collects at least $\lfloor \sqrt{ F(u)} \rfloor$ labels. By Corollary 1, applying this procedure with $u=t$ we obtain a path from $s$ to $t$ that collects at least $\lfloor \sqrt{ OPT} \rfloor$ labels.

The following lemma is useful to prove that the algorithm ComputePath is correct.

Lemma 8

If $F(u)\ge 4$ then there is an arc $ww'$ in $P(u)$ such that $F(w) \le (\lfloor \sqrt{ F(u)} \rfloor -1)^2$ and $F(w') \ge (\lfloor \sqrt{ F(u)} \rfloor -1)^2.$ Moreover, for any such arc, $\varGamma (w',u) \ge \lfloor \sqrt{ F(u)} \rfloor + 1$.

Proof

The first assertion is true because $F(s)=1 \le (\lfloor \sqrt{ F(u)} \rfloor -1)^2$ and $F(u) \ge (\lfloor \sqrt{ F(u)} \rfloor -1)^2$. To verify the second assertion, let $ww'$ be an arc such that $F(w) \le (\lfloor \sqrt{ F(u)} \rfloor -1)^2$ and $F(w') \ge (\lfloor \sqrt{ F(u)} \rfloor -1)^2.$ Since $ww' \in P(u),$ $F(w) + \varGamma (w',u) \ge F(u).$ This implies $\varGamma (w',u) \ge F(u)-F(w) \ge \lfloor \sqrt{ F(u)} \rfloor ^2-(\lfloor \sqrt{ F(u)} \rfloor -1)^2 = 2 \lfloor \sqrt{ F(u)} \rfloor -1 \ge \lfloor \sqrt{ F(u)} \rfloor + 1$, because $\lfloor \sqrt{ F(u)} \rfloor \ge 2.$   $\Box$

Theorem 6

ComputePath $(u)$ computes a path $P$ that collects at least $\lfloor \sqrt{F(u)} \rfloor$ labels.

Proof

If $F(u)<4,$ any path from $s$ to $u$ collects at least $\lfloor \sqrt{ F(u)} \rfloor =1$ labels. Now suppose that $F(u)\ge 4.$ We proceed by induction on the number of recursive calls. If $u=s$ the algorithm returns the path $(s)$ that collects $F(s)=1$ labels. Otherwise, the first assertion of Lemma 8 ensures that $P(u)$ contains an arc $ww'$ such that $F(w) \le (\lfloor \sqrt{ F(u)} \rfloor -1)^2$ and $F(w') \ge (\lfloor \sqrt{ F(u)} \rfloor -1)^2.$ By induction hypothesis, ComputePath $(w')$ returns a path $P'$ collecting at least $\lfloor \sqrt{ F(u)} \rfloor -1$ labels. If $P'$ collects at least $\lfloor \sqrt{ F(u)} \rfloor$ labels, the path $P'.Q$ returned by the algorithm is a correct answer. Now, suppose that the path $P'$ collects exactly $\lfloor \sqrt{ F(u)} \rfloor -1$ labels. By Lemma 8, $\varGamma (w',u) \ge \lfloor \sqrt{ F(u)} \rfloor + 1.$ This implies that $D_{w',u}-\{w'\}$ contains at least $\lfloor \sqrt{ F(u)} \rfloor$ labels. Among them at least one is not collected by $P'.$ A BFS traversal of $D_{w',u}$ will find a vertex $v$ having this label together with a path $Q$ from $w'$ to $u$ passing via $v.$ Finally, the path $P'.Q$ that collects at least $\lfloor \sqrt{ F(u)} \rfloor$ labels is a correct answer.   $\Box$

Using standard data structures, computing $F(u)$ and $P(u)$ for every vertex $u\in V$ can be done in time $O(|V|^3).$