Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this chapter we review recent work on new adaptive Error Control B-spline Gaussian Collocation software for the efficient numerical solution of systems of 1D parabolic PDEs. BACOL [11] and BACOLR [13], two packages of this type, developed over the last decade, use high order methods in time and space and feature adaptive control of high order estimates of the temporal and spatial errors. They have been shown to be efficient, reliable, and robust, especially for problems having solutions with sharp moving layers and for stringent tolerances [12]. These packages employ adaptive Error Control B-spline Gaussian Collocation for the spatial discretization of the partial differential equations (PDEs), leading to a system of time-dependent differential–algebraic equations (DAEs), which is solved in BACOL using DASSL [5] and in BACOLR using RADAU5 [8]. Control of estimates of the temporal error is handled by the DAE solver. Control of spatial error estimates is handled using adaptive spatial mesh refinement based on high order estimates of the spatial error. These spatial error estimates are obtained by computing a second collocation solution (at substantial additional cost). Recent work to address this cost issue has focused on interpolation based schemes that allow a spatial error estimate to be obtained without the need for the computation of a second collocation solution. These schemes, called the superconvergent interpolant (SCI) scheme [1] and the lower order interpolant (LOI) scheme [3], have been implemented in the recently developed software package, BACOLI [10], obtained through a substantial modification of BACOL.

The problem class assumed by BACOL, BACOLR, and BACOLI has the form

$$\begin{aligned}\underline u_t(x,t) = {\underline f}(x,t, {\underline u}(x,t), {\underline u}_x(x,t), {\underline u}_{xx}(x,t)),\end{aligned}$$
(1)

with initial and boundary conditions of the form

$$\begin{aligned}\underline u(x,t_0) = {\underline u}_0(x), \quad{\underline b}_L(t, {\underline u}(a,t), {\underline u}_x(a,t)), \quad{\underline b}_R(t, {\underline u}(b,t), {\underline u}_x(b,t)),\end{aligned}$$
(2)

where \({\underline u}\), \({\underline f}\), \({\underline u}_0\), \({\underline b}_L\), and \({\underline b}_R\) are vector functions with NPDE components (where NPDE is the number of PDEs).

This chapter is organized as follows. In Sect. 2, we briefly review the adaptive Error Control B-spline Gaussian Collocation algorithm implemented in BACOL/BACOLR.

Section 3 briefly describes the SCI and LOI schemes employed in the new BACOLI code while Sect. 4 presents numerical results comparing the accuracy of the BACOL and BACOLI error estimates and the overall efficiency of the codes.

2 BACOL/BACOLR Error Control B-spline Gaussian Collocation

Assuming a spatial mesh of NINT subintervals that partitions \([a,b]\), the B-spline collocation algorithm employed by BACOL/BACOLR assumes that the collocation solution, \({\underline U}(x,t)\), is represented as a (vector) linear combination of known C 1-continuous piecewise polynomials of degree p on each spatial subinterval (represented in terms of a B-spline basis [6]) having the form

$$\begin{aligned} {\underline U}(x,t) = \sum_{i=1}^{NC} {\underline y}_i(t) B_i(x),\end{aligned}$$
(3)

where B i (t) is the ith B-spline basis function, \({\underline y}_i(t)\) is the vector of corresponding B-spline coefficients, and \(NC= \textit{NINT}(p-1)+2\). The coefficients, \({\underline y}_i(t)\), are determined by requiring the collocation solution to satisfy the boundary conditions (at x = a and x = b) and the PDE at p − 1 collocation points per subinterval that are the images of the set of p − 1 Gauss points [4] on [0,1]. This gives the DAE system

$$\begin{aligned} {\underline 0} &= {\underline b}_L(a,t, {\underline U}(a,t), {\underline U}_x(a,t)), \end{aligned}$$
(4)
$$\begin{aligned} {\underline U}_t(\xi_j,t)&={\underline f}(\xi_j,t,{\underline U}(\xi_j,t), {\underline U}_x(\xi_j,t), {\underline U}_{xx}(\xi_j,t)), \end{aligned}$$
(5)
$$\begin{aligned} {\underline 0} &= {\underline b}_R(b,t, {\underline U}(b,t), {\underline U}_x(b,t)),\end{aligned}$$
(6)

where ξ j is the jth collocation point. As mentioned in the previous section, this DAE system is solved in BACOL using DASSL and in BACOLR using RADAU5. The spatial error estimate is obtained by using the same B-spline collocation algorithm, with a B-spline basis of degree p + 1, to obtain a second (higher order) collocation solution, \({\underline{\bar U}}(x,t)\). At the end of each timestep (let t be the current time), a norm of the difference between \({\underline{ U}}(x,t)\) and \({\underline{\bar U}}(x,t)\) is computed to provide a spatial error estimate for \({\underline{ U}}(x,t)\) over \([a,b]\). BACOL/BACOLR accepts \({\underline{ U}}(x,t)\) provided that this spatial error satisfies the user tolerance. If it does not, the codes compute a second spatial error estimate, again based on the difference between the two collocation solutions, giving an estimate of the spatial error on each spatial subinterval, which is then used as the basis for a spatial remeshing, and the timestep is repeated. See [11] for further details.

As mentioned in the previous section, the computation of the second collocation solution represents a significant computational cost, essentially doubling the overall cost of the algorithm.

3 Review of the SCI/LOI Schemes and BACOLI

In order to improve the efficiency of the BACOL/BACOLR spatial error estimate, [1] and [3] consider, respectively, the SCI and LOI schemes, in which one of the two collocation solutions computed by BACOL/BACOLR is replaced with an interpolant.

The SCI scheme is based on theoretical results [7] that prove that, for (1), the collocation solution and its first spatial derivative are superconvergent at the spatial mesh points. Furthermore, based on similar theory for collocation methods for boundary value ordinary differential equations (ODEs)—see, e.g., [4]—and from experimental results for (1) [2], it is apparent that there are several (known) points internal to each subinterval, where the collocation solution is also superconvergent. The SCI scheme replaces the higher order collocation solution with a C 1-continuous piecewise polynomial, of the same order, specified on each subinterval by requiring it to interpolate the superconvergent meshpoint collocation solution and derivative values, the internal superconvergent collocation solution values, and the closest superconvergent collocation solution values from within each adjacent subinterval. Because the SCI interpolates at points from multiple subintervals, the interpolation error can be large when adjacent subinterval size ratios are large. See [1] for further details.

In contrast, the LOI scheme replaces the lower order collocation solution with a C 1-continuous piecewise polynomial specified on each subinterval by requiring it to interpolate the higher order collocation solution and its first spatial derivative at the mesh points and collocation solution at certain points within each subinterval such that the interpolation error of the resultant interpolant agrees asymptotically with the collocation error of the lower order collocation solution. See [9] for related work and [3] for further details.

As mentioned earlier, these schemes are implemented in the new code, BACOLI, in which only one collocation solution is computed and there is the option to obtain the spatial error estimate using either the SCI or LOI scheme. When BACOLI uses the SCI scheme it computes the lower order collocation solution and controls an error estimate for this solution; this is called standard (ST) error control mode. The original BACOL code also uses ST error control mode. When BACOLI uses the LOI scheme, it computes the higher order collocation solution but controls an error estimate for the lower order collocation solution; this is known as local extrapolation (LE) error control mode. If the original BACOL code were to be modified slightly to return the higher order collocation solution rather than the lower order collocation solution, it would be using LE error control mode.

4 Numerical Results

A standard test problem of the form (1) is the One Layer Burgers’ Equation (OLBE):

$$\begin{aligned} u_t = \epsilon u_{xx} - u u_x,\end{aligned}$$
(7)

with an initial condition at t = 0 and boundary conditions at x = 0 and x = 1 taken from the exact solution

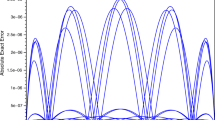
$$u(x,t) =\frac{1}{2}-\frac{1}{2}\tanh\left(\frac{x-\frac{t}{2}-\frac{1}{4}}{4\epsilon}\right),$$

where ϵ is a problem dependent parameter. In Fig. 1, we compare the BACOL, SCI, and LOI error estimation schemes with the true error, for the OLBE (\(\epsilon=10^{-3}\)) at t = 1, with p = 4 and a tolerance, \(tol=10^{-4}\). (BACOL error estimates control the mesh.)

Fig. 1
figure 1

BACOL, SCI, LOI error estimates and the true error for OLBE (\(\epsilon=10^{-3}\)) at t = 1, with p = 4, \(tol=10^{-4}\). (BACOL error estimates control the mesh.) The error estimates are in good agreement with each other and the true error except for the SCI estimates on subintervals for which the adjacent subinterval size ratios are large

Full size image

We see that the error estimates are generally in good agreement with the true error except for the SCI scheme on subintervals where an adjacent subinterval ratio is large. However, this issue is less significant when the SCI error estimates are used to control the mesh. See additional results in [2].

In Fig. 2, we compare BACOL in ST and LE modes (BAC/ST, BAC/LE) with BACOLI in SCI/ST and LOI/LE modes (SCI/ST, LOI/LE) with respect to efficiency. We again consider the OLBE (\(\epsilon=10^{-3}\)) with final time t = 1. We consider p = 5 and a set of 91 tol values over the range from \(10^{-1}\) to \(10^{-11}\).

Fig. 2
figure 2

Accuracy vs. time for OLBE (\(\epsilon=10^{-3}\)) at t = 1, for BACOL in ST and LE error control modes (BAC/ST, BAC/LE) and BACOL in SCI/ST and LOI/LE error control modes (SCI/ST, LOI/LE), p = 5. SCI/ST and LOI/LE are about twice as fast as BAC/ST and BAC/LE

Full size image

We see that BAC/ST and BAC/LE have comparable execution times and that these times are significantly greater than the BACOLI code in either SCI/ST or LOI/LE mode. However BACOLI in SCI/LOI mode has 14 failures over the 91 test cases. See [10] for additional results. An examination of the relative execution times for this problem (see [10]), averaged over \(tol =10^{-4}, 10^{-6}, 10^{-8}\) and \(p=4,\dots,11\), gives \(\frac{BAC/LE}{BAC/ST}=0.93\), \(\frac{SCI/ST}{BAC/ST}=0.57\), \(\frac{LOI/LE}{BAC/ST}=0.62\), and \(\frac{LOI/LE}{SCI/ST}=1.16\).

The BACOLI webpage, where the source code for BACOLI, a number of examples, and a Fortran 95 wrapper for the package are posted, ishttp://cs.smu.ca/∼muir/BACOLI-3_Webpage.htm.