Asymptotic Approximations

Abstract

Leonhard Euler (1707–1783) , among others in the eighteenth century, was adept at manipulating divergent series, though usually without careful justification (cf. Tucciarone [487], Barbeau and Leah [26], and Varadarajan [493]). Note, however, Hardy’s conclusion

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

(a) Background

Leonhard Euler (1707–1783) , among others in the eighteenth century, was adept at manipulating divergent series, though usually without careful justification (cf. Tucciarone [487], Barbeau and Leah [26], and Varadarajan [493]). Note, however, Hardy’s conclusion

$\ldots$ it is a mistake to think of Euler as a “loose” mathematician.

As with singular perturbations, the ideas behind asymptotic approximations were not well understood until about 1900. They were presumably unknown to Prandtl in Munich and Hanover. For a classical treatment of infinite series , see, e.g., Rainville [404].

See Olver [360] for an example of a semiconvergent or convergently beginning series . They were defined as follows in P.-S. Laplace’s Analytic Theory of Probabilities (whose third edition of 1820 is now available online as part of his complete work):

The series converge fast for the first few terms, but the convergence worsens, and then comes to an end, turning into a divergence. This does not hinder the use of the series if one uses only the first few terms, for which convergence is rather fast. The residual of the series, which is usually neglected, is small in comparison to the preceding terms.

(This translation is from Andrianov and Manevitch [10].)

Throughout most of the nineteenth century, a strong reaction against divergent series , led by the analyst Cauchy, nearly banned their use (especially in France). (Augustin-Louis Cauchy (1789–1857) was a professor at École Polytechnique from 1815–1830. Afterwards, he held other positions, sometimes in exile, because his conservative religious and political stances made him refuse to take a loyalty oath.) Note, however, Cauchy [73]. In 1828, the Norwegian Niels Abel (1802–1829) wrote:

Divergent series are the invention of the devil, and it is shameful to base on them any demonstrations whatsoever. By using them, one may draw any conclusion he pleases and that is why these series have produced so many fallacies and so many paradoxes.

Verhulst [500] has a similar quote from d’Alembert. Kline [255] includes considerable material regarding divergent series. In particular, he points out that Abel continued

That most of the things are correct in spite of that is extraordinarily surprising. I am trying to find a reason for this; it is an exceedingly interesting question.

Further, Kline quotes the logician Augustus De Morgan of University College London as follows:

We must admit that many series are such as we cannot at present safely use, except as a means of discovery, the results of which are to be subsequently verified and the most determined rejector of all divergent series doubtless makes use of them in his closet $\ldots$

Finally, the practical British engineer Oliver Heaviside wrote

The series is divergent; therefore, we may be able to do something with it.

In his Electromagnetic Theory of 1899, Heaviside also wrote

It is not easy to get up any enthusiasm after it has been artificially cooled by the rigorists $\ldots$ There will have to be a theory of divergent series.

Attitudes and developments no doubt somewhat reflect the alternations in French and European politics during those turbulent times. Abel summability of power series was originated by Euler, but it is usually named after Abel. Roy [427] reports that Abel called the technique

$$\displaystyle{\mbox{ horrible},}$$

saying

$$\displaystyle{\mbox{ Hold your laughter, friends.}}$$

In 1886, however, Henri Poincaré (1854–1912) and Thomas Joannes Stieltjes (1856–1894), simultaneously and independently, provided the valuable definition of an asymptotic approximation and illustrated its use and practicality. Their papers were, respectively, published in Acta Math. and Ann. Sci. École Norm. Sup. (cf. Poincaré [393] and Stieltjes [475]). The latter was Stieltjes’ dissertation. Stieltjes called the series semi-convergent. Poincaré (a professor at the Sorbonne and École Polytechnique) had studied with Hermite, who was in close contact with Stieltjes, primarily through letters (cf. Baillaud and Bourget [20]). Like most others, we tend to emphasize the special significance of Poincaré because of his important later work on celestial mechanics, basic to the two-timing methods we will later consider (see the centennial biographies, Gray [182] and Verhulst [502]). Stieltjes was Dutch, but successfully spent the last 9 years of his short life in France.

In contrast to convergent series, a couple of terms in an asymptotic series, in practice, often provide a good approximation. This is especially true for singular perturbation problems, as we shall find. McHugh [310] and Schissel [435] connect the topic to the classical ordinary differential equations literature. One’s first contact with asymptotic series may be for linear differential equations with irregular singular points (cf. Ford [151], Coddington and Levinson [91], or Wasow [513]). An example is provided by the differential equation

$$\displaystyle{x^{2}y^{{\prime\prime}} + (3x - 1)y^{{\prime}} + y = 0}$$

which has the formal power series solution

$$\displaystyle{\sum _{k=0}^{\infty }k!x^{k},}$$

convergent only at x = 0. The same series arises (as we will find) in expanding the exponential integral, while the series

$$\displaystyle{x\sum _{k=0}^{\infty }(-1)^{k}k!x^{k}}$$

formally satisfies

$$\displaystyle{x^{2}y' + y = x.}$$

The most popular book on asymptotic expansions may be Erdélyi [141]. (My copy cost $1.35.) The Dover paperback (now an e-book) was based on Caltech lectures from 1954 and was originally issued as a report to the U.S. Office of Naval Research. The material is still valuable, including operations on asymptotic series, asymptotics of integrals, singularities of differential equations, and differential equations with a large parameter. Arthur Erdélyi (1908–1977) came to Caltech in 1947 to edit the five-volume Bateman Manuscript Project (based on formulas rumored to be in Harry Bateman’s shoebox collection. Bateman was a prolific faculty member at Caltech from 1917 to 1946.) Erdélyi remained in Pasadena until 1964 when he returned to the University of Edinburgh to take the Regius chair that had been held by his hero, E. T. (later Sir Edmund) Whittaker, from 1912 to 1946. (Whittaker wrote A Course in Modern Analysis in 1902 and was coauthor with G. N. Watson of subsequent editions from 1915 (cf. [521]).) Influenced by the work feverishly underway among engineers at GALCIT, Erdélyi and some math graduate students also got involved in studying singular perturbations (one was the author’s own thesis advisor, Gordon Latta , whose 1951 thesis [281] had H. F. Bohnenblust as advisor). Erdélyi’s Asymptotic Expansions was much influenced by E. T. Copson’s Admiralty Computing Service report of 1946, commercially published by Cambridge University Press in 1965 [98], and by the work of Rudolf Langer, Thomas Cherry, and others in the 1930s regarding turning points. Much more applied mathematical activity involving asymptotics took place in Pasadena after Caltech started its applied math department about 1962, initially centered around Donald Cohen, Julian Cole, Herbert Keller, Heinz-Otto Kreiss, Paco Lagerstrom, Philip Saffman, and Gerald Whitham, among others contributing to practical applied asymptotics. Their students have meanwhile been most influential in the field.

The historical background to Cauchy’s own work on divergent series is well explained by the French mathematician Émile Borel (1871–1956) in Borel ([52], originally from 1928). Borel wrote:

The essential point which emerges from this hasty review of Cauchy’s work on divergent series is that the great geometer never lost sight of this matter and constantly searched this proposition, which he called

$$\displaystyle{\mbox{ a little difficult,}}$$

that a divergent series does not have a sum. Cauchy’s immediate successors, on the contrary, accepted the proposition with neither extenuation nor restriction. They remembered the theory only as applied in Stirling’s formula , but the possibility of practical use of that divergent series seemed to be a totally isolated curiosity of no importance from the point of view of general ideas which one could try to develop on the subject of analysis.

Andrianov and Manevitch [10], among others, report that Borel traveled to Stockholm to confer with Gösta Mittag-Leffler , after realizing that his summation method of 1899 gave the “right” answer for many classical divergent series. Placing his hand on the collected works of his teacher Weierstrass, Mittag-Leffler said, in Latin,

$$\displaystyle{\mbox{ The master forbids it.}}$$

Nonetheless, Borel had won the first prize in the 1898 Paris Academy competition “Investigation of the Leading Role of Divergent Series in Analysis.” See Costin [101] for an update on Borel summability .

Another important early book [196] on divergent series is by the British mathematician G. H. Hardy (1877–1946), a leading British pure mathematician and a professor successively at both Oxford and Cambridge. It was published posthumously in 1949 with a preface by his colleague J. E. Littlewood saying:

about the present title, now colourless, there hung an aroma of paradox and audacity.

Hardy’s introductory chapter is especially readable, filled with interesting and significant historical remarks. The book has none of the anti-applied slant nor personal reticence (cf. Hardy [195], Littlewood [296], or Leavitt [282]) often linked to Hardy. Overall the monograph is quite technically sophisticated, as is his related Orders of Infinity [194].

Olver’s Asymptotics and Special Functions [360] includes a rigorous, but very readable, coverage of asymptotics, with a computational slant toward error bounds. (British-born and educated, Olver came to the United States in 1961.) At age 85, Frank Olver (1924–2013) was the mathematics editor of the 2010 NIST Digital Library of Mathematical Functions [361] and of the associated Handbook, the web-based successor to Abramowitz and Stegun [2] (which originated at the U.S. National Bureau of Standards, the predecessor of the National Institute of Standards and Technology, and which may have been the most popular math book since Euclid.) It demonstrates that asymptotics is fundamental to understanding the behavior of special functions, which still remain highly relevant in this computer age.

Among many other mathematics books deserving attention by those wishing to learn asymptotics are Dingle [123], Bleistein and Handelsman [45], Bender and Orszag [36], Murray [338], van den Berg [40], Wong [525], Ramis [405], Sternin and Shatalov [473], Jones [229], Costin [101], Beals and Wong [33], Paris [386], and Paulsen [387]. Readers will appreciate their individual uniqueness and may develop their own personal favorites.

(b) Asymptotic Expansions

In the following, we will write

• (i)
  $$\displaystyle{ f(x) \sim \phi (x)\ \ \ \mbox{ as}\ \ \ x \rightarrow \infty }$$

  (2.1)

  if $\frac{f(x)} {\phi (x)}$ then tends to unity. (We will say that f is asymptotic to ϕ as x > 0 becomes unbounded.)

• (ii)
  $$\displaystyle{ f(x) = o(\phi (x))\ \ \ \mbox{ as}\ \ \ x \rightarrow \infty }$$

  (2.2)

  if $\frac{f(x)} {\phi (x)} \rightarrow 0$ (Alternatively, one can write $f \ll \phi$.) and

• (iii)
  $$\displaystyle{ f(x) = O(\phi (x))\ \ \ \mbox{ as}\ \ \ x \rightarrow \infty }$$

  (2.3)

  if $\frac{f(x)} {\phi (x)}$ is then bounded.

We often call these relations asymptotic equality and the little o and big O Landau (or Bachmann–Landau) order symbols (after the number theorists who introduced them in 1894 and 1909, respectively). (Olver [360] calls the O symbol a fig leaf, since the implied bound (which would be very useful when known) isn’t provided.) Warning: We need to be especially careful when the comparison function ϕ has zeros as $x \rightarrow \infty$. The symbol tilde $\sim$ is used to distinguish asymptotic equality from ordinary equality.

As our basic definition, we will use (after Olver): A necessary and sufficient condition that f(z) possess an asymptotic (power series) expansion

$$\displaystyle{ f(z) \sim a_{0} + \frac{a_{1}} {z} + \frac{a_{2}} {z^{2}} +\ldots \ \ \ \mbox{ as}\ \ \ z \rightarrow \infty \ \ \ \mbox{ in a region }R }$$

(2.4)

is that for each nonnegative integer n

$$\displaystyle{ z^{n}\left \{f(z) -\sum _{ s=0}^{n-1}\frac{a_{s}} {z^{s}}\right \} \rightarrow a_{n} }$$

(2.5)

as $z \rightarrow \infty$ in R, uniformly with respect to the allowed phase (i.e., argument) of z. The coefficients a _j are uniquely determined (as for convergent series). They’re not always the Taylor series coefficients, however. Also note that the limit point ∞ can be replaced by any other point and that (2.5) can be interpreted to be a recurrence relation for the coefficients a _n of (2.4).

An important case, often arising in applications , occurs when the asymptotic expansion with respect to $\frac{1} {z}$ depends on a second parameter , say θ. When the second parameter takes on (or tends to) a critical value θ _c , the expansion may become invalid. The asymptotic expansion is then said to be nonuniform with respect to θ.

Convergence factors are sometimes introduced to “make” divergent series converge. Likewise, the Borel–Ritt theorem is often invoked to provide a holomorphic sum to a divergent series (cf. Wasow [513]).

We also note, less centrally, that Martin Kruskal [266] perceptively introduced the term asymptotology as the art of handling applied mathematical systems in limiting cases, formulating seven underlying “principles” to be adhered to (cf. the original paper and Ramnath [406]). (They are simplification, recursion, interpolation, wild behavior, annihilation, maximum balance, and mathematical nonsense.)

A very useful elementary technique to obtain asymptotic approximations is the common method of integration by parts . We illustrate the technique by considering the exponential integral

$$\displaystyle{ Ei(z) \equiv \int _{-\infty }^{z}\frac{e^{t}} {t} \,dt, }$$

(2.6)

with integration taken along any path in the complex plane, cut on the positive real axis, with $\vert z\vert$ large. Repeated integration by parts gives

$$\displaystyle{Ei(z)\ =\ \frac{e^{z}} {z} +\int _{ -\infty }^{z}\frac{e^{t}} {t^{2}}\,dt\ =\ \frac{e^{z}} {z} + \frac{e^{z}} {z^{2}} + 2\int _{-\infty }^{z}\frac{e^{t}} {t^{3}}\,dt,}$$

etc., so for any integer n > 0, we obtain

$$\displaystyle{ Ei(z) = \frac{e^{z}} {z} \left (\sum _{k=0}^{n} \frac{k!} {z^{k}} + e_{n}(z)\right ) }$$

(2.7)

for the (scaled) remainder

$$\displaystyle{ e_{n}(z) \equiv (n + 1)!\ ze^{-z}\int _{ -\infty }^{z} \frac{e^{t}} {t^{n+2}}\,dt. }$$

(2.8)

If we define the region R by the conditions $\mbox{ Re}z < 0$ and $\vert \arg (-z)\vert <\pi$, so that $\vert e^{t-z}\vert \leq 1$ there, we find that

$$\displaystyle{ \vert e_{n}(z)\vert \leq \frac{(n + 1)!} {\vert z\vert ^{n+1}}, }$$

(2.9)

i.e. the error after using the first n + 1 terms in the power series for ze ^−z Ei(z) is less in magnitude than the first neglected term in the series when $z \rightarrow \infty$ in the sector of the left half plane. Thereby, as expected, the series expansion is asymptotic there. (Recall an analogous error bound, and the related pincer principle, for real power series whose terms have alternating signs.)

For n = 1,

$$\displaystyle{Ei(z) = \frac{e^{z}} {z} \left (1 + \frac{1} {z} + e_{1}(z)\right )}$$

with $\vert e_{1}(z)\vert \leq \frac{2} {\vert z\vert ^{2}}$ in the open sector R. For z fixed, the error is bounded. Moreover, we can nicely approximate Ei(z) there by using the first two terms

$$\displaystyle{e^{z}\left (\frac{1} {z} + \frac{1} {z^{2}}\right )}$$

of the sum if we simply let $\vert z\vert$ be sufficiently large. This is in sharp contrast to using a convergent expansion in powers of $\frac{1} {z}$, where we would typically need to let the number n of terms used become large in order to get a good approximation for any given z within the domain of convergence.

More surprising is the idea of optimal truncation (cf. White [519] and Paulsen [387]). A calculus exercise shows that for any given z, the absolute values of successive terms (i.e., our error bound) in the expansion (2.7) reach a minimum, after which they increase without bound. (Numerical tables for this example are available in a number of the sources cited.) This minimum occurs when $n \sim \vert z\vert$, so if this asymptotic series is truncated just before then, the remainder will satisfy

$$\displaystyle{ \vert e_{n}(z)\vert \leq \sqrt{\frac{2\pi } {\vert z\vert }}e^{-\vert z\vert } }$$

(2.10)

when we use Stirling’s approximation

$$\displaystyle{ \varGamma (x) = (x - 1)! \sim \left (\frac{x} {e}\right )^{x}\sqrt{ \frac{2\pi } {x}}\left (1 + \frac{1} {12x} + \frac{1} {288x^{2}}+\ldots \right )\mbox{ as }x \rightarrow \infty }$$

(2.11)

for $(\vert z\vert + 1)!$ (cf., e.g., Olver [360]). The latter series diverges for all x, but gives the remarkably good approximation 5.9989 for the rather small x = 4.

Spencer [470] states

Surely the most beautiful formula in all of mathematics is Stirling’s formula $\ldots$ How do the two most important fundamental constants, e and $\pi$, find their way into an asymptotic formula for the product of integers?

Equation (2.11) seems actually to be due to both de Moivre and Stirling (cf. Roy [427]). This error bound for Ei(z) is, indeed, asymptotically smaller in magnitude as $\vert z\vert \rightarrow \infty$ than any term in the divergent series! Thus, this bound is naturally said to display asymptotics beyond all orders .

Paris [386] points out that similar exponential improvements via optimal truncation can often be achieved. He cites the following theorem of Fritz Ursell [489]:

Suppose f(t) is analytic for $\vert t\vert < R$ with the Maclaurin expansion

$$\displaystyle{f(t) =\sum _{ n=0}^{\infty }C_{ n}t^{n}}$$

there and suppose that

$$\displaystyle{\vert f(t)\vert < Ke^{\beta t}}$$

for $r \leq t < \infty$ and positive constants K and β. Then (using the greatest integer function [ ] ), he obtains

$$\displaystyle{\int _{0}^{\infty }e^{-xt}f(t)dt =\sum _{ n=0}^{[rx]}\frac{C_{n}n!} {x^{n+1}} + O(e^{-rx})}$$

as $x \rightarrow \infty$. Thus, the Maclaurin coefficients of f(t) (about t = 0) provide the asymptotic series coefficients for its Laplace transform (about x = ∞) (because the kernel e ^−xt greatly discounts other t values).

We shouldn’t extrapolate too far from the example Ei(z) or Ursell’s theorem. The often-made suggestion to truncate when the smallest error is attained is not always appropriate. (Convergent series, indeed, attain their smallest error (zero) after an infinite number of terms.) However, we point out that considerable recent progress has resulted using exponential asymptotics , by reexpanding the remainder repeatedly and truncating the asymptotic expansions optimally each time (cf. Olde Daalhuis [358] and Boyd [55, 56, 57]). Boyd tries to explain the divergence of the formal regular power series expansion

$$\displaystyle{ u(x,\epsilon ) =\sum _{ j=0}^{\infty }\epsilon ^{2j}\frac{d^{2j}f} {dx^{2j}} }$$

(2.12)

as an asymptotic solution of

$$\displaystyle{\epsilon ^{2}u^{{\prime\prime}}- u = f(x),\ \ \ - 1 \leq x \leq 1}$$

by using the representation

$$\displaystyle{u(x,\epsilon ) =\int _{ -\infty }^{\infty } \frac{F(k)} {1 +\epsilon ^{2}k^{2}}e^{ikx}\,dk}$$

of the solution as an inverse Fourier transform (cf. Boyd [56]) with F being the transform of f. A critical point is the finite radius of convergence of the power series for $\frac{1} {1+\epsilon ^{2}k^{2}}$. Boyd seems to be first of many authors to quote Gian-Carlo Rota [421]:

One remarkable fact of applied mathematics is the ubiquitous appearance of divergent series , hypocritically renamed asymptotic expansions. Isn’t it a scandal that we teach convergent series to our sophomores and do not tell them that few, if any, of the series they meet will converge? The challenge of explaining what an asymptotic expansion is ranks among the outstanding taboo problems of mathematics.

In addition to asymptotic power series to approximate a given function, it will often be helpful to use more general asymptotic expansions

$$\displaystyle{\sum _{n\geq 0}a_{n}\phi _{n}(\epsilon ).}$$

Here, the a _n s are constants and we will suppose that {ϕ _n } is an asymptotic sequence of monotonic functions (or scale) satisfying

$$\displaystyle{ \frac{\phi _{n+1}} {\phi _{n}} \rightarrow 0\ \ \mbox{ as}\ \ \ \epsilon \rightarrow 0,\ \ \ n = 0,1,2,\ldots, }$$

(2.13)

generalizing the powers. We will again let the symbol tilde $(\sim )$ denote asymptotic equality

$$\displaystyle{ f(\epsilon ) \sim \sum _{n=0}^{\infty }a_{ n}\phi _{n}(\epsilon ) }$$

(2.14)

where for any integer N > 0

$$\displaystyle{ f(\epsilon ) =\sum _{ n=0}^{N}a_{ n}\phi _{n}(\epsilon ) + O(\phi _{N+1}). }$$

(2.15)

Often, it will be helpful to limit N and to restrict ε to appropriate complex sectors (about, perhaps, the positive real half axis) . In the special case of an asymptotic power series, we simply have ϕ _n (ε) = ε ⁿ. Note that the coefficients in (2.14) are uniquely determined since

$$\displaystyle{ a_{J} =\lim _{\epsilon \rightarrow 0}\left (\frac{f(\epsilon ) -\sum _{n=0}^{J-1}a_{n}\phi _{n}(\epsilon )} {\phi _{J}(\epsilon )} \right )\ \ \ \mbox{ for each $J$}. }$$

(2.16)

To multiply asymptotic expansions (2.14), it is convenient if the sequence satisfies

$$\displaystyle{\phi _{n}(\epsilon )\phi _{m}(\epsilon ) =\phi _{n+m}(\epsilon )}$$

for all pairs n and m. (Determining an appropriate asymptotic sequence {ϕ _n }, to use for a given f arising in, say, some application may not be simple, however. In response, Murdock [335] suggests a method of undetermined gauges.) When we let the a _n s depend on ε, the series (2.14) is called a generalized asymptotic expansion . Their coefficients a _n (ε) are then no longer unique. Such expansions are, nonetheless, commonly used, here and elsewhere.

Some further write

$$\displaystyle{f \sim \sum _{n=0}^{\infty }f_{ n}(\epsilon )}$$

whenever

$$\displaystyle{f(\epsilon ) -\sum _{n=0}^{N}f_{ n}(\epsilon ) = o(\phi _{N}(\epsilon ))}$$

for every N.

An important scale is the Hardy field of “logarithmico-exponential” functions , consisting of those functions obtained from ε by adding, multiplying, exponentiating, and taking a logarithm a finite number of times.

We note the important fact that a convergent series is asymptotic. This follows since the terms a _k z ^k of a convergent power series or analytic function

$$\displaystyle{f(z) = a_{0} + a_{1}z + a_{2}z^{2}+\ldots }$$

ultimately behave like a geometric series, i.e. they satisfy

$$\displaystyle{\vert a_{k}z^{k}\vert \leq \vert a_{ k}\vert r^{k} \leq A}$$

for some bound A, all large k and $\vert z\vert \leq r$ for some r > 0. For $\vert z\vert < \frac{r} {2}$, this implies that the remainder for any n satisfies

$$\displaystyle{\sum _{k=n+1}^{\infty }a_{ k}z^{k} = O(z^{n+1}),}$$

so the convergent power series for f for $\vert z\vert \leq r$ is indeed asymptotic as $z \rightarrow 0$. More simply, recall Taylor series with remainder.

A general technique to obtain asymptotic expansions for integrals is again termwise integration . Consider, for example, the Laplace transform

$$\displaystyle{ I(x) =\int _{ 0}^{\infty } \frac{t^{\lambda -1}} {1 + t}e^{-xt}\,dt }$$

(2.17)

for λ > 0 and x large. Since $\frac{1} {1+t} =\sum _{ s=0}^{n-1}(-t)^{s} + \frac{(-t)^{n}} {1+t}$, we obtain

$$\displaystyle{ I(x) =\sum _{ s=0}^{n-1}\frac{(-1)^{s}\varGamma (s+\lambda )} {x^{s+\lambda }} + r_{n}(x) }$$

(2.18)

in terms of Euler’s gamma (or factorial) function

$$\displaystyle{\varGamma (z) \equiv \int _{0}^{\infty }e^{-t}t^{z-1}\,dt,\ \ \ \mbox{ Re }z > 0}$$

(cf. Olver et al. [361]) for the remainder

$$\displaystyle{r_{n}(x) \equiv (-1)^{n}\int _{ 0}^{\infty }\frac{t^{n+\lambda +1}} {1 + t} e^{-xt}\,dt.}$$

Since $\vert r_{n}(x)\vert \leq \frac{\varGamma (n+\lambda )} {x^{n+\lambda }}$,

$$\displaystyle{ I(x) \sim \sum _{s=0}^{\infty }\frac{(-1)^{s}\varGamma (s+\lambda )} {x^{s+\lambda }} \ \ \ \mbox{ as }x \rightarrow \infty. }$$

(2.19)

Again, even though the Maclaurin series for $\frac{1} {1+t}$ only converges for 0 ≤ t < 1, its coefficients determine the asymptotics for I(x) as $x \rightarrow \infty$. (Readers should understand such typical arguments.) Generalizations of this procedure to integrals

$$\displaystyle{\int _{0}^{\infty }f(t)e^{-xt}\,dt}$$

often are labeled Laplace’s method (or Watson’s lemma ). A real variables approach to obtain such results is found in Olver [360], while a complex variables approach is presented in Wong [525]. More general techniques for the asymptotic evaluation of integrals include the stationary phase and saddle point methods (called Edgeworth expansions in statistics).

(c) The WKB Method

The WKB method (cf. Olver [360], Schissel [436], Miller [318], Cheng [83], Wong [526], and Paulsen [387]) concerns asymptotic solutions of the scalar linear homogeneous second-order differential equation

$$\displaystyle{ y^{{\prime\prime}} +\lambda ^{2}f(x,\lambda )y = 0 }$$

(2.20)

when the real parameter $\lambda \rightarrow \infty$ and f is bounded. Introducing the logarithmic derivative

$$\displaystyle{ u(x,\lambda ) = \frac{y^{{\prime}}(x,\lambda )} {y(x,\lambda )} = (\ln y)^{{\prime}}, }$$

(2.21)

or equivalently setting

$$\displaystyle{ y = e^{\int ^{x}u(s,\lambda )\,ds }, }$$

(2.22)

converts the given linear second-order differential equation (2.20) to the nonlinear first-order generalized Riccati equation

$$\displaystyle{ u^{{\prime}} + u^{2} +\lambda ^{2}f = 0 }$$

(2.23)

(since y ^′ = uy and $y^{{\prime\prime}} = (u^{{\prime}} + u^{2})y$) which, generally, can’t be solved directly. (This is not the simple version solved by Count Riccati (or Johann Bernoulli) (cf. Roy [427]).) We will further suppose that the expansion

$$\displaystyle{ f(x,\lambda ) \sim \sum _{n=0}^{\infty }\frac{f_{n}(x)} {\lambda ^{n}} }$$

(2.24)

is known and valid on an interval α < x < β as $\lambda \rightarrow \infty$. Then, we will seek a (formal) asymptotic solution

$$\displaystyle{ u(x,\lambda ) \sim \lambda \sum _{n=0}^{\infty }\frac{u_{n}(x)} {\lambda ^{n}}, }$$

(2.25)

of (2.23) with corresponding series for u ² and u ^′. Equating coefficients of λ ² and λ ²⁻ⁿ in the differential equation, we will successively need

$$\displaystyle{u_{0}^{2} + f_{ 0} = 0}$$

and

$$\displaystyle{u_{n-1}^{{\prime}} + 2u_{ 0}u_{n} +\sum _{ k=1}^{n-1}u_{ k}u_{n-k} + f_{n} = 0\ \ \ \mbox{ for each }\ \ n \geq 1.}$$

Thus, we will take

$$\displaystyle{ u_{0}(x) = u_{0}^{\pm }(x) = \left \{\begin{array}{@{}l@{\quad }l@{}} \pm i\sqrt{f_{0 } (x)} \quad &\mbox{ if }f_{0}(x) > 0 \\ \pm \sqrt{-f_{0 } (x)}\quad &\mbox{ if }f_{0}(x) < 0 \end{array} \right. }$$

(2.26)

and

$$\displaystyle{ u_{n}(x) = - \frac{1} {2u_{0}(x)}\left (u_{n-1}^{{\prime}} +\sum _{ k=1}^{n-1}u_{ k}u_{n-k} + f_{n}\right )\ \ \mbox{ for each}\ \ n \geq 1. }$$

(2.27)

In particular,

$$\displaystyle{u_{1}(x) = -\frac{1} {2} \frac{d} {dx}\left (\ln u_{0}(x)\right ) - \frac{f_{1}(x)} {2u_{0}(x)}}$$

implies two linearly independent WKB approximates

$$\displaystyle{ y^{\pm }(x,\lambda ) = \frac{1} {\root{4}\of{f_{0}(x)}}e^{\pm i\lambda \int _{x_{0}}^{x}\left (\sqrt{(f_{ 0}(s))}-\frac{1} {2\lambda } \frac{f_{1}(s)} {\sqrt{f_{0 } (s)}} \right )ds }(1 + o(1))\mbox{ if }f_{0}(x) > 0 }$$

(2.28)

and

$$\displaystyle{ y^{\pm }(x,\lambda ) = \frac{1} {\root{4}\of{\vert f_{0}(x)\vert }}e^{\pm \lambda \int _{x_{0}}^{x}\left (\sqrt{\vert f_{ 0}(s)\vert }-\frac{1} {2\lambda } \frac{f_{1}(s)} {\sqrt{\vert f_{0 } (s)\vert }} \right )ds }(1 + o(1))\mbox{ if }f_{0}(x) < 0 }$$

(2.29)

for (2.20). The algebraic prefactor comes from the first term of u ₁. See Keller and Lewis [245] for connections to geometrical optics and Keller [244] regarding the related Born and Rytov approximations. Note, further, that one consequence of the leading term approximation, important in quantum mechanics, is the so-called adiabatic invariance (cf. Arnold et al. [12] and Ou and Wong [385]). Knowing these linearly independent approximate solutions also allows us to solve the nonhomogeneous equation, i.e. to determine an asymptotic Green’s function (cf. Stakgold [472]).

As defined above, the o(1) symbol in (2.28–2.29) indicates an expression that goes to zero as $\lambda \rightarrow \infty$. Its approximate form would be determined by u ₂. Miller [318] proves the validity of the WKB approximation using a contraction mapping argument, while Olver [360] bounds the error involved in terms of the total variation of a natural control function. Note the singularities of y that result at any turning points where f ₀ has a zero. Also note that the solutions (2.28–2.29) change from being exponential to oscillatory (or vice-versa) as such points are crossed with f ₀ changing signs.

As an alternative to (2.28), we could directly seek asymptotic solutions of (2.20) in the form

$$\displaystyle{ A(x,\lambda )e^{i\lambda \int ^{x}\sqrt{f_{ 0}(s)}\,ds} + \overline{A(x,\lambda )}e^{-i\lambda \int ^{x}\sqrt{f_{ 0}(s)}\,ds} }$$

(2.30)

for a complex-valued asymptotic power series A(x, λ) whose terms could be successively found using an undetermined coefficients scheme. Thus

$$\displaystyle{y = Ae^{i\lambda \int ^{x}\sqrt{f_{ 0}(s)}\,ds} + \mbox{ c.c.}}$$

must satisfy the differential equation. Because

$$\displaystyle{y^{{\prime\prime}} = \left [A^{{\prime\prime}} + 2i\lambda \sqrt{f_{ 0}(x)}A^{{\prime}} + \frac{i\lambda } {2} \frac{f_{0}^{{\prime}}(x)} {\sqrt{f_{0 } (x)}}A -\lambda ^{2}f_{ 0}(x)A\right ]e^{i\lambda \int ^{x}\sqrt{f_{ 0}(s)}\,ds} + \mbox{ c.c.},}$$

we will need A to satisfy

$$\displaystyle{ \frac{1} {\lambda } \left [A^{{\prime\prime}} + \left (\frac{f(x,\lambda ) - f_{0}(x)} {\lambda } \right )A\right ] + 2i\sqrt{f_{0 } (x)}A^{{\prime}} + \frac{i} {2} \frac{f_{0}^{{\prime}}(x)} {\sqrt{f_{0 } (x)}}A = 0 }$$

(2.31)

as a power series

$$\displaystyle{A\left (x, \frac{1} {\lambda } \right ) \sim \sum _{j\geq 0}\frac{A_{j}(x)} {\lambda ^{j}}.}$$

Murray [338] works out a variety of WKB examples quite explicitly.

Olver points out that the separate results of the physicists Wentzel, Kramers, and Brillouin in 1926 and those of Jeffreys in 1924 were actually obtained independently by Joseph Liouville and George Green in 1837. Carlini had even treated a special case involving Bessel functions in 1817. See Heading [200] and Fröman and Fröman [164] for further history . Nonetheless, the WKB(J) label seems to persist. (William Thomson, later Lord Kelvin, visited Paris in 1845 after his Cambridge graduation and introduced Jacques Sturm and Liouville to the work [183] of Green, a recently deceased former miller from Nottingham, memorialized in 1993 with a plaque in Westminster Abbey near the tomb of Newton and plaques to Kelvin, Maxwell, and Faraday (cf. Cannell [69]). (Green’s mill is now restored as a science center.) As late as 1953, Sir Harold Jeffreys called WKB

$$\displaystyle{\mbox{ approximations of Green's type.}}$$

First, note that the WKB results provide existence and uniqueness theorems for the singularly perturbed linear ODE

$$\displaystyle{ \epsilon \frac{d^{2}y} {dx^{2}} + a(x)\frac{dy} {dx} + b(x)y = 0 }$$

(2.32)

when ε > 0 is small, a and b are smooth, and a(x) ≠ 0, when Dirichlet boundary conditions are applied at two endpoints, say α and β. Also note that the Sturm transformation

$$\displaystyle{ y(x) = w(x)e^{-\frac{1} {2\epsilon } \int ^{x}a(s)\,ds }, }$$

(2.33)

requires w to satisfy

$$\displaystyle{ \epsilon \frac{d^{2}w} {dx^{2}} + f(x,\epsilon )w = 0 }$$

(2.34)

for

$$\displaystyle{f(x,\epsilon ) \equiv b(x) -\frac{1} {2}a^{{\prime}}(x) -\frac{1} {4\epsilon }a^{2}(x).}$$

The transformation (2.33) holds for all ε, but we will be especially concerned with the more challenging situation that ε is small but positive . Multiplying (2.34) by w and integrating by parts, supposing homogeneous boundary conditions w(α) = w(β) = 0, implies that

$$\displaystyle{\epsilon \int _{\alpha }^{\beta }\left (\frac{dw} {ds} \right )^{2}ds =\int _{ \alpha }^{\beta }f(s,\epsilon )\,w^{2}(s)\,ds}$$

since the boundary terms $\epsilon w\frac{dw} {dx}$ at α and β then vanish. Thus, $w(x) \equiv 0$ must hold when

$$\displaystyle{ f(x,\epsilon ) \leq 0\mbox{ on }\alpha \leq x \leq \beta, }$$

(2.35)

and the given two-point problem for y then has a unique solution (just let w be the difference between any two of them). Note that the sign condition (2.35) on f is satisfied if either

• (i) a(x) ≠ 0 and ε > 0 is small,

or

• (ii) $2b \leq a^{{\prime}}$ and ε > 0.

Uniqueness conditions for more general Sturm-Liouville boundary value problems can be found in Courant-Hilbert [103] and Zettl [532].

Existence of the solutions y of (2.32) follows from using the two linearly independent real WKB solutions , which take the form

$$\displaystyle{ A(x,\epsilon )\ \ \mbox{ and }\ \ B(x,\epsilon )e^{-\frac{1} {\epsilon } \int ^{x}a(s)\,ds } }$$

(2.36)

for asymptotic series A and B. (Note that this A is not the complex amplitude A used in the WKB solution (2.30).) In particular, the exponential factor in (2.33) is cancelled or doubled in the corresponding solutions (2.36).

The resulting outer solution A(x, ε) of (2.32) must satisfy

$$\displaystyle{ \epsilon A^{{\prime\prime}} + a(x)A^{{\prime}} + b(x)A = 0 }$$

(2.37)

as a real power series in ε, so its leading term must satisfy

$$\displaystyle{a(x)A_{0}^{{\prime}} + b(x)A_{ 0} = 0,}$$

i.e.

$$\displaystyle{A_{0}(x) = e^{-\int _{x_{0}}^{x} \frac{b(s)} {a(s)} \,ds}\,A_{0}(x_{0}).}$$

Likewise $\left (Be^{\frac{1} {\epsilon } \int ^{x}a(s)\,ds }\right )^{{\prime}} = \left (B^{{\prime}}-\frac{Ba} {\epsilon } \right )e^{-\frac{1} {\epsilon } \int ^{x}a(s)\,ds }$ and $\left (Be^{-\frac{1} {\epsilon } \int ^{x}a(s)\,ds }\right )^{{\prime\prime}}$ $= \left (B^{{\prime\prime}}-\frac{2} {\epsilon } B^{{\prime}}a -\frac{1} {\epsilon } Ba^{{\prime}} + \frac{B} {\epsilon ^{2}} a^{2}\right )e^{-\frac{1} {\epsilon } \int ^{x}a(s)\,ds }$, so the differential equation for y requires that

$$\displaystyle{ \epsilon B^{{\prime\prime}}- aB^{{\prime}} + (b - a^{{\prime}})B = 0. }$$

(2.38)

Its leading term $B_{0}$ must satisfy $aB_{0}^{{\prime}} + (a^{{\prime}}- b)B_{0} = 0$, so

$$\displaystyle{B_{0}(x) = \frac{a(x_{0})} {a(x)} e^{\int _{x_{0}}^{x} \frac{b(s)} {a(s)} \,ds}B_{0}(x_{0})}$$

and the general solution of (2.32) on x ≥ x ₀ takes the form

$$\displaystyle{ y(x,\epsilon ) = e^{-\int _{x_{0}}^{x} \frac{b(s)} {a(s)} \,ds}A_{0}(x_{0}) + e^{-\frac{1} {\epsilon } \int _{x_{0}}^{x}\left (a(s)-\epsilon \frac{b(s)} {a(s)} \right )\,ds}B_{0}(x_{0})\frac{a(x_{0})} {a(x)} + O(\epsilon ) }$$

(2.39)

when a(x) > 0. If bounded values y(x ₀) and $\epsilon y^{{\prime}}(x_{0})$ are prescribed, we will need

$$\displaystyle\begin{array}{rcl} y(x_{0})& =& A_{0}(x_{0}) + B_{0}(x_{0}) + O(\epsilon ) {}\\ \end{array}$$

and

$$\displaystyle\begin{array}{rcl} y^{{\prime}}(x_{ 0})& =& -\frac{1} {\epsilon } a(x_{0})B_{0}(x_{0}) + O(1), {}\\ \end{array}$$

so

$$\displaystyle\begin{array}{rcl} A_{0}(x_{0})& =& y(x_{0}) - B_{0}(x_{0}){}\end{array}$$

(2.40)

and

$$\displaystyle\begin{array}{rcl} B_{0}(x_{0})& =& -\frac{\epsilon y^{{\prime}}(x_{0})} {a(x_{0})}.{}\end{array}$$

(2.41)

Having these two linearly independent solutions (2.36) to the linear differential equation (2.32) will allow us to asymptotically solve many boundary value problems for it and its nonhomogeneous analog. The errors made using such approximations are asymptotically negligible like e ^−Cx∕ε for some C > 0 and x > 0, so smaller than O(ε ⁿ) for any n > 0. See Fig. 2.1 and Howls [219]. Note that the solution (2.39) will feature an initial layer of nonuniform convergence. The asymptotic solutions of (2.32) for a(x) ≠ 0 will be more satisfactory throughout boundary layer regions than those traditionally found by matched expansions, as we shall later demonstrate. When such restrictions as f(x, ε) ≤ 0 in (2.34) don’t hold, and for nonlinear generalizations, we must expect either multiple solutions to such two-point problems or none at all.

Figure 2.1:

e ^−x∕ε for a small ε > 0 is ultimately smaller than ε ^κ for any κ > 0. Here, n > m > 0

To illustrate typical behavior near a (simple) turning point , consider the equation

$$\displaystyle{ \epsilon ^{2}y^{{\prime\prime}}- xh^{2}(x)y = 0 }$$

(2.42)

for a smooth h(x) > 0. Oscillatory behavior for x < 0 and exponential behavior for x > 0 are provided by the WKB solutions. Locally, i.e. near the turning point x = 0, we naturally use the Airy equation

$$\displaystyle{ \ddot{w} - tw = 0 }$$

(2.43)

as a comparison equation . Its linearly independent solutions are the Airy functions Ai(t), and Bi(t) (cf. Olver et al. [361]). Their asymptotic behavior as $t \rightarrow \pm \infty$ is well known, e.g.,

$$\displaystyle{\begin{array}{*{10}c} Ai(t) & \sim \frac{1} {2\sqrt{\pi }t^{1/4}} e^{-\frac{2} {3} t^{3/2} }\ \ \ \mbox{ as }\ \ \ t \rightarrow \infty \\ \mbox{ and}& \\ Ai(t) &\sim \frac{1} {\sqrt{\pi }} \frac{1} {(-t)^{1/4}} \sin \left (\frac{2} {3}(-t)^{3/2} + \frac{\pi } { 4}\right )\ \ \ \mbox{ as }\ \ \ t \rightarrow -\infty. \end{array} }$$

The connections to the WKB solutions follow the Langer transformation

$$\displaystyle{ y \sim \left (\frac{xh^{2}(x)} {S(x)} \right )^{1/4}\left [C_{ 1}Ai\left (\frac{S(x)} {\epsilon ^{2/3}} \right ) + C_{2}Bi\left (\frac{S(x)} {\epsilon ^{2/3}} \right )\right ] }$$

(2.44)

for constants C ₁ and C ₂,

$$\displaystyle{S(x) = \left [\frac{3} {2}\int _{0}^{x}\sqrt{\vert r\vert }\,h(r)\,dr\right ]^{2/3},}$$

and the corresponding limits as $t = \frac{S(x)} {\epsilon ^{2/3}} \rightarrow \pm \infty$ (cf. Wasow [515] for details of the so-called connection problem ). Expansions can also be found for multiple and, even, coalescing turning points. Fowkes [152] solves the problem using multiple scale methods.

More generally, it’s often valuable to realize the equivalence of the Riccati differential equation

$$\displaystyle{ y^{{\prime}} = a(x)y^{2} + b(x)y + c(x) }$$

(2.45)

and second-order linear homogeneous differential equations. The transformation

$$\displaystyle{ y = \frac{-w^{{\prime}}} {aw} \mbox{ or }w = e^{-\int ^{x}a(s)\,y(s)\,ds } }$$

(2.46)

in (2.45) implies that w will satisfy the linear equation

$$\displaystyle{ w^{{\prime\prime}}-\left [\frac{a^{{\prime}}(x)} {a(x)} + b(x)\right ]w^{{\prime}} + a(x)c(x)w = 0. }$$

(2.47)

Many times, its solutions can be provided in terms of special functions, thereby giving solutions y of the Riccati equation (2.45) as well through (2.46). On the other hand, if we can guess (or otherwise ascertain) a differentiable solution y of the Riccati equation, it determines a nontrivial solution w of the linear equation (2.47) and, by reduction of order, the general solution. Other transformations for linear equations are given in Kamke [232] and Fedoryuk [145].

Note, in particular, that the second-order linear equation

$$\displaystyle{ \epsilon u^{{\prime\prime}} + b_{ 1}(x)u^{{\prime}} + b_{ 0}(x)u = 0 }$$

(2.48)

can be converted to

$$\displaystyle{ \epsilon q^{{\prime\prime}} + (q^{{\prime}})^{2} + b_{ 1}(x)q^{{\prime}} +\epsilon b_{ 0}(x) = 0 }$$

(2.49)

by setting

$$\displaystyle{ u = e^{q/\epsilon } }$$

(2.50)

and that the latter equation can be solved asymptotically by taking

$$\displaystyle{ q(x,\epsilon ) \sim \sum _{j\geq 0}\epsilon ^{j}q_{ j}(x) }$$

(2.51)

or, equivalently, by setting

$$\displaystyle{u = C(x,\epsilon )e^{q_{0}(x)/\epsilon }}$$

for a power series C (cf. Bender and Orszag [36]), which can be sought termwise with respect to ε.

(d) The Regular Perturbation Procedure

In the following, we shall consider it natural and straightforward (even central to singular perturbations) to use a regular perturbation method to find power series solutions to nonlinear vector initial value problems

$$\displaystyle{ \dot{x} = f(x,t,\epsilon ),\ \ t \geq 0,\ \ x(0) = c(\epsilon ) }$$

(2.52)

based on knowing a smooth vector solution x ₀(t) to the limiting nonlinear problem

$$\displaystyle{ \dot{x}_{0} = f(x_{0},t,0),\ \ t \geq 0,\ \ x_{0}(0) = c_{0}(0) }$$

(2.53)

on some bounded interval 0 ≤ t ≤ T. Assuming sufficient smoothness of f and c and the series expansions

$$\displaystyle{f(x,t,\epsilon ) \sim \sum _{j\geq 0}f_{j}(x,t)\epsilon ^{j}}$$

with smooth coefficients f _j and

$$\displaystyle{c(\epsilon ) \sim \sum _{j\geq 0}c_{j}\epsilon ^{j},}$$

we shall let

$$\displaystyle{ x(t,\epsilon ) \sim \sum _{k\geq 0}x_{k}(t)\epsilon ^{k}. }$$

(2.54)

Expanding about ε = 0,

$$\displaystyle\begin{array}{rcl} f(x(t,\epsilon ),t,\epsilon )& =& f(x_{0}(t),t,0) +\big (f_{x}(x_{0}(t),t,0)(\epsilon x_{1}(t) +\epsilon ^{2}x_{ 2}(t)+\ldots ) {}\\ & +& \epsilon f_{\epsilon }(x_{0},t,0)\big) + \left (\frac{1} {2}((f_{xx}(x_{0}(t),t,0)))(\epsilon x_{1}(t)+\ldots )\right )\!(\epsilon x_{1}(t)+\ldots ) {}\\ & +& \epsilon f_{x\epsilon }(x_{0}(t),t,0)(\epsilon x_{1}(t)+\ldots ) + \frac{\epsilon ^{2}} {2}f_{\epsilon \epsilon }(x_{0}(t),t,0)+\ldots {}\\ \end{array}$$

and equating successive coefficients of powers of ε in (2.52), we naturally require

$$\displaystyle\begin{array}{rcl} \dot{x}_{1}& = & \frac{\partial f} {\partial x}(x_{0}(t),t,0)x_{1} + \frac{\partial f} {\partial \epsilon } (x_{0}(t),t,0),\ \ x_{1}(0) = c_{1}{}\end{array}$$

(2.55)

$$\displaystyle\begin{array}{rcl} \dot{x}_{2}& = & \frac{\partial f} {\partial x}(x_{0}(t),t,0)x_{2} + \frac{1} {2}\left (\frac{\partial ^{2}f} {\partial x^{2}}(x_{0}(t),t,0)x_{1}(t)\right )x_{1}(t) \\ & & \quad + \frac{\partial ^{2}f} {\partial x\partial \epsilon }(x_{0}(t),t,0)x_{1}(t) + \frac{1} {2} \frac{\partial ^{2}f} {\partial \epsilon ^{2}} (x_{0}(t),t,0)),\ \ x_{2}(0) = c_{2},{}\end{array}$$

(2.56)

etc. These linear equations for x _j with j ≥ 1 can be successively and uniquely solved using the nonsingular fundamental matrix Φ for the linearized homogeneous system

$$\displaystyle{ \dot{\varPhi }= A(t)\varPhi \ \ \ \mbox{ with }\ \ \ \varPhi (0) = I }$$

(2.57)

for the Jacobian

$$\displaystyle{A(t) = f_{x}(x_{0}(t),t,0)}$$

and the identity matrix I (cf. Brauer and Nohel [59]). When A is constant, Φ is the matrix exponential e ^At. Recall the variation of constants (parameters) method to solve the linear vector initial value problem

$$\displaystyle{ \dot{y} = A(t)y + b(t),\ \ y(0)\mbox{ given.} }$$

(2.58)

Set

$$\displaystyle{y =\varPhi (t)w(t)}$$

for an unspecified vector w. First note that the unique Φ can be found by iterating in the integral equation

$$\displaystyle{\varPhi (t) = I +\int _{ 0}^{t}A(s)\varPhi (s)\,ds}$$

corresponding to (2.57). This yields the approximations

$$\displaystyle{\varPhi (t) = I +\int _{ 0}^{t}A(s)\,ds +\int _{ 0}^{t}A(s)\int _{ 0}^{s}A(r)\,dr\,ds+\ldots,}$$

etc. (sometimes called the matrizant ) which converge. Differentiating y, we get $\dot{y} =\dot{\varPhi } w +\varPhi \dot{ w} = A\varPhi w + b(t)$, so we will need

$$\displaystyle{\varPhi \dot{w} = b\ \ \ \mbox{ and }\ \ \ y(0) = w(0).}$$

Integrating, we uniquely obtain $w(t) = y(0) +\int _{ 0}^{t}\varPhi ^{-1}(s)b(s)\,ds$ (since Φ will be, at least locally, nonsingular). Thus,

$$\displaystyle{ y(t) =\varPhi (t)y(0) +\int _{ 0}^{t}\varPhi (t)\,\varPhi ^{-1}(s)\,b(s)\,ds, }$$

(2.59)

as can be readily checked.

Knowing the solution x ₀(t) (of (2.53)) for ε = 0 and the resulting Φ (cf.(2.57)), we next obtain

$$\displaystyle{ x_{1}(t) =\varPhi (t)c_{1} +\int _{ 0}^{t}\varPhi (t)\,\varPhi ^{-1}(s)\,f_{\epsilon }(x_{ 0}(s),s,0)\,ds }$$

(2.60)

and, then, in turn

$$\displaystyle\begin{array}{rcl} & & x_{2}(t) = \varPhi (t)c_{2} +\int _{ 0}^{t}\varPhi (t)\,\varPhi ^{-1}(s)\bigg[\bigg(\frac{1} {2}f_{xx}(x_{0}(s),s,0)\,x_{1}(s)\, + \\ & & \qquad \qquad f_{x\epsilon }(x_{0}(s),s,0)\bigg)x_{1}(s) + \frac{1} {2}f_{\epsilon \epsilon }(x_{0}(s),s,0)\bigg]ds, {}\end{array}$$

(2.61)

etc. We expect the series (2.54) for x to converge uniformly for ε small and bounded t. This justifies the regular perturbation technique, which we will henceforth apply routinely. When the assumptions don’t apply, the asymptotic solution may not simply be a power series in ε. Puiseaux expansions in fractional powers of ε (cf. [17]) are a possibility. As we will ultimately find, however, we cannot expect to blindly use these approximate solutions on intervals where t becomes unbounded. A proof on finite intervals is given in de Jager and Jiang [224]. See Smith [466] for the celebrated example of Einstein’s equation for the motion of Mercury about the sun.

More generally, one might also use such regular perturbation (i.e., power series) methods to solve operator equations

$$\displaystyle{ T(u,\epsilon ) = 0 }$$

(2.62)

for small ε, justified by applying the implicit function theorem under appropriate conditions (cf. Miller [318]) to get an analytic solution u(x, ε) (cf. Baumgärtel [32] and Krantz and Parks [262]). Also, see Kato [243] and Avrachenkov et al. [17] regarding linear operators.

A classic example involves the zeroes of the Wilkinson polynomial

$$\displaystyle{\mathop{\varPi }\limits _{k=1}^{20}(z - k) +\epsilon z^{19}}$$

(cf. Wilkinson [523], Bender and Orszag [36], and Moler [324]). Its complex roots are extremely sensitive to perturbations. Corresponding to k = 15, the first correction is of the order 5 ε 10¹⁰, providing extreme sensitivity of the perturbation.

In ending the chapter, we want to emphasize that we have severely restricted the topics covered, keeping in mind our limited later needs. More generally, the use of iteration methods to obtain asymptotic expansions is often very efficient, as is the use of convergence acceleration methods (cf. Weniger [518]), among many other computational techniques. We recommend Barenblatt [27] and [28]’s unique development of intermediate asymptotics , relating and extending basic concepts from dimensional analysis, self-similarity, and scaling. Consulting the extensive literature cited is highly recommended! Bosley [53] even provides a numerical version of asymptotics.

Among recent texts, Zeytounian [533] attempts to model viscous, compressible, heat-conducting, Newtonian, baroclinic, and nonadiabatic fluid flow using

the art of modeling assisted, rationally, by the spirit of asymptotics.

Motivation for such rational asymptotic modeling is found in the autobiography Zeytounian [534].

Example 1

Gobbi and Spigler [171] consider the scalar singular linear two-point boundary value problem

$$\displaystyle{ \epsilon ^{2}u^{{\prime\prime}}- u = - \frac{1} {\sqrt{x(1 - x)}},\ \ \ 0 \leq x \leq 1,\ \ \ u(0) = u(1) = 0. }$$

(2.63)

Since the auxiliary polynomial ε ² λ ² − 1 = 0 provides the complementary solutions e ^−x∕ε and e ^{−(1−x)∕ε}, we can use variation of parameters to find the general solution

$$\displaystyle{ u(x,\epsilon ) = e^{-x/\epsilon }C_{ 1} + e^{-(1-x)/\epsilon }C_{ 2} + \frac{1} {2\epsilon }\int _{0}^{x}\frac{e^{-(x-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}} + \frac{1} {2\epsilon }\int _{x}^{1} \frac{e^{(x-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}} }$$

(2.64)

of the nonhomogeneous differential equation (2.63). The boundary conditions imply that

$$\displaystyle{C_{1} \sim -\frac{1} {2\epsilon }\int _{0}^{1} \frac{e^{-t/\epsilon }\,dt} {\sqrt{t(1 - t)}}\ \ \ \mbox{ and }\ \ \ C_{2} \sim -\frac{1} {2\epsilon }\int _{0}^{1}\frac{e^{-(1-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}} }$$

up to asymptotically negligible amounts. Since $\varGamma (\frac{1} {2}) = \sqrt{\pi }$,

$$\displaystyle\begin{array}{rcl} u(x,\epsilon ) \sim & -& \frac{1} {2}\sqrt{\frac{\pi } {\epsilon }}\left (e^{-x/\epsilon } + e^{-(1-x)/\epsilon }\right ) \\ \quad & +& \frac{1} {2\epsilon }\left [\int _{0}^{x}\frac{e^{-(x-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}} +\int _{ x}^{1} \frac{e^{(x-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}}\right ].{}\end{array}$$

(2.65)

Within (0, 1), the first two terms are asymptotically negligible, while the primary contributions to the two integrals come from near t = x. Indeed,

$$\displaystyle{\frac{1} {2\epsilon }\int _{0}^{x}\frac{e^{-(x-t)/\epsilon }\,dt} {\sqrt{t(1 - t)}} \sim \frac{1} {2\sqrt{x(1 - x)}}}$$

and the second integral has the same limit. Thus, as expected,

$$\displaystyle{ u(x,\epsilon ) \sim \frac{1} {\sqrt{x(1 - x)}}\ \ \ \mbox{ within }\ \ (0,1). }$$

(2.66)

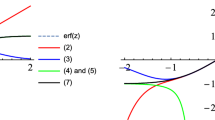
Because the asymptotic solution is symmetric about 1∕2 and the outer limit is unbounded at the endpoints, further analysis is necessary to determine the asymptotic behavior in the endpoint boundary layers. Computations for ε = 0. 01 and 0. 0025 provide spikes near 0 and 1 with $O(1/\sqrt{\epsilon })$ maxima, as found.

Example 2

$$\displaystyle{ \dot{y} = y^{2}(1 - y),\ \ y(0) =\epsilon }$$

(2.67)

(cf. Kapila [234]). Because $\dot{y} > 0$ for 0 < y < 1, we know that the solution y increases monotonically from ε to the rest point 1 at $t = \infty$. The exact solution can be obtained by separating variables since integrating $\left (\frac{1} {y} + \frac{1} {1-y} + \frac{1} {y^{2}} \right )dy = dt$ implies that

$$\displaystyle{ \ln \left ( \frac{y} {1 - y}\right ) -\frac{1} {y} = t -\frac{1} {\epsilon } +\ln \left ( \frac{\epsilon } {1-\epsilon }\right ). }$$

(2.68)

This implicit result shows, e.g., that

$$\displaystyle{y = \frac{1} {2}\ \ \mbox{ when }\ \ t = \frac{1} {\epsilon } -\ln \left ( \frac{\epsilon } {1-\epsilon }\right ) - 2}$$

while

$$\displaystyle{y = \frac{9} {10}\ \ \mbox{ when }t = \frac{1} {\epsilon } -\ln \left ( \frac{\epsilon } {1-\epsilon }\right ) -\frac{10} {9} +\ln 9}$$

and

$$\displaystyle{y = \frac{99} {100}\ \ \mbox{ when }t = \frac{1} {\epsilon } -\ln \left ( \frac{\epsilon } {1-\epsilon }\right ) -\frac{100} {99} +\ln 99.}$$

Thus, the ultimate explosion is long delayed when ε is small.

For bounded values of t, the preignition solution can be represented by a small regular perturbation expansion

$$\displaystyle{Y (t,\epsilon ) =\epsilon Y _{1}(t) +\epsilon ^{2}Y _{ 2}(t)+\ldots }$$

satisfying

$$\displaystyle{\dot{Y }_{1} = 0,\ \ Y _{1}(0) = 1}$$

and

$$\displaystyle{\dot{Y }_{2} = Y _{1}^{2},\ \ Y _{ 2}(0) = 0,}$$

etc. termwise. Thus

$$\displaystyle{ Y (t,\epsilon ) =\epsilon +\epsilon ^{2}t +\ldots. }$$

(2.69)

This breaks down as the slow-time $\tau \equiv \epsilon t$ grows. Indeed, the explosion takes place about

$$\displaystyle{ \tilde{t} = \frac{1} {\epsilon } -\ln \left ( \frac{\epsilon } {1-\epsilon }\right ) - 2, }$$

(2.70)

as can be verified numerically for, say, ε = 1∕10. One might say that a boundary layer (nonuniform convergence) occurs as $t \rightarrow \infty$.

Readers should be aware that one of the most successful texts presenting asymptotic methods has been Bender and Orszag [36], reprinted by Springer in 1999. Originated at MIT to teach the ubiquitous course in advanced mathematical methods for scientists and engineers, it featured easy, intermediate, difficult, and theoretical sections, corresponding exercises, and quotes from Sherlock Holmes at the beginning of each chapter. Paulsen [387] is a well-written new textbook seeking to simplify Bender and Orszag and make its subject more accessible.

To illustrate the centrality of asymptotics, we quote Dvortsina [128] regarding the prominent Soviet physicist I. M. Lifshitz (co-author of many outstanding texts with Nobel prizewinner Lev Landau):

Everyone who knew Lifshitz remembers well that every time he began a discussion of any work he asked first of all: “What small parameter did you choose?” He meant to say that in the majority of problems solved by theoretical physics the smallness of some quantity is always used.

After reading this chapter, and perhaps trying the exercises, the author hopes you no longer think asymptotic approximations are some sort of mystical constructions. They’re down to earth!

Exercises

• 1. (Awrejcewicz and Krysko [18]) Show that

  $$\displaystyle\begin{array}{rcl} \sin 2\epsilon & \sim & 2\epsilon -\frac{4} {3}\epsilon ^{3} + \frac{4} {15}\epsilon ^{5} +\ldots {}\\ & \sim & 2\tan \epsilon - 2\tan ^{3}\epsilon - 2\tan ^{5}\epsilon +\ldots {}\\ & \sim & 2\ln (1+\epsilon )+\ln (1+\epsilon ^{2})-2\ln (1 +\epsilon ^{3})+\ln (1 +\epsilon ^{4})+\frac{2} {5}\ln (1+\epsilon ^{5})+\ldots {}\\ & \sim & 6\left ( \frac{\epsilon } {3 + 2\epsilon ^{2}}\right ) -\frac{756} {5} \left ( \frac{\epsilon } {3 + 2\epsilon ^{2}}\right )^{5} +\ldots. {}\\ \end{array}$$

• 2. (Awrejcewicz and Krysko [18]) Consider

  $$\displaystyle{f(x,\epsilon ) = \sqrt{x+\epsilon }.}$$

  Note that $f(0,\epsilon ) = \sqrt{\epsilon }$. Show that

  $$\displaystyle{f(x,\epsilon ) = \sqrt{x}\left (1 + \frac{\epsilon } {2x} - \frac{\epsilon ^{2}} {8x^{2}} + \frac{\epsilon ^{3}} {16x^{3}}-\ldots \right )}$$

  when $\frac{\epsilon }{x} \rightarrow 0$, so the expansion is nonuniform.

• 3.

  • a. Find a power series expansion for the solution of the initial value problem

    $$\displaystyle{y^{{\prime}} = 1 + y^{2},\ \ y(0) =\epsilon.}$$

  • b. Find the exact solution and determine the first four terms of its power series about ε  = 0.

• 4. Find the first three terms of two power series solutions

  $$\displaystyle{u(x,\epsilon ) = u_{0}(x) +\epsilon u_{1}(x) +\epsilon ^{2}u_{ 2}(x)+\ldots }$$

  of the nonlinear differential equation

  $$\displaystyle{\epsilon u^{{\prime\prime}} = u^{2} - u +\epsilon x.}$$
• 5.

  • a. Find a regular perturbation solution to the initial value problem

    $$\displaystyle{y^{{\prime}} = 1 + y^{2} +\epsilon y,\ \ \ y(0) =\epsilon.}$$

    Where does it become singular?

  • b. Solve the equation

    $$\displaystyle{w^{{\prime\prime}}-\epsilon w^{{\prime}} + 1 = 0}$$

    and determine

    $$\displaystyle{y = -\frac{w'} {w}.}$$

    Where is it singular?

• 6. (cf. Hoppensteadt [213]) Consider the initial value problem

  $$\displaystyle{\dot{x} = -x^{3} +\epsilon x,\ \ \ x(0) = 1,\ \ t \geq 0.}$$

  • a. Find the first two terms of the regular perturbation expansion.

  • b. Find the exact solution and its limit as $t \rightarrow \infty$.

  • c. Explain the breakdown of the regular perturbation expansion.

• 7. (Hsieh and Sibuya [220]) Consider the two-point problem

  $$\displaystyle{y^{{\prime\prime}} =\epsilon \sin \left ( \frac{x} {100 - y^{2}}\right ),-1 \leq x \leq 1,\ \ \ y(-1) = y(1) = 0.}$$

  Obtain the solution y = ϕ(x, c, ε) by “shooting,” i.e. by solving the initial value problem

  $$\displaystyle{y^{{\prime\prime}} =\epsilon \sin \left ( \frac{x} {100 - y^{2}}\right ),\ \ y(-1) = 0,\ \ y^{{\prime}}(-1) = c(\epsilon )}$$

  for an appropriate c(ε). Determine the first two terms in the power series for y(x, ε) and c(ε). Observe the extensive and effective use of the shooting method in Hastings and McLeod [198].

• 8. A typical ODE exercise is to compute the terms of the power series solution to the initial value problem

  $$\displaystyle{y^{{\prime}} = x^{2} + y^{2},\ \ \ y(0) = 2.}$$

  • a. Set

    $$\displaystyle{y(x) =\sum _{ n=0}^{\infty }C_{ n}x^{n}}$$

    and show that C ₀ = 2, C ₁ = 4, C ₂ = 8, $C_{3 } = \frac{49} {3}$, and $C_{n+1} = \frac{1} {n+1}\sum _{p=0}^{n}C_{ p}C_{n-p}$, n ≥ 3.

  • b. Convert the equation to the Weber equation

    $$\displaystyle{w^{{\prime\prime}} + x^{2}w = 0}$$

    by using the representation w = e ^−∫ ₀ ^x y(s) ds .

  • c. Find the power series for w about x = 0, checking that $y = -\frac{w^{{\prime}}} {w}$. The radius of convergence for w is infinite. Note that w can be expressed in terms of parabolic cylinder (or Weber) functions .

• 9. (Kevorkian and Cole [249]) Consider the initial value problem

  $$\displaystyle{u^{{\prime\prime}} + u =\epsilon f(x)u}$$
  $$\displaystyle{u(0) = 0,\ \ u^{{\prime}}(0) = 1,\ \ x \geq 0.}$$

  Show that a necessary condition that the regular perturbation expansion of the solution be uniformly valid on x ≥ 0 is to have ∫ ₀ ^x f(s) ds bounded there.