Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A classical method in dMRI is Diffusion tensor imaging (DTI) [3] which assumes the EAP to be a single Gaussian centered at the origin. However, this over-simplified assumption has limitations in voxels where there are more complicated structures. To resolve this issue, Diffusion spectrum imaging (DSI) was proposed in [17]. However, a large number of measurements and a long acquisition time makes it impractical to use DSI in clinical setting. To this end, many imaging methods have been proposed, which reduce the number of measurements by using suitable signal models or by using compressed sensing techniques. For example, Hybrid diffusion imaging (HYDI) [18], Diffusion Propagator Imaging (DPI) [5], the SHORE basis [9, 11], the Bessel Fourier basis [6], the Spherical Polar Fourier (SPF) basis [2, 4] and the spherical ridgelet basis [14] extend the spherical representation of the signal on a single shell to multiple shells with a continuous radial term. On the other hand, MAP-MRI [12] represents the diffusion signal using Hermite polynomials. Finally, the method of [19] (NODDI) estimates axonal dispersion while the CHARMED model [1] uses very high b-value to estimate the axon diameter distribution.

2 Our Contributions

In this work, we use 3D Gaussian functions for representing the diffusion signal and computing the EAP. The diffusion signal is expressed as a linear combination of Gaussian basis functions centered at several locations in the q-space at which measurements are available. This is in contrast to other mixture models, which typically center the basis functions at the origin in q-space [7, 13]. The present work is a generalization of the radial basis functions method in [15], incorporating directional anisotropic (non-radial) Gaussians for continuous representation of the diffusion signal and the propagator. Since the Fourier transform of a Gaussian is another Gaussian, one obtains simple analytical expressions for the EAP, the ODF, the return-to-the-origin probability (RTOP) and the mean-squared-displacement (MSD). We validate our method on a physical phantom data set with known fiber crossing and on in-vivo human brain data set. We also compare our method to the one using radial basis functions (RBF) [15], 3D-SHORE [9], and show that adding constraints helps in improving the performance of 3D-SHORE.

3 Signal Representation

Accurate reconstruction of high dimensional continuous functions from finite number of samples can be achieved using as a linear combination of radial basis functions centered around the given data points [8]. We use a similar methodology to represent the dMRI signal continuously in the q-space. Given a sampling of diffusion signal \(E(\boldsymbol{q})\) at N data locations \(\{\boldsymbol{q}_{1},\ldots,\boldsymbol{q}_{N}\}\) in q-space, we consider its reconstruction using

$$\displaystyle{ \hat{E}(\boldsymbol{q}) =\sum _{ n=0}^{N}w_{ n}\phi _{n}(\boldsymbol{q} -\boldsymbol{q}_{n}),\;\text{with}\;\phi _{n}(\boldsymbol{q} -\boldsymbol{q}_{n}) =\exp (-(\boldsymbol{q} -\boldsymbol{q}_{n})^{T}D(\boldsymbol{q} -\boldsymbol{q}_{ n})), }$$
(1)

\(\boldsymbol{q}_{0} = 0\) and \(\phi _{0}(\boldsymbol{q}) = e^{-\boldsymbol{q}^{T}D_{ 0}\boldsymbol{q}}\). The tensor D is assumed to have a cylindrical shape with eigenvalues \(\sigma _{0},\sigma _{1},\sigma _{2}\) such that σ 1 = σ 2. The interpolation weights w n’s can then be computed by solving the following linear system: \(E(\boldsymbol{q}_{i}) =\sum _{ n=0}^{N}w_{n}\phi _{n}(\boldsymbol{q}_{i} -\boldsymbol{q}_{n})\text{for}i = 0,\ldots,N\) with E(0) = 1. Due to antipodal symmetry, we enforce equal coefficients for \(\phi _{n}(\boldsymbol{q} -\boldsymbol{q}_{n})\) and \(\phi _{n}(\boldsymbol{q} + \boldsymbol{q}_{n})\).

3.1 Closed Form Expressions for EAP and ODF

The EAP is given by the Fourier transform of \(\hat{E}(\boldsymbol{q})\). Since the constructed \(\hat{E}(\boldsymbol{q})\) is a linear combination of Gaussian functions, its Fourier transform is given by a linear combination of the Fourier transforms of the individual basis functions. Hence, the estimated EAP is of the form \(P(\boldsymbol{r}) = \mathcal{F}(\hat{E}(\boldsymbol{q})) =\sum _{ n=0}^{N}w_{n}\varPhi _{n}(\boldsymbol{r})\) with \(\varPhi _{0} = \mathcal{F}(\phi _{0}(\boldsymbol{q}))\) and \(\varPhi _{n} = \mathcal{F}(\phi _{n}(\boldsymbol{q} -\boldsymbol{q}_{n}) +\phi _{n}(\boldsymbol{q} + \boldsymbol{q}_{n}))\). In particular, Φ 0 is given by

$$\displaystyle{ \varPhi _{0}(\boldsymbol{r}) =\int _{\mathbb{R}^{3}}e^{-i2\pi \boldsymbol{r}^{T}\boldsymbol{q} }e^{-\boldsymbol{q}^{T}D_{ 0}\boldsymbol{q}}d\boldsymbol{q} =\pi ^{\frac{3} {2} }\vert D_{0}\vert ^{-\frac{1} {2} }e^{-\pi ^{2}\boldsymbol{r}^{T}D_{ 0}^{-1}\boldsymbol{r} }. }$$
(2)

A translation of a basis function leads to a phase shift of its Fourier transform, i.e. \(\mathcal{F}(\phi _{n}(\boldsymbol{q} + \boldsymbol{q}_{n})) = e^{i2\pi \boldsymbol{r}^{T}\boldsymbol{q}_{ n}}\mathcal{F}(\phi _{n}(\boldsymbol{q}))\). Hence, for n ≥ 1,

$$\displaystyle{ \varPhi _{n}(\boldsymbol{r}) = 2\pi ^{\frac{3} {2} }\vert D\vert ^{-\frac{1} {2} }\cos (2\pi \boldsymbol{r}^{T}\boldsymbol{q}_{n})e^{-\pi ^{2}\boldsymbol{r}^{T}D^{-1}\boldsymbol{r} }. }$$
(3)

The ODF is computed from the EAP by evaluating the integral \(\varPsi (\boldsymbol{u}) =\int _{ 0}^{\infty }P(r\boldsymbol{u})r^{2}\mathit{dr}\) [17], where \(\boldsymbol{u}\) is a unit vector and r is the radial co-ordinate. From the propagator \(P(\boldsymbol{r})\), \(\varPsi (\boldsymbol{u})\) is given analytically as \(\varPsi (\boldsymbol{u}) =\sum _{ n=0}^{N}w_{n}\varPsi _{n}(\boldsymbol{u})\) with

$$\displaystyle{ \varPsi _{0}(\boldsymbol{u}) = \frac{1} {4\pi \vert D_{0}\vert ^{\frac{1} {2} }(\boldsymbol{u}^{T}D_{0}^{-1}\boldsymbol{u})^{\frac{3} {2} }} }$$
(4)

and

$$\displaystyle{ \varPsi _{n}(\boldsymbol{u}) = \frac{1} {2\pi \vert D\vert ^{\frac{1} {2} }(\boldsymbol{u}^{T}D^{-1}\boldsymbol{u})^{\frac{3} {2} }} \left (1 -\frac{2(\boldsymbol{u}^{T}\boldsymbol{q}_{n})^{2}} {\boldsymbol{u}^{T}D^{-1}\boldsymbol{u}} \right )e^{-\frac{(\boldsymbol{u}^{T}\boldsymbol{q}_{n})^{2}} {\boldsymbol{u}^{T}D^{-1}\boldsymbol{u}} },\;n \geq 1. }$$
(5)

3.2 Expressions for RTOP and MSD

Similarly, closed form expressions for RTOP and MSD can be computed. RTOP, which is given by \(\int _{\mathbb{R}^{3}}\hat{E}(\boldsymbol{q})d\boldsymbol{q}\), is simply \(P(0) =\pi ^{\frac{3} {2} }(w_{0}\vert D_{0}\vert ^{-\frac{1} {2} } + 2\vert D\vert ^{-\frac{1} {2} }\sum _{n=1}^{N}w_{n})\). Similarly, the MSD, which is given by \(\int _{\mathbb{R}^{2}}P(\boldsymbol{r})\|\boldsymbol{r}\|^{2}d\boldsymbol{r}\), can be computed from \(\int _{\mathbb{R}^{2}}\varPhi _{0}(\boldsymbol{r})\|\boldsymbol{r}\|^{2}d\boldsymbol{r} = \frac{1} {2\pi ^{2}} \mathop{trace}\nolimits (D_{0})\), and

$$\displaystyle{\int _{\mathbb{R}^{2}}\varPhi _{n}(\boldsymbol{r})\|\boldsymbol{r}\|^{2}d\boldsymbol{r} = \frac{1} {\pi ^{2}} \left (\mathop{trace}\nolimits (D) - 2\boldsymbol{q}_{n}^{T}D^{2}\boldsymbol{q}_{ n}\right )e^{-\boldsymbol{q}_{n}^{T}D\boldsymbol{q}_{ n}}.}$$

3.3 The Relation to Radial Basis Functions Method

The radial basis functions method [15] is a special case of the proposed framework where radially symmetric Gaussian functions centered at the sample locations are used to represent diffusion measurement. The basis function is of the form \(\phi _{n}^{\mathrm{rbf}} = e^{-\sigma \|\boldsymbol{q}-\boldsymbol{q}_{n}\|^{2} }\) which corresponds to an isotropic tensor D = σ I 3×3. The corresponding EAP is expressed as \(P(r) =\sum _{ n=1}^{N}w_{n}\varPhi _{n}^{\mathrm{rbf}}(\boldsymbol{r})\) with

$$\displaystyle{\varPhi _{n}^{\mathrm{rbf}}(\boldsymbol{r}) = 2\left (\frac{\pi } {\sigma }\right )^{\frac{3} {2} }\cos (2\pi \boldsymbol{r}^{T}\boldsymbol{q}_{n})e^{-\frac{\pi ^{2}\|\boldsymbol{r}\|^{2}} {\sigma } }.}$$

The ODF is given by \(\varPsi (\boldsymbol{u}) =\sum _{ n=1}^{N}w_{n}\varPsi _{n}^{\mathrm{rbf}}(\boldsymbol{u})\) with

$$\displaystyle{\varPsi _{n}^{\mathrm{rbf}}(\boldsymbol{u}) = \frac{1} {2\pi }\left (1 - 2\sigma (\boldsymbol{u}^{T}\boldsymbol{q}_{ n})^{2}\right )e^{-\sigma (\boldsymbol{u}^{T}\boldsymbol{q}_{ n})^{2} }.}$$

3.4 Estimation Procedure

We discuss different methods for estimating the coefficients w n. From the samples at N locations in the q-space, we obtain an N + 1 dimensional vector e with the first entry being the measurement at the origin. The tensor D 0 is computed as in standard DTI [3], while the tensor D is chosen to have the same eigenvectors as D 0. One constructs an \((N + 1) \times (N + 1)\) dimensional matrix A with

$$\displaystyle{A(i,1) =\phi _{0}(\boldsymbol{q}_{i-1})\text{and}A(i,j) =\phi _{j}(\boldsymbol{q}_{i-1} -\boldsymbol{q}_{j-1}) +\phi _{j}(\boldsymbol{q}_{i-1} + \boldsymbol{q}_{j-1})}$$

for j ≥ 1 and \(i = 1,\ldots,N + 1\). We denote by w, an N + 1 vector whose entries are the coefficients w n to be estimated. A simple method to estimate w is \(w = A^{-1}e\). However, to avoid ill conditioned matrices A, a Tikhonov regularized solution is given by \(w_{\ell_{2}} = (A^{T}A +\lambda I)^{-1}A^{T}e\) where λ > 0 is a regularization parameter.

This method, however, does not account for the fact that the diffusion measurements are monotonically decreasing with increasing b-values. Moreover, the diffusion propagator should be positive and the value of the measurement at the origin is known to be one. Thus, one could numerically enforce these constraints while estimating the vector of weight w. The corresponding function then becomes: \(\min _{w}\|Aw - e\|^{2} +\lambda \| w\|^{2},\text{s.t.}Bw \geq 0,c^{T}w = 1.\) The matrix B is of the form B = [B 1 T, B 2 T]T with each column of B 1 being the difference of a Gaussian basis functions ϕ n along a given set of gradient directions at several b-value shells and each column of B 2 being the evaluation of Φ n at given set of locations for \(\boldsymbol{r}\). The vector c contains the values of the basis functions at the origin. We note that these constraints are always feasible and a trivially feasible element is given by w = [1, 0, …, 0]T.

4 Experiments

We tested our method on a data set acquired from a spherical physical phantom with a crossing angle of 45 degree [10]. We acquired ten separate scans of the phantom with the 5 different b-values \(b =\{ 1,000,2,000,3,000,4,000,5,000\}\,\mathrm{s}/\mathrm{mm}^{2}\) and each b-value shell consisted of 81 gradient directions. The ten scans were averaged to obtain the “gold-standard” data. The test data set was acquired as follows: For each of the following number of gradient directions K = { 16, 20, 24, 26, 30, 36, 42, 60, 81} we acquired the diffusion measurement over 2 b-shells corresponding to \(b =\{ 1,000,3,000\}\,\mathrm{s}/\mathrm{mm}^{2}\). Further, five repetitions were acquired for each of these data samples to test the effect of noise on signal reconstruction quality. Each acquisition had an average SNR of about 8.5.

4.1 Comparison Metrics

We used several quantitative metrics to test the ability of the proposed algorithm. Let \(\hat{E}_{\boldsymbol{x}}\) denote the reconstructed signal in the voxel at location \(\boldsymbol{x}\) and \(E_{\boldsymbol{x},\mathrm{gold}}\) be the “gold-standard” signal. The Normalized mean squared error (NMSE) in signal reconstruction was computed as

$$\displaystyle{\mathrm{NMSE} = \frac{1} {\vert \varOmega \vert }\sum _{\boldsymbol{x}\in \varOmega }\frac{\|\hat{E}_{\boldsymbol{x}} - E_{\boldsymbol{x},\mathrm{gold}}\|^{2}} {\|E_{\boldsymbol{x},\mathrm{gold}}\|^{2}} }$$

where Ω denotes the set of locations for all voxels. The estimated angle between the two principal diffusion directions (in case of crossing) was computed as the average estimated angle (EA) given by

$$\displaystyle{\mathrm{EA} = \frac{1} {\vert \varOmega _{2}\vert }\sum _{\boldsymbol{x}\in \varOmega _{2}}\vert \arccos (\boldsymbol{u}_{\boldsymbol{x},1}^{T}\boldsymbol{u}_{\boldsymbol{ x},2})\vert }$$

where \(\boldsymbol{u}_{\boldsymbol{x},1}\) and \(\boldsymbol{u}_{\boldsymbol{x},2}\) denote the direction of the two peaks in the voxel at location \(\boldsymbol{x}\) and Ω 2 denote the set of locations for voxels that have two peaks. The estimated angle was computed only in the voxels where only two peaks are detected. In order to know if the recovered signal missed or exaggerated the number of peaks, we computed the percentage of false peaks (PF) given as

$$\displaystyle{\mathrm{PF} = \frac{1} {\vert \varOmega _{\mathrm{gold}}\vert }\sum _{\boldsymbol{x}\in \varOmega _{\mathrm{gold}}}\mathcal{B}(n_{\boldsymbol{x}} - n_{\mathrm{gold}})}$$

where Ω gold denotes the set of locations for voxels that have n gold peaks in gold standard data which equals to 2 in this case, \(\mathcal{B}\) is an indicator function whose value is 1 if \(n_{\boldsymbol{x}} = n_{\mathrm{gold}}\) and 0 otherwise.

We used all of these metrics to quantify the reconstruction quality of the data using Gaussian basis function. We used two methods to estimate the vector \(w\). For the first one, w was chosen as \(w_{\ell_{2}}\) where the ℓ 2 regularization coefficient λ is chosen such that the condition number of A T A +λ I is bounded by 107. The second estimate of w was computed by solving a constrained quadratic programming problem. We compared the proposed methods with the ℓ 1 3D-SHORE method [4], the ℓ 2 3D-SHORE method [9], the ℓ 2 3D-SHORE method with constraint of monotonic decrease of the signal along gradient directions and the radial basis functions (RBF) method [15].

4.2 Phantom Results

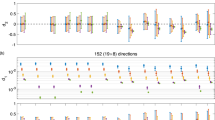
Results on the “gold standard” data (where the actual angle  = 45∘) with different methods are summarized in Table 1. For the test data set, the estimated angle (averaged over the five acquisitions) with different number of gradient directions are shown in Fig. 1. The percentage of false peaks and NMSE are shown in Fig. 1b, c respectively. The parameters σ 0 = 0. 002 and σ 1 = 0. 001 were used for all the Gaussian basis functions and for all experiments done on the test data set. The estimated ODF’s with 42 gradient directions (two b-values, so a total of 84 measurements) with constrained Gaussians, constrained ℓ 2 3D-SHORE, ℓ 1 3D-SHORE and radial basis functions are shown in Fig. 2a–d, respectively.

Table 1 Gold standard error metrics
Full size table
Fig. 1
figure 1

(a) Estimated angle vs. gradient directions. (b) Percentage of false peaks vs. gradient directions. (c) NMSE vs. gradient directions

Full size image
Fig. 2
figure 2

Estimated ODF from measurements on 2 b-value shells with 42 gradient directions each using: (a) Gaussian basis functions with constraints, (b) ℓ 2 3-D SHORE with constraints, (c) ℓ 1 3-D SHORE, (d) radial basis functions

Full size image

Note that, the proposed method produces much sharper ODF’s compared to the 3D-SHORE method. Further, from the error metrics shown in Fig. 1, it becomes clear that the proposed method, while having a slightly higher error in terms of the estimated angle, is yet very successful in detecting the two peaks (i.e. significantly lower percentage of false negatives) compared to 3D-SHORE (see Fig. 1b). Further, the method of 3D-SHORE itself does much better if constraints are added, which was not done in the method presented in [4, 9].

4.3 In Vivo Results

We tested our method on in-vivo human brain data with scan parameters: b-values of {900, 2, 000, 3, 600, 5, 600} s∕mm2 with each b-value shell having 60 gradient directions. This data set was considered as the “gold-standard” data. To obtain the test data, we used two subsets of this data. The first set consisted of data with b-values \(b =\{ 900,3,600\}\,\mathrm{s}/\mathrm{mm}^{2}\) and 60 gradient directions on each shell, while the second set had the same b-values but 30 gradient directions per shell. For the rectangular region (white box) shown in Fig. 3c, the NMSE for these two sets compared to the “gold standard” are given in Table 2. The estimated ODF for the data set with 2 b-value shells and 60 gradient directions using the constrained Gaussians (proposed) and the constrained ℓ 2 3D-SHORE are shown in Fig. 3a and b.

Fig. 3
figure 3

Estimated ODF for the rectangle region in the color FA image (c) from measurements on 2 b-value shells with 60 gradient directions using: (a) Gaussian basis functions with constraints; (b) ℓ 2 3-D SHORE with constraints; (c) color FA image

Full size image
Table 2 NMSE compared to “gold standard”
Full size table

5 Conclusion

In this work, we proposed a novel method of using anisotropic Gaussian functions centered at several locations in q-space to represent the diffusion signal and derive analytical expressions for the EAP, the MSD and RTOP. By using the same set of parameters, we showed the robustness of the proposed method to different number of gradient directions on a physical phantom data with very high noise (SNR  = 8.5). We also showed that the 3D-SHORE method works better if it is constrained to ensure monotonic decrease of the signal with increasing b-value. Quantitatively, the proposed method seems to have lower error in detecting the crossing peaks compared to 3D-SHORE and RBF. A limitation of the current method is that the user has to choose the eigenvalues of the tensor for the Gaussian basis functions, which can be also be chosen by minimizing the fitting error in a leave-one-out cross-validation scheme [16].